Introduction

The hybrid Korteweg-de Vries-Burgers (KdV-B) equation

$$\begin{aligned} \frac{\partial \psi }{\partial t} +a \, \psi \frac{\partial \psi }{\partial x} + b \, \frac{\partial ^{3}\psi }{\partial x^{3}} = c \, \frac{\partial ^{2} \psi }{\partial x^2} \,, \end{aligned}$$
(1)

incorporating constant (real) coefficients representing nonlinearity (a), dispersion (b) and dissipation (c), is a widely used paradigm adopted in various fields of physics and engineering. It describes the propagation of an excitation – expressed by a (real) dependent variable \(\psi (x, t)\), where the (real) independent variables x and t denote space and time, in the usual way. (The ad hoc notation adopted here will later be modified to be adopted to a plasma-physical context). Obviously, upon formally setting \(c=0\), the integrable Korteweg-de Vries (KdV) equation is obtained1,2,3,4. On the other hand, setting \(b = 0\), one obtains the Burgers equation5,6.

The properties of this PDE have been explored, from first principles, in various studies and analytical solutions in the form of (kink-soliton-like) shock excitations – that will form our focus here – have been obtained; see e.g. in Refs.7,8,9. In plasma physics, in particular, the KdV-B equation can be derived from fluid dynamical models, where all coefficients are parametrically dependent on the composition of the plasma.10,11. For a positive-valued dispersion coefficient B, which is generally the case in beam-free electron-ion plasma, this partial-differential equation (PDE) possesses analytical solutions representing positive (or negative) shock profiles for positive (or negative, respectively) values of the nonlinearity coefficient (A). These excitations represent a monotonic transition between two (different) asymptotic values of the electrostatic potential \(\phi\), associated with a monopolar (i.e. bell-shaped) disturbance of the electric field (E).

Contrary to widespread prior belief (based on the description of a beam-free plasma, assumed in the majority of plasma studies), an investigation of nonlinear electrostatic waves in beam-permeated plasmas reveals that that the sign(s) of all (i.e. any) of the coefficients may be reversed, independently from one another, depending on the beam velocity (value); see e.g. in earth’s reconnection jets12, as well as some earlier studies14,15,16. In the light of this result, we have reexamined the analytical solutions, in an effort to elucidate their applicability in plasma-physical scenarios (e.g., reconnection jets and other planetary plasma environments)12 in terms of the different sign combination possibilities, as regards the coefficients involved in the KdV-B equation. Emphasis will be made on the physical interpretation of the relevant algebraic expressions, focusing on the impact of one or the other coefficients changing value or sign, as a result of a change in the plasma configuration considered in a (any) specific physical situation.

We emphasize from the outset that we do not intend to rescale Eq. (1) into a reduced (“canonical”) form, since this would result in losing grasp of the underlying physics. Indeed, the coefficients in this equation reflect the specific characteristics of the plasma system considered in a given problem, as will be shown below, so tracking their relative magnitude (and sign) and its impact on waves’ (or shock fronts’) propagation characteristics is meaningful, for practical applications.

The structure of this paper is as follows. In the following “Plasma fluid model and derivation of KdV-Burgers equation” Section, the main steps involved in the derivation of Eq. (1) from a plasma-fluid model will be outlined. An analytical solution of the KdV-B equation thus derived will be presented in “Traveling wave (weak shock) solution of Eq. (10)” Section. The physical interpretation and the role of the different coefficients appearing in the solution will be discussed in “Qualitative characteristics of the solutions (17)-(18): interpretation and underlyingphysics" section. A parametric analysis is carried out in “On the role of (the sign of) the coefficients A, B and C” section, to showcase the role of the sign (plus or minus) of each of the coefficients. Finally, our results are summarized in the concluding “Conclusions” section.

It must be emphasized that, asides the fluid-plasma model related results presented in the next Section , the remaining part of the paper, including the qualitative discussions carried at every step, has its own merit, as it is based on Eq. (1) as it stands and may therefore be useful in any physical context or discipline, where an evolution equation in the form of Eq. (1) may be relevant. In other words, Section is only provided as a (one, among many) example of application of the theory, and may be neglected, while reading the paper; the remaining sections might just as well be read independently. (The exception to this point is the part regarding the electric field waveform features, to be discussed later, that is only relevant in a plasma-dynamical context.)

Plasma fluid model and derivation of KdV-Burgers equation

We have considered a physical plasma model consisting of a pair of ion (e.g. proton) beams, both modeled as streaming cold fluids, in the presence of electrons in the background. This plasma model is based on the observations of the MMS mission as reported by Liu et al.18.

A system of fluid equations, describing the plasma state in terms of the two ion fluid densities (\(n_j\)), the corresponding fluid speeds (\(u_j\)) – where \(j=1\) or 2 respectively – and the electrostatic potential (\(\phi\)) can be expressed as12,17,18

$$\begin{aligned} \frac{\partial n_j}{\partial t}+\frac{\partial (n_j u_j)}{\partial x}= & 0 \,, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial u_j}{\partial t}+ u_j \frac{\partial u_j}{\partial x}= & -\frac{\partial \phi }{\partial x}+\eta _j\frac{\partial ^2 u_j}{\partial x^2} \,, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial ^2 \phi }{\partial x^2}= & n_e -\delta _1 n_1-\delta _2 n_2 \,, \end{aligned}$$
(4)

where \(\delta _{1}=\frac{n_{1, 0}}{n_{0}}\) and \(\delta _{2}=\frac{n_{2, 0}}{n_{0}}\) are real parameters (\(\in [0, 1]\)) expressing the ratio(s) of the respective (subscript 1 or 2) beam-ion density over the total ion (or the electron) density \(n_0\) (note that the plasma is considered to overall charge-neutral). In writing the above equations, all state variables have been normalized over suitable quantities (not defined here, for brevity), hence the above fluid system is actually dimensionless – and so will be all of the algebraic expressions that will follow. The electron component is assumed to obey a statistical (velocity) distribution given by \(n_e(\phi ) = f(\phi )\) in terms of \(\phi\). Charge neutrality at equilibrium imposes \(\delta _1 +\delta _2 =1 \,\).

Assuming small excitations near equilibrium (\(\phi = 0\)), the electron density can be expanded in a Mc Laurin series as

$$\begin{aligned} n_{e} \approx 1 + c_1 \phi + c_2 \phi ^2+...\,. \end{aligned}$$
(5)

where the coefficients \(c_j\) are analytical functions of \(\delta _j\), which depends on the details of the distribution function \(f(\phi )\), viz. \(c_1 = f'(0)\) and \(c_2 = f''(0)/2\). It is important to note that \(c_1>0\) is a positive quantity, irrespective of the specific characteristics of the plasma (configuration) and wave (mode) under consideration, as fact that is essential to ensure the validity of certain algebraic expressions that will follow.

The reductive perturbative technique, first introduced by Washimi and colleagues19, can be used to obtain a closed evolution equation (a PDE) for the plasma state. This method relies on introducing a set of stretched (slow) coordinates, as

$$\begin{aligned} \xi =\epsilon ^{\frac{1}{2}}(x-\lambda t) \quad \textrm{and}\quad \tau =\epsilon ^{\frac{3}{2}}t\,, \end{aligned}$$
(6)

where \(\epsilon \ll 1\) is a small (real) parameter representing the strength of nonlinearity. The real variable \(\lambda\) represents the phase speed of the anticipated waveform (solution), to be determined later, as dictated by the algebra. The dependent variables \(n_{j}\), \(u_j\) and \(\phi\) can be expanded near their equilibrium values into power series in \(\epsilon\) as

$$\begin{aligned} \begin{bmatrix} n_{j} \\ u_j \\ \phi \\ \end{bmatrix} \approx \begin{bmatrix} 1\\ u_{j,0}\\ 0\\ \end{bmatrix} + \epsilon \begin{bmatrix} n_{j,1} \\ u_{j,1} \\ \phi _{1}\\ \end{bmatrix} + \epsilon ^{2} \begin{bmatrix} n_{j,2} \\ u_{j,2}\\ \phi _{2}\\ \end{bmatrix} + ... \end{aligned}$$
(7)

A weakly damped medium will be assumed, by considering an infinitesimal value of the kinematic viscosity, i.e.

$$\begin{aligned} \eta _j \approx \epsilon ^{1/2} \, \eta _{j0} \,, \end{aligned}$$
(8)

where \(\eta _{j0}\) is a finite quantity. The above ordering (scaling) assumption, in particular, given by Eqs. (6) and (8), will be justified a posteriori, as it enables dispersive, nonlinear and dissipative terms to appear on equal footing (i.e. at the same order in \(\epsilon\)) in the perturbative analysis. We note that an alternative path exists, relying on different stretching coordinates (relaxing the weakly damped medium assumption given by Eq. (8))20,21,22,23, which leads to the Burgers equation. In that case, the nonlinear and dissipation terms arise at the same order in \(\epsilon\) (while dispersion is absent). That other scenario will not be considered further here.

Substituting Eqs. (5)–(8) in Eqs. (2)–(4), an algebraic compatibility condition arises that needs to be imposed, in the form

$$\begin{aligned} \frac{\delta _1}{(\lambda -u_{1,0})^2}+\frac{\delta _2}{(\lambda -u_{2,0})^2}= c_1 \,, \end{aligned}$$
(9)

thus prescribing the phase speed \(\lambda\). In the single-ion case, i.e. for \(\delta _2 = 1 - \delta _1 = 0\), the expression for the phase speed simplifies to \(\lambda = u_{1,0} \pm 1/\sqrt{c_1}\). Moreover, in a beam-free electron-ion (e-i) plasma scenario (i.e., \(u_{1, 0} = 0\)), this relation reduces to \(\lambda = \pm 1/\sqrt{c_1}\), as expected from earlier works24.

Proceeding to higher orders in \(\epsilon\), some straightforward algebraic manipulation leads to

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \tau } +A\phi _{1}\frac{\partial \phi _{1}}{\partial \xi } + B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}} = C \frac{\partial ^{2} \phi _{1}}{\partial \xi ^2} \,, \end{aligned}$$
(10)

that is a closed partial differential equation (PDE) bearing the general structure of the KdV-B equation (1), albeit with different notation. Indeed, we have adopted a different notation, for what refers to our plasma model, for clarity in what will follow. The details of the algebraic procedure that led to the above evolution equation (omitted here) can be found in the literature, e.g. in12,13.

The coefficients appearing in the KdV-B equation (10) obtained from the fluid model consist of:

  • the nonlinearity coefficient

    $$\begin{aligned} A=B\left\{ 3\left[ \frac{\delta _1}{(\lambda -u_{1,0})^4}+\frac{\delta _2}{(\lambda -u_{2,0})^4}\right] -2c_{2}\right\} \,, \end{aligned}$$
    (11)

    i.e.,

    $$\begin{aligned} A=\frac{3}{2}\left[ \frac{\delta _1 (\lambda -u_{2,0})^4+\delta _2(\lambda -u_{1,0})^4}{\delta _1(\lambda -u_{2,0})^4(\lambda -u_{1,0})+\delta _2(\lambda -u_{1,0})^4(\lambda -u_{2,0})}\right] -\frac{c_{2}(\lambda -u_{1,0})^3(\lambda -u_{2,0})^3}{\delta _1(\lambda -u_{2,0})^3+\delta _2(\lambda -u_{1,0})^3} \,, \end{aligned}$$
    (12)

  • the dispersion coefficient

    $$\begin{aligned} B=\frac{1}{2}\left[ \frac{\delta _1}{(\lambda -u_{1,0})^3}+\frac{\delta _2}{(\lambda -u_{2,0})^3}\right] ^{-1} \, \end{aligned}$$
    (13)

    and

  • the dissipation coefficient

    $$\begin{aligned} C=B\left[ \frac{\eta _{1,0}\delta _1}{(\lambda -u_{1,0})^3}+\frac{\eta _{2,0}\delta _2}{(\lambda -u_{2,0})^3}\right] \,. \end{aligned}$$
    (14)

    i.e.

    $$\begin{aligned} C=\frac{1}{2}\left[ \frac{\eta _{1,0}\delta _1(\lambda -u_{2,0})^3+\eta _{2,0}\delta _2(\lambda -u_{1,0})^3}{\delta _1(\lambda -u_{1,0})^3+\delta _2(\lambda -u_{2,0})^3}\right] \,. \end{aligned}$$
    (15)

Recall that \(\lambda\) may be eliminated in the above formulae by using (9), and also that \(\delta _2 = 1- \delta _1\). Therefore, all three coefficients depend parametrically on \(c_1\), \(\delta _1\) and on the beam speed(s) \(u_{j, 0}\) (\(j=1,2\)). Additionally, A (alone) also depends on \(c_2\) (pinpointing the nonlinearity featured in the electron background profile statistics), while C also depends crucially on the viscocity coefficient(s) \(\eta _j\) (and vanishes in their simultaneous absence).

It should be clear from the above definitions that the coefficients are independent functions, i.e. neither their sign nor their magnitude may be linked to each other, since these may vary independently, in their own merit.

2.1 Beam-free plasma case (\(u_{1,0} = u_{2,0} = 0\)) In the absence of streaming (\(u_{j,0}=0\)), the latter two coefficients, B and C) are clearly positive-valued, while A may change sign (depending on the relative magnitude of the various parameters). Inserting (9) for \(\lambda\) into (12), one obtains an expression for the nonlinearity coefficient (\(A \gtrless 0\)) that turns out (see in25 for details) to be proportional to the quantity

$$\begin{aligned} A\sim \rho =3 c_{1}^2 - 2c_2 \,. \end{aligned}$$
(16)

It is obvious that the sign of A will depend on the background electron statistics, via the coefficients \(c_1\) and \(c_2\), defined earlier, whose relative magnitude may prescribe either a positive or a negative value for the above quantity (\(\rho\)). Different models have been proposed for the electron distribution in the past, including (but not limited to):

  • the Maxwell-Boltzmann distribution, for which \(c_1=1\) and \(c_2=1/2\)19,24 (thus, \(A \sim \rho = 2\)25),

  • the kappa distribution24,26, for which \(c_1=\frac{\kappa -1/2}{\kappa -3/2}\) and \(c_2 = \frac{\kappa ^2-1/4}{2(\kappa -3/2)^2}\), hence25

    $$\begin{aligned} \rho =\frac{(\kappa -1/2)(\kappa -5/2)}{(\kappa -3/2)^2} > 0 \qquad \forall \, \kappa \in (3/2,\infty ), \end{aligned}$$

    and

  • the Cairns distribution27, for which \(c_1=1-\frac{4\alpha }{1+3\alpha }\) and \(c_2=1/2\), hence the quantity

    $$\begin{aligned} \rho =3\left( 1-\frac{4\alpha }{1+3\alpha }\right) ^2-1, \end{aligned}$$

    possesses a root where it changes sign, in the interval \(\alpha \in [0,1)\).

It is obvious that A is positive in the former two cases, while it may either be positive or negative in the latter one (Cairns distribution); also see in Ref25. Based on different physical arguments, various alternative electron distribution functions may be considered, each showing a different analytical behavior of A and providing different predictions. Comparing these scenarios lies beyond our scope here.

To proceed, we may retain that A is a real function, while B and C are positive (definite) quantities in the beam-free plasma case.

2.2 General case (\(u_{j,0} \ne 0\), for \(j = 1\) or 2) It is obvious from the above definitions of the three coefficients A, B and C that they can take either positive or negative values, depending on the value of the (two) beam velocities \(u_{1, 0}\) and \(u_{2, 0}\). In fact, eight (8) combinations may exist, if one considers the sign (+/-) of these parameters. This fact, that actually motivated the work presented in this paper, raises a number of questions, as regards the physical applicability of the analytical shock-wave solution(s) of the KdV-B (to be presented below). These aspects will be discussed in detail in the following.

Traveling wave (weak shock) solution of Eq. (10)

To obtain a stationary-profile solution of the KdV-B equation, one may apply the traveling wave transformation \(\chi =\xi -V \tau\). Let us consider the function \(\Phi = \phi _1(\xi ,\tau )\), obeying Eq. (10), which now becomes \(\Phi (\chi )\) in the moving reference frame. An analytical solution to the KdV-Burgers equation can be obtained by adopting e.g., the hyperbolic tangent (tanh) method8,28 in the form

$$\begin{aligned} \Phi =\Phi _m\left\{ 1-\frac{1}{4}\left[ 1+\tanh \left( \frac{\xi - V \tau }{\Delta }\right) \right] ^2\right\} \,. \end{aligned}$$
(17)

Here, \(\Phi _m=\frac{12C^2}{25A B}\) is the shock amplitude while \(\Delta =\frac{10B}{C}\) is related to the shock width. The shock speed is actually not a free variable (as in the case of the KdV equation) but instead prescribed as \(V = \frac{6 C^2}{25 B}\).

Recalling that \({\textbf{E}} = -\nabla \Phi\) (in the electrostatic approximation), we can derive the following expression (in 1D geometry) for the electric field:

$$\begin{aligned} E = - \frac{\partial {\Phi (\xi , \tau )}}{{\partial \xi }} = E_0 \, \mathrm{sech^{2}}\left( \frac{\xi - V \tau }{\Delta }\right) \left[ 1+\tanh \left( \frac{\xi - V \tau }{\Delta }\right) \right] \,, \end{aligned}$$
(18)

where \(E_0=\frac{\Phi _m}{2\Delta }=\frac{3C^3}{125 A B^2}\) represents the maximum (or minimum, depending on the sign of \(E_0\)) value of E-field.

Since the above solution describes a monotonic (kink-soliton like) excitation for the electrostatic potential \(\Phi\), the latter expression represents a “monopolar” (i.e. bell-shaped) excitation for the electric field.

It is worth noting that both waveforms move at a weakly superacoustic (supersonic) speed given by \(v_{shock} = \lambda + \epsilon V = \lambda + \epsilon \, \frac{6 C^2}{25 B}\), where the “sound speed” \(\lambda\) is given by the solution of (9).

Qualitative characteristics of the solutions (17)–(18): interpretation and underlying physics

The solution (17) above depends on three parameters, namely \(\Phi _m\), \(\Delta\) and V. They have different roles:

  • the velocity \(V = \frac{6 C^2}{25 B}\) changes sign with B, i.e. for \(B > 0\) the wave propagates “to the right” (i.e. along the positive semi-axis), while for \(V < 0\), it propagates to the left;

  • the shock width \(\Delta =\frac{10 B}{C}\) is positive when B and C have the same sign, in which case the tanh function is written as it is; for \(B C <0\), however, \(\Delta\) is negative and the tanh functions changes sign (note that this is an odd function, since \(\tanh (-x) = \tanh x \quad \forall x \in {\mathbb {R}}\));

  • the amplitude \(\Phi _m=\frac{12C^2}{25A B}\) is positive when \(A B>0\) and negative when \(A B<0\).

Interestingly enough, the electric field maximum amplitude \(E_0=\frac{\Phi _m}{2\Delta }=\frac{3C^3}{125 A B^2}\), appearing in expression (18), does not show the same behavior (with respect to polarity reversal). In particular,

  • the E-field amplitude \(E_0=\frac{\Phi _m}{2\Delta }=\frac{3 C^3}{125 A B^2}\) is positive when \(A C > 0\), while it is negative when \(A C < 0\).

Given the above definitions, a number of algebraic considerations (reflecting different physical situations) are in row, based on the sheer fact that any of these coefficients affects (not only by its value, i.e. quantitatively, but also via its sign, qualitatively) the physical meaning of the above traveling wave solution. It is obvious that a “simple” sign change in A (keeping both B and C the same, say) will result in a polarity reversal in both \(\Phi _m\) and E. On the other hand, a sign change in B (keeping A and C the same) will affect the argument of the tanh and sech function(s) above, by altering the sign of the traveling wave’s speed V and width \(\Delta\). Finally, rather counter-intuitively, C may also change its sign (due to the beam characteristics, remember), in fact affecting the sign of \(\Delta\) and E (assuming A and B staying unchanged, that is).

It is obvious, in light of the above considerations, that eight (8) different regimes may exist, in terms of the sign (combination) of the three coefficients. Each of these depicts a different physical situation, as we intend to show in the following, by considering selected simple examples. Recall that this wealth of possibilities arises exclusively due to (and depends on) the beams’ strength and speed. Indeed, in the absence of the beams (both), only two (2) of these options survive: A positive or negative (since B and C are positive quantities in that case).

In the next section, we will focus on showcasing the different possibilities outlined above, by using simple algebraic arguments (based on the parity of the tanh and sech functions) in addition some qualitative (symmetry-based) considerations. However simple (or simplistic) these “book-keeping” considerations might appear to an “algebraically literate” (and symmetry-minded) reader, their impact on the physical interpretation of the above solutions in a given physical problem (in plasma dynamics or beyond) may be non-trivial and is often evidently not well understood in the literature.

On the role of (the sign of) the coefficients A, B and C

As discussed above, A, B and C are real quantities of arbitrary sign ( + or - ), in the general case. To simplify the presentation, we shall first consider the cases where the dissipation coefficient is positive (\(C>0\)), then further distinguishing among sub-cases where \(A \gtrless 0\) and/or \(B \gtrless 0\). The effect of a negative-valued coefficient C will then be treated separately.

Case I: \(C>0\)

For \(C>0\), one has four sub-cases, each of which will be discussed in detail.

Sub-case I(a): \(A, B, C > 0\)

In the most general case, all coefficients are positive. Therefore, \(\Phi _m\), \(\Delta\), V and \(E_0\) appearing in Eqs. (17) and (18) are all positive, so these may now be expressed as

$$\begin{aligned} \Phi =\frac{12C^2}{25A B}\left\{ 1-\frac{1}{4}\left[ 1+\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \right] ^2\right\} \,, \end{aligned}$$
(19)

and

$$\begin{aligned} E = \frac{3C^3}{125 A B^2} \, \mathrm{sech^{2}}\left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \left[ 1+\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \right] \,, \end{aligned}$$
(20)

respectively.

Figure 1
figure 1

[Sub-case I(a)] (a) A “standard” polarity shock wave (anti-kink) \(\Phi\) and (b) the associated electric field (E) are depicted in the \(\xi - \tau\) plane, for (arbitrarily chosen) fixed values \(A=B=C=1\). Propagation towards the right (i.e. in the positive direction of the axis) is assumed.

Full size image

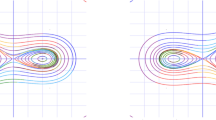
This is the “standard” case in plasma (where \(A > 0\) is associated with a “positive polarity” in the KdV soliton sense): a monotonic, anti-kink shaped (shock) excitation is then obtained for \(\Phi\), leading to a positive monopolar (bell-shaped) \(E-\)field profile. The corresponding profiles are depicted in Figure 1, assuming propagation towards the right.

Sub-case I(b): \(A<0\), \(B>0\) and \(C>0\)

Let us assumed that \(A<0\), while B and C remain positive. It is obvious that \(\Phi _m\) and \(E_0\) now change sign (become negative), while \(\Delta\) and V remain unchanged. This amounts to a simple polarity reversal, as obvious in Eqs. (17) and (18), which may now be rewritten as

$$\begin{aligned} \Phi = -\frac{12C^2}{25|A| B}\left\{ 1-\frac{1}{4}\left[ 1+\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \right] ^2\right\} , \end{aligned}$$
(21)

and

$$\begin{aligned} E = - \frac{3C^3}{125 |A| B^2} \, \mathrm{sech^{2}}\left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \left[ 1+\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{C}}\right) \right] \,. \end{aligned}$$
(22)
Figure 2
figure 2

[Sub-case I(b)] (a) An “inverse” polarity shock wave (kink-soliton like profile) \(\Phi\) and (b) the associated electric field (E) are depicted in the \(\xi - \tau\) plane, for arbitrary fixed values \(A=-1\) and \(B=C=1\). Propagation towards the right (i.e. in the positive direction of the axis) is assumed.

Full size image

The resulting \(\Phi\) and E profiles are depicted in Fig. 2. We see that the solution now represents a kink-soliton like (“negative polarity” shock) excitation, while the corresponding electric field profile will be a negative monopolar waveform (a pulse), i.e. a propagating dip in the electric field.

Sub-case I(c): \(A>0\), \(B<0\) and \(C>0\) (reversing B)

Let us consider a situation where the sign of B is reversed with respect to the “standard” reference case I(a) above. It is now obvious that the kink (shock) amplitude \(\Phi _m\), its width \(\Delta\) and its speed V all change sign (becoming negative), while the maximum E-field \(E_0\) (only) remains positive. Noting that the tanh function is an odd function (\(\tanh (-x) = - \tanh x\)) while the sech function is an even function in x (viz. \(\textrm{sech}(-x)=\textrm{sech} x\)), Eqs. (17) and (18) may be expressed as

$$\begin{aligned} \Phi = -\frac{12C^2}{25 A |B|}\left\{ 1-\frac{1}{4}\left[ 1-\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \right] ^2\right\} , \end{aligned}$$
(23)

and

$$\begin{aligned} E = \frac{3C^3}{125 A B^2} \, \mathrm{sech^{2}}\left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \left[ 1-\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \right] \,. \end{aligned}$$
(24)
Figure 3
figure 3

[Sub-case I(c)] (a) A kink-shaped shock excitation (for \(\Phi\)) and (b) its corresponding electric field (E) are depicted in the \(\xi - \tau\) plane. Upon a space reversal (\(\xi \rightarrow -\xi\)), the left panels (a,b) give their place to the right panels (c, d). Arbitrary fixed values \(A= C =1\) and \(B=-1\) have been considered.

Full size image

The resulting \(\Phi\) and E profiles are depicted in Fig. 3. Since the velocity is now negative, one may consider a space-reversal (\(\xi \rightarrow -\xi\)) to retrieve the physical picture in a convenient representation. One thus obtains a negative polarity shock (i.e. a kink-soliton-like excitation) for \(\Phi\) and a positive \(E-\)field profile, propagating toward the right; cf. panels (c, d) in Fig. 3, emanating from panels (a, b) upon a space reversal.

Sub-case I(d): \(A<0\), \(B<0\) and \(C>0\) (reversing B)

Let us now consider the previous case, but also reversing the sign of A (viz. \(A<0\), \(B<0\) and \(C>0\)). Thus, the potential amplitude will be positive \(\Phi _m\) (rather counter-intuitively, actually, given that \(A < 0\)), while \(\Delta\), V and \(E_0\) now become negative. Eqs. (17) and (18) may now be expressed as

$$\begin{aligned} \Phi = \frac{12C^2}{25 |A B|}\left\{ 1-\frac{1}{4}\left[ 1-\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \right] ^2\right\} , \end{aligned}$$
(25)

and

$$\begin{aligned} E = - \frac{3C^3}{125 |A| B^2} \, \mathrm{sech^{2}}\left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \left[ 1-\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{C}}\right) \right] \,. \end{aligned}$$
(26)
Figure 4
figure 4

[Sub-case I(d)] (a) An anti-kink \(\Phi\) and (b) its corresponding electric field (E) are depicted in the \(\xi - \tau\) plane. Upon a space reversal(\(\xi \rightarrow -\xi\)), the left panels (a, b) take the form of the right panels (c, d). Arbitrary fixed values \(A = B = -1\) and \(C=1\) have been considered.

Full size image

The resulting \(\Phi\) and E profiles are depicted in Fig. 4: note that the structures in the left column (i.e. panels (a, b)) now move towards the left (since \(V < 0\)): upon a space reversal transformation (cf. the right column, panels (c, d) in the same Figure), a “standard” polarity shock (i.e. an anti-kink profile) is obtained – see panel Fig. 4c – associated with a negative \(E-\)field profile – see panel Fig. 4d – both propagating towards the right.

Case II: \(C<0\)

For \(C<0\), we have four sub-cases, each of which will be discussed in detail.

Sub-case II(a): \(A, B > 0\), \(C < 0\)

Let us consider what happens in the “standard” (reference) case I(a) above, when the sign of C (only) is reversed. It is straightforward to show that the signs of \(\Phi _m\) and V will remain unchanged, while \(E_0\) and \(\Delta\) now become negative. Eqs. (17) and (18) may now be expressed as

$$\begin{aligned} \Phi =\frac{12C^2}{25A B}\left\{ 1-\frac{1}{4}\left[ 1-\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{|C|}}\right) \right] ^2\right\} \,, \end{aligned}$$
(27)

and

$$\begin{aligned} E = -\frac{3|C|^3}{125 A B^2} \, \mathrm{sech^{2}}\left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{|C|}}\right) \left[ 1-\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{|C|}}\right) \right] \,. \end{aligned}$$
(28)
Figure 5
figure 5

[Sub-case II(a)] (a) A shock wave (kink soliton) for \(\Phi\) and (b) the corresponding electric field (E) in \(\xi\)-\(\tau\) plane for fixed \(A=B=1\),\(C=-1\).

Full size image

The resulting excitations now represent a kink-profile (“negative polarity” shock) for \(\Phi\) – shown in Fig. 5 – and a negative pulse (a monopolar excitation) for E – shown in Fig. 5b; the structures in both panels propagate towards the right.

Sub-case II(b): \(A < 0\), \(B > 0\) and \(C < 0\)

Let us now consider what happens in the previous case, if one reverses the sign of A too (i.e. considering \(A < 0\), \(B > 0\) and \(C < 0\)). It is easy to see that \(\Phi _m\) and \(\Delta\) become negative, while \(E_0\) and V will remain positive in this case. Eqs. (17) and (18) now take the form:

$$\begin{aligned} \Phi = - \frac{12C^2}{25A B}\left\{ 1-\frac{1}{4}\left[ 1-\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10 B}{|C|}}\right) \right] ^2\right\} \,, \end{aligned}$$
(29)

and

$$\begin{aligned} E = \frac{3|C|^3}{125 |A| B^2} \, \mathrm{sech^{2}}\left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{|C|}}\right) \left[ 1-\tanh \left( \frac{\xi - \frac{6 C^2}{25 B} \tau }{\frac{10B}{|C|}}\right) \right] \,. \end{aligned}$$
(30)
Figure 6
figure 6

[Sub-case II(b)] (a) A shock wave (anti-kink soliton) \(\Phi\) and (b) the corresponding electric field (E) are depicted in the \(\xi - \tau\) plane. We have considered the arbitrary fixed values \(A=C=-1\) and \(B=1\), in these plots.

Full size image

The resulting excitation for \(\Phi\) and the corresponding E profile are depicted in Fig. 6. Physically speaking, this is a situation similar to Sub-case I(a): an anti-kink (or “positive polarity” shock) propagating towards the right, associated with a positive (monopolar) pulse for the \(E-\)field.

Sub-case II(c): \(A > 0\), \(B < 0\) and \(C < 0\)

Let us now consider the case when \(A>0\), \(B<0\) and \(C<0\). In this case, \(\Phi _m\), V and \(E_0\) change sign (become negative), while \(\Delta\) remains positive. Eqs. (17) and (18) can now be written as

$$\begin{aligned} \Phi = - \frac{12C^2}{25A |B|}\left\{ 1-\frac{1}{4}\left[ 1+\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10 |B|}{|C|}}\right) \right] ^2\right\} \,, \end{aligned}$$
(31)

and

$$\begin{aligned} E = - \frac{3|C|^3}{125 A B^2} \, \mathrm{sech^{2}}\left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10 |B|}{|C|}}\right) \left[ 1+\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10 |B|}{|C|}}\right) \right] \,, \end{aligned}$$
(32)

suggesting a sign reversal in both \(\Phi\) and E waves but also propagation towards the left (since V is negative). This situation is depicted in Fig. 7; see the left column panels (a, b) therein. However, if one visualizes these structures “from behind” the plane of the paper surface, i.e. considering a space reversal, viz. \(\xi \rightarrow -\xi\), one realizes that this situation describes an anti-kink (i.e. a “positive/standard polarity” shock) for \(\Phi\), accompanied by a negative pulse for E, both propagating “towards the right”; see in the right column panels (c, d) in Fig. 7.

Figure 7
figure 7

[Sub-case II(c)] Traveling waves: (a) a shock wave (antikink), for \(\Phi\), and the corresponding (negative pulse) for the electric field E, are depicted in the \(\xi - \tau\) plane. Upon a space reversal (\(\xi \rightarrow -\xi\)), the left panels (a, b) (for left-ward propagation) cede their place to the right panels (c, d), where propagation takes place in the forward direction, i.e. to the right of the axis. We have taken \(A=1\) and \(B=C=-1\), in these plots.

Full size image

Sub-case II(d): \(A, B, C<0\)

As a final combination (sub-case), we may now consider what happens when all (three) of the coefficients are negative: \(A<0\), \(B<0\) and \(C<0\). In this case, \(\Phi _m\), \(E_0\) and \(\Delta\) all remain positive, while V (only) becomes negative. Thus, Eqs. (17) and (18) may be cast in the form

$$\begin{aligned} \Phi =\frac{12C^2}{25|A B|}\left\{ 1-\frac{1}{4}\left[ 1+\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10 |B|}{|C|}}\right) \right] ^2\right\} \,, \end{aligned}$$
(33)

and

$$\begin{aligned} E = \frac{3|C|^3}{125 |A| B^2} \, \mathrm{sech^{2}}\left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10|B|}{|C|}}\right) \left[ 1+\tanh \left( \frac{\xi + \frac{6 C^2}{25 |B|} \tau }{\frac{10 |B|}{|C|}}\right) \right] \,. \end{aligned}$$
(34)
Figure 8
figure 8

3D profiles of (a) shock wave (anti-kink) \(\Phi\) and corresponding electric field (E) in \(\xi\)-\(\tau\) plane; the space reversal (\(\xi \rightarrow -\xi\)) for panels (a, b) is showed in (c, d) for fixed \(A=B=C=-1\).

Full size image

This situation prescribes a “standard” polarity anti-kink (\(\Phi\)) / positive pulse (E) pair (i.e. as in Sub-case I(a)), but propagating backward: see the left column plots (a, b) in Fig. 8. It is straightforward to see that, upon a space reversal (\(\xi \rightarrow -\xi\)), this situation is tantamount to an inverse-polarity (i.e. kink soliton like) shock (for \(\Phi\)), associated with a positive E-field pulse, should one consider forward propagation: see the right column plots (c, d) in Fig. 8.

Conclusions

We have considered the Korteweg-de Vries-Burgers (KdV-B) equation, incorporating constant (real) coefficients in account of nonlinearity (A), dispersion (B) and dissipation C, as an evolution equation for a function \(\psi\) of space (in a 1D geometry) and time. (The definition and the physical meaning of \(\psi\) will depend on the physical framework considered in a given problem.) The value(s) of the (3) coefficients (assumed to be similar in order of magnitude), has (have) been left arbitrary, since they may actually depend parametrically on the problem’s specific characteristics. For consistency, therefore, we deliberately chose not to rescale the original equation, casting it in e.g. a “canonical” form.

As one representative example, among other possibilities, we have shown how this equation arises in a plasma-fluid dynamical context, by adopting a bi-ion/electron plasma model and applying a multi-scale perturbation technique to derive an evolution equation for the electrostatic potential \(\Phi\) (here playing the role of the function \(\psi\)). In this model, B and C are both strictly positive (while \(A \in {\mathbb {R}}\)) in a standard (“textbook”) electron-ion plasma where all fluids are quiescent at equilibrium (i.e. in the absence of a beam component), thus only two possibilities exist, depending on the sign of the nonlinearity coefficient A. However, if either (or both) or the ion fluids show a streaming behavior in the laboratory reference frame (i.e. they behave as a particle beam), it turns out that any of the (3) coefficients may change sign (independently), thus allowing for eight (8) different combinations in terms of their sign. Based on the KdV-B equation as our starting point, we have considered an exact traveling wave (localized) solution for \(\phi\), for which we have relied on an analytical expression established in the literature8, in the form of a monotonic transition between two states, i.e. a shock (often called “a weak shock”) essentially identical to a kink (or anti-kink, mainly depending on the sign of A) excitation. Based on this solution, an analytical expression was obtained for the electric field (E), naturally involving the same (three) coefficients, in turn representing a monopolar (bell-shaped) localized excitation propagating alongside the shockwave. Elaborating on (and combining) the above considerations, we have discussed the physical interpretation of the combined “shock/pulse” localized excitation (for \(\phi\)/E, respectively) obtained above, by assuming different ad hoc hypotheses (all of which are plausible in the plasma context, for one) regarding the sign(s) of the various coefficients. Eight (8) sub-cases were discussed, and explicit expressions for observable quantities (the E-field, mainly, in the plasma case) were proposed in each case. From an algebraic point of view, our interpretation relied on a rigorous exploitation of the parity of the solution (note that the solution for \(\phi\) is an odd function of its argument, while the associated expression for E is an even function of the same argument), in combination with symmetry considerations (i.e., reversing spatial orientation in account of the propagation direction being reversed, when so prescribed by a negative value of the traveling wave’s speed). In this sense, our meticulous analysis was based on a tedious but perfectly straightforward procedure. From a physical point of view, our results are non-trivial, as they may allow a straightforward interpretation and classification of different structures observed e.g. in the laboratory or in a Space (planetary) context (eg., earth’s reconnection jets17,18), in the case of plasma dynamics. Beyond the limits of a plasma-fluid framework, our study may be of interest in any other area (among many), where the basic PDE (1) that was our starting point is of relevance.