Introduction

Epilepsy is a common chronic neurological disorder, which is a temporary disturbance of the function of the brain’s nervous system caused by sudden abnormal discharges of neuronal cells in the brain1,2. It presents as recurrent and sudden episodes of motor, sensory, psychiatric, and consciousness disturbances, commonly known as seizures3,4. Epilepsy affects an estimated 70 million individuals worldwide, approximately 20–30% of epilepsy patient do not experience effective relief from available medications or surgical interventions, unfortunately5,6,7. Seizures typically occur without warning, and their unpredictable nature profoundly affects the daily lives of patients8,9,10,11. The suddenness and unpredictability of seizures pose significant challenges to patients’ normal functioning. If a reliable seizure prediction algorithm can be developed, it can provide effective early warning to patients, safeguard their personal safety and mitigate the adverse effects of seizures.

Electroencephalogram (EEG) signals record the electrical activity of the cerebral cortex by amplifying the brain’s spontaneous biological potentials12,13,14. These contain valuable information about brain activity and have found extensive applications in diagnosing brain diseases and facilitating medical rehabilitation, which serve as an essential tool to aid doctors in clinical diagnosis15,16. The essence of seizure prediction research is to classify pre-ictal and inter-ictal EEG signals, but epilepsy EEG pre-ictal and inter-ictal periods are not like seizures with obvious high-frequency and high-amplitude characteristics, and there is still room for improvement of the prediction results of some subjects17,18,19. In recent years, an increasing number of researchers have incorporated machine learning20,21,22,23 and deep learning algorithms like convolutional neural network (CNN)24,25,26,27, Transformer28,29,30, long short-term memory (LSTM)31,32,33, and so on into medical diagnosis. In particular, offering notable advantages over traditional machine learning algorithms, deep learning models have the capacity to automatically extract and select relevant features, making them well-suited for processing epileptic EEG signals characterized by long-term temporal and spatial features.

Although existing studies have achieved praiseworthy average outcomes using deep learning models in subject-specific experiments on CHB-MIT datasets, there are still certain patients for whom the experimental results fall short of expectations. Zhou et al. successfully distinguished between inter-ictal and pre-ictal periods by directly feeding the frequency-domain raw signal into CNN, yielding an impressive mean accuracy of 95.6% while their performance on the Chb21 resulted in a lower accuracy of only 84%34. In contrast, despite achieving an impressive average accuracy of 92.07% and a sensitivity of 89.25% in discriminating spectrograms using RDANet with spectrum attention and channel attention modules, Yang et al. encountered a comparatively lower experimental accuracy of 73.7% on the Chb1435. Ji et al. introduced the GAMRNN model, which combines gate recurrent unit (GRU) and a convolutional attention module, and utilized the lion optimization algorithm for prediction, exhibiting an average classification accuracy of 91.73% and a specificity of 92.09%36. However, when applied to the Chb10 and Chb14 datasets, the accuracy dropped to 78.11% and 77.11%, respectively. These experimental findings suggest that the models used in the aforementioned studies might not have thoroughly investigated the features within the data of these challenging-to-separate subjects, potentially overlooking pertinent information. They also imply that there remain opportunities for enhancement in this area.

The intricate and complex brain networks are often modeled using graphs, and epileptic seizures also propagate within the brain network in the form of spreading patterns. Utilizing graph neural networks for analysis allows for a better consideration of the propagation of neural electrical signals in the brain network during seizures, which is beneficial for seizure prediction. Chen et al. developed the MESPF framework, leveraging wavelet packet decomposition, CNN, and GRU to explore the role of EEG signals in epilepsy, resulting in a successful multidimensional enhanced prediction model with promising outcomes37. Lian et al. built a global-local graph convolutional neural network (GCNN) in a data-driven way to jointly learn the graph structure and link weights in the task-related learning process of intracranial electroencephalography (iEEG) signals to optimize the learned graphs and feature representations to achieve the goal of seizure prediction, and the experimental results were significantly better than the CNN and GCNN models38. Jia et al. utilized graph convolutional network (GCN) to predict epilepsy by exploring the structure of EEG signals achieving an average sensitivity of 96.51% and an average area under the curve (AUC) of 0.9239. Zhao et al. focused on learning the spatial connectivity of the brain to distinguish between seizure and non-seizure phases of epilepsy using an optimized graph attention network (GAT), resulting in a model that achieved a sensitivity of 98.33% on the CHB-MIT datasets40. Perhaps this model can be applied to seizure prediction studies with good results. Although these studies have yielded satisfactory mean results, they do not fully account for EEG timing information and there is still room for further improvement in the application of the results to difficult-to-score subjects.

The EEG signal in epilepsy represents a typical time series data characterized by cyclic patterns. The dynamic and non-stationary nature of neural electrical activity underscores the importance of capturing time-varying information for accurate seizure prediction. The Transformer model leverages self-attention mechanisms to model dependencies effectively which enables parallel computation and facilitates the processing of long sequential data, making it particularly suitable for EEG analysis due to its extensive temporal resolution41. Applying the Transformer model to extract temporal relationships in EEG signals for seizure prediction offers distinct advantages. Therefore, to optimize the prediction performance for challenging-to-distinguish subjects, we propose an advanced approach that combines the strengths of the Transformer model and a graph model. By integrating the GAT, we effectively extract spatial information from synchronized graphs, while harnessing the power of the Transformer to capture temporal information from EEG signals. This fusion enables us to fully exploit the critical spatio-temporal interactions, thereby significantly enhancing the prediction performance. Briefly, the main contributions of this study are as follows:

  • We propose SGSTAN, a synchronization-based graph spatio-temporal attention network for seizure prediction. SGSTAN maximizes the utilization of the intricate information present in EEG recordings by exploiting spatio-temporal correlations.

  • We perform experiments on the widely used CHB-MIT database, both in subject-specific and subject-independent settings. The obtained results are comparable to or surpass the performance of existing state-of-the-art methods, validating the effectiveness of our model.

  • Our model exhibits a remarkable capability to capture essential features and significantly improves classification performance when dealing with challenging subjects in the public dataset.

The organization of the rest of this paper is as follows. Section “Materials and methods” describes the architecture of the proposed SGSTAN model, the public datasets and preprocessing. In Section “Results and discussion”, the results under different experimental methods, analysis and discussion are introduced. Conclusions are given in Section “Conclusion”.

Materials and methods

Proposed model

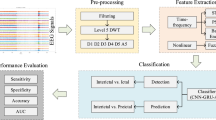
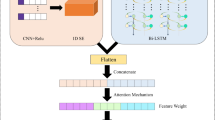
Figure 1 illustrates the flow chart of the SGSTAN model. The experimental process begins with preprocessing and segmentation of raw scalp EEG signals to mitigate noise and balance the ratio of data samples by overlapping sliding windows. Then, the correlation between pairs of EEG channels is calculated, and a graph structure is constructed by sparsifying the correlation matrix through thresholding. This graph structure, along with the original EEG signals, is then fed into a graph attention network model for spatial feature extraction. The GAT model assigns varying weights to nodes based on their significance and aggregates information from neighboring nodes. The raw signals and the output of the GAT model are further processed by linear projection and superimposed for enhancement, and then fed into the Transformer encoder for temporal feature extraction. The Transformer encoder captures temporal features and long-range dependencies from the spatially enhanced data. Finally, classification is performed using the softmax function, which assigns probabilities to each category based on the extracted features, allowing the model to make predictions.

Spatial information extractions

To begin, the GAT network takes the node features \(X=\{{x}_{1},{x}_{2},\dots\:,{x}_{N}\}\), where \(\:{x}_{i}\in\:{R}^{F}\), and the correlation matrix at time \(\:t\) as inputs. Here, \(\:N\) represents the number of electrode channels, and \(\:F\) denotes the feature dimension of each node. Within the GAT layer, a self-attention mechanism is applied to each node in the graph, assigning varying weights based on their importance. Subsequently, the layer aggregates the nodes and their adjacent nodes according to the weight magnitudes. For a

Fig. 1
figure 1

The framework of SGSTAN including preprocessing, spatial information extraction and temporal information extraction.

Full size image

pair of nodes with input feature vectors \(\:{x}_{i}\) and \(\:{x}_{j}\), the influence of node \(\:i\) on node \(\:j\), denoted as \(\:{e}_{ij}\), can be mathematically expressed as follows:

$${e}_{ij}=a\left(W{x}_{i},W{x}_{j}\right)$$
(1)

The weight matrix \(\:W\) is utilized to establish the relationship between the input features and the output features, enabling the transformation of node features. The attention mechanism, denoted as \(a(\cdot)\), is implemented as a feedforward neural network that maps features to a real number. The formula calculates the significance of node \(\:j\) to node \(\:i\), without considering the structural information of the graph. To incorporate the correlation coefficient between a node and its first-order neighborhood, the calculation of \(\:{e}_{ij}\) is limited to nodes \(\:j\in\:{V}_{i}\), where \(\:{V}_{i}\) represents the neighborhood of node \(\:i\). First-order neighbors are nodes that are directly connected to node \(\:i\) by a non-zero edge in the correlation matrix. By introducing the LeakyReLU activation function and expanding the equation, the attention coefficient calculated by the attention mechanism can be expressed as follows:

$${\alpha\:}_{ij}=\frac{{exp}\left(\text{LeakyReLU}\left({a}^{T}\left[W{x}_{i}\parallel\:W{x}_{j}\right]\right)\right)}{\sum\:_{l\in\:{V}_{i}}\:{exp}\left(\text{LeakyReLU}\left({a}^{T}\left[W{x}_{i}\parallel\:W{x}_{l}\right]\right)\right)}$$
(2)

where \(\:\parallel\:\) represents the concatenate operation, the attention coefficient \(\:{\alpha\:}_{ij}\) represents the attention between node \(\:i\) and node \(\:j\), where \(\:l\) denotes a node in the first-order neighbor set of \(\:i\).

The capability of a single-layer attention mechanism to learn from neighboring nodes is relatively limited. To enhance the accuracy of the learned features, this study incorporates multiple attention mechanisms. By employing multiple attention mechanisms to calculate attention coefficients for the surrounding nodes, the learning process of the model becomes more stable. The resulting fused feature output, denoted as \(\:{x}_{i}^{{\prime\:}}\), can be expressed as follows:

$${x}_{i}^{{\prime\:}}=\sigma\:\left(\frac{1}{k}\sum\:_{k=1}^{k}\:\sum\:_{j\in\:{V}_{i}}\:{\alpha\:}_{ij}^{k}{W}^{k}{x}_{j}\right)$$
(3)

where \(\:k\) represents a head, \(\:{W}^{k}\) is the weight matrix for head \(\:k\), \(\:\sigma\:\) is the sigmoid activation function, and \(\:{x}^{{\prime\:}}\) represents the output of GAT.

The attention mechanism in our model learns and parameterizes the connections between nodes, allowing for the assignment of different weights to each edge. Moreover, each head in the multi-head attention mechanism operates independently and in parallel, which makes the computation very efficient. With the introduction of the attention mechanism, only the weight is shared with adjacent nodes, eliminating the need for information from the entire graph. This robustness allows the model to handle disruptions effectively. If the connection between two nodes is lost, their attention coefficient will not be calculated. As a result, the model efficiently extracts the spatial relationships between channels.

Temporal information extractions

After extracting spatial information using the GAT model, we overlay this intermediate result with the linearly transformed original signal to enhance it and input it into the timing information extraction module. The Transformer model follows an encoder-decoder architecture, commonly used in neural sequence transduction models. In our study, we employ the Transformer encoder to capture the remote dependencies present in EEG sequences and temporal features. To facilitate network convergence and mitigate overfitting, each sub-layer incorporates a residual connection and layer normalization. The Transformer architecture consists of L stacked encoder modules, with each module containing two sub-modules: a multi-headed self-attention and a fully connected feed-forward network (FFN). The use of residual connections in each Transformer encoder helps retain the input feature information and enhances the stability of the model.

The multi-head attention layer incorporates scaled dot-product attention, which involves the matrices queries \(\:Q\in\:{\mathbb{R}}^{{d}_{r}\times\:{d}_{k}}\), keys \(\:K\in\:{\mathbb{R}}^{{d}_{r}\times\:{d}_{k}}\), and values \(\:V\in\:{\mathbb{R}}^{{d}_{r}\times\:{d}_{k}}\). The queries \(\:Q\) and keys \(\:K\) have the same dimensionality for the dot product operation. The attention matrix is obtained by \(\:V\), and then activated using the softmax function. The resulting score matrix represents the contribution value of each feature across the entire classification. In addition, the multi-head attention mechanism enables the model to attend to different representation subspaces at different positions in parallel by mapping the Q, K, and V with different learned linear transformations. The attention scores from each head are then concatenated using the Concat(⋅) function. This process enables the model to capture diverse and complementary information across multiple attention heads, facilitating a more comprehensive representation of the input data.

In addition to the attention sub-layers, each encoder module in the Transformer architecture incorporates a fully connected FFN. The FFN operates independently and identically on each position or node in the sequence. It consists of two linear transformations, separated by a non-linear activation function, typically ReLU:

$$FFN\left(x\right)=ReLU\left(0,x{W}_{1}+{b}_{1}\right){W}_{2}+{b}_{2}$$
(4)

The features generated by the encoder are passed through a reshape layer and a linear layer for dimensionality transformation, ultimately yielding the final classification results. During the model training process, we utilize cross entropy as the loss function to quantify the dissimilarity between the predicted values and the actual labels. To optimize the model parameters, we employ the Adam optimizer, a popular choice for gradient-based optimization algorithms, in our experiments.

Datasets

This work utilizes two publicly available epileptic EEG datasets, namely the CHB-MIT and the Siena datasets. The CHB-MIT dataset encompasses extended-duration scalp EEG recordings from 23 pediatric patients (18 females and 5 males) diagnosed with refractory epilepsy. The age range of the patients spans from 1.5 to 22 years. These scalp EEG signals were captured at a sampling rate of 256 Hz using the 10–20 international system for electrode placement, employing a bipolar montage. Compared to referential montages, bipolar montage can provide better artifact suppression and clearer spatial localization, which can keep away from volume conduction problems42,43,44,45. The dataset comprises an extensive collection of 916 h of continuous scalp EEG data, encompassing 157 occurrences of seizure events. Given the variability in electrode usage across multiple experiments for each patient, analyzing the data necessitates the selection of common channels. In order to mitigate the complexities arising from variations in electrode usage across multiple experiments and ensure methodological consistency, a rigorous approach is employed in this study. Specifically, the 18 channels common to all patients were retained in this experiment with reference to the selection of existing studies46,47, including FP1-F7, F7-T7, T7-P7, P7-O1, FP1-F3, F3-C3, C3-P3, P3-O1, FP2-F4, F4-C4, C4-P4, P4-O2, FP2-F8, F8-T8, T8-P8, P8-O2, FZ-CZ, and CZ-PZ. This meticulous selection process is undertaken to eliminate any potential inconsistencies caused by differences in electrode placement, and to facilitate further experimental setups.

The Siena dataset comprises data from 14 epileptic patients, which were collected as part of the PANACEE national interdisciplinary research project. The dataset includes recordings of cerebral activity of the patients, captured using a video scalp EEG system with a sampling rate of 512 Hz. The electrodes were positioned on the scalp based on the international 10–20 system. It is anonymized and freely available, featuring data from 14 patients, with 9 males ranging in age from 36 to 71, and 5 females ranging in age from 20 to 58. We select 19 channels common to each patient in this study, Fp1, F3, C3, P3, 1, F7, T3, T5, Fz, Cz, Pz, F4, C4, P4, O2, F8, T4, T6, Fp2.

EEG preprocessing

The CHB-MIT dataset contains a significant presence of 60 Hz power line noise in the recorded EEG signals. Consequently, in our experiment, we implemented a filtering procedure to remove frequency components within the range of 57–63 Hz, which corresponds to the power line frequency. Additionally, we also eliminated the direct current (DC) component at 0 Hz to ensure a convenient and highly effective means of mitigating the interference caused by power line noise and the DC component.

Different from numerous methods that take manually extracted features as input, our model automatically learns deep discriminative representations from raw EEG signals. It can reduce extra overhead in domain transformation and potential information degradation of the raw EEG signals. Then to mitigate inter-patient discrepancies and enhance the efficiency of convergence for deep learning models, the raw EEG signal is subjected to standardized preprocessing. However, the traditional maximum-minimum standardization method may be susceptible to unpredictable distortions due to the presence of false spikes within lengthy EEG segments. Therefore, to ensure a more robust standardization technique, this study employs Z-score normalization \(\:{X}^{{\prime\:}}\left(t\right)=\left(X\left(t\right)-\mu\:\right)/\sigma\:\), where \(\:\mu\:\), \(\:\sigma\:\) are the mean value and standard deviation of original signal \(\:X\left(t\right)\), respectively. Then \(\:{X}^{{\prime\:}}\left(t\right)\) is the normalized signal.

Before defining the scope of the inter-ictal and pre-ictal states, it is crucial to account for a crucial aspect wherein patients and physicians should be provided with a response time as an intervention period before an epileptic seizure. This period is commonly referred to as the seizure prediction horizon (SPH). The SPH allows doctors enough time to administer clinical interventions, with the optimal duration typically being 3–5 min48. Additionally, it is important to define the seizure occurrence period (SOP), which indicates the anticipated period when seizures are likely to happen and is equivalent in duration to the pre-ictal period. It is essential to strike a balance when setting the SOP duration, ensuring it is not excessively long, otherwise it may cause heightened psychological pressure for subjects. Drawing insights from other relevant literature sources49,50, we have set the SPH to 5 min and the SOP to 30 min in this paper.

Given that the exact point of transition from the inter-ictal to pre-ictal state cannot be discerned, it is necessary to define a specific time frame. To minimize interference, we have defined the inter-ictal period for the CHB-MIT dataset as the duration of 4 h preceding the ictal period, as well as the 4 h following the conclusion of the seizure. On the other hand, for the Siena scalp database, the inter-ictal period has been set to 1 h.

In order to overcome the severe data imbalance between inter-ictal and pre-ictal data in the datasets, caused by some patients having fewer recorded seizures, we implement a robust strategy. By utilizing the overlapping sliding windows to extract additional pre-ictal fragments, we can effectively divide the long-range EEG signals into distinct segments, ensuring the availability of a sufficient number of samples for training deep neural networks. This approach enables us to generate a robust training dataset that adequately represents the underlying characteristics of the EEG signals. Specifically, we apply a sliding window with a step size denoted as S along the time axis of the time-series EEG signals. The choice of S is determined on a per-subject basis to achieve a comparable number of samples per class (pre-ictal or inter-ictal) within the training set. Statistical analysis reveals that the proportion of inter-ictal to pre-ictal data samples in the CHB-MIT dataset is approximately 0.999, whereas in the Siena dataset, it is about 0.9978. These ratios meet the balance requirement. This meticulously designed method effectively addressed the issue of data imbalance, enabling us to construct a more representative and well-balanced training dataset.

Graph modeling

The phase-locking value (PLV) is a widely used metric for assessing the strength of functional connectivity in networks. It quantifies the absolute value of the average phase difference between two time-series51, reflecting the correlation from the perspective of instantaneous phase. A higher degree of synchronization indicates that the fluctuation patterns of the two signals are more closely aligned, suggesting a stronger correlation. The PLV is calculated as follows:

$$P\left(t\right)=\frac{1}{N}\left|\sum\:_{n=1}^{N}\:{e}^{i\left(\varDelta\:{\phi\:}_{n}\left(t\right)\right)}\right|$$
(5)

where \(\:\varDelta\:{\phi\:}_{n}\left(t\right)={\phi\:}_{a}\left(t\right)-{\phi\:}_{b}\left(t\right)\) is the instantaneous phase difference of the time series of a pair of EEG channels \(\:a\) and \(\:b\) at time \(\:t\). Instantaneous phase \(\:\phi\:\left(t\right)\) is obtained by the Hilbert transform.

Constructing a binary network involves identifying nodes and edges, whereas constructing a weighted functional network involves determining nodes, edges, and the corresponding edge weights. In our work, each channel is designated as a node. We calculate the phase-locking value between each pair of time-series and apply a threshold to sparsify the fully connected matrix. Values exceeding the threshold are retained, while those below are set to zero, resulting in the target network. A non-zero value in the sparsified matrix implies a direct edge between nodes \(\:i\) and \(\:j\).

Evaluation indicators

In the experiment, the prediction system achieves its performance by learning and classifying the distinctive EEG data characteristics of pre-ictal and inter-ictal segments. In this paper, we utilize Accuracy, Sensitivity, Specificity, False Positive Rate (FPR), and F1-Score as evaluation measures for our model to evaluate the effectiveness.

$$\:\begin{array}{c}Accuracy=\frac{TP+TN}{TP+FP+TN+FN} \end{array}$$
(6)
$$\:\begin{array}{c}Sensitivity=Recall=\frac{TP}{TP+FN} \end{array}$$
(7)
$$\:\begin{array}{c}Specificity=\frac{TN}{TN+FP}\end{array}$$
(8)
$$\:\begin{array}{c}Precision=\frac{TP}{TP+FP}\end{array}$$
(9)
$$\:\begin{array}{c}\text{F}\text{P}\text{R}\text{=}\frac{FP}{TN+FP}\end{array}$$
(10)
$$\:\begin{array}{c}F1-score=\frac{2\times\:Recall\times\:Precision}{Recall+Precision}\end{array}$$
(11)

Results and discussion

Subject-specific experiments

Subject-specific validation entails conducting each experiment exclusively for a single subject, without involving any other subjects in the process. The experimental outcomes specific to each subject are presented in Table 1; Fig. 2. Our model demonstrates an average accuracy, sensitivity, and specificity of 98.2%, 97.85%, and 98.07% respectively. The average F1-score and FPR achieved by the SGSTAN are 97.62% and 0.019/h, respectively. A higher F1-score indicates superior performance of the SGSTAN, implying that the proposed model exhibits high accuracy and consistent stability for each individual subject. Notably, subject Chb1 obtains an exceptional F1-score of 99.95%, while the lowest value is observed for subject Chb6 at 95.27%. Furthermore, subject Chb14 demonstrates 100% sensitivity, and the best FPR of 0.000/h is observed for subjects Chb1 and Chb23.

Table 1 Subject-specific experiments results using CHB-MIT dataset.
Full size table
Fig. 2
figure 2

Subject-specific experiments results using CHB-MIT dataset.

Full size image

To assess the model’s generalization capability, we fully replicated the entire experimental process including the data preprocessing and training phases using the Siena dataset and examined the metric results. The outcomes of these experiments are presented in Table 2; Fig. 3. The table reveals that the model achieved an average accuracy of 97.48%, specificity of 98.37%, sensitivity of 98.14%, and a FPR of 0.016/h. Notably, subject PH06 attained 100% across all indicators, while subjects PH05 and PH09 displayed similar metric values. The sensitivity of five subjects reached 100%, with subject PH17 exhibiting the lowest value of 90.75%.

The subject-specific experiments serve as evidence of the exceptional feature extraction capabilities and precise prediction accuracy exhibited by our proposed model. The notable superiority of our approach lies in the effective integration of connections between EEG channels. Additionally, we have successfully concatenated the features obtained from the GAT layer and Encoder layer, enabling the capture of crucial information necessary for distinguishing pre-ictal and inter-ictal EEG epochs.

Table 2 Subject-specific experiments results using Siena dataset.
Full size table
Fig. 3
figure 3

Subject-specific experiments results using Siena dataset.

Full size image

Subject-independent experiments

Unlike subject-specific methods, which train a model for each subject, subject-independent methods try to find a general model for all the subjects, which is more meaningful in clinical applications. In subject-independent experiments, data from N-1 patients are utilized for training, while the data from the remaining patient is reserved for testing. Since new models were not trained using EEG data specific to the test dataset, the variability of EEG signals poses a significant challenge to leave-one-subject-out experiment. Our model attained an average accuracy of 84.11%, an average sensitivity of 84.64%, and an average specificity of 82.96% on the CHB dataset. Meanwhile, on the Siena dataset, the model achieved 81.27%, 82.85%, 79.16% respectively.

Subject-independent seizure prediction experiments use the same model for multiple subjects and try to identify their common epileptic features. This approach may be more general, but it needs to deal with differences in EEG from different subjects. These differences may be due to physiological differences between subjects, different equipment, etc., which can make it difficult for the algorithm to identify common features of epilepsy. As a result, subject-independent seizure prediction experiments often lead to poorer results compared to subject-specific experiments.

Comparison with other methods

Additionally, we selected the results of other algorithms that have also conducted subject-specific experiments on the CHB-MIT dataset in recent years for a comprehensive comparison, and the results are shown in Table 3. Sensitivity and specificity serve as essential measures for assessing the classifier’s accuracy, making them meaningful indicators in clinical diagnoses. Upon examining the table, our model exhibited superior stability and a well-balanced performance across all metrics, outperforming other models that excelled in specific metrics. This highlights the consistent and exceptional capabilities of our model in various aspects.

Table 3 Comparison with prior works which have conducted subject-specific experiments on the CHB-MIT dataset.
Full size table

To further showcase the improvements made by our model on biased subjects,Table 4 presents a comparison between our results and the accuracy metrics reported in published papers. It is worth noting that some subject metrics in the published papers may have null values due to variations in subject screening criteria. Upon reviewing the results, it becomes apparent that while certain subjects, such as Yuan Zhang, 2020 Chb1017, Xinwu Yang, 2021 Chb1835, IMENE JEMAL, 2022 Chb252, and Hong Ji, 2023 Chb236, achieved better results in the published papers, their overall performance has been enhanced in our current modeling experiments. This suggests that our model has successfully improved the outcomes of these subjects as a whole.

Table 4 Comparison of the accuracy for challenging-to-distinguish subjects with prior works which have conducted subject-specific experiments on the CHB-MIT dataset.
Full size table

Ablation experiments

To effectively demonstrate the performance of our models, we conducted subject-specific ablation experiments on all subjects in the CHB-MIT dataset using several benchmark models, focusing on spatial networks, temporal networks, and spatio-temporal fusion neural networks, all utilizing the same experimental setup. The results of these experiments are presented in Table 5. Notably, our proposed model achieved over 97% for all evaluation metrics, with a remarkable specificity of 98.07%. The F1-score, which combines precision and recall, provides a comprehensive assessment of the classifier’s overall performance. Among all the models, our model achieved the highest F1-score, demonstrating its superior performance. These experimental results serve as strong validation for the effectiveness of our approach.

Table 5 Comparison of the subject-specific ablation results using baseline algorithms on CHB-MIT dataset.
Full size table

In Table 6, we provide a comparison of the accuracy rate for the specific subjects. Notably, our present model outperforms the baseline model in terms of accuracy for subjects that initially yielded poor experimental results. This notable improvement signifies the effectiveness and superior performance of our model compared to the baseline model in addressing the challenges posed by these specific subjects.

Table 6 Comparison of the accuracy of the subject-specific ablation results for challenging-to-distinguish subjects using baseline algorithms on CHB-MIT dataset.
Full size table

Both GCN and GAT are graph neural networks that aggregate information from neighboring nodes to the central vertex and learn feature representations in the graph domain. In Tables 6 and 7, GAT outperforms GCN across all evaluation metrics. This can be attributed to the fact that GCN treats each node equally using a fixed Laplacian matrix, while GAT calculates feature weights using attention coefficients. Furthermore, GCN’s convolutions have identical graphs and are more reliant on the structure of the prior graph, which imposes limitations. Conversely, GAT introduces attention mechanisms to replace GCN’s static normalized convolution operation. By assigning different importance to edges between nodes, GAT facilitates better learning of structural information.

While GAT excels in capturing the topological structure of non-Euclidean, it falls short in fully leveraging the temporal information embedded within EEG signals. To address this limitation, we integrated the Transformer mechanism into GAT to fully exploit the time domain characteristics of EEGs. Significantly, our model demonstrates noteworthy enhancements in average accuracy, specificity, and sensitivity compared to GAT when subjected to identical experimental conditions. The improvements amount to 2.24%, 2.62%, and 2.77%, respectively. Moreover, our model surpasses both GAT and Transformer in the case of 9 challenging-to-distinguish subjects, exhibiting superior performance with improvements of 2.89% and 3.82%, respectively.

We developed the GCN + Transformer and GAT + LSTM models by substituting various layers within the GAT + Transformer architecture. This allowed us to explore different combinations and configurations for capturing the spatio-temporal correlation of EEG signals. The SGSTAN, with its multilayer attention mechanism, effectively integrates the correlation between electrode nodes into the model. The results in Table 6 demonstrate that our proposed models outperform the baseline across multiple metrics, showcasing their superior performance.

Our proposed model has demonstrated superior performance in various metrics when compared to baseline algorithms. The experimental results highlight the model’s significant potential in EEG classification tasks. The fusion model’s superiority lies in its ability to effectively utilize the information contained within EEG signals by integrating both spatial characteristics and temporal information. This comprehensive integration allows for a more holistic understanding of the data and contributes to the improved performance of our model.

Influence of the parameters

Influenced by threshold changes

We constructed the weighted network by applying a threshold to sparsify plv matrix, which is set to 0 if the value of the coefficient between two nodes in the matrix is less than the threshold we set, otherwise the original weights are retained. To evaluate the effect of the chosen threshold on the model performance, we conducted subject-specific experiments on the CHB-MIT dataset for comparison. Experimentally, the optimal thresholds for subjects were clustered between 0.25 and 0.45, with 0.35 being the most frequent, so we used 0.35 as the threshold value for subject-independent experiments. Considering the differences in brain synchronization caused by individual differences, we used the optimal thresholds for different subjects in subject-specific experiment. Figure 4. illustrates the variation of accuracy versus threshold for subject chb3, chb6, chb7, chb9, chb10 and chb21 experiments.

Fig. 4
figure 4

Effect of different thresholds on model accuracy for subject chb3, chb6, chb7, chb9, chb10, chb21 on CHB-MIT dataset.

Full size image

Influenced by sliding window length

By employing the sliding window analysis technique, we can partition continuous long-term EEG signals into smaller segments, measured in seconds, and employ these segments as training data for deep neural networks. The results of these experiments are presented in Table 7. Optimal window length selection is pivotal in enhancing generalization performance. Within a 5-second interval, augmenting the window length captures an increased amount of discriminative feature information, thereby significantly enhancing performance. Nevertheless, surpassing the 5-second threshold for EEG window length leads to a bottleneck in the model’s learning capacity, resulting in a slight decline in performance. Consequently, considering all factors, employing a 5-second time window length yields optimal experimental outcomes.

Table 7 Effects of different sliding window length conducted subject-specific experiments on CHB-MIT dataset.
Full size table

Conclusion

In this study, a synchronization-based graph spatio-temporal attention network is proposed for seizure prediction. We model the phase synchronization information of the full-lead EEG signals as a graph structure and extracts the spatial information of different channels using GAT. Meanwhile, the temporal features aggregated in the signals are extracted using the Transformer model to fully exploit the spatio-temporal correlation of EEG sequences. The validity of the model was verified by conducting experiments such as subject-independent and subject-specific on public datasets, and the overall prediction results for focused subjects were enhanced.

Nevertheless, there is still much room for improvement in the study, for example, the plv method is susceptible to noise and volume conduction issues, indicating that more robust techniques should be employed in future work. Furthermore, the model would benefit from refinement to enhance accuracy in subject-independent experiments. At the same time, although the attentional mechanism in the model can automatically learn the key information in EEG and understand its spatio-temporal features, the model still has some limitations to fully understand its classification mechanism. Therefore, in future studies, we will further explore the introduction of interpretable learning methods to meet the clinical requirements for model interpretability.

In conclusion, the synchronization-based graph spatio-temporal attention network model proposed in this study has significant potential for seizure prediction. Meanwhile, for better application in clinical practice, we will aim to further improve the interpretability, robustness and generalizability of the model and gain a deeper understanding of its classification mechanism.