Reconfigurable security solution based on hopfield neural network for e-healthcare applications

Abstract

In the healthcare sector, e-diagnosis through medical images is essential in a multi-speciality hospital; securing the medical images becomes crucial for preserving an individual’s privacy in e-healthcare applications. So, this paper has proposed a novel encryption scheme implemented on reconfigurable hardware. Realising image encryption schemes on FPGA hardware platforms offers substantial advantages over software implementations. The image-specific key and Hopfield Neural Network (HNN) carry out the diffusion process using the suggested encryption method. The confusion is accomplished simultaneously by the pseudo-random memory addresses derived via a 16-bit stream cipher circuit, which incorporates cryptography and neural network dynamics methods. By breaking up the spatial redundancy in image data, this diffusion mechanism increases the data’s resilience against statistical attacks, yielding an average entropy of 7.99 and near zero correlation. When implemented on an FPGA platform, this dual-layer encryption technique’s fast processing speed, parallelism, and reconfigurability are substantial benefits, especially for real-time and resource-constrained applications. FPGA implementation occupies 20% of the total hardware and 424.71 mW of power dissipation on Intel Cyclone V FPGA.

Introduction

Neurocomputing, an interdisciplinary field at the intersection of neuroscience and computer science, focuses on developing computational models frequently based on Artificial Neural Networks (ANNs). These models have many applications, including target identification, clinical diagnosis, voice authentication, intelligent searching, image analysis, and data security. A particularly promising application is image security, which leverages ANNs to protect digital images from unauthorised access and manipulation. The neurons’ inherent random and chaotic behaviour makes them well-suited for complex tasks such as image encryption, owing to their intricate structures, adaptive learning capabilities, and dynamic nature¹. Field-Programmable Gate Arrays, or FPGAs, have become a potent platform for applying artificial neural networks (ANNs) to encryption techniques in recent years. Biological neural network-inspired encryption algorithms are executed by FPGAs using their parallel processing capabilities, providing a safe and effective solution for data transfer and storage. Large data volumes may be encrypted in real-time thanks to FPGAs’ parallelism, significantly improving the performance. Moreover, quicker encryption and decryption processes appropriate for high-throughput data applications are made possible by the reconfigurable design of FPGAs, which enables the investigation and development of numerous customisable ANN structures and encryption algorithms. The benefits of employing FPGAs for ANN-based image encryption are examined in the proposed paper, especially when compared to more conventional sequential processing environments like MATLAB. While MATLAB executes commands one after the other, slowing down the encryption.

Literature survey

A Hopfield attractor-trusted neural network for picture encryption was introduced by Chandrasekaran et al., who also showed off how resilient it was to several attacks. The dynamic and chaotic nature of the Hopfield network is effectively used for complex encryption tasks, ensuring robust security measures for image data¹. Ravichandran et al. described a penta-layer cryptosystem for encrypting biological images with FPGAs. The benefits of FPGA-based systems, like real-time processing and speedy throughput, are demonstrated by this system and are crucial for securely and swiftly handling enormous volumes of biomedical imaging data².

A hardware-accelerated Chao(S)-box triplet technique for encrypting colour medical images was presented by Vinoth Raj et al. This encryption method was optimised because of FPGAs’ reconfigurability, which produced strong security and quick processing speeds—two essentials for medical applications where data integrity and confidentiality are required³. The team also examined the best concurrent strategies for lightweight medical image encryption with FPGAs. Their study demonstrates how the parallel processing capabilities of FPGAs increase efficiency and allow for quick and safe encryption for real-time medical applications⁴.

Using FPGA reconfigurability, Ramalingam et al. developed a chaos-triggered image encryption system. Their method uses chaotic sequences to simplify and secure encryption, providing a strong defence against future cryptographic attacks⁵. Hyperchaos in the Hindmarsh-Rose neuron and the introduction of its use in encryption are among other areas that have been looked into by Li et al.⁶. Qin has proposed a novel approach to developing chaotic neural networks. The framework, however, can be used as a basis for image security applications that exploit the naturally chaotic behaviour of neural networks to produce powerful encryption algorithms⁷. As regards privacy-preserving techniques for learning backpropagation neural networks, Chen and Zhong⁸ studied these. Their results imply that secured photo encryptions would require data privacy while training on neurons⁸. However, Yu and Cao studied their effects on cryptography, showing how they could enhance the security of encryption systems through delayed feedback in neural networks^9,10.

In their study, Kassem et al. introduced a novel image encryption technique called Efficient neural chaotic generator that exploits the chaotic features of neural networks to make encryption more robust. In other words, they showed how effective chaotic neural generators can produce secure encryption keys as required for reliable image encryption systems¹¹. Bigdeli et al. provided a robust hybrid method for image encryption using Hopfield neural networks. This approach fuses the dynamic capabilities of Hopfield networks with conventional cryptographic techniques to form an unbreakable code technique protected against various attacks¹².

Devipriya et al. developed a reconfigurable three-layer artificial neural network architecture for image encryption. Their research demonstrates FPGA adaptiveness for better configurations of neural networks and improved encryption performance, demonstrating high-speed and secure FPGA-based implementations to achieve fast and secure encryptions¹³. Silva-García et al. investigated the use of chaotic systems to generate substitution boxes (S-boxes), key components in many encryption algorithms. Their work indicates how chaos theory can produce ultra-secure S-boxes, thereby enhancing the security of image encryption methods in general¹⁴. In another research, Fu et al. developed a medical image protection scheme employing chaotic maps. The authors employed complex behaviour of chaotic maps to guarantee medical image security, thus providing a strong safeguard for sensitive medical data against unauthorised access¹⁵.

DICOM images can be more secure using chaotic systems combined with number theory. This method increases encryption strength levels by taking advantage of the unpredictability of chaotic systems and the strict mathematical nature of number theory. It provides high security for medical imaging data¹⁶. The authors presented a new chaos-based image encryption system that emphasises utilising chaotic sequences to enhance the complexity of encryption. This system has shown significant security improvements, enabling it to be used for secure image encryption applications¹⁷. They also reported on FPGA implementation and explored a new pseudo-random number generator (PRNG) based on a memristive Hopfield neural network). Memristive devices can improve randomness and security for keys employed in data-hiding methods or other cryptographic techniques¹⁸.

Sulaiman et al. conducted a detailed review of FPGA-based system design and implementation. Their study examines several FPGA architectures and applications, emphasising FPGAs’ adaptability and efficiency in performing complicated tasks such as picture encryption¹⁹. Maazouz et al. investigated the development of a chaos-based picture encryption technique using an FPGA. Their research illustrates the viability of employing FPGAs to run sophisticated chaotic algorithms, resulting in fast and secure picture encryption appropriate for real-time applications²⁰.

Ciylan et al. (2019) have constructed an FPGA-based chaotic image encryption system using systolic arrays. The key idea behind this approach is that the parallel processing capabilities of systolic arrays are leveraged to implement chaotic encryption algorithms cost-effectively, resulting in significant improvements in encryption speed and security²¹. In their work, Kumari and Soni (2020) analysed the FPGA implementation of the Advanced Encryption Standard for secure communication applications. While they were specifically interested in AES, it can be noted that these findings provide insights on how to optimise different encryption algorithms for FPGA platforms with efficiency consideration of ANN-based image encryption techniques²². Prasad and Sai (2021) designed and implemented a hardware encryption module for picture security on embedded systems. To introduce ANN-based encryption into embedded systems, there was an emphasis on real-time encrypted solutions at a hardware level²³.

Adil Yazdeen et al’s (2021) study is dedicated to the FPGA-based cryptographic accelerators. It reviews several cryptographic algorithms and their FPGA implementations, providing crucial knowledge about using FPGAs for purposes such as cryptography²⁴. Raja and Murali created one of the lightweight image encryption techniques using the FPGA platform. The study emphasises that for resource-constrained scenarios, effective and fast encryption schemes and lightweight encryption techniques may be needed in secure image processing²⁵. Alwan and Hamad proposed a high-performance picture encryption implementation on FPGAs utilising chaotic maps. In this research, the inherent unpredictability of chaotic maps is used to enhance the security of picture encryption systems; it also shows that the FPGA-based approach can offer a breakthrough for rapid encryption²⁶. Chaos has several important features, like being unexpected, extremely random, sensitive to beginning values, adaptable to all multimedia data, scalable, and helpful in contemporary communication situations like cloud storage and blockchain requirements^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44}.

Chaos-based encryption techniques are software-oriented and lack physical separation and hardware, which makes them vulnerable to OS-based and software virus assaults, according to the literature review. Although lightweight encryption techniques offer physical separation, they have limited memory capacity, lack hardware that can be reconfigured, and have inflexible algorithms that are ineffective against emerging threats. Due to its hardware isolation, FPGA-based encryption is less sensitive to threats like malware and viruses than software-based techniques. FPGA provides Physical isolation, making it more difficult for attackers to retrieve important encryption keys or data. FPGAs allow for the dynamic updating or reconfiguration of encryption algorithms to address new threats. The literature claims that neural networks may now represent non-linear statistical data, opening the door to creating complex input-output prototypes. When making the pseudo-random sequence for image encryption, the neural network must exhibit both chaotic behaviour and recurrence.

The proposed work implements the neural-based encryption scheme and is realised on FPGA hardware. Hopfield attractor-based image encryption, particularly in comparison to more traditional sequential processing environments like MATLAB, FPGAs can conduct several computations simultaneously, but MATLAB conducts operations sequentially, slowing down the encryption process and hiding the natural parallelism of neural networks. This parallelism accelerates the encryption process and fully leverages the neural network’s capabilities, offering significant improvements in speed and efficiency. Thus, this research highlights the potential of FPGA-based implementations to revolutionise image security by overcoming the limitations of sequential processing systems.

Proposed methodology

Preliminaries

Recurrent Hopfield Neural Network (HNN)

Hopfield Neural Network (HNN) is a recurrent neural network version abstracted from the dynamics of the human brain. All HNN nodes have been updated with Eqs. (1) and (2). Each node receives the signal from other nodes as well as external input according to Eq. (1), and the node output is then calculated using the sigmoid transfer function, as shown in Eq. (2)^1,43.

$$N({x_{i+1}})={e_i}+\sum\limits_{{i=1}}^{4} {{x_i}}$$

(1)

$$\begin{gathered} {X_{i+1}}=\frac{1}{{1+{e^{ - Net({X_{i+1}})}}}} \hfill \\ \hfill \\ \end{gathered}$$

(2)

Adaptive key generation using BPN network

The cryptosystem’s security will be jeopardised once the key has been discovered. This study uses neural networks to create a defence against a specific plaintext attack¹⁷. Each image creates a unique session key. A feed-forward neural network maps a set of image characteristics from the dataset to the key during training. The set of image characteristics such as minimum intensity value & maximum intensity value, DC component of an image, histogram mean, entropy of an image, mean of each segment(8 × 8), DC component of segments, and histogram mean of segments. The network was trained using a multilayer BPN network as the target and image attributes as inputs. The output key must change whenever at least one image feature changes since the trained neural system creates a unique key in this manner¹.

The proposed E-healthcare schema

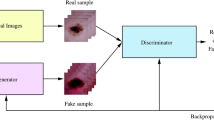
The proposed image encryption scheme is illustrated in Fig. 1. It has unique advantages such as an ANN on standalone reconfigurable hardware, parallelism increases the throughput, enhanced security through image-specific key, and simple key management through the integration of Hopfield attractor and stream cipher. The suggested approach improves security in two steps: first, it uses the Hopfield neural network’s chaotic dynamics to diffuse pixel values effectively. By utilising its associative memory capabilities, HNN integration for diffusion modifies the image data and guarantees a highly non-linear and unpredictable distribution of pixel values.

The proposed scheme can be applied to real-time applications such as live video streams, Wi-Fi communication, and secure communication between IoT devices. Further, the proposed algorithm is divided into three phases: stream cipher confusion, image-specific key generation, and Hopfield attractor-based diffusion. Stream cipher, an intrinsic FPGA method, is employed to initially confuse, and then the Hopfield neural network attractor is used for diffusion. Since these are two distinct extreme approaches, block diagrams roadmap to the proposed work.

Fig. 1

The Proposed Encryption Methodology.

Image-specific random key generation

The security of the cryptosystem will be jeopardised once the key has been discovered. So, the proposed work develops the image-dependent key using neural networks. It can be called a session key. Because for each image, it creates a unique session key. A multilayer BPN network with customised architecture is proposed to develop image-dependent keys. BPN is trained with the set of extracted spatial features and the key as a target. The BPN is trained to change the output key whenever at least one of the extracted spatial features changes since the trained neural system creates a unique key. Once the BPN is trained, it can produce an image-dependent key for each input image.

Stream Cipher based confusion

Stream cipher can produce a disoriented pattern for the plaintext, So it resists frequency analysis attacks. While working with real-time data streaming, stream cipher introduces low latency and high throughput. Non-linear polynomials can also be implemented in stream cipher, resulting in random sequences required for encryption. Later, the proposed algorithm is implemented in FPGA hardware. FPGA can process multiple operations simultaneously, and stream cipher implementation on FPGA makes the hardware simple and efficient. Because Stream cipher is implemented on FPGA using Flip-flops and XOR, stream cipher on FPGA offers resource constraint hardware architecture. The proposed scheme can be scalable to any size by utilising reconfigurable hardware. The stream cipher needs only a seed and polynomial, so key management is effortless.

Hopfield attractor-based diffusion

Data security is influenced by AI, in which HNN is a recurrent model with feedback. So, the HNN is well suited for diffusion HNN, which can generate random cyclic sequences and dynamic properties of the network that mutate in such a way. While defining the HNN architecture, the number of states or nodes, connection between states, feedback, external input to the specific state, and random value assumption of the initial state must be customised. Also, the activation function of each state is customised. The customised architecture has four nodes; all the nodes work concurrently under the support of FPGA configuration. Under the training, the weight matrix values are obtained. While diffusion is in progress, generated seed from the BPN model, The customised architecture provides the unique random sequences for an image.

Image encryption on FPGA

An FPGA’s interconnection is comparable to the neural wiring found in the human brain. Similar connections exist within the programmable logic fabric of an FPGA, which is one.

The reason why neural networks and other AI workloads are an excellent fit for FPGAs as implementation targets. Comparable to the brain’s ability to shift focus back to specific activities at hand is the bit-level dynamic programmability of FPGAs at both the logic and connecting wire levels. Furthermore, FPGA offers high flexibility through reconfigurable hardware not found in other architectures.

Results and discussion

The robustness of the developed encryption algorithm was tested using a variety of attack analyses, such as statistical analysis, differential analysis, quality assessment of the encryption, correlation and entropy examination, evaluation of key space and key sensitivity, analysis of computational and time complexity, and investigation of selected plaintext attacks^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44}.

In total, 12 numbers of 256 × 256 DICOM images (https://www.dicomlibrary.com/; https://www.osirix-viewer.com/resources/dicom-image-library/., 20 typical grayscale images (256 × 256, 512 × 512), and colour image (256 × 256) from the USC-SIPI Image Database (https://sipi.usc.edu/database/ ; https://in.mathworks.com/matlabcentral/answers/54439-list-of-builtin-demo-images ) were used to evaluate the method. Among these images, the results were presented for 5 grayscale images and 3 medical images, shown in Fig. 2.

Fig. 2

Test Images.

The software part of the work has been done in MATLAB R2022b with system configuration of 12th Gen Intel(R) Core (TM) i5-1235U 1.30 GHz with RAM 16.0 GB, and the hardware part has been done on Intel Cyclone V (5CSEMA5F31C6) FPGA using Verilog HDL as a programming language. Also, Fig. 3 (a – f) expresses the original, encrypted and decrypted images through the proposed encryption schema.

Fig. 3

DICOM 3 – (a) Original, (b) Encrypted (c) Decrypted & Grayscale – (d) Original e) Encrypted (f) Decrypted; Color image- (g) Original h) Encrypted (i) Decrypted.

Statistical analysis

Statistical analysis is utilised in image processing to understand and analyse images^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43}. Pixel values can be analysed mathematically to identify patterns and relationships in the image data. This facilitates object detection, image encrypting for security, and quality enhancement. For instance, it may measure how dissimilar or similar different areas of an image are by computing the correlation between pixels. Encrypted images cannot reveal original data patterns; hence, this knowledge is essential for enhancing image processing techniques. Here, correlation, entropy, and histogram analyses were performed to confirm the statistical resistivity of the created work.

Correlation analysis

Correlation analysis is one of the statistical analyses where the correlation between the pixel values of the original and encrypted images is referred to as ideally 1 or -1, which proves that statically neighbouring pixels are highly related to creating the pattern in the image block^{27,28,29,30,31,32,33,34,35}. A correlation study was conducted, and the findings are included in Tables 1 and 2. The charting of intensity values between neighbouring pixels in the encrypted DICOM images and plain mages is displayed in Table 1 (a-f), Table 1 (g-l) grayscale and encrypted images. The table values ensure that stream cypher-based confusion breaks the relation between the pixels. The average correlation of an encrypted image is around 10 − 3 due to the simple and efficient method of LFSR. The stream cipher confusion is compared with the chaotic confusion, and the resultant metrics are tabulated in Table 2. The reconfigurable hardware makes the cnfusion process more flexible with any image size. The lower correlation value proves that attackers cannot retrieve the image if they guess the pixel value.

Table 1 Results of the histogram of the original and the encrypted images.

Table 2 Results of correlation analyses.

Table 1 Graphical representation of the correlation between the adjacent pixels of the original images and their respective encrypted images. In the Table 1, figures (a-c) represent the correlation of the original DICOM3 image and (d - f) show the results for the encrypted image. Similarly, figures (g - i) illustrate the correlation of the original grayscale (Cameraman) image, and figures (j - l) represent its correlation for the encrypted image. Further, Table 2 summarises the coefficients of the correction analyses’ horizontal, vertical and diagonal directions for the test images. Upon analysing the numerical values, the proposed schema outperforms some of the existing encryption works stated in^16,27,28 that prove the efficacy of the proposed scheme.

Information entropy analysis

Entropy is another statistical analysis that ensures the effectiveness of the proposed diffusion part, as it measures the randomness and unpredictability of the encrypted image. The proposed scheme is considered the 8-bit image for this evaluation. After the diffusion, calculated entropy approaches 8, proving that diffusion makes maximum uncertainty. HNN generates a new synthetic image for each input image by updating the weight matrix. Consequently, it provides adaptive diffusion to get an average entropy of 7.99. The entropy values from Table 3 are close to 8, which is the ideal value. This finding indicates a significant alteration of the original image into random noise that ensures confidentiality preservation.

Table 3 Results of global entropy for original and encrypted images.

Comparison of confusion strategies

In general, chaos-governed image confusion schema can attain better entropies due to its stochasticity, ergodicity, and non-repudiation. However, chaotic maps or attractors demand enormous hardware resources to implement them since numerous arithmetic functions are required to generate the random number. In contrast, stream ciphers were the simplest and most effective form of random number generator that could offer the same security level yielded by the chaos-based schemes. To prove this claim, the results of the tent map-assisted confusion scheme were compared with those of the stream cipher-based confusion scheme, whose results are tabulated in Table 4.

Table 4 Results of the comparison of confusion strategies.

Table 4 shows that the LFSR-based confusion method, combined with Hopfield network diffusion, achieves slightly higher entropy values, indicating greater randomness and more robust encryption. Additionally, the LFSR method generally exhibits lower and more favourable horizontal and vertical correlation coefficients than the Tent map method, suggesting better decorrelation of the encrypted images. These metrics demonstrate that the LFSR-based approach provides more effective encryption. Furthermore, LFSR’s simplicity, efficiency, and low resource usage make it well-suited for FPGA implementation, offering high-speed performance and ease of scalability, thereby justifying its use in practical image encryption applications.

Histogram analysis

The test image and cipher image histogram are displayed in Table 5. According to the visual interpretation, the encrypted image histograms differ from the original images and are equally distributed. There is visual proof that the original image content is modified irregularly. The redundancy of the plain image was utterly disturbed. It generates the cipher image with non-linear displacement from the actual pixels.

Table 5 Results of the histogram of the original and the encrypted images.

Differential attack analysis

In image processing, differential analysis looks at changes and variances in pixel values within an image. Comparing the differences in pixel intensities helps identify edges, textures, and other essential elements. Examining these variations can locate items, highlight significant details, and enhance the image’s quality. For example, edge detection includes identifying regions with abrupt pixel value changes, which is critical for object identification and image segmentation tasks. Enhancing image analysis and processing methods requires the use of this technology.

Differential attack analysis with pixel change

The Normalised Pixel Change Rate (NPCR) and the Unified Average Changing Intensity (UACI) are two measures frequently employed to assess the efficacy of encryption systems. The Metrics are calculated between two cipher images of the same image, the original image and the original image with pixel change. Table 6 ensures the proposed algorithm resists the differential attack. The single bit of any pixel that differs between the original and encoded images is determined by NPCR. A good image encryption technique should have UACI values of approximately 33% and NPCR values of greater than 99%. Table 6 confirms the suggested encryption scheme’s efficacy and displays the differential findings of the scheme.

Table 6 Results of differential analyses.

Key sensitivity analysis

Key sensitivity is a critical property of the proposed encryption scheme; even a minor change, such as a fractional part in the encryption key, results in entirely different encrypted outputs. This ensures the cipher image exhibits a substantial diffusion property, preventing attackers from deducing the key or plaintext. A significant part of the proposed work is key generation. The key is generated through a Back Propagation Neural network. By leveraging image attributes, the proposed work provides an independent and adaptable key for every image. Minor changes in the characteristics of the image can be reflected in the key. So, the picture content(pixel) is slightly altered, and the key is changed, which alters the cipher image. NPCR and UACI are measured in between the encrypted images. For investigation, pixels are chosen from different positions to modify the image attributes. The original image with the pixel-altered version of the same image is used for the analysis. Results are tabulated in Table 6.

Keyspace analysis

While more minor key results limit the exhaustive search, the proposed approach gives vast key space to achieve a more robust algorithm. The key set for the suggested algorithm is {k1,…k8}, the key space is 10¹¹², the key precision is 10¹⁴ and the total key space is more significant than 2¹²⁸, implying the algorithm is more resistant to brute force attack. The keyspace is large enough that it is computationally impossible to brute-force every probable key using existing and predictable technology. Moreover, the suggested technique offers session keys, which are produced using the features of the original image.

Image transparency metric analysis

Image transparency metric analysis quantifies how much an image has been changed from its original state in image processing. This aids in evaluating the precision and quality of image processing techniques. Standard metrics that compare images and assess processing quality include Mean Squared Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). This guarantees that as much quality and detail as possible from the original image are retained in the processed version.

MSE and PSNR

Two popular error metric studies used to assess the quality of the encrypted images are Mean Square Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). The MSE and PSNR values are displayed in the Table 7. MSE compares the pixel-by-pixel differences between the original and encrypted images to assess the amount of noise in the encrypted image. A higher MSE value indicates considerable variations between the original and encrypted images.

Table 7 Results of MSE & PSNR.

Peak signal-to-noise ratio (PSNR) is a statistic that uses the ratio of the maximum achievable intensity value of the image to the mean square error (MSE) to represent the quality of the recovered image. A lower PSNR denotes a high noise level relative to the information and a noticeable difference between the encrypted and original plaintext images. The MSE and PSNR results are shown in Table 7.

Encryption quality analysis

The encryption quality was evaluated using Maximum Deviation (MD), Irregular Deviation (ID), and Deviation from Uniform Histogram (DH). Since the diffusion process has a greater influence on encryption quality than the confusion process, the randomness of the diffusion process will inevitably be validated using the previously mentioned measurements.

Table 8 displays the MD results for many test images. A greater value of MD indicates that the cipher image has strayed significantly from the original image. The obtained results are near the optimal value since the suggested technique first examines the intensity distribution of the plain image and redundancy attribute before performing the adaptive diffusion procedure. As a result, the cipher pixels are significantly offset from the plain image. The deviation from the uniform histogram quantifies the effectiveness of our image encryption method. Table 8 shows that the cameraman image achieved the lowest deviation at 0.0595, indicating a highly balanced intensity spread post-encryption. This consistent reduction in deviation across diverse images demonstrates the ability of the proposed method to obscure original data effectively. Thus, our encryption approach proves robust, ensuring enhanced security by closely approximating a uniform histogram.

Table 8 Results of encryption quality analyses.

Table 8 reveals that the DH values are shallow; this demonstrates that the suggested technique created a histogram that deviated less from the ideal histogram. Some intensities do not exist in the primary image, while others become redundant as an image becomes more significant. But the proposed diffusion method employs complex, dynamic, and non-linear encoding to provide uniform occurrences for each intensity value (between 0 and 255 for a grayscale image). Thus, the suggested system exhibits nearly little departure from the ideal histogram.

NIST SP 800 − 22 batteries of tests

The National Institute of Standards and Technology (NIST) has several standards and evaluation practices to verify the quality of the crypto schemes and outcomes. NIST SP 800–22 is one such evaluation benchmark that deals with the 16 different statistical test models to validate the randomness of any random number generator or ciphers. In this context, the input data has been tested on three fundamental properties: (a) Equidistribution, (b) Unpredictability, and (c) No pattern production. To conduct this test, pixel values of the encrypted images are stored in the on-chip RAM of the Cyclone V FPGA. Following extraction, the encrypted pixel values are transformed into a binary bitstream and put through the NIST SP 800 − 22 test suite battery of statistical randomness tests with critical parameters. Table 9 presents the results of NIST SP 800–22 in which tests have attained a probability greater than 0.01, which evidence the confidence level of α = 0.01. This shows that the proposed encryption algorithm has successfully passed NIST SP 800–22 tests with a randomness percentage of 99.9, ensuring the proposed encryption schema is cryptographically strong.

Table 9 Results of NIST SP 800 − 22 batteries of tests.

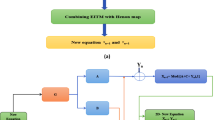
Hardware implementation analysis

The proposed HNN image-dependent encryption scheme was designed using Verilog HDL, synthesised through the Quartus II EDA (Electronic Design Automation) tool, and implemented on Cyclone V FPGA. The major on-chip features of 5CSEMA5F31C6 FPGA utilised in this implementation include (DICOM and Gray images) 1,048,576 (26%) of memory bits, 45 (10%) pins, 259 logic registers, 5(6%) DSP blocks and 1(17%) PLL (Phase Locked Loop). Figure 4 depicts the portion of the RTL (Register Transfer Level) diagram that shows the implementation strategy followed by the EDA tool. Further, a complete prototype of the proposed encryption on Cyclone V FPGA is illustrated in Fig. 5, which presents the integration of LCD (Liquid Crystal Display) to show the original and encrypted images. Logic utilisation of the test images has been tabulated in Table 10, displaying the change in the logic consumption due to the different sizes of the test images.

Table 10 Logic utilisation of various images.

Fig. 4

A section of the RTL diagram of the encryption algorithm on Cyclone V FPGA.

Fig. 5

A complete prototype of proposed encryption architecture on Cyclone V FPGA with cameraman image.

Power dissipation analysis

The power dissipation by FPGA hardware is contingent upon several parameters, including but not limited to device switching speed, memory utilisation, and algorithm implementation-related processes. The various types of power dissipation for the suggested concurrent architecture, giving rise to the overall power dissipation, are examined and show that regardless of the number of concurrent blocks employed, the quantity of static and I/O power dissipation is constant. The Total thermal power dissipation is equal to the sum of Static power dissipation, Dynamic power dissipation, and I/O power dissipation. This work calculated power using the Power Play Power Analyzer tool, the built-in power tool available in the Quartus II EDA tool. The tool calculated the total power as 424.71mW, with minimal power dissipation.

Encryption time complexity analysis

Time complexity analysis ensures the encryption process is reliable and effective by balancing security and speed. Analysing time complexity is essential for assessing and improving image encryption techniques. Analysis of the temporal complexity of the encryption algorithm guarantees that it can process images fast enough to satisfy real-time demands. The proposed scheme has balanced the speed and security, and it takes 1.2 s(as an average) to encrypt the image with the size of 512 × 512 × 3, which is tabulated in Table 11 and comparable with recent works.

Table 11 Time complexity of the proposed scheme.

The time complexity of the proposed image encryption is quick enough to meet real-time requirements. The reason behind that Several LFSR and Hopfield node calculations may be performed simultaneously on FPGAs because of their strong parallel capabilities. Variation in encryption time depends on FPGA resources and implementation, so it is possible to parallelise neuron updates and reduce effective time complexity by completely pipelined LFSR.

Occlusion attack analysis

Effective encryption should be able to withstand noise jamming. So, the robustness of the proposed scheme is tested by white Gaussian noise and salt & pepper noise, respectively. The noise level variance is chosen from 0.001 to 0.01, although the deciphered image is still discernible. The Structural Similarity Index Metric (SSIM) is the metric for the robustness of the image quality, which is calculated between the original image and the deciphered image. The SSIM value is close, confirming the image recovery’s robustness after decryption. Gaussian noise is verified with different filter dimensions, Yet the decoded DICOM 1 image remains identifiable even after adding the white Gaussian noise. The SSIM values are tabulated in Table 12.

Table 12 Robustness of the proposed scheme against occlusion attack.

Discussion about the strengths and future scope of the proposed work

Strengths

A proposed scheme assures high security by offering high, near-ideal entropy (7.99) and providing near-zero correlation coefficients, thus demonstrating excellent diffusion and confusion properties. Extensive dynamic session key generation using a Back Propagation Neural Network (BPN) guarantees unique and secure session keys to each invocation of encryption and strengthens against differential attacks. So, the FPGA-based implementation provides real-time performance with low resource utilisation (20% logic utilisation), minimal power dissipation (424.71 mW), and an encryption speed of around 1.3 s, making it well-suited for resource-constrained real-time environments. The system is scalable to images of all sizes and modalities, such as grayscale, medical, and colour images. It is also resilient to statistical, differential, noise, and occlusion attacks, having a vast key space of more than (2^{128}) and resistant to brute-force attacks.

Future scope

The runtime cost is introduced by the initial training of the BPN but can be minimised through the pre-trained model. The scheme is validated for grayscale and medical images, but further optimisation is required for high-resolution medical videos. Hardware dependence on FPGA-based technology improves speed and efficiency. High-end FPGA architectures might be utilised to enhance the speed of the proposed work further.

Conclusion

HNN and stream cipher-based image encryption on FPGA have shown a viable path toward secured image transmission. The proposed scheme has proven with the analysis part, emphasising the combined effect of parallel processing. The proposed scheme has arrived with a challenging image-specific key and unique HNN architecture, making for non-linear and stochastic pixel variation. Several measures are used to examine the proposed work and confirm its effectiveness in real-time applications. A neural attractor in an FPGA configuration boosts scalability and flexibility quickly, utilising a lower-end FPGA configuration. This work may be expanded to include video encryption using a higher-end FPGA architecture. The scalability of the FPGA implementation is confirmed, and with the right advanced FPGA versions, various deep-learning model architectures may be created for high-speed video encryption.