Introduction

Oil shale is widely distributed worldwide and regarded as an essential alternative energy source to traditional oil resources1. However, like other shales, the permeability, porosity, and thermal conductivity are extremely low, which hinders the migration of pyrolysis products to the production wells2,3,4. It is challenging to rely on its matrix and discontinuous structural planes to achieve commercial exploitation of this resource. Hydraulic fracturing is recognised as a major stimulation technique for enhanced hydrocarbon recovery. An in-depth investigation of the initiation and extension mechanism of hydraulic fractures is of great significance in guiding fracturing operation design and predicting the morphology of the hydraulic fractures.

Theoretical derivations5, numerical simulations6 and fracturing simulation experiments7,8 are the main methods to study the behaviour of hydraulic fractures. The results of previous studies have shown that the initiated fracture has an extremely tortuous morphology at a small distance to the wellbore9,10. The tortuous morphology of hydraulic fractures will cause high near-wellbore friction and extremely high initiation pressures, which can be solved through a rational design of perforated fracturing11. The extension and morphology of hydraulic fractures near-wellbore can be facilitated and complicated through perforated fracturing12. The perforated fracturing technology can be divided into spiral, co-planar, and oriented perforating13. Spiral perforating usually produces higher initiation pressures, while co-planar perforating is more costly14. Thus, oriented perforating technology is widely used to optimise fracture extension behaviour and improve the permeability of oil and gas reservoirs15. However, excavating the horizontal wellbore and formatting the perforation in the strata greatly disturb the geo-stress field near-well, resulting in an extremely complex stress field around the fracture tip. The evolution of this stress field has a crucial influence on the initiation and extension behaviour of the hydraulic fracture.

Many researchers have investigated the influence of perforation boreholes on hydraulic fracture initiation and extension behaviour16,17. As the deviation angle of perforation increases, it reduces near-wellbore fracture width6 and makes it difficult to control and predict the initiation and expansion of hydraulic fracture18,19. For the length of the perforated borehole, it was concluded that as the perforation length increases, the fracture initiation pressure decreases, and re-fracture becomes facilitated20. Furthermore, reducing the initiation pressure and the tortuous morphology of the fractures near-wellbore can also be achieved by increasing the density of the perforations21. The increase in perforation azimuth will result in fewer boreholes in the same plane, which is not favourable to the connection between the perforated boreholes and will lead to a rise in fracture pressure13.

In addition to the perforated borehole parameters, the fracturing fluid parameters also impact the effectiveness of the perforation fracturing. The flow rate and viscosity of fracturing fluid should not be ignored when discussing the initiation and extension of hydraulic fractures. The increase in flow rate and viscosity of the fracturing fluid will improve the effect of reservoir modification. However, many scholars have pointed out that there exists a threshold of flow rate and viscosity for different reservoirs, beyond which the fracturing effect is no longer significantly improved6,22. Reviewing the previous investigation results, we considered it essential to understand the mechanism of fracturing initiation pressure and initiation location for different perforation and fracturing fluid parameters within the perforated boreholes to predict the hydraulic fracture extension behaviour and improve the efficiency of reservoir modification.

In this paper, based on the superposition principle, the stress regime distribution around the perforated borehole was obtained, considering the effects of geo-stress, fracturing fluid pressure, filtration effect of fracturing fluid and temperature differences. Utilising the “Bucket theory” and combining the typical rock damage criterion for rocks, a theoretical model for calculating hydraulic fracture initiation pressure and location was established based on the abovementioned stress distribution. The typical rock damage criterion used in this paper were shown below:

  1. (1)

    Tensile failure criterion

$${\sigma}_{3}-\alpha{P}_{por}<-{\sigma}_{T}$$
(1)

where \({\sigma}_{3}\) is the minimum geo-stress; \(\alpha\) is the Biot coefficient; \({P}_{por}\) represents the pore pressure within the reservoir, and \({\sigma}_{T}\) represents the tensile strength of the reservoir rock.

  1. (2)

    Mohr-Coulomb criterion

Mohr criterion considered the pure shear damage to be related only to the maximum and minimum principal stresses and not to the intermediate principal stresses. The damage can be expressed as Eq. (2).

$$\left|\tau\right|=f\left(\sigma\right)$$
(2)

Based on the Mohr criterion, the Mohr-Coulomb criterion assumed that shear damage would occur at the damaged surface when the shear stress generated on the damaged surface by an external force exceeds the sum of the rupture surface’s shear strength \({{\upsigma}}_{\tau}\) and the frictional force F. Thus, the expression for the Mohr-Coulomb criterion can be obtained, as shown in Eq. (3).

$$\tau>{{\upsigma}}_{\tau}+\text{F}$$
(3)
  1. (3)

    Drucker-Prager criterion

The expression for the Drucker-Prager criterion is shown as Eq. (4):

$$\sqrt{\frac{1}{6}\left[{\left({\sigma}_{1}-{{\upsigma}}_{2}\right)}^{2}+{\left({{\upsigma}}_{2}-{{\upsigma}}_{3}\right)}^{2}+{\left({{\upsigma}}_{3}-{{\upsigma}}_{1}\right)}^{2}\right]}=\frac{C\sqrt{3}\text{cos}\phi}{\sqrt{3+{\text{sin}}^{2}\phi}}+\frac{\sqrt{3}\text{sin}\phi}{3\sqrt{3+{\text{sin}}^{2}\phi}}\left(\left.{\sigma}_{1}+{\sigma}_{2}+{\sigma}_{3}\right)\right.$$
(4)

where \({\sigma}_{1}\), \({\sigma}_{2}\), \({\sigma}_{3}\) are the principal stresses in the calculation cell, and φ and C denoted the angle of internal friction and cohesion, respectively.

  1. (4)

    Griffith Criterion

The criteria above view rocks as intact, fissure-free and continuous media, whereas in reality, they are structural bodies with multiple internal fissures. The Griffith criterion assumed that external forces would produce stress concentrations at the ends of fractures within the rock, leading to macroscopic fractures. The equation of this criterion was shown in Eq. (5):

$$\left\{\begin{array}{c}{\left({\sigma}_{1}-{{\upsigma}}_{3}\right)}^{2}=8{\sigma}_{T}\left({\sigma}_{1}+{{\upsigma}}_{3}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{\sigma}_{1}+3{\sigma}_{3}\ge\:0\\\:{{\upsigma}}_{3}=-{\sigma}_{T}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{\sigma}_{1}+3{\sigma}_{3}<0\end{array}\right.$$
(5)

where \({\sigma}_{1}\) and \({{\upsigma}}_{3}\) are the maximum and minimum principal stresses to which the rock is subjected, respectively, and \({\sigma}_{T}\) is the uniaxial tensile strength of the rock.

  1. (5)

    Modified Griffith Criterion

The Griffith theory above is a two-dimensional theory derived from the flat elliptical fracture theory, and when the effect of the intermediate geo-stress \({{\upsigma}}_{2}\) is taken into account, the Griffith Murrel’s derivation formula can be obtained, as shown in Eq. (6).

$${\left({\sigma}_{2}-{{\upsigma}}_{3}\right)}^{2}+{\left({{\upsigma}}_{3}-{{\upsigma}}_{1}\right)}^{2}+{\left({{\upsigma}}_{1}-{{\upsigma}}_{2}\right)}^{2}=24{\sigma}_{T}({\sigma}_{1}+{\sigma}_{2}+{\sigma}_{3})$$
(6)

where \({\sigma}_{1}\), \({{\upsigma}}_{2}\) and \({{\upsigma}}_{3}\) are the maximum, intermediate and minimum principal stresses, respectively, and \({\sigma}_{T}\) is the uniaxial tensile strength of the rock.

Based on the above damage criterion, we calculated the initiation pressure required for different perforated borehole cross-sections separately, and then obtained the initiation pressure and initiation location of the sample. Then, the true triaxial hydraulic fracturing experiments were performed to verify the accuracy of the theoretical model. Finally, the rigorousness of the findings of this paper was demonstrated by combining theoretical derivation and fracturing experiments. The research results will provide theoretical and technical support for predicting and evaluating perforation fracturing in oil shale reservoirs.

Methodology

Fundamental assumptions

Drilling a horizontal well in a low permeability reservoir will cause a redistribution of stresses in the rock around the wellbore. The generation of the perforation borehole will further complicate the stress field distribution around the horizontal well and the perforation hole. Therefore, the following assumptions need to be made before building a mathematical model of the stress field distribution around the horizontal wellbore and the perforation hole wall.

  1. (1)

    The reservoir rock is an isotropic elastic medium;

  2. (2)

    Assuming that the rock matrix around the wellbore is in plane strain and the fluid pressures are equal on the horizontal wellbore and perforation hole;

  3. (3)

    When performing the stress field analysis of the perforation hole, the perforation hole is treated as a small-sized cylindrical bare borehole wellbore connected to the horizontal wellbore, with no damage to the wellbore and borehole wall connectivity;

  4. (4)

    Ignore changes in the mechanical properties of the rock due to the physicochemical interaction between the fracturing fluid and the rock matrix.

Stress field distribution around the horizontal wellbore and the perforation borehole

The calculation unit of an oil shale formation was subject to three-dimensional geo-stress in the subsurface. The stress state of this stratigraphic unit can be expressed in terms of three-way principal stress, including the vertical principal stress σv, the horizontal maximum principal stress σH, and the minimum horizontal principal stress σh imposed by the overlying formation. The angle between the wellbore and the maximum horizontal and vertical ground stress was assumed to be \({\upgamma}\) and \({\uppsi},\) respectively. According to the coordinate transformation equation., the stress state at a point on the horizontal wellbore can be expressed through the principal geo-stresses. Considering the effect of the wellbore azimuth \({\upgamma}\) and the deviation angle \({\uppsi}\), the stress distribution around the wellbore can be obtained, as shown in Eq. (7).

$$\left\{ {\begin{array}{*{20}l} {\sigma _{x} = \left( {\sigma _{H} \cdot \sin ^{2} \gamma + \sigma _{h} \cdot \cos ^{2} \gamma } \right)\sin ^{2} \psi - \sigma _{v} \cdot \cos ^{2} \psi } \hfill \\ {\sigma _{y} = \left( {\sigma _{H} \cdot \sin ^{2} \gamma + \sigma _{h} \cdot \cos ^{2} \gamma } \right)\cos ^{2} \psi + \sigma _{v} \cdot \sin ^{2} \psi } \hfill \\ {\sigma _{z} = \sigma _{H} \cdot \cos ^{2} \gamma + \sigma _{h} \cdot \sin ^{2} \gamma } \hfill \\ {\tau _{{xy}} = \frac{1}{2}~\left( {\sigma _{h} \cdot \cos ^{2} \gamma + \sigma _{H} \cdot \sin ^{2} \gamma - ~\sigma _{v} } \right)\sin 2\psi } \hfill \\ {\tau _{{yz}} = \frac{1}{2}\left( {\sigma _{H} - \sigma _{h} } \right)\sin 2\gamma \cdot \cos \psi } \hfill \\ {\tau _{{zx}} = \frac{1}{2}\left( {\sigma _{H} - \sigma _{h} } \right)\sin 2\gamma \cdot \sin \psi } \hfill \\ \end{array} } \right.$$
(7)

According to Eq. (7), when the wellbore deviation angle \({\uppsi}\) = 90° and the wellbore azimuth angle \({\upgamma}\)\(\ne\)0°, the stress distribution around the horizontal wellbore in ideal conditions can be expressed by the three-way principal stress, as shown in Eq. (8)

$$\left\{ {\begin{array}{*{20}l} {\sigma _{x} = \sigma _{H} \cdot \sin ^{2} \gamma + \sigma _{h} \cdot \cos ^{2} \gamma } \hfill \\ {\sigma _{y} = \sigma _{v} } \hfill \\ {\sigma _{z} = \sigma _{H} \cdot \cos ^{2} \gamma + \sigma _{h} \cdot \sin ^{2} \gamma } \hfill \\ {\tau _{{xy}} = 0} \hfill \\ {\tau _{{yz}} = 0} \hfill \\ {\tau _{{zx}} = \left( {\sigma _{h} - \sigma _{H} } \right)\sin \gamma \cdot \cos \gamma } \hfill \\ \end{array} } \right.$$
(8)

Stress field distribution around the open-hole horizontal borehole wall

When a horizontal well was formed, the original stress balance within the formation was disturbed, causing a redistribution of stress in the surrounding rock near the wellbore and local stress concentrations. During the fracturing process, the injection of fracturing fluid caused an increase in the internal pressure in the wellbore, and the seepage of fracturing fluid into the formation produced an increase in pore pressure on the surrounding rock. According to the elastoplasticity theory, compressive stress was defined as positive and tensile stress as negative. The problem can be simplified to an infinite plane where the circular hole in the horizontal wellbore section was subjected to the additional stresses generated by the uniform internal pressure \(\:{\text{P}}_{\text{w}}\) and the plane of the borehole is also subjected to the plane strain problem of σx, σy, σz.

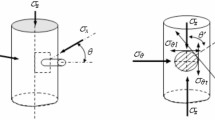
As shown in Eq. (9), the stress field distribution around the horizontal wellbore can be obtained considering the effect of fluid pressure, stress state, seepage conditions of the fracturing fluid, and temperature differences. The corresponding mechanical model was shown in Fig. 1.

Fig. 1
figure 1

Mechanical model of the stress field around a horizontal well.

Full size image
$$\left\{ \begin{gathered} \sigma _{{rh}} = P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) + \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }} - \frac{{4R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta ~ \hfill \\ \; + \tau _{{xy}} \left( {1 + 3\frac{{R^{4} }}{{r^{4} }} - 4\frac{{R^{2} }}{{r^{2} }}} \right)\sin 2\theta ~ + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) - \emptyset } \right]\left( {P_{w} - P_{p} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{\theta h}} = - P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) - \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \; - \tau _{{xy}} \left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\sin 2\theta + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 + \frac{{R^{2} }}{{r^{2} }}} \right) - \emptyset } \right]\left( {P_{w} - P_{p} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{zh}} = - c\frac{{R_{{hw}} ^{2} }}{{r^{2} }}~P_{w} + \sigma _{z} - 2\mu \left( {\sigma _{x} - \sigma _{y} } \right)\left( {\frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta - 4\mu \tau _{{xy}} \frac{{R_{{hw}} ^{2} }}{{r^{2} }}~\sin 2\theta \hfill \\ \; + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{\left( {1 - \mu } \right)}} - \emptyset } \right]\left( {P_{w} - P_{p} } \right)~ - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \tau _{{r\theta h}} = \tau _{{xy}} \cos 2\theta ~\left( {1 - \frac{{3R_{{hw}} ^{4} }}{{r^{4} }} + \frac{{2R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \tau _{{\theta zh}} = ( - \tau _{{zx}} \sin \theta + \tau _{{zy}} \cos \theta )\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \tau _{{rzh}} = (\tau _{{zy}} \sin \theta + \tau _{{zx}} \cos \theta )\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(9)

where the radial, circumferential and axial stresses at a point in the horizontal wellbore envelope in polar coordinates are \({\varvec{\sigma}}_{\mathbf{r}\mathbf{h}}\), \({\varvec{\sigma}}_{\varvec{\uptheta}\mathbf{h}}\), \({\varvec{\sigma}}_{\mathbf{z}\mathbf{h}}\), and the corresponding shear stress components are \({\varvec{\tau}}_{\mathbf{r}\varvec{\uptheta}\mathbf{h}}\), \({\varvec{\tau}}_{\varvec{\uptheta}\mathbf{z}\mathbf{h}}\), \({\varvec{\tau}}_{\varvec{r}\varvec{z}\varvec{h}},\) respectively. \({\mathbf{R}}_{\varvec{h}\varvec{w}}\)is the radius of the horizontal wellbore; r is the radius of the horizontal wellbore in polar coordinates; θ is the angle between the radial and the x-axis direction of the calculated point in the surrounding rock around the horizontal wellbore; \({\mathbf{P}}_{\varvec{w}}\) is the fluid pressure in the horizontal wellbore; \(\varvec{\mu}\) is the rock Poisson’s ratio; \(\varvec{\updelta}\) is the permeability coefficient; \(\varvec{\upxi}\) is the Biot coefficient; \({\mathbf{P}}_{\varvec{p}}\) is the pore fluid pressure; \({\varnothing}\) is the porosity; \(\mathbf{c}\) is the pressure correction factor, generally taken as 0.9 to 1; Δ is the rock temperature difference

Since the fracturing fluid pressure inside the wellbore was approximately the same as the pore fluid pressure inside the surrounding rock of the near-wellbore. The fluid temperature was essentially the same as the formation temperature. Equation (9) can be optimised as Eq. (10).

$$\left\{ \begin{gathered} \sigma _{{rh}} = P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) + \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }} - \frac{{4R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta ~ \hfill \\ \; + \tau _{{xy}} \left( {1 + 3\frac{{R^{4} }}{{r^{4} }} - 4\frac{{R^{2} }}{{r^{2} }}} \right)\sin 2\theta \hfill \\ \sigma _{{\theta h}} = - P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) - \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \; - \tau _{{xy}} \left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\sin 2\theta \hfill \\ \sigma _{{zh}} = - c\frac{{R_{{hw}} ^{2} }}{{r^{2} }}~P_{w} + \sigma _{z} - 2\mu \left( {\sigma _{x} - \sigma _{y} } \right)\left( {\frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta \hfill \\ \; - 4\mu \tau _{{xy}} \frac{{R_{{hw}} ^{2} }}{{r^{2} }}~\sin 2\theta \hfill \\ \tau _{{r\theta h}} = \tau _{{xy}} \cos 2\theta ~\left( {1 - \frac{{3R_{{hw}} ^{4} }}{{r^{4} }} + \frac{{2R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \tau _{{\theta zh}} = ( - \tau _{{zx}} \sin \theta + \tau _{{zy}} \cos \theta )\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \tau _{{rzh}} = (\tau _{{zy}} \sin \theta + \tau _{{zx}} \cos \theta )\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(10)

As shown in Eq. (11), the distribution of the stress field at the wall of the open-hole horizontal well (r = \({\text{R}}_{\text{h}\text{w}}\)) can be obtained.

$$\left\{ {\begin{array}{*{20}l} {\upsigma _{{rh}} = P_{w} } \hfill \\ {\upsigma _{{\theta h}} = - P_{w} + \left( {\upsigma _{x} + \upsigma _{y} } \right) - 2\left( {\upsigma _{x} - \upsigma _{y} } \right)\cos 2\theta - 4\uptau _{{xy}} \sin 2\theta ~} \hfill \\ {\upsigma _{{zh}} = - cP_{w} + \upsigma _{z} - \mu \left[ {2\left( {\upsigma _{x} - \upsigma _{y} } \right)\cos 2\theta + 4\uptau _{{xy}} \sin 2\theta } \right]} \hfill \\ {\uptau _{{r\theta h}} = 0} \hfill \\ {\uptau _{{\theta zh}} = 2\left( { - \uptau _{{xz}} \sin \theta + \uptau _{{yz}} \cos \theta } \right)} \hfill \\ {\uptau _{{rzh}} = 0~} \hfill \\ \end{array} } \right.$$
(11)

Equation (11) gave that \({{\uptau}}_{\text{r}{\uptheta}\text{h}}={{\uptau}}_{\text{r}\text{z}\text{h}}=0\), \({{\uptau}}_{{\uptheta}\text{z}\text{h}}\ne0\). Therefore, the circumferential stress \({{\upsigma}}_{{\uptheta}\text{h}}\) at the surface of the wellbore and the circumferential stress \({{\upsigma}}_{\text{z}\text{h}}\) are not the principal stress in the tangential plane (z-\({\uptheta}\) plane) of the wellbore. However, the radial stress \({{\upsigma}}_{\text{r}\text{h}}\) should be a principal stress since the bi-directional shear stress in the plane it was located was zero. The principal stresses in the zh-θh plane can be calculated using the composite stress theory, and the three-way principal stresses at any point on the surface of the wellbore as shown in Eq. (12).

$$\left\{ {\begin{array}{*{20}l} {\sigma _{1} = \sigma _{{rh}} } \hfill \\ {\sigma _{2} = \frac{1}{2}\left[ {\left( {\sigma _{{\theta h}} + \sigma _{{zh}} } \right) + \sqrt {\left( {\sigma _{{\theta h}} - \sigma _{{zh}} } \right) + 4\tau _{{\theta zh}}^{2} } } \right]} \hfill \\ {\sigma _{3} = \frac{1}{2}\left[ {\left( {\sigma _{{\theta h}} + \sigma _{{zh}} } \right) - \sqrt {\left( {\sigma _{{\theta h}} - \sigma _{{zh}} } \right) + 4\tau _{{\theta zh}}^{2} } } \right]} \hfill \\ \end{array} } \right.$$
(12)

Stress field distribution around the perforation borehole

Based on the stress distribution around the open-hole horizontal well, the wall shear of the perforation borehole was subject to the stresses of \(\sigma _{{\theta h}}\) and \(\sigma_{z h}\), in the horizontal direction, and \({\sigma}_{rh}\) was the stress in the axial direction of the perforation borehole. The perforations were usually in the reservoir as boreholes perpendicular to the horizontal well. Considering the additional stresses generated by seepage stresses and temperature differences, the stress field distribution surrounding the perforation borehole was obtained by superimposing the effect of each stress component. This state of stress can be represented by the axial stress \({\sigma}_{zp}\), radial stress \({\sigma}_{rp}\), circumferential stress \({\sigma}_{{\phi p}}\), and shear stresses \({\tau}_{{rp \phi}}\), \({\tau}_{rpz}\), \({\tau}_{\phi zp}\) in the polar coordinate system of the perforation, as shown in Fig. 2. The stress distribution in the surrounding rock around the perforation borehole can be expressed by Eq. (13) considering the combined effect of fracturing fluid pressure in the perforation, geo-stress and the seepage effect of fracturing fluid filtration loss.

Fig. 2
figure 2

Mechanical modelling of the stress field in the surrounding rock at the wall of the perforation borehole.

Full size image
$$\left\{ \begin{gathered} \sigma _{{rp}} = P_{P} \left( {\frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) + \frac{1}{2}\left( {\sigma _{{\theta h}} + \sigma _{{zh}} } \right)\left( {1 - \frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) + \frac{{\sigma _{{\theta h}} - \sigma _{{zh}} }}{2}\left( {1 + \frac{{3R_{P}^{4} }}{{r_{P}^{4} }} - \frac{{4R_{P}^{2} }}{{r_{P}^{2} }}} \right)\cos 2\varphi \hfill \\ + \tau _{{\theta zh}} \left( {1 + \frac{{3R_{P}^{4} }}{{r_{P}^{4} }} - \frac{{4R_{P}^{2} }}{{r_{P}^{2} }}} \right)\sin 2\varphi + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 - \frac{{R_{P} ^{2} }}{{r_{P}^{2} }}} \right) - \emptyset } \right]\left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{\varphi p}} = - P_{P} \left( {\frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) + \frac{1}{2}\left( {\sigma _{{\theta h}} + \sigma _{{zh}} } \right)\left( {1 + \frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) - \frac{{\sigma _{{\theta h}} - \sigma _{{zh}} }}{2}\left( {1 + \frac{{3R_{P}^{4} }}{{r_{P}^{4} }}} \right)\cos 2\varphi ~ \hfill \\ - \tau _{{\theta zh}} \left( {1 + \frac{{3R_{P}^{4} }}{{r_{P}^{4} }}} \right)\sin 2\varphi + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 + \frac{{R_{P} ^{2} }}{{r_{P}^{2} }}} \right) - \emptyset } \right]\left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{zp}} = \sigma _{{rh}} - 2\mu \left( {\sigma _{{\theta h}} - \sigma _{{zh}} } \right)\left( {\frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right)\cos 2\varphi - 4\mu \tau _{{\theta zh}} \left( {\frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right)\sin 2\varphi \hfill \\ + \delta \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 + \frac{{R_{P} ^{2} }}{{r_{P}^{2} }}} \right) - \emptyset } \right]\left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \tau _{{r\varphi p}} = \left( { - \frac{{\sigma _{{\theta h}} - \sigma _{{zh}} }}{2}\sin 2\varphi + \tau _{{\theta zh}} \cos 2\varphi } \right)\left( {1 - \frac{{3R_{P}^{4} }}{{r_{P}^{4} }} + \frac{{2R_{P}^{2} }}{{r_{P}^{2} }}} \right) \hfill \\ \tau _{{rzp}} ~~ = \left( {\tau _{{rzh}} \sin \varphi + \tau _{{r\theta h}} \cos \varphi } \right)\left( {1 - \frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) \hfill \\ \tau _{{\varphi zp}} ~ = \left( { - \tau _{{r\theta h}} \sin \varphi + \tau _{{rzh}} \cos \varphi } \right)\left( {1 + \frac{{R_{P}^{2} }}{{r_{P}^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(13)

where \({\varvec{\upsigma}}_{\mathbf{r}\mathbf{p}}\), \({\varvec{\upsigma}}_{\varvec{\upphi}\mathbf{p}}\), \({\varvec{\upsigma}}_{\mathbf{z}\mathbf{p}}\), \({\varvec{\uptau}}_{\mathbf{r}\varvec{\upphi}\mathbf{p}}\), \({\varvec{\uptau}}_{\varvec{\upphi}\mathbf{z}\mathbf{p}}\), \({\varvec{\uptau}}_{\mathbf{r}\mathbf{z}\mathbf{p}}\) are the radial stress, circumferential stress, axial stress and shear stress component at that point in the polar coordinate system for the calculated points around the perforation borehole; \(\varvec{\phi}\) is the angle between the direction of the \({\sigma}_{\theta h}\) and the radial direction of the calculated points; \({\mathbf{R}}_{\varvec{P}}\) is the radius of the perforation borehole, and the radius in polar coordinates of the perforation is \({\mathbf{r}}_{\varvec{P}}\); \({\mathbf{P}}_{\mathbf{P}}\) is the pressure of the fracturing fluid inside the perforation; \(\varvec{\mu}\) is the Poisson’s ratio of the rock; δ is the permeability coefficient; \(\varvec{\upxi}\) is the poroelasticity coefficient (Biot coefficient); \({\mathbf{P}}_{0}\) is the pore pressure of the formation; \({\varnothing}\) is the porosity; \(\mathbf{c}\) is the pressure correction factor, generally taken from 0.9 to 1; \({\varvec{\alpha}}_{\varvec{T}}\) is the expansion coefficient of the rock around the perforation borehole; \(\varDelta\varvec{T}\) is the rock temperature difference.

The stress distribution at the surface of the perforation (\({\text{r}}_{P}\)=\({\text{R}}_{P}\)) was shown in Eq. (14).

$$\left\{ \begin{gathered} \sigma _{{rp}} = P_{P} - \emptyset \left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{\varphi p}} = - P_{P} + \sigma _{{\theta h}} + \sigma _{{zh}} - 2\left( {\sigma _{{\theta h}} - \sigma _{{zh}} } \right)\cos 2\varphi - 4\tau _{{\theta zh}} \sin 2\varphi \hfill \\ + \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{\left( {1 - \mu } \right)}} - \emptyset } \right]\left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \sigma _{{zp}} = \sigma _{{rh}} - 2\mu \left( {\sigma _{{\theta h}} - \sigma _{{zh}} } \right)\cos 2\varphi - 4\mu \tau _{{\theta zh}} \sin 2\varphi \hfill \\ + \left[ {\frac{{\xi \left( {1 - 2\mu } \right)}}{{\left( {1 - \mu } \right)}} - \emptyset } \right]\left( {P_{P} - P_{0} } \right) - \frac{{E\alpha _{T} \Delta T}}{{1 - 2\mu }} \hfill \\ \tau _{{r\varphi p}} = \tau _{{rzp}} = 0 \hfill \\ \tau _{{\varphi zp}} = 2\tau _{{r\theta h}} \sin \varphi \hfill \\ \end{gathered} \right.$$
(14)

Similarly, since the injected fluid temperature was approximately the same as the reservoir temperature. The fluid pressure \({\text{P}}_{\text{P}}\) inside the perforation was roughly equal to the pore pressure \({\text{P}}_{0}\) around the perforation. Therefore, substituting Eq. (10) into Eq. (14) yields the stress field distribution around the perforated hole as shown in Eq. (15).

$$\left\{ \begin{gathered} \begin{array}{*{20}c} {\sigma _{{rp}} = P_{w} } \\ \end{array} \hfill \\ \sigma _{{\varphi p}} = - P_{w} + \left( {1 - 2\cos 2\varphi } \right)\left[ { - P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) - \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\cos 2\theta } \right] \hfill \\ + \left( {1 + 2\cos 2\varphi } \right)\left[ {\sigma _{z} - 2\mu \left( {\sigma _{x} - \sigma _{y} } \right)\left( {\frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta } \right] + 4\sin 2\varphi \left[ {\tau _{{zx}} \sin \theta - \tau _{{zy}} \cos \theta } \right] \hfill \\ \left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) \hfill \\ \sigma _{{zp}} = P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 - \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) + \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }} - \frac{{4R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta ~~ \hfill \\ - 2\mu \cos 2\varphi \left[ { - P_{w} \frac{{R_{{hw}} ^{2} }}{{r^{2} }} + \frac{{\sigma _{x} + \sigma _{y} }}{2}\left( {1 + \frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right) - \frac{{\sigma _{x} - \sigma _{y} }}{2}\left( {1 + \frac{{3R_{{hw}} ^{4} }}{{r^{4} }}} \right)\cos 2\theta - \sigma _{z} } \right. \hfill \\ \left. { + 2\mu \left( {\sigma _{x} - \sigma _{y} } \right)\left( {\frac{{R_{{hw}} ^{2} }}{{r^{2} }}} \right)\cos 2\theta } \right] \hfill \\ \tau _{{r\varphi p}} = \tau _{{rzp}} = 0 \hfill \\ \tau _{{\varphi zp}} = 2\tau _{{r\theta h}} \sin \varphi \hfill \\ \end{gathered} \right.$$
(15)

Since \({{\uptau}}_{r\phi p}={{\uptau}}_{rzp}=0\), \({\sigma}_{\text{r}\text{p}}\) was a principal stress on the face and was not a minimum principal stress. However, the circumferential stress \({{\upsigma}}_{\phi\text{p}}\) and the axial stress \({{\upsigma}}_{\text{z}\text{p}}\) in the perforation were not the principal stresses on the \(\phi p-zp\) plane. According to the composite stress theory, two mutually perpendicular principal stresses at any point on the \(\phi p-zp\) plane can be obtained, as shown in Eq. (16).

$$\left\{ {\begin{array}{*{20}l} {\sigma _{1} = \sigma _{{rp}} } \hfill \\ {\sigma _{2} = \frac{1}{2}\left[ {\left( {\sigma _{{\varphi p}} + \sigma _{{zp}} } \right) + \sqrt {\left( {\sigma _{{\varphi p}} - \sigma _{{zp}} } \right)^{2} + 4\tau _{{\varphi zp}}^{2} } } \right]} \hfill \\ {\sigma _{3} = \frac{1}{2}\left[ {\left( {\sigma _{{\varphi p}} + \sigma _{{zp}} } \right) - \sqrt {\left( {\sigma _{{\varphi p}} - \sigma _{{zp}} } \right)^{2} + 4\tau _{{\varphi zp}}^{2} } } \right]} \hfill \\ \end{array} } \right.$$
(16)

Calculation model of hydraulic fracture initiation pressure and initiation location for perforation fracturing

According to Eq. (15) and Eq. (16), the principal stresses \({\sigma}_{1}\), \({\sigma}_{2}\)and \({\sigma}_{3}\) of the perforation borehole, combined with the five-rock damage criteria selected at the end of section Introduction, can calculate the fluid pressure \({p}_{w}\) at different perforation hole cross-sections in the direction of the perforation length to reach the critical state of each damage criterion. This critical fluid pressure \({p}_{w}\) was considered to be the fracture initiation pressure. The location of the first perforation section to reach the damage condition is the corresponding crack initiation location. As the critical fluid pressure required for each perforation section to reach the damage state is different, according to the “barrel-effect” principle, a hydraulic fracture will be produced when the fluid pressure in the perforation comes to the minimum critical fluid pressure required in the whole perforation sections. The fluid pressure \({p}_{i}\) was the fracture initiation pressure for the perforation fracturing, and the location of the damaged perforation section is the fracture initiation location corresponding to the fracture initiation pressure.

In this calculation model, the theoretical calculation process generated two variables (fluid pressure in the perforation and the distance between the calculation section and the horizontal wellbore). The calculation process was carried out using a trial method of progressively increasing fluid pressure \({p}_{w}\) in the perforation, as shown in the following steps:

  1. (1)

    Determine the primary data, such as in-situ ground stress, the orientation of horizontal wellbore and perforation borehole, porosity and pore pressure. According to Eqs. (7), (10), (15) and (16) jointly to obtain the principal stresses \({\sigma}_{1}\), \({\sigma}_{2}\), \({\sigma}_{3}\) on the wall surface of the perforation borehole;

  2. (2)

    The parameters such as the principal stresses applied to the wall of the perforation borehole and the physical parameters of the rock (tensile strength, Poisson’s ratio, etc.) were brought into the rock damage criterion;

  3. (3)

    Defining the horizontal well radius, perforation length, the distance between the perforation section to be calculated and the axis of the horizontal wellbore. An initial value \({P}_{w}\) was preset for the fluid pressure in Eq. (16) and calculated whether the perforation hole section reached a destruction state according to the rock damage criterion;

  4. (4)

    \({P}_{w}\) that satisfied the damage state was the critical fluid pressure for the calculated perforation cross-section;

  5. (5)

    If the initial value of \({P}_{w}\) did not satisfy the critical conditions of the rock damage criterion, the fluid pressure value in Eq. (16) needed to be adjusted to \({P}_{w}+\nabla p\). Then, repeat steps (2) to (4) until the given fluid pressure value (\({P}_{w}+\nabla p\)) brought the calculated perforation cross-section to a state of destruction;

  6. (6)

    By increasing \({P}_{w}\) until the damage criterion was satisfied, we considered the corresponding fluid pressure \({P}_{w}\) as the initiation pressure \({P}_{i}\) and the corresponding cross-section as the initiation location.

Based on the critical fluid pressure at which each perforation cross-section reaches damage conditions, a curve of the cross-section location and critical fluid pressure curve can be plotted, where the lowest value of critical fluid pressure was the required initiation pressure \({P}_{i}\) and the corresponding cross-section was the fracture initiation location. The calculation process was shown in Fig. 3.

Fig. 3
figure 3

Calculation process for initiation pressure and location of hydraulic fractures for horizontal well injection fracturing.

Full size image

Theoretical solution of fracture initiation pressure and initiation location for perforation fracturing of oil shale

The physical parameters of the oil shale sample and the perforation borehole parameters impact the damaged criteria. Thus, the parameters used in calculating each damaged criterion need to be determined according to the physical conditions of the oil shale, the surrounding pressure conditions and the perforation arrangement to maximise the authenticity and validity of the theoretical calculations.

In the validation model of this paper, the horizontal wellbore diameter in the oil shale sample was 12 mm, and the length of the perforation borehole was 30 mm. Therefore, the calculated radius (\(\mathbf{r}\)) of \(6\text{m}\text{m}\le \text{r}<30\text{m}\text{m}\) could be obtained. The corresponding θ values were 90° and 0° when the perforation direction was the direction of maximum geo-stress and the direction of maximum horizontal ground stress, respectively. The maximum geo-stresses (\({\sigma}_{v}\)) selected for the theoretical model was 10Mpa, and the maximum (\({{\upsigma}}_{\text{H}}\)) and minimum (\({{\upsigma}}_{h}\)) horizontal geo-stresses were 7 MPa and 4 MPa, respectively. Furthermore, the mechanical parameters of oil shale were shown in Table 1. Based on the above-calculated parameters, the critical fluid pressure \({p}_{w}\) could be plotted for different perforation cross-sections with variable damage criteria, as shown in Fig. 4.

Table 1 Mechanical parameters of oil shale sample.
Full size table
Fig. 4
figure 4

Fracture pressure curves calculated for each fracture criterion at different perforation cross-sections ((a) θ=90°; (b) θ=0°).

Full size image

Experimental verification of theoretical solutions for fracture initiation pressure and initiation location for perforation fracturing

In this section, four hydraulic fracturing experiments were designed to verify the accuracy of the theoretical calculation method proposed in this paper, as shown in Table 2. The natural oil shale specimens were mined from the outcrop of the Lower Cretaceous Dalazi Formation at the Luozigou basin of WangQing county in Jilin province, China. Diamond abrasive wire was employed to cut the samples and remove the weathering layer from the surface, as shown in Fig. 5-(a). To prevent stress concentration on the surface of the specimen, cement paste was applied to wrap the sample. The overall dimensions of the specimen before the fracturing experiment is 200 mm*200 mm*200 mm to accommodate the size of the fracturing cabin, as depicted in Fig. 5-(b).

Fig. 5
figure 5

The shape of the oil shale specimens (a). Oil shale samples with weathered layers removed; (b) Cement-covered oil shale sample to be fractured; ).

Full size image

The burial depth of the oil shale samples ranges from 470 m to 500 m underground. The horizontal well inside the samples was always parallel to the minimum horizontal stress in all experiments. Here, the horizontal wellbore was simulated by a unique stainless-steel tube. Unlike previous studies on the influence of perforation, a small hole was drilled perpendicular to the centre borehole to simulate the perforation in this paper.

Table 2 Validation experimental program for perforated fracturing of oil shale samples.
Full size table

The experiments were carried out using a true triaxial hydraulic fracturing system, as shown in Fig. 6, which consists of a true triaxial pressurisation fracturing cabin, a constant velocity and constant pressure pump and a data acquisition and control system. The overall dimension of the true triaxial chamber was 2850*1520*1520 mm, and the internal fracturing cabin was 200*200*200 mm. Three pressure platens independently applied the in-situ stresses to the samples along the X-, Y-, and Z-axes. The platens can provide a maximum pressure of up to 30 MPa. The fracturing fluid was injected by a high-pressure pump which can be artificially selected to provide constant fluid pressure or a stable flow rate. The injecting equipment has a maximum volume of 250 ml, and the maximum injection pressure and flow rate of fracturing fluid were 70 MPa and 0.1-100 ml/min, respectively.

Fig. 6
figure 6

True triaxial hydraulic fracturing apparatus.

Full size image

Result and discussion

According to Fig. 4, each curve in this diagram represented the initiation pressure calculated for different perforation cross-sections along the perforation length by variable damage criteria. The fracture initiation pressure values calculated for each criterion increase as the perforation length increases. Based on the “barrel effect”, the lowest point of the fracture initiation pressure curve in Fig. 4 was the fracture initiation pressure value pi of the perforation fracturing for different damage criteria. From Fig. 4, we considered that the fracture initiation pressure for each damage criterion during the perforation fracturing process was minimised at the intersection of the perforation borehole and the horizontal wellbore. According to the calculation method proposed in this paper, the theoretically calculated value of the fracture initiation location for perforation fracturing of oil shale should be located at the intersection of the perforation borehole and the horizontal wellbore.

Perforation fracturing of oil shale specimens was carried out according to the protocol shown in Table 1, and the fracture morphology on the surface of the models after fracturing was shown in Fig. 7.

Fig. 7
figure 7

Fractures distribution on the surfaces of oil shale samples.

Full size image

As shown in Fig. 7, the different fracturing parameters significantly affected the fracture morphology on the surface of the oil shale samples. To explore the location of the fracture initiation and the extension behaviour of the fractures by perforation fracturing, CT scan technology was performed on the oil shale samples from the above fracturing experiments and the fracture network within the models was reconstructed using the software Avizo 2019. The inversion of the CT scan data from the fracturing experiment clearly showed the location of the hydraulic fracture initiation and the intersecting extension pattern between fractures, as shown in Fig. 8.

Fig. 8
figure 8

Local enlargement of the intersection of the horizontal wellbore and the perforation borehole for different experiments inverted by software Avizo 2019(a Test 1; b Test 2; c Test 3; d Test 4).

Full size image

As shown in Fig. 8, the hydraulic fracturing results of the perforation fracturing showed that the hydraulic fractures were initiated at the location between the perforation borehole and the horizontal wellbore. Consistent with the theoretically calculated results in Sect. 3.1, the hydraulic fractures all started near the intersection of the perforation borehole and the horizontal wellbore. The pumping pressure curve recorded by the actual laboratory experiments was conducted in Fig. 9.

Fig. 9
figure 9

Pressure-time curve for Test 1–4, showing various pressures during fracturing test.

Full size image

The results of the hydraulic fracture initiation pressure calculations for perforation fracturing based on different damage criteria were shown in Tables 3 and 4 below.

Table 3 Fracture initiation pressure values calculated for different damage criterion (θ = 90°).
Full size table
Table 4 Fracture initiation pressure values calculated for different damage criterion (θ = 0°).
Full size table

In Test 2, the perforation direction was in the intermediate geo-stress. The corresponding fracture initiation pressure was 10.1 MPa, similar to the calculated fracture initiation pressure value based on the Mohr-Coulomb damage criterion of 10.114 MPa, as shown in Table 4. We considered that the fracture morphology inside the specimen was a single double-wing-shaped transverse hydraulic fracture, with the formation of the hydraulic fracture dominated by the tensional damage of the oil shale matrix as the fracturing fluid continued to be injected.

When the perforation borehole was in the direction of maximum geo-stress (vertical stress direction), the experimentally measured fracture initiation pressure was 7.3 MPa, basically consistent with the calculated fracture initiation pressure of 7.544 MPa based on the Mohr-Coulomb criterion, as shown in Table 3. We believed that the induction and communication of the perforation borehole during the hydraulic fracturing contributed to the generation of branching and laminated fractures. Finally, a fracture network dominated by shear damage was formed by the internal fluid and surrounding external pressure. Furthermore, when hydraulic fracturing was carried out at very high fracturing fluid viscosities, the experimentally measured fracture initiation pressure was 15.1 MPa, which is generally consistent with the fracture initiation pressure of 15.423 MPa calculated based on the Drucker-Prager criterion, as shown in Table 3. The analysis suggested that when high-viscosity fluids were used for fracturing, extremely high fluid pressure would be generated inside the hydraulic fracture, resulting in a large additional stress in the direction of maximum horizontal geo-stress (\({\sigma}_{2}\) direction). As the \({\sigma}_{2}\) increased, the hydraulic fracture extension process can no longer ignore the effect of \({\sigma}_{2}\). The Drucker-Prager criterion in “Fundamental assumptions” section of this paper considers the effect of the intermediate principal stress \({\sigma}_{2}\). Therefore, when hydraulic fracturing was carried out using high-viscosity fracturing fluids, the Drucker-Prager criterion was more accurate for predicting the initiation pressure.

Conclusions

In this study, a novel model for calculating fracture initiation pressure and fracture initiation location for perforation fracturing was developed, and the accuracy of the theoretical model was verified by the true triaxial hydraulic fracturing experiments. The main findings are as follows.

  1. (1)

    A theoretical calculation model of fracture initiation pressure and fracture initiation location for perforation fracturing was developed based on clarifying the stress field distribution around the horizontal wellbore and the perforation borehole. The model calculations indicated that perforation fracturing of the oil shale started at the intersection of the perforation borehole and the horizontal wellbore. However, variable damage criteria correspond to different initiation fracturing pressures.

  2. (2)

    Hydraulic fracturing experiments on oil shale samples containing perforation borehole structures were implemented to verify the accuracy of the theoretical model. By magnifying the local CT inversion image, it can be found that the oil shale perforation fractures started at the intersection of the perforation borehole and the horizontal wellbore, which was highly consistent with the calculation results of the theoretical model.

  3. (3)

    Comparing the initiation pressure of theoretical and experimental values, we found that the theoretical fracture initiation pressure calculated by the Mohr-Coulomb damage criterion agreed well with the experimental values when the perforation borehole was in the direction of maximum horizontal geo-stress, and when the perforation direction was parallel to the maximum geological stress. For perforation fracturing with high-viscosity fracturing fluid, the theoretical fracture initiation pressure calculated by the Drucker-Prager criterion closely agreed with the experimental values.