Assessment of landslide susceptibility in watersheds during extreme rainfall using a complex network of slope units

Abstract

Rainfall-induced landslides present significant challenges in regional landslide prediction and management. Traditional regional landslide susceptibility assessment models often evaluate individual units in isolation, neglecting the hydrological connections between slope units within a watershed. This approach fails to account for the occurrence of landslides in groups. To address this limitation, we propose the “Network-based Landslide Susceptibility Assessment Model” (NLSAM). This model incorporates the impact of water transfer between slope units using a complex network and integrates a physically-based model to account for interactions between slopes. In this study, we applied the NLSAM to a watershed in Fuyang District, Zhejiang Province, China. Experimental results show that extreme rainfall increases water transfer between slope units, destabilizing more slopes and elevating landslide susceptibility. Validation results demonstrate that the recall of NLSAM is 0.93, confirming the model’s ability to identify group-occurring landslides. NLSAM captures rainfall propagation paths and quantifies their impacts, assisting decision-makers in formulating more effective management strategies.

Introduction

The occurrence of landslides frequently leads to severe loss of life and destruction of public and private property^1,2. Rainfall is one of the main factors triggering landslides³. Global climate change has led to an increase in the frequency and intensity of extreme rainfall events, exacerbating the risk of rainfall-induced landslides⁴. Assessing regional landslide susceptibility under different rainfall conditions to aid government disaster prevention and mitigation initiatives is a significant focus in landslide research.

Regional landslide susceptibility assessment is a way to obtain the landslide susceptibility area of a certain place for the management and application of related departments^5,6. Four prevalent regional landslide susceptibility models exist: expert-based models^7,8,9, physically-based models^10,11,12, statistical models, and machine learning models^13,14. These models use raster units or slope units as assessment units^15,16. The expert-based model assesses the landslide susceptibility of the study area by obtaining the relevant variables of the study area through the assessment of the experts, but it is only localizable and cannot be generalized to other study areas⁸. Statistical models and machine learning models use historical landslide datasets to analyze the factors that influence landslides. While they can produce more precise assessment results, they neglect the intricate physical process that occurs during landslide movement and present ambiguity and uncertainty^17,18. In contrast to the above methods, physical models can take into account the geotechnical characteristics of landslides and usually quantify slope stability by combining infinite slope stability methods and hydrological assumptions¹². Existing physical models for rapid assessment of landslide susceptibility in a region include SHALSTAB¹⁹, SINMAP²⁰, FSLAM¹², and others. Among them, the “Fast Shallow Landslide Assessment Model” (FSLAM) considers both lateral and vertical groundwater flow, which better reflects the mechanism of landslide occurrence¹². However, these physical models assess individual slope units in isolation and only consider the physical properties and hydrological characteristics of individual slope units, while ignoring the hydrological connections between slope units.

The current study is primarily a qualitative analysis of a specific study area for group-occurring landslides. Rainfall is identified as the primary factor contributing to group-occurring landslides²¹. Furthermore, the aggregation of depressions may be an additional significant factor that influences the initiation of landslides²². This implies that the hydrological conditions of adjacent slopes, such as infiltration or runoff, can be influenced by groundwater flow caused by rainfall running between slopes, which in turn affects the stability of the surrounding slopes. Conversely, physical models like FSLAM are incapable of capturing the impact of the aggregation of depressions on the landslide susceptibility of each slope unit. Consequently, they may not help identify group-occurring landslide phenomena.

To reflect the hydrological connections between slope units, this work uses complex networks to model their relationships within a watershed. Complex networks are abstractions that describe the interactions and correlations between units in a system^23,24,25, which helps us understand the hydrological flow and rainfall distribution among slope units.

This paper proposes the “Network-based Landslide Susceptibility Assessment Model” (NLSAM) to quantify the impact of physical interactions among slope units on landslides. NLSAM models the transfer of water between slope units using a complex network, where rainfall within a watershed is represented as transmission across slope units. The model improves upon FSLAM by incorporating surface runoff, infiltration, and slope saturation to evaluate the water flow spread and its effect on landslide susceptibility. Using a watershed in Fuyang District, Zhejiang Province, it can be found that extreme rainfall enhances water flow transfer between slope units, causing more slope units to become unstable and increasing the susceptibility of landslides in the watershed’s slope system. It also illustrates the necessity of considering the hydrological connections under extreme rainfall conditions.

Study area

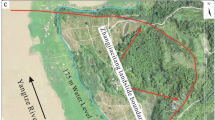
Zhejiang Province, situated on the southeast coast of China, is characterized by its intricate topography, extensive mountains, and hills. It is susceptible to extreme rainfall events due to its geographic location and monsoon climate, which is marked by frequent typhoon disasters and heavy and concentrated rainfall. In mountainous and hilly regions, extreme rainfall events can result in group-occurring landslides. Therefore, a watershed unit in Zhejiang Province was selected as our case study. The watershed is located in the southeastern part of Fuyang District, Hangzhou City, Zhejiang Province, near 29°52’52” N to 29°55’41” N and 120°00’32” E to 120°02’38” E. It is a catchment unit surrounded by ridgelines, covering an area of about 10 km², with a peak elevation of 623 m and a slope range of 0 ~ 44°.

On July 22, 2023, Fuyang District, Zhejiang Province, was hit by an extreme rainstorm that resulted in more than 145 shallow landslides in a 20-square-kilometer mountainous area of Fuyang District, including 60 landslide events that occurred in the study area (Fig. 1).

Fig. 1

Overview of the study area.

Methods and data

This paper proposes a landslide susceptibility assessment model considering water flow transfer between slopes in a watershed. We divided each slope in the watershed into slope units, established a complex network based on the flow relationship between water flows among the slope units, and assessed the susceptibility of the slope units based on the cascade relationship among the nodes and FSLAM. Figure 2 briefly describes the main steps of our model.

Fig. 2

The steps of the study.

Establishment of a complex network based on slope units

A slope unit is a topographic unit defined by a watershed line (ridge line) and a catchment line (valley line) (Fig. 3 (A), (B)). A watershed unit, also known as a catchment unit, is a river catchment region surrounded by watershed lines²⁶. This study was conducted in a watershed unit, and we extracted slope units within the watershed unit using hydrologic analysis (Fig. 3 (C)). Figure 3 illustrates a schematic diagram of the slope units and the results of the actual delineation of the slope units.

Rain falls on each slope unit in the watershed. If the area bordering a slope unit and a neighboring slope unit is depressional (i.e., valley area), uninfiltrated rainfall forms surface runoff on the surface of the slope unit into the depressions, and water flows from the low-lying areas infiltrate into the neighboring slope units through groundwater. Considering the relationship between slope units in flow transfer, we extracted all the depressions (i.e., the river network with flow 0) in the study area (brown connecting lines in Fig. 3 (D)), cut the river network with slope units to obtain the catchment point of the slope units on the river network (blue nodes in Fig. 3 (D)), and connected the slope units that have the same catchment point to obtain the actual catchment network of the slope units.

To clearly represent the relationship between slope units, a schematic diagram of the network construction rules is given (Fig. 3 (E)). In the figure, nodes A, B, C, and D represent the slope units, and nodes a, b, and c represent the catchment points of the slope units on the river network. The network constructed in this study uses slope units as nodes, and if a portion of the water flow generated by both slope unit A and slope unit C goes to the catchment point a, then a connecting edge is established between A and C. The physical significance of this connecting edge is that the water flow generated by slope unit A affects the groundwater elevation in slope unit C. At the same time, the water flow generated by slope unit C affects the groundwater elevation in slope unit A. Similarly, node A and node D, as well as node B and node D, also produce connected edges. Under this rule, complex networks based on slope units can be created within a watershed unit.

Fig. 3

(A) Profile of slope units (dashed lines show locations of ridges and valleys). (B) Plan view of slope units (blue line for ridgeline, orange line for valley line, and the enclosed area represents the slope unit). Created using ArcGIS Pro 3.4 (https://www.esri.com/en-us/arcgis/products/arcgis-pro), with satellite imagery provided by the software’s default base map (https://t0.tianditu.gov.cn/img_w/esri/wmts), at image level 16 with a spatial resolution of 1.19 m. (C) Schematic of slope unit delineation in a watershed. (D) Schematic diagram of a stream network with a flow of 0 (the brown line in the diagram represents a stream network with a flow of 0, and the blue point represents the intersection of a slope unit with that network, i.e., the slope catchment). (E) Complex network construction method depicting water flow transfer relationships between slope units (nodes A, B, C, D represent slope units, and nodes a, b, c represent slope catchments).

Overview of FSLAM

The landslide susceptibility assessment in this paper is mainly realized based on the results of the “Fast Shallow Landslide Assessment Model” (FSLAM) for slope units¹². FSLAM combines geotechnical modeling with groundwater modeling, which not only makes the model more interpretable but also takes into account the effects of hydrological conditions and rainfall on slope stability. At present, many scholars have used FSLAM to assess regional landslide susceptibility. Guo et al. used FSLAM to assess landslide susceptibility in southeastern China and found that the accuracy of FSLAM was higher than TRIGRS²⁷. Cui et al. realized a more accurate and efficient landslide susceptibility mapping by coupling FSLAM with a first-order reliability method²⁸.

The main assumption of FSLAM is to consider rainfall as a landslide-triggering mechanism, and the model consists of 2 main components, including a geotechnical model and a groundwater model.

FSLAM uses the infinite slope theory as the basis of the geotechnical model, and the calculated factor of safety is the ratio of the slip resistance to the downward sliding force on the assumed sliding surface of the slope body. Consequently, the calculation results have a more reliable physical interpretation compared to the data-driven model. The following equation can calculate the safety coefficient FS of a slope:

$$\:\begin{array}{c}FS=\frac{c}{g{\rho\:}_{s}zcos\theta\:sin\theta\:}+\left(1-\left(\frac{h}{z}\right)\left(\frac{{\rho\:}_{w}}{{\rho\:}_{s}}\right)\right)\left(\frac{tan\phi\:}{tan\theta\:}\right)\end{array}$$

(1)

Where $\:g$ (m/s²) = 10 is the gravity, $\:{\rho\:}_{s}$ (kg/m³) is the density of saturated soils, $\:{\rho\:}_{w}$ (kg/m³) is the density of water, $\:\theta\:$ (◦) is the terrain slope, $\:h$ (m) and $\:z$ (m) are respectively the water table depth and sliding soil depth, $\:\phi\:$ (◦) denotes the internal friction angle of the soil shear strength, and $\:c$ (kPa) denotes total cohesion of the soil shear strength, which is composed of the effective cohesion $\:{c}_{s}$ (kPa), and root cohesion $\:{c}_{r}$ (kPa), such that $\:c={c}_{s}+{c}_{r}$. In this model, the average saturation of the soil can be expressed as $\:\frac{h}{z}$, which is always numerically less than or equal to 1 (numerical equality of 1 indicates saturation of the soil). Specifically, it should be $\:\text{m}\text{i}\text{n}(\frac{h}{z},1)$.

The groundwater model determines groundwater levels by analyzing rainfall infiltration on various time scales. Antecedent rainfall is indicative of effective rainfall infiltration on medium to long-term time scales, as per the “water balance” theory, while event rainfall represents short-term rainfall replenishment of the groundwater level. The specific calculation formula is as follows:

$$\:\begin{array}{c}h={h}_{a}+{h}_{e}\end{array}$$

(2)

Where $\:{h}_{a}$ (m) is the pre-existing groundwater level, $\:{h}_{e}$ (m) is the height of the groundwater level due to vertical rainfall.

Considering the soil porosity, $\:{h}_{e}$ (m) can be determined according to the following equation:

$$\:\begin{array}{c}{h}_{e}=\frac{{q}_{e}}{n}\end{array}$$

(3)

Where $\:{q}_{e}$ (m) is the effective infiltration of rainfall $\:Pe$ from the induced event rainfall, $\:n$ is the porosity of the soil.

To convert the actual rainfall $\:Pe$ into effective groundwater recharge $\:{q}_{e}$, this paper adopted the event-oriented SCS-CN model proposed by the United States Department of Agriculture (USDA)²⁹. The model can calculate surface runoff associated with a rainstorm event, or it can calculate rainfall infiltration using implicit formulas, as described below:

$$\:\begin{array}{c}qe=Pe-\frac{{\left(Pe-\left(\frac{5080}{CN}-51\right)\right)}^{2}}{Pe+4\left(\frac{5080}{CN}-51\right)}\end{array}$$

(4)

Where $\:CN$ is the runoff curve number, which reflects the surface and soil characteristics of the pre-rainfall area about factors such as slope, land use type, soil type, and pre-existing soil moisture.

FSLAM can obtain the FS value of each slope unit. A lower FS value indicates that the slope unit is more unstable and more susceptible to landslides. Since FS is the ratio of the slip resistance to the downward sliding force on the hypothetical sliding surface of a slope unit, an FS of less than 1 means that a landslide has occurred in that slope unit.

The model (NLSAM) based on complex networks and FSLAM

Figure 4 shows the whole process of rainfall transfer between slope units in the watershed. When a slope unit is affected by rainfall, not only will vertical infiltration occur (Eq. 3), but surface runoff will also form and flow into the depression between the slope units (Eq. 5). This water flow will then affect the neighboring slope units through lateral infiltration (Eq. 6). If the neighboring slope units are not saturated at this time, the groundwater level in the neighboring slope units will rise, resulting in a decrease in FS for them. If the neighboring slope units are saturated, FS for that node does not change. The water flow in the depression will be passed along the network among the nodes (Eqs. 7-8) until the water flow is 0 or all the surrounding slope units are saturated at the end of the pass. We refer to the model of calculating FS of a slope unit by combining complex networks and synthesizing (Eqs. 1- 8) as the “Network-based Landslide Susceptibility Assessment Model” (NLSAM).

The other equations needed in the process of Fig. 4 are described below. First is the surface runoff calculation for Step C. Like the calculation of effective infiltration for induced event rainfall, the SCS-CN model is used in this paper.

$$\:\begin{array}{c}R=\frac{{\left(Pe-Ia\right)}^{2}}{Pe-Ia+s}\end{array}$$

(5)

Where $\:Pe$ (mm) is rainfall, $\:Ia$ is the amount of pre-existing losses, usually taken as 0.2S, and $\:S$ is infiltration, calculated as $\:S=\frac{25400}{CN}-254$.

In Step E2, The experiential equation is employed to determine the increase in groundwater elevation at adjacent nodes as a result of the infiltration of water flow in depressions.

$$\:\begin{array}{c}\varDelta\:h=Kt\end{array}$$

(6)

Where $\:K$ is the soil percolation coefficient, and $\:t$ is the rainfall time.

In Step F, the calculation of water flow transferred from the depressions varies for the source node, where surface runoff originates, compared to the other nodes that receive the water flow.

For the first type of node, the flow transferred by the node to its neighboring nodes is calculated as follows.

$$\:\begin{array}{c}{W}_{{i}_{0}m}=\frac{{R}_{{i}_{0}}{A}_{{i}_{0}}}{{N}_{{i}_{0}}}\end{array}$$

(7)

The node $\:{i}_{0}$ is the rain-affected node, node m is a neighboring node of $\:{i}_{0}$, $\:{W}_{{i}_{0}m}$ is the water flow accumulated on the edge connecting node $\:{i}_{0}$ and node m, $\:{R}_{{i}_{0}}$ is the surface runoff of node $\:{i}_{0}$, $\:{A}_{{i}_{0}}$is the area of node $\:{i}_{0}$, and $\:{N}_{{i}_{0}}$ is the degree of node $\:{i}_{0}$. If the water flow generated by the source node is not 0 after passing through the neighboring nodes, the water flow will flow along the network to other nodes.

For the second type of node, the flow of water from the non-initial neighbor node i to the node i’s neighbor node j is calculated as follows.

$$\:\begin{array}{c}{W}_{ij}=\left\{\begin{array}{c}\frac{{W}_{xi}-\varDelta\:{h}_{i}{A}_{i}\:}{{N}_{i}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{h}_{i}}{{z}_{i}}<1\\\:\frac{{W}_{xi}}{{N}_{i}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{h}_{i}}{{z}_{i}}\ge\:1\end{array}\right.\end{array}$$

(8)

Where $\:{W}_{xi}$ is the flow that node $\:i$ receives from other nodes, $\:\varDelta\:{h}_{i}{A}_{i}$is the flow absorbed by node $\:i$.

Fig. 4

The process of rainfall transfer between slope units and the flowchart of landslide susceptibility calculation.

Data preparation

The summary of input data required for the model is shown in Table 1. The terrain slope ($\:\theta\:$) and area (A) of each slope unit were generated from DEM data. The saturated soil density ($\:{\rho\:}_{s}$), soil porosity (n), angle of internal friction ($\:\phi\:$), and cohesion of the soil matrix ($\:{c}_{s}$) of each slope unit were obtained from SOIL data. Soil root cohesion ($\:{c}_{r}$) for each slope unit was generated by combining LULC data. CN data for each slope unit were generated from SOIL and LULC data. The pre-existing groundwater level ($\:{h}_{a}$) for each slope unit was obtained from the average of the day-by-day soil moisture for June 2023 in the assessment area. The soil depth (z) for each slope unit was generated from Soil depth data.

Table 1 Summary table of input data.

Experimental analysis

Complex network construction

In this paper, slope units were divided in the study area (Fig. 5 (A)), and a complex network describing the relationships among slope units was established (Fig. 5 (B)). The network consists of 125 nodes of slope units with 311 connected edges. The network can be represented as $\:G=(V,E)$. $\:V=\{{v}_{1},{v}_{2},\dots\:,{v}_{125}\}$ denotes the nodes of the network, which are the 125 slope units divided in the watershed. $\:E=\{{e}_{1},{e}_{2},\dots\:,{e}_{311}\}$ is the connecting edges of the network, that represent the transfer of water flow between nodes.

Figure 5 (C) shows the degree distribution of the complex network constructed in the study area of this paper, which can be seen to approximate the Poisson distribution, indicating that it is a random network. The network has a small average path length(6.08) and moderate clustering coefficient(0.52). We constructed a random network of the same size as the current network in order to investigate the type of network. The average clustering coefficient of the random network was approximately 0.04, and the average shortest path length was 3.20. The network in the study area exhibits the typical characteristics of a small-world network, with significantly higher clustering coefficients and slightly longer average path lengths than the random network.

The study area parameters required for the model were extracted from this paper’s study area dataset for the following calculations. The details of the study area extraction parameters are shown in Supplementary Table S1.

Fig. 5

(A) Results of the division of slope units in the study area. (B) Complex network map of the study area. (C) Complex network degree distribution in the study area.

Localized rainfall attacks

To analyze the cascading process among the nodes due to the diffusion of water flow, we attacked a single node in the network and observed the change in the size of the impacted nodes and their FS. This paper randomly chose slope unit 104 within the watershed. The model parameters were derived using the research area’s dataset, and the node was subjected to rainfall intensities of 50 mm/h and 100 mm/h for 48 h, respectively, to evaluate the variations in water flow and landslide susceptibility at all nodes under these conditions. The impact of the attack on node 104 on the watershed is shown in Fig. 6, with the blue area showing the spread of the rainfall through the network, and the red area showing the unstable slopes. It is evident that when rainfall intensity escalated, the extent of the water flow’s influence within the network expanded. When the rainfall intensity at the node was 50 mm/h (Fig. 6 (A)), the water flow spread from the starting node 104 to the eight nodes 102, 106, 101, 89, 92, 91, 95, and 107. When the rainfall intensity at the node was 100 mm/h (Fig. 6 (B)), the water flow spread from the beginning node 104 to the 16 nodes 102, 106, 101, 89, 92, 91, 95, 107, 103, 75, 77, 81, 85, 86, 88, 96. Meanwhile, the number of unstable slopes escalated with the augmentation of rainfall intensity. The unstable slopes changed from 4 nodes (Fig. 6 (A)) of 104, 106, 95, 107 to 5 nodes (Fig. 6 (B)) of 104, 106, 95, 107, 91.

Fig. 6

(A) Rainfall attack on node 104 with 48 h rainfall intensity of 50 mm/h. (B) Rainfall attack on node 104 with 48 h rainfall intensity of 100 mm/h. (The green node color is darker, which means the lower FS of the node, the red area means the slope units have been destabilized, and the blue area is the area where the water flows through)

The following is a specific analysis of the changes in FS for the rainfall directly affecting node 104 and the rainfall indirectly affecting node 107. Figure 7 shows the variation of FS of attacking node 104 and its adjacent node 107. With the rainfall attack on node 104, both the slope units’ FS decreased with increasing rainfall duration. Node 104 had a faster decrease in FS in the early stage and a slower decrease in FS in the later stage due to the influence of the vertical flow of rainfall. Node 107 had a slow decrease in FS in the early stages and a faster decrease in FS in the later stages due to groundwater supplements from lateral infiltration of water flow. In addition, FS of the nodes decreased with the increase in rainfall intensity. With the same rainfall duration, the amount of change in FS at node 104 was small and decreased slowly, while the amount of change in FS at node 107 was large and decreased significantly. The lateral infiltration of water flow between the nodes at subsequent stages had a more significant impact on the FS of the nodes than the vertical infiltration of rainfall. This shows the importance of considering the relationship between the slopes.

Fig. 7

Variation of FS with rainfall duration and intensity at nodes 104 and 107.

Global rainfall attacks

In reality, rainfall events are not limited to certain slope units but transpire across a broader region. This research analyzed the watershed for global rainfall to get the susceptibility assessment results for the watershed. Firstly, three rainfall attacks with 24-hour rainfall intensities of 10 mm/h, 20 mm/h, and 50 mm/h were carried out in the region respectively. The results and distribution of landslide susceptibility assessment for each node were obtained by calculating with FLSAM and NLSAM (Fig. 8 (A)). When the rainfall intensity was 10 mm/h, it was clear that the two models, considering and without considering network structure, had no effect on regional landslide susceptibility. For rainfall intensities of 20 mm/h and above, FS calculated using NLSAM was significantly smaller than those calculated using FSLAM for slope units. This suggests that the rainfall intensity must reach a certain threshold to significantly affect the FS of the nodes, at which point considering the network structure becomes necessary.

To investigate the critical value of daily rainfall in the region, this paper calculated FS for each slope unit for 24 h of the rain attack for 10 mm/h-20 mm/h rainfall intensities. Slope units with FS less than 1 were counted as a percentage of the total number of nodes in the watershed using the two models described above. The calculation results are shown in Fig. 8 (B). For rainfall intensities less than 15 mm, there was little difference between the two methods. When rainfall intensity was greater than 15 mm, the effect of using NLSAM on watershed landslide susceptibility was more significant than that of FSLAM. The cascading effect of the network structure on FS of slope units was shown. It illustrates that the effect of disaster transfer between nodes is more evident under extreme rainfall.

Fig. 8

(A) Boxplot of FS calculated using FSLAM and NLSAM for slope units in the watershed under different rainfall intensities. (B) Plot of the percentage of unstable landslides under different rainfall intensities for both methods.

Comparative analysis of the results for global rainfall

To reflect the influence of the rainfall threshold and network structure on the assessment results, we selected rainfall with intensities of 10 mm/h and 20 mm/h to attack the watershed for 24 h. FSLAM and NLSAM were used to assess the landslide susceptibility in the study area (Fig. 9).

Comparing Fig. 9 (A) and (C), the number of unstable slopes increased from 36 to 40 when FSLAM was used to attack the watershed for 24 h with rainfall intensities of 10 mm/h and 20 mm/h. Comparing Fig. 9(B) and (D), the number of unstable slopes increased from 36 to 98 when NLSAM was applied to the watersheds for 24 h with rainfall intensities of 10 mm/h and 20 mm/h. The number of unstable slopes increases as the intensity of rainfall increases. The consideration of water transfer between slope units results in a significant decrease in FS, which in turn leads to a significant increase in the number of unstable slopes.

Comparing Fig. 9 (A) and (B), the rainfall intensity of 10 mm/h attacked for 24 h. There was no difference between the two models in terms of the grading results as the rainfall intensity threshold had not been reached, and the number of unstable slopes was 36 in both cases. Comparing Fig. 9 (C) and (D), the rainfall intensity of 20 mm/h attacked for 24 h. The count of unstable slopes determined by NLSAM incorporated the findings from FSLAM, resulting in a significant rise from 40 to 98 unstable slopes. During extreme rainfall, the interactions among slope units intensify, leading to a greater decline in the stability of additional slope units, hence elevating the risk of landslides within the watershed. It also demonstrates the necessity of examining the cascade relationship between nodes to predict the susceptibility of landslides.

Fig. 9

(A) Landslide susceptibility assessment results using FSLAM for a 10 mm/h rainfall intensity attack for 24 h. (B) Landslide susceptibility assessment results using NLSAM for a 10 mm/h rainfall intensity attack for 24 h. (C) Landslide susceptibility assessment results using FSLAM for a 20 mm/h rainfall intensity attack for 24 h. (D) Landslide susceptibility assessment results using NLSAM for a 20 mm/h rainfall intensity attack for 24 h.

Model validation

Based on the group-occurring landslide event that occurred in the study area on July 22, 2023, the research validated the model. In the week before the landslides, the area received more than 404 mm of rainfall. During the 2 days from July 21 to 22, the rainfall amounted to 320 mm and was mainly concentrated on July 22 from 17:40 to 20:40. In light of this event, this paper used NLSAM and FSLAM to assess the landslide susceptibility of the area and validated the model’s reliability using the landslide inventory.

The results show that NLSAM calculations exhibit higher sensitivity under the same rainfall environment. Under extreme rainfall, the FS of NLSAM is lower than that of FSLAM. The landslides of this event were mainly concentrated in the areas where the FS assessment value of NLSAM was below 1.15 and that of FSLAM was below 1.3. (Fig. 10(A) and (B)). The results of the statistical analysis show in detail the percentage of predicted regional landslide susceptibility at each level (Fig. 10 (C)) and the percentage of actual landslide distribution at each susceptibility level (Fig. 10 (D)). This all indicates that NLSAM can better identify the landslides of this event. Comparing the ROC curves of FSLAM and NLSAM (Fig. 10 (E)), although the difference in AUC values between the two models is not significant (0.63 for FSLAM and 0.62 for NLSAM), NLSAM has a significantly higher recall (0.93) than FSLAM (0.45). This implies that NLSAM has the potential to identify a greater number of landslides, despite the possibility that its assessment of landslide susceptibility may be exaggerated.

Fig. 10

(A) Prediction results of FSLAM. (B) Prediction results of NLSAM. (C) Proportion of predicted regional landslide susceptibility at each level. (D) Proportion of actual landslide distribution for each susceptibility level. (E) ROC curves for FSLAM and NLSAM.

Discussion

Current physical methods for rapid assessment of regional landslide susceptibility are performed on a single isolated assessment unit and do not take into account the hydrologic linkages between slope units^12,28,32. Complex networks are an effective tool to reflect the interaction between nodes. Therefore, we abstract the hydrological connections of slope units into a complex network model. This is distinct from research that employs correlation analysis and multiple linear regression methods to examine the quantitative relationship between river network parameters and terrain parameters^33,34. The model effectively portrays the flow process of rainfall among slope units in the watershed, thus improving the traditional physical methods that ignore the interactions among slope units.

This paper examined the correlation between the degree of the nodes in the complex network and the distribution of the quantity of change in FS of the slope units in the study area (Fig. 11). The higher degree of the nodes indicates that the depressions around the slope units are more clustered and that the hydrological connections between the slopes are closer. Since the data did not conform to a normal distribution, this paper used Spearman’s correlation coefficient for hypothesis testing. The significance test was passed by all of the variables, which had r-values ranging from 0.4 to 0.5. This indicates that there is a positive correlation between the degree of the nodes and the amount of change in FS of that slope unit under various scenarios. The closer the hydrological connection of the slope unit, the more prone to landslides at that node. The small r-values may be attributed to the variability of the environmental parameters of the nodes. By combining the network structure with the landslide susceptibility analysis, we can understand more comprehensively the propagation paths of rainfall in the watersheds and their possible influence ranges, rendering decision-makers to make strategies to reduce potential disaster losses.

Compared to FSLAM, NLSAM is more effective in capturing group-occurring landslide events in the watershed. In the model validation, the recall of NLSAM was significantly higher than that of FSLAM, although the disparity in the AUC values between these two models is not substantial. In addition, the model aims to provide a rapid and straightforward physical model; therefore, simplifications were made in the hydrological calculations for FS, and some non-key parameters were not addressed in this paper. In future research, we will further analyze parameter sensitivity and discuss its impact.

There are several directions for further research, including the impact of various network structures on the susceptibility of landslides, the changes in network stability following the occurrence of geological disasters, and the potential to mitigate the occurrence and spread of geological disasters by modifying network structures.

Fig. 11

Correlation analysis between the amount of change in the node’s FS and the degree of the node.

Conclusions

This paper proposes a rapid landslide susceptibility assessment model (NLSAM) designed for watershed scale, taking into account the hydrological connections between slope units. The new model enhances the ability to capture group-occurring landslide events by improving upon the limitations of current physical models that typically assess isolated units. This enhancement is beneficial for the prevention and control of watershed landslide disasters. The main findings of this study are as follows:

• (1) Due to the application of a complex network in the NLSAM model to represent hydrological connections between slope units, the model can effectively simulate rainfall lateral infiltration. As the rainfall intensity increases, it is found that the sensitivity of slope unit FS to lateral infiltration is greater than its sensitivity to vertical infiltration.

• (2) As rainfall intensity increases, the hydrological connections between slope units have a greater impact on the susceptibility to landslides, leading to further decreased stability of more slope units and an increased susceptibility of landslides in the watershed. In the study area, when the rainfall intensity exceeds 15 mm/h for a continuous 24 h, the hydrological connections between slope units become a crucial influencing factor.

• (3) Compared to FSLAM, NLSAM is better at detecting group-occurring landslides. While the AUC values for both models are nearly identical, NLSAM shows a significant improvement in recall.