Introduction

With the increasing depth of coal mining operations, there has been a notable rise in the occurrence of coal and gas outburst incidents. The occurrence of coal and gas outburst incidents can be attributed to energy driven result. When the accumulated energy in coal and rock strata reaches its ESL, the surrounding rock mass will be deformed and damaged. As a result, those fractures would create pores or voids for gas migration and energy release1,2,3,4. Coal seams are not found in isolation underground; rather, they cohabit in the form of inter-bedded coal rock. Most coal seams were influenced by geological conditions in the form of inclined coal seams. Thus, it is vital to study the fracture mechanisms of coal–rock combinations under static loading conditions to ensure the sustainability of coal mining and to decrease the number of rock burst accidents.

Some scholars established the evolution Eq of rock damage in the process of rock deformation and failure5,6, and someone announced the deformation characteristics of shale under different loading conditions through cyclic loading and unloading tests7,8,9. it was discussed that the influence of coal-rock height ratio, loading rate, moisture content and other factors on rock mechanics and acoustic emission characteristics under cyclic loading conditions, the law of rock mechanics and AE (acoustic emission) energy evolution during loading and unloading stages10,11,12,13. Li SG’s research group and Yin systematically investigated the mechanical properties, energy changes and permeability characteristics of "solid–gas" coupling similar materials under uniaxial conditions14,15,16,17. Many scholars studied the effect of the combination method on the overall failure of the specimen through experiments and numerical simulation, leading to the clarification of macroscopic collapse mechanism of the CRC (Coal and rock combination)18,19,20. The difference in the mechanical parameters and structural characteristics of the CRC leads to a large difference in the energy dissipation law of the CRC compared with a single coal or rock mass. At the moment, most scholars analyzed the mechanical properties and AE properties of CRC during the loading process, which could not really explain the energy dissipation law of CRC due to interface inclination angles. Afterwards, someone carried out experiments on coal body, rock mass and coal-rock combination, analyzed its mechanical characteristics, energy characteristics, and failure characteristics, established the energy failure mechanism of coal-rock combination21,22. Zhang analyzed the fracture behavior of coal–rock combinations with different water contents under uniaxial compression using AE technology; they found that the AE counts showed different forms of decreasing with the expansion of cracks in the specimens23. Some scholars studied the energy dissipation features of coal under dynamic load conditions, and a damage load model under dynamic load was established24,25. The above research works provide some foundation for understanding the failure form and energy characteristics of coal and rock mass.

This paper presents an analysis of the strength and energy characteristics of the CRC with varying interface inclination angles under a uniaxial load. Therefore, from the perspective of energy study coal-rock-like material combination deformation damage law, establish coal combination damage in the process of energy change and the relationship between the fissure evolution law, may be more universal, more close to the coal deformation damage nature, for quantitative characterization of mining rock fracture domain and deep understanding of mine power disaster brings a new perspective. Designed to provide insights into the prevention and control of coal and gas outbreaks.

Experimental scheme

Preparation of specimen

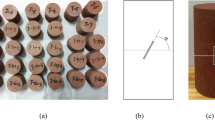
This study displays the format of proper nouns that may appear in the article (Table 1). To study the interface inclination effect of the mechanics and energy of the static load fracture process of the CRC, the coal-like material was selected to simulate the coal seam and the upper and lower roof and floor with a series of ratios to conduct physical similar simulation experiments. In the experiment, a total of 5 inclination angles (25°, 30°, 35°, 40°, 45°) levels were set, and the CRC was made according to a series of mix designs (Table 2). There were six groups of cylinder specimens with diameter of fifty millimeter and height of a hundred millimeter26. For the rock part of the coal-rock combination specimens, we used sand, cement, and plaster for production. Among them, the mass of sand was 1200g, the mass of cement was 180g, and the mass of plaster was 216g. The experimental system was composed of a DYD-10 uniaxial compression system. The DYD-10 uniaxial compression system was composed of a load frame, a servo motor, a transmission system, a data acquisition system, and a displacement protection device; the maximum load capacity was 10 KN. The specific test pieces production process was shown in Fig. 1.

Table 1 Table of word abbreviation meanings.
Full size table
Table 2 Proportioning table of test pieces.
Full size table
Fig. 1
figure 1

Preparation system of specimen.

Full size image

Experimental design

  1. (1)

    In this experiment, five different angles of inclination (25, 30, 35, 40 and 45) were set up to carry out the mechanical and energy characteristic experiments of the specimens to collect deformation and failure readings under uniaxial load.

  2. (2)

    After polishing the two end faces of the specimen, the height error would not exceed 1 mm.

  3. (3)

    The displacement control mode was used through the entire experiment. The displacement load speed was set to 0.01 mm/s, and the test was finished when the compressive strength decays to 60% of the peak strength.

  4. (4)

    In the experiment, the axial strain and deformation characteristics of the specimen were monitored, and the micro-fracture characteristics of the CRC were analyzed.

  5. (5)

    To ensure the stability and complementary of the experimental results, 3 sets of experiments were completed using different angles of interface inclination.

Experimental results

Stress and strain characteristics of specimens during uniaxial compression

The stress–strain curve and ultimate failure characteristics of the CRC were determined using a uniaxial static pressure loading experiment. As seen in Fig. 2.

Fig. 2
figure 2

Stress–strain curve of coal-rock combination with different interface inclination angle (a) 25°, (b) 30°, (c) 35°, (d) 40°, (e) 45°.

Full size image

According to the data presented in Fig. 2a,b, it was observed that the compressive strength values of the CRC were measured at 1.71 and 1.61 MPa when the interface inclination angles reached 25° and 30°, respectively. At an interface inclination angle of 35°, the compressive strength of the CRC material was measured to be 1.43 MPa, as shown in Fig. 2c. An increase in the interface inclination angle was observed to result in a decrease in the compressive strength of the CRC. The observed damage in the specimen, which had an interface inclination angle of 35°, can be attributed to the underlying deterioration of the coal seam. However, in comparison to the specimens with interface inclination angles of 25° and 30°, there had been a notable reduction in the final fracture length. That is, as the angle of the interface increased, the final penetration length of the CRC decreased. For the specimens with interface inclination angles of 40° and 45°, the final fracture length was relatively short, and the slip phenomenon had obviously appeared at coal-rock interface from the view of the failure morphology. The compressive strength values of the specimen at those angles were 1.29 and 1.19 MPa (Fig. 2d,e), which are further reduced as compared to the CRC with a smaller interface inclination angle.

The slip is due to the inclination effect, and the friction extrusion of the coal rock combination causes the large area of the coal block, and an extended crack appears at the lower end of the rock formation. Subsequently, the coal rock combination test enters the peak failure stage, and the specimen loses the bearing capacity. At this time, the coal rock combination test is mainly slip failure, and the horizontal distance of the specimen displacement to the lateral section in the original observation position is called the slip volume.According to the analysis of the axial strain, the larger the interface inclination angles, the greater the axial strain of the specimen, and the variation range was between 2.11 and 2.51%. When the interface inclination angle reaches 40°, the axial strain increases further with the appearance of interface slip. Figure 3 showed the law of slip amount of each specimen in the final failure mode. For the CRC with interface inclination angles of 25 to 35, the failure was splitting failure, and there was no sliding phenomenon in the interface direction, that is, the slip amount was 0 mm. Although the CRC with a dip angle of 35 was damaged as a whole, the shear stress (Fx) on the interface was not enough to make the specimen slide, but showed the characteristics of transverse strain in coal seam. For the CRC with interface inclination angle of 40, the slip amount was 3.79 mm, while that of 45° was 6.69 mm.

Fig. 3
figure 3

The amount of slip in the final failure form of the CRC.

Full size image

Energy evolution characteristics of specimens under uniaxial compression

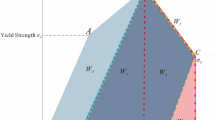
According to the energy conservation theory, the energy associated with the constrained rigid body motion can be classified into two distinct forms: the first form pertains to the irreversible dissipation of energy that occurs when the internal particles lose their restraints, while the second form refers to the elastic energy that is stored within the constrained rigid body. When considering the absence of energy exchange between the CRC and the external environment, the resulting Eq is as follows:

$$W = W_{{\text{e}}} + W_{{\text{d}}} ,$$
(1)

where W is the energy generated by the external force during uniaxial compression, which can be expressed as the total area covered by the curve, MJ/m3; We is the stored elastic energy of the specimen, expressed as the area of the shaded part, MJ/m3; Wd is the irreversible dissipated energy generated during the destruction of the CRC, MJ/m3. W, We and Wd were shown in Fig. 4.

Fig. 4
figure 4

Schematic diagram of the relationship between elastic energy and total energy.

Full size image

In the process of uniaxial static fracturing, the total energy W can be obtained by Eq. (2), and the reversible elastic energy We can be calculated by Eq. (3). In that way, the dissipation energy Wd can be obtained by Eq. (1).

$$W = \int {\sigma_{1} d\varepsilon_{1} = \sum {_{i = 1}^{n} } } \frac{1}{2}\left( {\sigma_{i + 1} + \sigma_{i} } \right)\left( {\varepsilon_{i + 1} - \varepsilon_{i} } \right),$$
(2)
$$W_{{\text{e}}} = \frac{1}{2}\sigma_{1} \varepsilon_{1} = \frac{{\sigma_{1}^{2} }}{{2E_{{\text{i}}} }},$$
(3)

where σi is an arbitrary point on the stress–strain curve, MPa; εi is the strain corresponding to this point, and the initial values are 0. Ei is the unloading elastic modulus.

The initial elastic modulus E is generally used instead of Ei (Fig 5)27. The correlation between the inclination angle θ of a contact and energy has been established and is represented by Eq. (4). Given the strain was divided into i segment and the corresponding stress is also i segment, the relationship between stress, strain and interface inclination angles was established as f(θ)i, g(θ)i (where i = 1, 2, 3, 4…). The inclination of each interface was defined as θj (j=1,2,3,4,5. j1=25°, j2=30°…), yielding the following19:

$$W_{{\text{j}}} = \int f \left( {\theta_{{\text{j}}} } \right)_{1} dg\left( {\theta_{{\text{j}}} } \right)_{1} = \sum {_{i = 1}^{n} } \frac{1}{2}\left( {f\left( {\theta_{{\text{j}}} } \right)_{{\text{i + 1}}} + f\left( {\theta_{{\text{j}}} } \right)_{{\text{i}}} } \right)\left( {g\left( {\theta_{{\text{j}}} } \right)_{{\text{i + 1}}} - g\left( {\theta_{{\text{j}}} } \right)_{{\text{i}}} } \right),$$
(4)
$$W_{{{\text{ej}}}} = \frac{1}{2}\sigma_{1} \varepsilon_{1} = \frac{{f\left( {\theta_{{\text{j}}} } \right)_{1}^{2} }}{{2E_{{\text{i}}} }}.$$
(5)
Fig. 5
figure 5

Energy distribution characteristics of the CRC.

Full size image

As presented in Fig 5, in the initial stage of static loading, the internal pores and primary microcracks of the specimen were closed at a low stress level. At this time, no obvious fracture was generated in the specimen, and the energy was low and fluctuates slightly (stage I). When the specimen was loaded into elastic stage, the stress and strain were linearly related. The elastic energy increased steadily during elastic stage (stage II). In the plastic fracture stage, the stored elastic energy of the specimen reaches the peak value. The elastic energy increased mainly in the elastic stage and the plastic fracture stage, and the elastic energy accounted for more than 90% in the two stages. In the plastic rupture stage, the internal fractures developed to the surface of the specimen, and the dissipation energy of the CRC began to increase (stage III). When the stress peak was reached, the fracture on the surface of the specimen was connected to form the main fracture. The proportion of dissipated energy was between 55.48% and 78.39% in the post peak failure stage, the ultimate bearing capacity was lost (stage IV).

Discussion

The effect of interface inclination angles on uniaxial compressive strength of specimen

When the interface inclination angles of the CRC were between 25° and 35°, during the whole static loading process, specimen would rupture firstly in the bottom of interface place and secondly in the coal body. When the axial stress was close to the compressive strength, fracture occurred in the upper and lower rock mass and continuously to break through the entire specimen. Based on an observation of a specimen, the degree of fracture in the coal was more severe than in the rock mass. When the fractures of coal body developed to the coal-rock interface, the further increase of stress would lead to the formation of partial fractures of rock mass, and finally the whole ended in the form of tensile failure. When the interface angles inclined to 40 and 45, a sliding failure occurred along the interface. Especially for the CRC with an interface inclination angle of 45, the failure of “rock-coal-rock” system caused by interface slip brought about the ultimate failure and instability of the CRC, and the failure mode was completely transformed from tensile failure to sliding failure. Primarily, the specimen exhibiting an interface dip angle ranging from 25 to 35 demonstrated a straightforward occurrence of tensile failure. In contrast, the specimen with an interface dip angle of 40 exhibited a combination of both tensile failure and slip failure. Lastly, the specimen with an interface dip angle of 45 only displayed slip failure. The critical juncture at which the two failure modes diverged was seen at an interface inclination angle of 40.

As shown in Fig 6, the compressive strength and elastic modulus of the CRC decrease with the increase of the interface angle. Table 3 showed the fitting relationship between them and the interface inclination angles, and the determination coefficient R2 is greater than 0.9.

Fig. 6
figure 6

The relationship between interface inclination angle-compressive strength-modulus of elasticity.

Full size image
Table 3 Fitting relationship between interface inclination angle-compressive strength-elastic modulus.
Full size table

Influence of the interface dip effect on the impact tendency and fracture development

Failure condition of other coal-rock-like materials was that the shear stress (τ) on the interface should be equal to or larger than the shear strength of the specimen28. For the CRC of inclined interface, the shear stress (Fx) on the interface was equal to or greater than the friction resistance (f) caused by normal stress (Fy) on the surface. As shown in Fig. 7:

$${\text{d}}F_{{\text{x}}} = {\text{d}}F\sin \theta \ge f.$$
(6)
Fig. 7
figure 7

Analysis diagram of the force on the dip interface.

Full size image

The mechanics analysis showed that the increase in interface inclination angles made the shear stress (Fx) on the interface increases, and the friction force caused by normal stress (Fy) decreases. Therefore, the failure and instability conditions of the specimen was easier to achieve, as shown in Fig. 8. The correlation between the interface inclination angles and elastic energy was fitted as follows in Table 4. The elastic energy of CRC was negatively correlated with the interface inclination angle. Combined with the analysis of the destruction form of the specimen, the destruction of the larger dissipative energy of composite was more severe. The specimen failure started from the coal-rock interface and propagates along the interface to the rock formation, and finally caused the failure and instability of the whole specimen.

Fig. 8
figure 8

Relationship between different interface inclination angles and peak energy.

Full size image
Table 4 Fitting relationship between different interface inclination angles and peak energy.
Full size table

Interfacial inclination angle effect of energy dissipation coefficient (EDC)

To quantitatively analyze the energy evolution mechanism of the CRC during uniaxial compression, the EDC “μ” was defined as the ratio of elastic energy to dissipated energy during uniaxial static loading as expressed below:

$$\mu = W_{{\text{e}}} /W_{{\text{d}}} .$$
(7)

According to Eqs. (1–3) and (7), the energy values and energy distribution law during the compression fracture process of the specimens were calculated, as presented in Fig. 9. The stress–strain process of the CRC had similarity with the energy change as explained below.

Fig. 9
figure 9

EDC under different inclination conditions: (a) 25°, (b) 30°, (c) 35°, (d) 40°, and (e) 45°.

Full size image

The first stage corresponds to the initial compaction stage. The initial compaction stage can be divided into particle friction section and internal void closure section. In the stage of particle friction, the dissipative energy was generated due to the friction between particles in the CRC, and the dissipated energy value was slightly greater than the elastic energy. The EDC µ was less than 1. However, after the particle friction segment, the void closure segment had greater elastic energy than dissipated energy due to the continuous increase in axial stress, which showed that the EDC "μ" was slightly greater than 1.

The second stage correspond to the elastic stage. The energy applied to the CRC by the testing machine gradually shifted from dissipation of energy to the elastic energy storage. At this time, with the increase of elastic energy, the EDC increased, and the curve had an obviously growing trend (the stage II of each image in Fig. 9). The dissipation coefficient "μ" is greater than 1 and increases rapidly.

The third stage corresponds to the plastic fracture stage. At this stage, fractures had been formed inside the specimen and spread to its surface, which showed the releasing of energy obviously. Compared with the elastic stage, as the increase of dissipated energy in the plastic fracture stage, the μ had obviously decreased, but it was still greater than 1.

The fourth stage corresponds to the post-peak failure stage. Under the same strain, the stress and elastic energy reach their respective peaks at the same time. At this stage, part of the elastic energy was transformed into the dissipative energy and then being released, and part of the elastic energy still retained in the CRC. The dissipation coefficient "μ" was greater than 1.

Combined with Fig. 5 to Fig. 9, the EDC curves of the CRC with different interface inclination angles were very similar. As the axial stress increases, the curves all showed a trend of first increasing and then decreasing. As a whole, with the increased of interface inclination angles, the strain of the specimen increases, and the corresponding elastic energy sudden increase region also moved back obviously in the diagram, corresponding to the respective elastic stage. The area mapped by the sudden increase of the EDC curve also reflects the size of elastic energy.

The interface inclination angles effect of the ESL and dissipated energy conversion rate of the specimen

In the uniaxial compression process, the energy characteristics could be divided into: steady, storage, peak and rapid release phases. The interconnection of these four processes was evident, as the energy transformation process coincided with the accumulation of elastic energy and the dissipation of energy. The specimen experiencing maximal stress was situated at the point of energy equilibrium, and the introduction of an external energy disturbance results in the abrupt release of elastic energy, ultimately causing the collapse of the CRC. After the accumulated energy exceeded peak value, the transformation rate of dissipated energy was accelerated rapidly, and the deformation and damage degree of coal sample were intensified. Therefore, combined with the above experiments, to effectively identify the severity of fracture instability of the CRC, the ESL and dissipation energy conversion rate of the CRC under different interface inclination angles were comprehensively analyzed. The calculation Eq of the ESL was29:

$$\mathop W\nolimits_{{\text{e}}}^{{\text{m}}} = \sigma^{2} {\text{c}}/2E_{{\text{t}}}$$
(8)

Putting the compression strength and elastic modulus fitting Eq in Table 2 into the Eq. (8), we can obtain:

$$\mathop W\nolimits_{{\text{e}}}^{{\text{m}}} = \frac{{\left( {2.398 - 0.0272\theta } \right)^{2} }}{{2\left( {157.415 - 1.9462\theta } \right)}},$$
(9)

where \({\text{W}}_{\text{e}}^{\text{m}}\) is the elastic energy stored when the specimen reaches the compressive strength limit, that is, the storage limit, MJ/m3; σc is the compressive strength of the CRC, MPa;\({\text{E}}_{\text{t}}\) is the elastic modulus of the CRC, MPa; θ is the interface inclination angles of the CRC.

After the specimen reaches the peak stress, the energy was quickly released and the specimen loses its bearing capacity. The dissipative energy conversion rate was defined as:

$$K = dW_{{\text{d}}} /dt,$$
(10)

where K is the DECR of the specimen, MJ·m-3·s-1; dt is the time from the peak stress to the failure instability of the specimen, s; d \({\text{W}}_{\text{d}}\) is the change in dissipated energy within dt, MJ/m3.

For the specimens with the same material ratio, the composites with smaller interfacial inclination angle had higher compressive strength. It meaned that the specimen had higher energy storage capacity during failure and instability, so the ESL was higher. For the CRC of smaller interface inclination angles, the dissipated energy exhibited a rapid increase during the post-peak failure period. While the major factor in this process was the release of energy, it was important to note that energy dissipation also played a significant role and accounted for a certain proportion. Nevertheless, the CRC featuring a greater interface dip angle exhibited the occurrence of interface sliding phenomenon during the post-peak failure stage. The proportion of the ultimate fracture area was significantly reduced compared to the CRC with tiny interface dip angle. This indicated that the energy dissipation was relatively low. In contrast to the process quantity of energy dissipation, the duration of energy release was comparatively shorter. The prompt discharge of energy resulted in heightened susceptibility to instability in the specimen. As seen in Fig. 10.

Fig. 10
figure 10

Relation diagram of combined ESL and DECR with interface inclination angles.

Full size image

Conclusions

This paper uses laboratory experiments to study the mechanical properties and energy characteristics of the coal-rock assembly during uniaxial compression under different interface inclination angles, and obtains the stress–strain curves of the coal-rock assembly at different interface inclination angles. And combined with a specific formula to calculate the energy of coal-rock-like material combination, the following conclusions were obtained.

  1. (1)

    The compressive strength and elastic modulus of in the coal-rock-like material combination with the angle of 25° to 45° were 1.19–1.71 MPa and 70.55–107.32 MPa, respectively. The compressive strength and elastic modulus of coal rock combination had negative correlation with the interface inclination angle.

  2. (2)

    The energy dissipation coefficient of the coal-rock-like material combination with different interface inclination angles was similar. In the first stage, the energy dissipation coefficient was small. In the second stage, the energy dissipation coefficient increases, and the curve increased obviously. In the third stage, the energy dissipation coefficient decreased obviously, but it was still greater than 1. In the fourth stage, the elastic energy was transformed into dissipative energy and released, but part of the elastic energy still retained in the coal-rock-like material combination, which showed that dissipation coefficient was greater than 1.

  3. (3)

    The storage of elastic energy mainly occurred in the second and third stages, and the proportion of elastic energy in the two stages was more than 90%; the growth of dissipated energy increased significantly in the post-peak failure stage, accounting for 55.48–78.39%. The energy storage limit was decreased with the interface inclination angles, and the dissipation energy conversion rate was increased with the interface inclination angles.