Hemodynamic effects of stenosis with varying severity in different segments of the carotid artery using computational fluid dynamics

Abstract

Carotid atherosclerosis is a leading cause of ischemic stroke. As a result of atherosclerotic plaque formation, the carotid artery lumen narrows, leading to significant hemodynamic alterations. These changes can further contribute to the development of subsequent lesions. In this study, we built 54 idealized carotid artery stenosis (CAS) models by using a single healthy carotid artery to simulate six different degrees of stenosis at nine various locations. Computational fluid dynamics (CFD) was applied to analyze blood flow changes, focusing on three key hemodynamic indicators: wall shear stress (WSS), oscillatory shear index (OSI), and relative residence time (RRT). Numerical simulations and model validations were conducted to ensure the correctness and validity of the results. The results show that increasing stenosis severity leads to higher WSS values at the site of stenosis, which may facilitate plaque rupture, while OSI and RRT decrease at the stenosis site. In the external carotid artery (ECA) and internal carotid artery (ICA), increasing stenosis severity results in a reduction in WSS at bifurcation sites, promoting plaque formation. These findings offer new insights into the hemodynamic changes associated with carotid artery stenosis and provide a solid foundation for future research and clinical applications.

Introduction

It is well known that carotid artery stenosis (CAS) may lead to unexpected events such as stroke or even death. It occurs due to the formation of carotid atherosclerotic plaques, which can disrupt normal blood flow. A key factor in plaque formation is the proliferation of the carotid intima, which is driven by an unfavorable hemodynamic environment. Studies have shown that hemodynamic parameters such as wall shear stress (WSS) and oscillatory shear index (OSI)^1,2 play critical roles in the formation, development, and rupture of carotid atherosclerotic plaques. Specifically, low WSS promotes plaque formation, while high WSS can induce plaque rupture^3,4,5. In addition to this, arterial stenosis due to plaque also affects hemodynamic characteristics, further complicating the flow dynamics. Therefore, computational fluid dynamics (CFD) is used to analyze the hemodynamic properties of different parts of the carotid artery under various degrees of stenosis. This approach helps identify high-risk areas for further stenosis or plaque rupture, which could aid in the early diagnosis and targeted interventions to prevent catastrophic events such as stroke.

Hemodynamics plays a critical role in analyzing blood flow patterns, atherogenesis, and the progression of atherosclerosis in patients with CAS⁶. Geometric measurements and blood flow characteristics in CAS are commonly assessed using clinical tools such as Doppler ultrasound⁷, phase-contrast magnetic resonance imaging (PC-MRI)⁸, and computed tomography angiography (CTA)⁹. CTA has been demonstrated to be an effective method for assessing the degree of stenosis¹⁰ and detecting CAS¹¹. In addition, CFD serves as an important non-invasive technique for visualizing blood flow^12,13, and can accurately replicate intra-arterial hemodynamics^14,15,16,17. CFD also enables the analysis of the relationship between flow parameters, such as velocities, pressures, WSS fields, and plaque onset and progression^{18,19,20,21,22}. This allows for further assessment of the location and severity of stenosis²³. References^24,25 have conducted numerical investigations of carotid arterial hemodynamics using the sharp interface latent boundary methodology. Yeh H H et al.²⁶ analyzed the effect of hematocrit on the hemodynamics of prosthetic heart valves using the Fluid-Structure Interaction (FSI) method. Birchall D et al.²⁷ conducted an extensive CFD analysis of abnormal hemodynamics at the carotid bifurcation in atherosclerotic carotid arteries, using patient-specific data. This lays the foundation for further research into the causal relationship between hemodynamic variables and the development of atherosclerosis and unstable plaque formation. CFD and FSI methods are used to study fluid flow and heat transfer in carotid arteries with three different sinusoidal geometries and locations, as well as four varying hematocrit levels²⁸. Studies have shown that atherosclerosis is more likely to develop when the carotid sinus is enlarged or displaced from the bifurcation point. The above analysis demonstrates the feasibility and broad acceptance of combining CTA and CFD techniques for the hemodynamic analysis of CAS.

Different locations and degrees of stenosis can significantly affect hemodynamic characteristics. Morphological parameters such as carotid lumen stenosis severity, bifurcation angle, plaque length, and lumen area may affect hemodynamics²⁹. The anisotropic elasticity of the arterial wall was taken into account by the FSI approach³⁰. The impact of plaque formation as well as key structural changes (especially bifurcation angle and degree of stenosis) on the development of carotid stenosis is investigated. It became clear that at lower levels of stenosis, the risk of further plaque buildup increased with increasing angle of bifurcation. The risk of plaque rupture increased with higher degrees of stenosis. Jędrzejczak K et al.³¹ found a correlation between blood flow and stenosis geometry and maximum shear stress (one of the most important indexes of hemolytic risk). As the diameter of the artery decreases, the critical flow rate decreases reducing the risk of hemolysis above this flow rate. The characterization of blood flow dynamics and heat transfer at arterial bifurcations with varying degrees of stenosis has been studied³². This study found that thrombus-induced arterial stenosis has a significant impact on blood delivery as the pulsation velocity reaches its peak. Abhilash H N et al.³³ found that since the shape of the carotid artery geometry, the bloodstream status changed significantly. Lower values of Time-averaged wall shear stress (TAWSS) are observed close to the carotid bifurcation region and carotid bulb position. Larger OSI values are found in the location of the internal carotid artery (ICA) and curvature of the carotid artery. Oyejide A J et al.³⁴ found that inductive forces lead to surface deformation and rupture of large plaques using a bidirectional FSI method. The carotid sinus plaques have the most significant effect on the external carotid artery (ECA). Plaques have higher yield strength to hemodynamic forces at the edge of attachment. From the above analysis, it can be seen that the degree of stenosis and its location will significantly change the geometric shape of the vessel. Thus affecting the hemodynamic characteristics. However, there has been no systematic analysis of the hemodynamic characteristics of the common carotid artery (CCA), ECA, and ICA as different degrees of stenosis occur in the proximal, middle, and distal portions of arteries. It is difficult to guide the prediction of the high-risk areas where stenosis or rupture may subsequently occur.

The selection of metrics is crucial for the rational assessment of hemodynamic properties. Kwak B R et al.³⁵ found that WSS regulates plaque formation. Unidirectional high WSS provided protection by upregulating anti-atherosclerotic, anti-thrombotic, and anti-inflammatory gene signatures. In contrast, low WSS induces pro-thrombotic and pro-inflammatory genes that facilitate the onset and progression of atherosclerotic lesions. It is found that low TAWSS and high OSI may appear to occur in ICA with moderate stenosis³⁶. This hemodynamic situation may contribute to atherosclerosis. Previous studies^37,38 showed that high OSI (> 0.2) is more predictive of atherosclerosis and vulnerable plaques than WSS. OSI is a statistical index of blood flow instability. A long-term state of oscillatory regurgitation is a very poor hemodynamic status for the endothelial and is likely to cause the formation of vascular plaques and lesions. It is found that areas of high OSI corresponded to areas of low WSS and were atherosclerosis prone³⁹. Subramaniam T and Rasani M R⁴⁰. studied the effect of different degrees and locations (before and after the bifurcation) of stenosis on carotid hemodynamics. As the degree of stenosis that occurs before the bifurcation increases from 30 to 70%, ICA maximal velocity rises from 12 to 65%, and ECA maximal velocity rises from 5 to 45%. If the degree of stenosis increases after bifurcation, the ICA maximal velocity takes longer to decrease after the peak systolic velocity. Dinh H et al.⁴¹ analyzed flow velocity and pressure data obtained from an intravascular guidewire and compared these data with CFD flow velocity and pressure simulations using a simplified carotid stenosis model. Increasing stenosis length is found to produce a larger WSS zone within and distal to the stenosis. Fukuda S et al.⁴² found those carotid arteries after plaque removal show significantly stronger WSS disturbances. The WSS is lower in the bifurcation and its more distal regions than in the healthy carotid artery. This could potentially lead to severe stenosis in the future. In summary, it can be seen that WSS, TAWSS, OSI, RRT (relative residence time), and so on have good evaluation guidance for stenosis development and prediction. However, in the current study, a single index or a small number of indexes are mostly used in the evaluation. Few studies comprehensively consider the effects of each index for the prediction of subsequent stenosis development risk areas.

In this study, we constructed 54 CAS models in an idealized manner by introducing varying degrees of stenosis at different locations in the CCA, ICA, and ECA segments of a single healthy artery. The objective was to investigate the specific effects of stenosis at different locations and severities on key hemodynamic parameters, such as WSS, OSI, and RRT, while minimizing the influence of other confounding factors. However, it is important to acknowledge that this study relies on idealized, simplified models of stenosis, which may not fully capture the anatomical and pathological complexities observed in real patients. In clinical practice, stenosis develops gradually and is influenced by multiple patient-specific factors such as vascular geometry and plaque characteristics. These factors result in irregular, asymmetric stenotic regions that our current model does not reflect. Nevertheless, this study provides valuable insights into the relationship between the location and severity of stenosis and hemodynamic parameters, offering a preliminary reference for both research and clinical applications.

Methodology

Physical model

Fig. 1

(Left) A schematic representation of a healthy carotid artery, highlighting the blood flow inlet and outlet. (Right) Illustration of various stenosis locations within the CCA, ECA, and ICA.

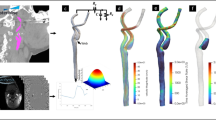
Here, in this study, a normal carotid artery is utilized, as illustrated in Fig. 1. CTA provides a clear visualization of the patient’s carotid arteries. A three-dimensional (3D) model of the realistic carotid artery is constructed by importing the CTA images into Mimics Medical 21.0 (https://www.materialise.com/). The resulting model is then exported and further refined using Geomagic Studio 2014 (https://www.3dsystems.com/) to enhance its smoothness. Based on the North American Symptomatic Carotid Endarterectomy Trial method⁴³, stenosis degrees of 10%, 30%, 40%, 60%, 70%, and 90% are introduced at nine locations within the carotid artery. The stenosis is distributed across the proximal, middle, and distal segments of the CCA, ECA, and ICA, which are potential regions for the development of stenotic lesions²³. For the CCA, the selected locations are at 8.77 mm, 42.05 mm, and 81.35 mm. For the ECA, the locations are 8.80 mm, 18.17 mm, and 31.38 mm, while for the ICA, the locations are 5.09 mm, 25.32 mm, and 46.08 mm. Tables 1, 2, and 3 provide the average diameters of the stenoses along with the corresponding percentages and locations. It is important to note that the decision to model stenosis at predefined locations limits the ability to capture the variability of stenosis formation in real patients. In clinical settings, stenosis develops at irregular sites influenced by a variety of factors, such as vascular geometry, wall stiffness, and the extent of atherosclerotic plaques. These factors may significantly impact the hemodynamic parameters, such as wall shear stress and oscillatory shear index, which our model may not fully represent.

Table 1 Stenosis severity and corresponding locations introduced into the CCA.

Table 2 Stenosis severity and corresponding locations introduced into the ECA.

Table 3 Stenosis severity and corresponding locations introduced into the ICA.

Mathematical model

In hemodynamic analysis, both the continuity equation and the Navier-Stokes equations are employed to describe the flow behavior of blood. The continuity equation ensures mass conservation for an incompressible fluid, while the Navier-Stokes equations govern the momentum conservation, incorporating the effects of fluid inertia, pressure gradients, and viscous forces. The continuity equation is expressed as²³:

$$\:\frac{\partial\:u}{\partial\:x}+\frac{\partial\:v}{\partial\:y}+\frac{\partial\:w}{\partial\:z}=0$$

(1)

here u, v, w represent the velocity components in the x, y, and z directions, respectively. x, y, z are the spatial coordinates.

The Navier-Stokes equations are given as²³:

$$\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{\mu }{\rho }\left( {\frac{{\partial ^{2} u}}{{\partial x^{2} }} + \frac{{\partial ^{2} u}}{{\partial y^{2} }} + \frac{{\partial ^{2} u}}{{\partial z^{2} }}} \right)$$

(2a)

$$\:\frac{\partial\:v}{\partial\:t}+u\frac{\partial\:v}{\partial\:x}+v\frac{\partial\:v}{\partial\:y}+w\frac{\partial\:v}{\partial\:z}=-\frac{1}{\rho\:}\frac{\partial\:p}{\partial\:y}+\frac{\mu\:}{\rho\:}\left(\frac{{\partial\:}^{2}v}{\partial\:{x}^{2}}+\frac{{\partial\:}^{2}v}{\partial\:{y}^{2}}+\frac{{\partial\:}^{2}v}{\partial\:{z}^{2}}\right)$$

(2b)

$$\:\frac{\partial\:w}{\partial\:t}+u\frac{\partial\:w}{\partial\:x}+v\frac{\partial\:w}{\partial\:y}+w\frac{\partial\:w}{\partial\:z}=-\frac{1}{\rho\:}\frac{\partial\:p}{\partial\:z}+\frac{\mu\:}{\rho\:}\left(\frac{{\partial\:}^{2}w}{\partial\:{x}^{2}}+\frac{{\partial\:}^{2}w}{\partial\:{y}^{2}}+\frac{{\partial\:}^{2}w}{\partial\:{z}^{2}}\right)$$

(2c)

where p is the pressure field. ρ is the fluid density. t is time. $\:\mu\:$ is the dynamic viscosity of blood. For Newtonian fluids, $\:\mu\:$ is constant, while for non-Newtonian fluids, it depends on the shear rate and is defined using different rheological models.

CFD simulations

In this study, a numerical simulation of the three-dimensional Navier-Stokes (N-S) equations is developed to analyze the hemodynamics of the carotid artery and explores the risks associated with carotid artery stenosis. Blood flow is assumed to be incompressible due to its high water content and negligible compressibility under physiological conditions. Blood is modeled as a non-Newtonian fluid, reflecting its shear-thinning properties under physiological conditions⁴⁴. A rigid wall model is adopted in this study to simplify the simulation and improve computational efficiency. While this approach neglects arterial wall elasticity, previous studies^25,26 have demonstrated that differences in key hemodynamic parameters, such as WSS and OSI, are minimal between rigid and elastic wall models under similar conditions.

• (1) Rheological model

In the study of⁴⁴, symmetrical 30–60% stenosis in a CCA under unsteady flow condition for both Newtonian and non-Newtonian viscosity models are investigated numerically. Results show that the power-law model overstates non-Newtonian behavior because it creates viscosities far from Newtonian viscosity at both low and high shear rates and so it is not a proper model. The generalized power-law and modified Casson models also underestimate non-Newtonian behavior, while Carreau is a suitable model. The Carreau non-Newtonian model is chosen to represent blood viscosity due to its ability to accurately capture the shear-thinning behavior of blood at varying shear rates. This model has been widely used in CAS hemodynamic studies^45,46. Because it effectively describes the transition from a Newtonian fluid at high shear rates to a non-Newtonian fluid at low shear rates, which is characteristic of blood flow in the human body.

In order to further evaluate the influence of different viscosity models on the hemodynamic parameters, two models with 30% and 60% stenosis at ICA-L1 were selected from the 54 models established in this article. For each model, a point was selected at a narrow location and WSS variation over time was calculated under different viscosity models for comparative analysis. The viscosity models are selected as Carreau, Power-law, Cross, and Newtonian model. The parameters for the viscosity models are primarily obtained from previously published studies^44,47. These parameters represent commonly accepted values in computational hemodynamics and were not recalibrated in this study.

The results in Fig. 2a and b indicate that the Power-Law model tends to overestimate non-Newtonian behavior. The Cross model underestimates non-Newtonian behavior, and only the Carreau model can accurately capture the shear-thinning behavior of blood at varying shear rates while maintaining the differences from the results of the Newtonian model. The results obtained for Carreau and Power-law models are consistent with those reported in⁴⁴. However, reference⁴⁴ did not include the Cross model, the Cross model allows for a more precise characterization of blood viscosity at both low and high shear rates, making it a valuable addition to this comparative analysis. In addition, as observed in Fig. 2, the WSS results stabilize after two cardiac cycles (1.6 s). Therefore, the hemodynamic data in this paper are based on the results from the third cycle.

Fig. 2

WSS trend over time at a certain point of stenosis in different viscosity models (Carreau, Power-law, Cross, and Newtonian models) with varying degrees of stenosis (a) 30% stenosis model at ICA-L1 position (b) 60% stenosis model at ICA-L1 position.

Therefore, in this study, the Carreau model is adopted. The following correlation is found between dynamic blood viscosity ($\:\mu\:$) and strain rate ($\:\dot{\gamma\:}$)⁴⁸:

$$\:\mu\:={\mu\:}_{{\infty\:}}+\left({\mu\:}_{o}-{\mu\:}_{{\infty\:}}\right)\times\:{\left[1+(\lambda\:\dot{\gamma\:}{)}^{2}\right]}^{\frac{n-1}{2}}$$

(3)

where zero shear rate viscosity $\mu _{o} = 0.056{\text{Pa}} \cdot {\text{s}}$, infinite shear rate viscosity $\:{\mu\:}_{{\infty\:}}=0.00345\:\text{P}\text{a}\cdot\:\text{s}$, $\:n$=0.3568 indicates the power index that determines the degree of shear thinning, $\:\lambda\:$=3.131 $\:\text{s}$ is the time constant, and $\:\dot{\gamma\:}$ is the shear rate ($\:{\text{s}}^{-1}$).

The Navier-Stokes equations (2a-2c) describe the unsteady flow of an incompressible Newtonian fluid and form the fundamental framework for fluid dynamics analysis. In this study, the non-Newtonian behavior of blood is incorporated by modifying the viscosity term using the Carreau model. This approach allows the Navier-Stokes framework to accurately capture the shear-thinning properties of blood while maintaining its generality and applicability.

• (2) Laminar flow assumption.

In the severe stenosis model, at the peak inlet velocity, the Reynolds number at the stenosis reaches approximately 3568 (exceeding 2000). At other times, the Reynolds number at the stenosis ranges between 556.38 and 1873.46 (below 2000). It is well established that the transition from laminar to turbulent flow does not occur instantaneously. Instead, it takes place in a region where the flow oscillates between laminar and turbulent states before fully transitioning to turbulence, typically requiring a Reynolds number exceeding 4000. However, in this study, the maximum Reynolds number of approximately 3568 persists for less than 0.1 s and is confined to a very short distance at the stenosis. Beyond this region, the Reynolds number drops below 2000, reverting to laminar flow. The Womersley number, calculated based on the pulse frequency and characteristic vessel dimensions, was determined to range between 4 and 8 across all cases. For carotid artery blood flow, this range typically corresponds to pulsatile flow. Furthermore, due to the geometric and flow velocity constraints of the carotid artery, the blood flow tends to predominantly maintain laminar characteristics.

Based on the analysis, it is evident that localized flow separation and transient vortices may occur in regions of severe stenosis or under extremely high flow velocities in the carotid artery. However, these phenomena are generally insufficient to induce a full transition to turbulence. Therefore, it is reasonable to assume that blood flow within the carotid artery remains laminar. This assumption aligns with the findings of Saqr K M et al.⁴⁹, who demonstrated that despite the presence of eddies, a turbulence model is not required when simulating laminar blood flow in cerebral arteries.

• (3) Boundary conditions.

At the inlet: The Doppler ultrasound waveform, obtained clinically, is utilized as the inlet velocity²³, as depicted in Fig. 3. This waveform represents spatially averaged velocity over the cross-section.

Fig. 3

Pulsatile flow profile applied at the inlet boundary over a complete cardiac cycle.

At the outlet: The boundary conditions are modeled using a simplified version three-element lumped Windkessel model. According to references [46] and [50], the three-element lumped Windkessel model consists of two resistances (proximal R_p and distal R_d) and one compliance element (C), representing the vascular resistance and elastic storage of blood, respectively. In three-element lumped Windkessel model, $\:C={\Delta\:}V/{\Delta\:}P$ represents the ability of blood vessels to store and release blood, defined as the ratio of volume change ($\:{\Delta\:}V$) to pressure change ($\:{\Delta\:}P$). Due to the rigid wall assumption adopted in our study, which assumes the elastic modulus of the blood vessel wall is infinite, the blood vessel walls tend to be non-deformable. Thus, the volume change of blood vessel approaches zero ($\:{\Delta\:}V\approx\:0$). This means that the compliance component can be reasonably approximated as zero ($\:C\approx\:0$) under the rigid wall assumption. This analysis is consistent with the result calculated under the assumption of a rigid wall in reference [46] (C=8.36 × 10⁻¹⁶~2.08 × 10^− 12 kg⁻¹ m⁴ s²). On the other hand, the reason for choosing this simplification is partly because our main focus is on analyzing the impact of different stenosis locations and severity on blood flow, rather than fully representing the compliance characteristics of the entire cardiovascular system. Consequently, only R is included in the model, which is calculated by⁴⁶.

$$\:R=\frac{128\mu\:l}{\pi\:{D}^{4}}$$

(4)

whereas $\:\mu\:$ is the blood viscosity. $\:D$ represents the vessel diameter. Measurements indicate that the diameters of the ECA and ICA without stenosis are 7.81 mm and 8.88 mm proximally to the bifurcation, and 3.9 mm and 5.0 mm distally to the bifurcation, respectively. The diameters of the CCA is 6.7 mm. $\:l$ represents the length, the length of the ECA and ICA without stenosis are 5.27 mm and 3.42 mm proximally to the bifurcation, and 46.67 mm and 50.49 mm distally to the bifurcation, respectively. R_p and R_d are calculated using the parameters of the ECA and ICA proximally and distally to the bifurcation, respectively.

The resistance R is applied as an outlet boundary condition via a User-Defined Function (UDF). Specifically, the outlet pressure (P_outlet) is dynamically calculated as:

$$\:{P}_{\text{o}\text{u}\text{t}\text{l}\text{e}\text{t}}={Q}_{\text{o}\text{u}\text{t}\text{l}\text{e}\text{t}}\cdot\:R$$

(5)

where Q_outlet is the flow rate at the outlet. This approach ensures a physiologically realistic pressure-flow relationship.

The UDF enforces this condition during each simulation time step. The implementation involves the following steps:

• (a) Calculate R for each outlet using Eq. (4).

• (b) Develop a UDF to dynamically update the outlet pressure (P_outlet) based on the calculated resistance and the simulated flow rate.

• (c) Apply the pressure boundary condition in the CFD solver at each time step, ensuring consistency with physiological flow conditions.

• (4) Solution settings.

CFD software (ANSYS Fluent 2022 R1, https://www.ansys.com/) is used to perform hemodynamic simulations in the carotid artery. The governing partial differential equations are discretized using the finite volume method. A fully implicit second-order time integration scheme, combined with second-order upwind spatial discretization, is employed to solve the discretized Navier-Stokes equations. This approach ensures numerical stability and accuracy, particularly for capturing the highly non-linear and transient nature of hemodynamic flows. The fully implicit scheme is well-suited for large time steps and avoids numerical instabilities associated with stiff equations. This implementation utilizes the SIMPLE algorithm for pressure-velocity coupling⁵¹. The simulations are conducted on a workstation with an Intel Xeon^® processor running at 2.30 GHz and 80 GB of installed memory.

Hemodynamics indicators

WSS was directly computed by the ANSYS Fluent 2022 R1 (https://www.ansys.com/) as part of the post-processing output. The software utilizes the velocity gradients near the vessel wall and the dynamic viscosity of the fluid to determine WSS values in accordance with the Navier-Stokes equations. As these calculations are handled internally by the software using well-established numerical schemes, the explicit formula for WSS is not presented here. The equations for TAWSS, OSI, and RRT in hemodynamics are presented as follows^52,53:

TAWSS represents the mean value of WSS over a complete cardiac cycle. In this study, TAWSS was determined using the results from the third cardiac cycle to ensure solution stability and periodicity.

$$\:\text{TAWSS}=\frac{1}{T}{\int\:}_{0}^{T}\:\left|\text{W}\text{S}\text{S}\right|dt$$

(6)

where T is the cardiac cycle.

OSI quantifies the directional changes in the WSS over a cardiac cycle, providing an indicator of disturbed flow. It is expressed as:

$$\:\text{OSI}=0.5\:\left(1-\frac{\left|{\int\:}_{0}^{T}\:\text{W}\text{S}\text{S}\:dt\right|}{{\int\:}_{0}^{T}\:\left|\text{W}\text{S}\text{S}\right|\:dt}\right)$$

(7)

RRT reflects the residence time of blood in contact with or near the endothelium and is considered an important factor in plaque genesis⁵⁴_, with values reported in Pa ^− 1. It is defined as:

$$\:\text{R}\text{R}\text{T}=\frac{1}{\text{T}\text{A}\text{W}\text{S}\text{S}\:(1-2\text{}\text{OSI})}$$

(8)

Grid and time step independence tests

The grid independence analysis is shown in Fig. 4a, where the healthy carotid artery model is used with varying number of grid elements to assess the impact on WSS. Once WSS converges with finer grid resolutions, we can infer that the OSI and RRT will also exhibit similar convergence. Since OSI and RRT are derived from WSS, ensuring the convergence of WSS across different grid resolutions is sufficient to indirectly validate the accuracy of the OSI and RRT calculations. The peak average WSS values of the third cardiac cycles are compared across different grid resolutions to determine when the results converge. The number of grid elements used include 540,280, 761,138, 1,031,332, and 1,429,980, spanning a wide range to ensure robustness in the analysis. The corresponding grid sizes for these number of grid elements range from 0.4 mm to 0.15 mm, with progressively finer resolutions used to test for convergence. The analysis shows that when the number of grid elements exceeds 1,031,332, the impact on the peak average WSS becomes negligible, indicating grid independence beyond this resolution. Thus, the grid size of 0.2 mm is selected for the final simulations, ensuring sufficient accuracy without unnecessary computational expense.

Fig. 4

(a) Mesh independence test, (b) Time-step independence test.

Figure 4b also presents the results of the time-step independence test, with four different time intervals (0.1 s, 0.01 s, 0.001 s, and 0.0001 s) used to determine the stability of the simulation. The peak average WSS values of the third cardiac cycles are compared across these time intervals to assess the impact of time step on the results. The comparison showed that minimal changes in the WSS values occurred beyond a time step of 0.001s, so a time step of 0.001s was selected for all subsequent simulations to ensure computational efficiency and result stability.

In this study, the boundary layer mesh is carefully refined to ensure accurate computation of near-wall hemodynamic parameters (as shown in Fig. 5). A total of 8 inflation layers are applied near the arterial walls to adequately resolve the boundary layer. The first layer of cells was set to a cell height of approximately 0.02 mm, depending on the local flow conditions. The cell growth rate was set to 1.2, ensuring a smooth transition of mesh density from the wall to the core region.

Fig. 5

Cross section and boundary layer mesh of ECA and ICA.

Model validation

To ensure the validity and reliability of the study’s findings, two key hemodynamic parameters, WSS and OSI, were selected for model validation in this study. The results of this study were compared with those reported by⁴⁴. As shown in Fig. 6, the outcomes are in good agreement with the findings of⁴⁴. Minor discrepancies between the two studies may arise from differences in research methodologies. Therefore, the results of this study demonstrate both accuracy and credibility.

Fig. 6

Validation of current predicted results and those obtained by⁴⁴ at the geometry wall for 60% stenosis with Carreau non-Newtonian blood model and pulsatile inlet velocity: (a) WSS validation and (b) OSI validation.

To further validate the reliability of the proposed hemodynamic analysis method, clinical data from a patient with mild carotid stenosis were incorporated. Using Doppler ultrasound, we measured the inlet and outlet velocities of the CCA, ICA, and ECA. Subsequently, a patient-specific computational model was constructed based on CTA imaging data, and hemodynamic simulations were performed using the proposed methodology. The simulation results for velocity waveforms in the ICA and ECA were compared with the corresponding Doppler ultrasound measurements. As shown in Fig. 7, the simulated velocity waveforms demonstrate good agreement with the clinical measurements, thereby enhancing the confidence in the reliability and accuracy of our proposed method.

Fig. 7

Validation of the current predicted centerline velocity for Carreau non-Newtonian blood model with the clinical measurements obtained by a Doppler ultra sound at distances of 10.8 mm and 10.5 mm from the ICA and ECA bifurcations, respectively.

Result and discussion

In this study, six different degrees of stenosis are introduced at nine locations of a single realistic carotid artery model to construct 54 CAS models. The objective is to calculate and analyze the effects of different stenotic regions and severities on blood flow. This study does not account for crucial factors such as plaque morphology, composition, and eccentricity, which are known to influence hemodynamic parameters and the natural progression of stenosis. However, the results of this research provide valuable insights for the preliminary understanding of the relationship between stenosis at different locations and severities in the carotid artery and key hemodynamic parameters (WSS, OSI, and RRT).

Wall shear stress

WSS is the tangential force exerted by blood flow on the vascular endothelium. Studies have shown that WSS is a critical parameter for carotid atherosclerotic plaque formation⁵⁵. Research indicates that elevated WSS values (> 2.5 Pa) are often associated with the formation of high-risk plaques⁵⁶, while reduced WSS values (< 0.4 Pa) are linked to an increased risk of atherosclerosis development⁵⁷.

We simulated three cardiac cycles, defining each complete cycle as 0.8 s. The WSS values presented in Figs. 8, 9 and 10 represent instantaneous WSS contour maps captured at 1.81 s (corresponding to 0.21 s in the third cardiac cycle). These instantaneous snapshots designed to illustrate the spatial distribution of WSS at this particular moment. 1.81 s corresponds to the deceleration phase of systole, which is the transitional time point where the flow velocity shifts from a high state to a lower state. It represents a critical transition from high shear stress and high-velocity flow to the low-velocity, steady flow characteristic of diastole. During the deceleration phase of systole, WSS typically undergoes rapid changes, which can have significant effects on endothelial cells. In the region of carotid artery stenosis, shear stress gradients are likely to be more pronounced, and these dynamic changes are critical factors contributing to the formation and destabilization of atherosclerotic plaques. Therefore, the selection of the WSS at 1.81 s can help analyze its potential impact on plaque rupture or vascular endothelial damage.

Fig. 8

The contour maps illustrate WSS variations at the 1.81 s in the CCA for stenosis degrees (10–90%) and locations, with maxima observed at bifurcations and stenotic regions.

Figure 8 shows that as stenosis at CCA-L1 (location one) increases in severity, the WSS in the CCA decreases. Patients with higher degrees of stenosis are at greater risk of developing new atherosclerotic plaques in the CCA. The maximum WSS at the stenosis site (WSS_smax) rises significantly, from 0.8 Pa to 192.3 Pa, while the maximum WSS at the bifurcation site (WSS_bmax) increases from 2.9 Pa to 15.1 Pa. For stenosis exceeding 70%, WSS_smax escalates sharply from 5.9 Pa to 192.3 Pa, indicating a high risk of plaque rupture. Similarly, for stenosis greater than 60%, WSS_bmax increases from 3.6 Pa to 14.4 Pa, suggesting that the vascular endothelium at the bifurcation site is highly susceptible to damage and prone to thrombosis formation.

At the CCA-L2 and CCA-L3 locations, the WSS in the CCA progressively increases with higher degrees of stenosis, indicating an elevated risk of endothelial damage. This condition facilitates early atherogenesis, secondary plaque formation, and thrombosis. At CCA-L2, WSS_smax rises significantly from 0.9 Pa to 527.8 Pa, while WSS_{bmax_}increases from 5.8 Pa to 27.5 Pa. For stenosis exceeding 60%, WSS_smax sharply escalates from 5.1 Pa to 73.8 Pa and then to 527.8 Pa, while changes at the bifurcation remain more moderate. At CCA-L3, WSS_smax increases from 0.5 Pa to 448.2 Pa, but WSS_bmax decreases from 25.6 Pa to 9.3 Pa. Studies suggest that elevated WSS levels can trigger plaque rupture. Although the risk of bifurcation lesions at CCA-L3 decreases with increasing stenosis, it does not completely vanish, as WSS values exceeding 2.5 Pa still pose a risk.

As shown in Fig. 9, at the three stenosis locations in the ECA, the overall WSS in the carotid artery decreases with increasing stenosis severity. However, this does not indicate a reduced vascular risk, on the contrary, lower WSS values are associated with a higher risk of vasculopathy. At the ECA-L1 location, WSS_smax rises from 19.2 Pa to 152.4 Pa, while WSS_bmax decreases from 6.2 Pa to 0.5 Pa. At the ECA-L2 location, WSS_smax increases from 28.6 Pa to 192.4 Pa, and WSS_bmax decreases from 4.8 Pa to 0.4 Pa. At the ECA-L3 location, WSS_smax rises from 42.2 Pa to 115.3 Pa, peaking at 143.3 Pa at 70% stenosis, while WSS_bmax declines from 5.2 Pa to 0.4 Pa. The increase in WSS_smax suggests that greater stenosis severity heightens the likelihood of plaque rupture at the site of stenosis. Conversely, the reduction in WSS_bmax promotes plaque formation and progression.

Fig. 9

The contour maps illustrate WSS variations at the 1.81 s in the ECA for stenosis degrees (10–90%) and locations, with maxima observed at bifurcations and stenotic regions.

As shown in Fig. 10, at the three stenosis locations in the ICA, the WSS values in both the ICA and CCA tend to decrease as stenosis severity increases. At the ICA-L1 location, WSS_smax rises from 3.9 Pa to 161.9 Pa. At ICA-L2, WSS_smax​ increases from 14.9 Pa to 164.3 Pa, while at ICA-L3, it grows from 15.9 Pa to 212.2 Pa. These data suggest that greater narrowing of stenosis increases the risk of plaque rupture and raises the likelihood of secondary plaque formation or blood clot development in healthy regions. The changes in WSS_bmax show no clear trend. Notably, the sharp drop in WSS_bmax at 90% stenosis does not indicate a lower risk of lesions; rather, it highlights a significantly higher likelihood of plaque formation. Extremely low WSS values can damage the vascular endothelium, further contributing to lesion development.

Fig. 10

The contour maps illustrate WSS variations at the 1.81 s in the ICA for stenosis degrees (10–90%) and locations, with maxima observed at bifurcations and stenotic regions.

Oscillatory shear index

One of the key factors influencing arterial endothelial cells is the OSI, which is affected by blood flow disturbances and arterial geometry. OSI quantifies the oscillatory nature of WSS and helps identify regions prone to atherosclerosis. OSI values range between 0 and 0.5, with values approaching 0.5 indicating a progressive narrowing of the vessel. It is widely acknowledged that OSI values exceeding 0.3 (highlighted as red and yellow regions in the cloud maps) can adversely impact the arterial intima, contributing to the initiation and progression of plaque formation.

Figure 11 illustrates the distribution of the OSI at different stenosis locations in the CCA. Across the three locations, OSI values at the stenosis sites tend to decrease with increasing stenosis severity. This may be attributed to the narrowing of the vessel lumen, which causes a jet-like blood flow and reduces flow oscillation at the stenosis site. At CCA-L1, both the bifurcation and the downstream regions of the stenosis exhibit a decreasing trend in OSI values. At CCA-L2, no significant changes are observed in OSI values downstream, while upstream regions show an increase. At CCA-L3, OSI values increase both upstream and downstream of the stenosis, with more pronounced changes upstream. These findings suggest that endothelial injury is more severe and poses greater risks upstream of the stenosis. The red and yellow regions, indicative of higher OSI values, are more prominent near the CCA bifurcation, the bifurcation itself, and the ICA. This indicates that stenosis in the CCA significantly raises the risk of secondary plaque formation in these areas.

Fig. 11

Cloud maps illustrating OSI variations in the CCA across different degrees and locations of stenosis.

Figure 12 illustrates the distribution of OSI values in the ECA for varying degrees and locations of stenosis. Across all three stenosis locations in the ECA, OSI values increased upstream of the stenosis and decreased downstream, while OSI at the stenosis itself varied with the degree of stenosis. These findings suggest that endothelial injury is more likely to occur upstream of the stenosis. For stenoses less than 90%, OSI values at the ICA and bifurcation tended to increase. However, at 90% stenosis, OSI values in these regions decreased significantly. This does not imply a reduced risk of secondary lesions at the ICA. On the contrary, it warrants closer examination and risk analysis using additional relevant evaluation metrics. The bifurcation, the CCA near the bifurcation, the upstream region of the stenosis, and the ICA are identified as high-risk areas for secondary plaque formation.

Fig. 12

Cloud maps illustrating OSI variations in the ECA across different degrees and locations of stenosis.

As depicted in Fig. 13, with increasing stenosis, the OSI decreased downstream of the stenosis and at the stenosis itself, while OSI at the bifurcation increased. However, at 90% stenosis, bifurcation OSI appeared to decrease, likely influenced by the downstream changes. This suggests that the bifurcation remains a high-risk region. At ICA-L1 and ICA-L2, OSI upstream of the stenosis varied irregularly, but regions with OSI > 0.3 are observed, indicating a potential risk of endothelial injury and subsequent plaque formation in these areas. At ICA-L3, a high-risk region with elevated OSI is present upstream only at 90% stenosis. For other stenosis levels, OSI values are smaller, implying a reduced risk of endothelial injury. Overall, the ICA, the bifurcation, and the CCA near the bifurcation are identified as high-risk areas for secondary lesion development.

Fig. 13

Cloud maps illustrating OSI variations in the ICA across different degrees and locations of stenosis.

Relative residence time

RRT quantifies the duration that blood remains in contact with or near the endothelium, making it a critical factor in plaque formation. An increased risk of atherosclerosis is observed when RRT exceeds 8 Pa⁻¹, as indicated by the red and yellow regions in the cloud maps.

As shown in Fig. 14, as the degree of stenosis increases, RRT values decrease at the bifurcation, stenosis, and the ICA near the bifurcation. This suggests that blood flow is faster at these locations, leading to a reduced risk of secondary lesions. At CCA-L1, RRT decreases downstream of the stenosis. At CCA-L2 and CCA-L3, there are no significant changes in downstream RRT values, except for the higher risk observed downstream of CCA-L3. Upstream RRT values also decrease. Therefore, in most cases, the ICA and CCA near the bifurcation are high-risk areas for secondary atherosclerosis.

Fig. 14

Cloud maps illustrating changes in RRT within the CCA across varying degrees and locations of stenosis.

As shown in Fig. 15, the RRT at the stenosis site decreases as the degree of stenosis increases. However, at the bifurcation, both upstream and downstream of the stenosis, RRT values increase, suggesting a higher risk of lesions in these regions. Stenosis in the ECA has a significant impact on the ICA, with more pronounced changes observed in the ICA as stenosis severity increases. At 90% stenosis, the RRT in the ICA is significantly reduced, but risk areas still remain. The risk at the bifurcation increases with stenosis greater than 60%. For stenoses less than 70%, the CCA near the bifurcation and the ICA are at higher risk for lesions. At 90% stenosis, in addition to the areas mentioned above, the ECA also becomes a high-risk region for secondary atherosclerosis.

Fig. 15

Cloud maps illustrating changes in RRT within the ECA across varying degrees and locations of stenosis.

As depicted in Fig. 16, RRT values at the stenosis site decrease with increasing stenosis severity. At 90% stenosis, RRT values downstream of the stenosis increase sharply, indicating a significantly higher risk of secondary atherosclerosis in these regions. At ICA-L1 and ICA-L2, RRT values near the bifurcation in the CCA initially increase (10–40% stenosis), then decrease (60%, 70%), and finally increase again (90%). In contrast, at CCA-L3, RRT values have shown a consistent upward trend. Therefore, in most cases, the areas near the bifurcation of the CCA and ICA are high-risk regions for subsequent lesions.

Fig. 16

Cloud maps illustrating changes in RRT within the ICA across varying degrees and locations of stenosis.

The results of this study can provide a preliminary reference for early diagnosis and targeted intervention. Specifically, it can help to preliminary identify high-risk areas for plaque rupture or progression that are not easily captured by traditional imaging techniques such as CTA or Doppler ultrasound. For example, in patients with moderate to severe stenosis, CFD results of WSS, OSI and RRT in regions of the carotid bifurcation can be used to assess the likelihood of plaque instability. This information can be integrated with existing diagnostic methods to help clinicians decide whether surgical intervention, such as carotid endarterectomy or stenting, is necessary. Additionally, hemodynamic simulation results can be personalized by incorporating patient-specific data from advanced imaging techniques (e.g., MRI or CT) to improve the precision of risk assessment and guide tailored treatment plans.

Conclusion

In this study, 54 idealized CAS models were constructed by using a single carotid artery model. Various locations and different degrees of stenosis were simulated. Hemodynamic simulations were performed using CFD, and the correctness of the results was validated by comparing them with reference studies. The WSS, OSI, and RRT were calculated based on the CFD results. While this study preliminary explores the effects of different stenosis locations and severities on the hemodynamic parameters, we acknowledge that the reliance on a single carotid artery model may limit the generalizability of our findings. The geometry of the carotid artery varies significantly between individuals, and these anatomical differences can affect hemodynamic outcomes. As such, the findings presented in this study are more suited for helping researchers deepen their understanding of the relationship between stenosis and hemodynamic characteristics, and should be applied with caution in clinical practice.

• (1) When stenosis occurs at the proximal, middle, and distal segments of the CCA, ECA, or ICA, an increase in the degree of stenosis leads to a continuous rise in WSS values at the stenosis, while OSI and RRT values decrease.

• (2) In the CCA, WSS values consistently increase upstream of the stenosis and at the bifurcation. The WSS_smax and WSS_bmax are observed at L2, measuring 527.8 Pa and 27.5 Pa, respectively. Upstream WSS and OSI values show an increasing trend, while RRT values decrease. These changes indicate disturbed blood flow direction and an increase in flow velocity, which predispose the endothelium to damage, potentially leading to secondary plaque formation or plaque rupture.

• (3) In the ECA, stenosis affects the ICA and bifurcation, leading to a continuous decrease in WSS values. The WSS_smax is 192.4 Pa at L2, while the WSS_bmax is 0.4 Pa at both L2 and L3. Upstream and downstream of the stenosis, OSI and RRT values show an increasing trend at the ICA and bifurcation but decrease significantly at 90% stenosis. These observations suggest that the ICA and bifurcation, particularly upstream and downstream of the stenosis, are prone to thrombus and plaque formation. At 90% stenosis, the risk of plaque rupture is notably high.

• (4) In the ICA, the WSS values in both the ICA and CCA decrease with increasing stenosis severity. The WSS_smax is observed at L3, reaching 212.2 Pa, while at 90% stenosis, the WSS_bmax decreases sharply to a minimum of 0.5 Pa at L2 and L3. As stenosis increases, OSI values decrease downstream of the stenosis and at the stenosis itself, while OSI at the bifurcation increases. In most cases, RRT values are higher near the bifurcation in both the CCA and ICA, indicating a greater likelihood of secondary plaque formation in these regions.

Limitations

This study provides valuable insights for researchers and clinicians to preliminarily understand the impact of the location and severity of carotid artery stenosis on hemodynamic parameters. However, it is important to note that this study uses a simplified, idealized model of carotid artery stenosis. It introduces stenosis at fixed, predefined locations, which may not fully capture the complexity of stenosis as observed in real patients. In reality, stenosis develops gradually and is influenced by a range of patient-specific factors, leading to irregular geometries that this model does not capture. These anatomical differences can affect hemodynamic outcomes. Thus, the current model may have limited applicability to real-world conditions.

In addition, the absence of factors, such as plaque morphology, composition, and eccentricity in our model may limit the ability to predict the full range of hemodynamic changes that occur in real-world clinical cases, as plaque characteristics can significantly alter blood flow patterns and shear stress distributions. Therefore, the findings presented in this study should be used with caution, particularly with respect to their applicability to a broader patient population.

Recommendations

In future studies, we plan to validate these results using multiple patient-specific models, each representing different anatomical features. Meanwhile, to improve the accuracy and clinical relevance of the model, future studies should integrate various plaque geometries and compositions, including eccentric plaques, into the model. Moreover, patient-specific data from advanced imaging techniques (e.g., CT, MRI) could also be used to create more accurate models, which would allow for more realistic simulations of stenosis at varied and irregular locations. This approach can better reflect individual variations in vascular geometry and stenosis progression. By incorporating personalized anatomical and hemodynamic data, future models could more effectively predict the impact of stenosis on hemodynamic parameters and improve the clinical relevance, particularly in predicting plaque vulnerability and informing personalized treatment strategies for patients with carotid artery stenosis.