Underwater image enhancement via multiscale disentanglement strategy

Abstract

Underwater images suffer from color casts, low illumination, and blurred details caused by light absorption and scattering in water. Existing data-driven methods often overlook the scene characteristics of underwater imaging, limiting their expressive power. To address the above issues, we propose a Multiscale Disentanglement Network (MD-Net) for Underwater Image Enhancement (UIE), which mainly consists of scene radiance disentanglement (SRD) and transmission map disentanglement (TMD) modules. Specifically, MD-Net first disentangles original images into three physical parameters which are scene radiance (clear image), transmission map, and global background light. The proposed network then reconstructs these physical parameters into underwater images. Furthermore, MD-Net introduces class adversarial learning between the original and reconstructed images to supervise the disentanglement accuracy of the network. Moreover, we design a multi-level fusion module (MFM) and dual-layer weight estimation unit (DWEU) for color cast adjustment and visibility enhancement. Finally, we conduct extensive qualitative and quantitative experiments on three benchmark datasets, which demonstrate that our approach outperforms other traditional and state-of-the-art methods. Our code and results are available at: https://github.com/WYJGR/MD-Net.

Introduction

Due to the complex physical characteristics of underwater environments, including light absorption and scattering, underwater images are often plagued by color distortion and reduced visibility^1,2. Moreover, the degradation of underwater images significantly impairs various vision tasks, such as depth estimation³, scene understanding⁴, and object detection underwater⁵. To solve the above problems, some deep learning methods have been applied to UIE in recent years. For example, Li et al. proposed a weakly supervised color transfer method⁶ to correct color distortion based on CycleGAN⁷ network structure. Li et al. designed a Water-Net which utilizes a straightforward multi-scale convolutional network⁸. However, these underwater image enhancement models typically employ standard deep network structures designed for solving general purpose image enhancement tasks, overlooking the distinct characteristics specific to underwater imaging. Subsequently, methods combining underwater physical imaging and deep learning have been developed to address the limitations mentioned above. Fu et al. proposed an UnSupervised Underwater Image Restoration method (USUIR) to achieve UIE by estimating the physical parameters and the homology between the original underwater image and the re-degraded image⁹. While these techniques demonstrate significant enhancement improvements, the precise estimation of underwater imaging parameters remains a considerable challenge for current deep learning approaches grounded in physical models.

To make up for the shortcomings of the above methods, and at the same time absorb the idea of combining physical imaging, we develop a Multiscale Disentanglement Network (MD-Net). MD-Net mainly consists of Transmission Map Disentanglement (TMD) and Scene Radiance Disentanglement (SRD) block. TMD and SRD are used to obtain transmission map and scene radiance (clear images), respectively. These parameters (including global background light) are then coupled through the underwater imaging model to form the original image, with self-supervised constraints applied to ensure the precision of each parameter to approximate the ground truth. In SRD and TMD, we have developed a Multi-level Fusion Module (MFM) and Dual-layer Weight Estimation Unit (DWEU) based on pixel and channel weights. Experimental results reveal that our MD-Net produces more realistic underwater colors and clearer visibility and shows favorable results in both trainable parameters (Params) and running times (Runtimes). The main contributions of this paper can be summarized as follows:

• 1. We propose a Multiscale Disentanglement Network (MD-Net) for UIE, which utilizes both shallow spatial features and deep semantic feature scales to improve the disentanglement accuracy of underwater scenarios.

• 2. To obtain richer shallow spatial features and deep semantic feature scales, we design a Multi-level Fusion Module (MFM) and Dual-layer Weight Estimation Unit (DWEU) based on pixel and channel weights.

• 3. Extensive experiments have demonstrated the superiority of the proposed method. Specifically, our method achieves promising results in quantitative experiments on three real underwater image datasets.

Related works

Underwater imaging model

Based on the model of Jaffe¹⁰ and McGlamery¹¹, As shown in Fig. 1a, the imaging process is described as a combination of three components: the direct component (the light reflected from an object that has not been scattered), the backward scattering component (the light reflected from floating particles), and the forward scattering component (the light reflected from an object scattered at small angles). Nevertheless, the direct component is usually neglected, enabling the imaging model to be simplified as follows¹²:

$$\begin{aligned} I_\lambda (x)=J_\lambda (x)t_\lambda (x)+B_\lambda \left( 1-t_\lambda (x)\right) , \end{aligned}$$

(1)

where I(x) represents the degraded underwater image, J(x) denotes the scene radiance (clear image), t(x) signifies the transmission map of I(x), B stands for the global background light, x refers to the pixel coordinate and $\lambda$ indicates a color channel. The forward scattering, $J_\lambda (x)t_\lambda (x)$, is primarily responsible for the blur and fog effects, whereas the backward scattering, $B_\lambda \left( 1-t_\lambda (x)\right)$, leads to contrast degradation and color distortion, $\lambda \in \{R,G,B\}$.

Figure 1

Illustrations of (a) the underwater imaging model and (b) the varying degrees of light color attenuation in water.

In addition, as shown in Fig. 1b, different wavelengths of light are absorbed differently in water, resulting in a significant degradation of underwater image quality with increasing depth and distance from the shore. The energy of the light is absorbed as it penetrates the water. When the depth reaches 4-5 meters, red light, having the longest wavelength, disappears first. The green wavelength is completely absorbed at a depth of 30 meters. Blue wavelengths travel farther due to their higher frequencies, typically reaching more than 50 meters below the surface. This explains why underwater images often appear in blue-green hue.

Model-free UIE methods

In the early stages, researchers focused on adjusting pixel values to produce visually pleasing underwater images. Zhang et al. proposed an iterative thresholding approach based on dual histograms for Attenuated color channel Correction and Detail-preserving Contrast enhancement, respectively¹³. Zhang et al. proposed a locally adaptive color correction method built on the minimum color loss principle and the maximum attenuation map-guided fusion strategy, which reduces the color loss of the color-corrected image¹⁴. Kang et al. developed a general Structural Patch Decomposition and Fusion method, which merges two complementary preprocessed images in perceptually and conceptually independent image space¹⁵. Zhuang et al. proposed a Retinex variational model based on Hyper-Laplacian Reflectance Priors to enhance underwater images¹⁶. Although these model-free methods improve visual quality marginally, they overlook the underwater imaging mechanism, making it difficult to achieve better consistency between subjective and objective results, which may lead to over-enhancement or insufficient enhancement.

Model-based UIE methods

The methods based on physical models estimate potential model parameters using various priors, then restore a clear underwater image by underwater imaging model. Drews et al. proposed an Underwater Dark Channel Prior (UDCP) to estimate underwater transmission and achieved significant improvements using the blue and green channels, which is an adaptation of the DCP method¹⁷. Peng et al. proposed a depth estimation method for underwater scenes based on Image Blurriness and Light Absorption (IBLA), which can be used in the Image Formation Model (IFM) to restore and enhance underwater images¹⁸. Peng et al. developed a Generalized Dark channel Prior (GDCP), and utilized it to estimate underwater scene transmission based on depth-dependent color variation¹⁹. Chiang et al. integrated DCP with wavelength-dependent compensation and image dehazing techniques to mitigate the effects of haze and blur²⁰. These model-based methods tend to be either resource-intensive or highly sensitive to prior assumptions and information. Furthermore, the accurate estimation of complex parameters in underwater imaging poses significant challenges for current physics-based techniques.

Data-driven UIE methods

In recent years, data-driven methods have become a significant research direction in UIE. These approaches rely on vast amounts of data for model training, with the aim of better understanding and restoring underwater images within complex environments. Data-driven methods in UIE primarily fall into two major categories: Generative Adversarial Networks (GANs) and Convolutional Neural Networks (CNNs). Islam et al. presented a conditional generative adversarial network-based model for real-time UIE²¹. Espinosa et al. proposed an architecture built from a minimal encoder-decoder structure to address underwater image degradations while maintaining efficiency²². Li et al. developed a CNN structure that uses a connectionist approach to learn mapping coefficients for color correction and channel-level refinement²³. Yang et al. pioneered a conditional generative adversarial network featuring dual discriminators²⁴. Guo et al. proposed a novel MultiScale Dense Block without constructing the underwater degeneration model and image prior, which effectively combines residual learning, dense concatenation, and multiscale²⁵. Wang et al. proposed a UIE method utilizing both RGB and HSV color spaces, skillfully integrating the advantages of the two color spaces²⁶. Li et al. presented a multi-color space embedding network guided by medium transmission, which successfully improves the visual quality of underwater images by leveraging the advantages of multi-color space embedding²⁷. Zhang et al. proposed a Synergistic Multiscale Detail Refinement via Intrinsic Supervision for UIE, which addresses the limited scale-related features in current UIE methods²⁸. Typically, these underwater image enhancement models utilize conventional deep network architectures designed for general applications, overlooking the distinct features of underwater imaging.

Figure 2

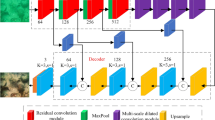
The overall network architecture of MD-Net that follows a decompose-reconstruct process. The branches from top to bottom are Gaussian blur, TMD, and SRD, used for acquiring global background light, transmission maps, and scene radiance respectively. The intermediate sections of TMD and SRD consist primarily of MFM, DWEU, GAP, and convolutional layers. Besides, the red line is a skip connection that carries information from the shallow layer to a deep layer. The far right consists of the Jaffe-McGlamery model (the underwater imaging model), aiming to achieve image detail restoration capabilities beyond the reference image by reconstructing the acquired parameters into underwater images, supervising the accuracy of the three parameters’ acquisition..

Proposed method

The full architecture of the proposed Multiscale Disentanglement Network (MD-Net) is presented in Fig. 2. MD-Net consists of a Gaussian Blur (GB) block, a Transmission Map Disentanglement (TMD) block, a Scene Radiance Disentanglement (SRD) block and a Jaffe-McGlamery model. The GB, TMD and SRD blocks disentangle raw images into global background light, transmission maps and scene radiance (clear images), respectively. The Jaffe-McGlamery model reconstructs the original image using the three parameters described above. Subsequently, we introduce adversarial reconstruction loss (${\mathcal {L}}_A$) that capitalizes on the feature contrast between the original and reconstructed images. This loss function enables a class adversarial learning process, which enhances the image’s disentanglement accuracy and structural consistency. Since the transmission map and scene radiance have the same dependence on pixel values and contrast of the original image, MD-Net adopts the same network structure for TMD and SRD. MD-Net jointly estimates the transmission map and scene radiance map by sharing a network architecture, thereby achieving superior image enhancement results while simultaneously reducing the number of parameters in the network model. This is illustrated in Fig. 3. The steps to disentangle raw images into transmission maps and scene radiance (clear images) are as follows: (1) Multi-level Fusion Module (MFM) employs varying receptive fields ($3\times 3$, $5\times 5$, $7\times 7$) to extract shallow spatial features $I_s$ and multi-layer fusion features $I_{mf}$, (2) the $I_{mf}$ are fed into both the Global Average Pooling layer (GAP) and the Dual-layer Weight Estimation Unit (DWEU) group to obtain the downsampling pooling feature $I_{dp}$ and the dual-level weight feature $I_{dw}$, (3) the $I_d$ is obtained by multiplying $I_{dw}$ and $I_{dp}$, (4) after the multi-scale features $I_m$ are obtained by adding $I_s$ and $I_d$, a convolution layer is adapted to adjust the number of channels for the final output of the transmission maps and scene radiance.

In what follows, we detail the key components of MD-Net, including MFM, DWEU and loss function.

Figure 3

Visual results of TMD and SRD with different structural versions, simple versions are composed of three layers of convolution and complex versions are composed of two MFMs and six DWEUs. Compared to the simple and complex versions of TMD and SRD (b,e,c,f), the current version’s TMD and SRD (a,d) have already achieved excellent parameter estimation..

Multi-level fusion module

Figure 4

MFM mainly consists of convolutional layers with varying kernel sizes and two convolutional blocks. The convolutional kernels of the three branches increase sequentially from top to bottom, with the red line at the bottom indicating skip connections. Convblock-1 comprises two convolutional layers a ReLU function, and a normalization operation. Convblock-2 comprises two convolutional layers, a ReLU function, and a sigmoid function..

Different sizes of receptive fields have different perceptual ranges for images. For example, the small receptive field can capture local detailed features but may need to include broader contextual information. The large receptive field can capture global information but may overlook some detailed features. To combine their properties for UIE, we design an MFM shown in Fig. 4 to capture multi-layer fusion features $I_{mf}$ that integrate global information and shallow spatial features $I_s$ for multiscale fusion.

Specifically, we first extract shallow spatial features through convolution layers with different receptive field sizes ($3\times 3$, $5\times 5$, $7\times 7$), which capture diverse levels of spatial information features ($I_s^{11}$, $I_s^{22}$, $I_s^{33}$) from the input images. As shown in Fig. 5, $I_s^{11}$ emphasizes the local details of the fish, while $I_s^{22}$ and $I_s^{33}$ contain the fine global structure. However, as observed in the first row of Fig. 5, noise artifacts still persist in the feature maps after one layer of convolution. Therefore, we propose the Convblock-1 $(Conv_1)$ to further capture detailed information from shallow layers:

$$\begin{aligned} I_S={\left\{ \begin{array}{ll}I_s^1,& I_s^1=Conv_1(I_s^{11}),\\ I_s^2,& I_s^2=Conv_1(I_s^{22}),\\ I_s^3,& I_s^3=Conv_1(I_s^{33}),\end{array}\right. } \end{aligned}$$

(2)

where $I_s$ refers to the collective term for shallow spatial features, each includes two convolutional layers of the original kernel size, a ReLU activation and a normalization layer. Notably, convolution blocks perform standard convolution operations within each smaller block, which effectively reduces the computational cost associated with convolution. Compared with Fig. 5b $I_s^{22}$ and (c) $I_s^{33}$, Fig. 5e $I_s^2$ and (f) $I_s^3$ show increased texture details and the removal of artifacts.

Figure 5

Visualization of feature maps $I_s^{11}$ to $I_s^{33}$ and $I_s^{1}$ to $I_s^{3}$. Higher brightness denotes greater weight. The brightness value is ranged in [0,1].

Subsequently, we perform tensor concatenation and feature fusion to acquire dynamic weights $W_f$:

$$\begin{aligned} W_f=Conv_2(cat(I_s^1,I_s^2,I_s^3)), \end{aligned}$$

(3)

where cat denotes a channel-wise concatenation. Convblock-2 $(Conv_2)$ generates dynamical weight $W_f$ for feature fusion, which includes two $3\times 3$ convolution layers, a ReLU activation and a Sigmoid function. $W_f$ dynamically weights different input features according to the $Conv_2$.

To allocate weights to each branch, we perform tensor splitting on $W_f$ to obtain $W_1$, $W_2$, $W_3$:

$$\begin{aligned} W_1,W_2,W_3=spl(W_f), \end{aligned}$$

(4)

As illustrated in Fig. 6, $W_1*I_s^1$, $W_2*I_s^2$, $W_3*I_s^3$ obtain better global structure and finer local details than $I_s^1$, $I_s^2$ and $I_s^3$ in Fig. 5, demonstrating that the dynamic weighting of $W_f$, $W_1$, $W_2$ and $W_3$ achieves superior results compared to direct feature fusion. The multi-layer fusion feature $I_{mf}$ obtained by fusing the above three fully integrates the information of image features at various scales of receptive fields.

Figure 6

Visualization of feature maps $W_f$, $W_1$ to $W_3$, $W_1*I_s^1$ to $W_3*I_s^3$ and $I_{mf}$. Higher brightness denotes greater weight. The brightness value is ranged in [0,1].

Dual-layer weight estimation unit

To learn complex relationships between illumination features and color information, we sequentially apply DWEU, which integrates channel and pixel weight estimation as shown in Fig. 7, to capture the dual-level weight feature $I_{dw}$ in SRD and TMD blocks.

Figure 7

DWEU takes the output of the MFM as input, passes it through a convolutional layer, and subsequently directs the features separately to the pixel estimation unit positioned above and the channel estimation unit located below. Next, the weighted sum proceeds through an additional convolutional layer combined with the unprocessed input features. Eventually, the assigned weight features are input to the subsequent module..

Specifically, we first use a convolutional layer with a kernel size of $3\times 3$ to extract features from $I_{mf}$. Then, we input it into the channel estimation unit and pixel estimation unit respectively to obtain the pixel weights and the channel weights $W_c$.

For obtaining $W_p$:

$$\begin{aligned} W_p=conv.s(conv.r.i(I_i)), \end{aligned}$$

(5)

where $I_i$ are pr-extracted features from convolution, conv.r.i includes a convolutional layer with the kernel size of $3\times 3$ for processing image features followed by a ReLU activation for nonlinear transformation and a normalization layer for standardizing feature maps, conv.s includes a convolutional layer with the kernel size of $3\times 3$ for further processing the feature maps followed by a Sigmoid function to compress the output values into the [0, 1] range.

For obtaining $W_c$:

$$\begin{aligned} W_c=conv.s(conv.r(gap(I_i))), \end{aligned}$$

(6)

where gap represents the global average pooling layer used to extract global features, conv.r is used to extract and nonlinearly transform channel features.

Next, the estimated weights are used for pixel-wise weighted allocation and channel-wise weighted allocation of $I_i$ to obtain $I_p$ and $I_c$:

$$\begin{aligned} {\left\{ \begin{array}{ll} I_p=W_p*I_i, \\ I_c=W_c*I_i,\end{array}\right. } \end{aligned}$$

(7)

where $I_p$ represents the pixel-weighted feature with a size of $1\times H\times W$, and $I_c$ represents the channel-weighted features with a size of $C\times 1\times 1$. We pass the sum of $I_p$ and $I_c$ through a convolutional layer to obtain the final dual-level weight features $I_{dw}$:

$$\begin{aligned} I_{dw}=conv(I_p+I_c), \end{aligned}$$

(8)

where conv is used to balance illumination features and color information, the size of $I_{dw}$ is $C\times H\times W$. Fig. 8 displays the gray visual comparison of $I_p$, $I_c$ and $I_{dw}$. As shown in Fig. 8a, $I_p$ enhances the contrast between pixels, but the contour details of the image are not clear. In Fig. 8b, $I_c$ exhibits better smoothness. In contrast, Fig. 8c shows that $I_{dw}$ integrates the advantages of pixel and channel weight estimation, making the image not only more prominent in details but also enhancing the overall smoothness.

Figure 8

Visualization of feature maps $I_p$, $I_c$ and $I_{dw}$. Higher brightness denotes greater weight. The brightness value is ranged in [0,1].

By performing operations mentioned above, DWEU completes one iteration. Fig. 9 shows the visual comparison of DWEU after 4 iterations. As shown, compared to Fig. 6h, Fig. 9a exhibits better color reproduction and low light enhancement effects, confirming that the construction of a dual-level weight estimation unit can significantly improve visibility and color restoration. It is noteworthy that four iterations are sufficient to produce satisfactory underwater colors and image visibility.

Figure 9

Visual comparison of different DWEU iterations.

Loss function

The overall loss function of MD-Net consists of three components: adversarial reconstruction loss (${\mathcal {L}}_{A}$), color correction loss (${\mathcal {L}}_{C}$) aimed at preventing oversaturated colors, and mean square error loss (${\mathcal {L}}_{M}$) to further improve the quality of target image. The fundamental concept of adversarial learning involves optimizing the model within a “game” framework. Building on this principle, we introduce a feature-based ${\mathcal {L}}_{A}$ to enable a pseudo-adversarial process. This feature-level contrastive loss replaces the conventional generative adversarial game, allowing the network to focus on pixel-level discrepancies and the consistency of high-level image features. The ${\mathcal {L}}_{A}$ is formulated as the following mean squared error:

$$\begin{aligned} {\mathcal {L}}_{A}=\frac{1}{n}\sum _{i=1}^{n}(I(x)_{i}-x_{i})^2, \end{aligned}$$

(9)

where x represents the original underwater image, and $I(x)_{i}$ represents the reconstructed image using the underwater imaging model presented in Eq. (1). To limit color correction oversaturation, we introduced color correction loss (${\mathcal {L}}_{C}$). ${\mathcal {L}}_{C}$ first sums and averages each color channel c in the color channel set $\lambda \in \{R, G, B\}$, then calculates the square of the difference between this mean and 0.5 (assuming the scene’s average reflectance is gray, known as the gray world assumption) using the ${\mathcal {L}}_{2}$ norm, to correct color deviations from the gray world assumption. Its formula is given as:

$$\begin{aligned} {\mathcal {L}}_{C}=\sum _{c\in \lambda }\left\| \mu ({\hat{S}}_{i}^{c})-0.5\right\| _{2}^{2},\lambda \in \{R,G,B\},\end{aligned}$$

(10)

where $\mu (\hat{S}_{i}^c)$ represents the mean of the color channel c. ${\mathcal {L}}_{M}$ is defined as:

$$\begin{aligned} {\mathcal {L}}_{M}=\frac{1}{n}\sum _{i=1}^{n}({\hat{S}}_{i}-S_{i})^2, \end{aligned}$$

(11)

where ${\hat{S}}_{i}$ represents the scene radiance, $S_{i}$ is the ground truth, and n is the number of pixels. This function computes the average of the squared differences between the predicted values and ground truth.

The overall loss function is defined as follows:

$$\begin{aligned} {\mathcal {L}}_{total}={\mathcal {L}}_{D}+{\mathcal {L}}_{C}+{\mathcal {L}}_{M}. \end{aligned}$$

(12)

Experiments

Experiment settings

We train MD-Net using PyTorch 2.1 framework, running on an Intel(R) i9-12900K CPU, 64GB of RAM, and an NVIDIA RTX 4090 GPU. We set the learning rate to $10^{-4}$ and use the Adam optimizer for network optimization. The model is trained for 50 epochs with a batch size of 4, and all input images are resized to $350\times 350$ pixels. We compared the proposed method with seven UIE methods including four non-data-driven methods (DCP²⁹, UDCP¹⁷, ACDC¹³, UIEF³⁰) and data-driven methods (PUIE-Net³¹, P2CNet³², TCTL-Net³³). For a fair comparison, we employ the source code provided by the authors, retrain each method on our training set and produce the best enhancement results. Our performance evaluation utilizes real UIE benchmark datasets containing LSUI³⁴ and UIEB³⁵ datasets. Each dataset is divided into a training dataset and a testing dataset. For training, we use 3,794 images from the LSUI³⁴ dataset and 800 images from the UIEB³⁵ dataset. For testing, we use the rest 485 images from the LSUI³⁴ dataset (Test-485) and the rest 90 images from the UIEB³⁵ dataset (Test-90). It is noteworthy that the current underwater image datasets have certain limitations. As depicted in Fig. 10, the reference images in panels (a), (c), and (d) exhibit substantial color distortion, whereas the detailed textures in the reference images of panels (b), (e), and (f) appear less refined compared to the results produced by our method. We employ four metrics to measure the performance of different methods on Test-485, and Test-90. These metrics include full-reference and non-reference metrics which are Peak Signal-to-Noise Ratio (PSNR)³⁶, Structural Similarity Index Measure (SSIM)³⁷, Underwater Color Image Quality Evaluation (UCIQE)³⁸ and Underwater Image Quality Measure (UIQM)³⁹. Higher PSNR³⁶ and SSIM³⁷ scores indicate that the enhanced images more closely resemble the reference images in both content and structure. Higher UCIQE³⁸ and UIQM³⁹ values indicate a better balance among colorfulness, sharpness, and contrast.

Figure 10

Visual comparison of reference images and our proposed MD-Net for test-485³⁴ and Test-90³⁵. The second row is the enlarged pictures of the red boxes in the first row..

Figure 11

The visual comparison of various methods on bluish underwater images from Test-485³⁴ and Test-90³⁵. The compared methods are DCP²⁹, UDCP¹⁷, ACDC¹³, PUIE-Net³¹, P2CNet³², UIEF³⁰, TCTL-Net³³, and the proposed MD-Net, respectively..

Figure 12

The visual comparison of various methods on greenish underwater images from Test-485³⁴ and Test-90³⁵. The compared methods are DCP²⁹, UDCP¹⁷, ACDC¹³, PUIE-Net³¹, P2CNet³², UIEF³⁰, TCTL-Net³³, and the proposed MD-Net, respectively..

Figure 13

The visual comparison of various methods on yellowish images from Test-485³⁴ and Test-90³⁵. The compared methods are DCP²⁹, UDCP¹⁷, ACDC¹³, PUIE-Net³¹, P2CNet³², UIEF³⁰, TCTL-Net³³, and the proposed MD-Net, respectively..

Figure 14

The visual comparison of various methods on low visibility images from Test-485³⁴ and Test-90³⁵. The compared methods are DCP²⁹, UDCP¹⁷, ACDC¹³, PUIE-Net³¹, P2CNet³², UIEF³⁰, TCTL-Net³³, and the proposed MD-Net, respectively..

Qualitative evaluation

We conduct visual comparisons among different methods using Test-760, Test-485 and Test-90, as shown in Figs. 11, 12, 13, and 14. As shown in Figs. 11b and 12b, the overall illumination of the image is improved under the DCP²⁹ method, but some areas exhibit unnatural color balance. UDCP¹⁷ enhances the color vividness, but there are issues with color oversaturation in Figs. 12c and 13c. ACDC¹³ achieved good results in underwater image visibility, but it also increased color bias as shown in Figs. 12d and 13d. PUIE-Net³¹ effectively addresses UIE by breaking it down into distribution estimation and a consensus process, resulting in relatively satisfactory visualization but its performance to deblur images needs improvement, as evidenced in Figs. 13e and 14e. As depicted in Figs. 11f and 14f, P2CNet³² restores image details, yet it does not remove color casts and introduces severe artificial colors. UIEF³⁰ adjusts the color casts and enhances brightness realistically but introduces purple artifacts and unnatural sharpness in Figs. 11g and 14g. As shown in Figs. 11h and 13h, while TCTL-Net³³ achieves color correction, the problems of darkness and gray artifacts are common in the enhanced images. In contrast, the proposed MD-Net effectively corrects color casts, leveraging the designed SRD. It achieves favorable results by enhancing low contrast images under poor lighting conditions, owing to the fusion of the disentanglement strategy and the Jaffe-McGlamery model¹².

Quantitative assessment

We evaluate the performance of various UIE approaches using PSNR³⁶, SSIM³⁷, UCIQE³⁸ and UIQM³⁹ on Test-485 and Test-90, as summarized in Table 1. For PSNR³⁶ and SSIM³⁷, the proposed MD-Net yields four best scores, which indicates that our results closely resemble the reference images in terms of both content and structure. For UCIQE³⁸, in contrast to our competitors, MD-Net achieves a best score and a second-best score, demonstrating that the proposed approach mitigates non-uniform color bias, reduces blurriness and enhances contrast. Besides, MD-Net secures two second-best UIQM³⁹ score, showcasing exceptional performance in terms of colorfulness, sharpness, and contrast enhancement.

Table 1 The average scores for PSNR³⁶, SSIM³⁷, UCIQE³⁸, UIQM³⁹ and Mean using different methods on TEST-485 and TEST-90. The best and second-best performances are highlighted in italics and bold, respectively.

Ablation study

We systematically analyze the impact of various components within MD-Net through comprehensive ablation studies on bluish, greenish, yellowish and low-visibility degeneration scenes, including 3 settings: (1) MD-Net without SRD and Disentangle strategy (Our-settingI), (2) MD-Net without Disentangle strategy (Our-settingII), (3) full method (Our). Figure 15 presents the visual results. Our-settingI underperforms in both mitigating color casts and improving visibility. Our-settingII improves color and increases visibility but fails to fully restore color casts. Our full method not only attains true-to-life colors but also enhances sharpness and visibility. Furthermore, we show a quantitative comparison in Table 2. As depicted, the PSNR³⁶ and SSIM³⁷ index results show a progressive improvement from Our-setting I to Our-setting II, as the SRD module is incorporated. Compared with Our-settingII, our comprehensive approach achieves the highest PSNR³⁶ and SSIM³⁷ scores, underscoring the superior performance of our MD-Net in restoring underwater content and structure.

Figure 15

Ablation study on underwater images exhibiting various color degradation.

Table 2 The average PSNR³⁶ and SSIM³⁷ scores from the ablation study on TEST-90. The best and second-best performances are highlighted in italics and bold, respectively.

Complexity and runtime

We compare the FLOPs (G) and trainable parameters (M) of diverse UIE methodologies to gauge their computational efficiency, as illustrated in Table 3. The implementations of DCP²⁹, UDCP¹⁷ and UIEF³⁰ are executed within the Matlab environment, and as such, they do not have associated FLOPs and parameters. While MD-Net did not perform well in FLOPs detection on image sizes 256 $\times$ 256, 512 $\times$ 512 and 1024 $\times$ 1024 compared to other competitors, its architecture parameters has resulted in outstanding performance. Table 4 illustrates that MD-Net achieves respectable processing speeds across various image dimensions and notably achieves the second-fastest speed at a resolution of 256 $\times$ 256 and 512 $\times$ 512, highlighting its ability to efficiently handle diverse image sizes.

Table 3 Comparison of complexity across various methods. The best and second-best performances are highlighted in italics and bold, respectively.

Table 4 The average runtime of various methods over one hundred trials on different image sizes. The best and second-best performances are highlighted in italics and bold, respectively.

Figure 16

These images display application tests for various underwater imaging tasks. The top row illustrates underwater depth estimation, the second row shows underwater edge detection, the third row presents underwater keypoint detection, the fourth row features underwater saliency detection, and the bottom row demonstrates underwater image segmentation. The compared methods are DCP²⁹, UDCP¹⁷, ACDC¹³, PUIE-Net³¹, P2CNet³², UIEF³⁰, TCTL-Net³³, and the proposed MD-Net, respectively..

Application tests

We show the effectiveness of our MD-Net through various underwater application tests in Test-90³⁵, including depth estimation, edge detection, keypoint detection, saliency detection, and image segmentation. For underwater depth estimation, we employ the non-local prior⁴⁰, utilize the Canny operator⁴¹ for underwater edge detection, employ the SIFT keypoint detection⁴² for underwater keypoint detection, adopt BASNet⁴³ for underwater saliency detection, and apply a superpixel-based clustering algorithm⁴⁴ for underwater image segmentation. All results are illustrated in Fig. 16. Although the generated depth maps and edge detection results did not rank first among competitors, they still demonstrated commendable performance. Additionally, MD-Net detected more key points, and captured sharper structures. Moreover, MD-Net’s segmentation results demonstrated higher consistency and accuracy, while its saliency maps contained more distinct objects and sharper boundaries. These findings suggest that MD-Net effectively can effectively enhance both underwater image segmentation and saliency detection.

Conclusion

This paper proposes MD-Net, a multi-scale disentanglement network for underwater image enhancement. MD-Net embeds a multi-scale feature fusion CNN and an underwater imaging model into the architecture of underwater image inverse-reconstruction through a disentanglement strategy. Specifically, the disentangled physical parameters (global background light, transmission map and scene radiance) are fed into the underwater imaging model to reconstruct underwater images. Furthermore, the designed multiscale feature fusion CNN integrates shallow spatial features and deep semantic features by focusing on multi-level receptive field features, and allocation of pixel and channel weights. We conducted extensive experiments on MD-Net, including qualitative and quantitative comparative experiments, as well as a series of computer vision application experiments. Experimental results demonstrate that the proposed method outperforms existing state-of-the-art methods in terms of color cast correction and visibility enhancement on different datasets, providing significant performance enhancement in multiple computer vision tasks.