Introduction

Microirrigation, as a precise and efficient irrigation technology, is widely used worldwide because of its controllable irrigation and fertilization quantities, adaptability to different terrains, and labor cost savings1,2,3. According to statistics, China has 5.27 million hectares (Mha) of farmland utilizing microirrigation technology, accounting for approximately one-third of the world’s total microirrigation area, making it the leading country in terms of microirrigation applications globally4.

Nevertheless, in China, the adoption rate of precision irrigation technology remains relatively low, with sprinklers and microirrigation accounting for only 13.7% of the total irrigated area. China is a mountainous country with limited flat land, and the per capita arable land area is only 0.078 hectares. Therefore, it is essential to develop advanced irrigation technologies in hilly areas to increase crop yields. Compared with traditional surface irrigation, the most significant feature of microirrigation is pressurized irrigation. Water is transported from the source through various levels of irrigation pipelines under pressure, allowing users to control the system’s pressure for the centralized management of complex terrains or large-scale irrigation systems5,6,7,8,9. In hilly areas, variations in elevation, hydraulic friction losses, and differences in the control areas of rotating irrigation systems result in significant pressure fluctuations within the irrigation pipeline network. To ensure the safety of the system and irrigation uniformity, multistage pressure regulation equipment must be used to control the irrigation system10,11,12,13,14,15,16,17.

For hilly irrigation systems with complex topography and significant elevation changes, multistage pressure regulation equipment can work together to gradually adjust the high-pressure water from the mountaintop to different elevation levels of the rotating irrigation system, delivering water to the fields according to the working pressure requirements of the emitters18,19,20,21 The advantage of this approach is that the system’s pipeline design becomes more flexible and better suited to complex terrains, avoiding excessive pressure reduction tasks at any single stage of the pressure regulation equipment, which would otherwise increase the demands on equipment performance and pipelines, thereby increasing system investment costs22,23.

The common pressure regulation equipment used in irrigation systems, from the water source to the field, includes pressure relief valves for the main pipe, pressure regulators for the submain pipe, pressure and pressure regulators for the drip tapes inlet, and pressure compensating emitters at the end of the system24,25,26,27.

The basic working principle of these pressure regulating devices is the same: they dissipate the high upstream water pressure into a predetermined lower pressure (Fig. 1). This means that regardless of where the pressure regulating device is installed in the system, it adjusts only the upstream pressure and does not have a direct regulating function for the pressure changes in the downstream irrigation system. Therefore, pressure regulators located closer downstream, such as pressure compensating drip emitters, have a more direct effect on improving water uniformity. However, since each device controls a smaller area, multiple units are needed, which can increase the overall investment in the system. On the other hand, pressure regulating devices located upstream, such as main and submain pipe pressure relief valves, control larger areas but cannot eliminate pressure discrepancies at the inlets of drip tapes and emitters. In hilly areas, these devices must be used in conjunction with other downstream pressure regulating devices to achieve better irrigation uniformity.

Clearly, the selection and combination of pressure-regulating devices in hilly regions directly affect the design complexity, economy, and irrigation uniformity of the system.

Currently, the most commonly used pressure control scheme in hilly drip irrigation systems involves installing pressure relief valves on the main and branch lines in conjunction with pressure compensating drip tapes in the field. This approach balances the ease of system design with high irrigation uniformity, as the pressure relief valves only need to ensure that the water pressure does not exceed the pressure limits of the pipelines and emitters, whereas the pressure compensating emitters ensure high irrigation uniformity in the field.

However, this pressure control scheme has a high initial investment due to the significant cost of individual pressure relief valves. Extensive use of these valves is often uneconomical for small-scale irrigation systems, particularly in hilly areas where the controlled area is usually small and where rotating irrigation groups cover irregular plots28,29,30. Additionally, the large number of pressure-compensating drip emitters needed increases the total investment, since the price of pressure compensating drip tapes is typically 4 to 8 times greater than that of non-pressure compensating options. The initial investment is a major concern for farmers in developing countries. As a result, optimizing the selection and configuration of irrigation pressure control devices is crucial to reduce system costs when promoting and developing microirrigation technology in the hilly areas of these countries.

An additional level of pressure regulation device known as the pressure regulator for lateral (PRL) at the inlet of the drip tape exists between the submain pressure regulators and pressure compensating emittes. The PRL can eliminate pressure discrepancies at the inlet of the drip tape along the submain pipe direction. Therefore, the use of PRLs makes it possible for hilly areas to utilize economical non-pressure compensating drip tapes. Additionally, since the PRL protects the drip tape, it allows for higher pressures on the submain pipes, which helps reduce the need for branch pressure regulators. In recent years, with advancements in the research and development of PRL technologies, performance improvements, and industrial production, the application of PRL in hilly drip irrigation systems has gradually increased31,32,33.

However, very little information is available regarding the design methods for hilly drip irrigation systems that utilize PRL. Users lack theoretical guidance for selecting and configuring equipment, especially when they need to comprehensively assess system design, investment costs, and irrigation uniformity. The complex hilly terrain makes it difficult to weigh these factors. The method of constructing mathematical models and utilizing computer tools to design and solve optimization problems has been widely applied in the optimization design of complex systems and is considered an efficient and accurate approach34,35,36.

In summary, this article proposes a design method for hilly drip irrigation systems utilizing PRLs that leverages computer programming techniques. Based on this, a real hilly drip irrigation system is taken as an example for systematic design optimization, and the differences in design schemes, investment costs, and irrigation uniformity before and after optimization are compared. This study aims to provide design solutions and irrigation uniformity evaluation methods for the application of PRL in drip irrigation systems in hilly areas. This research will help developing countries reduce microirrigation system investments, improve irrigation uniformity, and better promote microirrigation technology.

Materials and methods

The irrigation system is located in a plantation in Wumao Township, Yuanmou County, Yunnan Province. The area is hilly, covering 6.67 ha. A water storage tank is built at the top of the hill, with an elevation of 1,173 m. The maximum elevation difference in the area is 53 m, utilizing natural elevation differences for gravity-fed drip irrigation. The crops planted are avocados, with the fruit trees cultivated in strip terraces along the contour lines.

Figure 1 shows a schematic diagram of the pressure regulation characteristics of the irrigation pressure regulating device. As illustrated, when the inlet pressure is low, the outlet pressure of the regulating device increases as the inlet pressure increases. When the inlet pressure exceeds a certain threshold, the outlet pressure of the pressure regulating device fluctuates within a certain range around its preset pressure. This fluctuation range is referred to as pressure deviation, which is influenced by the device’s flow rate, inlet pressure, and manufacturing tolerances. A more efficient regulating device will exhibit a smaller output pressure deviation under varying operating conditions.

Fig. 1
figure 1

Schematic diagram of the pressure regulation characteristics of irrigation pressure regulating devices.

Full size image

Original irrigation system

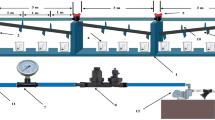
The original irrigation system was established in 2019, and the layout of the pipeline network is shown in Fig. 2. The entire irrigation system is divided into four irrigation sectors, numbered 1, 2, 3, and 4, with areas of 2.00, 1.86, 1.53, and 1.28 ha, respectively. The main pipeline uses Φ90 PVC pipes (internal diameter of 80 mm), whereas the submain pipes use Φ75 PVC pipes (internal diameter of 70 mm). The drip tape has an outer diameter of 16 mm, with a nominal flow rate of 1.4 L/h for the emitters and an emitter spacing of 40 cm. The distance between adjacent drip tapes is 5 m, and the tapes are connected via bypass to the submain pipes. During irrigation, a rotational irrigation system is implemented, with each of the four irrigation sectors forming one rotation group.

The hydraulic performance of the pressure compensating drip tape is shown in Fig. 3, with a flow index of 0.0407 and a flow coefficient of 1.2838. The bursting pressure of the pressure compensating drip tape used in the original system is 0.30 MPa. When excessive elevation differences lead to high pressures at the submain pipe outlets, which threatens the safety of the drip tape, a pressure-reducing valve must be installed (as shown in the blue pressure-reducing valve in Fig. 3). This pressure-reducing valve is an adjustable preset type, with each valve manually adjusted to set the output pressure (downstream pressure) at 20 m. The original system requires five pressure-reducing valves.

Fig. 2
figure 2

Original irrigation system.

Full size image
Fig. 3
figure 3

Hydraulic performance of the pressure compensating drip emitter.

Full size image
Fig. 4
figure 4

Modified irrigation system.

Full size image
Fig. 5
figure 5

Hydraulic performance of the non-pressure compensating drip irrigation emitter.

Full size image

Renovated irrigation system

As shown in Fig. 4, the original system’s drip irrigation tape bypass and pressure compensating drip irrigation tape were replaced with PRLs and non-pressure compensating drip irrigation tape, resulting in a renovated drip irrigation system. The system’s water source, main and submain pipe dimensions, and layout remain consistent with those of the original system. The PRL now replaced the original bypass connection between the drip tape and the submain. The PRL selected for the system retrofit is independently developed and designed by our team. Compared to traditional PRLs, its biggest advantage is that its output pressure is minimally affected by changes in inlet pressure and flow rate. This performance advantage makes it particularly suitable for irrigation systems in complex hilly terrains. Detailed information regarding the main structures and operational principles of these PRLs is provided in Zhang and Li (2017)37.

With the PRLs installed at the inlet of the drip irrigation tapes to provide protection, the number of pressure-reducing valves required for the renovated system has been reduced from five to two. The hydraulic performance of the emitters when non-pressure compensating drip irrigation tape was used in the renovated system is illustrated in Fig. 5, with a flow index of 0.5411 and a rated emitter flow rate of 1.4 L/h. The outer diameter of the drip irrigation tape and the emitter spacing are the same as those used in the original system with pressure compensating drip irrigation tape, measuring 16 mm and 40 cm, respectively. The bursting pressure of the drip irrigation tape was 0.20 MPa. An overview of the modified system and the connection method for the PRL are shown in Fig. 6.

Fig. 6
figure 6

A current view of the modified hilly drip irrigation system with PRL installation.

Full size image

Hydraulic performance assessment methods for irrigation systems

Figure 7 shows the process of designing and assessing the hydraulic performance of the drip irrigation system with PRL installation: (1) A mathematical model for the PRL output pressure that comprehensively considers manufacturing deviations, inlet pressure effects, and flow rate impacts is established based on a large amount of measured PRL data. (2) Various levels of pipes should be selected and arranged according to topographic maps and planting needs, and a parametric statistical analysis of pipe positions and dimensions should be conducted. (3) MATLAB programming was used to perform preliminary hydraulic calculations for the irrigation system, and the pressure and flow distributions throughout the system were obtained as basic parameters for subsequent calculations. (4) The mathematical model of the pressure regulating device is embedded into the irrigation system calculation program for hydraulic performance simulation analysis. (5) A comprehensive evaluation of the system is conducted on the basis of the calculation results.

Fig. 7
figure 7

Flowchart of the design and hydraulic performance evaluation method for drip irrigation systems with PRL installation.

Full size image

Establishing a mathematical model for the PRL outlet pressure

The actual outlet pressure Pout of the pressure regulator is influenced by the inlet pressure Pin, flow rate (Q), and manufacturing deviation (M), resulting in a discrete distribution around its preset nominal pressure value. Pout is affected by Pin and (Q) as part of the pressure regulation characteristics of the pressure regulator itself, which is related to its operating conditions. In contrast, (M) represents the random deviations in performance caused by manufacturing processes and is independent of the specific operating conditions of the pressure regulator. Therefore, when the model for the outlet pressure of the pressure regulator is constructed, Pout is first defined as a function of Pin and (Q). Then, the manufacturing deviation (M) is added to this outlet pressure function, causing Pout to follow a random normal distribution with a certain standard deviation.

Figure 8 shows the relationships of the inlet and outlet pressures during the pressure regulation stage for four different performance pressure regulators (A, B, C, and D) under a flow rate of 1000 L/h (Fig. 8a), the relationship between the outlet pressure and flow rate under an inlet pressure of 0.20 MPa (Fig. 8b), the linear fitting results of the relationship between the starting pressure and flow rate (Fig. 8d), and the outlet pressure of the pressure regulators under different manufacturing deviations (Fig. 8c). The A-type PRL with the best performance was used for the modification of the drip irrigation system. Detailed information regarding the main structures and operational principles of these PRLs is provided in Zhang and Li (2017)37.

As shown in Fig. 8, the correlation coefficients R2 are all greater than 0.85, indicating a good fitting effect. The slopes of the linear fits obtained in Fig. 6a and b, and 6c represent the pressure increase coefficient kp due to an increase in Pin leading to a rise in Pout, the pressure decrease coefficient kQ due to an increase in Q leading to a decrease in Pout, and the pressure increase coefficient k0 due to an increase in Q leading to a rise in starting pressure Pa.

Therefore, without considering manufacturing deviations, Pout can be expressed as:

$${P_{{\text{out}}}} {\text{=}}{P_{{\text{out0}}}}+{k_{\text{p}}}\left( {{P_{in}} - {P_{\text{a}}}} \right)+{k_{\text{Q}}}\left( {Q - {Q_{\hbox{min} }}} \right)$$
(1)
$${P_{\text{a}}} {\text{=}}{P_0}+{k_0}\left( {Q - {Q_{\hbox{min} }}} \right)$$
(2)

where Pout, Pin and Pa represent the outlet pressure, inlet pressure, and the minimum inlet pressure required for operation of the PRL, respectively, in MPa; Q and Qmin represent the flow rate and the minimum applicable flow rate of the PRL, respectively, in L/h; P0 and Pout0 represent the starting pressure and outlet pressure of the pressure regulator at the flow rate Qmin, respectively, in MPa; kP and kQ represent the pressure increase coefficient and pressure decrease coefficient of the PRL, respectively; kP indicates the increase in outlet pressure due to an increase in inlet pressure; kQ indicates the decrease in outlet pressure due to an increase in flow rate; and k0 represents the pressure increase coefficient due to an increase in flow rate leading to an increase in starting pressure.

Assuming that Pout follows a random normal distribution influenced by the manufacturing deviation M (Fig. 8c), the outlet pressure model of the pressure regulator considering the manufacturing deviation M can be expressed as:

$${P_{{\text{out}}}}(M)=NORMINV(s,{P_{{\text{out}}}},\sigma )$$
(3)
$$s=Random\left( {0,1} \right)$$
(4)
$$\sigma ={P_{{\text{out}}}} \cdot {C_{{\text{VM}}}}$$
(5)

where s is a number randomly generated between 0 and 1 by the Random function, representing random probability; Pout is the outlet pressure of the pressure regulator generated by Eq. (1) under certain inlet pressure and flow rate conditions, not considering the impact of manufacturing deviation; σ is the standard deviation; NORMINV is the inverse function of the normal distribution probability density function; and the CVM represents the manufacturing deviation of the pressure regulator.

Fig. 8
figure 8

Fitting results of outlet pressure and minimum operating pressure of the PRL under the influence of various factors.

Full size image

The measured results of the outlet pressure of the PRL are presented and compared with the corresponding theoretical calculations in Fig. 9. The findings reveal that Eq. (3) demonstrates a high level of accuracy in the theoretical calculations, with an nRMSE (normalized root mean square error) of less than 1.0%. This indicates a very high level of accuracy in the model’s predictions compared with the observed values.

Fig. 9
figure 9

Theoretical and measured results of the outlet pressure of PRL.

Full size image

Preliminary hydraulic calculations for the irrigation system

For most hilly drip irrigation systems, the shapes of the irrigation plots are often irregular, and the lengths of the drip tapes vary within the system. Taking the irrigation plot labeled No. 1 in Figs. 1 and 3 as an example, the following method uses Origin’s image digitization tool to measure the lengths of various drip tapes within a complex drip irrigation system.

Using Origin’s image digitization tool, the field image is automatically gridded, with the x-axis overlapping with the branch pipe. Figure 10 shows the results of grid-based point capture along the field boundary after using Origin’s image digitization tool for equidistant spacing. The identified feature points are sufficient to represent the characteristics of the plot shape. However, depending on the pixel differences, the x value spacing of the automatically recognized points may not equal the actual spacing of the adjacent drip tapes. Therefore, a linear interpolation method is employed for the x values, setting the distance from each lateral pipe inlet (branch water outlet) to the branch pipe inlet as the x-external interpolation for the desired lateral pipe length. The automatically recognized data serve as input, allowing the calculation of the true lengths of the drip tapes on the basis of their actual positions.

Fig. 10
figure 10

Obtaining the installation length of the drip tape based on the shape of the field.

Full size image

When the length of the drip tape is known, the total flow rate of the drip tape (PRL flow rate) can be estimated via the following formula:

$${Q_{\text{D}}}=\frac{{{L_{\text{D}}}}}{{{L_{\text{L}}}}} \cdot {q_{\text{e}}}$$
(6)

where QD represents the estimated total flow rate of the drip tape, L/h; LD denotes the total length of the drip tape, m; LL indicates the spacing between emitters, m; and qe is the rated flow rate of the emitters under the nominal preset pressure conditions of the pressure regulator, L/h.

Figure 11 shows a schematic diagram of the hydraulic calculations for the submain. When the inlet pressure HB of the submain and the total flow rate QD of the drip tape are known, the pressure at the submain bleeders (the inlet pressure of the PRL or pressure compensation drip tape inlet) can be estimated via the following formula:

$$\Delta {{\text{H}}_{{\text{B}}i}}=f\frac{{Q_{{Bi}}^{m}}}{{{D^{\text{b}}}}}{L_{\text{B}}}{\text{+}}{L_{\text{B}}} \cdot {I_{{\text{B}}i}}$$
(7)
$${Q_{Bi}}={Q_B} - {q_{B1}} - \cdots - {q_{Bi}}$$
(8)
$${{\text{h}}_{\text{B}}}i={{\text{H}}_{\text{B}}} - \Delta {{\text{H}}_{{\text{B0}}}} - \cdot \cdot \cdot - \Delta {{\text{H}}_{{\text{Bn}} - {\text{1}}}}$$
(9)

where ∆HBi represents the head loss along the submain, m; IBi denotes the slope between adjacent branch water distribution outlets; f represents the head loss coefficient; QBi represents the flow rate in the segment between adjacent submain bleeders, in L/h; D represents the internal diameter of the pipeline, mm; LB represents the spacing between submain bleeders (drip tapes spacing), m; m represents the flow exponent; and b represents the diameter exponent. For the PVC submain, f, m and b are typically taken as 0.464, 1.77, and 4.77, respectively; qBi is the flow rate at the submain bleeders (equal to the total flow rate of the connected drip tapes QD), L/h; HB is the inlet pressure of the submain, m; and hBi is the pressure at the branch water distribution outlet (the inlet pressure of the PRL or pressure compensation drip tape inlet pressure), m.

Fig. 11
figure 11

Schematic diagram of submain pipe hydraulic calculations.

Full size image

Hydraulic calculations for systems with installed pressure regulation devices

On the basis of preliminary hydraulic calculations, the length and inlet pressure (outlet pressure of the PRL or inlet pressure of the pressure compensating drip tape) of each drip tape in the system can be determined. These are used as input parameters in a program developed in MATLAB, which employs the stepping method to perform iterative calculations for each drip tape in the system.

The calculation principle is illustrated in Fig. 12. First, the pressure at the end of the drip emitter hL0 is assumed. Using the relationship between the emitter flow and pressure, the emitter flow qL0 and the segment flow QL0 can be determined. Then, via the head loss formula (11), the pressures and flow rates at each emitter are recursively calculated from the end of the lateral pipe to the inlet. After multiple iterations, the calculation is complete when the computed inlet pressure of the lateral pipe equals the outlet pressure of the pressure regulator. The relationships among the emitter flow and pressure, pressure differences between adjacent emitters, microtopography deviations, and segment flow and the formulas for recursively calculating the inlet pressure of the drip tapes are as follows:

$${q_i}=k \cdot {h_i}^{x}$$
(10)
$$\Delta {{\text{H}}_{{\text{L}}i}}=f\frac{{Q_{{{\text{L}}i}}^{{\text{m}}}}}{{{D^{\text{b}}}}}{L_{\text{L}}}{\text{+}}{L_{\text{L}}} \cdot {I_{{\text{L}}i}}{\text{+}}{W_{\text{H}}}$$
(11)
$${W_{\text{H}}}=Random\left( { - {\text{C}},{\text{C}}} \right)$$
(12)
$${Q_{{\text{L}}i}}={Q_{{\text{L}}i - 1}}{\text{+}}{q_{{\text{L}}i}}$$
(13)
$${{\text{H}}_{\text{L}}}={h_{{\text{L}}0}}{\text{+}}\Delta {{\text{H}}_{{\text{L1}}}}{\text{+}}\Delta {{\text{H}}_{{\text{L}}2}}{\text{+}} \cdots {\text{+}}\Delta {{\text{H}}_{{\text{Ln}} - {\text{1}}}}{\text{+}}\Delta {{\text{H}}_{{\text{Ln}}}}$$
(14)

where qLi represents the emitter flow rate in L/h; k denotes the emitter flow coefficient; hLi represents the emitter pressure, m; x represents the flow index; HL represents the inlet pressure of the drip tape, m; ∆HLi represents the head loss along the drip tapes, m; ILi represents the slope between adjacent emitters; f represents the head loss coefficient; QLi represents the flow rate in the segment between adjacent emitters in L/h; D denotes the inner diameter of the pipe in mm; LL represents the spacing between emitters, m; WH represents the microtopography deviation randomly generated in the interval (-C, C), m; C represents the absolute value of the maximum microtopography deviation, m; m represents the flow coefficient; and b denotes the diameter coefficient. For a polyethylene (LDPE) drip tape with a diameter of 16 mm, the values of f, m and b are generally 0.505, 1.75, and 4.75, respectively.

Fig. 12
figure 12

Schematic diagram of drip tape hydraulic calculations.

Full size image

Results

Pressure distribution of the pipeline network

The original system used pressure compensating drip tape, which was connected to the submain via the bypass, with the pressure at the outlet of the submain being the inlet pressure of the pressure compensating drip tape. After the modification, the system uses non-pressure compensating drip tape, which is connected to the submain through the PRL. The pressure at the outlet of the submain bleeder is the inlet pressure of the PRL, whereas the outlet pressure of the PRL is the inlet pressure of the non-pressure compensating drip tape.

Figure 13 shows the coefficient of variation (CV) of the drip tapes inlet pressure for each zone and the entire system before and after the modification. As shown in the figure, although the original system used a greater number of pressure-reducing valves to reduce the pressure deviation in the submain, the overall CV of the drip tapes inlet pressure in the system was still as high as 18.9%. After the installation of the PRLs, the overall CV of the drip tapes inlet pressure in the modified system decreased to less than 5.5%. The CV for Field No. 2 of the irrigation system is slightly greater than that of the other irrigation zones (still less than 6.5%), mainly because of the irregular shape of the area where Field No. 2 is located, which results in the greatest variation in the length of the drip tapes within that zone.

Fig. 13
figure 13

Coefficient of variation of inlet pressure for the drip tape inlet (PRL outlet).

Full size image

Figure 14 shows the pressure distribution at the submain bleeder (PRL inlet/pressure compensating drip tape inlet) and non-pressure compensating drip tape inlets of the original system and the modified system. As illustrated, the increase in pressure at the submain bleeders due to the elevation drop in the submain direction across the four irrigation zones is quite evident. For the original system, when the pressure at the submain bleeders approaches the bursting pressure of the pressure compensating drip tape at 0.30 MPa, a submain pressure-reducing valve is needed to lower the pressure and protect the drip tape (shown in blue in Fig. 14b). In the modified system, the bursting pressure of the non-pressure compensating drip tape is 0.20 MPa. However, since the installed PRL provides protection, a pressure-reducing valve only needs to be installed on the submain when the pressure exceeds the upper limit of the PRL’s set point at 0.40 MPa (shown in black in Fig. 14c). As a result, the number of pressure-reducing valves used in the modified system is significantly lower than that used in the original system (see Figs. 1 and 3).

Figures 13 and 14 show that the installation of the PRLs significantly reduces the impact of submain pressure fluctuations on the inlet pressure of the drip tape. This allows non-pressure compensating drip tapes, which have a lower bursting pressure, to be used safely in hilly irrigation systems with significant elevation changes. After the PRL adjustment, the inlet pressures of the drip tapes in the four irrigation zones were maintained at approximately 0.10 MPa. Even in a hilly irrigation system with a maximum elevation difference of 53 m, the coefficient of variation for the inlet pressures (PRL outlet pressures) of the entire system’s drip tapes remains below 6%.

Fig. 14
figure 14

Pressure distribution of each irrigation zone before and after the modification.

Full size image

Irrigation uniformity of the system

Table 1 shows the simulation results of the irrigation uniformity (CU) and average emitter flow rate for each irrigation zone and the entire system before and after the drip irrigation system was modified. The formula for calculating the Christiansen uniformity coefficient (CU) is presented as follows:

$$CU=\left( {1 - \frac{{\sum\limits_{{i=1}}^{n} {\left| {{q_i} - \overline {q} } \right|} }}{{\sum\limits_{{i=1}}^{n} {{q_i}} }}} \right) \times 100\%$$
(15)

As indicated in the table, the irrigation uniformity of the modified system decreased by 3–6% compared with that of the original system; however, the irrigation uniformity for each irrigation zone and the entire system still reached over 90%. The measured irrigation uniformities of the entire irrigation system before and after the renovation were 95.2% and 91.2%, respectively. The simulated irrigation uniformities before and after the renovation were 98.3% and 93.4%, with an absolute error of less than 3.3% compared to the measured results, indicating that the simulation method is reliable and effective. The average emitter flow rate for each irrigation zone and the entire system after the modification is approximately 1.36 L/h, which is very close to the designed flow rate of 1.40 L/h, essentially meeting the design requirements. In summary, the hydraulic performance of the modified system fully meets the needs of precise irrigation.

Table 1 Irrigation uniformity and average emitter flow rate for each zone and the entire system.
Full size table

Taking Field No. 1 as an example, Fig. 15 shows the distribution of the emitter flow rate in the original system using pressure compensating drip tape and in the modified system using non-pressure compensating drip tape with a PRL. As shown in the figure, the overall emitter flow rate of the original system is slightly higher than that of the modified system, and the emitter flow rate distribution is more uniform along the lateral direction. This is because the PRL only stabilizes the pressure at the inlet of the drip tape, and it does not address the issue of uneven pressure at the emitters caused by minor topographical variations and hydraulic friction losses laterally. However, overall, the emitter flow rate distribution in the modified system remains relatively uniform.

Fig. 15
figure 15

Distribution of emitter discharge in field No. 1 before and after modification.

Full size image

Investment analysis of the irrigation system

Table 2 shows the investment details before and after the modification of the drip irrigation system. The table accounts for only the main materials in the main line, branch line, and lateral pipe systems, excluding equipment such as pumps, filters, fertilizer injectors, pressure gauges, and flow meters. The table shows that the main differences between the original system and the modified system are the type of drip tape used and the number of pressure reducing valves used. Compared with the original system, the one-time investment in the modified system was reduced by 48%, with savings of 25,000 Chinese yuan (CNY) attributed solely to the drip tape. Considering the useful life of various materials in the system, the average annual investment of the modified system decreased by 35.3% compared with that of the original system.

Table 2 Investment details before and after the drip irrigation system modification.
Full size table

Discussion

Taking the system in this study as an example, with all other conditions unchanged, the unit price of pressure compensating drip tape needs to be reduced to 0.9 CNY/m for the average annual investment to be on par with the conditions under which non-pressure compensating drip tape and PRL are used. Considering that using pressure compensating drip tape can achieve a higher CU, if the unit price of pressure compensating drip tape can be lowered to below 1 CNY/m (approximately 0.14 USD/m), it would provide a better cost‒performance ratio for the average annual investment, thus attracting farmers in developing countries to use it. However, the unit price of pressure compensating drip tape would need to be reduced to 0.3 CNY/m for the one-time investment to match that of using PRL and non-pressure compensating drip tape, which is clearly nearly impossible given the current production processes and market conditions.

For developing countries, using PRL and non-pressure compensating drip tape in hilly areas is a balance between cost-effectiveness and irrigation uniformity. By sacrificing some irrigation uniformity, farmers can significantly reduce one-time investment, which they are willing to accept. The benefits of this approach include the following: (1) Replacing the originally expensive pressure compensating drip tape with cheaper options; (2) the use of PRLs protects the drip tapes and greatly reduces the number of submain pressure reduce valves needed; and (3) the PRLs can also replace the bypass connection between the drip tape and the submain, and their low unit price does not significantly increase the overall system investment.

The topography and terrain of the irrigation system are the main factors influencing the choice of PRL. The farmland studied in the manuscript has significant elevation changes and irregular shapes, resulting in large pressure variations along the submain direction within an irrigation area, as well as considerable variations in the laying length of the drip tape (design flow rate). Therefore, it is essential to choose the A-type PRL, which is less affected by changes in the inlet pressure and flow rate. In a similar scenario, when the parameters of the D-type PRL, which is most influenced by flow variations, are input into the drip irrigation system simulation program established in this paper, the simulated CU is 85%, which is less than 90%. Considering both water application uniformity and the investment in the PRL itself (the unit price and quantity of A-type PRLs are not high), the irrigation system discussed in this study opted for the A-type PRL. Clearly, different hilly drip irrigation systems have complex and varied operating conditions. The selection and configuration of drip tape and pressure regulation equipment must comprehensively consider design difficulty, economic efficiency, and water application uniformity. The hydraulic performance evaluation method for hilly drip irrigation systems proposed in this paper aims to address this issue. Users can use this method to preliminarily assess the hydraulic performance of the system under different pressure control schemes after the basic operating conditions of the irrigation system are obtained while also considering the economic feasibility of the investment.

This study is built upon the previous research conducted by our team. Through CFD methods and incorporating 3D printing technology, we significantly improved the performance of the PRL and developed a series of products with different output pressure specifications6,37. On this basis, we proposed system evaluation indicators for the PRL32 and assessed the potential performance enhancement of the PRL after optimization in an experimental system38.

The main innovation of this study lies in the retrofit of a complex hilly drip irrigation system using our self-developed PRL, which maintains efficient irrigation uniformity while greatly reducing system investment, especially the one-time investment. Additionally, we proposed a mathematical model for the PRL output pressure that comprehensively considers the impacts of manufacturing deviations, flow rate, and inlet pressure. This mathematical model serves as an important foundation for simulating the hydraulic performance of drip irrigation systems with PRL installations, particularly in addressing the calculation of inlet flow and pressure in drip tapes.

Of course, this study also has certain limitations. Since it involves the retrofit of an existing irrigation system and aims to reduce investment by utilizing the original system’s pipeline as much as possible, the dimensions and layout of the submain and main pipes were not altered in this study. In the next phase of our research, we plan to leverage artificial intelligence and deep learning techniques to refine and construct a comprehensive decision-making model that takes into account the layout of the irrigation system’s pipeline network, as well as the performance and installation positions of multi-stage pressure regulation equipment.

Conclusions

This study establishes a design and evaluation method for hilly drip irrigation systems utilizing PRL, employing computer programming techniques. Using a real hilly drip irrigation system as a case study, it performs a systematic optimization design and comprehensively compares the differences in design schemes, investment costs, and irrigation uniformity before and after optimization. The main conclusions are presented as follows:

  1. (1)

    A mathematical model for the PRL outlet pressure is constructed, taking into account the combined effects of the inlet pressure, flow rate, and manufacturing deviations, with an nRMSE of less than 1.0%.

  2. (2)

    A real hilly drip irrigation system was modified by replacing the pressure compensating drip tape used in the original system with PRL and non-pressure compensating drip tape. This modification maintained a uniformity of irrigation (CU) greater than 90% while reducing the system’s one-time investment and average annual investment by 48.0% and 35.3%, respectively.

  3. (3)

    In developing countries, the cost of pressure compensating drip tape is significantly greater than that of non-pressure compensating drip tape, making it difficult to promote pressure compensating systems. The main economic reason for the greater promotional potential of PRL and non-pressure compensating drip tape lies in this cost difference. Taking the system in this study as an example, the use of pressure compensating drip tape can achieve greater irrigation uniformity. From the perspective of average annual investment, the cost of pressure compensating drip tape can be reduced to 1 CNY/m (approximately 0.14 USD/m) while maintaining existing performance, thereby increasing its potential for promotion in hilly areas of developing countries.