An enhanced denoising system for mammogram images using deep transformer model with fusion of local and global features

Abstract

Image denoising is a critical problem in low-level computer vision, where the aim is to reconstruct a clean, noise-free image from a noisy input, such as a mammogram image. In recent years, deep learning, particularly convolutional neural networks (CNNs), has shown great success in various image processing tasks, including denoising, image compression, and enhancement. While CNN-based approaches dominate, Transformer models have recently gained popularity for computer vision tasks. However, there have been fewer applications of Transformer-based models to low-level vision problems like image denoising. In this study, a novel denoising network architecture called DeepTFormer is proposed, which leverages Transformer models for the task. The DeepTFormer architecture consists of three main components: a preprocessing module, a local-global feature extraction module, and a reconstruction module. The local-global feature extraction module is the core of DeepTFormer, comprising several groups of ITransformer layers. Each group includes a series of Transformer layers, convolutional layers, and residual connections. These groups are tightly coupled with residual connections, which allow the model to capture both local and global information from the noisy images effectively. The design of these groups ensures that the model can utilize both local features for fine details and global features for larger context, leading to more accurate denoising. To validate the performance of the DeepTFormer model, extensive experiments were conducted using both synthetic and real noise data. Objective and subjective evaluations demonstrated that DeepTFormer outperforms leading denoising methods. The model achieved impressive results, surpassing state-of-the-art techniques in terms of key metrics like PSNR, FSIM, EPI, and SSIM, with values of 0.41, 0.93, 0.96, and 0.94, respectively. These results demonstrate that DeepTFormer is a highly effective solution for image denoising, combining the power of Transformer architecture with convolutional layers to enhance both local and global feature extraction.

Introduction

Digital mammography plays a crucial role in the detection and diagnosis of breast cancer. However, the task of identifying subtle signs of cancer, particularly in the presence of microcalcifications (MCs)—small calcium deposits ranging from 0.1 to 1 mm in diameter—can be complicated by noise in the images. This challenge is exacerbated for radiologists, as MCs serve as early indicators of breast cancer, but they are difficult to detect. Various types of noise, including salt and pepper, Poisson, speckle, and Gaussian noise, can be introduced during the acquisition, transmission, and storage of mammographic images. These disturbances degrade the image quality and can obscure critical features like MCs, making it harder to identify early signs of cancer¹.

Despite their low apparent presence, noise disturbances misplace and distort pixel values, resulting in the omission of fine details in the mammogram. This degradation of image quality negatively impacts the diagnostic process. As a result, denoising has become an essential first step in mammogram image processing. By reducing noise, denoising improves image quality, enabling radiologists to detect subtle abnormalities more effectively. This enhancement not only improves diagnostic accuracy but also aids in generating more reliable classification results for breast cancer detection².

In recent years, Deep Convolutional Neural Networks (DCNNs) have gained widespread recognition for their exceptional performance in computer vision tasks, particularly in object classification³. The typical DCNN architecture consists of multiple layers that combine convolutional filters, pooling layers, and nonlinear activation functions. These networks are designed to extract high-level features from input data, while the final fully connected layers perform classification. Prominent DCNN models, such as LeNet⁴, GoogLeNet⁵, AlexNet⁶, VGGNet⁷, ZFNet⁸, and ResNet⁹, have proven successful in various imaging applications, including mammogram analysis¹⁰.

An important task in image processing is feature point matching, which is fundamental to many visual tasks, such as image alignment or object recognition. Traditional feature-matching techniques, such as FAST⁷, SIFT^9,11, ORB¹², and SURF¹³, rely on detecting specific points (e.g., corners or edges) in an image and matching them between different images. These methods use pixel gradients or brightness variations to identify feature points. However, they often struggle in areas with weak or missing textures, which can lead to inaccurate feature detection and poor matching performance¹⁴.

The advent of deep learning has revolutionized feature point matching by providing more robust and efficient methods. Deep learning-based approaches can extract features and match points with much higher accuracy, overcoming the limitations of traditional techniques. These new methods are particularly valuable in challenging imaging scenarios, such as mammogram analysis, where detecting fine details like MCs is essential^15,16.

In summary, the combination of denoising techniques and deep learning-based methods—such as DCNNs for classification and advanced feature point matching—has significantly improved the quality and accuracy of mammogram image analysis. This combination not only aids radiologists in detecting early signs of breast cancer but also enhances the overall efficiency and reliability of automated diagnostic systems^17,18.

Instead of using feature detectors, featureless detector-based methods generate dense descriptors or dense feature matches through convolutional layers, such as DualRC-Net¹⁹, NCNet²⁰, Sparse-NCNet²⁰, LoFTR²¹, etc. By implementing a dual-resolution correspondence network to get pixel-level correspondences from coarse to fine resolution, DualRCNet extracts feature maps in both coarse and fine resolution categories, and by using the 4D correlation tensor extracted from the coarse resolution and the fine-resolution feature mapping to obtain dense correspondences between feature points finally. NCNet solves the problem of finding reliable dense correspondences between a pair of images through a trainable convolutional neural network structure from end to end that obtains matching pairs by analyzing the neighborhood consistency of all possible correspondences between a pair of images in a 4D space.

By analyzing all these points, the objectives of the proposed work are to Reduce noise in mammography pictures to improve their quality and enable more accurate diagnosis and analysis, to create a network that efficiently combines local and global characteristics to remove noise more accurately, particularly from complex textures like those seen in mammography pictures, to construct a deep network design that avoids problems like vanishing gradients, which are frequently seen in deep learning models, and yet maintains excellent performance and to make sure that during the denoising process, important local structures in mammography images are maintained.

The main contributions are: An end-to-end Transformer-based network that combines local and global properties is used in the suggested method. By effectively removing noise from mammography pictures, this fusion preserves important diagnostic data; the deeper network architecture improves performance by using residual connections that merge numerous Transformer and convolutional layers. This is important because the network may learn more intricate patterns connected to breast tissue, which is useful for denoising mammograms. The Transformer incorporates a depth-wise convolutional layer to maintain local features that are essential for the interpretation of mammograms. This makes sure that during the denoising process, important local information—like delicate breast tissue structures—is preserved. As a part of quantitative analysis, a new performance metric is introduced by combining the weighted traditional quality metrics.

The further contents of the article are organized as follows: “Related works” summarizes the existing literature in denoising medical images. “Proposed transformer model for mammogram denoising” explains the proposed method in detail. “Result analysis” describes the dataset and analyses the performance of the proposed method by comparing it with the state-of-the-art denoising methods. Finally, “Conclusion” concludes the work.

Related works

Researchers have tried a variety of approaches to get rid of noise in mammography images. The mammogram images are subjected to a combination of conventional and efficient filters to eliminate salt-and-pepper noise, speckle noise, and Gaussian noise. These filters include the Wiener filter, the Median filter, and the Gaussian filter, with the latter type of filter achieving superior results compared to the other methods²².

In a study conducted by Vikramathithan et al.²³, a dual median filter was employed to improve the image quality of mammography. This was achieved by effectively reducing the presence of salt and pepper noise, which had a high density of up to 95%. Liu et al.²⁴ employed a mixed methodology in their research, incorporating noise detection using the Modified Robust Outlyingness Ratio (mROR) and a nonlocal mean filter for noise reduction.

The authors employed the contrast-limited Adaptive Histogram Equalization (CLAHE) strategy in¹⁹ to enhance the contrast of mammograms for the purpose of detecting breast tumor boundaries through the utilization of thresholding approaches. The purpose of this action was to enhance the precision of medical diagnosis. The objective of this work²⁰ is to develop an improved preprocessing technique for the conventional breast cancer computer-aided diagnosis (CAD) system by the application of wavelet transform. The objective of this technique is to diminish noise and enhance contrast.

The method based on feature detectors xtract each group of points of interest in the image, generates corresponding descriptors for each group of points of interest, and then finds the corresponding relationship between the points of interest through feature matching algorithms, such as LIFT¹¹, SuperGlue¹², D2-net¹⁴, ASLfeat¹³, DISK²⁵, and improved algorithms based on the above algorithms. LIFT is the first end-to-end neural network that simultaneously implements three tasks: feature point detection, direction estimation, and descriptor generation. SuperGlue is the first technique for matching features that uses attention mechanisms and graph neural networks. It leverages attention mechanisms to derive deeper relationships between features and achieve higher matching accuracy by creating dense undirected graphs between them.

D2-net detects features using a single convolutional neural network while extracting dense feature descriptors. It then performs non-maximum suppression on each descriptor to obtain detected feature points, solving the problem of reliable pixel-level matching under difficult imaging conditions. ASLfeat employs a deformable convolutional network¹³ for dense estimation, applying local transformations to leverage the inherent feature hierarchy. It introduces a multilevel detection mechanism that recovers spatial resolution without the need for extra weights, while also preserving low-level details to improve keypoint localization. By using peak measurements to correlate feature responses and compute detection scores, the method addresses the issues of localized shape variations (such as scale and orientation) often ignored in the joint learning of feature detectors and descriptors, and the problem of inaccurate keypoint localization.

DISK is a framework for local feature extraction using the strategy gradient of reinforcement learning, which achieves high feature-matching accuracy by optimizing end-to-end learning through end-to-end optimization. Sarlin et al.¹² designed an exact matching algorithm that includes outlier filtering based on the principle of SuperGlue local similarity. Without affecting the correct matching results, it can enhance matching accuracy by efficiently filtering out results with significant matching errors.

Proposed transformer model for mammogram denoising

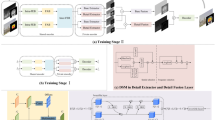
The proposed method is a transformer architecture that has a series of five DeepTformer blocks with residual connections to learn the global and local features. The fusion of global and local features is applied to perform denoising. As the proposed method aims to enhance real medical images, the model’s performance is performed with two sets of metrics. The DeepTformer has three phases say, preprocessing, feature extraction and image reconstruction phase as shown in Fig. 1.

Fig. 1

The framework of the proposed method.

Preprocessing

The preprocessing phase has a single 3 × 3 convolutional layer that can extract the local features. Let $\:{I}^{H\times\:W\times\:C}$ be the image to be denoised. $\:{F}_{1}$ is the preprocessing function as mentioned in Eq. (1).

$$\:{F}_{1}={Conv\left({I}^{H\times\:W}\right)}_{3\times\:3}$$

(1)

where $\:{Conv(.)}_{3\times\:3}$ refers to a $\:3\times\:3$ Convolutional layer. $\:{F}_{1}$ is the deep local features. The output of preprocessing is shown in Fig. 2. Figure 2a is the original mammogram image, and Fig. 2b is the output of one of the 3 × 3 convolution filters used that visualizes the hidden features.

Fig. 2

(a) Original image. (b) Output of 3 × 3 convolution.

Feature extraction

The feature extraction phase contains a series of five DeepTformer blocks; each block has four improved Transformers (ITransformers). The functional units of Itransformers are shown in Fig. 3. This phase extracts global features with residual connections. The output of preprocessing ($\:{F}_{1})$ is passed through the five DeepTformer block functions ($\:{F}_{2})$ as shown in Eq. (2).

$$\:{F}_{2}={T}_{DT}\left({F}_{1}\right)$$

(2)

$\:{T}_{DT}$ is the function of DeepTformer blocks, which have an M number of transformers. The output of $\:{F}_{2}$ are deep features that are passed to the final layer through the residual connection to concatenate with $\:{F}_{1}$. This produces high-quality denoised image $\:(\widehat{I}$) as shown in Eq. (3).

$$\:\widehat{I}={F}_{2}+{F}_{1}$$

(3)

$\:{F}_{2}^{r}$ refers to the reconstruction function. $\:{F}^{d}$ is the mathematical function of the transformer series in DeepTformer block. For the $\:N\:$medical images with noisy ($\:{I}_{N}$)and noise-free image $\:{(I}_{NF})$ the loss function $\:\left(L\right(\theta\:\left)\right)\:$with model parameters $\:\theta\:$ is defined by the absolute average difference between $\:{I}_{N}$ and $\:{I}_{NF}$ as shown in Eq. (4).

$$\:L\left(\theta\:\right)=\frac{1}{N}\sum\:\left|{I}_{N}-{I}_{NF}\right|$$

(4)

Stohastic gradient descent is used to find the optimal parameters.

Fig. 3

tth Itransformer block.

DeepTformer blocks

The feature extraction phase contains five improved Transformers (ITransformer). There is a 3 × 3 deep convolutional layer behind all the ITransformer along with a long-residual connections. The sequence of functions applied are normalization on deep convoluted features. There are two parts in the ITransformer block. They are auto-attention module and a multi-layer perceptron.

In auto-attention module, the image from preprocessing is subjected to three different convolutions as shown in Eqs. (5) to (7) and the results obtained are used further to extract global features. The sample output of the three convolution operations are shown in Fig. 4.

$$\:{W}_{1}{X}_{i}={Conv}_{1}\left({X}_{i}\right)$$

(5)

$$\:{W}_{2}{X}_{i}={Conv}_{2}\left({X}_{i}\right)$$

(6)

$$\:{W}_{3}{X}_{i}={Conv}_{3}\left({X}_{i}\right)$$

(7)

Fig. 4

Output of (a) $\:{Conv}_{1}$ (b) $\:{Conv}_{2}$ and (c) $\:{Conv}_{3}$

Then, the first two outputs ($\:{W}_{1}{X}_{i}\:$and $\:{W}_{2}{X}_{i}$) are combined by a simple matrix multiplication to produce the concatenated features ($\:{X}_{i}^{12})$as shown in Eq. (8). The concatenated features are shown in Fig. 5.

$$\:{X}_{i}^{12}={W}_{1}{X}_{i}\:\times\:\:{W}_{2}{X}_{i}$$

(8)

Fig. 5

Concatenation of Conv₁ and Conv₂ outputs.

In the next step, the combined features ($\:{X}_{i}^{12})$ are applied with a softmax function to extract the stochastic ranking of features. Then, these values are multiplied with the output of the third convolution to boost up the important features. Finally, a linear projection is applied to obtain the global features ($\:{X}_{i}^{G}$) as shown in Eq. (9).

$$\:{X}_{i}^{G}=LP\left(Softmax\right({X}_{i}^{12})\times\:{X}_{i}^{12})$$

(9)

where, LP is the linear projection. The projected features are joined with $\:{X}_{i}$ to produce the auto attention output ($\:{X{\prime\:}}_{i})$ as shown in Eq. (10).

$$\:{X{\prime\:}}_{i}={X}_{i}^{G}\:+\:{X}_{i}$$

(10)

The output of final feature concatenation is shown in Fig. 6.

Fig. 6

Output of final concatenation.

The second part of Itransformer is a multi-layer perceptron that contains a layer level normalization as used in the auto attention module, a linear projection layer following a resizing step, a 3 × 3 convolutional layer and a linear projection. Finally, the concatenated features ($\:{X}_{i}^{12})$ from auto attention module and the projected features from MLP are added together to find the transformed context ($\:{X}_{i}^{t}$) of the image at tth Itransformer block.

The introduction of ResNet²⁶ and DenseNet²⁷ has demonstrated that using skip-connection in neural networks enhances their robustness and stability during training. Additionally, the residual connection technique has the capability to ease the fusing of specific features. The exchange of information among several layers, particularly when traversing numerous layers. Moreover, the implementation of dense residual connections among various layers has the potential to enhance performance. In a general sense, shallow features primarily encompass low-frequency information, whereas deep features prioritize the retrieval of high-frequency information. By utilizing a variety of residual connections, both long and short, it is possible to combine low and high-frequency information. The DeepTformer model involves the utilization of convolutional operations with a multi-head auto-attention mechanism to collect both local and global data effectively. In this paper, the utilization of a dense residual connection as a means to effectively connect the local and global features is proposed. The reconstruction of the denoised image is done by concatenation of the global-local feature combinations $\:{X}_{i}^{N}$ with the original image I.

Result analysis

The proposed approach was tested using the Anaconda runtime environment. It provides faster GPUs and more RAM and disk space, making it appropriate for training massively parallel ML and DL models. We employed Python 3.6 and the other Python packages like TensorFlow and Keras are used to implement the proposed models. Our dataset was loaded using the OpenCV library, and the scikit-learn package was used to divide it and calculate the results. To represent the plots, Matplotlib was also used. In addition, the following are the computer’s primary component specifications: (1) Intel Core i5 CPU 2.40 GHz, (2) NVIDIA Quadro RTX 3000, (3) 32 GB of RAM, and (4) other components. 64-bit operating system and x64-based CPU operating system type.

Dataset description

The Digital Database for Screening Mammography (DDSM) is revised and standardized into the CBIS-DDSM (Curated Breast Imaging Subset of DDSM)²⁸. A database of 2,620 scanned film mammography investigations constitutes the DDSM. It contains pathology information that has been verified for normal, benign, and malignant cases. In conjunction with ground truth validation, the DDSM’s database size and scope render it a valuable instrument during the testing and development phases of decision support systems. A trained mammographer has selected and curated a subset of the DDDSM data for inclusion in the CBIS-DDSM collection. Figure 7 shows the sample mammogram images from the CBIS-DDSM dataset. The training set and test set are taken with a ratio of 70:30.

Fig. 7

Sample mammogram images.

Evaluation metrics

Through visual inspection, the denoising of images can be evaluated. Nonetheless, the success of an algorithm cannot be determined just based on the level of visual gratification it provides. Figure 5 shows the local and global features extracted from the preprocessing and feature extraction phases for the samples shown in Fig. 8.

Fig. 8

(a) Local features. (b) Global features.

To provide a numerical value to the outcomes, it is essential to measure certain performance measures. This paper presents the many metrics that were utilized to evaluate the performance of the research activity quantitatively. These metrics are described in this section.

The peak signal-to-noise ratio (PSNR) is defined as the ratio between the greatest power that can be present in a signal and the power of noise that interferes with the signal. A noise-free signal P with dimensions of W × H and a denoised signal I are considered in the calculation of the PSNR of $\:\widehat{I}$ as shown in Eq. (11). Large value of PSNR ensures a better quality image.

$$\:PSNR\left(I,\widehat{I}\right)=10\:{log}_{10}\left(\frac{{255}^{2}}{MSE}\right)$$

(11)

Where $\:MSE=\frac{1}{W\:x\:H}\sum\:_{i=1}^{W}\sum\:_{j=1}^{H}{\left[I\right(i,j)-\widehat{I}(i,j\left)\right]}^{2}$

The edge preservation index (EPI) is a metric used to quantify the extent to which edges remain intact in a denoised image²⁹. The identification of lesions using edges is a crucial aspect in the field of medical picture denoising. The range of EPI will be [0,1]; larger value of EPI ensures a better denoising result. The EPI, where I represent the noise-free image and $\:\widehat{I}$ represents the denoised image, is defined as shown in Eq. (12).

$$\:EPI(I,\widehat{I})=\frac{\sum\:(\varDelta\:I-MEAN(\varDelta\:I\left)\right)(\varDelta\:\widehat{I}-MEAN(\varDelta\:\widehat{I}))}{\sqrt{\sum\:{(\varDelta\:I-MEAN(\varDelta\:I\left)\right)}^{2}{(\varDelta\:\widehat{I}-MEAN(\varDelta\:\widehat{I}\left)\right)}^{2}}}$$

(12)

where, $\:\varDelta\:I$ and $\:\varDelta\:\widehat{I}$ are the images obtained by a high-pass filtering on the images I and $\:\widehat{I}$. Let $\:\mathcal{F}$ be the high pass filter, which uses a 3 × 3 spatial domain filter as mentioned in Eq. (13).

$$\:\mathcal{F}(i,j)=\left\{\begin{array}{cc}1,&\:i,j=\text{1,2},3\:and\:i,j\ne\:2\\\:\sum\:_{i=1,j=1}^{3}\mathcal{F}(i,j)&\:i=j=2\:and\:\:i=j\ne\:2\end{array}\right.$$

(13)

An indication of the degree to which the denoised images are comparable to the original image is provided by the structural similarity index (SSIM). Therefore, it is computed as shown in Eq. (14).

$$\:SSIM(I,\widehat{I})=\frac{(2\times\:MEAN(I)\times\:MEAN(\widehat{I})+{\alpha\:}_{1})(2\times\:STD.DEV(I,\widehat{I})+{\alpha\:}_{2})}{({MEAN\left(I\right)}^{2}+{MEAN\left(\widehat{I}\right)}^{2}+{\alpha\:}_{1})({STD.DEV\left(I\right)}^{2}+{STD.DEV\left(\widehat{I}\right)}^{2}+{\alpha\:}_{2})}$$

(14)

$$\:\text{W}\text{h}\text{e}\text{r}\text{e},\:{\alpha\:}_{1}=0.02\times\:L,\:{\alpha\:}_{2}=0.03\times\:L\:\text{a}\text{n}\text{d}\:{L=2}^{bits\:per\:pixel}$$

Based on the idea that the human visual system (HVS) interprets images primarily based on their low-level characteristics, the Feature Similarity Index (FSIM)³⁰ measures how closely the denoised image resembles the original image, as shown in Eq. (15).

$$\:FSIM(I,\widehat{I})=\frac{\sum\:_{x\in\:H\times\:W}\left(\frac{({2\times\:PC}_{I}\times\:{PC}_{\widehat{I}}+0.75)\:\times\:\:max({PC}_{I},{PC}_{\widehat{I}})(2{{\times\:G}_{I}\times\:G}_{\widehat{I}}+0.75}{({{PC}_{I}}^{2}+{{PC}_{\widehat{I}}}^{2}+165)({{G}_{I}}^{2}+{{G}_{\widehat{I}}}^{2}+165)}\right)}{\sum\:_{x\in\:H\times\:W}\left(max({PC}_{I},{PC}_{\widehat{I}})\right)}$$

(15)

PC is the phase congruency map, G is the magnitude of gradient maps, and the two constant values are arbitrarily selected. Given that there are no noise-free images, the human eye might not be sufficient to assess medical images. Therefore, measuring the traditional measures mentioned above is not possible. Even after denoising, attention must still be paid to feature preservation, noise reduction, and the existence of any artifacts. The following non-reference measures are used to assess how well denoising algorithms perform when applied to actual medical images.

The Fourier phase spectrum of an image is considered by the Sharpness Index (SI), which is a key metric for assessing image quality and is recognized to contain vital information about the geometry and contours of the image. Equation (16) defines the sharpness index of an image. The higher the SI, the better the denoised image.

$$\:SI\left(\widehat{I}\right)=-{log}_{10}\left(\frac{Mean\left(\widehat{I}\right)-Total\:variance\:\left(\widehat{I}\right)}{Variance\left(\widehat{I}\right)}\right)$$

(16)

A statistical measure of unpredictability called entropy (E) can be used to describe the texture of an input image. It shows how much information is contained in the picture. An image is better the higher its entropy. We define the entropy of a noisy image (I) as Eq. (17).

$$\:E\left(I\right)=-\sum\:p\times\:log\left(p\right)$$

(17)

p is the probability of each pixel. The proposed denoising model is compared with a number of state-of-the-art linear denoising filters. The noise is synthetically added with the original image and the labeled metrics like PSNR, EPI, SSIM and FSIM.

Fig. 9

Comparison of PSNR.

The proposed image denoising is compared with the state of the art methods like FROST³¹, LEE³², SARBM3D³³, NPD³⁴, WFB³⁵, WGB³⁶, OBNLM³⁷, NLMW³⁸, and DLRA³⁹. The denoising ability of the various methods for varying noise levels is displayed in Fig. 9 based on their PSNR values. Although FROST, LEE, and SRAD all perform well at speckle reduction, it is evident from the PSNR that LEE tends to lessen contrast while FROST and SRAD tend to introduce artifacts. The proposed algorithms provide greater performance than the multiscale approaches NPD, WFB, and WGB, even if these methods also outperform the conventional methods. Nonlocal means filtering and clustering of comparable patches is also the foundation of the OBNLM and NLMW techniques. They also frequently report significantly lower PSNR values when using the suggested techniques. Therefore, when compared to all other filters that have been shown thus far, the low rank-based approaches, DLRA and proposed method, provide the greatest results in terms of PSNR at all noise levels.

The probability distribution of PSNR for the proposed method using the range of noise levels of 10%, 20%, 40%, 80%, 90% and 100% are shown as a boxplot in Fig. 10 for all the images in the training set. This proves that the range of PSNR with the minimum noise (10%) is 0.39 to 0.43, while the maximum noise level (100%) generates the PSNR in the range of 0.33 and 0.37.

Fig. 10

Noise level vs. PSNR distribution.

Fig. 11

Comparison of EPI.

Edge preservation is an essential component of medical imaging because it plays a significant role in the process of disease differentiation. All of this is determined with the assistance of EPI. Figure 11 illustrates the findings of the study. Once more, DLRA, Sparse 3D⁴⁰, and SARBM3D demonstrate superior edge retention, but multiscale approaches NPD, WFB, and WGB provide just minor performance. The spatial domain filters, specifically the FROST filter and the LEE filter, exhibit the least amount of performance available.

Fig. 12

Noise level vs. EPI distribution.

The probability distribution of EPI for the proposed method using the range of noise levels of 10%, 20%, 40%, 80%, 90% and 100% are shown as a boxplot in Fig. 12 for all the images in the training set. This proves that the range of EPI with the minimum noise (10%) is 0.99, while the maximum noise level (100%) generates the EPI around 0.94.

Table 1 shows the global features and local features obtained by the proposed model for various views of mammograms. The proposed denoising model is compared with the existing denoising neural network architectures like our recent work USCUNT⁴¹, ABN⁴², Hybrid filter⁴³, UDNET⁴⁴, FC-AIDE⁴⁵, and FOCNet⁴⁶. Table 1 compares the proposed method with the state-of-the-art denoising models with a corresponding PSNR. The visual output, as well as the quantitative value of PSNR, shows that the proposed denoising outperforms other methods with a PSNR value of 39.4. Floating-point operations per second (FLOPs) are the metric that is used to analyze the complexity of the CNN models. Table 1 shows the FLOPs of the state-of-the-art CNN models and proposed method. The higher the FLOPs value, the faster the learning process. Hence, the FOCNet has the highest FLOPs value and is faster in this case. The proposed methods need optimization to improve the speed of the estimation.

Table 1 Comparison with the state-of-the-art deep learning models.

Figure 13 shows that a higher SSIM value index indicates more robust Denoising success at maintaining the structure of the denoised image. Figure 14 clarifies that FROST, LEE, and SRAD tend to even out the image and lessen contrast variations. There is significant edge preservation in the multiscale-based approaches (NPD, WFB, WGB, and group matching-based methods (OBNLM and NLMW). Nonetheless, DLRA and the proposed method provide the best outcomes.

Fig. 13

Comparison of SSIM.

Fig. 14

(a) Original image, Output of (b) SARBM3D (c) SRAD (d) NPD (e) WFB (f) WGB (g) DLRA (h) Proposed method.

Fig. 15

Comparison of SI.

Compared to the denoised images, the noisy images are observed to have a very low estimation of SI. The low-rank strategy, DLRA, as well as multiscale methods, NPD, WFB, and WGB, demonstrate noteworthy performance in this instance. Filtering-based techniques, including Sparse 3D, SARBM3D, and FROST have worse noise reduction capabilities due to their lower SI values. The visual outputs are shown in Fig. 15.

Fig. 16

Comparison of FSIM.

A representation of the change of FSIM with varying degrees of noise can be found in Fig. 16. A measure of the degree to which low-level features in a picture are preserved is referred to as FSIM. Comparatively speaking, the performance of the nonlocal means approaches, such as INLM⁴⁷ and ANLM⁴⁸, is significantly poorer in terms of FSIM values. Even though BM3D⁴⁹ and KSVD⁵⁰ produce superior outcomes, the TVTSVD⁵¹ algorithm itself achieves the highest level of performance.

Fig. 17

Noise level vs. FSIM distribution.

The probability distribution of FSIM for the proposed method using the range of noise levels of 10%, 20%, 40%, 80%, 90% and 100% are shown as a boxplot in Fig. 17 for all the images in training set. This proves that the range of FSIM with the minimum noise (10%) is 0.98, while the maximum noise level (100%) generates the FSIM around 0.93.

A quantitative metric known as a Figure of Merit (FoM) is employed to assess the efficacy or efficiency of a system, method, or procedure by considering multiple factors. The FoM was created to evaluate how well a denoising algorithm minimizes undesired noise in the context of denoising applications, all the while maintaining the key characteristics of a signal or image, like clarity, structural integrity, and visual quality.

Developers and engineers can use the FoM as a benchmark to compare various denoising approaches and evaluate which algorithm works best in a certain application. Usually, it incorporates several metrics, each of which represents a distinct performance characteristic, including computational efficiency, edge preservation, signal integrity, and noise reduction. In this paper, FoM is defined as a weighted sum of PSNR, EPI, SSIM, FSIM and EI with weights $\:{w}_{1},\:{w}_{2},\:{w}_{3},{w}_{4}\:$and $\:{w}_{5}$ respectively as shown in Eq. (18).

$$\:FoM={w}_{1}PSNR+{w}_{2}EPI+{w}_{3}SSIM+{w}_{4}\:FSIM+{w}_{5}EI$$

(18)

To give more weightage for feature-based metrics, EPI, FSIM and EI are assigned with weight of 0.25 each, PSNR is weighted with 0.15 and SSIM with 0.10. Table 2 compares the FoM obtained for various denoising methods over various noise levels.

Table 2 Comparison of FoM.

The evaluation of the Figure of Merit (FoM) among various denoising techniques at distinct noise levels (10%, 20%, 40%, 80%, and 100%) illustrates the exceptional efficacy of the suggested method. This approach consistently attains the highest Figure of Merit (FoM) across all noise levels, with a FoM of 15.1313 even at 100% noise, demonstrating its resilience to harsh noise conditions. The DLRA approach exhibits commendable performance, securing the second position overall; however, its figure of merit diminishes considerably with rising noise levels. Among conventional techniques like FROST, LEE, SRAD, NPD, WFB, and WGB, LEE and WGB are notable; however, they remain inferior to both the DLRA and the suggested method. Techniques such as SARBM3D, OBNLM, and NLMW have reduced FoM values, especially at elevated noise levels, signifying their diminished efficacy in managing significant noise. The suggested method exhibits superior denoising performance, especially in high-noise situations, surpassing all other methods in the comparison.

Conclusion

This research offers an efficient picture denoising scheme based on DeepTformer, a dense residual connection network. The preprocessing, local-global feature extraction and reconstruction modules comprise DeepTformer. The proposed ITransformer layer utilizes a dense residual connection to better extract features and reconstruct the details. In the meantime, to extract the deep features and connect the data from various layers, we use dense residual connections amongst DeepTformer groups. The outcomes on the images showed that, compared to other current methods, our DeepTFormer produces better results in color and grayscale images. Furthermore, DeepTFormer exhibits a reasonable balance between model size and experimental performance in actual noise reduction studies. The enhanced Transformer and dense residual connection can help fuse local-global characteristics better for image restoration jobs. The proposed framework lacks in denoising image without a reference image. To address this, in the future, a self-learning mechanism can be used. To improve the speed of estimation, optimization can be included.