Introduction

Drowsiness is the same as being drowsy. The effects of the drowsiness might be severe, even if it may only last for a few minutes. Most often, fatigue—which lowers alertness as well as attention—is primary cause of drowsiness; additional factors that may contribute include difficulty focusing, drugs, sleep disorders, alcohol consumption, shift work1. Roughly one in twenty drivers report having dozed off while operating a vehicle. Truck as well as bus drivers who commute for ten to twelve hours a day are most at risk for fatigued driving. These people put other drivers in danger more than they do themselves. NHTSA (National Highway Traffic Safety Administration) states that approximately 1,500 fatalities as well as 100,000 auto accidents annually are attributed to drivers’ fatigue. These statistics are based on police and hospital reports. An estimated 1,550 fatalities, 71,000 injuries, $12.5 billion in monetary damages are attributed to sleep-related driving2. In 2019, drowsy driving contributed to 697 fatalities. The NHTSA admits that it is difficult to determine exact number of crashes or fatalities brought on by drowsy driving and that numbers provided are underestimates. A range of symptoms, including frequent yawning, prolonged eye closure, abrupt lane changes, are present in drowsy drivers. Methods for diagnosing driver drowsiness (DDD) is thoroughly studied in last few years. There are a lot of cars on the road at night, including trucks with big machinery. Continuously operating these kinds of vehicles for extended periods of time increases their susceptibility to these extreme circumstances3. Over the past 20 years, a number of techniques have been developed, such as GPS systems that can identify when a motorist starts to stray from their lane out of inattention. Other methods employed electrocardiographic equipment to gauge the driver’s level of tiredness by monitoring the driver’s heart rate. A primary objective of intelligent transport systems (ITS) is to enhance public health and reduce accident rates. The fatigue and boredom of drivers are major contributors to accidents, particularly on congested highways. Drowsiness impairs decision-making and attentiveness, which are necessary for operating a motor vehicle. Some study indicates that drivers experience drowsiness after short drives, especially in the early afternoon, after, and late at night, when their level of fatigue is high and their mental state is atypical4. Moreover, alcohol consumption and the use of hypnotic drugs impair judgement. Distracted driving was the cause of entirely different kinds of accident statistics that were reported in other countries. Driver’s temporary condition and carelessness are the main causes of the 200 accidents. Research indicates that implementing a sleepiness detection system can substantially lower the frequency of accidents by at least 20%. To identify the driver’s sleepiness, a sequence of face photos is taken, tracking the driver’s head motions and eye blinks. A classification model may predict a class label for a given collection of input data once it has been trained. Machine learning (ML) based classification is extensively used because it can work with large amounts of data, reducing it to smaller dimensions5. This is very appropriate for real-life applications. Above all, the and analysis of biosignals like as EEG, EOG, ECG for the purpose of identifying driver drowsiness is a common use of machine learning techniques. Unfortunately, there isn’t much help available when selecting a categorization model, hence different models have been applied without carefully taking the particular application into account. Prior research took into account variables like the categorization model’s flexibility, computing cost, complexity. Artificial Neural Networks, Support Vector Machine, Random Forest Classifier, K-Nearest Neighbours are classifiers that are utilised most up to this point. As a result, a comparison of the most popular classification models and the ensuing performance results can offer some insight into the usefulness of these classifiers6.

Contribution

To analyse brain signal activity using wavelet time frequency transform model and classification using multi-layer convolutional designed transfer VGG-16 neural network. It was first created by processing electroencephalography (EEG) signals after they were captured. Twelve subjects’ EEG data were subjected to several machine learning algorithms in this study in order to gauge each subject’s performance. The initial phase involved segmenting the recorded data into second epochs for every subject. For every epoch, brain signals were classified as alert or drowsy. Preprocessing is utilized to extract pertinent data from captured signal before machine learning algorithms are applied.

Literature review

Numerous strategies were explored to enhance accuracy of the driver drowsiness system detection. A model to identify tiredness based on electroencephalography (EEG) data has been proposed in work7. The logarithm of the signal’s energy and extracted chaotic properties are used to distinguish between alertness and drowsiness. 83.3% accuracy was obtained in the classification process using an artificial neural network. A model for determining drowsiness based on the combination of electrooculography, EEG, and driving quality signals was proposed by author8. A class separability feature selection technique was applied to find which subset of features was best. For categorization, a selforganized map network was employed, accuracy rate was 76.51 ± 3.43%. Method to determine drowsiness based on steering patterns was created by author9. To capture steering patterns, they developed 3 feature sets for this strategy utilizing advanced signal processing techniques. Performance is calculated utilizing five ML methods, such as SVM and K-Nearest Neighbour. The accuracy rate for recognising tiredness was 86%. Work10 created a technique to detect tiredness based on changes in eye blink rate. Facial region of the photos was identified using the Viola Jones detection technique. The pupils’ locations were then determined using an eye detector based on neural networks. Determined the number of blinks per minute if a rise in blinks suggested that the driver was getting drowsy. A method for detecting tiredness through yawning was presented by author11. This approach detected the regions of the mouth and eyes after the face. They computed a hole in the mouth due to the wide open mouth. The face with the biggest aperture shows a wide open mouth. work12 created a model to use CNNs to determine drowsiness. This approach produced 78% classification accuracy by first using a convolutional neural network to extract latent information, followed by a SoftMax layer for classification. A sleepiness detection method based on EAR measure was created by author13. They computed EAR values for successive frames as well as fed those values into machine learning methods, such as SVM, RF, multilayer perceptrons. When14 investigated sleepiness as an input for a binary SVM classifier, they also employed EAR metric. With 97.5% accuracy, the model identified the driver’s level of tiredness. Because mouth behaviour has elements that are helpful for DDD, it is a good sign of sleepiness. The authors of15 suggested using mouth movement tracking to identify yawning as a sign of tiredness. They employed a dataset of more than 1000 normal photos and 20 yawning photographs for their investigation. The system employed an SVM classifier to detect yawning as well as notify driver after using a cascade classifier to locate driver’s mouth from face images. A yawning detection rate of 81% was reported in the final results. The mouth opening ratio is an additional mouth-based characteristic16. Another name for it is the MAR. It characterises the extent of mouth opening as a sign of yawning. In17, an SVM classifier was fed this feature, and it produced a 97.5% accuracy rate. Head motions are another helpful parameter for sleepiness detection in image-based systems, as they can indicate tired behaviour. As a result, they can be utilised to extract characteristics that are helpful for machine learning-based sleepiness detection. These head characteristics include head position, head nodding frequency, and head nodding direction. The forehead was utilised in18 as a point of reference to determine driver’s head posture. In18, infrared sensors were employed to track movements as well as identify driver weariness. A unique micro-nod detection sensor was employed in19 to track head posture feature in 3D in real-time prior to head position analysis. The most noticeable indicators of drowsiness were identified using a manually created compact face texture descriptor in a face-monitoring sleepiness-detection system reported by author20. At first, three signs of fatigue were identified: head nodding, frequency of yawning, and blinking rate. In the end, they employed a non-linear SVM classifier, yielding an accuracy of 79.84%. the comparison for brain signal activity analysis has been shown in Table 1.

Table 1 Comparison for brain signal activity analysis.
Full size table

Research gap: Current driver drowsiness detection systems have a number of drawbacks, such as high false alarm rates, challenges in identifying microsleeps, requirement for calibration or individualised customisation. Furthermore, the driver may find certain devices obtrusive or uncomfortable, and ambient conditions may have an impact on how successful they are. Current methods for detecting drowsiness involve intricate procedures and expensive machinery, like an electroencephalography (EEG) that tracks brain activity. Certain techniques employ 68 facial points for face detection, storing coordinates in a dynamic storage system. However, because all coordinates are associated, these approaches are unable to identify the precise target regions in cases where the entire face is not visible in the frame. Convolution neural networks (CNNs), which provide greater accuracy but perform poorly under certain circumstances including shifting angles, dim light, and transparent glasses, have been the basis for the majority of modern techniques. The primary cause of the failure was CNN’s operation, since it needed to analyse the item from three different angles (0, + 200, and − 200). The angle issue persists in all driver-based approaches since they all concentrate on improving number of hidden layers, which results in significant data loss.

Materials and methods

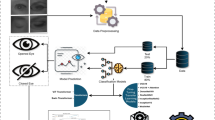
The primary goal of this effort is to identify tiredness as accurately as possible using single-channel EEG signals. In contrast to current approaches, as illustrated in Fig. 1, the suggested work conducts classification straight from the raw EEG data, omitting the need for hand-engineered features and signal processing procedures. There are two primary possible causes of the artefacts in the EEG readings. One is a result of the equipment utilised to read the EEG data. For instance, artefacts may occasionally result from the EEG sensor’s improper contact with the scalp. Artefacts may also be caused by power fluctuations in the EEG reading unit. Physiological artefacts, which are associated with specific motions like eye movements and blinks, as well as artefacts connected to muscles, especially those resulting from the forehead muscles, comprise the other category of artefacts. Artefacts cause interference with EEG signals and decrease their informational value. These objects could appear sometimes or not at all. Complete removal of artefacts without altering associated brain activity is required.

Fig. 1
figure 1

proposed drowsiness detection based on EEG signal pattern analysis.

Full size image

Brain activity patterns analysis using wavelet time frequency transform (WTFT) model

A feature is a single, quantifiable quality or characteristic of a data point that is used as input for a machine learning algorithm. In the context of machine learning, a feature is also referred to as a variable or attribute. Features are various features of the data that are pertinent to the problem at hand and might be text-based, category, or numerical. Features might include the age, location, square footage, and number of bedrooms in a dataset of home costs, for instance. Features in a consumer demographic dataset may include age, gender, occupation, and income level. In machine learning, the selection and calibre of features are crucial since they have a big influence on the model’s performance and accuracy. The WTFT’s non-stationary properties make it a popular tool for time-frequency analysis of biological signals, particularly EEG signals. Good time-frequency analysis is produced by the WTFT. Two down samplers by two and sequential high pass as well as low pass filtering of time series are used in the WTFT decomposition of a signal. Until desired number of breakdown levels is attained, the A1 is further broken down and the process is repeated. Wavelet function \(\:{\psi\:}_{\text{j},\text{k}}\left(\text{n}\right)\), which is indicated as follows, comes after high pass filter, while dilation function \(\:{\phi\:}_{\text{j},\text{k}}\left(\text{n}\right)\) depends on low pass filter by Eq. (1)

$$\:{\phi\:}_{\text{j},\text{k}}\left(\text{n}\right)={2}^{\text{j}/2}\text{}\text{h}\left({2}^{\text{j}}\text{n}-\text{k}\right)$$
$$\:{\psi\:}_{\text{j},\text{k}}\left(\text{n}\right)={2}^{\text{j}/2}\text{}\text{g}\left({2}^{\text{j}}\text{n}-\text{k}\right)$$
(1)

where M is the signal’s length and n, j, k, and 2j -1, as well as J and log2(M), are the values of 0, 1, 2,… and M. The primary frequency components of the provided signal determine the highest level of decomposition. The coefficients of the selected basis functions and the original time series are called the dot product of the DWT. In the ith level, the detailed coefficients Di and the approximation coefficients Ai are represented as Eq. (2)

$$\:{A}_{i}=\frac{1}{\sqrt{M}}\sum\:_{n}\:\:x\left(n\right)\times\:{\phi\:}_{j,k}\left(n\right)\:$$
$$\:{\text{D}}_{\text{i}}=\frac{1}{\sqrt{\text{M}}}\sum\:_{\text{n}}\:\:\text{x}\left(\text{n}\right)\times\:{\psi\:}_{j,k}\left(\text{n}\right)\:$$
(2)

where M is EEG time series length in discrete points and k = 0, 1, 2, …, 2j -1. wavelet sub-band energy, both relative and total. The following formula is used to get wavelet energy at every decomposition level, i = 1,…, L by Eq. (3)

$$\:{E}_{{D}_{i}}=\sum\:_{j=1}^{N}\:\:{\left|{D}_{ij}\right|}^{2},\:i=\text{1,2},3,\dots\:,L$$
$$\:{\text{E}}_{{\text{A}}_{\text{i}}}=\sum\:_{\text{j}=1}^{\text{N}}\:\:{\left|{\text{A}}_{\text{i}\text{j}}\right|}^{2},\:\text{i}=L$$
(3)

The highest degree of decomposition is indicated by a “L.” Thus, the total energy can be defined as follows from Eq. 4:

$$\:{\text{E}}_{\text{Total\:}}=\left(\sum\:_{i=1}^{L}\:\:{\text{E}}_{{\text{D}}_{\text{i}}}+{\text{E}}_{{\text{A}}_{L}}\right)$$
(4)

The relative wavelet energy is represented by the normalised energy values by Eq. (5)

$$\:{\text{E}}_{\text{r}}=\frac{{\text{E}}_{\text{j}}}{{\text{E}}_{\text{Total\:}}}$$
(5)
$$\:\text{where\:}{\text{E}}_{\text{j}}={E}_{{D}_{i-1},\dots\:}\text{\:or\:}{E}_{{\lambda\:}_{i-L}}$$

Because it directly affects classification performance, extracting pertinent information from raw signals is an essential stage in the categorization of EEG patterns. Detailed and approximative coefficients were calculated. Table 2 shows the frequency range and sub-band percentage relative energy of a single participant for a single channel. The collected wavelet coefficients were used to calculate total as well as relative sub-band energy. Equation 8 was used to calculate the relative wavelet energy ErD1; ErD2…ErA4. For every participant and every channel’s data, the relative energy features were calculated.

Table 2 Frontal F3 channel’s sub-band percentages’ relative energy as well as their frequency range.
Full size table

Level 1 detailed coefficients D1 and D2 detailed coefficients D3 and D4 detailed coefficients of level 4 and A4 approximation level 4 respectively.

Time-Frequency analysis. Every EEG data underwent a time-frequency analysis utilising the wavelet time frequency transform (WTFT). A wavelet is a time- and frequency-localized zero-mean function with finite duration. For a given EEG time series x(t), the WTFT is described as follows by Eq. (6)

$$\:(\alpha\:,\beta\:)=\frac{1}{\sqrt{\alpha\:}}\int\:\:x\left(t\right){\psi\:}^{\text{*}}\left(\frac{t-\beta\:}{\alpha\:}\right)$$
(6)

where * indicates the complex conjugate operator, ψ is wavelet basis function known as the mother wavelet, β is translation parameter. Energy distribution in time-scale plane is represented by square modulus of WTFT coefficients (|WTFT (α, β)| 2). In fact, there is a rough correlation between scale and frequency: low frequencies are associated with high scale values by Eq. (7).

$$\:{f}_{\alpha\:}=\frac{{f}_{c}}{{T}_{s}\alpha\:}$$
(7)

where Ts is the sampling time, fα is the pseudo-frequency associated with the scale α, fc is centre frequency of selected mother wavelet. Mexican Hat Mother wavelet function was employed in this investigation due to its suitability for analysis of EEG signals.

WTFT features. Equation 1 is used to evaluate the CWT for each channel in an EEG epoch. This results in 19 TFM. The five sub-matrices that each aTFM is divided into correspond to the five sub-bands that are being examined. The following CWT properties are calculated for each sub-matrix, or subband: entropy (h), skewness (v), kurtosis (k), mean (m), and standard deviation (d). The size of the generated WTFT vector is 5 (# features) × 5 (# sub-bands) = 25 features. Thus, the matching WTFT feature vector (sized 1 × 25) for each EEG epoch is retrieved and fed into the suggested classification structures. For every participant and every channel’s data, the relative energy features were calculated. As a result, the relative energy feature matrix for a single subject in every EEG task as well as every sub-band by Eq. (8)

$${\rm Relative\, Energy\, Feature \,Matrix }\:\left(\overrightarrow{{\text{F}}_{r}}\right)=\left[{\text{E}}_{\text{r}\text{A}(280\times\:128)}\right]$$
(8)

There were 128 channels and 280 instances in each class. Consequently, for each of the eight students in a class, relative energy feature matrix of first detailed coefficients was represented by symbol \(\:\left[{\text{E}}_{\text{r}\text{A}(280\times\:128)}\right]\).

Multi-layer convolutional designed transfer VGG-16 neural network (MLCDT-VGG-16) based brain signal classification

Advantages of the multi-layer convolutional neural network include its quick operation, ease of installation, and lower training set needs. Information input to the output layer is processed and transmitted by the hidden levels. One mapping between two Euclidean spaces (RRn1 n1, R n2) is called a multi-layer convolutional. A sequence of Euclidean spaces R n1, R n2,… R nL and the mapping (F) connecting them is the definition of the mapping by Eq. (9)

$$\:{F}_{1}:{R}^{{n}_{1}}\to\:{R}^{{n}_{1}},{F}_{2}:{R}^{{n}_{1}}\to\:{R}^{{n}_{1}}\dots\:{F}_{L-1}:{R}^{{n}_{L-1}}\to\:{R}^{{n}_{L}},\:$$
(9)

where L is the total number of convolutional layers in a multilayer architecture. Every neuron j in hidden layer of multi-layer CNN adds up its input signals (xi), then calculates its output (yj) as a function of sum. In terms of math by Eq. (10)

$$\:{y}_{j}=f\left(\sum\:\:{w}_{ij}\text{*}{O}_{i}\right)$$
(10)

Here, O stands for the hidden layers, while w stands for the weights, which are changed in accordance with the gradient descent process. Let’s say that W0 and W1 represent the two subwindows, with W1 holding the most recent examples. |µW0 − µW1 | ≤ 2ε, where ε is the Hoeffding bound and µW0 and µW1 are the means of two subwindows, with probability 1− by eqn (11)

$$\:\begin{array}{c}P\left(t\right):{p}_{P\left(t\right)}=\left({p}_{i,P\left(t\right)},{p}_{j,P\left(t\right),}{p}_{k,P\left(t\right)}\right)\in\:{1}_{++,}^{3}{l}_{P\left(t\right)}\\\:=\left({l}_{i,P\left(t\right)},{l}_{j,P\left(t\right)},{l}_{k,P\left(t\right)}\right)\in\:{\mathbb{I}}_{++}^{3}\\\:{L}_{i,P\left(t\right)}=\frac{{l}_{x,P\left(t\right)}}{{1}_{x}},{l}_{j,P\left(t\right)}=\frac{{l}_{y,P\left(t\right)}}{{1}_{y}},{l}_{k,P\left(t\right)}=\frac{{l}_{z,P\left(t\right)}}{{1}_{z}}\\\:C:{p}_{C}=\left({p}_{i,C},{p}_{j,c},{p}_{k,C}\right)=(\text{1,1},1),{l}_{C}=L\\\:=\left({L}_{i},{L}_{j},{L}_{k}\right)\in\:{\mathbb{I}}_{++}^{3}\\\:{L}_{i}=\frac{{L}_{x}}{{1}_{x}},{L}_{j}=\frac{{L}_{y}}{{1}_{y}},{L}_{k}=\frac{{L}_{z}}{{1}_{z}}\end{array}$$
(11)

Assume µ to be the real mean of W. The Hoeffding bound states that |µW0 − µ| < ε and |µW1 − µ| ≤ ε can be obtained independently. It is therefore possible to convert them into −ε ≤ |µW0 − µ| ≤ ε and −ε ≤ | µ − µW1 |≤ ε. Once these two disparities are added up by eqn (12)

$$\:\left|{\mu\:}_{{W}_{0}}-{\mu\:}_{{W}_{i}}\right|\le\:2\epsilon\:.$$
$$\:\left|{\mu\:}_{{W}_{0}}-{\mu\:}_{{W}_{1}}\right|\le\:\sqrt{\frac{2R\text{l}\text{n}(1/\delta\:)}{n}.}$$
(12)

Two subwindows of equal length were created out of the sliding window W: a right subwindow WR and a left subwindow WL. The definition of the Kullback-Leibler distance between X and Y is by Eq. (13)

$$\:\text{K}\text{L}\left({W}_{L}\parallel\:{W}_{R}\right)=\sum\:_{x\in\:X}\:\:{p}_{{W}_{L}}\left(x\right)\text{l}\text{o}\text{g}\frac{{p}_{{W}_{L}}\left(x\right)}{{p}_{{W}_{L}}\left(x\right)}$$
(13)

The CNN model is trained using the following parameters: (i) learning rate; (ii) momentum; and (iv) lambda (regularisation). To attain optimal performance, these parameters can be adjusted based on dataset. The lambda is used to stop data from being overfit. Momentum aids in convergence of data, whereas learning rate regulates how quickly network learns during training. Trial as well as error is used to determine these parameters. To best of authors’ knowledge, this study is first to use CNN for seizure identification in particular as well as EEG signal processing in general. Three distinct layer types make up the CNN architecture: a fully connected layer, a pooling layer, convolutional layer.

(1) Convolutional layer: It is made up of filters, or kernels, that move over the EEG signal. Matrix is convolved with input EEG signal is called a kernel, stride of filter determines how much of the input signal it convolves across. Equation (3) is used by this layer to perform convolution on input EEG signals using kernel. Another name for the convolution’s output is a feature map. Following is convolution operation by Eq. (14)

$$\:{y}_{k}=\sum\:_{n=0}^{N-1}\:\:{x}_{n}{h}_{k-n}$$
(14)

where N is number of elements in x, h is filter, x is signal. Y is output vector. nth element of vector is indicated by subscripts.

(2) Pooling layer: The down-sampling layer is another name for this layer. In order to lower the computational intensity as well as avoid overfitting, pooling process minimizes dimension of convolutional layer’s output neurons. Max-pooling operation is utilised. By choosing only highest value from every feature map, max-pooling procedure lowers total number of output neurons.

(3) Fully connected layer: Each and every activation in the layer before it is fully connected to this layer.

In this work, two different kinds of activation functions are used:

(1) Rectified linear activation unit: To use an activation function after every convolutional layer. An operation that maps an output to a set of inputs is known as an activation function. They are employed to give the network structure non-linearity. An established deep learning activation function is RLU. Activation function for convolutional layers is leaky rectifier linear unit (LeakyRelu). Due to LeakyRelu’s characteristics, the network structure gains nonlinearity and sparsity. Consequently, offering resilience to minute variations like noise in the input. We can see the LeakyRelu function in Eq. (15).

$$\:\:f\left(x\right)=\left\{\begin{array}{cc}x&\:\text{\:if\:}x>0\\\:0.01x&\:\text{\:otherwise\:}\end{array}\right.$$
(15)

(2) Softmax: Probability distribution of k output classes is calculated by this function. Therefore, Layer 13 predicts class to which input EEG signal belongs by using softmax function by Eq. (16)

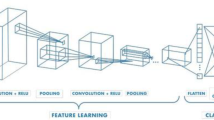
$$\:{p}_{j}=\frac{{e}^{{x}_{j}}}{\sum\:_{1}^{k}\:\:{e}^{{x}_{k}}}\text{\:for\:}\text{j}=1,\dots\:\text{k}$$
(16)

The net input is represented by x. P’s output values range from 0 to 1, and their total adds up to 1. VGG uses very small receptive fields instead of massive fields like AlexNet. So it uses 3 × 3 with a stride of 1. The decision function is more discriminative now that there are three ReLU units instead of simply one. There are also fewer parameters (27 times the number of channels vs. 49 times the number of channels in AlexNet). Without modifying the receptive fields, VGG uses 1 × 1 convolutional layers to make the decision function more non-linear. The VGG architecture is a convolutional neural network architecture that has been around for a while. It was developed as a result of research on how to make specific networks denser. The network employs tiny 3 × 3 filters. Aside from that, the network stands out for its simplicity, with simply pooling layers and a fully linked layer as extra components. VGG net deep learning model is one of the most widely employed image-recognition models today.

Table 3 presents the model’s architecture and layers. A 3 × 3 convolutional layer was employed in 2D, with Relu serving as the activation function. To minimise the number of features, a 2 × 2 maxpooling technique is utilised. As a link learns to prevent overfitting, 25% of connections deactivate. To convert data to a vector format for the following levels, use the flatten tool. We employed the Sigmoid function as the last activation layer to get binary classification results. Each network’s chosen hyperparameter is also described in that section. When it comes to real-time jobs, MLCDT-VGG-16 excels above other proposed networks due to its simplicity and speed. Pre-trained CNN and the idea of transfer learning were utilised in second and third networks to extract features.

Table 3 Proposed MLCDT-VGG-16 structure.
Full size table

In this case, 2D kernel, K, has a size of p × r, I is input matrix. Convolution blocks in Eq. (3) further employ ReLU activation function to introduce non-linearity into output. You can think of ReLU’s operation as f being a function of x by Eq. (17)

$$\:f\left(x\right)=\text{m}\text{a}\text{x}\text{i}\text{m}\text{u}\text{m}(0,x)\:$$
(17)

Of all the pooling layers, max-pooling is the approach that is most frequently utilised. By taking a sample of greatest stimulation factor derived from an array or represent space, it lowers the number of parameters. Equation (4) provides a description of max-pooling by Eq. (18)

$$\:{P}_{i,j}=\text{m}\text{a}\text{x}\text{i}\text{m}\text{u}\text{m}\left(f\left(x\right):x={A}_{i+m,j+n}\right)$$
(18)

where P is the max-pooling layer’s output and A is the ReLU’s activation output. the transposed convolution process, which upsamples the encoding in place of maxpooling. Equation (5) uses a kernel of size k × k in transposed convolution to process an image of size i × i. The result is an upsampled matrix whose dimensions are determined by following formula by Eq. (19)

$$\:(j-2)\times\:r-(1\times\:q)+(g-2)+3$$
(19)

where s is padding’s development. Feature extraction weights of every CNN were acquired by the application of transfer learning. Each of the three CNNs underwent the identical categorization procedure. In Fig. 2, the suggested architecture is displayed.

Fig. 2
figure 2

Architecture proposed with transfer learning based on VGG_16NN.

Full size image

Drowsiness analysis

Data for Training, Validating, Testing: A total of 1963 eyeblink artefacts with 25 features were chosen for training as well as testing following classification as shown in Fig. 3. As a result, there were 49,075 features that were needed for the models’ testing and training. Out of the total number of 1963 eye-blink artefacts, 1288 were classified as “Drowsy” artefacts, and the remaining 675 were classified as “Alert” artefacts. To create a highly accurate model for predictive modelling, it is crucial to divide data into training, validation, testing sets. Dataset that was utilised to train the model was called training set, it was from this dataset that model discovered its underlying patterns. 30% of data in this study was used for model testing, with the remaining 70% being used for model validation and training. To avoid overfitting in this investigation, 10-fold cross-validation was employed. Dataset is divided into 10 groups, or folds, at random using this method. Each fold has around the same size. One group was used as a hold-out or test dataset for every iteration, while other nine groups were used as training set. To train every data point, ten iterations were carried out in this manner. Consolidated cross-validation accuracy score was calculated by taking average of accuracy scores that method returned for each iteration.

Fig. 3
figure 3

Drowsiness detection model.

Full size image

Results and discussion

Experimental setup: An Alienware Desktop running 64-bit Windows 10 with an NVIDIA GeForce GTX 1080 graphics card as well as Intel(R) Core(TM) i7-6700 CPU was used for the comparison. The Python 3.6.6 platform was utilized to implement as well as test codes. Pytorch was utilized to implement suggested model, the SincShallowNet model, and its variants. TensorFlow’s Keras API was used to download and execute the EEGNet models. Our preliminary experiments revealed that, when utilising the default batch normalisation layer offered by the Pytorch and TensorFlow libraries, all of these deep learning models exhibit a rapid convergence followed by a notable decline in the accuracies for this dataset. To address the issue, we made small adjustments to each comparison model by turning off the computation of the mean and variance (we set momentum = 0 and track_running_stats = False for the batch normalisation layers that the Pytorch and Tensflow libraries included, respectively).

Dataset description: Two primary steps in the EEG data capture process are signal collection with Emotiv EPOC + headset. Hardware as well as software components work together to create signal gathering step. Emotiv EPOC + hardware is a non-invasive BCI (brain-computer interface) for contextual studies as well as human brain development. In comparison with therapeutic congeal, brine elucidation is simpler to administer as well as effectively maintains touch of scalp on both genders. Professionals can obtain outstanding access to high-quality brain data using the Emotiv EPOC + headset. Electrodes are placed on participant’s scalp in following areas: frontal as well as anterior parietal, temporal, occipital-parietal. Some of key features of Emotiv EPOC + helmet are shown in Table 4.

Real-time data stream visualisation, encompassing all data sources, is possible with the EmotivPRO programme. This application sets EEG Graphics’ vertical scaling for both single- as well as multi-channel display modes. Raw EEG data are then exported in formats that are used as input for data preparation step: EDF (European Data Format) or CSV (Comma-Separated Values).

Table 4 Features of Emotiv EPOC + helmet.
Full size table

Real-time data captured utilizing a single channel device is necessary for analysis of the EEG signal. We used pre-recorded EEG sleep data from the National Institutes of Health (NIH) research database called Physionet for this study. The participant in the experiment was instructed to use the driving simulation platform while seated in a chair. Using a 32-channel electrode cap, the EEG was recorded during the experiment in accordance with the international 10–20 lead standard. The Brain Vision recorder uses a 1000 hz sample rate to record EEG. The laboratory is kept at a constant 22 °C, giving the subjects a steady and comfortable atmosphere in which to conduct experiments. The distinct functional makeup of distinct brain regions results in variations in the EEG signal bands observed in certain regions. Furthermore, noise waves can easily interfere with EEG signals due to their low frequency and low amplitude. Thus, it is crucial to understand how to select the right electrode position. The majority of the electrodes are in good contact with the scalp when the EEG is recorded while driving using Brain Vision recorder recording software, and all signals satisfy the requirements for EEG collection. The EEGs of normal driving and fatigued driving were recorded, respectively. Twenty minutes of tiredness signals and twenty minutes of normal signals were recorded by each participant. Training and test samples were created using the signals that were gathered every ten seconds as a sample. Six participants in this study gathered a total of 720 groups of EEG samples from normal subjects and another 720 groups from fatigued people. The 1440 groups of EEG data samples that were collected were then processed and analysed. The number of blink events that were taken from each individual in the alert and drowsy states is summarised in Table 5. To address the class imbalance observed in the dataset, oversampling techniques like SMOTE were applied during training. Additionally, metrics such as F1-score and precision-recall were used to provide a balanced evaluation of the model’s performance.

Table 5 The number of observations obtained Table-6 comparative based on various EEG dataset.
Full size table

Table 6 shows parametric comparison between proposed and existing techniques. Comparative analysis has been carried out for Physionet and Emotiv EPOC + datasets in terms of prediction accuracy, precision, recall, F-1 score, SNR, RMSE, MAP. Existing techniques compared are STFT, SVM_LDA with proposed model. Analysis has been carried out for both the datasets between proposed and existing techniques.

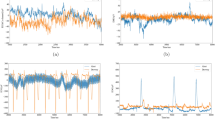
Table 6 Comparative based on various EEG dataset.
Full size table

For Physionet dataset proposed model achieved prediction accuracy 89%, precision 79%, recall 72%, F-1 score 61%, SNR 45%, RMSE 36%, MAP 55% as shown in Fig. 4 (a-g); whereas STFT prediction accuracy 81%, precision 75%, recall 66%, F-1 score 54%, SNR 41%, RMSE 32%, MAP 51%, SVM_LDA obtained prediction accuracy 85%, precision 77%, recall 68%, F-1 score 59%, SNR 43%, RMSE 34%, MAP 53%. From the above analysis for the Emotiv EPOC + dataset, the proposed technique obtained an enhanced accuracy rate with precision and minimal RMSE compared with other existing techniques and other parameters. Secondly, for Emotiv EPOC + dataset, proposed model achieved prediction accuracy 92%, precision 85%, recall 78%, F-1 score 71%, SNR 52%, RMSE 44%, MAP 60% as in Fig. 5 (a-g); whereas STFT prediction accuracy 85%, precision 81%, recall 73%, F-1 score 63%, SNR 47%, RMSE 39%, MAP 56%, SVM_LDA obtained prediction accuracy 88%, precision 83%, recall 75%, F-1 score 65%, SNR 49%, RMSE 42%, MAP 58%.

Fig. 4
figure 4

(a-g) Parametric comparison for Physionet dataset.

Full size image
Fig. 5
figure 5

(a-g) Parametric comparison for Emotiv EPOC+ dataset.

Full size image

The suggested system performs Drowsiness Detection utilising a single channel EEG input by utilising a deep learning technique based on MLCDT-VGG-16. As the research discusses, choosing a single channel instead of multi-channel EEG lowers time complexity. In a real-time application like driving, it is critical that method responds quickly. The suggested method predicts whether or not a signal sample is drowsy in two steps. The training phase, which is the first stage, is completed offline. Real-time online predictions are made during the second phase, which is when driver is really operating car. There is a trade-off between classification accuracy and training duration. Compared to many other existing methodologies, training time complexity of our suggested technique is considerable. Prediction phase’s temporal complexity isn’t very high, though. The EEG signal prediction occurred in a linear amount of time. The linear temporal complexity results from prediction of a signal occurring as a weighted sum of trained weights.

Conclusion

By employing a machine learning model, this study suggests a novel method for automatically detecting tiredness when driving. Utilising the wavelet time frequency transform paradigm, the input EEG signal was processed to classify patterns of brain activity. thereafter a multi-layer convolutional designed transfer VGG-16 neural network was used to classify this examined pattern. The ability to recognise tiredness is essential for safe driving, and this study suggested a new method to stop drowsiness-related accidents. Our EEG data is labelled to indicate fatigue according to an primary assessment as well as θ- frequencies as of sequential as well as occipital regions. The results show that careful consideration must be given to the pre-processing pipeline’s architecture in order to handle various types of noise as well as objects in signals based on how they affect classification task. It is inevitable that the nature of EEG signals makes them more difficult to comprehend than other types of data, such as pictures and natural languages. As a pilot investigation, only a small subset of the samples were analysed in this paper. Further work will be done in the future to understand deep learning models and develop techniques in a way that addresses the issues encountered in the pursuit of brain computer interfaces that don’t require calibration.