PIA-A secure and efficient identity authentication scheme in telemedicine via the PUF method

Abstract

With the rise of IoT technology, remote medical services have gained increasing attention. These services became particularly popular during the COVID-19 pandemic due to their convenience, privacy, and ability to transcend geographical boundaries. In remote medical networks, identity authentication protocols are a crucial component, playing a vital role in ensuring that healthcare providers can operate in a secure and efficient environment. However, some existing identity authentication protocols in remote medical environments are vulnerable to various security threats, such as privileged insider attacks, session key security issues, unauthorized data access, and failure to meet both three-factor security and anonymity. These threats can compromise patient privacy and the integrity of healthcare systems.Therefore, the development of a secure and efficient identity authentication protocol for remote medical services is of utmost importance. To address this need, we propose a Physically Unclonable Function-based identity authentication scheme for telemedicine. In our scheme, we use symmetric encryption and Elliptic Curve Cryptography to encrypt critical information, ensuring a high level of security. We leverage PUF technology to associate devices with users, creating a “device fingerprint” for enhanced authentication. Furthermore, we have provided security proofs for our scheme using the Random Oracle model and the ProVerif protocol analysis tool. Through comprehensive security analysis, we demonstrate that the proposed scheme can resist most known attacks and meets anonymity, forward/backward security, and three-factor security. Lastly, we compared our scheme with existing protocols in terms of computational overhead, storage overhead, and communication overhead using a unified performance benchmark. The results indicate that, while there is no advantage in communication overhead, our scheme reduces computational overhead by approximately 50.71% and storage overhead by 16.32%.

Introduction

The emergence of the Internet of Things (IoT) and remote healthcare technologies has transformed the traditional healthcare model, enabling individuals to access medical treatment without being constrained by geographical barriers. Particularly during the COVID-19 pandemic, remote medical services have played a crucial role in facilitating off-site consultations^1,2. The IoT enhances communication between medical devices and healthcare professionals through the internet, creating new business opportunities and scenarios for medical institutions. However, this advancement also introduces new challenges and security risks. For instance, sensors utilized in remote medical devices often possess limited memory and computational capabilities. Furthermore, data transmitted over public channels in remote medical settings is susceptible to tampering and interception. While identity authentication protocols are essential for ensuring data security in remote medical environments³, current protocols still encounter issues such as anonymity, impersonation attacks, and man-in-the-middle attacks. Insecure identity authentication protocols not only elevate the risk of theft and tampering with medical data but also endanger patients’ lives by potentially leading to incorrect medical decisions due to compromised data. Consequently, developing secure and efficient identity authentication protocols for devices with low power, limited computational resources, and inadequate storage capacity has become a focal point for many researchers⁴. Currently, in many fields such as healthcare, industry, and smart homes, many identity authentication protocols are vulnerable to issues like offline password guessing attacks, node capture attacks, and man-in-the-middle attacks, and fail to meet required security objectives such as anonymity and three-factor security. In the login process, fuzzy extractor functions are primarily used, but they do not associate the user with the device. Therefore, to better meet these requirements and enhance the use of the protocol in resource-constrained devices, as well as to address security issues in the protocol used for remote medical diagnosis and treatment by doctors for patients, we propose our PIA protocol.

Motivation and contributions

Current protocols frequently exhibit vulnerabilities, including susceptibility to offline password-guessing attacks, insufficient forward secrecy, and the potential for user anonymity tracing. In response, we have developed a robust identity authentication protocol that not only reduces computational time and storage costs but also strengthens defenses against prevalent attacks. Consequently, the primary contributions of this paper are as follows.

• (1) We have developed a robust and efficient protocol for remote healthcare identity authentication. Local validation leverages the use of Physically Unclonable Functions (PUFs). Biohashing techniques enhance biometric recognition, thereby improving accuracy in feature identification and reducing computational burden. The implementation of symmetric cryptography and Elliptic Curve Cryptography (ECC) facilitates secure parameter exchange and ensures secure session key negotiation.

• (2) The proposed scheme has undergone a formal security proof utilizing both the Random Oracle (RoR) model and the ProVerif tool, thereby ensuring the security of the session key. Additionally, the security analysis demonstrates that our scheme is resilient against common attacks and specific vulnerabilities, thereby affirming its classification as a secure protocol.

• (3) We conducted a comparative analysis of our proposed solution against similar alternatives, evaluating performance across various metrics, including computation time, communication, storage costs, and security. The results clearly demonstrate the superior security measures and reduced computational and storage requirements of our solution, rendering it highly suitable for deployment in resource-limited remote medical settings.

The structure of the paper

The upcoming chapters are structured as follows: The “Related Work” section analyzes classification-based studies on remote medical identity authentication protocols and the evolution of authentication factors. The “Foundational Theoretical” chapter delves into fundamental concepts, with a particular focus on Biohashing functions and Physical Unclonable Functions (PUF). The “Proposed Scheme” presents a comprehensive framework that emphasizes mutual authentication and key negotiation between doctors’ and patients’ devices within a remote medical network, including a proof of the security of the protocol. In the "Efficiency and Security Comparisons" section, we evaluate our solution against similar schemes in terms of computational overhead, storage overhead, communication overhead, and security, utilizing a unified performance benchmark. Lastly, Section VI provides a conclusive summary of the findings.

Related work

In recent decades, researchers have proposed numerous authentication schemes suitable for Wireless Medical Sensor Networks (WMSNs). In 2012, Kumar et al.⁵ introduced an authentication scheme for medical applications that utilized smart card technology and symmetric encryption to establish session keys between users and medical sensor nodes. However, He et al.⁶ identified vulnerabilities to password guessing attacks and insider threats in Kumar et al.'s scheme and proposed an enhanced version of authentication. Subsequently, Mir et al.⁷ demonstrated vulnerabilities in He et al.'s scheme to offline password guessing and user impersonation attacks, introducing an authentication and key negotiation scheme that employed hash functions and XOR operations.

When two-factor authentication schemes fail to meet the security requirements of Wireless Multimedia Sensor Networks (WMSNs), researchers have proposed three-factor authentication schemes. In 2018, Challa et al.⁸ introduced a tri-factor authentication and key negotiation protocol in WMSNs utilizing bilinear pairings to address common security vulnerabilities such as smart card theft, offline password guessing, and insider privilege attacks. Following this, in 2019, Li et al.⁹ put forward a secure tri-factor user authentication protocol with forward secrecy in WMSN systems. This protocol incorporates biometric verification with error-correcting codes and fuzzy extraction functions, claiming resistance against various security attacks. However, Muhammad et al.¹⁰ identified shortcomings in Li et al.'s scheme concerning user anonymity and sensor spoofing attacks. In response, Shin et al.¹¹ proposed an identity authentication and key negotiation scheme that ensures user privacy protection by leveraging the Elliptic Curve Diffie-Hellman (ECDH) technique. Furthermore, Ali et al.¹² introduced an identity authentication and access control protocol for WMSNs that combines ECC with biometrics. In 2020, Hsu et al.¹³ presented a fast tri-factor authentication and privacy-preserving scheme utilizing hash functions and XOR operations, primarily designed for the single sign-on of users in remote medical information systems.

Despite the advantages of lightweight communication between doctors and patients, existing schemes^11,12,13 are susceptible to physical attacks on sensor nodes and cloning attacks. To mitigate these vulnerabilities, Physical Unclonable Functions (PUF) present an effective solution. In 2021, Wang et al.¹⁴ proposed a lightweight authentication protocol for Wireless Multimedia Sensor Networks (WMSNs), highlighting its resilience against network and physical security threats. However, Yu et al.¹⁵ identified several weaknesses in this protocol, including vulnerabilities to man-in-the-middle attacks and session key leakage, thereby underscoring the absence of mutual authentication. Conversely, Servati et al.¹⁶ introduced an IoT-based medical environment authentication scheme that purports to safeguard against various attacks. Nonetheless, an analysis by Thakur et al.¹⁷ revealed that this scheme remains vulnerable to impersonation attacks targeting users, servers, and gateway nodes.

Guo et al.¹⁸ introduced an innovative IoT privacy-preserving authentication protocol that utilizes ECC. This protocol incorporates four authentication factors—password, smart card, biometrics, and PUF. By integrating hash and XOR operations, the the protocol’s design achieves a balance between security and computational efficiency. Nyangaresi et al.¹⁹ proposed a pseudonymous authentication protocol for wearable computing environments, which uses elliptic curve cryptography (ECC) and pseudonym-based protocols to address issues of vulnerability to malicious entities, as well as high computational, storage, and communication overheads, making them suitable for use in resource-constrained sensors. Nyangaresi et al. ²⁰ developed a three-factor authentication protocol that includes patient biometric data, smart cards, and passwords. Formal analysis using the Real-or-Random (ROR) model and the Dolev-Yao (BAN) logic demonstrated that the protocol is secure. Nyangaresi et al. ²¹ proposed a protocol utilizing a lightweight anti-collision one-way hash function and pseudonyms to mitigate threats such as spoofing attacks, edge attacks, and physical attacks. Additionally, the confidentiality of derived sessions was proven.

Shukla et al.²² designed an innovative, multi-factor, ECC-based multi-server authentication protocol, combined with an offline registration center, specifically targeting multi-server architectures in cloud environments. The protocol aims to address threats such as replay attacks, user impersonation attacks, and denial-of-service attacks, while introducing a registration center to authenticate each user-server connection, potentially leading to computational bottlenecks and a single point of failure in the registration center. Patel et al.²³ proposed a cloud-enhanced protocol based on fuzzy validators and elliptic curve encryption, offering privacy features while also providing security against attacks. However, its repeated use of ECC point multiplication results in low computational efficiency, making it unsuitable for resource-constrained environments.

Mathematical preliminaries

To enhance the readability of our protocol, we will provide a brief introduction to some basic concepts.

(1) Biohashing Function.

Due to the presence of noise, slight variations in the extracted biometric features occur each time a user accesses them. To address this issue, Jin et al.²⁴ introduce the Biohashing function, which is designed to manage the subtle variations in the input biometric features. Consequently, Biohashing has emerged as a widely utilized identity authentication scheme, particularly in the field of revocable biological authentication.The input to a biometric hash function is a biometric feature, and the output is a hash value. Below is a simplified mathematical formula from input to output:

Input: Biometric feature vector ${\text{F}} = (f_{1} ,f_{2} ,f_{3} ....f_{k} )$, where each ${\text{f}}_{{\text{i}}}$ is a numerical value of a biometric feature (such as parameters in a fingerprint, iris, etc.).

The output steps can be described as follows:

Normalization or Mapping of Biometric Features: Convert the biometric feature ${\text{f}}_{{\text{i}}}$ into numerical form.

Weighted Sum: Calculate the weighted sum of each feature, with weights ${\text{w}}_{{\text{i}}}$.

Modulo Operation: Finally, apply the modulo operation to the weighted sum to ensure the output is within a certain range.

The mathematical formulas can be expressed as:${\text{H(F)}} = \left( {\sum\nolimits_{{{\text{i}} = {1}}}^{{\text{k}}} {{\text{f}}_{{\text{i}}} \cdot w_{i} } } \right){\text{ mod p}}$, ${\text{p}}$ is a prime number that ensures the output is within a certain range.

(2) PUF Function.

PUF, or Physical Unclonable Function, is a technology that utilizes the intrinsic physical structure of materials to uniquely identify them. The underlying principle of PUF technology involves constructing a circuit that collects and amplifies the subtle physical differences that arise during the manufacturing process of each chip, which serve as the sole ‘feature’ information of the chip, referred to as the PUF value. These minor physical variations include the initial state of the SRAM unit and the random differences in the transistor threshold voltage, contributing to the uniqueness of the PUF value for each chip. Moreover, PUF values are not only unique but also unclonable. The PUF operates based on a "challenge-response" mechanism. Formally, a PUF can be defined as a physical system that maps a challenge ${\text{R}} = {\text{\{ 0,1\} }}^{{{\text{l}}_{{2}} }}$ selected from a finite space ${\text{C}} = {\text{\{ 0,1\} }}^{{{\text{l}}_{{1}} }}$ to a response rrr in a finite space ${\text{c}}$. That is:${\text{r}} \leftarrow {\text{PUF}}_{{\text{k}}} {\text{(c)}}$.

(3) Elliptic Curve Cryptography.

The ECC algorithm is a cryptographic algorithm based on elliptic curve theory. Compared to RSA, it offers higher transmission speed and shorter key lengths²⁵. Therefore, this protocol utilizes the ECC algorithm to encrypt transmitted data, ensuring confidentiality. Below are two common fundamental concepts related to the ECC algorithm:

• (a) Elliptic Curve Equation: Typically, it appears as ${\text{E(a,b)}}$:${\text{y}}^{{2}} = ({\text{x}}^{{3}} + {\text{ax}} + {\text{b}})\bmod p$, where ${\text{p}}$ is a large prime number.$\forall {\text{a,b}} \in {\text{Z}}_{{\text{p}}}^{*}$ is such that $\left( {{\text{4a}}^{{3}} + {\text{27b}}^{{2}} } \right)\bmod p \ne {0}$²⁶. G is an arbitrary base point on the curve ${\text{E(a,b)}}$.

• (b) Elliptic Curve Diffie-Hellman Problem: On the elliptic curve ${\text{E(a,b)}}$, G is a base point. Assuming $\forall {\text{a,b}} \subseteq {\text{Z}}_{{\text{p}}}^{*}$ , ${\text{c}} = a \cdot b$ and ${\text{M}} = a \cdot {\text{G}}$ , ${\text{N}} = {\text{b}} \cdot {\text{G}}$, ${\text{R}} = {\text{c}} \cdot {\text{G}}$ exist together, it is impossible for an attacker to compute R in polynomial time, given M and N , while a and b are unknown.

Proposed scheme

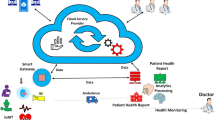
To establish a secure and efficient telemedicine network environment, we propose a novel protocol comprising six distinct phases. The relevant symbols utilized within the protocol, along with their descriptions, are presented in Table 1. Our protocol comprises three primary entities: physician users, trusted gateways (TGW), and medical sensor devices. Figure 1 illustrates the structural diagram of these entities and their interrelationships. Doctor users (e.g., User1, User2, etc.) are primarily responsible for collecting patients’ physiological data to provide treatment recommendations or, through medical devices, for offering remote diagnosis and treatment. The gateway mainly stores the registration information of doctor users and medical sensors, as well as forwarding information to assist users in negotiating session keys with the sensors. Medical sensors (e.g., HD1, HD2, etc.) are primarily attached to the patient’s body to collect physiological data or assist doctors in remote diagnosis and treatment.When a physician user requires access to remote sensor devices, both the physician user and the medical sensor devices must pre-register with a trusted gateway via a secure communication channel. Following this reciprocal registration, the trusted gateway stores essential confidential parameters associated with both the physician user and the medical sensor devices, thereby streamlining the session key negotiation process between the physician and the sensors.As three independent entities, the information transmitted between them is conveyed over public channels. However, public channels are unreliable, and the information transmitted may be intercepted, tampered with, or even forged. The physiological data of patients face risks of leakage, misdiagnosis, and potential connection interruptions in emergency situations. To address the aforementioned risks, this solution has been proposed, aiming to ensure high security while improving the efficiency of such solutions and reducing storage requirements, making it suitable for use in resource-constrained environments or devices.

Table 1 Symbol and descriptions.

Fig. 1

Framework structure.

1. Initialization

The system initialization process starts with the TGW selecting specific parameters. During this process, the TGW chooses primary private keys x and y from a random number space, where x and y are secret parameters. Additionally, the public parameter P is selected and made available to the public.

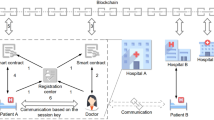
2. Physician Users Registration.

To gain authorization as a legitimate physician user communicating with medical sensors, one must undergo registration with the TGW under secure communication protocols. The registration procedure is outlined below and depicted in Fig. 2.

Fig. 2

Physician user registration.

Step A1 Physician users ${\text{U}}_{{\text{i}}}$ input both their PW and BIO on the device. Subsequently,device computes $C_{i} = {\text{biohashing}}(BIO)$,

$E_{i} = PUF(C_{i} )$. Lastly, $C_{i}$ and $E_{i}$ are sent to the TGW over a secure channel.

Step A2 Upon receiving the message containing $C_{i}$ and $E_{i}$, TGW initially verifies the message’s authenticity. If TGW deems the message illegitimate, thereby terminating the session. When TGW determines the message to be legitimate, it performs the following computations:$D_{y} = h(C_{i} ||x)$, $A = E_{i} \oplus D_{y}$. Afterward, generated R, calculates $M_{0} = h(A||R)$,then save $\{ M_{0} ,(C_{i} ,E_{i} ,R)\}$ in its database. Finally, it sends $\{ D_{y} ,A,R\}$ to $U_{i}$ through a secure communication channel, maintaining a one-to-one mapping of $M_{0}$ with $\{ C_{i} ,E_{i} ,R\}$ in the database.

Step A3 When $U_{i}$ receive the message $\{ D_{y} ,A,R\}$, start computing $B = h(PW||C_{i} )$ and $C = h(A||B||D_{y} )$. Once the computation is completed, store $\{ D_{y} C,R\}$ in the device.

3. Medical Sensor Device Registration.

The sensor node first generates $S_{D} = PUF \, (SID)$ and sends $S_{D}$ and $SID$ to the TGW through a secure channel. Upon receiving the message, the TGW calculates $K_{j} = h(SID||y||S_{D} )$. Subsequently, the TGW saves $S_{D}$ and $SID$, and sends $K_{j}$ to the sensor. Upon receiving it, the sensor saves it.

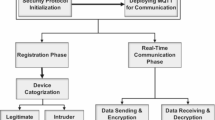
4. Physician Users Login and Key Negotiation.

Before accessing the data from the sensor node, the physician user first logs in through the device used during registration, and after successful login authentication, negotiates the session key with the medical sensor device through the TGW. After successful three-way authentication of the physician user, the gateway and the sensor node, a secure session key is generated. The user will be able to securely interact with the sensor device for data through the session key. This phase is described in further detail in the next section, as shown in Fig. 3.

Fig. 3

Physician Users Login and Key Negotiation.

Step A1 Physician user ${\text{U}}_{{\text{i}}}$ inputs their password (${\text{PW}}^{1}$) and biometric data (${\text{BIO}}^{1}$) using the mobile device. It calculates.

$C_{i} = biohashing(BIO^{1} )$,$E_{i} = PUF(C_{i} )$,$A = E_{i} \oplus D_{y}$,$B = h(PW^{1} ||C_{i} )$,$C^{\prime} = h(A||B||D_{y} )$,and checks whether $C^{\prime} = C$. The request is aborted if $C^{\prime} \ne C$. Otherwise, Local identity authentication has been successfully completed. Then, it produces a timestamp $T_{1}$. Calculates $M_{1} = h(A||R)$,$M_{2} = h(M_{1} ||B||R||E_{i} )$,$M_{3} = SID \oplus R \oplus M{}_{2}$,$M_{4} = h(M_{2} ||M_{3} )$,$M_{5} = h(M_{1} ||M_{2} ||M_{3} ||M_{4} )$,$V = h(A||R||D{}_{y})$,$M_{6} = E_{\left( V \right)} (M_{2} ,M_{3} ,M_{4} )$. Finally, ${\text{U}}_{i}$ sends the login request $\{ M_{1} ,M_{5} ,M_{6} ,T_{1} \}$ to the TGW.

Step A2 Upon receiving the request message $\{ M_{1} ,M_{5} ,M_{6} ,T_{1} \}$, the TGW initially verifies ${|}T_{1} - T^{\prime}_{1} | < \Delta T$. Then TGW checks $M_{1}$ in the database whether $M_{1}$ exists. If it does not exist, the session terminates. If it exists, the corresponding user information is extracted. Then, TGW computers $D_{y}^{\prime } = h(C_{i} ||x)$,$A^{\prime} = E_{i} \oplus D_{y}$,$V^{\prime} = h(A^{\prime}||R||D_{y}^{\prime } )$, $(M^{\prime}_{2} ,M^{\prime}_{3} ,M^{\prime}_{4} ) = D_{{(V^{\prime})}} (M_{6} )$,$M^{\prime}_{5} = h(M^{\prime}_{2} ||M^{\prime}_{3} ||M^{\prime}_{4} )$, and checks whether $M^{\prime}_{5} = M_{5}$. The request is aborted if $M^{\prime}_{5} \ne M_{5}$. If not, the login request is deemed legitimate. TGW proceeds to.

generate two random nonce values a, b, and a timestamp ${\text{T}}_{{2}}$, and computers $SID^{\prime} = M^{\prime}_{3} \oplus M^{\prime}_{2} \oplus R$, $K^{\prime}_{j} = h(SID||y||S_{D} )$, $M_{7} = aP$,

$M_{8} = K^{\prime}_{j} \oplus b \oplus S_{D}$,$M_{9} = h(SID^{\prime}||b||M_{7} ||K^{\prime}_{j} )$.At last, TGW forwards the message $\{ M_{5} ,M_{7} ,M_{8} ,M_{9} ,T_{2} \}$ to the sensor node ${\text{S}}_{j}$.

Step A3 Upon receiving message $\{ M_{5} ,M_{7} ,M_{8} ,M_{9} ,T_{2} \}$,${\text{S}}_{j}$ verifies ${|}T_{2} - T^{\prime}_{2} | < \Delta T$. Then calculates $S_{D} = PUF(SID)$, $b{\prime} = M_{8} \oplus K{}_{j} \oplus {\text{S}}_{{\text{D}}}$,$M^{\prime}_{9} = h(SID||b^{\prime}||M_{7} ||K_{j} )$, and checks whether $M^{\prime}_{9} = M_{9}$. The request is aborted if $M^{\prime}_{9} \ne M_{9}$. Otherwise, the request is legitimate. ${\text{S}}_{j}$ creates a random nonce, denoted as c, and calculates $M_{10} = cP$,$M_{11} = cM_{7}$,$M_{12} = M_{10} \oplus b^{\prime} \oplus S_{D}$, $M_{13} = h(K_{j} ||M_{10} ||M_{11} ||b^{\prime})$,$SK = h(M_{5} ||M_{10} ||M_{11} )$,$M_{14} = h(SID||M_{5} ||M_{11} ||SK)$. At last,${\text{S}}_{j}$ forwards the message $\{ M_{12} ,M_{13} ,M_{14} \}$ to TGW.

Step A4 While receiving the message $\{ M_{12} ,M_{13} ,M_{14} \}$, TGW computers $M^{\prime}_{10} = M_{12} \oplus b \oplus S_{D}$,$M_{11} = aM_{10}$,

$M^{\prime}_{13} = h(K_{j} ||M^{\prime}_{10} ||M^{\prime}_{11} ||b)$, and checks whether ${\text{M}}_{13}{\prime} = {\text{M}}_{13}$. If they are equal, TGW generates a new random nonce ${\text{R}}^{{{\text{new}}}}$ and calculates $M_{15} = h(M^{\prime}_{4} \left| {\left| {M^{\prime}_{10} } \right|} \right|M^{\prime}_{11} ||A^{\prime})$,$M_{16} = E_{\left( V \right)} \left( {M^{\prime}_{10} ,M^{\prime}_{11} ,R^{new} } \right)$,$M_{0}^{new} = (A||R^{new} )$. Afterward, TGW updates the previously stored $M_{0}$ to $M_{0}^{new}$ and R to $R^{new}$. At last, TGW forwards the message $\left\{ {M_{14} ,M_{15} ,M_{16} } \right\}$ to ${\text{U}}_{i}$.

Step A5 Upon receiving message $\left\{ {M_{14} ,M_{15} ,M_{16} } \right\}$,${\text{U}}_{{\text{i}}}$ computes $(M^{\prime\prime}_{10} ,M^{\prime\prime}_{11} ,R^{new} ) = D_{\left( V \right)} \left( {M_{16} } \right)$,$M^{\prime}_{15} = h(M_{4} ||M^{\prime\prime}_{10} ||M^{\prime\prime}_{11} ||A)$ and check whether $M^{\prime}_{15} = M_{15}$. If it proves to be valid $,$ ${\text{U}}_{i}$ computers $SK = h(M_{5} ||M^{\prime\prime}_{10} ||M^{\prime\prime}_{11} )$, $M_{14} = h(SID||M_{5} ||M^{\prime\prime}_{11} ||SK)$, and checks whether $M^{\prime}_{14} = M_{14}$. If they are equal, update R to ${\text{R}}^{{{\text{new}}}}$. Finally, ${\text{U}}_{i}$ and ${\text{S}}_{j}$ can engage in subsequent communication through TGW using the shared key SK.

5) Password Alter

The user can alter the password by following these procedures.

Step A1${\text{U}}_{{\text{i}}}$ input ${\text{PW}}^{1}$ and BIO using the device. The mobile device computes $C_{i} = biohashing(BIO)$,$E_{i} = PUF(C_{i} )$,$A = E_{i} \oplus D_{y}$,

$B = h(PW^{1} ||C_{i} )$,$C^{\prime} = h(A||B||D_{y} )$, and checks whether $C^{\prime} = C$. If $C^{\prime} \ne C$, the protocol will result in a local login failure. Otherwise, local identity authentication has been successfully completed, continue with the subsequent operations.

Step A2${\text{U}}_{{\text{i}}}$ enters the new password ${\text{PW}}^{n}$, continue with the subsequent operations.

Step A3 The mobile device calculates $B^{new} = h(PW^{n} ||C_{i} )$,$C^{new} = h(A||B^{new} ||D_{y} )$.${\text{U}}_{i}$ updates the previously stored C to $C^{new}$. Completed the local password update operation.

6) Deregister and Re-Registration.

In the event of a physician device stolen, the subsequent measures can be implemented to revoke the device:

Step A1${\text{U}}_{i}$ forwards $C_{i} = biohashing(BIO)$ to TGW through secure channel, indicating a logout request.

Step A2 TGW checks the validity of $C_{i}$. If valid, TGW locks $C_{i}$ and revokes the user associated with it. Subsequently, no user can log in to TGW with identity $C_{i}$.

After a physician user deregisters their previous user identity information from the trusted gateway, accessing the medical sensor device from a new device simply requires re-registering using the same method.

Security analysis

The segment employs a variety of security analysis techniques to demonstrate the security of the proposed solution. The random oracle model’s formal analysis highlights semantic security attainment. Utilizing the Proverif formal analysis tool, simulation experiments affirm the solution’s resistance against prevalent known attacks. Furthermore, a security analysis establishes the realization of multiple security attributes, encompassing anonymity and three-factor security.

(1) Formal Security Analysis

A) Real-or Random model.

Feng et al.²⁷ used a three-factor multi-cloud server authentication security model. In the proposed model, three distinct entities are presumed to exist: user ${\text{U}}_{i}$, TGW, and sensor nodes ${\text{S}}_{j}$. Each oracle model has three states to describe the outcomes.

• Accept: receives the expected correct message.

• Reject: receives the incorrect expected message.

• ⊥: no response was received for the input information.

Partnership: Among the three entities, both are accepting if two instances simultaneously meet the following three conditions: Both of them are in receptive states;

They authenticate each other and share identical session identifiers:

They are each other’s mutual partners;

They are reciprocal partners. Fulfilling these three criteria will establish a partnership.

Attacker: Here, as per the assailant model, we suppose that ${\mathcal{A}}$ can attack all information on the public channel. Within this model, ${\mathcal{A}}$ undermines the authentication protocol’s security by engaging with honest entities, initiating query oracles, and manipulating simulators to acquire the session key. These queries ${\mathcal{A}}$ can initiate the following types of operations:

Execute(${\text{U}}_{{\text{i}}} {\text{, S}}_{{\text{j}}} {\text{, TGW}}$): The query imitates a passive assault, bestowing the assailant entry to all data conveyed via a communal communication conduit. Send(${\text{U}}_{{\text{i}}}$/${\text{S}}_{{\text{j}}}$/ TGW, m): This query replicates active attacks. The attacker transmits message m to ${\text{U}}_{{\text{i}}} /{\text{S}}_{{\text{j}}} /$ TGW. If the message m proves valid, the oracle acknowledges it and responds with a message to the attacker. Additionally, the attacker can use Send(${\text{U}}_{{\text{i}}}$, start) to initialize an authentication process.

Reveal(${\text{U}}_{{\text{i}}} {\text{, S}}_{{\text{j}}}$): The oracle furnishes the attacker with the session key of either instance ${\text{U}}_{{\text{i}}}$ or ${\text{S}}_{{\text{j}}}$. If instance ${\text{U}}_{{\text{i}}}$ or ${\text{S}}_{{\text{j}}}$ hasn’t established a session key, it produces an invalid symbol 丄 as a response.

Corrupt(${\text{U}}_{{\text{i}}} {\text{, z}}$): The oracle provides the attacker with one or two sets of authentication information belonging to user ${\text{U}}_{{\text{i}}}$-. It’s important to note that the attacker is incapable of acquiring all three types of authentication information concurrently; doing so would erase any distinction from legitimate users.

When z = 1, it returns the password of ${\text{U}}_{{\text{i}}}$ to the attacker.

When z = 2, it returns the parameters stored in ${\text{U}}_{{\text{i}}}$ smart card.

When z = 3, it returns the biometric data of ${\text{U}}_{{\text{i}}}$.

Corrupt(${\text{U}}_{{\text{i}}} ,S_{j} ,TGW$): The oracle simulates forward secrecy, enabling the attacker to acquire the long-term secret values associated with ${\text{U}}_{{\text{i}}}$,${\text{S}}_{{\text{j}}}$, and TGW.

Test (${\text{U}}_{{\text{i}}} ,S_{j}$): The oracle assesses the semantic integrity of the session key, enabling a single query for the attacker. When ${\text{U}}_{{\text{i}}}$ or ${\text{S}}_{{\text{j}}}$ is fresh, the oracle acquires the session key SK from the Reveal(${\text{U}}_{{\text{i}}}$) outcome and forms a bit b. If not, it provides an invalid symbol ⊥. If b equals 1, it furnishes the session key to the attacker. Should b equal 0, it furnishes an equally lengthy random string to the attacker.

Freshness: A case where ${\text{U}}_{{\text{i}}}$ or ${\text{S}}_{{\text{j}}}$ is deemed fresh when these criteria align:

The occurrence has been acknowledged, and a session key has been established.

The attacker has not queried Reveal(${\text{U}}_{{\text{i}}} ,{\text{S}}_{{\text{j}}}$) for this instance or its partners in the same session.

The attacker has not queried Corrupt(${\text{U}}_{{\text{i}}}$, u = 1,2,3) for this instance.

The attacker has not queried Corrupt(${\text{S}}_{{\text{j}}}$, TGW) for this instance.

Semantic Security: If the attacker ${\mathcal{A}}$ is able to distinguish whether the query return result of Test(${\text{U}}_{{\text{i}}}$,${\text{S}}_{{\text{j}}}$) is a session key or a random string, then we can say that the ${\mathcal{A}}$ has breached the semantic security of the authentication protocol, and the advantage for the ${\mathcal{A}}$ to win the game is defined as ${\text{Adv}}_{{\mathcal{L}}}^{{{\text{AKE}}}} \left( {\mathcal{A}} \right)$ = 2Pr(b' = b)—1. If the above advantage is negligible for any attacker in polynomial time, then the authentication scheme has semantic security.

AKE Security: Let ${\text{E}}_{{\text{p}}}$ stand for the ECC, while D represents a password dictionary uniformly distributed with a size of |D|.${\mathcal{L}}$ represents the proposed protocol, and ${ }{\mathcal{A}}$ denotes an attacker against our scheme. Consider ${\text{Adv}}_{{\mathcal{L}}}^{{{\text{ECDHP}}}}$ as the advantage of ${\mathcal{A}}$ in efficiently solving the ECDH problem within a polynomial time frame. Given an upper limit of time t, ${\mathcal{A}}$ can execute a maximum of ${\text{q}}_{{\text{s}}}$ message sending queries, ${\text{q}}_{{\text{e}}}$ execution queries, ${\text{q}}_{{\text{h}}}$ hash queries, and ${\text{q}}_{{\text{b}}}$ biometric hash queries and ${\text{q}}_{{\upvarepsilon }}$ encryption\decryption queries within this time frame. Hence, we have

$${\text{ Adv}}_{{\mathcal{L}}}^{{{\text{AKE}}}} \left( {\mathcal{A}} \right) \le \frac{{{\text{q}}_{{\text{h}}}^{2} + 6{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{1} }} }} + \frac{{{\text{q}}_{{\text{b}}}^{2} + 2{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{2} }} }} + \frac{{{\text{q}}_{{\upvarepsilon }}^{2} }}{{2^{{{\text{l}}_{3} }} }} + \frac{{\left( {{\text{q}}_{{\text{s}}} + {\text{q}}_{{\text{e}}} } \right)^{2} }}{{\text{n}}} + \frac{{2{\text{q}}_{{\text{s}}} }}{{\text{Y}}} + 2{\text{q}}_{{\text{h}}} {\text{Adv}}_{{\mathcal{L}}}^{{{\text{ECDHP}}}} .$$

(1)

where ${\text{l}}_{1}$ is the length of the output bit from the hash function,${\text{l}}_{2}$ the length of the output bit from the biohashing function,${\text{l}}_{3}$ the length of the output bit from symmetric encryption, and Y represents the size of passwords dictionary space. It denotes the advantage an attacker has in solving ${\text{Adv}}_{{\mathcal{L}}}^{{{\text{ECDHP}}}}$ within polynomial time.

Proof:

We deduce the advantage an attacker has in breaking the proposed scheme through a series of games from ${\text{G}}_{0}$ to ${\text{G}}_{7}$.${\text{S}}_{{\text{i}}}$ represents the attacker correctly guessing the value of b in ${\text{Test}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,{\text{U}}_{{\text{j}}}^{{\text{a}}} } \right)$ in game ${\text{G}}_{{\text{i}}}$.${\text{ Pr}}\left[ {{\text{S}}_{{\text{i}}} } \right]$ represents the probability of event ${\text{S}}_{{\text{i}}}$ occurring.

${\text{G}}_{0}$: This game simulates the attacker’s real attack on the protocol, obviously ${\text{Adv}}_{{\mathcal{L}}}^{{{\text{AKE}}}} \left( {\mathcal{A}} \right) = 2\left( {{\text{Pr}}\left[ {{\text{S}}_{0} } \right]} \right) - 1$.

${\text{G}}_{1}$: This game simulates all the oracles involved in the security model. In this game, a new hash list ${\text{L}}_{{\text{h}}}$ is created to simulate the hash random oracle, a new biohashing list ${\text{L}}_{{\text{b}}}$ is created to simulate the biohashing random oracle, and a new encryption and decryption random oracle list ${\text{L}}_{{\upvarepsilon }}$ is created to simulate the encryption and decryption random oracle. For the hash query H (str), if a str and other values of the value exist in the hash list, the prophet returns the value to the attacker. Otherwise, a random number is returned to the attacker and added to the hash list ${\text{L}}_{{\text{h}}}$. Biohashing random oracle is modeled in the same way. For the encrypted query E (str), the ${\upgamma }$ is returned to the attacker if there is a correlation (k, str,${\upgamma }$) in the list ${\text{L}}_{{\upvarepsilon }}$. Otherwise, select a value from the ciphertext space to return it to the attacker. The decryption random oracle simulates in the same way. Obviously, the game is no different from the game ${\text{G}}_{0}$.

$${\text{Pr}}\left[ {{\text{S}}_{0} \left] { - {\text{Pr}}} \right[{\text{S}}_{1} } \right] = 0$$

(2)

${\text{G}}_{2}$: This game, ${\mathcal{A}}$ can fake messages to collide with the message space to further make the communication entity believe in itself. Following the birthday paradox principle, there are:

The probability of collision in the hash prediction machine’s output is lower than or equal to $\frac{{{\text{q}}_{{\text{b}}}^{2} }}{{2^{{{\text{l}}_{1} + 1}} }}$.

Biohashing the probability of a collision is less than or equal to $\frac{{{\text{q}}_{{\text{b}}}^{2} }}{{2^{{{\text{l}}_{2} + 1}} }}$.

The output of the symmetric encryption random oracle collides with a probability of less than or equal to $\frac{{{\text{q}}_{{\upvarepsilon }}^{2} }}{{2^{{{\text{l}}_{3} + 1}} }}$.

The selected random number (R, a, b, c) has a collision probability of less than or equal to $\frac{{\left( {{\text{q}}_{{\text{s}}} + {\text{q}}_{{\text{e}}} } \right)^{2} }}{{2{\text{n}}}}$.

Unless the output of the aforementioned prophet collides, ${\text{G}}_{2}$ and ${\text{G}}_{1}$ are indistinguishable.

$$\left| {{\text{Pr}}\left[ {{\text{S}}_{1} \left] { - {\text{Pr}}} \right[{\text{S}}_{2} } \right]} \right| \le \frac{{{\text{q}}_{{\text{h}}}^{2} }}{{2^{{{\text{l}}_{1} + 1}} }} + \frac{{{\text{q}}_{{\text{b}}}^{2} }}{{2^{{{\text{l}}_{2} + 1}} }} + \frac{{{\text{q}}_{{\upvarepsilon }}^{2} }}{{2^{{{\text{l}}_{3} + 1}} }} + \frac{{\left( {{\text{q}}_{{\text{s}}} + {\text{q}}_{{\text{e}}} } \right)^{2} }}{{2{\text{n}}}}$$

(3)

${\text{G}}_{3}$: This game, remove the attacker in the game ${\text{G}}_{2}$ without making the corresponding hash query and correctly guess < ${\text{M}}_{5}$, ${\text{M}}_{9}$, ${\text{M}}_{13}$,${\text{M}}_{14}$,${\text{M}}_{15}$ > situation, the probability is $\left| {{\text{Pr}}\left[ {{\text{S}}_{2} \left] { - {\text{Pr}}} \right[{\text{S}}_{3} } \right]} \right| \le \frac{{{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{1} }} }}$.

${\text{G}}_{4}$: In this game, remove the situation of the attacker directly guessing the authentication secret value ${\text{A}}_{{\text{i}}}$ in the game ${\text{G}}_{3}$, the probability is $\left| {{\text{Pr}}\left[ {{\text{S}}_{3} \left] { - {\text{Pr}}} \right[{\text{S}}_{4} } \right]} \right| \le \frac{{{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{1} }} }}$.

${\text{G}}_{5}$: In the game, remove the attacker in the game ${\text{G}}_{4}$ with the ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,{\text{z}}} \right)$ query to obtain the certified secret value ${\text{A}}_{{\text{i}}}$ situation, including the following three cases:

The attacker queries the ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,1} \right)$ and ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,2} \right)$. To obtain the certified secret value ${\text{A}}_{{\text{i}}}$, the attacker needs to obtain the biometric, and the probability that the attacker will correctly guess the user’s biometric BIO is less than or equal to $\frac{{{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{2} }} }}$.

The attacker queries the ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,2} \right)$ and ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,3} \right)$. The probability of the attacker guessing to the user password is less than or equal to $\frac{{{\text{q}}_{s} }}{Y}$.

The attacker queries the ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,1} \right)$ and ${\text{Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,3} \right)$. The probability of the attacker guessing to the user smart card parameter ${\text{D}}_{{\text{y}}}$ is less than or equal to $\frac{{{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{1} }} }}$.

The probability of obtaining the authentication secret value ${\text{A}}_{{\text{i}}}$ with the help of ${\text{ Corrupt}}\left( {{\text{U}}_{{\text{i}}}^{{\text{a}}} ,{\text{z}}} \right)$ query is less than or equal to ${\text{q}}_{{\text{s}}} {*(}\frac{1}{{2^{{{\text{l}}_{2} }} }} + \frac{1}{{\text{Y}}} + \frac{1}{{2^{{{\text{l}}_{1} }} }}{)}$. So there is

$$\left| {{\text{Pr}}\left[ {{\text{S}}_{4} \left] { - {\text{Pr}}} \right[{\text{S}}_{5} } \right]} \right| \le {\text{q}}_{{\text{s}}} {*(}\frac{1}{{2^{{{\text{l}}_{2} }} }} + \frac{1}{{\text{Y}}} + \frac{1}{{2^{{{\text{l}}_{1} }} }}{)}$$

(4)

${\text{G}}_{6}$: In that game, the SK is computed using the private hash predicate ${\text{H}}_{{1}}{\prime}$ instead of the hash predicate ${\text{H}}_{1}$. ${\text{H}}_{{1}}{\prime}$ is unknown to the attacker. So there is ${\text{Pr}}\left[ {{\text{S}}_{6} } \right] = \frac{1}{2}$.${\text{G}}_{6}$ and ${\text{G}}_{5}$ are indistinguishable unless the attacker makes a hash query ${\text{H}}_{1}{\prime} \left( {{\text{M}}_{5} {\text{||M}}_{10} {\text{||M}}_{11} } \right)$. By ${\Lambda }$ to the event, there have

$$\left| {{\text{Pr}}\left[ {{\text{S}}_{5} \left] { - {\text{Pr}}} \right[{\text{S}}_{6} } \right]} \right| \le {\text{Pr}}\left[ {\Lambda } \right]$$

(5)

${\text{G}}_{7}$: The game simulates the random self-reduction properties of the ECDHP. If the attacker query ${\text{H}}({\text{SID}}\left| {\left| {{\text{M}}_{5} } \right|} \right|{\text{M}}_{11} ||{\text{SK}})$, Then the list ${\Lambda }_{{\text{H}}}$ must have tuples containing the SK. By randomly selecting in the list, the probability of SK is $\frac{1}{{{\text{q}}_{{\text{h}}} }}$, There are ${\text{Pr}}\left[ {\Lambda } \right] \le {\text{q}}_{{\text{h}}} {\text{Adv}}_{{\mathcal{L}}}^{{{\text{ECDHP}}}}$.

Our goal is to prove that ${\text{Adv}}_{{\mathcal{L}}}^{{{\text{AKE}}}}$ can be neglected, so by using the above formula and the following transformation.

$$2\left( {{\text{Pr}}\left[ {{\text{S}}_{0} } \right]} \right) - 1 = 2\left( {{\text{Pr}}\left[ {{\text{S}}_{0} \left] { - {\text{Pr}}} \right[{\text{S}}_{6} } \right]} \right) + 2{\text{Pr}}\left[ {{\text{S}}_{6} } \right] - 1 = 2\left( {{\text{Pr}}\left[ {{\text{S}}_{6} } \right]} \right) - 1 + 2\sum_{{{\text{i}} = 0}}^{5} \left( {{\text{Pr}}\left[ {{\text{S}}_{{\text{i}}} \left] { - {\text{Pr}}} \right[{\text{S}}_{{{\text{i}} + 1}} } \right]} \right)$$

(6)

We can obtain:

$${\text{Adv}}_{{\mathcal{L}}}^{{{\text{AKE}}}} \left( {\mathcal{A}} \right) \le \frac{{{\text{q}}_{{\text{h}}}^{2} + 6{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{1} }} }} + \frac{{{\text{q}}_{{\text{b}}}^{2} + 2{\text{q}}_{{\text{s}}} }}{{2^{{{\text{l}}_{2} }} }} + \frac{{{\text{q}}_{{\upvarepsilon }}^{2} }}{{2^{{{\text{l}}_{3} }} }} + \frac{{\left( {{\text{q}}_{{\text{s}}} + {\text{q}}_{{\text{e}}} } \right)^{2} }}{{\text{n}}} + \frac{{2{\text{q}}_{{\text{s}}} }}{{\text{Y}}} + 2{\text{q}}_{{\text{h}}} {\text{Adv}}_{{\mathcal{L}}}^{{{\text{ECDHP}}}} .$$

(7)

B) Formal Validation Utilizing the ProVerif Tool.

Based on reference²⁸, a security proof of our scheme will be conducted using ProVerif. ProVerif is a tool specifically designed for automatically analyzing the security of cryptographic protocols, and its effectiveness has been extensively validated.

Definition of Code: In Table 2, we present comprehensive definitions for our code. Here, c1 and c2 denote public communication channels, while Cug and Cgs represent secure private communication channels. Specifically, c1 and Cug are utilized for communication between a physician user and TGW, whereas c2 and Cgs are employed between the TGW and sensor. Moreover, sku and sks denote session keys for the user and sensor, respectively. Additionally, corresponding functions have been defined, such as symmetric encryption/decryption, hash functions, XOR operations, etc. The last two query conditions are aimed at obtaining the security proof results of the protocol.

Table 2 Definition of code.

Process of Code: We segment the code into four sections, as depicted in Table 3. The 2nd to 5th rows in user code and the 2nd to 11th rows in gateway code correspond to the registration of medical professionals. Rows 2 to 3 in sensor code and rows 14 to 16 in gateway code pertain to the registration of medical sensor devices. The remaining sections cover login and key negotiation. The sentence "let Gateway = TGWRegUser | TGWRegSj | TGWAuth" denotes that the entire gateway process includes TGWRegUser, TGWRegSj, and TGWAuth. Furthermore, the usage of "process !DoUser |!Gateway | !Sj" indicates parallel execution of processes for the three entities.

Table 3 Process of Code.

ProVerif is a tool specifically designed for the automatic analysis of the security of cryptographic protocols, and its effectiveness in practical applications has been widely validated.In the Dolev-Yao model, the execution of the protocol involves three parallel processes: the user, the gateway, and the sensor device. The output results of the simulation script are shown in Fig. 4. The first two lines of the results confirm that the protocol operates under conditions of weak passwords (PW) and weak biometric traits (BIO).The next four lines demonstrate that the protocol successfully implements mutual authentication between the user and the gateway, as well as between the gateway and the sensor. The final two lines indicate that the session key of the protocol is secure and resistant to common attack types. Therefore, through formal security verification using the ProVerif simulation tool, it is proven that the protocol is secure under the Dolev-Yao model.

Fig. 4

Results of the code execution.

(2) Informal security analysis.

At the outset of the design process, the scheme was required to ensure anonymity, session key security, forward secrecy, backward secrecy, mutual authentication, and three-factor security. Additionally, it needed to be resilient against various potential attacks such as offline password guessing, replay, desynchronization, man-in-the-middle, and impersonation attacks. Our systematic security analysis confirms that the scheme is capable of meeting these security requirements. The following provides a comprehensive breakdown of the analysis.

Proposition 1

PIA has Physician User Anonymity.

Proof

In our scheme, both parameters $C_{i}$ and $E_{i}$ possess the unique identity characteristic, making them suitable as identity identifiers. The respective parameters and their generation processes are as follows:${C}_{i}={\text{biohashing}}(BIO)$$C_{i} = biohashing(BIO)$,$E_{i} = PUF(C_{i} )$,$A = E_{i} \oplus D_{y}$, $D_{y} = h(C_{i} ||x)$. Since attackers cannot obtain the trusted gateway’s master key x, nor clone the same PUF function, they are unable to recover $C_{i}$ and $E_{i}$ from the given parameter $D_{y}$. Additionally, in the publicly transmitted messages $M_{1} ,M_{5} ,M_{6}$, the involvement of the random number $R$ in the computation ensures that the data transmitted varies randomly with each transmission. The irreversibility of the hash function further prevents attackers from deducing the parameters involved in the computation. Therefore, our scheme meets the anonymity requirement as demanded by the doctor users.

Proposition 2

Session key and Backward/Forward Secrecy.

Proof

In our scheme, the session key $SK = (M_{5} ||M_{10} ||M_{11} ) = h(M_{5} ||cP||caP)$ is shared between the doctor user and the sensor. The parameter $M_{5} = h(h(A||R)||M_{2} ||M_{3} ||M_{4} )$, where R is a random number updated on the doctor’s device each time, and c is a random number generated by the sensor. Since $M_{10} = M_{12} \oplus b$, and $M_{11} = aM_{10}$, where both a and b are random numbers generated by the gateway, they cannot be obtained by attackers. In the verification $(M^{\prime}_{10} ,M^{\prime}_{11} ,R^{new} ) = D_{\left( V \right)} (M_{16} )$ process, $V = h(A||R||D_{y} )$, attackers cannot forge $D_{y}$, $A$ and $R$, thus they cannot forge the symmetric encryption key and decrypt $M_{16}$ to obtain $M_{10}$ and $M_{11}$. In addition, each per-session process involves the participation of a random number. Therefore, the disclosure of certain session keys does not affect the security of other session keys, and the security properties of session keys can be satisfied, meeting the requirement for backward/forward secrecy.

Proposition 3

Three-factor Security.

Proof

Three-factor security, as defined in our scheme, ensures that even if an attacker manages to obtain two of the user’s authentication factors, they will still be unable to access the third factor and impersonate the user. The analysis of three specific scenarios further elucidates the effectiveness of three-factor security in our system.

• (a) When an attacker gains access to the smart card parameters $\{ D_{y} ,C,R\}$ and the biometric features (${\text{BIO}}$) of the doctor user, and aims to obtain the user’s password (${\text{PW}}$), it’s important to note that the password only participates in the user’s local authentication process. The corresponding parameters and their generation processes $C_{i} = biohashing(BIO)$,$E_{i} = PUF(C_{i} )$, $A = E_{i} \oplus D_{y}$,$B = h(PW||C_{i} )$ and $C = h(A||B||D_{y} )$ are involved. An attacker, leveraging the compromised ${\text{BIO}}$, can generate C_i, but due to the unclonable nature of PUF, they cannot forge $E_{i}$. As a result, the attacker cannot compromise parameter $A$. Therefore, the attacker cannot breach the user’s password through the authentication process involving parameter $C$.

• (b) When an attacker gains access to the smart card parameters $\{ D_{y} ,C,R\}$ and the password (${\text{PW}}$) of the doctor user, and aims to obtain the user’s biometric features (${\text{BIO}}$), it’s crucial to understand that according to the user’s local login process, even if the attacker obtain the smart card parameters and password, the unclonable nature of PUF and the unilateral of the hash function prevent the attacker from compromising the user’s biometric features.

• (c) When an attacker obtains the doctor user’s biometric features (${\text{BIO}}$) and password (${\text{PW}}$) and attempts to reconstruct the smart card parameters, including $D_{y} = h(C_{i} ||x)$, where x represents the master key of the trusted gateway which the attacker cannot acquire, thus rendering the attacker unable to reconstruct $D_{y}$. Similarly, the attacker is unable to reconstruct C and the random number R.Therefore, the attacker is also unable to impersonate the user.

The attacker is unable to reconstruct C and the random number R, thus preventing them from impersonating the user. Therefore, our scheme guarantees three-factor security.

Proposition 4

Mutual authentication.

Proof

In our scheme, the validation of legitimacy through $M_{5}$,$M_{9}$,$M_{13}$ and $M_{15}$ also includes the verification of relevant attributes, thereby achieving mutual authentication.

Proposition 5

Resist Against Mobile Device Node Capture and Password Guess Attacks.

Proof

Based on the analysis of three-factor security (a), attackers can potentially obtain the user’s smart card parameters through side-channel attacks²⁹, and they may acquire the user’s biometric features. However, attackers cannot guess the user’s password. Therefore, our scheme can withstand password guessing attacks and attacks aimed at capturing user’s mobile device nodes.

Proposition 6

Resist Trust Gateway Simulation Attack.

Proof

To impersonate the gateway, attackers must generate messages $\{ M_{5} ,M_{7} ,M_{8} ,M_{9} ,T_{2} \}$ and $\{ M_{14} ,M_{15} ,M_{16} \}$. Because attackers cannot obtain the gateway’s master key y, they are unable to forge the parameter $M_{8} = K^{\prime}_{j} \oplus b \oplus S_{D}$. Similarly, they cannot forge $M_{9} = h(SID^{\prime}||b||M_{7} ||K^{\prime}_{j} )$. Additionally, attackers cannot generate parameter $A = E_{i} \oplus D_{y}$, hence they cannot forge $M_{15}$ and $M_{16}$. Therefore, they are unable to impersonate the gateway in sending data to users or sensors.

Proposition 7

Resist Physician User Impersonation Attack.

Proof

The attacker tries to fake being an authorized user by creating a fraudulent login request message. Based on the analysis of three-factor security (c), even if attackers acquire the user’s password and biometric features, they are still unable to impersonate the user and send legitimate request messages due to their inability to generate the crucial parameters stored in the smart card and replicate the same PUF function.

Proposition 8

Resist Sensor Devices Impersonation Attack.

Proof

Attackers intending to impersonate the sensor must be able to send legitimate message $\{ M_{12} ,M_{13} ,M_{14} \}$, where $M_{12} = M_{10} \oplus b^{\prime}$, $M_{13} = h(K_{j} ||M_{10} ||M_{11} ||b^{\prime})$ and $M_{14} = h(SID\left| {\left| {M_{5} } \right|} \right|M_{11} ||SK)$. The attacker must compute $K_{j}$, representing the identity information of $S_{j}$. Here, $K_{j} = h(SID||S_{D} ||y)$, where y is the secret value of TGW, inaccessible to the attacker. So, our protocol can resist this attack.

Proposition 9

Desynchronization Attack.

Proof

A desynchronization attack is an attack that attempts to disrupt the time or state synchronization between different entities in a system. In secure communication, such an attack can lead to communication failures or data errors. Our protocol is resilient against replay attacks and time synchronization issues due to the presence of timestamps and random numbers, providing resistance against these attacks. First, during the doctor user’s initial login and session key negotiation with the sensor, the messages sent by the user to the gateway and the gateway to the sensor both include timestamps, ensuring that the gateway and sensor can resist replay attacks. Secondly, the response messages from the sensor to the gateway and from the gateway to the user do not include timestamps, preventing attackers from tampering with the timestamps to desynchronize the system’s time baseline, which could lead to the failure of the RRR update and prevent the user from logging in again and negotiating the session key. Additionally, all publicly transmitted messages involve the participation of random numbers, ensuring that the messages meet the requirements of randomness and uniqueness. Therefore, our scheme is resilient to desynchronization attacks.

Proposition 10

Resist Insider Privilege Attack.

Proof

On one hand, the proposed solution does not leak user passwords or biometric features to the control server during the registration phase. On the other hand, during the login and authentication phases, users do not disclose any authentication information to either the control server or cloud service providers (such as passwords, biometric features, or smart card parameters). A more important point is that because the biometric information is processed through the PUF function, a binding is established between the device and the user. Even if an internal attacker obtains the user’s ID, password, and biometric information, the attacker will still be unable to log in using any device other than the user’s own device during the login authentication process.Therefore, the proposed solution is capable of resisting insider attacks.

Proposition 11

Resist Capture Attacks on Medical Sensor Device Nodes.

Proof

After capturing sensor devices in an attack, attackers can obtain parameters $\{ SID,K_{j} \}$ stored inside them. However, they cannot replicate the $S_{D}$ generated by the PUF, making it impossible to calculate the random number b and generate the corresponding $M_{13}$. As a result, they are unable to impersonate the sensor and send legitimate information to the gateway.

Proposition 12

Resist Replay Attacks.

Proof

In our scheme, we utilize timestamps and random numbers to prevent attackers from flooding the device with a large number of invalid messages, thus consuming device resources and rendering it unusable. Due to its nature, our scheme can resist replay attacks.

Proposition 13

Man-in-middle Attacks.

Proof

Attackers are unable to intercept and generate legitimate messages, whether between doctors and gateways or between gateways and sensors. The data transmitted between them is primarily generated by hashing, and attackers cannot obtain or generate key information to forge legitimate messages and send data to the other party. Both doctors and sensors have data generated by PUF in their parameters, and attackers cannot obtain the x and y in the gateway either. Therefore, our scheme can resist man-in-the-middle attacks.

Proposition 14

Non-traceability.

Proof

In our scheme, the use of random numbers enhances the randomness of scheme parameters. Every data operation includes the random number, ensuring that new data is generated each time session key negotiation occurs during login. There are no invariant parameters, enabling our scheme to achieve non-traceability.

Efficiency and security comparisons

1) Computation costs.

This section, we compare with other relevant protocols^{9,17,30,31,32}. To facilitate performance evaluation, based on³⁰, we define ${\text{T}}_{{\text{m}}} {,}\;{\text{T}}_{{\text{h}}} {,}\;{\text{T}}_{{{\text{fuz}}}} {,}\;{\text{T}}_{{\text{b}}}$ and ${\text{T}}_{{{\text{sye}}}}$ as the computational time for ECC point multiplication ($\approx$ 0.063075 s), hash function($\approx$ 0.0005 s), fuzzy extractor ($\approx$ 0.063075 s), biohashing function($\approx$ 0.01 s), and symmetric encryption/decryption $\approx$ 0.0087 s, respectively. In our scheme, the terminal device of the doctor used a biohashing function once during the login process, denoted as ${\text{1T}}_{{\text{b}}}$. In the key exchange process, the critical parameters are transmitted through encryption and decryption. On the user terminal device, encryption and decryption were utilized once each, denoted as ${\text{2T}}_{{{\text{sye}}}}$. Additionally, 10 times hash functions were used, denoted as ${\text{10T}}_{{\text{h}}}$. Therefore, the total computational costs on the doctor’s device is approximately ${\text{1T}}_{{\text{b}}} {\text{ + 2T}}_{{{\text{sye}}}} {\text{ + 10T}}_{{\text{h}}}$ $\approx$ 0.0324 s. For the sensor device, we utilized the ECC multiplication principle for encrypting critical data during transmission. Throughout, we employed two point multiplication and 4 times hash functions, denoted as ${\text{2T}}_{{\text{m}}}$ and ${\text{4T}}_{{\text{h}}}$, respectively, resulting in a total cost of ${\text{2T}}_{{\text{m}}} + {\text{4T}}_{{\text{h}}}$ $\approx$ 0.12815 s. In the gateway, we used encryption and decryption once each, along with two point multiplication and eight times hash function, denoted as ${\text{2T}}_{{\text{m}}}$,${\text{2T}}_{{{\text{sye}}}}$, and ${\text{8T}}_{{\text{h}}}$, respectively, resulting in a total cost of ${\text{2T}}_{{\text{m}}} + {\text{2T}}_{{{\text{sye}}}} + {\text{8T}}_{{\text{h}}}$ $\approx$ 0.14755 s. Under a unified performance benchmark, we calculated the computational costs of the schemes presented in references^{9,17,30,31,32}. The computational costs for user devices, sensor devices, and gateways, as well as the total computational costs, are listed in Table 4. Figure 5 represents the comparison of the schemes in terms of total computational overhead. Figure 6 shows the comparison of the computational overhead of each scheme at the user side, gateway side and sensor device side respectively.

Table 4 Comparison of computational overhead.

Fig. 5

Comparison of the total calculation times.

Fig. 6

Computational time comparison.

Currently, the main reason for the high computational overhead in most identity authentication protocols is the use of a large number of non-lightweight algorithms. The primary direction for reducing computational overhead is to decrease the number of times these algorithms are used, but there are still protocols that use a high number of operations. For example, the scheme proposed by Sahoo et al.³² uses 8 ECC point multiplication operations and 6 symmetric encryption/decryption operations, resulting in the highest computational overhead of 1.1958s. The scheme by Thakur et al.¹⁷ uses 10 ECC point multiplication operations, leading to a still very high computational overhead of 0.7028 s. Li et al.⁹ only use 6 ECC point multiplications, so their computational overhead is relatively small at 0.3895 s. The schemes by Ryu et al.³⁰ and Sahoo et al.³¹, which use fewer non-lightweight algorithms, have computational overheads of 0.3979 s and 0.4392 s, respectively. In contrast, our scheme only uses 4 ECC point multiplications and 4 symmetric encryption/decryption operations, resulting in a computational overhead of 0.3081 s, which represents an average reduction of approximately 50.71%.

2) Communication cost.

According to reference³¹, we define the output lengths of random numbers, point multiplication, hash functions, identity ID/password/biometrics, timestamps, and symmetric encryption/decryption as 32 bits, 160 bits, 160 bits, 32 bits, 32 bits, and 128 bits respectively. Based on the defined values above, let’s calculate the communication costs for the mutual data exchange between ${\text{U}}_{{\text{i}}}$ and TGW, and between TGW and $S_{{\text{j}}}$ in our scheme. Denote these costs as $\left\{ {{\text{M}}_{1} ,{\text{M}}_{5} ,{\text{M}}_{6} ,{\text{T}}_{1} } \right\}$ = 160 + 160 + 128 + 32 = 480 bits, $\left\{ {{\text{M}}_{5} ,{\text{M}}_{7} ,{\text{M}}_{8} ,{\text{M}}_{9} ,{\text{T}}_{2} } \right\}$ = 160 + 160 + 160 + 160 + 32 = 672 bits, ${ }\left\{ {{\text{M}}_{12} ,{\text{M}}_{13} ,{\text{M}}_{14} } \right\}$ = 160 + 160 + 160 = 480 bits, $\left\{ {{\text{M}}_{14} ,{\text{M}}_{15} ,{\text{M}}_{16} } \right\}$ = 160 + 160 + 128 = 448 bits respectively. Therefore, the total communication cost is calculated to be 2080 bits.

Although the solution proposed by Ryu et al.³⁰ has a significant advantage in terms of communication overhead, with a communication overhead of 864 bits, as it only involves the user and the sensor during the session key negotiation process, with the gateway not participating, thereby achieving the lowest communication overhead, it is evident from Table 6 that their solution suffers from vulnerabilities such as doctor user impersonation attacks, sensor device impersonation attacks, and desynchronization attacks. The solution by Sahoo et al.³² has a communication overhead of 1312 bits and a computational overhead that is approximately three times higher than our scheme, so its overall advantage is not significant, and it still has security issues. Thakur et al.¹⁷ have a communication overhead of 1600 bits, as they use multiple ECC point multiplications for encryption, which reduces the need to pass many parameters, thereby lowering communication overhead. The solutions proposed by Li et al.⁹ and Sahoo et al.³¹ have a communication overhead of 2080 bits, which is the same as our proposed scheme.

Our solution sacrifices some communication overhead to achieve higher security goals and lower computational overhead, making the communication overhead not as advantageous compared to related protocols, as shown in Fig. 7.

Fig. 7

Communication overhead comparison.

3) Storage cost.

The storage costs in both the doctor’s terminal device and the patient’s terminal device (sensor) were computed for accurate evaluation. In our scheme, the doctor’s terminal device stores $\{ D_{y} ,C,R\}$, where $D_{y}$ and C are generated by a hash function, and R is a random number, totaling 352 bits. The sensor stores $\{ K_{j} ,SID\}$, where $K_{j}$ is generated by a hash function and SID is the identity identifier, totaling 192 bits. Together, they store 544 bits. Using a unified benchmark and the same calculation principles, we computed the communication and storage costs of the compared schemes^{9,17,30,31,32}. Our scheme shows parity with relevant protocols^9,31 in terms of communication overhead, but surpasses^17,30,31. However, concerning storage overhead, our scheme demonstrates significant advantages in both inter-terminal device and total storage cost compared to other schemes. The overall storage overhead is reduced by approximately 16.32% on average. Detailed data are shown in Table 5 . Figure 8 represents the comparison of storage cost between users, sensors and the total cost.

Table 5 Storage Cost Comparison.

Fig. 8

Storage cost comparison.

3) Security Comparisons.

Based on the security issues provided in references^9,31, we conducted an analysis of the solution against 15 security aspects to determine if it meets the expected security objectives. We also performed a security analysis of the related protocols compared to our solution or referred to security vulnerabilities found in other published articles. For example, reference³⁰ explicitly pointed out that the solution in reference³² cannot resist insider privilege attacks, and a detailed analysis was provided. The final results are presented in Table 6. In the table, "√" indicates that the solution can resist the vulnerability, while " × " indicates that it cannot. The results show that our solution achieves the expected security objectives and demonstrates a significant security advantage over other solutions.

Table 6 Security features comparison.

Conclusion

With the rapid advancement of new technologies, the security of data transmitted over public channels faces unprecedented challenges. Identity authentication protocols have become a key focus for researchers aiming to protect data from theft and tampering. However, existing identity authentication protocols in remote healthcare lack anonymity and are vulnerable to various attacks, including offline password guessing and session key attacks. In response to these challenges, we propose a secure and efficient identity authentication scheme for remote healthcare. This scheme facilitates the secure exchange of critical data between users and sensors through a trusted gateway that negotiates session keys, leveraging the unique properties of Physical Unclonable Functions (PUF) to mitigate node capture attacks. Furthermore, we validate the security of our scheme using mathematical logic and the ProVerif simulation tool, and we conduct a comprehensive analysis of specific security vulnerabilities present in current remote healthcare identity authentication protocols.

Our analysis demonstrates that the proposed scheme effectively achieves the desired security objectives, which include anonymity, mutual authentication, three-factor security, and session key security, while also addressing its identified vulnerabilities. Furthermore, through comparative assessments with existing protocols regarding computational overhead, storage requirements, communication efficiency, and security measures, our findings indicate that, although the communication overhead advantage is not significant, the proposed scheme reduces computational overhead by approximately 50.17%, storage overhead by approximately 16.32%, and demonstrates significantly superior security compared to other solutions. Therefore, our solution is highly suitable for deployment in remote medical environments characterized by limited computational resources, insufficient storage capacity, and low-power devices.

Future research could continue to explore the reduction of communication overhead, biometric updates, and the development of cross-domain authentication mechanisms based on standardized protocols, ensuring seamless interoperability and secure communication across different systems.