Mix design and performance prediction of EPS lightweight structural concrete based on orthogonal experimentation

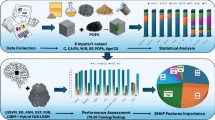
Abstract

This study explores mix proportion design and mechanical property prediction of EPS lightweight structural concrete using orthogonal experimentation and machine learning models. The research systematically analyzed the effects of EPS content, water-to-binder ratio, and POM fiber content on compressive strength, splitting tensile strength, thermal conductivity, and frost resistance. Key findings reveal that EPS content significantly enhances thermal insulation and frost resistance but reduces mechanical strength. POM fibers were shown to improve tensile strength and frost resistance by limiting crack propagation. A novel dataset was established and utilized in performance prediction using XGBoost, optimized with Seagull Optimization Algorithm (SOA), Whale Optimization Algorithm (WOA), and Particle Swarm Optimization (PSO). Among these, SOA-XGBoost achieved the highest prediction accuracy and stability. The optimal mix proportion, combining 35% EPS, 0.21 water-to-binder ratio, and 0.65% POM fiber content, was identified, providing an effective balance between mechanical and thermal performance. The proposed framework offers valuable insights and methodologies for optimizing lightweight concrete and serves as a reference for other composite materials in engineering applications.

Introduction

With the rapid development of the construction industry, lightweight concrete has been increasingly applied in green building projects due to its superior thermal performance, sound insulation, and low density^1,2,3. As a typical lightweight concrete material, expanded polystyrene (EPS)-based lightweight concrete combines the advantages of low weight and high efficiency^4,5. Prasittisopin et al.⁶ investigated the performance and environmental impacts of lightweight concrete incorporating EPS and found that EPS significantly reduces the material’s weight, making it suitable for prefabricated and modular construction while enhancing its thermal insulation and acoustic properties. The study revealed that partially replacing coarse and fine aggregates with EPS could improve the workability and mechanical properties of concrete. Alhnifat et al.⁷ studied the properties of lightweight concrete incorporating EPS beads and pozzolanic aggregates, reporting that the inclusion of EPS reduced the concrete’s density and achieved a 28-day compressive strength of 40.11 MPa when combined with a superplasticizer. Vinod et al.⁸ examined the performance of lightweight concrete blocks produced with EPS beads and foaming agents, highlighting that EPS significantly reduced the density of the concrete. Adding fly ash and ground granulated blast-furnace slag (GGBS) to the mix helped reduce hydration and carbon footprint, thereby minimizing shrinkage. El Gamal et al.⁹ explored the use of recycled EPS beads as a partial replacement in concrete to develop lightweight mixes with good thermal insulation properties. Their findings indicated that recycled EPS notably decreased density, thermal conductivity, and mechanical properties. However, challenges remain in optimizing mix proportions to enhance mechanical properties and durability while enabling rapid prediction of mechanical performance, given the low density and poor wettability of EPS beads.

In recent years, the rapid development of machine learning technologies has opened new avenues for concrete mix design and performance prediction^10,11,12. Shang et al.¹³ successfully applied decision tree (DT) and AdaBoost algorithms to predict the mechanical properties of recycled coarse aggregate (RCA)-based concrete, achieving effective predictions of compressive strength (CS) and splitting tensile strength (STS), thereby validating the applicability of machine learning in engineering material performance forecasting. Similarly, Golafshani et al.¹⁴ proposed a combination of artificial neural networks (ANN) and the multi-objective multiverse optimization (MOMVO) algorithm to develop a comprehensive dataset for concrete containing waste foundry sand (WFS) in MATLAB. Through model training and optimization, the method achieved precise predictions of compressive strength, splitting tensile strength, elastic modulus, and flexural strength, demonstrating high accuracy and stability. Jueyendah et al.¹⁵ investigated the compressive and flexural strength of cement mortar incorporating nano-silica and micro-silica using the support vector machine (SVM) approach. A comparison with multilayer perceptron (MLP), radial basis function networks (RBFN), and general regression neural networks (GRNN) revealed that the SVM-RBF model delivered superior predictive performance, further extending the application of machine learning in predicting complex concrete behaviors. Mustapha et al.¹⁶ applied the XGBoost algorithm to predict the compressive strength, tensile strength, density, and porosity of pervious concrete (PC), outperforming support vector regression (SVR) and demonstrating strong agreement with experimental results. Yu et al.² explored precast recycled aggregate concrete (PRAC) as a low-carbon alternative to traditional recycled concrete. Their study combined Bayesian model updating and the Cuckoo search algorithm to optimize PRAC mix proportions, highlighting that a minimum of 60% recycled aggregate achieves a balance between strength and environmental impact, offering a scalable solution for concrete mix design. Meanwhile, Safhi et al.¹⁷ addressed the challenge of predicting the rheological properties of self-consolidating concrete (SCC). Using 348 datasets from peer-reviewed literature and 12 critical variables, such as water-to-powder ratio and cement content, they developed an XGBoost model with exceptional accuracy (R² = 0.99), highlighting its advantages in handling nonlinear, multidimensional data.

These studies showcase the immense potential of machine learning in concrete mix design and performance prediction. By leveraging big data analysis and model training, machine learning effectively establishes quantitative relationships between material composition and performance indicators, providing a robust scientific basis for optimizing concrete properties. Among various machine learning methods, XGBoost has emerged as a preferred algorithm for material science applications due to its superior ability to handle nonlinear and high-dimensional data^18,19,20. However, the predictive performance of XGBoost is highly dependent on hyperparameter tuning. To address this, intelligent optimization algorithms such as Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), and Seagull Optimization Algorithm (SOA) have been introduced in recent years to enhance the generalization capability and accuracy of XGBoost models.

This study integrates three intelligent optimization algorithms into the XGBoost framework: Seagull Optimization Algorithm (SOA), Whale Optimization Algorithm (WOA), and Particle Swarm Optimization (PSO). These algorithms enable global searches across different mix proportion parameters, significantly improving the predictive accuracy and stability of the models. Furthermore, to comprehensively explore the performance characteristics of EPS lightweight concrete, this study employs orthogonal experimental design to construct a dataset, ensuring uniform coverage of the parameter space.

The innovation of this research lies in integrating orthogonal experimental design with machine learning techniques and intelligent optimization. This combined framework not only ensures efficient exploration of mix proportion parameters but also enhances the accuracy and stability of predictive models. This novel methodology provides theoretical and practical contributions to lightweight concrete mix design and establishes a reference for performance optimization in other composite materials. This research aims to establish an efficient and accurate method for EPS lightweight concrete mix design and performance prediction, providing theoretical support for the engineering application of lightweight concrete and offering new insights into the performance optimization of other composite materials. The specific research methods and experimental designs are introduced in the following sections.

This paper is organized as follows:

Section “Model principles” introduces the principles of the XGBoost algorithm and the three optimization algorithms employed for hyperparameter tuning.

Section “Experimental design” details the experimental design, including the selection of materials, mix proportions, and testing methods.

Section “Experimental results and analysis” presents the results and analysis, focusing on the effects of key factors on concrete performance and the outcomes of range analysis.

Section “Prediction of mechanical properties of EPS lightweight construction concrete based on multi-optimization models” evaluates the predictive performance of the proposed multi-optimization models, comparing them with conventional machine learning methods.

Section “Discussion” discusses the implications of the findings, including recommendations for future research and practical applications.

Section “Results” concludes the study by summarizing the main contributions and highlighting the significance of the proposed framework for lightweight concrete mix design.

Model principles

To accurately predict the mechanical properties of EPS lightweight concrete, this study employs the XGBoost algorithm as the core predictive model and integrates three intelligent optimization algorithms (SOA, WOA, and PSO) for hyperparameter tuning. This section introduces the theoretical foundations of these algorithms, laying the groundwork for their application in subsequent experimental and modeling analyses.

XGBoost

XGBoost (eXtreme Gradient Boosting) is an advanced machine learning algorithm based on gradient boosting decision trees (GBDT). It was proposed to address both efficiency and performance issues in large-scale and complex prediction tasks. XGBoost achieves superior predictive capabilities by introducing regularization, gradient-based optimization, and parallel computation. Compared to traditional gradient boosting methods, XGBoost offers robustness in handling nonlinear and high-dimensional data while minimizing overfitting risks.

The prediction model in XGBoost is established as an ensemble of decision trees. Each decision tree acts as a weak learner, and the final prediction is obtained by aggregating the results of all trees. The model iteratively improves the prediction accuracy by minimizing the loss function and updating tree weights.

The key formulation for XGBoost is as follows:

$$\hat{y}_{i} = \mathop \sum \limits_{{k - 1}}^{K} f_{k} \left( {x_{i} } \right),\;\;f_{k} \in \rm{\mathcal{F}} ,$$

(1)

where ${\hat {y}_i}$​ represents the predicted value for the i-th sample, K is the total number of trees, fk is the k-th tree in the model, and $\mathcal{F}$ is the space of all decision trees.

The objective function in XGBoost consists of two components: the loss function and the regularization term:

$$\rm{\mathcal{L}} = \mathop \sum \limits_{{i = 1}}^{n} l\left( {y_{i} ,\hat{y}_{i} } \right) + \mathop \sum \limits_{{k = 1}}^{K} {{\Omega }}\left( {f_{k} } \right) ,$$

(2)

where $l\left( {{y_i},{{\hat {y}}_i}} \right)$ is the loss function that measures the difference between the predicted value ${\hat {y}_i}$ and the true value ${y_i}$​, and ${\text{\varvec{\Omega}}}\left( {{f_k}} \right)$ represents the regularization term that controls the complexity of the model to prevent overfitting.

The regularization term is defined as:

$${{\Omega }}\left( {f_{k} } \right) = \gamma T + \frac{1}{2}\lambda \mathop \sum \limits_{{k = 1}}^{K} \omega _{k}^{2} ,$$

(3)

Where, T represents the number of leaf nodes; ${\text{\varvec{\Omega}}}\left( {{f_k}} \right)$ represents the weight of the leaf nodes; $\gamma$ and $\lambda$ are pre-defined hyperparameters that control the number and scores of leaf nodes, respectively.

To optimize the objective function, XGBoost uses a second-order Taylor expansion to approximate the loss function, which allows the model to incorporate both the first and second derivatives for more accurate updates.

For an iteration ttt, the objective function becomes:

$$\rm{\mathcal{L}}^{{(t)}} \approx \mathop \sum \limits_{{i = 1}}^{n} \left[ {g_{i} f_{t} \left( {x_{i} } \right) + \frac{1}{2}h_{i} f_{t}^{2} \left( {x_{i} } \right)} \right] + \Omega \left( {f_{t} } \right),$$

(4)

where ${g_i}$​ and ${h_i}$​ are the first and second derivatives of the loss function with respect to the prediction:

$${g_i}=\frac{{\partial l\left( {{y_i},{{\hat {y}}_i}} \right)}}{{\partial {{\hat {y}}_i}}},$$

(5)

$${h_i}=\frac{{{\partial ^2}l\left( {{y_i},{{\hat {y}}_i}} \right)}}{{\partial \hat {y}_{i}^{2}}},$$

(6)

By iteratively constructing new decision trees to minimize the objective function, XGBoost effectively improves prediction accuracy. Its ability to handle sparsity, use efficient parallel computations, and optimize tree-building strategies makes it particularly suitable for engineering applications involving complex relationships and large datasets.

Optimization algorithms

Seagull Optimization Algorithm (SOA)

The Seagull Optimization Algorithm, proposed by DHIMAN G and KUMAR V, is a novel swarm intelligence optimization algorithm²¹. This algorithm is suitable for solving multi-objective optimization problems. The primary inspiration for the algorithm comes from the migration and attack behaviors of seagulls in nature. These behaviors are mathematically modeled to emphasize exploration within specific search spaces. The position updates in the SOA are primarily composed of two phases: migration (global search) and attack (local search)^22,23. When migratory birds move from one place to another, seagulls often attack them, performing natural spiral motions during the attack. These motions can be correlated to the target function to be optimized.

The algorithm initializes parameters including the population size (Search Agents), the maximum number of iterations (Tmax), the dimensionality of variables (dim), the lower (ul) and upper (ub) bounds of variables, and the frequency and spiral parameters. The seagull population and other parameters are initialized, and the fitness value of the objective function is calculated.

The initial positions of the seagulls are given by the following equation:

$${\text{Positions}}=rand({\text{SearchAgents}},1) \times (ub - lb)+lb,$$

(7)

In the equation: ul represents the upper bound of the variables. ub represents the lower bound of the variables.

The fitness values of the objective function are calculated and sorted in ascending order using [fitness, index] = sort(fitness). The sort function arranges the array in ascending order, which allows the determination of the best fitness value for each seagull and the global best value (pbest) for the entire population. Based on the sorting indices (index), the positions are updated from Positions to x as the optimization process begins.

During the migration phase, seagulls move toward the best position to find the optimal location. The migration process ensures that seagulls meet the conditions of avoiding collisions, moving toward the best position, and approaching the optimal location.

To prevent collisions between neighboring seagulls, an additional variable A is introduced to compute the new positions of the seagulls.

$$\left\{ {\begin{array}{*{20}{l}} {{C_s}=X * A} \\ {A={f_c} - t * \left( {\frac{{{f_c}}}{{{T_{\hbox{max} }}}}} \right)} \end{array}} \right.,$$

(8)

In the equation: f represents the current iteration number. ${f_c}$ is a parameter that linearly decreases from 2 to 0.

The optimal position direction coefficient is denoted as ${M_s}$. Under the condition that collisions do not occur, seagulls move toward the optimal position direction.

$$\left\{ {\begin{array}{*{20}{l}} {{\text{rd}}=rand(1,\dim )} \\ {{\text{B}}=2 * {A^2} * {\text{rd}}} \\ {{M_s}={\text{B}} * (P{\text{best}} - X)} \end{array}} \right.,$$

(9)

The coefficient for approaching the optimal position is denoted as ${D_s}$. Seagulls move in the direction of the optimal position and reach a new position, marking the end of the migration process.

$${D_s}=|Cs+Ms|,$$

(10)

In the equation: ${D_s}$ represents the new position of the seagull that satisfies the three conditions.

$$\left\{ {\begin{array}{*{20}l} {\theta = rand(1,\dim ) * 2\pi } \\ {r = u * e^{{\theta * v}} } \\ {x = r * \cos \theta ,\;y = r * \sin \theta ,\;z = r * \theta } \\ \end{array} } \right.,$$

(11)

In the equation: $\theta$ is a random number within the range [0,2π], measured in radians (rad).

Finally, the formula for the seagull’s attack behavior is expressed as follows:

$${X_{{\text{new}}}}=x * y * z * {D_s}+{\text{~pbest~,}}$$

(12)

Whale optimization algorithm

Whale Optimization Algorithm (WOA) is a population-based optimization algorithm proposed by Mirjalili and Lewis in 2016. Inspired by the unique bubble-net hunting strategy of humpback whales, WOA has shown superior performance in solving complex nonlinear problems and is widely used in multi-objective optimization, parameter optimization, and other engineering and scientific fields^24,25,26. WOA simulates the following two hunting behaviors of humpback whales:

Step 1: Initialize the population.

Initialize the position of each individual Xi in the population (i.e., candidate solutions) and calculate their objective function values. Identify the current global best solution X^∗25.

Step 2: Update positions.

During each iteration, the position of each individual is updated based on one of the following two strategies:

Bubble-net attacking behavior is simulated using the following equation:

$$X(t+1)={X^ * }+D \cdot {e^{bl}} \cdot \cos (2\pi l),$$

(13)

Where: D=∣C⋅X∗−X(t)∣represents the distance between the current solution and the prey; b is the spiral shape parameter (commonly set to 1); l is a random number in the range [− 1,1]; e^bl and cos (2πlsimulate the spiral motion of the whale.

The prey position update (global search) is modeled using the following equation:

$$X(t+1)={X^ * } - A \cdot D,$$

(14)

Where: $D = \left| C \right. \cdot X^{ * } - X(t)$, $A = 2a \cdot r - a,\;{\text{~}}C = 2 \cdot r$, a gradually decreases with iterations, and r is a random number in the range [0,1].

Step 3: Exploring Prey Position.

When the random number p > 0.5, the whales perform a global search, modeled by the following equation:

$$X(t+1)={X_{{\text{rand}}}} - A \cdot \left| {C \cdot {X_{{\text{rand}}}} - X(t)} \right|,$$

(15)

Where Xrand​ is a randomly selected candidate solution.

Step 4: Convergence and Stopping Criteria.

The algorithm stops when the maximum number of iterations is reached or the convergence criteria are met, returning the optimal solution X*.

Particle swarm optimization (PSO)

Particle Swarm Optimization (PSO) is a population-based optimization algorithm inspired by the social behaviors of birds and fish schools. It is widely used for solving nonlinear and multidimensional optimization problems due to its simplicity and efficiency^33,34. The algorithm models a swarm of particles, each representing a candidate solution in the search space. Through iterative updates, particles adjust their positions based on individual and collective experiences to converge toward the global optimum³⁵. In PSO, the position and velocity of each particle are updated using the following equations:

• 1. Velocity Update

$${v_i}(t+1)=w \cdot {v_i}(t)+{c_1} \cdot {r_1} \cdot \left( {{p_{i,{\text{~best~}}}} - {x_i}(t)} \right)+{c_2} \cdot {r_2} \cdot \left( {{g_{{\text{best}}}} - {x_i}(t)} \right),$$

(16)

Where, ${v_i}(t)$: Velocity of particle iii at iteration t. w: Inertia weight controlling exploration and exploitation. ${c_1} \cdot {r_1}$ ​: Acceleration coefficients determining the influence of personal and global best positions. ${c_2} \cdot {r_2}$: Random values between 0 and 1.${p_{i,{\text{best}}}}$ ​: Personal best position of particle i. ${g_{{\text{best}}}}$ : Global best position found by the swarm.

• 2. Position Update

$${x_i}(t+1)={x_i}(t)+{v_i}(t+1).$$

(17)

Where, ${x_i}(t)$: Position of particle iii at iteration t. ${v_i}(t+1)$: Updated velocity of particle i.

By dynamically balancing exploration (global search) and exploitation (local refinement), PSO effectively finds near-optimal solutions in high-dimensional spaces.

Experimental design

Building on the theoretical principles outlined in the previous section, this section describes the experimental setup, including material selection, mix proportions, and testing methodologies. These experiments form the basis for analyzing the effects of EPS content, water-to-binder ratio, and POM fiber content on mechanical and thermal properties.

Raw materials

The cement used in the experiment is P·O 42.5 ordinary Portland cement with a density of 3.1 g/cm³. The fly ash selected is Grade I fly ash with a density of 2.55 g/cm³, and the density of silica fume is 2.1 g/cm³. The EPS particles used in the experiment have an apparent density of 0.025 g/cm³ and a thermal conductivity of 0.04 W/(m·K), with a particle size ranging from 3 to 5 mm. The morphology of the EPS is shown in Fig. 1. The fiber material used is POM fiber produced by Chongqing Yuntianhua Polymer Materials Co., Ltd., with its main performance indicators listed in Table 1, and its morphology is shown in Fig. 2. The sand used is natural river sand of medium type, with a fineness modulus of 2.68. The polycarboxylate-based superplasticizer is provided by Nantong Pudai Building Materials Co., Ltd., with a solid content of 40% (by mass), and its water-reducing efficiency can reach 25%.

Fig. 1

Morphology of EPS particles.

Fig. 2

Morphology of POM fibers.

Table 1 Main performance parameters of POM Fiber.

Experimental mix proportions

To investigate the influence of multiple factors and levels on the performance indicators, the orthogonal experimental design method was adopted in this study. The main factors considered in the experiment include the EPS content (A), water-binder ratio (B), and POM fiber content (C). To ensure that the strength of EPS lightweight concrete reaches C30, the EPS content was set at 30%, 35%, and 40% of the binder material volume based on the recommendations in reference¹⁴. The water-binder ratio was determined according to adjustments made to the fluidity and consistency of EPS lightweight concrete in preliminary experiments. The POM fiber content was divided into three levels: 0.29%, 0.65%, and 1.02% (mass fraction), as recommended by the manufacturer. The specific experimental design of factors and levels is shown in Table 2.

Table 2 Orthogonal experimental factors and levels.

Specimen preparation and test methods

EPS lightweight concrete specimens were prepared according to the relevant provisions of the Standard for Test Method of Performance on Ordinary Concrete Mixtures (GB/T 50080-2016). All test materials were measured based on the designed mix proportions. During the mixing process, sand, fly ash, silica fume, and cement were first mixed evenly as dry materials. Water and superplasticizer solution were then gradually added, and the mixture was thoroughly stirred until a uniform concrete mixture was obtained^27,28. Finally, EPS particles and POM fibers were added and mixed further until they were evenly distributed.

After mixing, the fresh concrete was placed in 100 mm × 100 mm × 100 mm cubic molds and ϕ50 mm × 50 mm cylindrical molds. The mixture was compacted in two layers using vibration. The formed specimens were cured under conditions of 20  ±  2 °C and a relative humidity of more than 95%. After demolding, the specimens continued to cure under the same conditions for 28 days until they met the testing requirements.

Compressive Strength and Splitting Tensile Strength:

Compressive strength and splitting tensile strength tests were conducted according to the requirements of the Standard for Test Method of Physical and Mechanical Properties of Concrete (GB/T 50081-2019). A hydraulic universal testing machine was used to apply the load at a rate of 0.5 MPa/s. Test data were recorded, and the strength values were calculated.

Thermal Conductivity:

The thermal conductivity test was performed using the guarded hot plate method as specified in the Test Method for Steady-State Thermal Resistance and Related Properties of Insulation Materials (GB/T 10294-2008). The specimen was placed in the testing apparatus, and the thermal conductivity of the concrete was calculated by measuring the heat flux and temperature difference under steady-state conditions.

Frost Resistance:

Frost resistance was tested using an improved rapid freezing method. According to the standard freezing and thawing cycle procedures, the specimens underwent alternating freezing at − 18 °C and thawing at 20 °C, with each cycle lasting 4 h. The frost resistance was evaluated by measuring the mass loss rate and relative dynamic elastic modulus loss rate of the specimens after different numbers of freeze-thaw cycles.

Tensile Strength:

In the tensile strength testing section, a detailed explanation of the measurement and calculation process has been provided. The tensile strength test was conducted using the split-cylinder method, where a load was applied perpendicular to the axis of the specimen, and the maximum load at failure was measured. The tensile strength was calculated using the following formula based on the rupture load and specimen dimensions:

$${f_t}=\frac{{2P}}{{\pi LD}}.$$

(18)

Where ft is the tensile strength (MPa), P is the maximum load at failure (N), L is the length of the specimen (mm), and D is the diameter of the specimen (mm).

In the specimen preparation section, we further clarified the dimensions of various specimens: the compressive strength specimens were 100 mm × 100 mm × 100 mm, the thermal conductivity specimens were 100 mm × 100 mm × 50 mm, and the freeze-thaw test specimens were 150 mm × 150 mm × 300 mm.

The experimental design described here provides a robust dataset for performance analysis and modeling. The results obtained from these tests will be used in the next section to quantify the influence of various factors on EPS lightweight concrete properties through range analysis.

Experimental results and analysis

Using the experimental data collected in the previous section, this section conducts range analysis to quantify the impact of EPS content, water-to-binder ratio, and POM fiber content on mechanical properties, thermal conductivity, and frost resistance. These insights serve as the foundation for performance optimization and predictive modeling in subsequent sections.

Range analysis

Based on the experimental data presented in Table 3, the influence of each factor on the mechanical properties, thermal insulation performance, and frost resistance of EPS lightweight concrete was analyzed. Relative dynamic elastic modulus is an important indicator that reflects the extent of internal damage in concrete, while the mass loss rate is more susceptible to the influence of water content. Therefore, this study selected the relative dynamic elastic modulus after 100 freeze-thaw cycles as the key indicator for evaluating frost resistance and conducted range analysis on it.

Table 3 Orthogonal test results of EPS lightweight concrete.

Based on the experimental data in Table 3, the orthogonal experimental method was used to quantify the influence of each factor, resulting in the range analysis results of the orthogonal experiment (as shown in Table 4). These analyses intuitively reveal the effects of EPS content, water-to-binder ratio, and POM fiber content on various performance indicators, providing important guidance for subsequent performance optimization design.

Table 4 Orthogonal test range analysis.

Analysis of compressive strength

The compressive strength generally decreases as the EPS content increases from 35 to 45%, as shown in Fig. 3. Groups Z-1, Z-2, and Z-3, with 35% EPS content, show the highest compressive strengths (42.09 MPa, 45.78 MPa, and 37.03 MPa, respectively).As the EPS content increases to 40% and then 45%, the compressive strength drops, with Z-4 showing the lowest value at 28.72 MPa.This reduction in compressive strength can be attributed to the decreasing density and increasing porosity of the concrete with higher EPS content, which reduces the concrete’s ability to withstand compressive forces.

Fig. 3

Compressive strength distribution of EPS lightweight concrete.

From the analysis of Table 4, the factors affecting apparent density are ranked as follows: EPS content (A) > POM fiber content (C) > water-to-binder ratio (B), with the optimal combination being A3B2C3. EPS content is the dominant factor influencing apparent density, accounting for 90.25%. Specifically, when the EPS content increases from 35 to 40%, the bulk density of concrete decreases by 8.14%; further increasing it to 45% results in a cumulative reduction of approximately 9.56%. This significant weight reduction is mainly attributed to the extremely low density of EPS particles, which effectively replace high-density components in the cementitious matrix, thereby reducing the overall density of the concrete.

POM fiber content ranks second in its impact on apparent density, accounting for 6.41%, and shows slight fluctuations as the fiber content increases, with apparent density first increasing and then decreasing. This phenomenon can be attributed to the excellent hydrophilicity and dispersibility of POM fibers, which are distributed in a three-dimensional random manner within the paste, filling micropores and partially entrapped air bubbles, thereby enhancing the internal compactness of the concrete. However, as the fiber content further increases, its dispersibility decreases, leading to fiber agglomeration and the generation of additional micro air bubbles and pores, which reduce the compactness of the concrete and consequently decrease its apparent density.

The water-to-binder ratio has the least influence, accounting for only 3.09% of the total range, indicating that changes in the water-to-binder ratio within the studied levels have limited effects on apparent density. EPS content is the key factor in regulating the apparent density of EPS lightweight concrete. Increasing the EPS content can significantly reduce concrete density. At the same time, the appropriate incorporation of POM fibers can optimize the internal structure, but their dosage must be controlled within a suitable range to avoid the negative effects caused by fiber agglomeration.

Under different POM fiber content conditions, the compressive failure modes of EPS lightweight concrete exhibit significant differences. With the incorporation of POM fibers, the crack length is significantly reduced, and the width of the main cracks is visibly narrower, as shown in Fig. 4. This phenomenon further demonstrates the critical role of POM fibers in enhancing the compressive performance of concrete, providing a scientific basis for optimizing the compressive properties of EPS lightweight concrete.

Fig. 4

Compressive failure morphology of EPS lightweight concrete.

Analysis of tensile strength

The tensile strength shows more variability across the groups, as shown in Fig. 5. Group Z-3, with 35% EPS content, has the highest tensile strength at 4.78 MPa, while Group Z-9, with 45% EPS, has the lowest tensile strength at 1.88 MPa. There is a noticeable decrease in tensile strength as EPS content increases, particularly from groups Z-7 to Z-9. This trend suggests that while EPS improves thermal properties, it reduces the material’s ability to resist tensile forces. The addition of POM fibers seems to have a positive effect on tensile strength, as higher fiber content in groups Z-2, Z-6, and Z-8 leads to a slight increase in tensile strength compared to other groups with similar EPS content.

Fig. 5

Tensile strength distribution of EPS lightweight concrete.

Analysis of the data in Table 4 reveals that the factors influencing the tensile strength of EPS lightweight concrete are ranked as follows: EPS content (A) > POM fiber content (C) > water-to-binder ratio (B). Among them, EPS content has the most significant impact on tensile strength, accounting for 72.63%; POM fiber content ranks second, accounting for 21.33%; while the water-to-binder ratio has a relatively smaller impact, accounting for only 6.09%.

Although the incorporation of EPS reduces the density of concrete, it has a certain adverse effect on tensile strength. However, with the addition of POM fibers, the tensile performance of concrete is significantly improved. Due to their high relative elastic modulus and tensile strength, POM fibers are randomly distributed in a three-dimensional manner within the concrete, effectively preventing crack propagation. During the splitting failure process, the fibers effectively limit the lateral deformation of the concrete, thereby reducing its Poisson’s ratio and indirectly enhancing the tensile strength of EPS lightweight concrete. Furthermore, the reinforcing effect of POM fibers is also evident in the improvement of crack morphology.

As the fiber content increases, the crack morphology in the split-cylinder test undergoes significant changes. The addition of fibers enhances the toughness and crack resistance of the concrete, especially at the initial crack stage, where fibers bridge the cracks and limit their propagation. With higher fiber content, the crack width generally decreases as the fibers effectively disperse stress and reduce crack expansion. Additionally, the presence of fibers restricts the longitudinal extension of cracks, making the cracks shorter compared to samples without fibers. The crack propagation mode changes from a single, direct extension to more complex intertwining or bending cracks, with cracks no longer extending in a straight line but branching or curving along the fiber distribution direction. As fiber content increases, the crack distribution becomes more uniform. The network structure formed by the fibers enhances the randomness and dispersion of cracks, improving the overall crack resistance of the concrete (see Fig. 6).

Fig. 6

Compressive failure morphology of EPS lightweight concrete.

Analysis of apparent density

From the analysis of Table 4, the factors affecting apparent density are ranked as follows: EPS content (A) > POM fiber content (C) > water-to-binder ratio (B), with the optimal combination being A3B2C3. EPS content is the dominant factor influencing apparent density, accounting for 90.25%. Specifically, when the EPS content increases from 35 to 40%, the bulk density of concrete decreases by 8.14%; further increasing it to 45% results in a cumulative reduction of approximately 9.56%. This significant weight reduction is mainly attributed to the extremely low density of EPS particles, which effectively replace high-density components in the cementitious matrix, thereby reducing the overall density of the concrete.

POM fiber content ranks second in its impact on apparent density, accounting for 6.41%, and shows slight fluctuations as the fiber content increases, with apparent density first increasing and then decreasing. This phenomenon can be attributed to the excellent hydrophilicity and dispersibility of POM fibers, which are distributed in a three-dimensional random manner within the paste, filling micropores and partially entrapped air bubbles, thereby enhancing the internal compactness of the concrete. However, as the fiber content further increases, its dispersibility decreases, leading to fiber agglomeration and the generation of additional micro air bubbles and pores, which reduce the compactness of the concrete and consequently decrease its apparent density.

The water-to-binder ratio has the least influence, accounting for only 3.09% of the total range, indicating that changes in the water-to-binder ratio within the studied levels have limited effects on apparent density. EPS content is the key factor in regulating the apparent density of EPS lightweight concrete. Increasing the EPS content can significantly reduce concrete density. At the same time, the appropriate incorporation of POM fibers can optimize the internal structure, but their dosage must be controlled within a suitable range to avoid the negative effects caused by fiber agglomeration.

Thermal conductivity analysis

According to Table 4, the factors influencing the thermal conductivity of EPS lightweight concrete are ranked as follows: EPS content (A) > water-to-binder ratio (B) > POM fiber content (C). The contribution of EPS content is as high as 91.28%, making it the dominant factor, followed by the water-to-binder ratio at 7.09%, while the influence of POM fiber content is minimal at only 1.33%. The optimal factor combination is A3B1C2.

Specifically, when the EPS content increases from 35 to 40%, the thermal conductivity decreases by 12.3%; further increasing the EPS content to 45% results in a cumulative reduction of approximately 21.6%. This indicates that the low thermal conductivity of EPS material effectively disrupts heat transfer pathways within the concrete, significantly reducing thermal conductivity and enhancing insulation performance. Therefore, optimizing the EPS content can effectively improve the thermal resistance of lightweight concrete, making it more suitable for applications with high thermal insulation requirements.

Frost resistance analysis

Based on the data in Table 4, the influence of factors on the frost resistance of EPS lightweight concrete is ranked as follows: EPS content (A) > POM fiber content (C) > water-to-binder ratio (B). The contribution of EPS content reaches 95.50%, making it the dominant factor affecting frost resistance; POM fiber content accounts for 2.56%, while the water-to-binder ratio has the least impact, at 1.57%.

As the EPS content increases, the frost resistance of the concrete significantly improves. This is primarily because the addition of EPS provides buffer space for the expansion of pore water during freezing, thus alleviating the hydraulic pressure generated during the freezing process and reducing damage to pore walls. Studies have shown that the maximum hydraulic pressure is positively correlated with the capillary pore distance. The inclusion of low-absorption EPS particles effectively shortens the migration path of unfrozen water, inhibits capillary infiltration in gel pores during freezing, and significantly reduces the osmotic pressure caused by freezing, thereby enhancing the frost resistance of the concrete²⁰.

For compressive strength, a key performance indicator for EPS lightweight concrete, EPS content is the most significant factor, followed by POM fiber content, while the water-to-binder ratio has a relatively minor effect. Through the range analysis, it is concluded that when the EPS content is 35%, the lightweight concrete meets the target requirement of C30 strength. Further optimization reveals that when the EPS content is 30% (A1), the water-to-binder ratio is 0.21 (B2), and the POM fiber content is 0.65% (C2), the compressive strength reaches its maximum value. Thus, the optimal mix design is A1B2C2.

Frost resistance analysis of EPS lightweight concrete

Mass loss rate and relative dynamic elastic modulus

After 100 freeze-thaw cycles, the freeze-thaw damage rate of EPS lightweight concrete remained below 25%, significantly better than the 40% limit specified in the failure evaluation criteria. This demonstrates the excellent frost resistance of EPS lightweight concrete, fully meeting the requirements of the Design Code for Hydraulic Concrete Structures (SL 191–2008)²⁴, which specifies a frost resistance grade of ≥ 100 for exposed structures on the sunny side in cold regions during dry winters.

As shown in Fig. 7a and b, the mass loss rate of EPS lightweight concrete gradually increases under freeze-thaw cycles, while the relative dynamic elastic modulus decreases with the number of cycles. Specifically, after 100 freeze-thaw cycles, the specimen with 45% EPS content exhibited the best frost resistance, with an average mass loss rate of only 0.156% and a relative dynamic elastic modulus as high as 95.9%. Compared to the group with 35% EPS content, its frost resistance was significantly improved. This phenomenon indicates that with the increase in EPS content, the concrete gains more internal buffer space, effectively mitigating the damage caused by hydrostatic pressure to pore walls during the freeze-thaw process.

Fig. 7

Mass loss and relative dynamic elastic modulus of EPS lightweight concrete under freeze-thaw cycles.

In summary, a moderate increase in EPS content not only enhances the frost resistance of lightweight concrete but also provides strong technical support for its application in building structures in cold regions.

Thermal conductivity

The thermal conductivity of EPS lightweight concrete is primarily influenced by factors such as aggregate and porosity. Under freeze-thaw cycles, the internal porosity of the concrete changes, and some EPS particles may be damaged, leading to corresponding changes in the material’s thermal insulation performance. To study this variation pattern, five groups of EPS lightweight concrete specimens with different mix proportions were randomly selected, and their thermal conductivity was tested under freeze-thaw cycling conditions.

As shown in Fig. 8, the thermal conductivity of each group of EPS lightweight concrete exhibits a similar trend under different freeze-thaw cycles. Overall, the variation in thermal conductivity follows a “decrease-increase-decrease” pattern. Initially, as the number of freeze-thaw cycles increases, the thermal conductivity gradually decreases due to the adjustment of the pore structure and the densification of some voids. However, as the freeze-thaw cycles intensify, the damage to EPS particles becomes evident, leading to an increase in the porosity of the concrete and a temporary rise in thermal conductivity. After more extensive freeze-thaw cycles, the ability of EPS particles to block heat conduction paths is further strengthened, resulting in another decline in thermal conductivity.

Fig. 8

Thermal conductivity of EPS lightweight concrete under freeze-thaw cycles.

Freeze-thaw damage model

To comprehensively analyze the damage behavior of EPS lightweight concrete under freeze-thaw cycles, the relative dynamic elastic modulus (D_N) before and after freeze-thaw cycling was used to indirectly characterize the extent of material damage. A damage variable D was introduced to describe the development of internal cracks in the material, which is defined as shown in Eq. (19):

$$D=1 - \frac{{{D_N}}}{{{D_{N0}}}}.$$

(19)

Where, D_N0 represents the initial relative dynamic elastic modulus, and DNDNDN denotes the relative dynamic elastic modulus after freeze-thaw cycling. The damage variable D ranges from 0 to 1 and reflects the accumulation of internal damage in the material.

To describe the evolution law of the damage variable, a two-parameter Weibull distribution model was adopted to construct the freeze-thaw damage evolution equation, as shown in Eq. (20):

$$D=1 - \exp \left[ { - {{\left( {\frac{n}{A}} \right)}^B}} \right].$$

(20)

Where, n is the number of freeze-thaw cycles, and A and B are the scale and shape parameters of the model, respectively, used to characterize the rate and form of damage evolution. For ease of fitting and calculation, Eq. (19) is transformed twice logarithmically, resulting in a linear expression as shown in Eq. (21):

$$\ln ( - \ln (1 - D))=B\ln n - B\ln A.$$

(21)

According to Eq. (21), calculate the corresponding variables X = ln n and Y = ln (− ln(1 − D)) for each group of specimens. Perform linear regression fitting on X and Y to determine the specific values of parameters A and B. The results are shown in Fig. 9.

Fig. 9

Parameters A, B, and correlation coefficient R² for the damage equation of EPS lightweight concrete.

The fitted parameters A and B are substituted into the Weibull distribution model, resulting in the freeze-thaw damage evolution equation for EPS lightweight concrete based on this distribution, as shown in Eq. (22):

$$D=1 - \exp \left[ { - {{\left( {\frac{n}{A}} \right)}^B}} \right].$$

(22)

The above freeze-thaw damage equation exhibits a certain level of accuracy and can effectively reflect the degree of freeze-thaw damage in EPS lightweight concrete. Based on practical experience, the damage evaluation criterion is set as D_N=40%. Substituting this criterion into the freeze-thaw damage equation yields the number of indoor freeze-thaw cycles. Using Eq. (23), the freeze-thaw durability of lightweight concrete as an exterior wall material in the region is predicted. The prediction results are shown in Fig. 10.

$$t=\frac{{K \times N}}{M}.$$

(23)

In this study, to investigate the freeze-thaw damage patterns of concrete structures and predict their service life, relevant parameters are introduced to supplement the freeze-thaw damage model. The specific meanings of the parameters in the equations are as follows:

t: The service life of the concrete structure in an outdoor natural environment, measured in years (a).

K: Experimental coefficient, representing the number of natural freeze-thaw cycles in the actual environment equivalent to one freeze-thaw cycle in the experiment. Based on related literature and empirical data, the range of K is generally 10 to 14. In this study, the average value K = 12 is adopted.

M: The number of natural freeze-thaw cycles the concrete structure may experience annually under actual environmental conditions, measured in cycles/year.

Fig. 10

Predicted freeze-thaw durability lifespan in different regions.

By incorporating the aforementioned parameters, the laboratory test results can be correlated with freeze-thaw damage in real-world environments, thereby establishing a more accurate freeze-thaw durability prediction model. This model provides significant theoretical support for evaluating the long-term performance of concrete structures in cold regions.

The results of the range analysis highlight the dominant influence of EPS content on concrete properties and the synergistic effects of water-to-binder ratio and fiber content. These findings will guide the development of machine learning models for performance prediction, as discussed in the next section.

Prediction of mechanical properties of EPS lightweight construction concrete based on multi-optimization models

Building on the experimental findings, this section explores the application of machine learning models, particularly XGBoost with intelligent optimization algorithms, to predict the mechanical properties of EPS lightweight concrete. The focus is on evaluating model performance and identifying optimal parameter combinations.

Data preparation

To achieve the prediction of mechanical properties for EPS lightweight concrete using multi-optimization models, this study utilized the experimental design described earlier. For each experimental setup, the results were averaged over three repeated experiments, yielding a total of 27 datasets. The specific experimental data include three primary factors: EPS content (A), water-to-binder ratio (B), and POM fiber content (C), as well as the corresponding 28-day compressive strength (fc) and splitting tensile strength (ft) indices.

To further enhance the dataset and improve the generalization ability and predictive accuracy of the machine learning model, additional experimental data from prior related studies were integrated into this study’s dataset. The resulting dataset comprises 100 experimental records, as illustrated in Fig. 11, covering a broad range of mix proportion parameters and mechanical performance indices. This comprehensive dataset provides diversity and reliability for training and testing the machine learning algorithms.

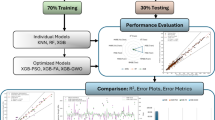
Due to the relatively small dataset size, five-fold cross-validation was employed to mitigate model overfitting and enhance prediction performance. Specifically, the dataset was split into training and testing sets in an 8:2 ratio, with 80% of the data used for training and 20% for testing the model’s predictive capability. Within the training set, five-fold cross-validation was applied by dividing the training data into five subsets. For each iteration, four subsets were used for training, while the remaining subset was used for validation. This process was repeated five times, and the average results across all folds were used to evaluate model performance.

The key parameters in the complete dataset include EPS content, water-to-binder ratio, and POM fiber content, as well as the 28-day compressive strength (fc​) and splitting tensile strength (ft). These form the input and output features for the machine learning models. Specifically, the input features are A, B, and C, while the output targets are fc​ and ft ​. This dataset provides a solid foundation for subsequent predictions of mechanical properties using multi-optimization models, while the application of five-fold cross-validation ensures the robustness and generalization of the experimental results.

Fig. 11

Distribution of sample dataset.

The normality test results in Fig. 11a show that the p-value for “28 d ft ​ (MPa)” is 0.5572, which is significantly greater than 0.05, indicating that this variable follows a normal distribution. However, the p-values for all other variables are less than 0.05, demonstrating that these variables deviate significantly from normality.

Figure 11b correlation matrix shows that “B” (water-binder ratio) has a strong positive correlation with “28 d fc (MPa)” with a correlation coefficient of 0.496514, indicating that the water-binder ratio significantly influences the compressive strength of concrete. In contrast, “C (%)” (fiber content) exhibits a negative correlation with “28 d ft (MPa)” with a correlation coefficient of -0.478062, suggesting that increasing fiber content may reduce the tensile strength of concrete.

The correlation between “A (%)” (EPS content) and “C (%)” is 0.390167, indicating a moderate positive correlation, which suggests a potential synergistic interaction between EPS content and fiber content in mix design. On the other hand, the correlation between “A (%)” and “28 d fc​ (MPa)” is -0.405352, implying that higher EPS content may lead to a reduction in compressive strength.

The correlation between “28 d ft (MPa)” and “28 d fc (MPa)” is relatively weak, with a correlation coefficient of 0.333408, indicating that tensile strength and compressive strength are somewhat independent and are influenced by different factors.

In summary, the results of the normality test and correlation analysis clearly reveal the characteristics of data distribution and the relationships between variables. For variables that deviate from normal distribution, data transformation or robust statistical methods can be used for further analysis. The correlation results provide valuable insights for optimizing concrete mix proportions and predicting performance, particularly highlighting the significant influence of water-binder ratio and fiber content on mechanical properties, which warrants further investigation.To assess the accuracy and performance of the multi-optimization model-based predictions of EPS lightweight concrete’s mechanical properties, the following commonly used regression evaluation metrics are adopted^29,30,31:

Model training and parameter optimization

To enhance the accuracy of predicting the mechanical properties of EPS lightweight concrete, a multi-optimization model based on XGBoost was employed for training and prediction. Various optimization algorithms were integrated to fine-tune the model parameters and achieve optimal performance. The dataset was randomly divided into a training set (80%) and a testing set (20%), with the training set used for model training and validation, and the testing set for evaluation. To avoid overfitting and improve generalization, a five-fold cross-validation approach was applied to the training set. The training data was split into five subsets, where four subsets were used for training, and the remaining subset for validation. The average performance across the five folds was used as the final evaluation metric for the model.

During model training, XGBoost iteratively optimized the loss function to predict the mechanical performance metrics, namely 28-day compressive strength (fc) and splitting tensile strength (ft​). The input variables were EPS content (A), water-to-cement ratio (B), and POM fiber content (C). To further improve model performance, Seagull Optimization Algorithm (SOA), Whale Optimization Algorithm (WOA), and Particle Swarm Optimization Algorithm (PSO) were introduced to fine-tune XGBoost’s hyperparameters. From the loss function curves, these three optimization algorithms demonstrated distinct characteristics in terms of loss reduction and convergence speed. WOA-XGBoost achieved the lowest loss and fastest convergence, followed by SOA-XGBoost, while PSO-XGBoost exhibited a higher loss and slower convergence but showed overall stability.

The main objective of parameter optimization was to adjust key hyperparameters, including the learning rate, maximum depth, subsampling ratio, and regularization parameters. The learning rate controls the step size for weight updates during each iteration and was set in the range of 0.01 to 0.3. Maximum depth determines the complexity of the decision tree and was set between 3 and 10. The subsampling ratio controls the proportion of samples used in each training iteration, with a range of 0.6 to 1. Regularization parameters were used to control model complexity and prevent overfitting. During optimization, the three algorithms searched these parameters differently. From the curve analysis, WOA showed high efficiency in parameter search, quickly identifying the optimal parameter combination. SOA effectively avoided local optima but required a slightly longer search time. PSO exhibited slower initial optimization but showed higher stability in later stages. Detailed results are shown in Fig. 12, and the parameter combinations based on minimum error are listed in Fig. 13.

Fig. 12

Loss function of models based on five-fold cross-validation.

Fig. 13

Parameter combinations with minimum error.

Prediction performance comparison

Analysis of single-model prediction performance

To evaluate the performance of the XGBoost algorithm in predicting the mechanical properties of EPS lightweight concrete, conventional machine learning algorithms such as Linear Regression (LR), Support Vector Regression (SVR), and Random Forest (RF) were selected as benchmarks. These models were trained and tested using the same dataset. By comparing the prediction results and error metrics of different models, the superiority of XGBoost in prediction performance was more intuitively analyzed.

Experimental results revealed that the XGBoost algorithm exhibited significant advantages in predicting the 28-day compressive strength (fc) and splitting tensile strength (ft). The predicted values by XGBoost closely matched the actual values, with the coefficient of determination (R²) consistently exceeding 0.98 across all metrics. In contrast, the Linear Regression model, constrained by its assumption of linear relationships among variables, performed poorly in capturing the nonlinear characteristics of concrete’s mechanical properties, resulting in an R² significantly lower than that of XGBoost. Furthermore, while SVR could capture certain nonlinear relationships in specific scenarios, its generalization ability was insufficient in larger sample spaces. The Random Forest model, though achieving results close to XGBoost in some metrics, fell short in model complexity and computational efficiency.

From the perspective of error metrics, XGBoost outperformed other conventional algorithms in MAE, MSE, and RMSE, demonstrating superior prediction accuracy and stability. For example, in predicting the 28-day compressive strength, XGBoost’s MAE was notably lower than that of SVR and Random Forest, indicating its ability to more effectively capture the nonlinear mapping relationship between input and target variables in complex data scenarios. Similarly, in predicting the 28-day splitting tensile strength, XGBoost exhibited sensitivity to small numerical changes, further reflecting the flexibility and adaptability of the model.

Figures 14 and 15 highlight the comparison, showing that XGBoost outperforms conventional algorithms such as Linear Regression, Support Vector Regression, and Random Forest in terms of both accuracy and stability in predicting the mechanical properties of EPS lightweight concrete. Its superiority lies not only in its robust expressiveness and ability to uncover feature importance but also in its built-in regularization mechanism, which effectively prevents overfitting. These findings demonstrate that XGBoost is an efficient and reliable algorithm, highly suitable for tasks involving the prediction of concrete’s mechanical properties.

Fig. 14

Scatter plot of single-model predictions.

Fig. 15

Accuracy of single-model predictions.

Optimized model prediction performance analysis

This section analyzes the prediction performance of SOA-XGBoost, WOA-XGBoost, and PSO-XGBoost models for predicting the 28-day compressive strength (fc) and splitting tensile strength (ft). Table X provides a comparison of the actual and predicted values for each optimized model, revealing noticeable differences in prediction accuracy. Overall, all three optimized algorithms effectively capture the relationship between input and target variables, although there are variations in their detailed performances.

Figures 16 and 17 demonstrate that SOA-XGBoost achieves the best prediction performance for both 28-day compressive and splitting tensile strengths. The prediction deviations are minimal, with the best coefficient of determination (R²) reaching 0.987, indicating that SOA-XGBoost captures the nonlinear relationship between input variables and target properties most effectively. Comparatively, WOA-XGBoost shows slightly lower performance, with fc and ft mean absolute errors (MAE) of 0.91 and 0.12, and R² values of 0.986 and 0.961, respectively. Although slightly less accurate, WOA-XGBoost still provides high prediction precision. PSO-XGBoost, on the other hand, shows lower prediction performance, with fc MAE at 1.23 and R² values of 0.968 for compressive strength and 0.945 for tensile strength. This suggests that PSO’s slower convergence or susceptibility to local optima in high-dimensional parameter optimization affects its overall performance. Nonetheless, the predicted values of PSO-XGBoost still show strong correlation with the actual values.

From the error metrics, SOA-XGBoost consistently outperforms the other two models. For instance, for 28-day compressive strength, SOA-XGBoost achieves MAE of 0.65, MSE of 0.89, and RMSE of 0.94, compared to WOA-XGBoost (MAE: 0.91, MSE: 1.42, RMSE: 1.19). Similarly, for splitting tensile strength prediction, SOA-XGBoost achieves an MAE of only 0.07, which is significantly lower than that of WOA-XGBoost and PSO-XGBoost. These results confirm the robustness of the SOA algorithm in optimizing model parameters and enhancing both the generalization ability and prediction accuracy of XGBoost.

Fig. 16

Prediction results of different optimized models.

Fig. 17

Evaluation metrics results of different optimized models.

SOA-XGBoost emerges as the best-performing model for predicting the mechanical properties of EPS lightweight concrete in this study, combining high accuracy and adaptability to complex data distributions. Its performance highlights its potential for optimizing concrete mix design. Meanwhile, WOA-XGBoost and PSO-XGBoost also show reliable prediction capabilities, with WOA being particularly effective at maintaining prediction consistency. These findings provide essential theoretical and technical support for optimizing lightweight concrete mix proportions and predicting mechanical performance in engineering applications.

Discussion

This study systematically analyzed the effects of EPS content, water-to-binder ratio, and POM fiber content on the mechanical and durability properties of EPS lightweight concrete through orthogonal experiments and machine learning models. The results indicate that EPS content is the dominant factor influencing concrete density, thermal conductivity, and frost resistance. As the EPS content increases, the concrete density significantly decreases, while thermal insulation and frost resistance improve markedly; however, excessive EPS content weakens the mechanical strength due to its low density and poor interfacial bonding characteristics. Furthermore, POM fibers demonstrated significant advantages in enhancing tensile strength and crack suppression. Proper fiber dosage effectively fills micro-cracks and limits crack propagation through a three-dimensional distribution, whereas excessive addition leads to fiber agglomeration, reducing the overall uniformity and mechanical performance of the structure. Compared to previous studies by Prasittisopin et al.⁶ and El Gamal et al.⁹, this research further quantified the interaction between EPS content and POM fiber content, and employed machine learning models to predict concrete performance. Notably, the SOA-XGBoost model achieved the best predictive performance after parameter optimization, significantly improving prediction accuracy and stability. While the findings provide a scientific basis for optimizing the mix proportions of EPS lightweight concrete, the experimental data were primarily obtained from laboratory tests, without considering long-term freeze-thaw conditions and loading effects. Therefore, future research should validate the long-term performance through field tests and further investigate the material’s deterioration mechanisms and durability using microscopic analysis and numerical simulations, offering more comprehensive technical support for the practical application of EPS lightweight concrete in engineering projects³².

Results

This study has successfully explored the mix design and performance prediction of EPS lightweight structural concrete through orthogonal experimentation and machine learning models. The results indicate that the EPS content is the most influential factor affecting the mechanical properties, thermal conductivity, and frost resistance of the concrete. While increased EPS content reduces the concrete’s density, it also significantly enhances its thermal insulation and frost resistance, albeit at the expense of mechanical strength. The inclusion of POM fibers has been shown to improve tensile strength and crack resistance, making it a promising additive for optimizing concrete performance.

Through the integration of three optimization algorithms—Seagull Optimization Algorithm (SOA), Whale Optimization Algorithm (WOA), and Particle Swarm Optimization (PSO)—into the XGBoost model, the study demonstrated that SOA-XGBoost achieved the highest prediction accuracy, followed by WOA-XGBoost and PSO-XGBoost. The optimal mix proportion, consisting of 35% EPS, 0.21 water-to-binder ratio, and 0.65% POM fiber content, provided an effective balance between mechanical and thermal performance.

While this research contributes valuable insights into lightweight concrete mix optimization and predictive modeling, it is limited by the laboratory-based experimental conditions and the absence of long-term field validation. Future studies should consider real-world environmental factors, such as freeze-thaw cycles and loading effects, to further evaluate the durability and performance of EPS lightweight concrete. Additionally, further investigation into the microscopic properties of the material and its degradation mechanisms will offer more comprehensive guidance for practical engineering applications.