Introduction

Antarctica, often referred to as the Earth’s largest cold source, exerts a profound influence on global ocean and atmospheric circulation due to its extensive sea ice cover and the high reflectivity (albedo) of the ice surface. Among the various sectors of the Southern Ocean, the Weddell Sea holds particular importance in regulating the climate of the Southern Hemisphere and beyond1,2,3. Its waters contribute to the formation of Antarctic Bottom Water—a fundamental driver of global thermohaline circulation—and its expansive seasonal sea ice strongly modulates air–sea heat exchanges. Consequently, shifts in Weddell Sea ice patterns can have cascading effects on weather systems, sea level, and coastal environments worldwide4. By studying the spatial and temporal dynamics of the Weddell Sea’s sea ice, we can gain deeper insights into how large-scale climate modes interact with polar processes, thereby improving our understanding of both regional climate vulnerability and global climate feedback mechanisms.

The Weddell Sea is a key region for studying sea ice variability due to its unique geographical position and interactions with atmospheric and oceanic forces. The passive microwave radiometers, including the Special Sensor Microwave Imager Sounder (SSMIS), Microwave Radiation Imager (MWRI), and Advanced Microwave Scanning Radiometer 2 (AMSR2)5,6, have long been the primary tools for monitoring sea ice concentration (SIC)7. Various algorithms are used to derive SIC products from passive microwave data, such as Bootstrap (BT), NASA Team (NT), Enhanced NASA Team (NT2)8,9, and the Arctic Radiation and Turbulence Interaction Study (ASI) algorithms. These products, released by institutions like the University of Bremen, the National Snow and Ice Data Center (NSIDC), and others, vary in spatial and temporal resolution, and their accuracy differs across regions. Therefore, assessing the accuracy and applicability of these products is an essential first step in sea ice research. Fig. 1

Fig. 1
figure 1

Weddell Sea spatial distribution map.

Full size image

Sea ice extent and concentration in the Weddell Sea are closely linked to atmospheric and oceanic dynamics10,11,12,13. Variability in the Southern Annular Mode (SAM), El Niño Southern Oscillation (ENSO)14,15,16,17,18,19,20, and net heat flux are key drivers of these changes. For instance, SAM is positively correlated with air temperature in the Weddell Sea but exhibits a negative correlation in parts of East and West Antarctica21,22. These teleconnections highlight the need for robust modeling approaches that can capture the spatial and temporal variability of sea ice and its response to environmental drivers23,24.

Traditional statistical models, such as linear regression, often assume uniform relationships across space and time, which limits their ability to capture the dynamic and heterogeneous nature of polar environments. In contrast, Geographically and Temporally Weighted Regression (GTWR) allows for parameter estimation that varies across both space and time, making it particularly suitable for studying spatiotemporal processes in sea ice data25,26. By incorporating spatial and temporal weights, GTWR provides a nuanced understanding of the localized effects of environmental variables such as wind speed, atmospheric pressure, sea surface temperature (SST), and heat fluxes on SIC27,28,29.

In this study, we employ the MODIS Sea Ice Concentration (SIC) dataset as a benchmark due to its high spatial resolution and multispectral capabilities, which enhance its accuracy in depicting sea ice characteristics. MODIS data have been validated extensively in previous studies and are capable of addressing challenges like cloud cover and varying solar illumination, which are common in polar regions. By comparing six SIC products derived from different satellite sensors and algorithms, we evaluate their accuracy against MODIS data and analyze the spatial and temporal patterns of sea ice changes in the Weddell Sea over 13 years. Using GTWR, we further investigate the localized and dynamic influences of environmental variables on SIC, providing deeper insights into the mechanisms driving sea ice variability in this critical region.

Results and discussion

Assessment of antarctic SIC products based on MODIS data

Through the preprocessing of 36 MODIS images and the inversion of SIC, the data albedo, ice-water binarization map, and MODIS 25 km \(\:\times\:\) 25 km spatial resolution SIC were obtained. By comparing the bias, mean absolute deviation (MAD), root mean square deviation (RMSD), and correlation coefficient (R) (see Table 1) between the SIC inverted from MODIS and the SIC products released by various organizations, the consistency between different SIC products and high-resolution optical remote sensing data-derived SIC was verified and analyzed. AMSR2/NT2, SSMIS/CDR, and MWRI/NT2 show high correlation coefficients with the verification data SIC, at 0.92, 0.91, and 0.94, respectively.

Table 1 Bias, MAD, RMSD and correlation coefficients between six sic products and the SIC of MODIS.
Full size table

The bias analysis indicates that the bias of MWRI/NT2 is the smallest, at just 0.23%, while the bias of SSMIS/NT is the largest, at −9.63%. Because the NT algorithm has a low recognition capacity for new ice and melt ponds, there is a significant bias compared to the SIC inverted from MODIS.

The analysis of MAD and RMSD shows that the MAD and RMSD of SSMIS/NT are the largest, at 11.20% and 15.35%, respectively, while those of MWRI/NT2 are the smallest, at 3.68% and 9.52%.

In summary, MWRI/NT2 has the highest correlation coefficient, the lowest MAD, and the lowest RMSD among the six SIC products, achieving the highest consistency with the SIC inverted from MODIS. Therefore, the MWRI/NT2 SIC product was used for subsequent research analysis. The NT2 algorithm reduces the effect of sea ice surface changes using the polarization ratio, making it more effective than the NT algorithm. The MWRI/NT2 product can detect finer-scale SIC changes than the 25 km \(\:\times\:\) 25 km spatial resolution SIC products. The influencing factors include variations in sensors used for obtaining brightness temperature data, differences in satellite observation times, algorithmic differences, variations in spatial resolution, differences in post-processing methods, and sensitivity to climate and environmental factors.

Seasonal sea ice changes

Summer changes

Over the past 13 years, the summer SIC in the Weddell Sea has shown an overall decreasing trend, with a decline rate of −8.9 ± 2.1 × 103km2yr−1 (Table A1). A strong inverse relationship exists between SST and SIC (r=−0.62, p < 0.01) (Table A2), which leads to a reduce of SIC with high SST (Fig. 2(a) and (b)). Due to the substantial increase in SST north of 70°S and the decrease south of 70°S (eastern Antarctic Peninsula), both thermal and pressure differences between low and high latitudes have resulted in the strengthening of the westerly belt3031,. As shown in Fig. 2(c), the wind speed and zonal wind between 60°S and 70°S significantly increase, indicating the strengthening of the westerlies. The intensification of the westerlies promotes the northward transport of colder surface waters through Ekman transport. This phenomenon leads to Ekman suction, enhancing the mid-layer water transport from mid-latitudes to high latitudes. Furthermore, a weakening of the westerlies leads to a reduction in the Weddell Gyre circulation, which in turn causes an upwelling of the thermocline, resulting in an increase in surface water temperatures and a subsequent reduction in sea ice31. Additionally, correlation analysis results demonstrate that both wind speed and zonal wind have an inverse relationship with SIC (zonal wind: r=−0.42, p < 0.05; wind speed: r=−0.62, p < 0.01) (Table A2). Changes in wind speed can affect the intensity of sea ice advection, which subsequently influences both increase and decrease of sea ice. As shown in Fig. 2(d), wind speed increases between 60°S and 70°S, promotes sea ice advection towards the northeastern Weddell Sea and reduces the SIC. Therefore, both SST and wind speed have a significant inverse relationship with SIC, which together affect the changes of sea ice during summe24.

Autumn changes

In autumn, the SIC in the northern and northeastern regions of the Weddell Sea decreases significantly, with a decline rate of −10.7 ± 2.3 × 103km2 year-1 (Table A1), marking it as the season with the most severe sea ice loss in the Weddell Sea. There is an inverse relationship between the trend in SST and SIC, indicated by a correlation of −0.66 (p < 0.01) (Table A2, Fig. 3(a) and (b)). The westerly winds strengthen in the northwestern and northeastern Weddell Sea (Fig. 3(c)). Correlation analysis shows that in autumn, there is a strong negative relationship between both wind speed and zonal wind and the SIC (zonal wind: r=−0.60, p < 0.01; wind speed: r=−0.77, p< 0.01) (Table A2)1. Northwestern region: This intensified circulation causes the thermocline to rise, subsequently leading to the northward migration of warm water into the Weddell Sea. Additionally, the enhanced Ekman transport increases the movement of cold surface water from high to low latitudes, triggering the Ekman suction phenomenon, which facilitates the influx of warm low-latitude water into the Weddell Sea. The rise in wind speed enhances the movement of sea ice, leading to its northwestward drift. These three factors collectively promote the melting of sea ice2. Northeastern region: In the northeastern Weddell Sea, changes in the wind speed and zonal wind are minimal24. A decrease in both the wind speed and zonal wind is observed in some areas, where sea ice experience loss (Fig. 3(c) and 3(d)). Therefore, we divided the Weddell Sea at the − 20°W meridian into eastern and western sections and separately analyzed the correlations of the SIC with the SST, wind speed and zonal wind. The results show that in the eastern Weddell Sea, the SST, wind speed and zonal wind all exhibit an inverse relationship with the SIC (Eastern SST: r = −0.62, p < 0.01; Eastern zonal wind: r = −0.70, p < 0.01; Eastern wind speed: r = −0.77, p < 0.01). In the western Weddell Sea, the correlation coefficients of the SIC with the SST, wind speed and zonal wind are − 0.68, −0.39 and − 0.40, respectively (Table A2). Therefore, in the northeastern Weddell Sea, the primary cause of changes in SIC is variations in SST, while the impacts of the wind speed and zonal wind on SIC are minor.

In summary, in the northwestern Weddell Sea during the autumn, the reduction in the SIC is primarily due to rising SST and the intensification of zonal and meridional winds. In the northeastern Weddell Sea, the dominant factor influencing the decrease in the SIC is the SST.

Fig. 2
figure 2

Spatial plots of summer trends in the Weddell Sea. (a) SIC (%year−1), (b) SST (℃year−1), (c) zonal wind (ms−1year−1), (d) wind speed (ms−1year−1) and wind vector trends. Areas with trends significant at a 95% confidence level are marked by black dots.

Full size image
Fig. 3
figure 3

The trends of autumn, Same as Fig. 2.

Full size image

Winter changes

In winter, the trend in SIC changes in the Weddell Sea is minimal, with a notable reduction primarily near 60°S, especially at the northern tip of the Antarctic Peninsula (Fig. 4(a)). The rate of sea ice loss is −1.3 ± 0.5 × 103km2yr−1(Table A1). Similar to autumn, the correlation between the SIC and SST, wind speed and zonal wind is different in the eastern and western Weddell Sea1. In the northwestern Weddell Sea, at the northern tip of the Antarctic Peninsula, the correlation coefficients between the SIC and the SST, zonal wind, and wind speed are − 0.57, −0.35, and − 0.53, respectively (Table A2). The correlation analysis results indicate that as the trend in changes in the SIC weakens, the correlation also diminishes. The findings from the correlation analysis suggest indicate that changes in the SIC are primarily influenced by variations in sea surface temperature and wind speed. The strengthening of westerly and northwesterly winds in this region (Fig. 4(d)) enhances both sea ice advection and Ekman suction. This, in turn, facilitates the influx of warm water from lower latitudes. As a result of this warm water intrusion, sea surface temperatures at the northern tip of the Antarctic Peninsula exhibit an upward trend (Fig. 4(b)). Consequently, the SIC at the northern tip of the Antarctic Peninsula significantly decreases2. In the northeastern Weddell Sea, SST has a strong negative correlation with SIC, as shown by a correlation coefficient of −0.71 (p < 0.01) (Table A2), and shows no significant correlation with the wind speed and zonal wind. Therefore, the decrease in the SIC in this region is primarily due to the increase in SST.

Spring changes

During spring, SIC in most areas of the Weddell Sea shows a declining trend, with the northwest experiencing the most pronounced decrease. The rate of sea ice decline is −6.2 ± 1.9 × 10³ km²yr⁻¹ (Table A1) (Fig. 5(a)). The SIC displays strong negative correlations with the SST, wind speed, and zonal wind, exhibiting correlation coefficients of −0.65, −0.71, and − 0.74, respectively (Table A2). The SST shows an upward trend in the northern Weddell Sea (Fig. 5(b)), resulting in higher seawater temperatures and hastening the dissolution of sea ice. During spring, the strengthening of westerly winds (Fig. 5(c)) enhances Ekman transport, which drives the movement of colder polar surface water toward lower latitudes. This intensified Ekman transport also increases Ekman suction, leading to the influx of warm water into the Weddell Sea. Additionally, the strengthening of westerly winds contribute to the intensification of the Weddell Gyre, which in turn promotes increased vertical mixing and the upward movement of warmer water from the thermocline32. The declining trend in SIC in the eastern Weddell Sea is driven by the substantial strengthening of westerly and northwesterly winds, which promotes sea ice advection and causes the ice to drift eastward (Fig. 5(c) and (d)). The pronounced declining trend in SIC at the northern tip of the Antarctic Peninsula is caused by intensified sea ice advection, a result of the increased wind speeds due to westerly winds from the Bellingshausen Sea being blocked by the Antarctic Peninsula. This phenomenon is also observed in the summer, autumn and winter. The SST along the eastern flank of the Antarctic Peninsula is showing a declining trend, while the western side exhibits an increasing trend. The Antarctic Peninsula acts as a barrier, preventing the transfer of temperature and wind between its eastern and western sides1,33. As can be seen from Fig. 5, as the SST in the west of the Antarctic Peninsula increases, the SIC decreases significantly. Due to the Antarctic Peninsula’s resistance to heat transfer, the SST in the east of Antarctic Peninsula changes very little, resulting in almost no change in SIC24.

Fig. 4
figure 4

The trends of winter, Same as Fig. 2.

Full size image
Fig. 5
figure 5

The trends of spring, Same as Fig. 2.

Full size image

Long-term sea ice changes

From 2011 to 2023, the SIE in the Weddell Sea exhibited significant seasonal variations and interannual fluctuations. In 2014, the SIE reached its maximum extent of 4.08 × 106km2, declining to its minimum extent of 3.17 × 106km2 by 2023 (Fig. 6). Overall, the SIE shows a decreasing pattern, characterized by an average yearly reduction rate of −6.6 ± 1.3 × 103 km²yr−1 (Table A1).

Seasonal analysis indicates that the most significant declining trend occurs in autumn, with a rate of −10.7 ± 2.3 × 10³ km² yr⁻¹, while the smallest decline is observed in winter, at −1.3 ± 0.5 × 10³ km² yr⁻¹ (Table A1). According to statistical analysis, there is a significant negative correlation between SIE and SST across seasons (r=−0.81, p < 0.01) (Table A3), with the negative correlation occurring in summer (r=−0.89, p< 0.01) (Table A4). Changes in SST are the primary factors affecting the expansion and retreat of sea ice34. The largest SIE in 2014 corresponded to the lowest SST of −0.21 °C, while the smallest SIE in 2023 corresponded to the highest SST of 0.25 °C (Fig. 7). This finding is consistent with existing research, which indicates that increases in SIE correspond with decreases in SST35.

The NHF represents the net exchange of heat between a system, such as the ocean, and its surrounding environment. A positive NHF indeed means that the ocean is losing heat to the atmosphere. Conversely, a negative NHF indicates that the ocean is gaining heat from the atmosphere. The NHF is crucial for driving atmospheric circulation, affecting ocean temperatures and influencing the formation and melting of sea ice. Statistical analysis reveals that the relationship between the NHF and SIE varies by season. In spring and summer, a substantial positive relationship is observed between NHF and SIE, with correlations of r = 0.72 (p < 0.01) for spring and r = 0.3 (p < 0.1) for summer. Conversely, in autumn and winter, the relationship becomes negative, with correlations of r=−0.65 (p < 0.01) for autumn and r=−0.52 (p < 0.01) for winter (Tables A4-A7, Fig. 7).

Fig. 6
figure 6

Timeseries of the annual anomalies showing interannual variation (2011–2023) of SIE (106 km2), SST (°C), NHF (Wm−2), ENSO, AMM and SAM over the Weddell Sea. The calculation of anomalies is based on climatological data from 1991–2020.

Full size image

Over the past 13 years, the sea ice cover in the Weddell Sea has undergone significant changes, which are closely related to the continuing ocean-atmosphere interactions. To deepen the understanding of these processes, a correlation analysis was conducted on Weddell Sea sea ice with various climate variability patterns (Fig. 5, Table A3). The SAM refers to the climate variations caused by the northward or southward shifts of the westerly wind belt or low-pressure systems surrounding Antarctica36,37, directly reflecting variations in the atmospheric pressure patterns around Antarctica. It significantly influences the SST and the strength of the westerly winds in the Weddell Sea. Although annually there is no significant correlation between the SIE and the SAM, seasonally, the SIE correlates positively with the SAM in summer (r = 0.29, p < 0.1), and negatively in winter (r=−0.28, p < 0.1) (Tables A3-A7, Fig. 7). The expansion and contraction of sea ice are driven by the positive phase of the SAM, which leads to changes in the westerlies and alters the pressure differences between the Antarctic low pressure belt and the subtropical high pressure belt31,38,39.

The IOD is associated with variations in the differences between the SST and sub-surface ocean temperatures in the eastern and western regions of the Indian Ocean. The IOD demonstrates significant negative correlations with the SIE during summer (r=−0.62, p < 0.01) and autumn (r=−0.33, p < 0.1), and a significant positive correlation in spring (r = 0.31, p < 0.1) (Tables A3-A7, Fig. 7). This may be attributed to the proximity of the Indian Ocean to the eastern Weddell Sea, where changes in the SST of the western Indian Ocean and variations in the IOD facilitate changes in the Southern Hemisphere westerlies, easily influencing sea ice changes in the eastern Weddell Sea. The results of this study indicate that there is no significant correlation between the ENSO and AMM with SIE throughout the year (Tables A3-A7, Fig. 7).

Fig. 7
figure 7

Interannual variations (2011–2023) in SIE (106 km2), SST (℃), NHF (W/m−2), ENSO, AMM and SAM are depicted through seasonal anomalies for (a) summer; (b) autumn; (c) winter; and (d) spring over the Weddell Sea. The calculation of anomalies is based on climatological data from 1991–2020.

Full size image

Spatial correlation and lag time distribution

Figure 8 shows the correlation coefficients of SST, NHF, wind speed, zonal wind, meridional wind, and SIC in the Weddell Sea of Antarctica and its surrounding seas (Fig. 8 (a–e)), as well as the lag months corresponding to the maximum correlation (Fig. 8 (f–j)).

As shown in Fig. 8(a), a significant negative correlation between SST and SIC is observed in the western Weddell Sea (approximately 50°W–30°W, 60°S–70°S), with correlation coefficients reaching as low as − 0.6. This indicates that in this region, higher SIC is often associated with a decreasing trend in SST. The corresponding lag distribution (Fig. 8(f)) shows that in the southwestern Weddell Sea (approximately 40°W–60°W, 70°S − 75°S), lags of − 3 to − 5 months are common, suggesting that SST changes in this area may precede SIC changes by about 3–5 months. In contrast, in parts of the eastern region (approximately 10°W–20°E), the lag extends to 4 to 6 months, indicating that SST in these areas may respond to SIC changes with a delay of 4–6 months.

Fig. 8
figure 8

Correlation and hysteresis distribution of main sea-air variables and sea ice concentration in the Weddell Sea. Black dots are areas with significant correlations. SST is the sea surface temperature, NHF is the sea-air heat flux, SI is the 10-meter wind speed, U10 is the 10-meter zonal wind, and V10 is the 10-meter meridional wind.

Full size image

Figure 8(b) shows that NHF exhibits a significant positive correlation across most of the Weddell Sea, with correlation coefficients mostly ranging from 0.3 to 0.6. Particularly in the region around 30° W–10° W, 60° S–75° S, local peaks can reach up to 0.7. This indicates that when SIC increases, the ocean-atmosphere net heat flux tends to strengthen correspondingly. However, negative correlations are observed in the northern and eastern areas, with values as low as − 0.4, suggesting an opposite coupling relationship in these peripheral and eastern regions. From the lag pattern (Fig. 8(g)), NHF in the southwestern region (50° W–40° W, approximately 65° S) typically shows a lag of 2–5 months, whereas in the eastern region (approximately 0°–20° E, 60° S–65° S), the lag extends to 6–8 months. This suggests that different regions exhibit varying response times to external forcing or internal variability.

The correlation distribution of sea ice concentration in Fig. 8(c) exhibits greater spatial heterogeneity. In the western sea area (~ 50°W–60°W, 65°S–70°S), the correlation coefficients range from approximately − 0.3 to − 0.5, indicating a moderate negative correlation with SIC. In contrast, the eastern region (around 20°W–10°E) shows multiple areas with high positive correlations, reaching up to 0.4. The lag distribution (Fig. 8(h)) reveals that the maximum correlations in these regions are mostly concentrated within a range of ± 3 to ± 6 months. Specifically, the negative correlation zones in the west often reach their peak at a lag of − 2 to − 4 months, while the positive correlation zones in the southeast tend to peak around + 4 months. This division of positive and negative correlations may reflect the differences in seasonal processes of sea ice between the western and eastern Weddell Sea, as well as the lagged response to external climatic signals, such as the Antarctic Oscillation or polar vortex activities, in different regions.

The wind field correlation maps exhibit “banded” or block-like patterns (Fig. 8(d, e) and (i, j)). For the 10 m zonal wind, the maximum correlation values, approximately 0.5, appear in a banded region around 60°S, while further south (65°S–70°S), there are areas with negative correlations ranging from − 0.3 to − 0.4. The meridional wind shows a more fragmented correlation distribution, though certain regions (e.g., 20°W–0°) feature bands of positive correlation as high as 0.5. The lag times of the wind field (Fig. 8(i, j)) also vary significantly: some regions show a lead (negative lag of 2–4 months), while others exhibit a lag (3–6 months). Notably, along the southeastern Antarctic margin (10°E–30°E, ~ 60°S), the lag for V10 extends up to 8 months.

Overall, in terms of correlation coefficients, the central and western Weddell Sea is often dominated by negative correlations, with the lowest values reaching − 0.6, while the eastern and northern margins are primarily characterized by positive correlations, with the highest values up to 0.7. The coupling between SIC and NHF is particularly pronounced: the central and southern sea areas exhibit high correlations (\(\:\mid\:r\mid\:\) > 0.4), indicating the sensitivity of sea ice to heat flux fluctuations. Regarding lag times, most are distributed within the ± 2–8 month range, showing significant spatial variability. Some regions exhibit leads (negative lags), such as − 3 to − 5 months in the southwestern end, as shown in Fig. 8(f, g), while other areas display lags of up to 6 or even 8 months, suggesting that the peaks of these variables occur later.

Spatial and temporal analysis of environmental factors influencing SIC

The GTWR accounts for spatial and temporal heterogeneity in modeling, allowing various environmental factors to have unique impacts on SIC at different geographic locations and time points28,29. Initially, correlation analysis and multicollinearity tests were conducted to screen the environmental factors, including 10 m zonal wind, 10 m meridional wind, 10 m wind speed, mean sea-level pressure (MSL), SST, LH, SH, and NR flux (NR), derived from the ERA5 reanalysis dataset. The results of the correlation analysis indicate a high degree of correlation between SST and other environmental factors, particularly with MSL and LH (Table A8). The results of the multicollinearity test show that the variance inflation factor (VIF) for SST is 27.4 (Table 3). The VIF is a statistical measure used to assess the degree of multicollinearity, indicating how the interrelationships among independent variables affect the precision and stability of a linear regression model42,43,44. Typically, the VIF of less than 10 is considered acceptable for multicollinearity. Since the VIF for SST exceeds 10, it was excluded from the analysis. We then employed 10 m zonal wind, 10 m meridional wind, 10 m wind speed, MSL, LH, SH, and NR as independent variables, with SIC as the dependent variable, to construct the GTWR model, quantifying the effects of these factors on SIC.

The statistical results of the regression coefficients for each environmental variable in the GTWR model are presented in the Table 2. The regression coefficients shown are standardized coefficients, where a larger absolute value indicates a greater impact on SIC45. The LH exhibits the most significant impact on SIC, with a median value of 1.44. This is followed by 10 m zonal wind, 10 m meridional wind, MSL, SH, and NR. The influence of 10 m wind speed is the least, with a median value of 0.09. Because the 10 m wind speed, net thermal radiation and sensible heat flux have a low impact on sea ice, they are not involved in the subsequent analysis of the spatiotemporal distribution of the impact coefficients.

Table 2 Statistics of regression coefficients of environmental factors in GTWR model.
Full size table
Table 3 Statistics of regression coefficients of environmental factors in GTWR model.
Full size table

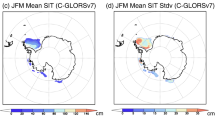
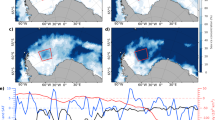
The Fig. 9shows the spatiotemporal distribution of the influence coefficient of zonal wind on sea ice from 2011 to 2023. It can be seen that in the Weddell Sea region, zonal wind primarily promotes sea ice growth. However, near the Larsen Ice Shelf at the junction of the Antarctic Peninsula and the Antarctic continent, zonal wind promoted sea ice growth from 2011 to 2015, but after 2016, it began to suppress sea ice growth. We extracted the corresponding data for this region and plotted time series of the relevant variables46. Figure 9(a)–(d) respectively present the annual mean zonal wind, sea surface temperature (SST), latent heat flux (LHF), and sea ice concentration (SIC) in that area. Before 2016, the zonal wind showed an upward trend, and SIC also increased, consistent with the zonal wind promoting sea ice growth. However, after 2016, the zonal wind gradually weakened, whereas SIC continued to increase. The main reason for this phenomenon is that after 2016, SST kept decreasing and LHF kept increasing. Since LHF tends to promote sea ice growth and SST tends to inhibit it, and both LHF and SST have a greater overall influence on sea ice than the zonal wind does, sea ice continued to grow even though the zonal wind diminished47,48. At the northern tip of the Antarctic Peninsula, the zonal wind suppresses sea ice growth. This is driven by the wind channel effect: as the zonal wind intensifies, wind speeds around the peninsula’s northern tip increase significantly, enhancing both sea ice advection and vertical mixing in the ocean, ultimately leading to reduced sea ice. Hence, in this region, the zonal wind inhibits sea ice growth.

Fig. 9
figure 9

Spatial and temporal distribution of the influence coefficient of 10 m zonal wind on SIC. The line graphs (a-d) are the annual averages of zonal wind, sea surface temperature, latent heat flux and sea ice concentration, respectively.

Full size image

Figure 10 shows the spatial distribution of the impact coefficients of meridional wind on sea ice from 2011 to 2023. It can be observed that meridional wind primarily promotes sea ice growth. This is because the meridional wind transports colder air from the Antarctic continent towards the equator, thereby enhancing sea ice formation.

However, in the region between 20° W–40° W and 55° S–65° S, the meridional wind inhibited sea ice growth during 2012–2015. According to the line chart on the right, before 2015, the meridional wind exhibited a downward trend, while SIC showed an upward trend50,51. This phenomenon can be attributed to the decline in SST and the increase in LHF during the period from 2011 to 2015. As a result, the meridional wind in this region acted to suppress sea ice growth.

Fig. 10
figure 10

Spatial and temporal distribution of the influence coefficient of 10 m Meridional wind on SIC. The line graphs (a-d) are the annual means of meridional wind, sea surface temperature, latent heat flux and sea ice concentration. respectively.

Full size image

The Fig. 11 shows the spatial distribution of the impact coefficients of MSLP on sea ice from 2011 to 2023. It is evident that in the northern Weddell Sea, MSLP inhibits sea ice growth, whereas in the southern Weddell Sea, MSLP promotes sea ice growth. This is because the northern Weddell Sea lies within the subpolar low-pressure belt, where a decrease in MSLP enhances westerly winds, thereby promoting sea ice formation. Consequently, MSLP in the northern Weddell Sea exerts a negative feedback effect on SIC.

In contrast, a decrease in MSLP in the southern Weddell Sea intensifies easterly winds, suppressing sea ice growth. Therefore, MSLP in the southern Weddell Sea exerts a positive feedback effect on SIC. Over time, the influence of MSLP on sea ice has gradually weakened.

The line chart on the right divides the Weddell Sea into northern and southern parts, showing that after 2014, the variations in MSLP became more subdued, but the fluctuations in SIC remained significant. This indicates that after 2014, the influence of MSLP on sea ice has gradually diminished.

Fig. 11
figure 11

Spatial and temporal distribution of the influence coefficient of MSLP on SIC. Line graphs (a, b) show the annual averages of MSL and SIC in the northern Weddell Sea. Line graphs (c, d) show the annual averages of MSL and SIC in the southern Weddell Sea.

Full size image

The Fig. 12 shows the spatiotemporal distribution of the impact coefficients of LHF on sea ice from 2011 to 2023. It can be observed that during this period, LHF consistently promoted sea ice growth, with a particularly significant impact. This effect is especially pronounced along the eastern coast of the Weddell Sea. This phenomenon occurs because the release of latent heat flux is accompanied by cooling of the sea surface or sea ice, which reduces sea ice melting and promotes the formation of new ice. Therefore, overall, LHF contributes to sea ice growth.

Fig. 12
figure 12

Spatial and temporal distribution of the influence coefficient of LHF on SIC.

Full size image

Conclusion

In this study, six publicly available sea ice concentration (SIC) products were evaluated against MODIS optical remote sensing data. The MWRI/NT2 product showed the highest consistency, characterized by the strongest correlation with MODIS (R = 0.94), and the smallest bias, MAD, and RMSD. Consequently, MWRI/NT2 was selected as the optimal product to investigate sea ice variability in the Weddell Sea from 2011 to 2023.

Analyses of seasonal SIC changes revealed that autumn experienced the most pronounced reduction in sea ice, whereas winter exhibited the smallest decline. Statistical results further indicated that sea surface temperature (SST) consistently exerted a significant negative correlation with SIC, and wind forcing (both wind speed and wind direction) served as another crucial factor driving sea ice reduction. In the northwestern Weddell Sea, intensified winds promoted upwelling of warm water from lower latitudes, enhancing sea ice melt. In contrast, in the northeastern Weddell Sea, increases in SST were primarily responsible for sea ice reduction. Over the 13-year period, the sea ice extent (SIE) showed a net decreasing trend at an average rate of.

A comprehensive analysis was conducted on the seasonal variations and trends in sea ice within the Weddell Sea region from 2011 to 2023, utilizing the MWRI/NT2 product, which shows the highest correlation with the SIC inverted from MODIS. This approach ensures the accuracy and reliability of the SIC data. Additionally, and the relationship between sea ice changes and climatic factors was explored and analyzed.

By comparing various the SIC products with the SIC inverted from MODIS, it was found that the MWRI/NT2 SIC product performs best in terms of correlation and error metrics, demonstrating its effectiveness in observing sea ice changes.

The SIE in the Weddell Sea has shown a significant declining trend over the past 13 years, particularly in the spring, summer and autumn seasons, with smaller changes in winter. The average annual decline rate is −6.6 ± 1.3 × 103km2 year-1. In the spring and summer of the Weddell Sea, the SIC exhibits a significant negative correlation with the SST, wind speed and zonal wind. In autumn and winter, different correlation results were found between the eastern and western parts of the Weddell Sea. In the east, the SIC is primarily influenced by the SST, with which it exhibits a significant negative correlation. In the west, the SIC shows a significant negative correlation with the SST, wind speed and zonal wind. We speculate that the occurrence of these conditions is due to the Antarctic Peninsula blocking the transfer of heat and wind between its eastern and western sides. The specific mechanisms responsible for this phenomenon will be the focus of our future research.

Research indicates that changes in SIC in the Weddell Sea during summer and spring are primarily influenced by the SST, while in autumn and winter, the SIC changes are jointly influenced by the NHF and SST. In summer and spring, the sea ice changes are primarily attributed to ocean warming, while in autumn and winter, they are driven by ocean-atmosphere interactions.

The GTWR was employed in this study to assess the spatial and time heterogeneity in the impact of various environmental factors on the SIC across the Weddell Sea. The complex and region-specific nature of these influences was highlighted by the analysis. For instance, LH was found to be a significant promoter of sea ice growth in most regions. The impact of wind speed exhibited no clear space-time pattern, likely due to its low overall influence and the lack of directional data in ERA5. The Zonal and meridional winds generally supported sea ice formation, though topographical effects near the Antarctic Peninsula sometimes led to suppression. SH promoted sea ice growth in the western and eastern regions but had a suppressive effect in the central Weddell Sea, likely due to the influx of warmer air and water. The varied responses of SIC to mean sea-level pressure further underscored the dynamic interactions between atmospheric and oceanic processes, particularly in the context of ongoing climate change. These findings demonstrate the critical importance of considering spatial heterogeneity in climate models and suggest that regional responses to environmental factors can significantly differ, influencing sea ice dynamics in complex ways.

Data and methods

Passive microwave sea ice concentration product

The institutions that release sea ice concentration products include the NSIDC in the United States, the UB in Germany, the European Organization for the Exploitation of Meteorological Satellites, and the NSMC of the China Meteorological Administration. The SIC products are generated based on algorithms such as BT, NT, NT2, and ASI, based on passive microwave data obtained by instruments onboard various satellites. The six commonly used Antarctic sea ice concentration products utilized in this study are presented in Table 4.

Table 4 6passive microwave remote sensing sea ice concentration products.
Full size table

MODIS data

In this study, The MODIS Sea Ice Concentration (SIC) data has been chosen as the benchmark to evaluate other SIC products derived from various satellite sensors and algorithms. The MODIS was selected due to its high spatial resolution and extensive validation in previous studies, which confirm its reliability in accurately depicting sea ice characteristics61. Unlike sensors limited to specific parts of the electromagnetic spectrum, MODIS integrates data from visible, infrared, and microwave spectral bands62,63. This multispectral capability enhances its ability to detect sea ice under diverse atmospheric conditions, such as cloud cover and varying levels of solar illumination, which are common challenges in polar regions.

The SIC is inverted by using 500 m × 500 m spatial resolution MODIS L1B images to compare and verify the differences between various passive microwave SIC products (https://ladsweb.modaps.eosdis.nasa.gov/). First, the MODIS L1B product is preprocessed, including radiometric calibration, reprojection, and bow-tie removal. The MODIS L1B product is zenith-corrected using the MOD03 product, and the MOD35 product is used for cloud mask processing to obtain cloudless clear sky pixels64,65. Before zenith angle correction, attention should be paid to whether the various observation angles in SolarZenith are within a reasonable dynamic range. In order to reduce the impact of excessive solar zenith angles, solar zenith angle data less than 85° should be selected.

ECMWF reanalysis v5 reanalysis data set

The ERA5 reanalysis dataset (0.25°×0.25° grid)66, obtained from the European Centre for Medium-Range Weather Forecasts (https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels-monthly-means?tab=overview), was used to analyze the impact of various climate parameters on sea ice, including 10 m wind speed, zonal wind, meridional wind, and 2 m SST.

NOAA data

The heat flux and monthly climate indicators used in this paper (such as LH, SH, LW, SW, SAM, ENSO, AMM and IOD) are obtained from the National Oceanic and Atmospheric Administration https://psl.noaa.gov/data67. This study utilizes the ENSO data derived from the Nino 3.4 region. (5°N-5°S, 120°−170°W).

Retrieving SIC from MODIS data

This paper uses the reflectivity data of bands 1 (0.620–0.670 μm), 3 (0.459–0.479 μm), and 4 (0.545–0.565 μm) of the MODIS L1B product to invert SIC, and the calculation formula is:

$$\:\text{A}=0.3265\times\:{\text{A}}_{1}+0.4364\times\:{\text{A}}_{3}+0.2366\times\:{\text{A}}_{4}\:\:$$
(1)

where A is the broad-band albedo of the top atmosphere, and A1, A3, and A4 are the corresponding reflectivity values of the 1st, 3rd, and 4th bands of MODIS, respectively.

The Otsu algorithm is used to classify ice and water in images68,69. Finally, the mean method is used to calculate the SIC of 25 km × 25 km.

Statistical and comparative analysis methods.

Four statistical parameters are utilized in this article for accuracy assessment: bias, MAD, RMSD, and correlation coefficient (r).

$$\:\text{b}\text{i}\text{a}\text{s}=\frac{\sum\:_{\text{i}=1}^{\text{n}}\left({\text{X}}_{\text{i}}-{\text{Y}}_{\text{i}}\right)}{\text{n}}$$
(2)
$$\:\text{M}\text{A}\text{D}=\frac{\sum\:_{\text{i}=1}^{\text{n}}\left|{\text{X}}_{\text{i}}-{\text{Y}}_{\text{i}}\right|}{\text{n}}$$
(3)
$$\:\text{R}\text{M}\text{S}\text{D}=\sqrt{\frac{\sum\:_{\text{i}=1}^{\text{n}}{\left({\text{X}}_{\text{i}}-{\text{Y}}_{\text{i}}\right)}^{2}}{\text{n}}}$$
(4)
$$\:\text{r}=\frac{\sum\:_{\text{i}=1}^{\text{n}}\left({\text{X}}_{\text{i}}-\stackrel{-}{\text{X}}\right)\left({\text{Y}}_{\text{i}}-\stackrel{-}{\text{Y}}\right)}{\sqrt{\sum\:_{\text{i}=1}^{\text{n}}{\left({\text{X}}_{\text{i}}-\stackrel{-}{\text{X}}\right)}^{2}}\sqrt{\sum\:_{\text{i}=1}^{\text{n}}{\left({\text{Y}}_{\text{i}}-\stackrel{-}{\text{Y}}\right)}^{2}}}$$
(5)

where \(\:{X}_{i}\:\) is the SIC of a product; \(\:{Y}_{i}\:\) is the SIC estimated by MODIS; \(\:\stackrel{-}{\text{X}}\) and \(\:\stackrel{-}{\text{Y}}\) are the means of \(\:{X}_{i}\) and \(\:{Y}_{i}\:\) respectively; n is the total number of samples.

Cross-correlation and maximum correlation lag

To measure the linear correlation strength between SIC and environmental factors at different lags, this study employs cross-correlation analysis. The basic definition is:

$$\gamma \left( \tau \right)=\frac{{\sum\limits_{t} {\left[ {X\left( t \right) - \overline {X} } \right]\left[ {Y\left( {t+\tau } \right) - \overline {Y} } \right]} }}{{\sqrt {{{\sum\limits_{t} {{{\left[ {X\left( t \right) - \overline {X} } \right]}^2}\sum\limits_{t} {\left[ {Y\left( {t+\tau } \right) - \overline {Y} } \right]} } }^2}} }}$$
(6)

Where \(\overline {X}\) and \(\overline {Y}\) denote the mean values of the sequences \({X}\) and \({Y}\) , respectively, and \(\tau\) represent the time lag (in units such as months). When \(\tau> 0\) it indicates that the \({X}\) sequence leads the \({Y}\) sequence by \(\tau\) time units. When, \(\tau<0\) it indicates that the \({X}\) sequence lags behind the \({Y}\) sequence by \(\mid\tau\mid\) time units. When \(\tau=0\) the two sequences are synchronous. If \(\gamma \left( \tau \right)\) is positive, it indicates that when \({X}\) (at a lag of \(\tau\)) is greater than its mean, \({Y}\) (at the current moment) is also greater than its mean, and vice versa. If \(\gamma \left( \tau \right)\) is negative, it indicates that the two variables are inversely related at the given lag.

In this study, the sequences were detrended, deseasonalized, and otherwise pre-processed to minimize the interference of strong seasonal cycles and long-term trends on the correlation and lag analysis.

SIE estimation method

The threshold of 15% SIC is widely adopted by leading sea ice research communities and data providers—such as the National Snow and Ice Data Center (NSIDC)—to define the presence of sea ice in a given pixel. This threshold stems from earlier global assessments aiming to establish a common standard that balances detection accuracy and noise reduction. However, it is important to note that some scholars, both domestically and internationally, have employed alternative cutoffs (20% or 30%) based on regional study objectives, sensor-specific characteristics, or algorithmic considerations.

In this study, we followed the commonly used 15% threshold to ensure consistency with internationally recognized datasets and facilitate comparisons with previous research on the Weddell Sea. The sea ice extent (SIE) was thus estimated by summing the SIC of each pixel exceeding the 15% threshold and multiplying by the respective pixel area (Eq. 7)70. Specifically:

$${\text{S}} = \mathop \sum \limits_{{{\text{i = 1}}}}^{{\text{n}}} {\text{Ci}} \times {\text{R}}^{2}$$
(7)

where S is the SIE, \(\:{\text{C}}_{\text{i}}\) is the SIC of the pixel (SIC > 15%), R is the spatial resolution of the image, and n is the number of pixels in the image.

NHF calculation method

The NHF is determined by the LH, the SH, the LW, and the SW. The NHF over the ocean surface (\(\:{Q}_{net}\)) is expressed as follows71:

$$\:{Q}_{net}={Q}_{LH}{+{Q}_{SH}+Q}_{LW}+{Q}_{SH}\:\:$$
(8)

where \(\:{\text{Q}}_{\text{n}\text{e}\text{t}}\) is the NHF, \(\:{\text{Q}}_{\text{L}\text{H}}\) is the LH flux, \(\:{\text{Q}}_{\text{S}\text{H}}\) is the SH flux, \(\:{\text{Q}}_{\text{L}\text{W}}\) is the LW, and \(\:{\text{Q}}_{\text{S}\text{W}}\) is the SW. \(\:{\text{Q}}_{\text{n}\text{e}\text{t}}\) is the NHF.

GTWR

The GTWR model can address spatial and temporal variations in sea ice data. Sea ice dynamics are influenced by highly localized environmental factors (such as ocean currents and wind directions) as well as broader temporal factors (such as seasonal cycles and long-term climate trends). Traditional regression methods often assume global stationarity, making them unable to capture these localized and dynamic interactions. In contrast, GTWR incorporates spatial and temporal weights, allowing the model to adapt to local variations in data distribution across space and time. This makes it particularly well-suited for sea ice analysis, where the spatiotemporal processes are inherently non-stationary and exhibit complex interdependencies.

The GTWR model is a localized linear regression model that reflects the spatiotemporal non-stationarity characteristics of research data by estimating parameters that vary across space and time. This model calculates the spatiotemporal weighting matrix by incorporating spatial and temporal coordinates into the model. Spatiotemporal non-stationarity implies that the parameters describing the spatiotemporal relationships change over time and space. The GTWR model used in this study to assess the impact of various environmental factors on sea ice concentration in the Weddell Sea is based on the following equation27:

$${Y_i}={\beta _0}\left( {{u_i},{v_i},{t_i}} \right)+\sum\limits_{k} {{\beta _k}\left( {{u_i},{v_i},{t_i}} \right)} {X_{ik}}+{\varepsilon _i}$$
(9)

Where \({Y_i}\) is the dependent variable of the \({i^{th}}\) sample point; \({X_{ik}}\) is the \({k^{th}}\) independent variable of the \({i^{th}}\) sample point; \({\varepsilon _i}\) is the random error; \({u_i}\) is the longitude coordinate of the \({i^{th}}\) sample point; \({v_i}\) is the latitude coordinate of the \({i^{th}}\) sample point; \({t_i}\) is the time coordinate of the \({i^{th}}\) sample point; \(\left( {{u_i},{v_i},{t_i}} \right)\) is the spatio-temporal dimension coordinates of the \({i^{th}}\) sample point; \({\beta _0}\left( {{u_i},{v_i},{t_i}} \right)\) is the constant term of the \({i^{th}}\) sample point; and \({\beta _k}\left( {{u_i},{v_i},{t_i}} \right)\) is the regression coefficient of the \({k^{th}}\) independent variable at the \({i^{th}}\)sample point, with the least squares estimation as follows72:

$${\widehat {\beta }_k}\left( {{u_i},{v_i},{t_i}} \right){\left[ {{X^T}W\left( {{u_i},{v_i},{t_i}} \right)X} \right]^{ - 1}}{X^T}W\left( {{u_i},{v_i},{t_i}} \right)Y$$
(10)

Where \(W\left( {{u_i},{v_i},{t_i}} \right)\)is ​​ the spatiotemporal weight matrix, which is the attenuation function of the spatiotemporal distance and is calculated by the following formula73:

$${W_{ij}}=\exp \left[ { - \frac{{{{\left( {d_{{ij}}^{{ST}}} \right)}^2}}}{{{h^2}}}} \right]$$
(11)

Where \({h}\) is a non-negative parameter, called the spatiotemporal bandwidth, which represents the spatiotemporal range of the sampling point. We select the spatiotemporal bandwidth corresponding to the minimum second-order corrected Akaike information criterion (AICc) value as the optimal spatiotemporal bandwidth. The spatiotemporal distance \({d^{ST}}\) is calculated as follows:

$${d^{ST}}=\sqrt {\lambda \left[ {{{\left( {{u_i} - {u_j}} \right)}^2}+{{\left( {{v_i} - {v_j}} \right)}^2}} \right]+\mu {{\left( {{t_i} - {t_j}} \right)}^2}}$$
(12)

where \({\left( {{u_i} - {u_j}} \right)^2}+{\left( {{v_i} - {v_j}} \right)^2}\) is the spatial distance between sample points \({i}\) and \({j}\) ; \({\left( {{t_i} - {t_j}} \right)^2}\) is the temporal distance between sample points \({i}\) and \({j}\) ; \(\lambda\) and \(\mu\) are the scaling factors of spatial distance and temporal distance, respectively.