Exploration of stagnation-point flow of Reiner–Rivlin fluid originating from the stretched cylinder for the transmission of the energy and matter

Abstract

This research focuses on non-Newtonian stagnation-bioconvective point flow near a stretched cylinder along the Reiner–Rivlin model. The study incorporates thermal and mass transfers, considering thermodynamic diffusion, bioconvection, and viscous heating. Entropy production analysis is included to assess the inherent uncertainty in transport processes. The computational framework is developed under prescribed wall temperature and concentration conditions, which are essential for achieving self-similar solutions. Numerical findings are collected using MATLAB’s “bvp4c” technique. The numerical outcomes are validated by comparing them with solutions for specific parameter values. The impact of curvature on boundary layer behavior is investigated for a range of governing parameters. For Reiner–Rivlin fluids, the skin friction coefficient is calculated to determine the force exerted by the straining cylinder. Additionally, a rise in the Reiner–Rivlin fluid factor causes a reduction in the surface cooling rate. Mainly the flow patterns observed by considering the quantity of parameters as $2.0 < Q < 3.5$, $1.2 < A < 1.5$, $0.5 < M < 0.8$, $0.2 < S < 0.8$, $0.1 < Nc < 0.4$, $0.1 < Nr < 0.7$, $7.5 < \Pr < 8.5$, $0.5 < \beta < 0.8$ on all profiles.

Introduction

Chamkha¹ examined an electrically conducting fluid’s steady, laminar flow near a porous body with heat generation/absorption. The impact of a magnetic field on the flow and heat transfer characteristics is investigated, and the results are presented graphically for various physical parameters. A nanofluid is a liquid involving nanometer-sized particles that are introduced for heat and mass transfer problems. Unsteady mixed convection flow near a vertical surface is analyzed under the influence of a time-varying free stream. Results demonstrate that a decelerating flow can induce flow reversal, a phenomenon mitigated by a magnetic field. The study further reveals that the magnetic field enhances heat transfer and primary flow shear while concurrently diminishing secondary flow shear stress by Nath et al.². Nabwey et al.³ investigated MHD conjugate forced and free convection of a Casson nanofluid flowing around a rotating sphere with convective boundary conditions. The impact of various physical parameters on the flow, heat transfer, and entropy generation is analyzed numerically, and the results are compared with existing literature. Mahdy et al.⁴ analyzed homogeneous and heterogeneous chemical reactions near a stagnation region on a rotating sphere in a nanofluid with Copper and Ferro nanoparticles. They used numerical methods and explored the effects of nanoparticles on velocity, temperature, and concentration profiles, along with skin friction and heat transfer rates. Baig et al.⁵ analytically examine the interplay effects between stagnation flow and stretching flow over a heated cylinder with multi-wall carbon nanoparticles in water, highlighting the dominance of stagnation flow under high oncoming pressure and lower stretching velocity through graphical heat transport analysis and flow visualization.

Sharma et al.⁶ studied the heat transfers in MHD nanofluid blood flow through a stenosed composite artery, optimized using response surface methodology (RSM), which analyzed the effects of physical parameters like magnetic field, and hematocrit on velocity, temperature, shear stress, and Nusselt number. They studied relevant biomedical applications and also explored artery abnormalities using magnetic resonance angiography (MRA). Khanduri et al.⁷ analyzed the effects of key parameters on blood flow with Al₂O₃ nanoparticles through constricted arteries under stenosis, thrombosis, and catheter influence. They used a mathematical model and Crank–Nicolson scheme, and the results provided insights into hemodynamics, aiding biomedical applications like magnetic resonance angiography (MRA). Mahabaleshwar et al.⁸ explored the axisymmetric stagnation point flow of Casson nanofluid with ${\text{Fe}}_{3} {\text{O}}_{4}$ nanoparticles on a stretchable plate or cylinder, focusing on thermal radiation, suction/injection, and how influences the flow, thermal transport, and applications in conductive nanomaterials for various industries. Ahmed⁹ studied numerically analyzing the stagnation-point flow and thermal transmission in the Maxwell fluid over a shrinking/stretching horizontal cylinder, revealing dual solution behaviors influenced by the stretching/shrinking parameter. Khan and Mahmood¹⁰ investigated the impact of mass suction and magnetic field on heat transmission in a polymer-based ternary dual phase nanofluid pass on a shrinking/stretching cylinder, finding that increased nanoparticle concentration enhances skin friction and heat transport, verified by comparison along existing studies. Kumar et al.¹¹ investigated the sensitivity analysis of Jeffrey fluid flow with copper nanoparticles in a polyvinyl alcohol-water base, influenced by factors like Joule heating, viscous dissipation, and Arrhenius activation energy. They used numerical methods and response surface methodology, and the effects of key parameters on drag coefficient, Nusselt number, and thermal transport were analyzed, highlighting applications in energy, electronics, and nano-drug delivery. Reddy et al.¹² examined entropy generation in MHD Williamson nanofluid flow over a stretching sheet, incorporating various heat and mass transfer effects. Numerical solutions highlight parameter impacts on flow, thermal fields, and entropy generation, offering insights for engineering and biomedical applications. Singh et al.¹³ investigated how nanoparticle shape and volume fraction in a ${\text{TiO}}_{2} - {\text{Al}}_{2} {\text{O}}_{3} - {\text{MoS}}_{{_{2} }} /$ kerosene oil ternary hybrid nanofluid impact heat transfer and drag reduction around a sinusoidal cylinder, revealing enhanced thermal performance and efficiency. Elattar et al.¹⁴. investigated the advanced thermal transport for a vertically oriented cylinder using a ternary hybrid nanofluid which shows enhanced temperature and reduced velocity compared to traditional nanofluids, with nonlinear solar thermal radiations further boosting thermal performance. Reddy et al.¹⁵ investigated entropy generation, energy, and mass transfer in the MHD flow of Carreau–Yasuda nanofluid over a porous stretching sheet, considering activation energy and chemical reactions. Numerical results highlight parameter effects on flow characteristics, with key insights for optimizing nanoparticle concentration and entropy generation. Moatimid et al.¹⁶. explored the energy and mass transfer of a non-Newtonian nanofluid around a rotating, stretchable disc under the influence of Stefan blowing, thermophoresis, and magnetic flux, showing enhanced nanoparticle diffusion and heat transfer, with potential applications in medical therapies. Nasir et al.¹⁷ analyzed Reiner–Rivlin nanofluid flow over a reactive stretched sheet, finding that cross-viscous and radiative effects significantly impact velocity, temperature, and concentration, with implications for nanofluid applications in thermal management. Khan et al.¹⁸ explored thermal and matter transmission incorporated with convection Reiner–Rivlin fluid flow around a stretching cylinder, showing that thermal relaxation, thermal conductivity, and solutal relaxation significantly influence temperature, velocity, and concentration profiles. Yasin et al.¹⁹ examined magneto hydrodynamic Reiner–Rivlin fluid peristalsis in a cylindrical porous tube, highlighting how parameters like the Hartman number, Hall current, and slip influence velocity, temperature, and concentration, with applications for modeling blood flow in arteries under electromagnetic effects. Khan et al.²⁰ investigated thermal bioconvection in magnetized Reiner–Rivlin nanofluids, showing how parameters like the Reiner–Rivlin constant, Peclet number, and external heating affect heat transfer, concentration, and microorganism distribution for improved stability in nanofluid applications. Dashes and Singh²¹ developed and compared perturbation and analytical solutions for axisymmetric Navier–Stokes equations in stenosed arteries, finding that the Reiner–Rivlin model closely simulates blood flow characteristics, especially in comparison with the Power Law model. Nebiyal et al.²² analyzed the flow entropy optimization in Reiner–Rivlin nanofluid originating a revolving disk, solving nonlinear equations with the Homotopy Analysis Method, and examining the impression of distinct factors on velocity, temperature, concentration, and entropy. Sadighi et al.²³ examined the energy and mass transmission in a nanofluid flow with an inclined magnetic field, showing how parameters like curvature, nanoparticle volume, and chemical reactions impact skin friction, velocity, and concentration profiles. Pasha et al.²⁴ employed the Finite Element Method to simulate thermal and mass transportation in Casson nanofluid through the cylinder, showing that the magnetic parameter reduces drag and lift, while concentration peaks at the channel center and decreases toward the walls. Yu et al.²⁵ investigated the impact of the buoyancy flux, Prandtl number, and surface curvature through the heated vertical cylinder. Bilal et al.²⁶ examined non-Newtonian nanofluid passes through a magnetized shrinking/expanding cylinder, incorporating effects of slip mechanisms and thermal radiation, and found that higher Weissenberg numbers decrease fluid speed for expanding cylinders while increasing it for contracting cylinders. Afzal et al.²⁷ explored the models of Dual-phase nanofluid through two rotating disks, exploring various nanoparticle shapes for entropy optimization in medical applications, finding that fluid velocity decreases with increasing unsteady parameters and Darcy number, at the same time the temperature is highest with brick-shaped nanoparticles and entropy is minimized with spherical nanoparticles. Najib and Bachok²⁸ investigated the influence of cylinder shrinkage on viscous fluid flow and heat transfer, revealing dual solutions with stability in the upper branch, showing that increased mass suction enhances the duality of the cylinder surface and diminishes skin friction and heat transfer rates. Abdel-Wahed and El-Said²⁹ investigated thermal transport in a moving cylinder within a nanoparticle-laden cooling medium, analyzing the effects of heat generation, convective constraints, Brownian migrations, and thermophoresis over the flow and transmission rates using an analytical approach. Islam et al.³⁰ numerically analyzed heat transport and flow-induced vibration in heated cylinders with varying diameters, revealing that closer spacing reduces oscillations, and increased spacing enhances vortex shedding and thermal transfer, particularly with uniform diameters at higher spacings. Shah and van der Heijden³¹ investigated and presented an elastic rod’s geometrically exact theory strained over a cylindrical surface, examining static friction models and buckling behavior under compression and torsion, with applications in engineering and medical fields.

Castro et al.³² connected a deformable main cylinder with holes to attached cylinders, but testing revealed occasional misalignment despite a flexible connecting geometry. Belhaou et al.³³ deeply studied an analytical solution of stress distribution originating in functionally graded cylinder under internal pressure is presented, validated by finite-element simulations, accounting for elastic, elastoplastic, and post-collapse behavior influenced by radial variations in material properties. Cham and Mustafa³⁴ analyzed the effects of viscoelasticity, electrical conductivity, and partial slip, over axial fluid flow with nonlinear boundary conditions, providing numerical solutions for momentum and heat transfer rates across varying parameters. Becks et al.³⁵ studied the uses of Reynolds-averaged Navier–Stokes simulations to investigate how upstream surface distortions on a cylinder affect the supersonic turbulent flow, revealing that these distortions can significantly decrease peak pressure and heat flux loads while altering corner separation length. Wu and Li³⁶ proposed a simulation device for deep-sea pressure along a pair of hydraulic cylinders, emphasizing the need to account for fluid compression and the cylinder’s distortion along sealed pressure when measuring small pressure changes in deep-sea environments. Robin et al.³⁷. presented numerical studies of laminar flow along mixed convection in a quadruple medium along two rotating hot cylinders, revealing that peak heat transmission and lessened entropy exist while the rotated cylinders are in opposing directions, while smaller cylinder sizes and decreased gap ratios enhance thermal performance. Malik et al.³⁸ investigated the viscous incompressible, steady flow of nanofluid across a whirling, stretchable permeable cylinder under a radial magnetic field, utilizing similarity transformations and MATLAB’s bvp4c to derive impression for various factors, revealing that increased magnetic and permeability parameters reduce velocity due to resistance. Saboj et al.³⁹ investigated buoyancy-driven natural convection heat transfer in a heptagonal cavity with a lukewarm cylinder, revealing that the presence of the cylinder enhances heat transfer rates, particularly in nanofluid, and that employing heat flux conditions improves Nusselt and Bejan numbers compared to isothermal conditions. Chokoe et al.⁴⁰ investigated the entropy dissipation rate in nanofluid unsteady flow across a cylindrical permeable surface with variable viscosity, finding that increasing volume fraction of nanoparticles, enlarges Nusselt number, skin friction, Bejan number, and entropy production. Rooman et al.⁴¹ examined entropy formation in the flow of Ellis nanofluid over a stretched permeable cylinder, focusing on heat transmission effects from magnetic fields, thermal radiation, and Joule heating, and analyzing velocity, temperature, and concentration profiles. Ali and Rahman⁴² investigated statistical analysis to explore the impacts of periodic MHD, heat radiation, and Casson nanofluids over entropy generation in chemical reactions over a sloping cylinder, revealing the periodic MHD reduces entropy creation against non-periodic Magnetohydrodynamics and that Casson fluids generate more entropy than Newtonian fluids. Ahmad et al.⁴³ numerically examine the axisymmetric mixed convective flow and entropy generation of hybrid nanofluid around a rotating, vertically stretching cylinder, incorporating the joule heating, Cattaneo-Christov theory, magnetic effects, and convective boundary conditions. Rezaee and Houshmand⁴⁴ presented a MATLAB-based approximation solution for 2D flow across a cylinder, employing the Runge–Kutta method, with results validated against analytical solutions. Yasmin et al.⁴⁵ numerically analyzed the flow of fluid with gyrotactic microorganisms, thermal, and mass transmission around an inclined stretchable cylinder, using bvp4c to solve transformed ODEs and examining the impacts of parameters on momentum, temperature, and microbial density. Najib and Bachok⁴⁶ analyzed the heat transfer and viscous fluid flow across a shrinking cylinder, examining the effects of curvature and mass suction parameters over dual solution stability, skin friction, and temperature profiles, with numerical results validating the stable upper branch solution. Nguyen et al.⁴⁷ studied the flow characteristics around rough and smooth circular cylinders, highlighting the influence of Reynolds number, disturbances, and three-dimensional effects relevant to structural design. Nikarya⁴⁸ analyzed the impact of blowing/injection and suction on mixed convective boundary layer flows over a vertical cylinder, using a spectral collocation method along Bessel functions and comparing results through the shooting method for validation. Gintrand and Moreno-Gelos⁴⁹ investigated the dynamics of magnetized blast waves from massive stars under azimuthal and axial magnetic fields, revealing differences in shock propagation and shell formation influenced by magnetic strength and field orientation. Takabe⁵⁰ deeply studied the self-similar analytical solutions for shock wave trajectories in spherical compression, highlighting applications in laser-driven implosions and supernova remnants, with transitions between Chevalier and Sedov–Taylor solutions. Lakshminarayana et al.⁵¹ examined the diffusion, heat source effects, and entropy generation in the flow of Casson and Maxwell nanofluids over a porous stretching sheet, considering viscous dissipation and thermal radiation. Numerical results reveal parameter impacts on flow, temperature, and concentration, offering insights for thermal energy applications like solar exchangers. Nath⁵² investigated models of impulsive wave propagation with a gravitating mixture of van der Waals gas and inert metal particles in a revolving medium, revealing how flow conditions and parameter variations affect shock strength and compressibility in both adiabatic and isothermal scenarios. Kirsur and Joshi⁵³ presented exact analytical solutions of the Falkner–Skan equation along heat transport, extending existing closed-form solutions to include multiple outcomes for momentum and temperature equations while validating results against numerical solutions for various pressure gradients and Prandtl numbers. Gad and Jedani⁵⁴ investigated a Bianchi type-III cosmological model along similarity transformations, revealing new exact solutions to Einstein’s field equations and discussing the kinematic and physical properties related to the homothetic vector field’s relationship with fluid elements and cosmic strings.

Tlili et al.⁵⁵ examined the thermal effects of cross-nanofluid flow on a stretchable cylinder, considering radiative energy transport, activation energy, viscous dissipation, and bioconvection, with findings obtained through numerical simulations. Khan et al.⁵⁶ analyzed mass and energy transmission in Maxwell nanofluid flow across a rotating, porous cylinder under magnetic, thermophoretic, and Brownian motion effects, using the homotopy analysis method to assess the impression of various parameters on fluid flow and microorganism density. Awwad et al.⁵⁷ examined nonlinear thermal transport in non-Newtonian polymer flows over a cylindrical surface, incorporating bioconvection, magnetic field effects, thermophoresis, and Brownian diffusion, with numerical exploration of mass and heat transport, surface drag, and the impact of governing parameters. Rashad and Mansour⁵⁸ deeply studied flow across a radiative vertical permeable cylinder along gyrotactic microorganisms, and nanoparticles examining the effects of Brownian motion, thermophoresis, and radiative heat flux while analyzing velocity, temperature, microorganism concentration, and heat/mass transfer for engineering applications in power generation and mechanical energy. Basit et al.⁵⁹ investigated the flow of Casson nanofluid in a conical gap, considering factors like microorganisms, thermal radiation, and magnetic fields. They used MATLAB’s bvp4c, the numerical results show how the rotation of the disc and cone affects the temperature, velocity, and transfer rates of the nanofluid. Basit et al.⁶⁰ examined the effects of motile microorganisms, activation energy, and thermal radiation on heat and mass transfer in Carreau nanofluid flow over an inclined stretchable cylinder. They used MATLAB’s bvp4c, numerical results highlighting parameter influences on velocity, thermal profile, nanoparticle concentration, and microorganism density, with insights for engineering and nanotechnology applications. Nima and Ferdows⁶¹ developed a mathematical model of flow along a bioconvection, and a vertical cylinder with a permeable channel, incorporating nanofluid effects, Brownian motion, thermophoresis, and gyrotactic microorganisms, with a focus on the impacts of key flow parameters on temperature, velocity, microorganism concentration, and heat/mass transfer, for applications in power generation and mechanical energy systems. Galal et al.⁶² analyzed the effects of activation energy, thermal radiation, magnetic fields, and slip conditions on bioconvective Casson nanofluid flow over a stretching cylinder. Numerical results, obtained by using MATLAB, highlight parameter influences on velocity, temperature, concentration, and motile microorganism density, offering novel insights into fluid dynamics.

The research gap is: the stagnation-point flow over a cylindrical exterior in a Reiner–Rivlin fluid, considering mass and thermal transfer, frictional heating, Soret effect, heat source/sink, Bio-convection, viscous dissipation, and ohmic heating, has not been previously investigated. This topic holds significant practical implications, as discussed earlier.

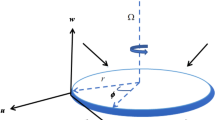
The numerical simulations, implemented using MATLAB’s “bvp4c” platform, explore the variation of similarity profiles under different governing parameters. The study highlights the influence of non-Newtonian behavior on crucial factors such as disk cooling rate, resistive torque, and volume flow rate. Streamline and isotherm visualizations enhance the presentation of the results. The organization of the nanofluid and its applications are shown in Figs. 1, 2 and 3.

Fig. 1

Real-life applications of the stagnation bioconvective nanofluids.

Fig. 2

Magnetized nanofluids.

Fig. 3

Thermal radiation applications.

Mathematical interpretation

A Reiner–Rivlin fluid stagnation-bioconvective point flow moving toward a cylindrical porous, stretchable surface along a linear speed $u_{s} \left( x \right) = u_{0} {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}},$ where $u_{0}$ and $L$ represent characteristic velocity, and the reference values for characteristic length, respectively. Suppose that the $x$- component of the distant field velocity is $u_{e} \left( x \right) = u_{1} {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}},$ where $u_{1}$ is a constant.

Assume that the surface concentration, denoted by $C_{s} \left( x \right),$ and the temperature on the cylindrical wall, expressed by $T_{s} \left( x \right),$ belongs to the following categories: $T_{s} \left( x \right) = T_{\infty } + T_{0} \left( {{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)^{2}$ and $C_{s} \left( x \right) = C_{\infty } + C_{0} \left( {{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)^{2}$ Where $T_{0}$ and $C_{0}$ are positive constants and $T_{\infty } ,$$C_{\infty }$ are the values of the ambient temperature and concentration. In order to guarantee a self-similar solution to the issue, the formulas $T_{s} \left( x \right)$ and $C_{s} \left( x \right)$ are particularly used.

As shown in Fig. 4, consider the axial coordinate $\left( x \right)$ is aligned parallel to the axis of the cylinder and normal to it along the radial coordinate $\left( r \right)$. Additionally,$\left( {u,v} \right)$ stand for the velocity projections towards $\left( {x,r} \right)$.

Fig. 4

Geometrical Configuration.

Tensor for inelastic fluids is:

$$\tau_{ij} = - p\partial_{ij} + \mu e_{ij} + \mu_{c} e_{ik} e_{kj} ,e_{ij} = \frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }},e_{jj} = 0,$$

(1)

The deformation rate tensor, Kronecker delta, coefficient of dynamic viscosity, pressure, and cross-viscosity coefficient, are denoted as $e_{ij} ,\partial_{ij} ,\mu ,p$ and $\mu_{c}$, respectively.

The stress tensor Eq. (1) can be used to generate the transport equations under the boundary layer assumptions⁶³:

$$\frac{\partial }{\partial x}\left( {ur} \right) + \frac{\partial }{\partial r}\left( {vr} \right) = 0,$$

(2)

$$\begin{gathered} \frac{\partial u}{{\partial x}}u + \frac{\partial u}{{\partial r}}v = \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{\partial u}{{\partial r}}\frac{1}{r}} \right)\vartheta + 2\frac{{\mu_{c} }}{\rho }\left\{ {\left( {\frac{\partial v}{{\partial r}} + \frac{\partial u}{{\partial x}}} \right)\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{\partial u}{{\partial r}}\frac{1}{r}} \right) + \left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + 2\frac{{\partial^{2} u}}{\partial x\partial r}} \right)\frac{\partial u}{{\partial r}}} \right\} \hfill \\ + \left( {u_{e} - u} \right)\frac{\sigma }{\rho }B_{0}^{2} + \frac{{du_{e} }}{dx}u_{e} - \frac{1}{{\rho_{f} }}g\left[ {\left( {1 - C_{f} } \right)\rho_{f} \beta^{*} \left( {T - T_{\infty } } \right) - \left( {C - C_{\infty } } \right)\left( {\rho_{p} - \rho_{f} } \right) - \left( {\rho_{m} - \rho_{f} } \right)\left( {n - n_{\infty } } \right)\gamma } \right], \hfill \\ \end{gathered}$$

(3)

$$\begin{gathered} v\frac{\partial T}{{\partial r}} + \frac{\partial T}{{\partial x}}u = \left( {\frac{\partial T}{{\partial r}}\frac{1}{r} + \frac{{\partial^{2} T}}{{\partial r^{2} }}} \right)\frac{{D_{T} }}{{c_{\rho } \rho }} + \left( {\frac{\partial u}{{\partial r}}} \right)^{2} \frac{1}{{c_{\rho } \rho }}\left\{ {\mu + \left( {\frac{\partial v}{{\partial r}} + \frac{\partial u}{{\partial x}}} \right)3\mu_{0} } \right\} \hfill \\ + \frac{1}{{c_{\rho } \rho }}\left( {\left( {u_{e} - u} \right)^{2} B_{0}^{2} \sigma + Q_{0} \left( {T - T_{\infty } } \right)} \right), \hfill \\ \end{gathered}$$

(4)

$$\begin{gathered} \frac{\partial C}{{\partial r}}v + \frac{\partial C}{{\partial x}}u = D\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{\partial C}{{\partial r}}\frac{1}{r}} \right) + \frac{{k_{T} D}}{{T_{m} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{\partial T}{{\partial r}}\frac{1}{r}} \right) - K_{0} \left( {C - C_{\infty } } \right)\exp \left( { - \frac{{E_{a} }}{kT}} \right), \hfill \\ \, \hfill \\ \end{gathered}$$

(5)

$$u\frac{\partial n}{{\partial x}} + v\frac{\partial n}{{\partial r}} = { - }\frac{{bW_{c} }}{{\left( {C_{w} - C_{\infty } } \right)}}\left[ {\frac{ \, \partial }{{\partial r}}\left( {n\frac{\partial C}{{\partial r}} \, } \right)} \right] + \, D_{m} \frac{\partial }{\partial r}\left( {\frac{\partial n}{{\partial r}}} \right).$$

(6)

where $\mu_{c}$ denotes the cross-viscosity coefficient and $\vartheta = {\raise0.7ex\hbox{$\mu $} \!\mathord{\left/ {\vphantom {\mu \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}$ represents the kinematic viscosity, where $\mu$ and $\rho$ are the fluid density and dynamic viscosity, respectively. The species’ diffusion coefficient is called $D$, the reaction rate and the heat source coefficient are called $K_{0}$ and $Q_{0}$, the electrical conductivity $\sigma$, activation energy coefficient is represented by $E_{a}$, $\exp \left( {\frac{{E_{a} }}{kT}} \right)$ is modified Arrhenius function, and magnetic field intensity is $B_{0}$, and the specific heat capacity is represented by $c_{\rho }$, $D_{T}$ be the thermal conductivity, $k_{T}$ stands for thermal diffusion ratio,$n$ denotes the concentration of the microorganisms, $n_{\infty }$ be the upstream concentrations of the microbes, $D_{m}$ is microorganism diffusion coefficient, and $W_{c}$ is the maximum cell swimming speed.

Here, we introduce the terms in the velocity that represent the contributions of the pressure gradient and magnetic force. The last terms in the energy equation represent the Joule heating and heat source/sink effects. Furthermore, the concentration equation incorporates novel elements: chemically reactive species, activation energy, and the Soret effect. Lastly, the microbial density equation represents the microbial cell speed and microbe’s diffusivity.

The permeability and no-slip assumptions impose the following boundary conditions:

$$\begin{gathered} r = R:u = \frac{{u_{0} x}}{L},v = - v_{0} ,T = T_{\infty } + T_{0} \left( \frac{x}{L} \right)^{2} ,C = C_{\infty } + C_{0} \left( \frac{x}{L} \right)^{2} ,n = n_{\infty } + n_{0} \left( \frac{x}{L} \right)^{2} , \hfill \\ r \to \infty :u \to u_{e} \left( x \right)\frac{{u_{1} x}}{L},T \to T_{\infty }^{2} ,C \to C_{\infty } ,n \to n_{\infty } . \hfill \\ \end{gathered}$$

(7)

The cylinder’s axial stretch in its plane along linearly increasing velocity assumes no wall slide, and the cylindrical surface’s constant suction velocity is taken into account, Variations in surface temperature, microbial density, and concentrations assume no thermal and concentration slip, which are represented in the Eq. (7).

The answers to Eqs. (3–6) with boundary constraint Eq. (7) are handled employing the similarity transformations Eq. (8).

$$\begin{gathered} \eta = \frac{{r^{2} - R^{2} }}{2R}\sqrt {\frac{{u_{0} }}{L\vartheta }} ,u = \frac{{u_{0} x}}{L}f^{\prime}\left( \eta \right),v = - \frac{R}{r}\sqrt {\frac{{\vartheta u_{0} }}{L}} f\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{S} - T_{\infty } }}, \hfill \\ \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{s} - C_{\infty } }},\chi \left( \eta \right) = \frac{{n - n_{\infty } }}{{n_{s} - n_{\infty } }}. \hfill \\ \end{gathered}$$

(8)

With the similarity variable. The prescribed Eqs. (3–6) are transformed into the following forms:

$$\begin{gathered} \left( {1 + 2\eta M} \right)f^{\prime \prime \prime } + 2Mf^{\prime \prime } + ff^{\prime \prime } - f^{\prime 2} + \left( {A - f^{\prime } } \right)Ha^{2} + A^{2} \hfill \\ + \alpha \left( {\theta - Nr\phi - Nc\chi } \right) + 2\beta \left\{ {f^{\prime \prime 2} \left( {1 + 2M\eta } \right) + f^{\prime } f^{\prime \prime } M + Mf^{\prime \prime \prime } f} \right\} = 0, \hfill \\ \end{gathered}$$

(9)

$$\begin{gathered} \theta^{\prime \prime } \left( {1 + 2M\eta } \right) + 2M\theta^{\prime } + \left( {f^{\prime \prime 2} \left( {1 + 2M\eta } \right) + 3\beta ff^{\prime \prime 2} M} \right)EcPr \hfill \\ + \Pr \left( {f\theta^{\prime } - 2f^{\prime } \theta + \left( {A - f^{\prime } } \right)^{2} Ha^{2} Ec + Q\theta } \right) = 0, \hfill \\ \end{gathered}$$

(10)

$$\begin{gathered} \phi^{\prime \prime } \left( {1 + 2M\eta } \right) + 2\phi^{\prime } M + ScSr\left\{ {\theta^{\prime \prime } \left( {1 + 2M\eta } \right) + 2\theta^{\prime } M} \right\} \hfill \\ - Sck\phi \exp \left( { - \frac{E}{{\left( {1 + \delta_{0} \theta } \right)}}} \right) + Sc\left( {f\phi^{\prime } - 2f^{\prime } \phi } \right) = 0, \hfill \\ \end{gathered}$$

(11)

$$\chi^{\prime \prime } \left( {1 + 2M\eta } \right) + Lb\chi^{\prime } M - Pe\left( {\phi^{\prime } \chi^{\prime } + \phi^{\prime \prime } \chi { + }\sigma \phi^{\prime \prime } } \right) = 0.$$

(12)

Altered boundary constraints are:

$$\begin{gathered} \eta = 0:f\left( \eta \right) = S,f^{\prime } \left( \eta \right) = 1,\theta \left( \eta \right) = 1,\phi \left( \eta \right) = 1,\chi \left( \eta \right) = 1, \hfill \\ \eta \to \infty : \, f^{\prime } \left( \eta \right) = A,f^{\prime \prime } \left( \eta \right) = 0,\theta \left( \eta \right) = 0,\phi \left( \eta \right) = 0,\chi \left( \eta \right) = 0. \hfill \\ \end{gathered}$$

(13)

The following parameters are part of the equations above: bioconvective Lewis $\left( {Lb} \right)$ Eckert $\left( {Ec} \right)$, Schmidt $\left( {Sc} \right)$, Prandtl $\left( {Pr} \right)$, Soret $\left( {Sr} \right)$, Peclet $\left( {Pe} \right)$ numbers, heat generation parameter $\left( Q \right)$, curvature parameter $\left( M \right)$, magnetic interaction parameter $\left( {Ha} \right)$, Reiner–Rivlin fluid variable $\left( \beta \right)$, suction parameter $\left( S \right)$, velocity ratio parameter $\left( A \right)$, and chemical reaction parameter $\left( K \right)$. The following are the expressions of these in mathematics:

$$\begin{gathered} A = \frac{{u_{1} }}{{u_{0} }},S = v_{0} \sqrt {\frac{L}{{u_{0} \vartheta }}} ,M = \sqrt {\frac{L\vartheta }{{u_{0} R^{2} }}} ,Ha = \sqrt {\frac{{L\sigma B_{0}^{2} }}{{u_{0} \rho }},} \beta = \frac{{\mu_{c} u_{0} }}{\mu L},Ec = \frac{{u_{0}^{2} }}{{c_{\rho } T_{0} }},Pe = \frac{{W_{c} b}}{{D_{m} }}, \hfill \\ Pr = \frac{{c_{p} \mu }}{k},Sc = \frac{\vartheta }{{D_{m} }},Sr = \frac{{k_{t} D_{m} \left( {T_{s} - T_{\infty } } \right)}}{{\left( {C_{s} - C_{\infty } } \right)T_{m} v}},Q = \frac{{LQ_{0} }}{{c_{p} u_{0} \rho }},K = \frac{{LK_{0} }}{{u_{0} }},Lb = \frac{\vartheta }{{D_{m} }}. \hfill \\ \end{gathered}$$

(14)

Keep in mind that the surface of the cylindrical stretchable velocity exceeds the ambient stream velocity when $u_{0} > u_{1}$. Consequently $f^{\prime \prime } \left( 0 \right) < 0$ and decreasing the function of $\eta$ is $f^{\prime}$ which is the axial velocity curve. Since the upstream velocity is greater than the stretchable velocity when $u_{0} < u_{1}$,$f^{\prime \prime } \left( 0 \right) > 0$. Note that in a specific scenario where $\beta = A = S = Ec = Sr = 0,$ the governing systems (9–12) show precise solutions. For further information on such precise solutions. The following form is achieved via the skin friction factor $C_{f} = S_{xr} |_{r = R} /\rho u_{s}^{2}$ with the help of transformations:

$$Re_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} C_{f} = \left( {1 + 2\beta Mf\left( 0 \right)} \right)f^{\prime \prime } \left( 0 \right),$$

(15)

and the local Reynolds number is given by $Re_{x} = u_{s} {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x v}}\right.\kern-0pt} \!\lower0.7ex\hbox{$v$}}$.

Additionally, the local Sherwood number $Sh_{x} = - x\left( {\frac{\partial C}{{\partial r}}} \right)|_{r = R} /\left( {C_{s} - C_{\infty } } \right)$, local Nusselt number $Nu_{x} = - x\left( {\frac{\partial T}{{\partial r}}} \right)|_{r = R} /\left( {T_{s} - T_{\infty } } \right)$ and microbial diffusivity rate $Sn_{x} = - x\left( {\frac{\partial n}{{\partial r}}} \right)|_{r = R} /\left( {n_{s} - n_{\infty } } \right)$ provide the following results:

$$Re_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} Nu = - \theta^{\prime } \left( 0 \right),$$

(16)

$$Re_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} Sh = - \varphi^{\prime } \left( 0 \right),$$

(17)

$$Re_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} Sn = - \chi^{\prime } \left( 0 \right),$$

(18)

The irreversibility of thermal transmission, Joule heating, and viscous dissipation are used to define the entropy generation rate. The following is its mathematical expression.

Here, the entropy creation phenomena are examined without a mass transfer process for simplicity’s sake.

$$S_{G} = \left( {\frac{\partial T}{{\partial r}}} \right)^{2} \frac{k}{{T_{\infty }^{2} }} + \left( {\frac{\partial u}{{\partial r}}} \right)^{2} \frac{1}{{T_{\infty } }}\left\{ {\mu + \left( {\frac{\partial v}{{\partial r}} + \frac{\partial u}{{\partial x}}} \right)3\mu_{0} } \right\} + \left( {u_{e} - u} \right)^{2} \frac{{B_{0}^{2} \sigma }}{{T_{\infty } }},$$

(19)

The non-dimensionalized form of Eq. (19) is given below:

$$N_{G} \left( \eta \right) = \left( {1 + 2M\eta } \right)\theta^{\prime 2} \alpha + \left( {1 + 2M\eta } \right)f^{\prime \prime 2} Br + 3Br\beta ff^{\prime \prime 2} M + Br\left( {A - f^{\prime } } \right)^{2} Ha^{2} ,$$

(20)

the temperature difference parameter is denoted by $\alpha = \left( {T_{s} - T_{\infty } } \right)/T_{\infty }$, the entropy generation number is $N_{G} \left( \eta \right) = \left( {S_{G} T_{\infty } vL/ku_{0} \left( {T_{s} - T_{\infty } } \right)} \right)$ and $Br = \Pr Ec$ is expressed.

Bejan number

The ratio of irreversible thermal transmission to total heat transmission in the given system is known as the Bejan number. Analyzing the effectiveness of heat transmission requires it. While a low Bejan number signifies effective heat transfer, a high number suggests possible areas for development. The definition of the Bejan number $Be$ is as follows:

$$Be = \frac{Entropy \, generation \, owing \, to \, heat \, transfer}{{total \, Entropy \, generation}}$$

The nondimensionalized form of $Be$ is:

$$Be = \frac{{\alpha \left( {1 + 2M\eta } \right)\theta^{\prime 2} }}{{\left( {1 + 2M\eta } \right)\theta^{\prime 2} \alpha + \left( {1 + 2M\eta } \right)f^{\prime \prime 2} Br + 3Br\beta ff^{\prime \prime 2} M + Br\left( {A - f^{\prime } } \right)^{2} Ha^{2} }},$$

(21)

Numerical methodology

One of the well-known tools for assessing numerical solutions for various boundary value issues is MATLAB’s “bvp4c” tool. In addition to being dependable and effective, the “bvp4c” package has error control features that guarantee accurate and trustworthy numerical answers. The BVP4C numerical algorithm, while a powerful tool, exhibits several limitations. Primarily, it can be sensitive to the selection of boundary conditions. Inappropriate choices can lead to numerical instability or inaccurate solutions. Convergence issues are another concern. The algorithm may converge slowly or fail to converge entirely, particularly when dealing with certain problem types or when the initial guess is far from the true solution. BVP4C may also struggle with problems involving singularities, such as those with discontinuous coefficients or singularities within the solution. It’s important to note that BVP4C is specifically designed for ordinary differential equations, limiting its applicability to other types of differential equations. Furthermore, the computational cost can be significant, especially for high-dimensional systems or problems with complex geometries. The algorithm’s dependence on the quality of the initial guess is another consideration. Obtaining a good initial guess may require trial and error, with no guarantee of finding the global optimum. Lastly, BVP4C may not perform well with problems involving highly oscillatory or discontinuous solutions as it assumes smoothness in the solution space. Despite these limitations, BVP4C remains a valuable tool when used judiciously with careful problem formulation and appropriate numerical techniques.

The steps adopted for the solution are shown in Fig. 5. Using this package begins with reducing the provided system of higher-order equations to a first-order system, which is accomplished by the following substitutions:

$$f = Y_{1} ,f^{\prime } = Y_{2} ,f^{\prime \prime } = Y_{3} ,\theta = Y_{4} ,\theta^{\prime } = Y_{5} ,\varphi = Y_{6} ,\varphi^{\prime } = Y_{7} ,\chi = Y_{8} ,\chi^{\prime } = Y_{9} .$$

(22)

Fig. 5

Shows the flow chart of the numerical scheme.

Using Eqs. (9–12) are transformed to obtain the following equations:

$$Y_{3}^{\prime } = \frac{{2Y_{3} M + Y_{3} Y_{1} - Y_{2}^{2} + \left( {A - Y_{2} } \right)Ha^{2} + A^{2} + 2\beta \left( {1 + 2M\eta } \right)Y_{3}^{2} + 2\beta Y_{2} Y_{3} M}}{{\left( {1 + 2M\eta } \right) + 2\beta Y_{1} M}},$$

(23)

$$\begin{aligned} Y_{5}^{\prime } & = \frac{{2Y_{5} M + \left( {Y_{5} Y_{1} - 2Y_{4} Y_{2} + \left( {A - Y_{2} } \right)^{2} Ha^{2} Ec + Y_{4} Q} \right)\Pr }}{{\left( {1 + 2M\eta } \right)}} \\ & \quad + \frac{{\left\{ {\left( {1 + 2M\eta } \right)Y_{3}^{2} + 3\beta MY_{3}^{2} Y_{1} } \right\}Ec\Pr }}{{\left( {1 + 2M\eta } \right)}}, \\ \end{aligned}$$

(24)

$$Y_{7}^{\prime } = \frac{{2Y_{7} M + \left( {Y_{7} Y_{1} - 2Y_{6} Y_{2} - Y_{6} K} \right)Sc + \left( {\left( {1 + 2M\eta } \right)Y_{5}^{\prime } + 2MY_{5} } \right)ScSr}}{{\left( {1 + 2M\eta } \right)}},$$

(25)

$$Y_{9}^{\prime } = \left( {Pe\left( {Y_{7} Y_{9} + Y_{7}^{\prime } Y_{8} { + }\sigma Y_{7}^{\prime } } \right) - LbY_{9} M} \right)/\left( {1 + 2M\eta } \right).$$

$$\begin{gathered} \eta = 0:Y_{1} \left( \eta \right) = S,Y_{2} \left( \eta \right) = 1,Y_{4} \left( \eta \right) = 1,Y_{6} \left( \eta \right) = 1,Y_{8} \left( \eta \right) = 1, \hfill \\ \eta \to \infty :Y_{2} \to A,Y_{3} \to 0,Y_{4} \to 0,Y_{6} \to 0,Y_{8} \to 0. \hfill \\ \end{gathered}$$

(26)

Results and discussion

Impacts on velocity profile of the flow

In Figs. 6, 7, 8 and 9 the context of stagnation-bioconvective point flow interacting with a stretchable cylinder in a Reiner–Rivlin fluid, the enhancement in velocity with an increase in source/sink $\left( Q \right)$, velocity ratio $\left( A \right)$, curvature parameter $\left( M \right)$, and suction parameters $S$ can be attributed to intricate physical interactions. When heat sources are presented, they contribute additional energy, accelerating the fluid particles, whereas heat sinks remove energy, influencing the boundary layer characteristics and impacting velocity distribution. The velocity ratio parameter adjusts the relative motion between the free stream and the cylinder, directly affecting the local flow speed and momentum transfer. As the curvature parameter increased, stretching near the cylinder’s surface intensified, enhancing the shear rate. This results in a greater velocity gradient and increased fluid velocity due to the fluid’s non-Newtonian response to deformation. Lastly, the suction parameter decreases the boundary layer thickness, minimizing resistance near the surface and promoting a faster, more streamlined flow. Collectively, these factors interact to increase the velocity in a complex, interdependent manner within the fluid surrounding the deforming cylinder.

Fig. 6

Variations on $f^{\prime }$ due to $Q.$

Fig. 7

Variations on $f^{\prime }$ due to $A.$

Fig. 8

Variations on $f^{\prime }$ due to $M.$

Fig. 9

Variations on $f^{\prime }$ due to $S.$

In Figs. 10, 11, 12, 13 and 14 the scenario of stagnation-bioconvective point flow impacting a deformable cylinder within a Reiner–Rivlin fluid, an enhancement in the Rayleigh number $\left( {Nc} \right)$, buoyancy ratio $\left( {Nr} \right)$, Prandtl number $\left( {Pr} \right)$, Reiner–Rivlin fluid variables $\left( A \right)$, and magnetic interaction parameter $\left( {Ha} \right)$ leads to a downfall in the velocity due to various physical effects. The Rayleigh number represents the impact of buoyancy-driven flow, so a higher value intensifies the convective currents, which interfere with the forward flow momentum, resulting in a decreased velocity near the cylinder. Additionally, a higher buoyancy ratio parameter disrupts flow uniformity by altering the density gradients, contributing to resistance against fluid acceleration. An increased Prandtl number, which indicates a larger ratio of momentum to thermal diffusivity, restricts thermal diffusion, thereby thickening the thermal boundary layer and reducing flow velocity near the surface. The Reiner–Rivlin fluid variable, characterizing the fluid’s non-Newtonian properties, enhances resistance within the fluid due to higher deformation rates, thus dampening the flow. Finally, the magnetic interaction parameter introduces Lorentz forces, which resist the flow movement through magnetic drag, decreasing the fluid’s velocity. These parameters introduce combined effects that slow down the flow around the deforming cylinder.

Fig. 10

Variations on $f^{\prime }$ due to $Nc.$

Fig. 11

Variations on $f^{\prime }$ due to $Nr.$

Fig. 12

Variations on $f^{\prime }$ due to $Pr.$

Fig. 13

Variations on $f^{\prime }$ due to $\beta .$

Fig. 14

Variations on $f^{\prime }$ due to $Ha.$

Impacts on temperature profile of the flow

In Figs. 15, 16, 17 and 18 the case of stagnation-bioconvective point flow on a deformable cylinder within a Reiner–Rivlin fluid, an enhancement in the suction parameter $\left( S \right)$, velocity ratio parameter $\left( A \right)$, Prandtl number $\left( {Pr} \right)$ and curvature parameters $\left( M \right)$ decrease in the fluid temperature around the cylinder due to several physical mechanisms. The suction parameter intensifies the fluid away from the boundary layer, which draws cooler fluid from the outer regions towards the cylinder, effectively reducing the temperature near the surface. The velocity ratio parameter, representing the ratio between the free-stream and wall velocities, influences the convective cooling effect by strengthening the fluid’s movement along the surface, which enhances heat transfer away from the cylinder and thereby reduces local temperatures. A higher Prandtl number, indicating a greater relative importance of momentum diffusion compared to thermal diffusion, results in a thicker thermal boundary layer and restricts the rate of thermal energy conduction relative to the flow, further cooling the region around the cylinder. Together, these parameters facilitate heat dissipation and reduce the temperature of the fluid in the vicinity of the deforming cylinder. When the curvature parameter of a cylinder increases, the surface area in contact with the fluid also increases. This increased surface area leads to a higher rate of heat transfer from the fluid to the cylinder’s surface. As a result, the fluid near the surface loses more heat, causing its temperature to decrease.

Fig. 15

Variations on $\theta$ due to $S.$

Fig. 16

Variations on $\theta$ due to $A.$

Fig. 17

Variations on $\theta$ due to $Pr.$

Fig. 18

Variations on $\theta$ due to $M.$

In Fig. 19 the context of stagnation-bioconvective point flow effecting on a deformable cylinder within a Reiner–Rivlin fluid, an increase in the heat source $\left( Q \right)$, leads to an enhancement in the fluid temperature around the cylinder due to distinct physical mechanisms. When a higher heat source parameter introduces more internal energy into the system, directly supplying heat to the fluid and thereby raising the temperature in the vicinity of the cylinder.

Fig. 19

Variations on $\theta$ due to $Q.$

Impacts on concentration profile of the flow

In Figs. 20, 21, 22 and 23 the case of stagnation-bioconvective point flow on a deformable cylinder within a Reiner–Rivlin fluid, increasing the heat source $\left( Q \right)$, curvature parameter $\left( M \right)$, chemical reaction $\left( K \right)$, and Schmidt number $\left( {Sc} \right)$ parameters lead to a reduction in concentration near the cylinder. The heat source parameter adds thermal energy, which can enhance molecular motion, causing solute particles to diffuse away from the surface, thus reducing concentration levels locally. The curvature parameter, which accounts for the cylinder’s shape, affects flow patterns and intensifies boundary layer thinning, which disrupts concentration gradients and facilitates outward diffusion. Additionally, a higher chemical reaction parameter indicates an increased rate of chemical transformation, consuming solute particles more rapidly near the cylinder and leading to a further drop in concentration. Lastly, a higher Schmidt number, the ratio of momentum diffusivity to mass diffusivity, suppresses mass diffusion relative to momentum diffusion, making it harder for particles to remain concentrated near the surface. These parameters collectively reduce the concentration in the region close to the deforming cylinder.

Fig. 20

Variations on $\phi$ due to $Q.$

Fig. 21

Variations on $\phi$ due to $M.$

Fig. 22

Variations on $\phi$ due to $K.$

Fig. 23

Variations on $\phi$ due to $Sc.$

In Fig. 24 stagnation-bioconvective point flow impinging on a stretchable cylinder within a Reiner–Rivlin fluid, an increase in the Soret number $\left( {Sr} \right)$ enhances concentration near the cylinder from start to $\left( {1.4} \right)$. The Soret effect, also known as thermophoresis, describes how a temperature gradient can drive mass diffusion, causing particles to move from warmer to cooler regions. With a higher Soret number, this thermophoretic force becomes more pronounced, leading solute particles to accumulate in areas of lower temperature near the cylinder’s surface. As the Soret number increases, this temperature-driven diffusion effect dominates, drawing more solute toward the cylinder and enhancing local concentration. This mechanism is especially significant in non-Newtonian fluids like the Reiner–Rivlin fluid, where temperature gradients strongly influence molecular motion, thus leading to an increased concentration close to the deforming cylinder. While in Fig. 24 from $\left( {1.4} \right)$ to onward depicts the decrease in the concentrations. The temperature gradient-induced mass diffusion, as described by the Soret effect, dominates over other factors, resulting in a lower concentration in the hotter regions.

Fig. 24

Variations on $\phi$ due to $Sr.$

Impacts on microbial density profile of the flow

In Figs. 25, 26 and 27 the case of stagnation-point flow impinging on a deforming cylinder within a Reiner–Rivlin fluid, a greater input in the Schmidt number $\left( {Sc} \right)$, Peclet number $\left( {Pe} \right)$, and curvature parameters $\left( M \right)$ contributes to a higher density of microbes near the cylinder surface due to several physical factors. A higher Schmidt number, the ratio of momentum diffusivity to mass diffusivity, reduces the rate of microbial diffusion away from the surface, allowing microbes to accumulate and enhancing their local density. Similarly, an increased Peclet number indicates that advective transport, or movement due to the flow, is more dominant than diffusive transport, causing microbes to be carried along and concentrated near the cylinder rather than dispersing. The curvature parameter, related to the shape of the cylinder, influences boundary layer behavior by shaping the flow around the surface; this can create regions where microbes are more likely to settle and accumulate due to reduced outward diffusion. Together, these parameters restrict the dispersion of microbes and promote their accumulation near the deforming cylinder, leading to an increase in microbial density.

Fig. 25

Variations on $\chi$ due to $Sc.$

Fig. 26

Variations on $\chi$ due to $Pe.$

Fig. 27

Variations on $\chi$ due to $M.$

Figures 28, 29, 30, 31 and 32 Illustrates the variations of the suction parameter $\left( S \right)$, heat source $\left( Q \right)$, bioconvection of the Lewis number $\left( {Lb} \right)$, velocity ratio parameter $\left( A \right)$, and the Soret number $\left( {Sr} \right)$. Increasing the suction parameter leads to a stronger extraction fluid from the surface, reducing the residence time of microbes near the surface and thus decreasing their density. A higher heat source parameter implies a more heated surface, which can adversely affect the survival and growth of microbes. A larger Bioconvection Lewis number corresponds to a higher diffusion rate of microorganisms relative to heat and mass, leading to their dispersion away from the stagnation point. A higher velocity ratio parameter indicates a stronger external flow, which can shear off the bioconvection layer and reduce microbial density. Finally, a larger Soret number implies a stronger thermal diffusion effect, causing the microbes to move away from the hotter regions, contributing to the observed reduction.

Fig. 28

Variations on $\chi$ due to $S.$

Fig. 29

Variations on $\chi$ due to $Lb.$

Fig. 30

Variations on $\chi$ due to $A.$

Fig. 31

Variations on $\chi$ due to $Sr.$

Fig. 32

Variations on $\chi$ due to $Q.$

In Table 1 the achieved numerical results of the current problem are compared with the exact solutions and found the great accord among the results on the basis of Skin friction, Nusselt number, and Sherwood number.

Table 1 Shows the comparison of numerical results with analytical results.

Concluding remarks

This research examines the stagnation-bioconvective point flow of energy and mass transport phenomena of the Reiner–Rivlin on a horizontal expandable cylinder. The investigation incorporates the effects of viscous dissipation, bioconvections, Soret effect, heat sink/ sour, reaction rate, and magnetic field. The governing equations are solved numerically using the bvp4c routine for various parameter values. The primary conclusions of the study are presented below.

• The Reiner–Rivlin fluid model enhances heat transfer and momentum diffusion in the streamwise direction. An increasing input of the material fluid parameter leads to a thinner concentration boundary layer.

• The inclusion of the curvature parameter results in a significant thickening of all boundary layers. However, this effect is counteracted by increasing the magnetic interaction parameter.

• The behavior of the parameters on the velocity profile is opposite in the cases where the velocity ratio parameter is less than or greater than 1.

• A larger curvature parameter necessitates force to maintain the cylinder’s uniform stretching rate. Additionally, an increase in the curvature parameter leads to a higher Nusselt number, indicating increased surface cooling.

• The temperature field decreases with increasing Prandtl number, while the opposite trend is observed for increasing Eckert number or heat source parameter.

• The concentration boundary layer thins with increasing Schmidt number, and it thickens with increasing reaction rate.

• The microbial density decreases with the Soret and bioconvective Lewis number, increasing with the Peclet and Schmidt numbers.

• The entropy production rate increases with a higher Brinkman it decreases with increasing Bejan number.

• The current findings show agreement with specific cases reported in previous studies.

Future research directions include exploring the model with more variety of nanoparticles-based fluids and investigating the effects of various other physical parameters.