Introduction

Surface mass loading, which includes the redistribution of terrestrial water, atmospheric, and oceanic fluid masses, leads to surface deformation, changes in the gravity field, and shifts in the Geo-center1,2,3. Of these, terrestrial water storage (TWS) change is the predominant factor affecting crustal vertical deformation in the land4. The Earth’s crust undergoes non-tectonic deformation as an elastic response to external forces. Although theoretical models for solid Earth and polar tides have been refined with high precision, and advanced geophysical models exist for atmospheric and ocean tidal and non-tidal effects, as well as other geodetic tidal effects, allowing for their removal or compensation, terrestrial water loading’s unmodeled effects introduce a higher level of complexity. This complexity is due to more pronounced crustal deformation, characterized by its intricate nonlinearity and non-stationary quasi-periodicity compared to atmospheric and non-tidal oceanic loading variations. Satellite gravity inversion and other geodetic techniques (such as GNSS, satellite altimetry, INSAR etc.) for quantitatively assessing spatiotemporal changes in terrestrial water loading facilitate understanding of the deformation effects of terrestrial water load using load deformation theory. Precisely monitoring of terrestrial water loading displacement and its variations over time is crucial for maintaining dynamic geodetic reference frameworks5,6,7. Moreover, the high precise terrestrial water loading deformation fusion model can provide effective data support for the inversion of terrestrial water storage changes for understanding global hydrological cycles, assessing climate change impacts, and managing water resources effectively, and it is possible to assume that the variations of the gravity field are due only to water redistribution and not to other processes2,8.

Recent advancements in satellite remote sensing technologies, notably GRACE/GRACE-FO and GNSS, have revolutionized research methodologies in this field, providing unprecedented insights into hydrological phenomena9,10,11,12,13. GRACE satellites, in particularly, excel in detecting changes in terrestrial water storage by accurately measuring minor variations in Earth’s gravity field, offering valuable data for exploring global hydrology loading displacement dynamics. However, GRACE’s sensitivity is generally limited to medium- to long-wavelength signals, posing challenges in identifying finer-scale variations in the surface gravity field. Consequently, hydrological loading signals derived solely from GRACE inversions predominantly reflect large-scale deformations and coarse spatial resolutions, lacking the granularity needed to capture localized hydrological loading deformation signals or to monitor specific hydrological events such as the closure of terrestrial water budgets in small to medium-sized river basins or the differentiation of surface mass balance from ice dynamics in individual glacier systems. In contrast, the global network of continuous GNSS stations provides highly precise, stable, and long-term geometric coordinate time series, especially for vertical displacements measured with millimeter precision. This higher precision renders GNSS data particularly sensitive to local, high-frequency loading deformation dynamics. Using internationally established independent model data, non-tidal atmospheric load, non-tidal oceanic load, and various tidal effects are removed from the GNSS vertical displacement time series, effectively extracting the contribution of terrestrial water loading. Subsequently, time series processing methods such as least squares fitting and Singular Spectrum Analysis (SSA) are employed to denoise this component and extract its primary periodic signals and long-term trend changes. Research in the domain of terrestrial water storage change and loading deformation has extensively leveraged the combined strengths of GRACE and GNSS technologies. Davis et al. (2004) analyzed time-variable gravity data from GRACE to assess surface vertical load deformation in the Amazon River Basin between 2002 and 2004, finding strong agreement with global positioning system (GPS) measurements14. Van Dam et al. (2007) used GRACE data to deduce surface loading deformations, comparing these with European GPS data and noting a subtle correlation potentially due to GPS data processing inaccuracies, which might introduce erroneous periodic signals15. Zhang et al. (2021) explored differences in seasonal surface mass load deformation as monitored by GRACE and GNSS, both regionally and at specific points16. Their analysis in the Amazon basin indicated a 30% mean discrepancy between methods, a variation likely influenced by several factors including GRACE’s data processing, geo-center motion corrections, GNSS station data’s high-frequency noise, and the choice of elastic parameters in Earth models. He et al. (2021) applied empirical orthogonal function methods to detect spatial and seasonal variations in surface deformation across five Tibetan Plateau regions, identifying a significant correlation with mass load changes recorded by GRAC17E. Similarly, Pan et al. (2021) used empirical spatial structure functions to map China’s vertical velocity fields comprehensively, refining vertical load velocity estimates with GRACE data for improved tectonic movement insights3. While considerable effort has been made to validate GRACE-derived hydrological load deformation against GNSS data and adjust GNSS elevation series to negate non-tectonic effects, advancing the integration of these geodetic techniques and developing sophisticated models is essential. Such efforts are crucial for achieving high precise regional terrestrial water storage analyses, detailed quantification of crustal elastic loading and corresponding nonlinear deformations.

Despite advancements in geodesy and geodynamics, uncertainties persist due to complex geological structures across different regions and partially understood geodynamic mechanisms. The reliance on limited observational data for geodynamic modeling introduces significant uncertainty. However, machine learning techniques, particularly in identifying higher-level nonlinear characteristics and solving nonlinear fitting and prediction challenges where mechanisms remain unclear, offer valuable insights that augment traditional physics-based models18,19,20,21,22.

This research employs a deep learning strategy using 3D-CNN alongside GNSS vertical displacement and GRACE-derived water storage data to model the elastic deformation caused by terrestrial water loads in Yunnan Province. By contrasting the high-resolution and locally sensitive GNSS data and traditional Green’s function convolution methods with 3D-CNN outcomes, this study aims to estimate the precision of deep learning in mapping terrestrial water load-induced elastic deformation. The objective is to ascertain the effectiveness of deep learning in assessing crustal deformation driven by TWS change, and to preliminarily investigate the potential of creating a comprehensive terrestrial water load deformation model by integrating GNSS and GRACE data. The structural framework of this paper is as follows. Firstly, the general situation of the research area and the data sources used are introduced, and the satellite inversion theory of time-varying TWS and crustal load deformation theory are preliminarily analyzed, and the TWLD research model and method adopted in this paper are proposed. Secondly, the temporal and spatial variation of TWS in the study area and its vicinity are analyzed in detail. The change of TWS in the near area is the main load source that causes the calculation of water load deformation, so it is necessary to study the spatiotemporal change of TWS in the area and its vicinity to understand the TWLD and the correlation between the two. Finally, the TWLD time series of GNSS stations in the study area were calculated by 3D-CNN and Green function method respectively, and the results were compared with the refined GNSS monitoring results to estimate the calculation precision of the two methods. On this basis, the temporal and spatial variation of TWLD in the study area are evaluated in detail, and then the research conclusion of this paper is drawn.

Materials and methods

Study area

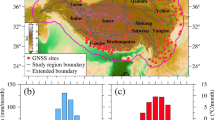
Yunnan Province, located on the eastern edge of the Tibetan Plateau within the collision zone of the Indian and Eurasian Plates, experiences significant tectonic activity. This activity, marked by frequent active faults and severe earthquakes, results from the ongoing collision between these plates over the past 45 million years23. The region is dissected by two principal active fault zones—the Red River and Xiaojiang Fault Zones—dividing Yunnan into several blocks like the Sichuan-Yunnan Rhombic Block, Yunnan-Myanmar Block, and South China Block. These divisions influence the unique regional stress fields16. GNSS stations across Yunnan must account for seismic activities and tectonic movements in data post-processing to ensure accuracy. Yunnan’s climate, a subtropical plateau monsoon, exhibits significant vertical climatic variation due to its geographic positioning. Influenced by the Indian and East Asian monsoons and temperature variances from the Tibetan Plateau, the region sees pronounced temperature fluctuations with elevation. Precipitation is spatially and temporally uneven, with the rainy season (May to October) accounting for approximately 85% of annual precipitation and the dry season (November to April) the remaining 15%. From 2011 to 2020, most areas received over 1000 millimeters of annual average precipitation, contributing to Yunnan’s rich biodiversity and status as a vital genetic resource for wild flora and fauna. However, the province faces ecological preservation challenges due to global warming and frequent extreme weather. Yunnan’s susceptibility to climate change, exacerbated by its monsoon influence and varied topography, underscores the importance of research into TWS and TWLD for effective water resource management and ecological conservation.

Data

GNSS data

The daily vertical displacement time series of GNSS stations used in this study were provided by the National Seismic Science Data Sharing Center in the form of single-day solution coordinate time series (https://www.eqdsc.com). The distribution of GNSS stations in Yunnan Province and its surrounding areas is shown in Fig. 1. Data processing was conducted using the GAMIT/GLOBK software, leveraging orbit and clock corrections provided by the International GNSS Service (IGS). Prior tropospheric delay corrections were applied using the GMF model, while corrections for solid Earth and ocean tides were implemented using the IERS03 model for solid tides and pole tides, and the FES2004 model for ocean tides24. Post-processing of the GNSS vertical displacement time series in this study involved three main steps. Firstly, gross errors and offset in the GNSS vertical displacement time series were mitigated using the TSAnalyzer software25. Subsequently, each GNSS vertical displacement time series underwent position fitting, linear trend fitting, and annual signal fitting using the least squares linear fitting method, followed by correction of abrupt changes and long-term trend variations (primarily induced by glacial isostatic adjustment or tectonic effects) using the Heaviside function. Lastly, the Kriged Kalman filtering method proposed by Liu et al. (2017) was employed to interpolate data gaps in the GNSS vertical displacement time series. Overall, the 41 GNSS stations utilized in this study exhibited favorable data availability throughout the research period, with an average data coverage of 95% per station26. Additionally, geophysical fluid loading products disseminated by the Earth System Modeling Group (ESM) within the GFZ (https://esmdata.gfz-potsdam.de:8080/repository) were utilized to alleviate non-tidal atmospheric and oceanic loading effects from the GNSS vertical displacement time series, enabling inference of the final changes in terrestrial water loading deformation27. Generally, post-processing of GNSS vertical displacement time series plays a pivotal role in enhancing the reliability of TWS change inference derived from GNSS data.

Fig. 1
figure 1

GNSS stations in Yunnan Province and its surrounding areas.

Full size image

GRACE data

The GRACE data used in this study were obtained from the Mascon monthly solutions provided by the University of Texas Center for Space Research (UT-CSR) (http://www2.csr.utexas.edu/grace/RL06_mascons.html). This dataset has been adjusted for C20 terms and Geo-center corrections and has been corrected for glacial isostatic adjustment (GIA) effects. It is normalized to the mean from January 2004 to December 2009 and exhibits high resolution, high signal-to-noise ratio, and minimal leakage errors. The spatial resolution of this data is 0.25°×0.25°, basically a subsampling of the raw data. In contrast to spherical harmonic coefficient products, Mascon products do not require filtering, smoothing, or scaling procedures, and increase the precision of the TWS estimates28,29.

Methodologies

Methodology for inverting TWS changes based on GRACE

The migration and redistribution of surface mass, including terrestrial water, causes the change of gravity field, so the surface mass variations can be inverted by observing the time-varying gravity potentials. In the application of GRACE satellite data, a crucial assumption is that the redistribution of Earth’s surface mass primarily occurs within a relatively thin layer near the surface, typically within a height range of 10–15 km. This assumption simplifies the processing and analysis of GRACE data, enabling us to more accurately estimate TWS changes. Based on this assumption, a methodology has been proposed for calculating equivalent water height using spherical harmonic coefficients. Equivalent water height refers to the conversion of changes in Earth’s gravity field into equivalent changes in the thickness of a water layer, providing an effective means of quantifying changes in TWS. The specific calculation formula is as follows30,31:

$$\:\varDelta\:h(\theta\:,\lambda\:)=\frac{a{\rho\:}_{e}}{3{\rho\:}_{w}}{\sum\:}_{n=0}^{\infty\:}{\sum\:}_{m=0}^{n}\frac{2n+1}{1+{k}_{n}}\cdot\:\left[\varDelta\:{C}_{nm}{cos}(m\lambda\:\right)+\varDelta\:{S}_{nm}{sin}(m\lambda\:\left)\right]\cdot\:{\bar{P}}_{nm}\left({cos}\theta\:\right)$$
(1)

In the equation, \(\:\theta\:,\lambda\:\) represent geocentric colatitude and longitude, respectively; \(\:a\) and\(\:\:\:{\rho\:}_{e}\:\)denote the average radius and average density of the Earth, respectively; \(\:{\rho\:}_{w}\) is the density of water; \(\:n,m\:\)represent the degree and order of the spherical harmonic coefficients, respectively; \(\:{\bar{P}}_{nm}\left({cos}\theta\:\right)\)denotes the fully normalized associated Legendre function; \(\:{k}_{n}\)is the Love number for vertical displacement load; \(\:\:\varDelta\:{C}_{nm}\)、\(\:\varDelta\:{S}_{nm}\) represent changes in the spherical harmonic coefficients.

In practical applications, GRACE data is initially processed to remove the effects caused by Earth tides, atmospheric and oceanic mass variations, among other factors. This process typically involves filtering the data to reduce the impact of errors and noise. Subsequently, by applying Eq. (1), variations in surface water storage can be estimated from GRACE satellite data. Furthermore, based on the theory of elastic loading, the crustal deformation induced by water mass loading can be calculated. Common methods for this purpose include spherical harmonic functions and convolution methods using load Green’s functions.

Recovery of TWLD based on 3D-CNN model

As mentioned above, the Yunnan region, situated among multiple structural faults zones, experiences frequent earthquakes and tectonic activities. These non-load deformations mainly influence the trend component of GNSS signals. To enhance consistency and comparability with GRACE data, which solely reflects terrestrial water load effects, this paper processed the trend components of time series as follows: (1) the line-trend components of GNSS and GRACE time series were separated using least squares fitting; (2) when constructing the TWLD model using the Green’s function method and 3D-CNN, time series of GNSS and GRACE data excluding line-trend component were used; (3) for analyzing terrestrial water storage changes using GRACE time series, the complete time series including detrended components were employed.

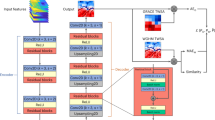
Subsequently, the 3D-CNN method is utilized to estimate TWLD based on preprocessed GNSS data and GRACE Mascon data. As illustrated in Fig. 2, a five-dimensional matrix with the form [N, T, H, W, C] is constructed. Here, N represents the number of GNSS stations, which amounts to 41 in this study; T denotes the number of time steps, set at 48 months for this investigation; H and W signify the spatial layout of grid points selected around each GNSS point. In this study, 12 grid points are chosen in each direction surrounding the GNSS station, resulting in H = W = 12. C represents the number of features, which is set to 5 in this study, including longitude, latitude, differences in longitude and latitude between grid points and GNSS points, and TWS data. Subsequently, the CNN model is designed, with convolutional layers featuring a kernel size of 3 × 3 × 3 and Relu activation functions. Through subsequent operations involving max-pooling layers, flattening layers, and fully connected layers, the model ultimately outputs the time series of TWLD for each station on monthly basis, and its accuracy of forward modeling is validated using the validation dataset.

Fig. 2
figure 2

3D-CNN for TWLD recovery.

Full size image

Estimation of TWLD based on Green’s function

The crustal displacement resulting from surface mass loading migration emerges from the cumulative impact of proximate load sources, specifically the total deformation induced by a sequence of unit mass load sources at deformation sites. The regional crustal elastic deformation caused by mass load redistribution can be solved using the Green’s function of the load. The load Green’s function is a classic method for calculating the deformation of the Earth’s surface caused by surface loading. The atmospheric load and sea level change load in environmental loading exhibit a globally continuous spatial distribution, which manifests more as medium to long wave signals in the spatial domain. Therefore, when calculating their load deformation effects, it is more suitable to use spherical harmonic analysis methods. In contrast, changes in terrestrial water storage, due to their relatively independent regional distribution characteristics, are primarily expressed by short wave signals in the energy spectrum. The surface load deformation caused by these changes mainly depends on near-field load variations, making the load Green’s function convolution method more appropriate for solving the deformation effects of terrestrial water loads.

The principal computational procedures include: (1) determining the Love numbers for loading and subsequently deriving the load’s Green’s function; (2) convolving the change in mass load with the Green’s function and integrating to ascertain the deformation magnitude at specific station locations. The ground will produce corresponding load effects under the action of unit point source loads, and these changes in physical quantities can be represented by response functions establishing mathematical relationships between the load source and the deformation or gravity field. Such a response function is known as the load Green’s function. As mentioned above, different surface environmental mass changes can be represented by equivalent water height \({\Delta {h_w}({\varphi^{'}},{\lambda ^{'}}})\). According to the theory of load Green’s functions, the general formula for load responses caused by changes in mass is given by32:

$$\Delta {Q_n}\left( {\varphi ,\lambda } \right)=G{\rho _w}\iint_{S} {\frac{{\Delta {h_w}({\varphi ^{'}},{\lambda ^{'}})}}{n}}G(\theta )dS$$
(2)

In the equation, \(({\varphi ^{'}},{\lambda ^{'}})\)represents the unit point source of integral flow on the ground; n denotes the spatial distance from the flowing point to the calculation point; \({\rho _w} \approx {10^3}kg \cdot {m^{ - 3}}\) stands for the density of water; \(G(\theta )\)represents the load Green’s function corresponding to different geodetic observables; and G is the universal gravitational constant.

The study utilizes gridded TWS change values from GRACE Mascons with load Green’s function convolution to calculate the monthly time series of TWLD for 41 GNSS stations in Yunnan Province and surrounding areas during the period from 2019 to 2022. Then, the outcomes of this traditional forward modeling are compared with results from the deep learning model constructed using 3D Convolutional Neural Networks (3D-CNN).

Results and analysis

Spatiotemporal variation of TWS in Yunnan region

Temporal variation patterns of TWS in Yunnan region

Initially, the terrestrial water storage changes for all grids within the same epoch, as inverted by GRACE data, are aggregated to derive the spatially averaged TWS change for the Yunnan region. This newly synthesized time series have been mean-centered, achieved by subtracting the mean of the original data from itself. The results are anomalies (deviations) based on the mean value of the study period and presented in Fig. 3.

Fig. 3
figure 3

The spatially averaged TWS change in the Yunnan region from 2019 to 2022.

Full size image

As illustrated in Fig. 3, the average TWS change in the Yunnan region between 2019 and 2022 demonstrates marked seasonal variations and a pronounced upward trend. A considerable fluctuation in water storage is observed from the latter half of 2020 through the end of 2021. To better understand the terrestrial water cycle and its seasonal variations, this study categorized months based on whether the water storage change was greater than or less than 0. The distribution of months with positive and negative water storage changes is depicted in Fig. 4.

Fig. 4
figure 4

The distribution of monthly TWS changes in the Yunnan region from 2019 to 2022.

Full size image

Figure 4reveals that water storage in Yunnan Province predominantly shows positive values from July to November annually, while negative values are more common from February to May. This pattern is influenced by Yunnan’s subtropical plateau monsoon climate, distinguished by its unique three-dimensional climatic attributes. The province’s location subjects it to significant impacts from the Indian monsoon, East Asian monsoon, and air masses originating from the Qinghai-Tibet Plateau, leading to pronounced precipitation variations across distinct wet and dry seasons. The dry season, spanning December to April of the following year, is influenced by tropical continental air masses, resulting in minimal precipitation, whereas the wet season, from May to November, is characterized by increased rainfall. This climatic rhythm closely correlates with the observed temporal water storage trends. However, a delay of 1 months is noted between water storage changes detected by GRACE and actual precipitation in some grids. This discrepancy arises because indirect TWS change inference via the time-varying Earth gravity field model fundamentally differs from direct, near-real-time precipitation data collection, attributable to disparate strategies and spatiotemporal resolutions, potentially inducing phase differences33,34.

To elucidate the periodicity and trend features of water storage changes in Yunnan Province more precisely, this research applied the Singular Spectrum Analysis (SSA) technique to decompose the time series into its constituent modal components. The period of 12 months for the annual component was chosen as the window length for the SSA method in this study. Additionally, the Fast Fourier Transform (FFT) technique was employed to identify periodic signals within the data. The findings from these analyses are illustrated in Fig. 5.

Fig. 5
figure 5

The periodic characteristic in average terrestrial water storage in Yunnan Province from 2019 to 2022.

Full size image

Following SSA decomposition and reconstruction, complemented by Fast Fourier Transform (FFT) period detection, distinct annual and semi-annual periodic signals were discerned. The amplitude of the annual periodic signal is estimated to be between 10 and 12 cm, peaking around November. Conversely, the amplitude of the semi-annual periodic signal varies between 0.5 and 2 cm. These findings align with the pronounced wet and dry seasonal patterns characteristic of the Yunnan region’s climate and further illustrate the lag observed in GRACE data relative to the peak precipitation period. Based on spectral energy statistics, the eigenvalue contribution rates of the annual periodic signal, trend component, and semi-annual periodic signal are 84.5%, 7.8%, and 7.3%, respectively. Together, these three signals account for over 99% of the total, signifying that they represent the principal components of water storage variation in the Yunnan region.

Spatial variation of TWS in Yunnan region

The average amplitudes of the TWS time series for each grid point in the Yunnan region, spanning from the beginning of 2019 to the end of 2022, were analyzed to derive the spatial distribution of average amplitudes. The results are presented in Fig. 6.

Fig. 6
figure 6

The spatial distribution of amplitude changes of TWS in Yunnan Province from 2019 to 2022.

Full size image

As illustrated in Fig. 6, the variation in TWS across Yunnan Province shows significant spatial differences, with a clear gradient of decreasing amplitude from the southwest to the northeast. Specifically, the regions in the northwest and southeast record the lowest amplitudes, experiencing a notable difference of approximately 20 cm between the highest and lowest values. The regional average amplitude is around 10.93 cm. The southwestern area of Yunnan, situated in the warm river valley region, benefits from a prolonged summer and copious rainfall, leading to more significant fluctuations in water storage. In contrast, the northwest, characterized by a cold temperate climate with brief periods of spring and autumn and limited rainfall, experiences less variation in water storage.

TWLD extraction from GNSS vertical time series

The vertical time series data from GNSS observations, corrected for various tidal phenomena, predominantly capture environmental loading effects, including terrestrial water loading, non-tidal atmospheric loading, and non-tidal ocean loading, alongside thermal expansion effects and other unidentified geophysical influences1,2. Atmospheric loading displacement is identified as a significant factor in the nonlinear movements observed in GNSS vertical coordinate time series, contributing roughly 10–20% in mid-latitude areas. Although the study region is located far from oceanic influences, non-tidal ocean loading still contributes to the observed nonlinear movements in GNSS vertical coordinate time series. The variations in nonlinear motion at selected stations within Yunnan Province, before and after corrections for atmospheric loading and non-tidal ocean loading, are documented in Table 1.

Table 1 Changes of nonlinear motion of the station before and after correction of atmospheric loading and non-tidal ocean loading.
Full size table

Table 1 illustrates that, after corrections for atmospheric loading and non-tidal ocean loading, a noticeable reduction in both annual and semi-annual periodic amplitudes at the individual stations is evident, with the decrease in annual periodic amplitude being particularly significant. Statistical analysis reveals that the average reduction in annual periodic amplitude across the monitored stations is 15.68%, and the semi-annual periodic signal experiences an average decrease of 6.03%. These findings highlight the significant impact of atmospheric loading and non-tidal ocean loading on the stations’ nonlinear motion, emphasizing the importance of pre-correction before estimating TWLD.

Moreover, GIA is identified as a significant factor affecting the linear motion detected in GNSS vertical coordinates. To ensure compatibility with GRACE data and eliminate interference from hydrological signals within the coordinate time series, corrections for GIA have been implemented in this study. Subsequent research has shown that hydrological loading displacement plays a crucial role in crustal deformation vertically, accounting for over 50% of the periodic characteristics observed in the GNSS coordinate time series at monitoring stations, particularly regarding the amplitude and phase of the annual component3,4,17,21,35,36. Consequently, after adjustments for atmospheric, non-tidal oceanic, ocean tidal loading, and GIA, it is deduced that the bulk of the residual non-linear components is predominantly due to hydrological signals.

In addition, considering the effects of thermal expansion and poroelastic deformation is also an important step in the processing of GNSS time series. Previous studies have investigated the impact of thermal expansion on GNSS stations and reached similar conclusions37,38. The overall impact of thermal expansion (including both the bedrock and observation monument effects) on the vertical displacement of GNSS stations in CMONOC is roughly divided by the Yangtze River: to the north of the Yangtze, the annual amplitude of the thermal expansion effect exceeds 1 mm, while to the south it is less than 1 mm. For GNSS stations in the study area, the annual amplitude of vertical displacement caused by thermal expansion is approximately 0.3 mm, while the average annual amplitude of terrestrial water load deformation is on the order of 10 mm. Therefore, the impact of thermal expansion on TWLD in the Yunnan region and surrounding areas is relatively small. However, in colder regions such as Northeast and Northwest China, where changes in terrestrial water storage are small, the thermal expansion effect for the vertical displacement amplitude of GNSS stations cannot be ignored. In the analysis of GNSS vertical displacement time series, particularly for stations located on sedimentary layers, poroelastic deformation is an important factor that must be considered. Due to the thick Quaternary cover in certain regions, there are currently 58 GNSS stations in CMONOC located on sedimentary (or Quaternary) layers, accounting for about 22% of the total number of stations. In this study, eight GNSS stations are located on sedimentary layers (SCXC, SCYX, SCYY, YNMH, YNMZ, YNJP, YNRL, YNHZ). For stations built on sedimentary layers, the displacement signals include not only the deformation caused by bedrock loading but also the combined deformation from both the sedimentary layer and the bedrock. This study, from the perspective of GNSS_TWLD (GNSS-based Terrestrial Water Load Deformation) data, performed poroelastic deformation detection and screening for those 41 CMONOC stations. A quantitative comparison was made with the periodic signals of the terrestrial water load deformation time series (GRACE_TWLD) derived from GRACE data. This helped to identify GNSS vertical displacement time series that primarily reflect TWLD. The specific steps involved using the cross-wavelet transform algorithm to analyze the amplitude and phase relationship of the GNSS_TWLD and GRACE_TWLD time series, calculating the correlation coefficient between the two. Stations with poor periodic signal correlation were excluded, and phase differences of significant periodic signals were calculated for the remaining stations. Through analysis of the amplitude and phase differences, it was found that for the eight sedimentary layer stations (SCXC, SCYX, SCYY, YNMH, YNMZ, YNJP, YNRL, YNHZ), the phase differences between GNSS_TWLD and GRACE_TWLD were all within one month (may be caused by the inherent differences between the two models, the data processing strategies, and the delay between load and deformation), and the amplitude match was good. Furthermore, the peak phase of GNSS_TWLD matches well with the trough phase of the TWS time series at the corresponding location. These findings preliminarily suggest that the poroelastic deformation interference at these stations is relatively minimal and does not significantly impact the quantification of TWLD.

TWLD estimation based on GRACE data

The influence of convolution radius on TWLD estimating via 3D-CNN

The choice of convolution radius plays a pivotal role in the estimation of loading displacement when convolving mass loading with load Green’s functions. A radius too small might induce signal leakage, whereas an overly large radius can cause inaccuracies in loading displacement and reduce computational efficiency. Similarly, in applying the 3D-CNN technique for TWLD estimation, identifying the appropriate convolution radius is crucial. This research explored the impact of various convolution radii, represented as grid numbers: 6, 8, 10, 12, 14, and 16. The TWLD estimations made by 3D-CNN were evaluated against GNSS observations, and both the standard deviation and computational efficiency for each convolution radius were assessed. Based on inversion accuracy and computational efficiency, the optimal convolution radius was identified, with findings detailed in Table 2.

Table 2 Statistical analysis of accuracy and efficiency in estimating TWLD using different convolution radius with 3D-CNN method.
Full size table

Table 2 demonstrates that for convolution radii below 10 grids, accuracy markedly improves as the radius increases. Beyond 10 grids, both the mean and the standard deviation of the differences between the TWLD estimations by 3D-CNN and the GNSS observations remain under 0.3 mm and 2 mm, respectively. Yet, the gains in accuracy taper off with larger convolution radii. Additionally, computational time escalates, following an exponential pattern, as the convolution radius expands. Balancing accuracy and computational efficiency, a convolution radius of either 10 or 12 grids emerges as optimal for estimating TWLD using 3D-CNN. To align with the convolution radius applied in Green’s functions (typically set at a boundary inclusion of 3°), this study opted for a convolution radius of 12 grids.

Terrestrial water loading displacement estimation

The assessment of TWLD was performed utilizing both the load Green’s function and the 3D-CNN methods as outlined in Sect. 1.2. Owing to constraints on space, this document details the outcomes for six GNSS stations only depicted in Fig. 7.

Fig. 7
figure 7

Comparison of TWLD of GNSS observations and based on 3D-CNN and loading Green’s function.

Full size image

Figure 7 illustrates that the time series of TWLD derived from all three methods reveal distinct annual periodic variations, with amplitude ranges between 5 and 15 mm across the study region. Compared to the results from the load Green’s function method, the TWLD estimated by the 3D Convolutional Neural Network (3D-CNN_TWLD) aligns more closely with the GNSS-observed terrestrial water load displacement (GNSS_TWLD). Notably, the amplitude of TWLD observed via GNSS exceeds those estimated through both GRACE-based methods. The precision of the classic Green’s Function (GF) method for calculating TWLD depends on the precision of the input terrestrial water storage change data and the accuracy of geophysical parameters. In contrast, the 3D-CNN method bypasses specific physical mechanisms, with the accuracy of the solution being dependent on the precision of the water storage change data input and the observation accuracy of GNSS vertical displacement as the learning target. Thus, the CNN method relies more on the precision and reliability of the input data, as well as on advanced machine learning models that are closer to the physical mechanisms, while the GF method is influenced by both the precision of the input data and the determinacy of geophysical parameters. Clearly, cleaner GNSS observation data (i.e., with contributions from other geophysical effects removed) and appropriate machine learning models are key to constructing a high-precision CNN fusion model. This discrepancy can likely be ascribed to the inclusion of various geophysical factors such as thermal expansion and poroelastic processes in the GNSS_TWLD measurements (if stations located on sedimentary layers). Statistical analysis was also performed on the discrepancies between the outcomes of the two GRACE-based inversion methods (3D-CNN or GF) and the GNSS observational results across all monitoring stations. Statistical indicators encompassed the maximum (MAX), minimum (Min), mean (MEAN), and standard deviation (STD) of the observed differences. The findings are detailed in Table 3.

Table 3 Difference statistics between the inversion results of 3D-CNN and loading green’s function and the observation results of GNSS.
Full size table

Table 3 clearly demonstrates that the 3D-CNN_TWLD closely aligns with the GNSS observations, outperforming the Green’s function method in accuracy. The maximum discrepancy between the 3D-CNN_TWLD and GNSS observations reduced by 1.34 mm, the absolute minimum difference lessened by 1.47 mm, the absolute mean difference shrank by 79.6%, and the standard deviation diminished by 31.4%. These statistical outcomes signify a notable enhancement in the precision of TWLD estimation with the 3D-CNN method relative to conventional approach.

To investigate the variations of hydrology loading displacement across the study region, TWLD estimations derived from 3D-CNN for all grid cells were averaged regionally. This process generated a fitted time series representing the regional TWLD. The findings are illustrated in Fig. 8.

Fig. 8
figure 8

The temporal variation of TWLD within the study area.

Full size image

Figure 8 reveals that TWLD demonstrates distinct periodic properties. The amplitude of TWLD within the study region initially rises before declining, generally exhibiting a downward trend. A notable peak is observed between June 2020 and June 2021. Predominantly, TWLD assumes negative values during the summer and autumn months and positive values throughout winter and spring. This pattern largely stems from the increased precipitation during summer and autumn, resulting in higher terrestrial water storage and subsequent surface subsidence. In contrast, reduced precipitation in winter and spring leads to a rebound of the ground. Given the phase delays, this behavior approximately mirrors an anti-phase relationship with the precipitation cycle.

To elucidate the periodic variation characteristics of TWLD more thoroughly, the FFT techinque was employed to identify the periodicities present in the time series. The outcomes are depicted in Fig. 9. The analysis identified clear annual, semi-annual, and approximately one-third-year periodic signals within the TWLD of the study area. Among these, the annual signal emerged as the most pronounced, while the one-third-year signal was the weakest in intensity.

Fig. 9
figure 9

The periodic signals detected in TWLD.

Full size image

Simultaneously, by applying Eq. (3), a comprehensive least squares fitting was performed on the time series for all grid points to determine the amplitudes of each seasonal component. Subsequently, the spatial distribution of these amplitudes was analyzed.

$$\:h={a}_{1}sin({b}_{1}t+{c}_{1})+{a}_{2}sin({b}_{2}t+{c}_{2})+{a}_{3}sin({b}_{3}t+{c}_{3})\:+{a}_{4}sin({b}_{4}t\:+\:{c}_{4})+e$$
(3)

Here, \(\:h\) denotes the TWLD of cells; \(\:{a}_{1},\:{a}_{2},\:{a}_{3},{a}_{4}\) is amplitudes of periodics; \(\:{b}_{1},\:{b}_{2},\:{b}_{3},{b}_{4\:}\:\)represent the angular frequencies of each periodic component;\(\:{c}_{1},\:{c}_{2},\:{c}_{3},{c}_{4}\:\:\)are phase parameters, and \(\:e\) represents the fitting residual.

Upon comparing the amplitudes of each seasonal component, it becomes clear that the amplitude of the annual cycle significantly surpasses those of other periodic components across all grid points. Consequently, the amplitude of the annual cycle within the study area has been selected for detailed analysis, as illustrated in Fig. 10.

Fig. 10
figure 10

The spatial distribution of TWLD annual amplitudes derived from 3D-CNN.

Full size image
Fig. 11
figure 11

The spatial distribution of GNSS_TWLD annual amplitudes.

Full size image

Figure 10 reveals that the amplitude of 3D-CNN_TWLD across the Yunnan region follows a generally ascending trend from the northeast towards the southwest. In the northeastern and northwestern sections of Yunnan Province, the amplitudes are notably modest, averaging around 5 mm. In contrast, the southwestern part of the province witnesses the highest amplitudes, with certain areas surpassing 15 mm. This pattern of spatial distribution for hydrology loading in Yunnan aligns closely with the spatial characteristics of TWS change, which are predominantly shaped by precipitation patterns. Additional, for verifying the “stability” of the GNSS data and to check if some stations are characterized by local effects or do not seem to work properly, the spatial distribution of the GNSS annual amplitudes is also shown in Fig. 11 (also from SSA and FFT). The comparison between Figs. 10 and 11 clearly demonstrates that the annual periodic signal amplitudes of GNSS_TWLD gradually decrease from the southwest to the northeast, exhibiting a smooth transitional spatial distribution. Furthermore, the annual periodic amplitude of GNSS_TWLD is of a similar magnitude to that of 3D-CNN_TWLD. This result not only validates the reliability of the GNSS time series processing approach used in this study but also confirms the stability of the 3D-CNN method for estimating TWLD.

Conclusions

Utilizing GNSS observations from 41 stations in Yunnan Province and adjacent regions of China, alongside GRACE Mascons data, this research introduces an innovative method for estimating hydrological load displacement employing 3D-CNN. The outcomes are evaluated against those derived from Green’s function conventional method and refined GNSS observational data.

The comparison of TWLD derived from 3D-CNN, traditional Green’s function method, and GNSS observations underscored the superiority of the 3D-CNN approach in precisely estimating hydrological loading displacement. Notably, there was a reduction of 1.34 mm in the maximum discrepancy from GNSS results, a decrease of 1.47 mm in the absolute minimum difference, a significant 79.6% decline in the absolute mean difference, and a 31.4% decrease in standard deviation. Furthermore, spectral-energy analysis of TWLD time series derived from 3D-CNN across the Yunnan region identified annual, semi-annual, and approximately one-third-year cycles, with the annual cycle being the most pronounced and the one-third-year cycle the least intense. The annual amplitude of TWLD exhibits a gradual increase from the northeast to the southwest, featuring lower amplitudes in the northeastern and northwestern areas of Yunnan Province around 5 mm, and higher amplitudes in the southwestern part, where some locations surpass 15 mm. This pattern of spatial distribution is strongly aligned with the regional precipitation patterns, indicating that the TWLD in this area are predominantly driven by precipitation and align with the local climate.

Based on the findings of this study, the 3D-CNN method demonstrates better precision in assessing TWLD and shows a high similarity in both the spatial distribution and magnitude of the GNSS-TWLD in term of amplitude. This further highlights the adaptability of advanced machine learning in the fields of geophysics and geodesy, as well as the feasibility of using appropriate machine learning methods to construct a TWLD model through the fusion of GNSS and GRACE data.