Introduction

A black hole is one of the important predictions in a general theory of relativity, due to the fact that the gravitational pull of a black hole is sufficiently strong that no object, including electromagnetic radiation, can be observed beyond its spacetime boundary, i.e., the event horizon (EH)1. In fact, almost all the evidences on the existence of gravitational black holes are indirect ones observed by a large number of astronomical observation experiments, typically such as the X-ray binaries, gravitational lensing, and gravitational wave detection2,3,4. Physically, an approach to detect gravitational black holes is to probe their thermal evaporation, i.e. Hawking radiation. However, the very low temperature of Hawking radiation from astrophysical gravitational black holes (e.g., for stellar-mass black holes, the Hawking temperature is only at the \(10^{-8}\) K level) has led to the fact that their associated Hawking radiation is not experimentally detectable5. In order to reveal the physical nature of black hole Hawking radiation, it is of great importance to detect Hawking radiation from a variety of possible artificial analogue black holes.

In recent years, a series of analogue black holes, based on their critical behaviors of certain experimentally observable physical quantities, have been constructed by experimental systems, including typically the acoustic systems6, \(^3\)He superfluid7, ion traps8, fiber-optic optics9,10, and Bose-Einstein condensations (BECs)11, etc. For example, based on the modulation of the water surface acoustic flow rate by water flow waves generated by pumps in a flume and by generators, the existence of acoustic horizons of the white holes has been experimentally confirmed12. In this system, the acoustic black hole horizons are defined at the \(c^2=v^2\) critical point in velocity space (where c and v are the propagation velocities of acoustic waves and fluid, respectively); the observed negative mode conversion of the flow velocity in the vicinity of the horizons and the exponential decrease of the ratio of the Bogoliubov coefficients with wavelength is regarded as the spontaneous excitation of the Hawking thermal radiation, although the estimated Hawking radiation temperature is only at the order of \(10^{-12}\) K. Interestingly, in Ref.13 Leonhardt et al. demonstrated that an artificial event horizon could be established by using the light pulses in nonlinear fiber, as the pulse could generate a moving perturbation of the refractive index, via the Kerr effect. Probe light perceives this as an event horizon, when its group velocity, slowed down by the perturbation, matches the speed of the pulse. It is estimated that the Hawking temperature of such an analogue optical black hole could be up to \(10^3\) K10. In particular, the critical behavior of the acoustic wave propagation in BEC systems had also been utilized to construct the analogue black hole14,15, whose Hawking radiation can be detected by measuring the density correlation function of the BEC particles on both sides of its acoustic horizon, when the flow rate of the BEC particles exceeds its mid-acoustic propagation velocity. The measured Hawking radiation temperature is on the order of \(10^{-10}\) K. Inspired by these pioneering experiments for analogue Hawking radiation detection, more gravity-like black holes are expected to be constructed to confirm the existence of analogs of Hawking radiation.

Specifically, certain critical phenomena of electromagnetic wave propagating in some electromagnetic systems had also been used to construct the analogue gravitational black holes, i.e., electromagnetic black holes (EBHs), for the implementations of the analogue Hawking radiation detections16,17. For example, by using the velocity critical behavior of electromagnetic waves along the usual right-handed transmission line (RH-TL), Schützhold18 first demonstrated the feasibility of constructing an EBH and the Hawking radiation temperature of such a black hole is estimated as in the order of mK, which is much higher than those expected for gravitational black holes. Furthermore, by adjusting the inductances of the dc-SQUID arrays, another EBH was proposed by Nation19. While, due to the thermal noise caused by the losses of the electromagnetic propagation, the Hawking radiation from these EBHs is practically very difficult to be experimentally detected. To overcome such a difficulty, the electromagnetic soliton black hole models were proposed by Katayama20,21, based on certain critical behaviors of the propagating electromagnetic soliton without energy loss22. The Hawking radiation from these electromagnetic soliton black holes should be detected more easily, as it does not generate any additional thermal noise background. Noted that in the recent work23,24 the Hawking radiation (\(\sim 10^{-5}\) K) from the analogously EBH, demonstrated by using the transitions of inter-bit coupling strengths from the negative to positive distributions in a one-dimensional array of superconducting quantum chips, was successfully simulated by probing the quasiparticle tunnelings.

In this paper, we further investigate how to construct the feasible electromagnetic soliton black hole with a controllable composite right/left-handed transmission line (CRLH-TL), which is a kind of electromagnetic metamaterials (MTMs) with nonlinear dispersion25. Physically, solitons possess stable propagation properties in dielectrics26, which makes it possible to construct soliton EBHs by exploiting certain critical behaviors of soliton propagation. Since the dispersion relation of the CRLH-TL is highly nonlinear25, the electromagnetic wave is able to propagate as a voltage soliton satisfying the relevant nonlinear Schrödinger equation27 without any energy loss. By adjusting the distributed nonlinear capacitors in the CRLH-TL, the group velocity of electromagnetic wave propagation can be changed to make it equal to the velocity of the voltage soliton. In this way, a voltage soliton EBH can be constructed in the velocity domain, and thus its Hawking radiation could be detected, in principle, by probing the voltage-fluctuation spectra beyond the thermal noise background. The work in this paper is based on this idea and specifically demonstrates how to construct a voltage soliton EBH by using the adjustment of the nonlinear capacitors in the CRLH-TL system. Furthermore, we demonstrate the existence of the negative frequency mode near the analogue black hole horizon, and thus the particles productions could be realized outside the horizon.

The paper is organized as follows. Firstly, we establish the wave equation for electromagnetic wave propagation in CRLH-TL based on the telegraph equation and show that the electromagnetic wave propagating along such a CRLH-TL with controllable capacitors can be described by a nonlinear Schrödinger equation. Using the discrete reduction perturbation method28,29, we construct a voltage soliton solution satisfying this equation. Secondly, we discuss the construction of voltage soliton EBHs by adjusting the nonlinear capacitors and determining the horizon on its velocity domain. The existence of negative frequency modes in the horizon and thus the corresponding particle production are demonstrated by using the Bogoliubov transformation. The average number of produced particles outside the horizon obeys the usual Planck spectrum distribution, and the corresponding analogue Hawking radiation temperature is estimated as about 20.91 mK for the typical experimental parameters. Finally, we summarize our results and discuss the possibility of generating the EBHs with the higher Hawking radiation temperatures.

Voltage soliton waves in CRLH-TL with controllable capacitors

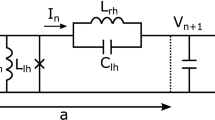
As shown in Fig. 1, We first consider the propagation of an electromagnetic wave along a CRLH-TL. According to Kirchhoff’s law, the voltage and current at the n-th unit cell in the CRLH-TL can be written as

Figure 1
figure 1

Equivalent circuit model of microwave-driven CRLH-TL. The unit cell length is a, which includes series inductance \(L_R\) and shunt inductance \(L_L\), and series capacitance \(C_L\) and shunt nonlinear capacitance \(C_R(V)\), respectively.

Full size image
$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} V_n-V_{n-1}&=-L_R\frac{\partial }{\partial t}I_{n-1}-\frac{1}{C_L}\int I_{n-1}dt,\\ I_n-I_{n-1}&=-C_R\frac{\partial }{\partial t}V_n-\frac{1}{L_L}\int V_ndt, \end{aligned} \right. \end{aligned} \end{aligned}$$
(1)

where \(L_{R/L}\), \(C_{R/L}\) denote RH- (LH-) inductance and capacitance respectively. According to the Eq. (1), we have

$$\begin{aligned} \begin{aligned} \frac{\partial ^{2}}{\partial t^{2}}(V_{n+1}-2V_n+V_{n-1})=L_{R}C_{R}\frac{\partial ^{4}}{\partial t^{4}}V_n+\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}}{C_{L}}\right) \frac{\partial ^{2}}{\partial t^{2}}V_n+\frac{1}{C_{L}L_{L}}V_n. \end{aligned} \end{aligned}$$
(2)

If the cell length \(a=10^{-3}\) m is sufficiently small, compared to the wavelength of the transmitted electromagnetic wave \(\lambda =(2\pi )/k=0.02\pi\) with \(k=100\) /m is the wave number, i.e., \(V_n\equiv V(x,t)\) and \(a\rightarrow 0\), we further have \(V_{n+1}-2V_n+V_{n-1}=a^2\partial ^{2}V(x,t)/\partial x^{2}\). Thus, Eq. (2) can be rewritten as

$$\begin{aligned} \begin{aligned} L_{R}C_{R}\frac{\partial ^{4}}{\partial t^{4}}V(x,t)+\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}}{C_{L}}\right) \frac{\partial ^{2}}{\partial t^{2}}V(x,t)+\frac{1}{C_{L}L_{L}}V(x,t)-a^2\frac{\partial ^{4}}{\partial t^{2}\partial x^{2}}V(x,t)=0. \end{aligned} \end{aligned}$$
(3)

In the frequency domain, it yields

$$\begin{aligned} \frac{\partial ^2}{\partial x^2}V(x,\omega )=\frac{(i\omega )^2}{v_p^2}V(x,\omega ), \end{aligned}$$
(4)

where \(v_p=a/\sqrt{L_{R}C_{R}-(L_{R}/L_{L}+C_{R}/C_{L})/\omega ^2 +1/(\omega ^4C_LL_L)}=\omega /k\) is the phase velocity of the electromagnetic wave with the frequency \(\omega =\omega (k)\), propagating along the CRLH-TL with the dispersion relation:

$$\begin{aligned} \omega =\omega (k)=\left( \frac{A\pm \sqrt{A^2-\frac{4L_RC_R}{L_LC_L}}}{2L_RC_R}\right) ^{\frac{1}{2}}, \end{aligned}$$
(5)

where \(A=(L_R/L_L+C_R/C_L)+4\sin ^2(ka/2)\). Obviously, the Eq. (4) can be rewritten as \([\partial ^2 V(x,t)/\partial t^2]/v_p^2=[\partial ^2 V(x,t)/\partial x^2]\) in the time-domain. This is the wave equation for electromagnetic waves propagating in CRLH-TL. In Ref.18, an EBH based on the modulation of the critical behavior of the electromagnetic wave transmission velocity was constructed for the first time by controlling the change of the capacitance in the RH-TL system. In addition, Refs.20,21 constructed EBHs based on the modulation of the critical behavior of current solitons by adjusting the junction inductance in RH-TL. In the following, we investigate how to use the modulation of distributed nonlinear capacitors in CRLH-TL to construct an EBH by using the critical behavior of the voltage solitary wave propagating along the controllable CRLH-TL.

Physically, let us assume that the RH capacitance in the CRLH-TL can be adjusted non-linearly with respect to the alternating voltage V(x, t)30,31, i.e., \(C_R(V)=C_R^{(0)}V_0/(V_0+V)=C_R^{(0)}(1+\tilde{\beta }V^2)\), where \(V=V(x,t)\) with \(C_R^{(0)}\) and \(V_0\) being the constant capacitance and bias voltage, and \(\tilde{\beta }=1/V_0^2\) is a positive parameter. With Eq. (3), we further have

$$\begin{aligned} \begin{aligned} L_{R}C_{R}(V)\frac{\partial ^{4}}{\partial t^{4}}V +\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}(V)}{C_{L}}\right) \frac{\partial ^{2}}{\partial t^{2}}V+\frac{1}{C_{L}L_{L}}V-a^2\frac{\partial ^{4}}{\partial t^{2}\partial x^{2}}V=0. \end{aligned} \end{aligned}$$
(6)

It can be further simplified as

$$\left( {\frac{\partial }{{\partial t}}\frac{1}{{v_{p'}^2(x,t)}}\frac{\partial }{{\partial t}} - \frac{{{\partial ^2}}}{{\partial {x^2}}}} \right)V = 0,{\mkern 1mu} {\mkern 1mu} {v_{p'}}(x,t) = \frac{a}{{\sqrt {{L_R}{C_R}(V) - \frac{1}{{{{\omega '}^2}}}\left( {\frac{{{L_R}}}{{{L_L}}} + \frac{{{C_R}(V)}}{{{C_L}}}} \right) + \frac{1}{{{{\omega '}^4}{C_L}{L_L}}}} }} = \frac{{\omega '}}{k},$$
(7)

where \(v_p'(x,t)\) is the phase velocity of an electromagnetic wave of frequency \(\omega '\) propagating in a CRLH-TL with the controllable nonlinear capacitor.

In the following we use the discrete reduction perturbation method32,33, by introducing the slow variable

$$\begin{aligned} \xi =\epsilon (x-\tilde{v}_gt),\,\,\tau =\epsilon ^2t, \end{aligned}$$
(8)

to construct the solitary wave solution to the Eq. (6), where \(\epsilon\) is a dimensionless parameter (\(0<\epsilon \ll 1\)), and \(\tilde{v}_g=\partial \tilde{\omega }/\partial k\) is the group velocity of an electromagnetic wave with frequency \(\tilde{\omega }\), respectively. From the Eq. (8), we get

$$\begin{aligned} \partial \xi =\epsilon (\partial x-\tilde{v}_{g}\partial t),\,\,\partial \tau =\epsilon ^2\partial t. \end{aligned}$$
(9)

Let f be a function of \(\xi\) and \(\tau\), which in turn are the functions of x and t. The chain rule allows us to find \(\partial f/\partial x\) and \(\partial f/\partial t\) as

$$\begin{aligned} \frac{\partial f}{\partial x}=\frac{\partial f}{\partial \xi }\frac{\partial \xi }{\partial x}+\frac{\partial f}{\partial \tau }\frac{\partial \tau }{\partial x},\,\,\frac{\partial f}{\partial t}=\frac{\partial f}{\partial \xi }\frac{\partial \xi }{\partial t}+\frac{\partial f}{\partial \tau }\frac{\partial \tau }{\partial t}. \end{aligned}$$
(10)

According to Eq. (9), the following partial derivatives can be obtained as \(\partial \xi /\partial x=\epsilon\), \(\partial \xi /\partial t=-\tilde{v}_g\epsilon\), \(\partial \tau /\partial x=0\), and \(\partial \tau /\partial t=\epsilon ^2\), we rewrite Eq. (10) as

$$\begin{aligned} \frac{\partial f}{\partial x}=\epsilon \frac{\partial f}{\partial \xi },\,\,\frac{\partial f}{\partial t}=-\epsilon \tilde{v}_g\frac{\partial f}{\partial \xi }+\epsilon ^2\frac{\partial f}{\partial \tau }. \end{aligned}$$
(11)

Given the space-time point voltage in the above coordinate system, it can be expanded as the plane-wave expansion, i.e.,

$$\begin{aligned} \begin{aligned} V=\sum _{\alpha =1}^\infty \epsilon ^\alpha V_{\alpha }(x,t),\,\,V_{\alpha }(x,t) =\sum _{l=-\alpha }^{\alpha }[U_{\alpha }^{(l)}(\xi ,\tau )e^{il(kx-\tilde{\omega }t)}+H.c.], \end{aligned} \end{aligned}$$
(12)

where l and \(\alpha\) are both integers and \(l\ne 0\), and H.c. denotes complex conjugate. Above, for the first order approximation term O\((\epsilon )\), we have

$$\begin{aligned} V_1\simeq \epsilon U_1^{(1)}(\xi ,\tau )e^{i(kx-\tilde{\omega }t)}+\epsilon U_1^{*(1)}(\xi ,\tau )e^{-i(kx-\tilde{\omega }t)}. \end{aligned}$$
(13)

Specifically, for the coefficients of the \(\epsilon\) term, we get \(V=\epsilon V_1,\,\,C_R(V)=C_R^{(0)}\), and thus

$$\begin{aligned} \begin{aligned} a^2\frac{\partial ^{4}}{\partial t^{2}\partial x^2}V_1=L_{R}C_{R}^{(0)}\frac{\partial ^{4}}{\partial t^{4}}V_1+\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}^{(0)}}{C_{L}}\right) \frac{\partial ^{2}}{\partial t^{2}}V_1+\frac{1}{C_{L}L_{L}}V_1. \end{aligned} \end{aligned}$$
(14)

Similarly, for the coefficients of the \(\epsilon ^2\) term we have \(V=\epsilon V_1+\epsilon ^2V_2,\,\,C_R(V)=C_R^{(0)}\), and

$$\begin{aligned} \begin{aligned}&L_{R}C_{R}^{(0)}\left( \frac{\partial ^{4}}{\partial t^{4}}V_2-4\tilde{v}_g\frac{\partial ^4}{\partial t^3\partial \xi }V_1\right) +\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}^{(0)}}{C_{L}}\right) \left( \frac{\partial ^{2}}{\partial t^{2}}V_2-2\tilde{v}_g\frac{\partial ^2}{\partial t\partial \xi }V_1\right) +\frac{1}{C_{L}L_{L}}V_2\\&\quad -a^2\left[ \frac{\partial ^{4}}{\partial t^{2}\partial x^{2}}V_2+(2\frac{\partial ^4}{\partial x\partial \xi \partial t^2} -2\tilde{v}_g\frac{\partial ^4}{\partial x^2\partial t\partial \xi })V_1\right] =0. \end{aligned} \end{aligned}$$
(15)

By comparing the coefficients of the \(\epsilon ^3\) term, we get \(V=\epsilon V_1+\epsilon ^2V_2+\epsilon ^3V_3,\,\,C_R(V)=C_R^{(0)}(1+\tilde{\beta }V^2)\), where the higher-order \(O(\epsilon ^4)\) terms have been neglected completely, and thus \(V^2\approx \epsilon ^2V_1^2+2\epsilon ^3V_1V_2\). This leads to

$$\begin{aligned} \begin{aligned}&L_{R}C_{R}^{(0)}\left[ \frac{\partial ^{4}}{\partial t^{4}}V_3-4\tilde{v}_g\frac{\partial ^4}{\partial t^3\partial \xi }V_2+\left( 6\tilde{v}_g^{2}\frac{\partial ^4}{\partial t^2\partial \xi ^2}+4\frac{\partial ^4}{\partial t^3\partial \tau }\right) V_1\right] \\&\quad +\left( \frac{L_{R}}{L_{L}}+\frac{C_{R}^{(0)}}{C_{L}}\right) \left[ \frac{\partial ^{2}}{\partial t^{2}}V_3 -2\tilde{v}_g\frac{\partial ^2}{\partial t\partial \xi }V_2+\left( \tilde{v}_g^{2}\frac{\partial ^2}{\partial \xi ^2} +2\frac{\partial ^2}{\partial t\partial \tau }\right) V_1\right] \\&\quad +\frac{1}{C_{L}L_{L}}V_3-a^2\left[ \frac{\partial ^{4}}{\partial t^{2}\partial x^{2}}V_3+\left( 2\frac{\partial ^4}{\partial x\partial \xi \partial t^2}-2\tilde{v}_g\frac{\partial ^4}{\partial x^2\partial t\partial \xi }\right) V_2\right. \\&\quad \left. +\left( \tilde{v}_g^{2}\frac{\partial ^4}{\partial x^2\partial \xi ^2}+2\frac{\partial ^4}{\partial x^2\partial t\partial \tau }-4\tilde{v}_g\frac{\partial ^4}{\partial x\partial t\partial \xi ^2}+\frac{\partial ^4}{\partial \xi ^2\partial t^2}\right) V_1\right] \\&\quad +\tilde{\beta }L_RC_R^{(0)}V_1^2\frac{\partial ^4}{\partial t^4}V_1+\frac{C_R^{(0)}}{C_L}\tilde{\beta }V_1^2\frac{\partial ^2}{\partial t^2}V_1=0. \end{aligned} \end{aligned}$$
(16)

Substituting Eq. (8) and Eq. (12) into Eq. (6), the equations corresponding to each order of \(\epsilon\) can be derived, and thus the series form of Eq. (13) can be determined. For example, for a first-order solution of \(\epsilon\) (where \(l=1\)), we have

$$\begin{aligned} V_1=U_1^{(1)}e^X+H.c., \end{aligned}$$
(17)

where \(X=i(kx-\tilde{\omega }t)\). Substituting Eq. (17) into Eq. (14), we get the following dispersion relation

$$\begin{aligned} \begin{aligned} \cos (ka)&=1-\frac{1}{2}\left[ \tilde{\omega }^{2}L_RC_R^{(0)}-\left( \frac{L_R}{L_L}+\frac{C_R^{(0)}}{C_L}\right) +\frac{1}{\tilde{\omega }^{2}L_LC_L}\right] ,\\ \tilde{\omega }&=\pm \left( \frac{A_1\pm \sqrt{A_1^2 -\frac{4L_RC_R^{(0)}}{L_LC_L}}}{2L_RC_R^{(0)}}\right) ^{\frac{1}{2}}=\frac{2}{a}\tilde{v}_p\sin \left( \frac{ka}{2}\right) , \end{aligned} \end{aligned}$$
(18)

where \(A_1=(L_R/L_L+C_R^{(0)}/C_L)+4\sin ^2(ka/2)\), and

$$\begin{aligned} \begin{aligned} \tilde{v}_p&=\frac{a}{\sqrt{L_{R}C_{R}^{(0)}-\frac{1}{\tilde{\omega }^{2}}\left( \frac{L_{R}}{L_{L}} +\frac{C_{R}^{(0)}}{C_{L}}\right) +\frac{1}{\tilde{\omega }^{4}C_LL_L}}}=\frac{\tilde{\omega }}{k}, \end{aligned} \end{aligned}$$
(19)

is the phase velocity of an electromagnetic wave of frequency \(\tilde{\omega }\) propagating in a CRLH-TL containing a nonlinear capacitor. Similarly, for the \(\epsilon ^2\) order term, we have

$$\begin{aligned} V_2=U_2^{(2)}e^{2X}+H.c., \end{aligned}$$
(20)

with \(U_2^{(1)}=U_2^{*(1)}=0\). Substituting Eqs. (17) and (20) into Eq. (15), the group velocity of an electromagnetic wave propagating in a nonlinear capacitor CRLH-TL can be expressed as

$$\begin{aligned} \begin{aligned} \tilde{v}_g=\frac{k\tilde{\omega }^{3}L_LC_La^2}{\left| \tilde{\omega }^{4}L_RC_R^{(0)}L_LC_L-1\right| }=\tilde{v}_p\cos {\left( \frac{ka}{2}\right) }, \end{aligned} \end{aligned}$$
(21)

which satisfies the relation \(\tilde{v}_g=\partial \tilde{\omega }/\partial k\). Similarly, for the \(\epsilon ^3\) order term, we have

$$\begin{aligned} \begin{aligned} V_3=U_3^{(2)}e^{2X}+U_3^{(3)}e^{3X}+H.c., \end{aligned} \end{aligned}$$
(22)

with \(U_3^{(1)}=U_3^{*(1)}=0\). Finally, substituting Eqs. (17),  (20) and (22) into Eq. (16), we get the nonlinear Schrödinger equation32,33

$$\begin{aligned} i\frac{\partial U_1^{(1)}}{\partial \tau }+P\frac{\partial ^2U_1^{(1)}}{\partial \xi ^2}+QU_1^{(1)}|U_1^{(1)}|^2=0,\,\,Q=\frac{3\tilde{\omega }^{3} \tilde{\beta }L_LC_R^{(0)}(L_RC_L\tilde{\omega }^{2}-1)}{2(\tilde{\omega }^{4}L_RC_R^{(0)}L_LC_L-1)}, \end{aligned}$$
(23)

and Q is the nonlinear coefficient, for the dynamical variable \(U_1^{(1)}\) with

$$\begin{aligned} P= & \frac{\tilde{\omega }^{3}C_LL_La^2}{2(\tilde{\omega }^{4}L_RC_R^{(0)}L_LC_L-1)^3}\left[ \tilde{\omega }^{6}L_RC_R^{(0)}L_LC_L(L_{R}C_{L}+C_{R}^{(0)}L_{L})-6\tilde{\omega }^{4}L_RC_R^{(0)}L_LC_L+3\tilde{\omega }^{2}(L_{R}C_{L}+C_{R}^{(0)}L_{L})-2\right] \nonumber \\= & \frac{1}{2}\times \frac{\partial \tilde{v}_g}{\partial k}, \end{aligned}$$
(24)

being the dispersion coefficient, denoting group velocity dispersion (GVD)34. Obviously, in the “balanced” case, i.e., \(L_RC_L=C_R^{(0)}L_L\), they can be simplified to28,29 \(P=\tilde{\omega }^{3}C_LL_La^2/[(\tilde{\omega }^{2}L_RC_L+1)^3]=-a\tilde{v}_p\sin {(ka/2)}/4<0\) and \(Q=3\tilde{\omega }^{3}\tilde{\beta }L_RC_L/[2(\tilde{\omega }^{2}L_RC_L+1)]=12\tilde{\beta }L_RC_L\tilde{v}_p^{3}\sin ^3{(ka/2)}/[a^3+4L_RC_La\tilde{v}_p^{2}\sin ^2{(ka/2)}]>0\), respectively. Since \(PQ<0\), it is easy to verify that the Eq. (23) possesses the following soliton solution

$$\begin{aligned} \begin{aligned} U_1^{(1)}(\xi ,\tau )=A\tanh \left( A\sqrt{\left| \frac{Q}{2P}\right| }(\xi -u\tau )\right) e^{i(k\xi -\tilde{\omega }\tau )},\,\,\sqrt{\left| \frac{Q}{2P}\right| }=\sqrt{\frac{24\tilde{\beta }\tilde{v}_p^{2}L_RC_L\sin ^2({\frac{ka}{2}})}{4\tilde{v}_p^{2}a^2L_RC_L\sin ^2({\frac{ka}{2}})+a^4}}, \end{aligned} \end{aligned}$$
(25)

with \(u=v_s-\tilde{v}_g\). Here, \(v_s\) is the soliton propagation velocity, A is the soliton amplitude and \(\tilde{v}_p=(a\tilde{\omega }^2\sqrt{L_LC_L})/(\tilde{\omega }^2L_RC_L-1)\). By substituting Eq. (25) into Eq. (23), one can easily verify that Eq. (25) is indeed a solution to the wave equation shown in Eq. (23). Thus, Eq. (25) can be served as a voltage solitary wave.

Voltage soliton black hole

In the following, we discuss how the critical behavior of the propagation of voltage solitary waves in CRLH-TL with controllable capacitors can be used to construct an EBH, called the voltage soliton black hole afterward. For this purpose, we introduce a variable \(\eta =\xi -u\tau\) in the co-moving coordinate system. As \(k\xi =\tilde{\omega }\tau\), Eq. (25) can be simplified as

Figure 2
figure 2

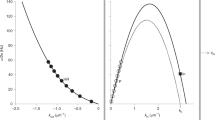
(a) The voltage soliton \(U_1^{(1)}(\eta )\) in the co-moving coordinate system with \(\eta =\xi -u\tau\). Here, the soliton parameters are set as \(A=0.1\) v and \(V_0=1\) v, respectively. The circuit parameters are set as31: \(L_R=L_L=2.5\times 10^{-9}\) H, and \(C_R^{(0)}=C_L=1\times 10^{-12}\) F, respectively; (b) the group velocity \(v'_g(\eta )\) transitions near the horizon point in the co-moving coordinate system \(\eta\). The relevant parameters are set as the same as in Fig. 2a.

Full size image
$$\begin{aligned} U_1^{(1)}(\eta )=A\tanh \left( A\sqrt{\left| \frac{Q}{2P}\right| }\eta \right) . \end{aligned}$$
(26)

Figure 2a gives the variation of the voltage soliton with spatial distribution in the co-moving coordinate system and shows an abrupt behavior near \(\eta =0\). The voltage soliton width can be calculated as \(w=2\tanh ^{-1}(1/2)\sqrt{|2P/Q|}/A\approx 6a\), for the typical parameters of \(L_R=L_L=2.5\times 10^{-9}\) H, \(C_R^{(0)}=C_L=1\times 10^{-12}\) F, \(A=0.1\) v, \(V_0=1\) v. This implies that, if the number of cells is larger than six, then the voltage soliton could be regarded as a continuous transport wave. According to Eq. (7), the phase velocity of electromagnetic wave, propagating along the CRLH-TL with the controllable capacitors, can serve as the transporting velocity of the voltage solitary wave in the co-moving coordinate system. With Eqs. (7) and (19), we have

$$\begin{aligned} v'_p(\eta )=\tilde{v}_p\frac{\omega '(\eta )}{\tilde{\omega }},\,\,\omega '(\eta )=\left( \frac{A_2\pm \sqrt{A_2^2-\frac{4L_RC_R^{(0)}}{L_LC_L}A_3}}{2L_RC_R^{(0)}}\right) ^{\frac{1}{2}}, \end{aligned}$$
(27)

with \(A_2=[A_3(L_R/L_L)+(C_R^{(0)}/C_L)]+4A_3\sin ^2((ka)/2)\) and \(A_3=1+U_1^{(1)}(\eta )/V_0=1+(A/V_0)\tanh (A\sqrt{\left| Q/(2P)\right| }\eta )\), respectively. Furthermore, using Eqs. (18) and (27), we rewrite Eq. (27) as

$$\begin{aligned} v_p^{\prime }(\eta )=\tilde{v}_p\left[ \frac{A_2\pm \sqrt{A_2^2-\frac{4L_RC_R^{(0)}}{L_LC_L}A_3}}{A_1\pm \sqrt{A_1^2-\frac{4L_RC_R^{(0)}}{L_LC_L}}}\right] ^{\frac{1}{2}}. \end{aligned}$$
(28)

Consequently, Eq. (7) can be rewritten as

$$\begin{aligned} \begin{aligned} \left[ \left( \frac{\partial }{\partial t}-v_s\frac{\partial }{\partial \eta }\right) \frac{1}{v'^{2}_p(\eta )}\left( \frac{\partial }{\partial t}-v_s\frac{\partial }{\partial \eta }\right) -\frac{\partial ^2}{\partial \eta ^2}\right] V=0, \end{aligned} \end{aligned}$$
(29)

in the form of a co-moving coordinate system.

Formally, with the wave equation in Eq. (29), one can define a Painlev\(\acute{e}\)-Gullstrand (PG) space-time with the line element; \(ds^2=g_{\mu \nu }d\eta ^{\mu }d\eta ^{\nu }=-(v_s^2-v'^{2}_p(\eta ))dt^2-2v_sd\eta dt-d\eta ^2\), where

$$\begin{aligned} g_{\mu \nu }=- \left( \begin{array}{ll} ~v_s^2-v'^{2}_p(\eta ) & v_s \\ ~~v_s & 1 \\ \end{array} \right) , \end{aligned}$$
(30)

is the relevant metric. Following Ref.35, the analogue black hole horizon for this spacetime can be defined as \(g_{00}=v_s^2-v_p^{'2}(\eta )=0\). Therefore, based on Eqs. (21) and (28), the group velocity of a voltage soliton propagating in such a co-moving coordinate system can be expressed as

$$\begin{aligned} \begin{aligned} v'_g(\eta )=v'_p(\eta )\cos {\left( \frac{ka}{2}\right) }=\tilde{v}_p\cos {\left( \frac{ka}{2}\right) }\left[ \frac{A_2\pm \sqrt{A_2^2-\frac{4L_RC_R^{(0)}}{L_LC_L}A_3}}{A_1\pm \sqrt{A_1^2-\frac{4L_RC_R^{(0)}}{L_LC_L}}}\right] ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$
(31)

This implies that the physical horizon of this voltage soliton black hole is at \(v_s^2=v'^{2}_g(\eta )\) in the co-moving coordinate system. Figure 2b gives the relationship between the group velocity of the electromagnetic wave as a function of the co-moving coordinate parameter \(\eta\). Obviously, at \(\eta _h\), we have \(v_s^2=v'^{2}_g(\eta )\); i.e., at the soliton black hole physical horizon, the group velocity of the electromagnetic wave propagating in the CRLH-TL equals to the propagation velocity of the voltage soliton. Moreover, the group velocity of this voltage solitary wave also exhibits a transition behavior near the horizon, i.e., at \(\eta =\eta _h\sim 0\). With the typical device parameters31, one can find that the propagation group velocity \(v'_g(\eta )\) of the voltage soliton occurs an abrupt change; from a constant value of \(v_g^{\prime }(\eta <0)=2.06\times 10^8\) m/s, to another constant value of \(v'_g(\eta >0)=2.16\times 10^8\) m/s, near \(v_s=\tilde{v}_p=2.1\times 10^8\) m/s. Correspondingly, as \(\omega _s=\tilde{\omega }=2.1\times 10^{10}\) Hz, the frequency of this voltage soliton can be calculated as \(f_s=\omega _s/(2\pi )=3.34\times 10^{9}\) Hz for the present circuit parameters31.

As motioned above, due to the nonlinear effect in the CRLH-TL with controllable capacitors, electromagnetic waves can be propagated as a soliton without any propagation loss. Then, in the co-moving coordinate system, the group velocity of such a voltage soliton possesses an obvious critical behavior in the velocity domain near the horizon of the voltage soliton black hole. Specifically, at the horizon point, the group velocity of the voltage soliton in the co-moving coordinate system equals that of the electromagnetic wave propagating in the realistic circuit. Thus, the frequency of the electromagnetic waves propagated as the voltage soliton wave is a critical frequency to define the voltage soliton black hole; below this frequency, the propagating electromagnetic wave possesses a constant group velocity, while those above such a critical frequency the electromagnetic wave propagates with another constant group velocity. Physically, similar to that of a gravitational black hole near its horizon, Hawking radiation from such a voltage soliton black hole must occur analogously.

Particle productions and the Hawking radiation temperature of the EBH

Quantum mechanics predicates that the so-called vacuum is not absolutely empty, which could be alternatively regarded as the process of uninterrupted creation and annihilation of certain virtual particle pairs. When these quantum vacuum fluctuations occur in the vicinity of a black hole’s horizon, the curvature of spacetime significantly affects the behavior of the virtual particle pairs. Specifically, the positive- and negative frequency modes mix around the horizon. Imaginably, the energy of negative frequency modes inside the horizon is ‘absorbed’ by the black hole, resulting in a reduction of its mass, while the energy of positive frequency modes outside the horizon may radiate out via the real particle productions, generating the so-called Hawking radiation. Therefore, Hawking radiation is physically related to the quantum vacuum fluctuation near the horizon. To verify whether the voltage soliton black holes proposed here can produce the corresponding analogue Hawking radiation, we first investigate the negative frequency modes within the horizon and then we analyze the production mechanism of particles outside the horizon. The analogue Hawking radiation temperature is calculated then accordingly.

Positive- and negative frequency modes near the horizon of the generated EBH

The wave equation of CRLH-TL in the co-moving coordinate system, i.e., Eq. (29), can be easily rewritten as

$$\begin{aligned} \frac{\partial ^2}{\partial t^2}\phi (\eta ,t)-2v_s\frac{\partial ^2}{\partial \eta \partial t}\phi (\eta ,t)-(v_p'^{2}(\eta )-v_s^2)\frac{\partial ^2}{\partial \eta ^2}\phi (\eta ,t)=0, \end{aligned}$$
(32)

with \(\phi (\eta ,t)=\int V(\eta ,\tau )d\tau\). It can be generated by the following Lagrangian

$$\begin{aligned} L=\frac{1}{2}\int _{-\infty }^{+\infty }d\eta \left\{ [\dot{\phi }(\eta ,t)]^2-2v_s\dot{\phi }(\eta ,t)\phi '(\eta ,t)-(v_p'^2(\eta )-v_s^2)[\phi '(\eta ,t)]^2\right\} , \end{aligned}$$
(33)

through the usual Lagrangian equation of motion. Here, \(\dot{\phi }(\eta ,t)=\partial _t\phi (\eta ,t)\) and \(\phi '(\eta ,t)=\partial _\eta \phi (\eta ,t)\). This Lagrangian gives the Hamiltonian

$$\begin{aligned} H=\frac{1}{2}\int _{-\infty }^{+\infty }d\eta \left\{ \Pi ^2(\eta ,t)+2v_s\Pi (\eta ,t)\phi '(\eta ,t)+v_p'^{2}(\eta )[\phi '(\eta ,t)]^2\right\} , \end{aligned}$$
(34)

by Legendre transformation, wherein \(\phi (\eta ,t)=h_k(t)e^{-v_skt}u(\eta )\) is the generalized field variable and \(\Pi (\eta ,t)=\dot{\phi }(\eta ,t)-v_s\phi '(\eta ,t)\) is the relevant canonical momentum, respectively. Consequently, the wave equation shown in Eq. (32) can be variably separated as \(u''_k(\eta )+k^2u_k(\eta )=0\) with k being a constant, whose solution can be generically written as \(u_k(\eta )=C_1e^{ik\eta }+C_2e^{-ik\eta }\) (with \(C_1\) and \(C_2\)) being constants), and

$$\begin{aligned} \ddot{h}_k(t)+\Omega '^{\,2}_{k,\eta }h_k(t)=0, \end{aligned}$$
(35)

where \(\Omega '_{k,\eta<0}=\sqrt{|\omega '^{2}_{k,\eta <0}-2k^2v_s^2|}\) and \(\Omega '_{k,\eta>0}=\sqrt{|\omega '^{2}_{k,\eta >0}-2k^2v_s^2|}\) refer to the kth negative and positive frequencies, respectively. As a consequence, Eqs. (33) and (34) can be rewritten as

$$\begin{aligned} L(h_k(t),\dot{h}_k(t))=\frac{1}{2}\sum _k\left[ \dot{h}_k^2(t)-\Omega '^{2}_k(\eta )h_k^2(t)\right] ,\,\,\,H(F_k(t),h_k(t))=\frac{1}{2}\sum _k\left[ F_k^2(t)+\Omega '^{2}_k(\eta )h_k^2(t)\right] , \end{aligned}$$
(36)

where \(F_k(t)=\dot{h}_k(t)\) is the generalized momentum.

The analogue Hawking radiation temperatures and Particle number productions

As motioned above, the inside and outside of the horizon can be described by the different modes of oscillating analogous space-time. Following Hawking1,5, in the framework of quantum field theory, the vacuum in the vicinity of the horizon is not a vacuum and could be described by the Hamiltonian as

$$\begin{aligned} \hat{H}(\hat{F}_k(t),\hat{h}_k(t))=\frac{1}{2}\sum _k\left[ \hat{F}_k^2(t)+\Omega '^{2}_{k,\eta }\hat{h}_k^2(t)\right] =\sum _k\Omega '_{k,\eta }\left[ \hat{a}_k^{\dag }(t)\hat{a}_k(t)+\frac{1}{2}\right] , \end{aligned}$$
(37)

in Heisenberg picture. Here, \([\hat{h}_k(t),\hat{F}_k(t)]=i\) is the canonical commutation relation, \(\hat{a}_k(t)=\sqrt{\Omega '_{k,\eta }/2}[\hat{h}_k(t)+i\hat{F}_k(t)/\Omega '_{k,\eta }]\), and \(\hat{a}_k^{\dag }(t)=\sqrt{\Omega '_{k,\eta }/2}[\hat{h}_k(t)-i\hat{F}_k(t)/\Omega '_{k,\eta }]\) are the kth generation and annihilation operators, which satisfies the usual canonical commutation relation: \([\hat{a}_k(t),\hat{a}_{k'}^{\dag }(t)]=\delta _{kk'}\). For the present problem, as motioned above, the horizon is defined by \(\eta _h=0\) at the co-moving coordinate, wherein \(\eta\) represents the spatial part and implicitly the temporal part t. Thus, in such a co-moving coordinate, we have

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} \hat{h}_k(t<0)&=\hat{a}_kf_k(t<0)+\hat{a}^{\dag }_kf_k^{*}(t<0),\\ \hat{h}_k(t>0)&=\hat{b}_kf_k(t>0)+\hat{b}^{\dag }_kf_k^{*}(t>0), \end{aligned} \right. \end{aligned} \end{aligned}$$
(38)

wherein \(\hat{a}_k\) and \(\hat{b}_k\) denote the annihilation operators of two independent sets of bosons, satisfying the corresponding canonical commutation relations, respectively. Also, \(f_k(t<0)=e^{-i\Omega '_{k,\eta<0}t}/\sqrt{2\Omega '_{k,\eta <0}}\) and \(f_k(t>0)=e^{-i\Omega '_{k,\eta>0}t}/\sqrt{2\Omega '_{k,\eta >0}}\) are the relevant mode functions, \(f_k^{*}(t<0)\) and \(f_k^{*}(t>0)\) are their complex conjugations, where \(\Omega '_{k,\eta <0}\) is the inside mode and \(\Omega '_{k,\eta >0}\) is alternatively the outside one of the horizon.

Physically, the inside- and outside modes of the horizon can be related by using the Bogoliubov transformation5,36; \(\hat{b}_k=\alpha _k\hat{a}_k+\beta _k\hat{a}_k^{\dag }\), with \(|\alpha _k|^2-|\beta _k|^2=1\). Without loss of the generality, we assume that \(f_k(t<0)=\alpha _kf_k(t>0)+\beta _kf_k^{*}(t>0)\), yielding

$$\begin{aligned} \frac{1}{\sqrt{2\Omega '_{k,\eta<0}}}=\frac{1}{\sqrt{2\Omega '_{k,\eta>0}}}\left( \alpha _k+\beta _k\right) ,\,\,\,-i\sqrt{\frac{\Omega '_{k,\eta <0}}{2}}=-i\sqrt{\frac{\Omega '_{k,\eta >0}}{2}}\left( \alpha _k-\beta _k\right) , \end{aligned}$$
(39)

as the mode function \(f_k(t)\) and its time derivative should be continuous at the horizon, i.e., \(\eta =\eta _h=0\) and \(t=0\). Therefore, one can easily get

$$\begin{aligned} \alpha _k=\frac{1}{2}\left( \sqrt{\frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}}+\sqrt{\frac{\Omega '_{k,\eta<0}}{\Omega '_{k,\eta>0}}}\right) ,\,\,\beta _k=\frac{1}{2}\left( \sqrt{\frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}}-\sqrt{\frac{\Omega '_{k,\eta <0}}{\Omega '_{k,\eta >0}}}\right) , \end{aligned}$$
(40)

and thus

$$\begin{aligned} |\alpha _k|^2=\frac{1}{4}\left( \frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}+\frac{\Omega '_{k,\eta<0}}{\Omega '_{k,\eta>0}}+2\right) ,\,\,|\beta _k|^2=\frac{1}{4}\left( \frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}+\frac{\Omega '_{k,\eta <0}}{\Omega '_{k,\eta >0}}-2\right) . \end{aligned}$$
(41)

As a consequence, the above Bogoliubov transformation can be rewritten as

$$\begin{aligned} \hat{b}_k=\frac{1}{2}\sqrt{\frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}}\left[ \left( 1+\frac{\Omega '_{k,\eta<0}}{\Omega '_{k,\eta>0}}\right) \hat{a}_k+\left( 1-\frac{\Omega '_{k,\eta <0}}{\Omega '_{k,\eta >0}}\right) \hat{a}_k^{\dag }\right] . \end{aligned}$$
(42)

Again, following Refs.1,5, we have \(|\alpha _k|^2=e^{2\pi \Omega '_{k,\eta >0}/g_H}|\beta _k|^2\), and thus the kth mode average particle number generated in the outside of the horizon could be calculated as

$$\begin{aligned} \langle \hat{n}_k\rangle =\langle 0|\hat{b}_k^{\dag }\hat{b}_k|0\rangle =|\beta _k|^2=\frac{1}{4}\left( \frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}+\frac{\Omega '_{k,\eta <0}}{\Omega '_{k,\eta>0}}-2\right) =\frac{1}{e^{\frac{2\pi \Omega '_{k,\eta>0}}{g_H}}-1}=\frac{1}{e^{\frac{\hbar \Omega '_{k,\eta >0}}{k_BT_H}}-1}, \end{aligned}$$
(43)

where

$$\begin{aligned} g_H=\frac{2\pi \Omega '_{k,\eta>0}}{\left| \ln \left( \frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}+\frac{\Omega '_{k,\eta<0}}{\Omega '_{k,\eta>0}}-2\right) -\ln {\left( \frac{\Omega '_{k,\eta>0}}{\Omega '_{k,\eta<0}}+\frac{\Omega '_{k,\eta <0}}{\Omega '_{k,\eta >0}}+2\right) }\right| },\,\,T_H=\frac{\hbar g_H}{2\pi k_B}, \end{aligned}$$
(44)

is the surface gravity on the present analogous horizon and \(T_H\) is the corresponding Hawking radiation temperature. Above, \(k_B=1.38\times 10^{-23}\) J/K is Boltzmann constant and \(\hbar =1.05\times 10^{-34}\) J\(\cdot\)s the reduced Planck constant. For the typical parameters31, i.e., \(a=10^{-3}\) m, \(k=100\) /m, \(A=0.1\) v, \(V_0=1\) v, \(L_R=L_L=2.5\times 10^{-9}\) H, and \(C_R^{(0)}=C_L=1\times 10^{-12}\) F, respectively. Also, we have \(\Omega '_{k,\eta <0}=2.14\times 10^{10}\) Hz and \(\Omega '_{k,\eta >0}=2.04\times 10^{10}\) Hz, and thus \(T_H=20.91\) mK. This temperature should be experimentally detectable, at least theoretically. Noted that the surface gravity on a horizon of an analogous black hole and the corresponding Hawking radiation temperature are usually calculated by the following Unruh’s formula6;

$$\begin{aligned} \bar{g}_H=\left| \frac{\partial v'_g(\eta )}{\partial \eta }\right| _{\eta =\eta _h},\,\,\bar{T}_H=\frac{\hbar \bar{g}_H}{2\pi k_{B}}. \end{aligned}$$
(45)

As a consequence, the corresponding Hawking radiation temperature for the present EBH can be numerically calculated as \(\bar{T}_H=5.13\) mK for the same physical parameters. Obviously, it is slightly lower than the value of \(T_H=20.91\) mK calculated above. The reason is that the above derivations are based on the continuity and its derivative continuity conditions for Bogoliubov’s coefficients at the horizon point. This can be understood as that, the radiation comes from the energy hopping between two flat spacetimes inside- and outside the horizon. While, the Unruh effect formula Eq. (45) takes into account the finite ‘width’ of the horizon, and thus the relevant radiation process can be understood as the energy inside the horizon is ‘gradually’ transferred into the flat spacetime outside the horizon. Taking into account the ‘width’ of the horizon effect, the radiation should weaken and thus the corresponding radiant temperature should be decreased. It is seen that the present Hawking radiation temperature is comparable with those (\(\sim\) mK) of the other analogous EBH systems, shown in Refs.18,19, and significantly higher than those (\(\sim 10^{-9}\) mK) of the acoustic black holes demonstrated in Ref.12. Interestingly, as the Hawking radiation temperature of such an analogue EBH can still be modulated by the velocity of the propagating voltage solitons. Therefore, in principle, by optimizing the circuit device parameters, the generated EBHs can possess higher Hawking radiation temperatures for direct experimental observations.

Figure 3
figure 3

The calculated average particle number produced outside the horizon \(\langle \hat{n}_k\rangle\). With different temperature as \(T_H=20.91\) mK and \(\bar{T}_H=5.13\) mK, respectively.

Full size image

Consequently, let us investigate the relevant particle productions. Obviously, the average particle number produced outside the horizon could be described by Eq. (43), satisfying the usual Bose-Einstein distribution law. With the above typical parameters and the calculated Hawking radiation temperature, in Fig. 3 we plot the relevant average number of the produced particles for the Hawking radiation temperatures; \(T_H=20.91\) mK and \(\bar{T}_H=5.31\) mK, respectively. Although they also show still the Planck spectra and thus possess the similar characteristics that, are shown in Ref.37, for astronomic Schwarzschild black holes with significantly low Hawking radiation temperatures.

Conclusions and discussions

In summary, by using the discrete reduction perturbation method, in this paper, we constructed a voltage soliton solution to the nonlinear wave equation for the electromagnetic transport along a CRLH-TL with controllable nonlinear capacitors. It was shown that the propagation speed of this voltage soliton exists as a critical behavior, which is related to the nonlinear effect of the distributed capacitors in the circuit. Based on such a critical behavior, a voltage soliton-based EBH was defined, by defining its horizon in the velocity domain, when the soliton velocity is equivalent to the group velocity of electromagnetic wave propagation. In addition, the existence of negative frequency modes in such an analogue black hole near the horizon is investigated by the relevant theoretical analysis. The production mechanism of particles outside the horizon is then discussed by the usual Bogoliubov transformation, and the analogue Hawking radiation temperature of such an EBH is altercated specifically for the experimental circuit parameters. The results showed that the corresponding Hawking radiation temperature of such a voltage soliton-based EBH could be sufficiently high at the order of a few tens of milli-Kelvins. This implies that the Hawking radiation of such an EBH should be significantly stronger than the usual astronomic and artificial acoustic black holes, and thus could be directly detected, in principle.

Certainly, the detection of Hawking radiation from either astrophysical black holes or artificial analogue black holes is actually very difficult. For the voltage soliton black holes constructed in the present work, two problems must be solved for the direct detection of Hawking radiation. Firstly, non-linearly modulating the distributed voltage in the CRLH-TL should be feasible, in order to realize the electromagnetic wave can be propagated in the CRLH-TL system in the form of the voltage soliton without any energy loss. Secondly, the temperature of the Hawking radiation of such a voltage soliton-based EBH was estimated theoretically as in the range of tens of milli-Kelvins, which is almost the same as the lowest environment temperature in the dilution refrigerator. Therefore, distinguishing the Hawking radiation from the background thermal noise still requires a very high voltage measurement sensitivity. In this sense, it is still desirable to construct the EBHs with the higher Hawking radiation temperatures for the direct observations.