Abstract
Phosphorus-31 magnetic resonance spectroscopic imaging (31P-MRSI) provides valuable non-invasivein vivoinformation on tissue metabolism but is burdened by poor sensitivity and prolonged scan duration. Ultra-short echo time (UTE) acquisitions minimize signal loss when probing signals with relatively short spin-spin relaxation time (T2), while also preventing first-order dephasing. Here, a three-dimensional (3D) UTE sequence with a rosette k-space trajectory (PETALUTE) is applied to 31P-MRSI at 3T. Conventional weighted MRSI employs highly regular Cartesian k-space sampling, susceptible to substantial artifacts when accelerated via undersampling. In contrast, this novel sequence’s “petal-like” pattern offers incoherent sampling more suitable for compressed sensing (CS). These results showcase the competitive performance of PETALUTE against conventional weighted 31P-MRSI with simulation, phantom, and in vivo leg muscle comparisons.
Similar content being viewed by others
Introduction
Phosphorous-31 magnetic resonance spectroscopy 31P-MRS), the longest-standing in vivo MRS modality, can be an invaluable tool for probing in vivo metabolites such as phosphocreatine (PCr), inorganic phosphate (Pi), phosphomonoesters (PMEs), phosphodiesters (PDEs), and adenosine triphosphate (ATP)1,2. As fundamental phospholipids and constituents of the high-energy phosphate pathway, these 31P metabolites provide noninvasive measures of tissue pH, lipid metabolism, and oxidative bioenergetics3,4. Thus 31, P-MRS possesses versatile diagnostic and prognostic potential. For instance, elevated PME/PDE ratios and reduced ATP levels have been reported in diseased and cancerous liver tissue, often correlated with classical plasma markers and Child-Pugh scores5,6,7,8,9. Furthermore 31, P-MRS has been used to assess whole-liver treatment efficacy, monitoring metabolite changes in malignant tissues following therapy10. Likewise, diminished PCr/ATP ratios and post-exercise PCr recovery rates have been measured in cardiac and skeletal muscles of patients with type 2 diabetes11. Numerous endeavors have employed 31P-MRS in the brain, heart, and muscle, seeking out alterations in neurodegenerative, cardiovascular, metabolic, and oncological diseases12,13,14,15,16,17,18,19,20.
While relevant1H-MRS metabolites can be obscured by contaminating fat, water, and macromolecular background signals, widely spaced 31P spectral peaks are more easily elucidated due to the absence of these nuisance signals. However, in contrast to1H-MRS 31, P-MRS is burdened by a lower gyromagnetic ratio and relatively short spin-spin metabolite relaxation times (T2);21,22 these factors engender extremely poor in vivo relative sensitivity and force a delicate balance between SNR, resolution, and scan duration. Low 31P-MRS tissue concentrations (approximately 2 mM γ-ATP in liver23) further exacerbate SNR challenges, so that commonly used acquisition delays (TE > 300 µs) with conventional methods result in prolonged acquisition, phase distortions, baseline roll, and subsequent operator errors during metabolite quantification. Such complications have been severely limiting factors in the clinical feasibility of 31P-MRS. Recent advances in coil engineering and the introduction of ultra-high field (UHF, B0 > 3T) scanners have assisted in mitigating these limiting factors; one experiment demonstrated a 2.8-factor increase in PCr SNR at 7T relative to 3T24. Conversely, UHF acquisitions also necessitate larger spectral bandwidth (SBW), with a 40-ppm range requiring approximately 2.0 kHz at 3T but 4.8 kHz at 7T. Still, excessive acquisition durations remain the clear barrier to clinical translation without innovative acceleration.
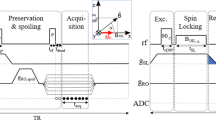
To address these points, we propose a novel three-dimensional (3D), ultra-short echo time (UTE) sequence with a rosette25 k-space trajectory (PETALUTE, previously validated in ultra-short-T2 imaging26,27, brain iron mapping28,29, and sodium quantification30) for 31P magnetic resonance spectroscopic imaging (MRSI)31. Compared to conventional Cartesian MRSI k-space trajectories, rosette’s “petal-like” pattern (Fig. 1) maps 3D k-space far more efficiently. Additionally, rosette’s relatively incoherent data sampling allows the possibility of significant acceleration through higher undersampling factors and compressed sensing (CS) reconstruction; offering better k-space coverage when compared to radial and spiral trajectories, generalized rosette’s curvature affords superior SNR performance under aggressive acceleration32. Furthermore, the rosette’s center-out k-space design enables UTE acquisition, thereby permitting capture of short-T2 signals before significant transverse signal decay and first-order dephasing occur; this enhances SNR, simplifies spectral pre-processing, and minimizes operator-dependent quantification errors.
Illustration of 3D rosette k-space trajectory and gradients. (A)–(C) Acquisition begins at k-space center for every petal, crossing k-space origin twice at each petal’s beginning and end. Petals can be manually separated into two halves, similar to odd and even echoes in EPSI MRSI. (D,E) Varied petal rotations form the rosette pattern, providing sufficient k-space coverage. (F) With the closed-loop trajectory, acquisition delay is further minimized by enabling the analog to digital converter (ADC) for sampling during gradient ramp-up.
Substantial efforts have been invested towards clinically feasible 31P-MRSI, experimenting with short repetition times (TR), measuring multiple k-space points per TR, k-space undersampling, enhancing reconstruction via prior knowledge, and their conceivable combinations33. 3D extensions of ISIS have shown promise in UHF preclinical and 3T cardiac studies but remain limited by time resolution and motion artifact sensitivity34,35. Non-localized or FID acquisitions are often preferred to minimize rapid 31P metabolite T2-decay, but also to overcome specific absorption rate (SAR) limitations at UHFs. Thus, variations of spatial-spectral encoding (SSE) schemes and their synergies with k-space undersampling appear to be the more promising avenue forward; several Cartesian and non-Cartesian acquisition designs offer varying degrees of SNR efficiency, k-space weighting, gradient system demands, and undersampling acceleration potential.
For example, flyback and multishot EPSI have been tested in brain36,37 and skeletal calf muscle38, offering considerable time savings over conventional phase encoding when combined with CS acceleration;39 despite its acceleration potential, EPSI36,40,41,42 offers lower SNR efficiency and SBW at fine resolutions than other SSE options. Density-weighted concentric ring43,44 trajectories (CRTs) grant increased SNR efficiency and SBW limits, enabling faster MRSI even with UHF systems. CRTs boast flexibility in weighting and temporal interleaves, allowing tailoring according to acceleration needs and gradient slew rates. Similarly, spiral-encoded4531P-MRSI has exhibited faster dynamic calf muscle mapping than conventional elliptical phase-encoded acquisition46. Though spirals offer high acceleration, SNR efficiency, and customizable weighting, they are also limited by SBW and gradient system hardware.
Conventional MRSI FIDs commonly possess TE on the order of 1–2 ms, restricted by the duration of constant excitation pulses and phase encoding gradients to reach the outermost k-space points. This acquisition delay can be decreased using variable pulse widths and amplitudes. Sampling throughout gradient transition periods, or ramp sampling, remains an additional option for minimizing TE. Studies have demonstrated TE as low as 480 µs and 520 µs for EPSI and radial EPSI, respectively39,47. Acquisitions using such UTE-MRSI techniques48 have achieved TE = 300 µs at 3T and TE = 500 µs at 7T49,50. In non-Cartesian center-out k-space trajectories employing ramp sampling, TE is primarily limited by the dead time between coil transmit-receive switching, permitting the shortest possible TE. Despite this possibility, SBW constraints and conventional sequence parameter (TA/FOV) matching have prevented extensive investigation of non-Cartesian UTE 31P-MRSI.
In this study, we evaluate the PETALUTE 31P-MRSI with a novel rosette k-space trajectory by comparing its performance to conventional 3D weighted Cartesian 31P-MRSI in the quadriceps muscle at 3T. We ultimately aim to demonstrate its potential value in clinical spectroscopic acquisitions.
Methods
k-space trajectory designs for MRSI
PETALUTE
General sequence parameters were as follows: TA = 36:00, TR = 350 ms, TE = 65 µs, matrix size (\(\:{N}_{x}{\times\:N}_{y}\times\:{N}_{z}\)) = 24\(\:\times\:\)24\(\:\times\:\)24, nominal voxel size = 8 mL, FOV = 480\(\:\times\:\)480\(\:\times\:\)480 mm3, SBW = 2083 Hz, time samples = 512. Parameters are summarized in Table 1.
As in prior work26, 3D PETALUTE k-space trajectory (Fig. 1) for 31P-MRSI was generated with Eqs. (1) and (2):
Where K max is the furthest distance in k-space (= 25 cycle/m in this study), the radial direction oscillation frequency (\(\:{\omega\:}_{1}\)) and the angular direction oscillation frequency (\(\:{\omega\:}_{2}\)) were set equally (\(\:{{\omega\:}_{1}=\omega\:}_{2}\)), \(\:\phi\:\) determines the z-axis location, which was sampled uniformly in the range of [-\(\:\pi\:\)/2, \(\:\pi\:\)/2], and \(\:\beta\:\) determines the initial angular direction phase, which was sampled uniformly in the range of [0, 2\(\:\pi\:\)].
Other imaging parameters included: hard rectangular RF pulse duration = 50 µs, flip angle α = 20°, dwell time Δt = 5 µs in the readout, and each rosette petal designed with Npp = 96 points. This leads to
as well as
and the resulting − 20 to + 20 ppm in the 3T spectral range is more than sufficient for 31P-MRS. In reconstruction, each petal was downsampled to Npp = 48 by averaging the oversampled points. With a matrix size of 24\(\:\times\:\)24\(\:\times\:\)24 for the reconstruction, the required number of petals (Np) to satisfy Nyquist criterion was calculated as
However, due to the rosette’s efficient sampling scheme, only 79.8% coverage (i.e., Np = 1444) was defined as full k-space acquisition. Thus, the acquisition time per average was calculated as
or roughly 9 min. A complete description including the influence of trajectory parameters, Nyquist criterion, and the specific gradient ramp-up of this 3D rosette k-space pattern is provided in earlier work (Shen et al.)26.
Conventional weighted MRSI
Conventional Cartesian 3D acquisitions used the vendor-provided 31P-MRSI FID with k-space weighting and Hanning filter. Sequence parameters were as follows: TA = 36:56, TR = 1000 ms, TE = 2.3 ms, matrix size (\(\:{N}_{x}\times\:{N}_{y}\times\:{N}_{z}\)) = 16\(\:\times\:\)16\(\:\times\:\)16, nominal voxel size = 8 mL, FOV = 320\(\:\times\:\)320\(\:\times\:\)320 mm3, SBW = 2200 Hz, time samples = 512. The acquisition used the vendor H-Sinc excitation pulse with 1.28 ms duration and α = 90°.
Parameters are summarized in Table 1.
Simulations
To assess the theoretical performance of the PETALUTE relative to conventional weighted MRSI, MATLAB (MathWorks, Natick, USA) simulations were run examining side lobes and SNR relative to the spatial response function (SRF). A simple, constant 3D object was placed at the origin of a 48\(\:\times\:\)48\(\:\times\:\)48 grid (FOV = 480 mm isotropic producing a nominal voxel size = 1 mL) and reconstructed using the non-uniform FFT (NUFFT) method51 and k-space information for each in vivo acquisition. We discuss both SRF and point spread function (PSF) since the former specifically estimates side lobes and signal bleed between adjacent voxels, while the latter measures contribution from a single object point to the entire population of voxels.
Experimental comparison
All data acquisition occurred on a 3T MRI system (Prisma, Siemens, Erlangen, Germany) with Gmax = 80 mT/m and slew rate = 200 mT/m/ms isotropic. This study conforms to the Declaration of Helsinki, with all protocols approved and conducted in accordance with the Institutional Review Boards of Purdue University. Written informed consent was obtained from all human subjects.
The rosette and conventional acquisitions were tested with a uniform 2-liter bottle phantom (0.17 mg/mL phosphoric acid) using a dual-tuned 1H/31P Tx/Rx flexible 11-cm surface coil (RAPID Biomedical). For in vivo comparison, five healthy volunteers (BMI = 26 ± 2 kg/m2; age = 29 ± 5 years; 2 f / 3 m) received leg scans with an 8-channel, dual-tuned 1H/31P Tx/Rx phased array coil52 (Stark Contrast, Erlangen, Germany). Quadriceps was chosen for its superior PCr SNR and absence of respiratory motion during prolonged scanning. Subjects were positioned feet-first and supine, with the upper quadriceps tightly surrounded by the coil plates. Following localizer imaging, the adjustment volume was manually positioned (spanning both legs), and linewidth was minimized using a 3D GRE field map and interactive Siemens shimming. Each subject was scanned first with the conventional weighted Cartesian acquisition followed uninterrupted by the PETALUTE 31P-MRSI.
Post-processing and reconstruction
Raw data files were exported for reconstruction and pre-processing in MATLAB. Gridding and FFT were completed using adjoint, type 2 (forward) NUFFT regridding53 and density compensation according to the Pipe method54. Data were Hanning filtered and, when necessary, coil-combined using whitened singular value decomposition (wSVD) with the noise covariance matrix (Σ) approximated from spectral regions without signal55. Spectra from the PETALUTE were zero-order phased by maximizing the integral of the largest peak (PCr, 0 ppm). Spectra from the conventional weighted MRSI were both zero-order phased and first-order phased to correct a 2.3-ms delay.
SNR and quantification
Spectra were fitted within the Oxford Spectroscopy Analysis (OXSA) toolbox56 using AMARES methods. Metabolite peak SNRs were calculated from real-valued spectra according to Eq. (3), with noise variance calculated from a residual region lacking metabolite signals. As an additional signal quantification metric, “raw SNR” (Eq. (4)) was estimated by dividing the highest absolute-value peak point by the noise variance in an off-spectrum region; this method carries the advantage of consistently assessing signal strength regardless of any interfering spectral phase.
Figures 2 and 3 summarize data acquisition, reconstruction, processing, and analysis workflow.
Workflow of data acquisition, reconstruction, processing, and analysis. Subjects were positioned feet-first supine with both quadriceps positioned between the 30-cm phased array coil plates. Raw data were exported, appropriately reconstructed, coil-combined, and phased prior to fitting and quantification.
Quantitative analysis
The performance of PETALUTE and weighted MRSI in phantom solution and quadriceps muscle were assessed using Pi and PCr metabolite signals, respectively. Quantification considered the central, highest signal axial slices within each subject, attempting to quantify every voxel. Only voxels with SNR > 3 and OXSA-AMARES Cramér-Rao lower bound (CRLB) goodness of fit smaller than 20% for PCr peak were included in the final analysis. The statistical significance of SNR results was assessed using right-tailed Welch’s t-tests.
Results
Spatial response function simulation comparison of PETALUTE with weighted MRSI
The impact of varying k-space sampling trajectories on image quality can be evaluated via SRF simulations as shown in Fig. 4. FWHMs along the x-axis at the center of the FOV were comparable between rosette (30.7 mm) and weighted MRSI (36.1 mm). Both acquisition schemes exhibit noticeable sidelobe noise, albeit with slightly reduced side lobes in the rosette trajectory close to the object origin.
Results of spatial response function (SRF) simulation for novel 3D PETALUTE and conventional 3D weighted MRSI sequences. (A) 2D (xy-plane) SRFs for simulated object and each k-space trajectory at center of the FOV. (B) 1D (x-axis) log10 decibel comparison between k-space trajectories at center of the FOV. (C) 1D (x-axis) comparisons between each normalized reconstruction and the true simulated object at center of the FOV.
Phantom comparison of PETALUTE with weighted MRSI
Figure 5 presents results and setup of phantom experiments with dual-tuned flexible surface coil. With approximately matched acquisition times, mean raw SNR (Eq. 4) was 69% higher in PETALUTE than in weighted MRSI. Spectral linewidth was approximately identical between the two acquisitions. Right-tailed t-test confirmed the statistical significance of rosette’s SNR advantage (p < 0.001).
Results from phantom measurements using “raw SNR” (Eq. 4) of absolute inorganic phosphate (Pi) metabolite signal. (A) With approximately matched acquisition times, PETALUTE’s mean SNR was 69% higher. (B) As both sequences share the same nominal resolution, example axial SNR maps show clear signal intensity across a width of 5 voxels (equivalent to 100 mm). (C) A uniform 100-mm diameter Pi bottle phantom was prepared and used for both measurements.
In vivo leg comparison of PETALUTE with weighted MRSI
Figure 6 shows representative PETALUTE and weighted MRSI axial PCr maps and spectra in the same volunteer. High-signal muscle regions are clearly distinguishable from low-signal bony femur regions. As expected, PCr predominates the 31P muscle spectrum alongside smaller Pi and ATP peaks.
(Left) Example axial slice raw PCr SNR maps from both acquisitions for one quadriceps subject. Both protocols clearly discriminate between high signal muscle tissue and low signal femur region. (Right) Unfiltered magnitude spectra from each method in the highlighted muscle (red) and bone (green) voxels scaled to the maximum PCr peak amplitude. Stated spectral SNR is for PCr peak.
Figure 7 provides the quantitative PCr results for all subjects, illustrating the different SNRs obtained from Eqs. (3) and (4), respectively. Tables 2 and 3, and 4 summarize these distinctions. While PETALUTE consistently outperformed weighted MRSI, the advantage was slightly more prominent in AMARES-fitting of the real data at 34% compared to raw SNR of absolute data at 18%. CRLBs for quantified voxels (see Supplementary Table S1) were well below the 20% limit, with a mean below 3% in all subjects. PCr peak spectral linewidth was nearly matched between the two acquisitions (see Supplementary Table S2) with FWHMs around 4 Hz or below. Right-tailed t-tests confirm the statistical significance of PETALUTE’s higher SNR in both cases (p < 0.001).
(A) Measured PCr SNR (mean ± SD) from OXSA-AMARES quantifiable voxels across all five quadriceps subjects using each acquisition scheme and real data (Eq. 3). By this quantification metric, PETALUTE outperforms weighted MRSI by approximately 34% in vivo. (B) Measured raw PCr SNR (mean ± SD) from quantifiable voxels across all five quadriceps subjects and bottle phantom using each acquisition scheme and absolute data (Eq. 4). By this quantification metric, PETALUTE outperformed weighted MRSI by approximately 69% in phantom and 18% in vivo. Detailed results are provided in Tables 2 and 3.
Discussion
Experimental overview
This study demonstrates the feasibility of using PETALUTE 31P-MRSI with a novel rosette k-space trajectory to acquire quality in vivo human subject data. Simulations showed the rosette trajectory produced acceptable image quality and SRF characteristics when compared to a conventional 3D weighted MRSI acquisition. Experimental phantom scans utilized a uniform Pi bottle solution, and the same scanning parameters were later applied to in vivo quadriceps subjects.
UTE advantages
The novel acquisition’s 70-µs acquisition delay is substantially lower than the 300-500-µs delays in previously published UTE 31P-MRSI methods49,50, minimizing transverse signal decay and first-order dephasing. Accurate phasing is key to spectral fitting and quantification of real spectral data; when fitting parameters must be tailored to hundreds of voxels across a large volume, such as for high resolution 3D MRSI, the challenge of avoiding phasing errors is most apparent. As expected, all PETALUTE data were intrinsically devoid of noticeable first-order phasing, thereby streamlining the quantification process. The SNR gap between PETALUTE and weighted MRSI acquisitions was narrowed when solely considering absolute data (Eq. 4). This distinction might be partially explained by the absence of phase in these magnitude spectra, whereby the PETALUTE (TE = 70 µs) acquisition loses a portion of its advantage over conventional weighted MRSI (TE = 2.3 ms). Notably, SDs for PETALUTE SNR were significantly higher (50% or more) compared to weighted MRSI. This elevated variation is partially explained by the novel acquisition’s significantly higher SNR; moreover, weighted MRSI’s slightly wider SRF engenders higher inter-voxel crosstalk, diminishing overall variation among quantified voxels.
Acceleration potential
Although these 36-minute acquisitions are quite lengthy, conventional ungated in vivo 3D 31P-MRSI typically requires a minimum of 20 min at 3T. Compared to a weighted Cartesian trajectory, this novel rosette k-space pattern’s relative incoherence makes it a very suitable candidate for CS acceleration via undersampling. Applying undersampling factors of 2 to 4, as demonstrated previously in ultra-short transverse relaxation time (uT2) brain imaging26 and sodium quantification30, could reduce PETALUTE 31P-MRSI’s TA to 9–18 min (or less with fewer averages)57. Such ongoing investigations58 could allow implementation of 31P-MRSI within realistic clinical constraints, while also being translatable to UHF research systems and higher resolutions.
As with all 31P-MRS, spectral quality can also see potential improvement via proton decoupling and nuclear Overhauser effect (NOE) enhancement, albeit with implications for SAR and measured metabolite ratios22. Furthermore, appropriately applied low-rank approximation and principal component analysis denoising have seen use in heightening SNR of MRSI data sets;59,60,61 nevertheless, in the absence of ground truths or precise simulation, care must be taken in estimating metabolite concentration uncertainties after denoising.
Resolution and SBW
Many non-Cartesian acquisitions face restrictions in spatial resolution, SBW, and SNR due to available gradient hardware33. For example, spiral trajectories face reduced SNR while waiting to return to k-space center between spirals; this inefficiency is addressed by closed-loop, out-in trajectories62, but these remain impractical outside UHF animal gradient systems. Concentric rings can be similarly adjusted to meet needs with temporal interleaves43. Recent work with silent EPSI and gradient insert hardware shows remarkable promise in addressing these constraints63.
Clearly, SBW limitations are a significant challenge; although 2.0 kHz might be sufficient for 31P-MRS at 3T, such a SBW would only offer a spectral range of around 17 ppm at 7T. While this rosette acquisition sampled 48 points per petal every 480 µs, the sequence remains highly customizable. By leveraging the second half of each petal (Fig. 1), it is possible to partially satisfy Nyquist criterion at even higher bandwidths and enable finer resolution reconstructions than the relatively coarse 8 mL voxels shown here. Additionally, this permits greater SBW acquisitions, opening the door to PETALUTE 31P-MRSI at UHF and 1H-MRSI at 7T and higher magnetic fields64. However, these petal halves are analogous to odd and even echoes of EPSI MRSI; since the timings between individual Npp are not equidistant, such “full-petal” spectra will suffer from some degree of noise amplification and aliasing artifact.
Other limitations
Further experimentation is required in exploring the potential and limitations of PETALUTE MRSI. Notably, these scans focused on quadriceps muscle with plentiful PCr signal in a healthy volunteer population. However 31, P-MRSI is frequently applied in measuring diverse brain, cardiac, and liver spectra, where nearby tissues may introduce contaminating metabolite signals. Minimal signal contamination was observed in noisy voxels within bony regions. Nonetheless, due to the relative uniformity of skeletal muscle spectra, it would be difficult to discern the rosette acquisition’s relatively incoherent aliasing. As clinical implementation of 31P-MRSI necessitates faster acquisition, future work will aim to assess accelerated performance in patient populations.
Notably, these acquisitions did not account for gradient delays in the reconstruction. Since rosette petals gradually evolve from Kz max (a straight line) to Kz = 0 (a round circle), the slew rate and velocity change for petals in different Kz locations. Thus, the gradient delays will have variable impact, introducing an uncertainty in reconstruction which must be better accounted for in rigorous quantitative mapping. Similarly, B1-homogeneity can substantially impact measured metabolite signals. While operators performed manual transmit voltage calibration on the vendor adjustment platform before acquisition, variability in B1 remains a clear limitation. Future applications should incorporate T1/B1 mapping to maximize quantitative accuracy across large volumes with multiple metabolites, especially at UHF.
Conclusions
Using the quadriceps of five healthy volunteers at 3T, we investigated a potential application to 31P-MRSI using a novel 3D UTE rosette sequence. In comparison to conventional weighted Cartesian MRSI with matched bandwidth, nominal resolution, and acquisition time, the novel rosette acquisition provided competitive resolution and superior SNR with straightforward quantification. As this proof-of-concept study was limited to five subjects and a relatively homogeneous region of PCr-plentiful muscle, additional testing is required to demonstrate efficacy in differentiating diverse and diseased tissue regions.
Data availability
Data are available upon reasonable request, by contacting the first author (bbozymsk@purdue.edu).
References
Ackerman, J. J. H., Grove, T. H., Wong, G. G., Gadian, D. G. & Radda, G. K. Mapping of metabolites in whole animals by 31P NMR using surface coils. Nature 283, 167–170 (1980).
Chance, B., Im, J., Nioka, S. & Kushmerick, M. Skeletal muscle energetics with PNMR: Personal views and historic perspectives. NMR Biomed. 19, 904–926 (2006).
Chance, B., Eleff, S., Leigh, J. S., Sokolow, D. & Sapega, A. Mitochondrial regulation of phosphocreatine/inorganic phosphate ratios in exercising human muscle: A gated 31P NMR study. Proc. Natl. Acad. Sci. U S A. 78, 6714 (1981).
Podo, F. Tumour phospholipid metabolism. https://doi.org/10.1002/(SICI)1099-1492(199911)12:7 (1999).
Cox, I. J. et al. In vivo and in vitro 31P magnetic resonance spectroscopy of focal hepatic malignancies. NMR Biomed. 5, 114–120 (1992).
Bell, J. D. & Bhakoo, K. K. metabolic changes underlying 31 P MR spectral alterations in human hepatic tumours. https://doi.org/10.1002/(SICI)1099-1492(1998110)11:7 (1998).
Dagnelie, P. C. et al. Abnormal liver metabolism in cancer patients detected by 31 P MR spectroscopy. https://doi.org/10.1002/(SICI)1099-1492(199912)12:8 (1999).
Dagnelie, P. C. & Leij-Halfwerk, S. Magnetic resonance spectroscopy to study hepatic metabolism in diffuse liver diseases, diabetes and cancer. World J. Gastroenterol.: WJG 16, 1577 (2010).
Glazer, G. M. et al. Image localized 31P magnetic resonance spectroscopy of the human liver. NMR Biomed. 1, 184–189 (1989).
Seelen, L. W. F. et al. Prospective of 31 P MR Spectroscopy in Hepatopancreatobiliary Cancer: a systematic review of the literature. J. Magn. Reson. Imaging 57, 1144–1155 (2023).
Scheuermann-Freestone, M. et al. Abnormal cardiac and skeletal muscle energy metabolism in patients with type 2 diabetes. Circulation 107, 3040–3046 (2003).
Jett, S. et al. Systematic review of 31P-magnetic resonance spectroscopy studies of brain high energy phosphates and membrane phospholipids in aging and Alzheimer’s disease. Front. Aging Neurosci. 15, 1183228 (2023).
Tsampasian, V., Cameron, D., Sobhan, R., Bazoukis, G. & Vassiliou, V. S. Phosphorus magnetic resonance spectroscopy (31P MRS) and cardiovascular disease: The importance of energy. Med. (Kaunas) 59(1), 174 (2023).
Rider, O. J. et al. Effects of catecholamine stress on diastolic function and myocardial energetics in obesity. Circulation 125, 1511–1519 (2012).
Levelt, E. et al. Cardiac energetics, oxygenation, and perfusion during increased workload in patients with type 2 diabetes mellitus. Eur. Heart J. 37, 3461–3469 (2016).
Maris, J. M. et al. 31P nuclear magnetic resonance spectroscopic investigation of human neuroblastoma in situ. N Engl. J. Med. 312, 1500–1505 (1985).
Pinggera, D. et al. Repeated 31P-Magnetic resonance spectroscopy in severe traumatic brain Injury: insights into cerebral energy status and altered metabolism. J. Neurotrauma 38, 2822–2830 (2021).
Gadian, D. G., Dawson, M. J. & Wilkie, D. R. Contraction and recovery of living muscles studies by 31P nuclear magnetic resonance. J. Physiol. 267, 703–735 (1977).
Ross, B. D. et al. Examination of a case of suspected McArdle’s syndrome by 31P nuclear magnetic resonance. N Engl. J. Med. 304, 1338–1342 (1981).
Valkovič, L., Chmelík, M. & Krššák, M. In-vivo31P-MRS of skeletal muscle and liver: A way for non-invasive assessment of their metabolism. Anal. Biochem. 529, 193–215 (2017).
Meyerspeer, M., Krššák, M. & Moser, E. Relaxation times of 31P-metabolites in human calf muscle at 3 T. Magn. Reson. Med. 49, 620–625 (2003).
Meyerspeer, M. et al. 31 P magnetic resonance spectroscopy in skeletal muscle: Experts’ consensus recommendations. NMR Biomed. 34(5), e4246 (2020).
Jonuscheit, M. et al. Reproducibility of absolute quantification of adenosine triphosphate and inorganic phosphate in the liver with localized 31P-magnetic resonance spectroscopy at 3-T using different coils. NMR Biomed. 37 (8), e5120 (2024).
Rodgers, C. T. et al. Human cardiac 31P magnetic resonance spectroscopy at 7 tesla. Magn. Reson. Med. 72, 304 (2014).
Noll, D. C. Multishot rosette trajectories for spectrally selective mr imaging. IEEE Trans. Med. Imaging 16, 372–377 (1997).
Shen, X. et al. Ultra-short T2 components imaging of the whole brain using 3D dual-echo UTE MRI with rosette k-space pattern. Magn. Reson. Med. 89, 508–521 (2023).
Shen, X. et al. 3D balanced SSFP UTE MRI for multiple contrasts whole brain imaging. Magn. Reson. Med. 92, 702–714 (2024).
Shen, X. et al. High-resolution 3D ultra-short echo time MRI with Rosette k-space pattern for brain iron content mapping. J. Trace Elem. Med. Biol. 77, 127146 (2023).
Monsivais, H. et al. Ultrashort-echo time magnetization transfer (UTE-MT) for brain iron imaging. in Presented During ISMRM Annual Meeting & Exhibition; June 3–8, 2023; Toronto, CA.
Villarreal, C. X. et al. An Accelerated PETALUTE MRI sequence for in vivo quantification of sodium content in human articular cartilage at 3T. Skeletal Radiol (2024).
Bozymski, B. et al. Comparison of compressed sensing accelerated rosette UTE and conventional 31P 3D MRSI at 3T in leg muscle. in Presented During ISMRM Annual Meeting & Exhibition; June 3–8, 2023; Toronto, CA.
Li, Y. et al. Analysis of generalized rosette trajectory for compressed sensing MRI. Med. Phys. 42, 5530–5544 (2015).
Bogner, W., Otazo, R. & Henning, A. Accelerated MR spectroscopic imaging: A review of current and emerging techniques. NMR Biomed. 34, e4314 (2021).
Bakermans, A. J. et al. In vivo mouse myocardial (31)P MRS using three-dimensional image-selected in vivo spectroscopy (3D ISIS): Technical considerations and biochemical validations. NMR Biomed. 28, 1218–1227 (2015).
de Wit-Verheggen, V. H. W. et al. PCr/ATP ratios and mitochondrial function in the heart: A comparative study in humans. Sci. Rep. 13, 8346 (2023).
Korzowski, A. & Bachert, P. High-resolution 31 P echo-planar spectroscopic imaging in vivo at 7T. Magn. Reson. Med. 79, 1251–1259 (2018).
Cunningham, C. H. et al. Design of flyback echo-planar readout gradients for magnetic resonance spectroscopic imaging. Magn. Reson. Med. 54, 1286–1289 (2005).
Santos-Díaz, A., Obruchkov, S. I., Schulte, R. F. & Noseworthy, M. D. Phosphorus magnetic resonance spectroscopic imaging using flyback echo planar readout trajectories. MAGMA 31, 553–564 (2018).
Santos-Díaz, A., Harasym, D. & Noseworthy, M. D. Dynamic 31 P spectroscopic imaging of skeletal muscles combining flyback echo-planar spectroscopic imaging and compressed sensing. Magn. Reson. Med. 81, 3453–3461 (2019).
Posse, S., Tedeschi, G., Risinger, R., Ogg, R. & Bihan, D. Le. High speed 1H spectroscopic imaging in human brain by echo planar spatial-spectral encoding. Magn. Reson. Med. 33, 34–40 (1995).
Cunningham, C. H. et al. Pulse sequence for dynamic volumetric imaging of hyperpolarized metabolic products. J. Magn. Reson. 193, 139–146 (2008).
Nam, K. M. et al. Deuterium echo-planar spectroscopic imaging (EPSI) in the human liver in vivo at 7 T. Magn. Reson. Med. 90, 863–874 (2023).
Clarke, W. T. et al. Three-dimensional, 2.5-minute, 7T phosphorus magnetic resonance spectroscopic imaging of the human heart using concentric rings. NMR Biomed. 36(1), e4813 (2023).
Furuyama, J. K., Wilson, N. E. & Thomas, M. A. Spectroscopic imaging using concentrically circular echo-planar trajectories in vivo. Magn. Reson. Med. 67, 1515–1522 (2012).
Adalsteinsson, E. et al. Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magn. Reson. Med. 39, 889–898 (1998).
Valkovič, L. et al. Dynamic 31P–MRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7 T. NMR Biomed. 29, 1825 (2016).
Ludwig, D., Korzowski, A., Ruhm, L., Ladd, M. E. & Bachert, P. Three-dimensional 31P radial echo-planar spectroscopic imaging in vivo at 7T. in Presented during ISMRM 25th Annual Meeting and Exhibition; April 22–27, 2017; Honolulu, HI.
Robson, M. D., Tyler, D. J. & Neubauer, S. Ultrashort TE Chemical Shift Imaging (UTE-CSI). Magn. Reson. Med. 53, 267–274 (2005).
Tyler, D. J. et al. Reproducibility of 31P cardiac magnetic resonance spectroscopy at 3 T. NMR Biomed. 22, 405–413 (2009).
Ellis, J., Valkovič, L., Purvis, L. A. B., Clarke, W. T. & Rodgers, C. T. Reproducibility of human cardiac phosphorus MRS (31P-MRS) at 7 T. NMR Biomed. 32(6), e4095 (2019).
Fessler, J. & Sutton, B. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 51, 560–574 (2003).
Panda, A. et al. Phosphorus liver MRSI at 3 T using a novel dual-tuned eight-channel 31P/1H H coil. Magn. Reson. Med. 68, 1346–1356 (2012).
Fessler, J. A. On NUFFT-based gridding for non-cartesian MRI. J. Magn. Reson. 188, 191–195 (2007).
Pipe, J. G. & Menon, P. Sampling density compensation in MRI: Rationale and an iterative numerical solution. Magn. Reson. Med. 41, 179–186 (1999).
Rodgers, C. T. & Robson, M. D. Receive array magnetic resonance spectroscopy: Whitened singular value decomposition (WSVD) gives optimal bayesian solution. Magn. Reson. Med. 63, 881–891 (2010).
Purvis, L. A. B. et al. An open-source magnetic resonance spectroscopy analysis toolbox in MATLAB. PLoS One 12, e0185356 (2017).
Farley, N., Bozymski, B., Dydak, U. & Emir, U. Fast 3D-P31-MRSI using custom rosette petal trajectory at 3T with 4x accelerated compressed sensing. in Presented during ISMRM Annual Meeting & Exhibition; June 3–8; Toronto, CA (2023).
Alcicek, S. et al. Multi-site ultrashort echo time 3D Phosphorous MRSI repeatability using novel rosette trajectory (PETALUTE). bioRxiv https://doi.org/10.1101/2024.02.07.579294 (2024).
Nguyen, H. M., Peng, X., Do, M. N. & Liang, Z. P. Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans. Biomed. Eng. 60, 78–89 (2013).
Clarke, W. T. & Chiew, M. Uncertainty in denoising of MRSI using low-rank methods. Magn. Reson. Med. 87, 574–588 (2022).
Froeling, M., Prompers, J. J., Klomp, D. W. J. & van der Velden, T. A. PCA denoising and Wiener deconvolution of 31P 3D CSI data to enhance effective SNR and improve point spread function. Magn. Reson. Med. 85, 2992–3009 (2021).
Esmaeili, M. et al. Whole-slab 3D MR spectroscopic Imaging of the human brain with spiral-out-In sampling at 7T. J. Magn. Reson. Imaging 53, 1237–1250 (2021).
Versteeg, E. et al. A silent echo-planar spectroscopic imaging readout with high spectral bandwidth MRSI using an ultrasonic gradient axis. Magn. Reson. Med. 91, 2247–2256 (2024).
Emir, U. E., Sawiak, S. Bridging the gap between Preclinical, Clinical, Metabolomics, MRI, MRS(I) methods via PETALUTE MRI. Presented at ISMRM Workshop on MR Spectroscopy: Frontiers in Molecular & Metabolic Imaging, Boston (2024).
Acknowledgements
This work was supported by grants to U.E. and S.S. from the Wellcome Trust Collaborative Award (223131/Z/21/Z). This project was funded with support from the Indiana Clinical and Translational Sciences Institute, funded in part by Award Number UM1TR004402 from the National Institutes of Health, National Center for Advancing Translational Sciences, Clinical and Translational Sciences Award.
Author information
Authors and Affiliations
Contributions
Conceptualization by U.E. & U.D.; Methodology contributions from all authors; Data collection by B.B., X.S. & U.E.; Data analysis by B.B., U.E., X.S. & W.T.C.; Results and conclusions reviewed and agreed upon by all authors. First manuscript draft and revision by B.B., U.E. & X.S.; Final revision and approval by all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bozymski, B., Shen, X., Özen, A. et al. Feasibility and comparison of 3D modified rosette ultra-short echo time (PETALUTE) with conventional weighted acquisition in 31P-MRSI. Sci Rep 15, 6465 (2025). https://doi.org/10.1038/s41598-025-90630-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-90630-y