Advanced predictive machine and deep learning models for round-ended CFST column

Abstract

Confined columns, such as round-ended concrete-filled steel tubular (CFST) columns, are integral to modern infrastructure due to their high load-bearing capacity and structural efficiency. The primary objective of this study is to develop accurate, data-driven approaches for predicting the axial load-carrying capacity (P_cc​) of these columns and to benchmark their performance against existing analytical solutions. Using an extensive dataset of 200 CFST stub column tests, this research evaluates three machine learning (ML) models – LightGBM, XGBoost, and CatBoost – and three deep learning (DL) models – Deep Neural Network (DNN), Convolutional Neural Network (CNN), and Long Short-Term Memory (LSTM). Key input features include concrete strength, column length, cross-sectional dimensions, steel tube thickness, and yield strength, which were analysed to uncover underlying relationships. The results indicate that CatBoost delivers the highest predictive accuracy, achieving an RMSE of 396.50 kN and an R² of 0.932, surpassing XGBoost (RMSE: 449.57 kN, R²: 0.906) and LightGBM (RMSE: 449.57 kN, R2: 0.916). Deep learning models were less effective, with the DNN attaining an RMSE of 496.19 kN and R² of 0.958, while the LSTM underperformed substantially (RMSE: 2010.46 kN, R²: 0.891). SHapley Additive exPlanations (SHAP) identified cross-sectional width as the most critical feature, contributing positively to capacity, and column length as a significant negative influencer. A user-friendly, Python-based interface was also developed, enabling real-time predictions for practical engineering applications. Comparison with 10 analytical models demonstrates that these traditional methods, though deterministic, struggle to capture the nonlinear interactions inherent in CFST columns, thus yielding lower accuracy and higher variability. In contrast, the data-driven models presented here offer robust, adaptable, and interpretable solutions, underscoring their potential to transform design and analysis practices for CFST columns, ultimately fostering safer and more efficient structural systems.

Introduction

Concrete-filled steel tubular (CFST) columns have garnered significant attention in modern construction due to their advantageous combination of steel and concrete properties. The steel tube provides confining pressure to the concrete core, enhancing its compressive strength, while the concrete prevents inward buckling of the steel tube¹. These synergistic interactions result in a composite system with high load-carrying capacity, improved ductility, and better energy absorption characteristics, making CFST columns ideal for structural applications subjected to axial and lateral forces². Despite their robust performance, predicting the axial load-carrying capacity of CFST columns remains a challenging task due to the complex interactions between their constituent materials and geometric configurations³.

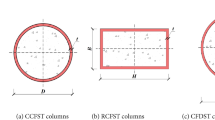
Traditionally, empirical and analytical models have been employed to estimate the axial load-carrying capacity of CFST columns. These models often rely on simplifying assumptions and idealized boundary conditions, which limit their accuracy, particularly for non-standard configurations such as stub columns with round ends⁴. Round-end CFST columns as shown in Fig. 1 exhibit unique stress distributions and failure mechanisms, further complicating the prediction process. Additionally, the axial load-carrying capacity is influenced by various factors, including the diameter-to-thickness ratio of the steel tube, the compressive strength of the concrete core, and the slenderness of the column. These interdependent variables demand a more sophisticated approach to achieve precise predictions.

Fig. 1

Round-ended CFST column (a) application in bridge (b) cross-section.

The advent of machine learning (ML) has opened new avenues for modelling complex engineering systems^5,6,7. ML algorithms, which leverage data-driven techniques, have shown remarkable potential in capturing nonlinear relationships between input parameters and output responses^8,9. In the context of CFST columns, ML models can integrate a wide range of parameters, including material properties, geometric configurations, and loading conditions, to predict the axial load-carrying capacity with high accuracy¹⁰. Several studies have demonstrated the efficacy of ML models, such as artificial neural networks (ANNs), support vector machines (SVMs), and decision tree-based ensembles, in predicting structural performance metrics^11,12. However, the application of ML to CFST columns with round ends remains relatively unexplored. ML approaches have sought to address the challenges posed by material nonlinearity, geometric effects, and boundary conditions, enabling the development of accurate predictive models and design guidelines¹³.

The progression of research into CFST columns is exemplified by studies such as Han et al.¹⁴, who explored double-skin tubular (DST) columns composed of stainless steel, concrete, and carbon steel. Their work highlighted the ductile behaviour of DST columns and provided simplified models for predicting their cross-sectional strengths, validated through extensive experimental testing. The findings underscored the influence of sectional parameters and tapering angles on structural performance, laying a foundation for subsequent explorations into confined concrete behaviour. A significant contribution to the understanding of round-ended CFST columns was made by Faxing et al.¹⁵ and Piquer et al.¹⁶, who employed finite element analysis (FEA) to simulate their behaviour under axial compression. These studies identified critical parameters such as the width–thickness ratio, concrete strength, and eccentricity, which significantly affect confinement and ultimate bearing capacity. Their models achieved high accuracy in replicating experimental observations, affirming the validity of FEA in addressing the intricacies of round-ended configurations. FEA has long been utilized as an effective tool for analysing and predicting structural behaviour across a wide range of applications^{17,18,19,20,21}.

Further refinement in modelling confined concrete systems was achieved^22,23, introducing advanced nonlinear FEA models tailored for eccentrically-loaded and round-ended rectangular CFST columns, respectively. These models successfully captured local buckling, shear failure, and the effects of geometric ratios on structural performance. Their work provided simplified empirical formulas that enhanced the applicability of CFST designs in practical engineering scenarios. Explorations into the effects of additional reinforcement within CFST systems were conducted^24,25. Ding et al.²⁴ demonstrated the enhanced ductility and bearing capacity achieved by incorporating rebars into track-shaped CFST columns, while Lu et al.²⁵ investigated the impact of stirrups in weathering steel tubular configurations. Both studies emphasized the role of reinforcement in improving structural stiffness, energy dissipation, and confinement effects, offering practical formulas for design optimization. Work has also expanded into specific geometric and material configurations^26,27,28. Wang et al.²⁶ highlighted the susceptibility of thin-walled, round-ended CFST columns to global buckling under slender geometries, whereas Ren et al.²⁷ examined the influence of central angles and tie bars on confinement efficiency and failure modes. Shen et al.²⁸ extended the understanding to cyclic loading scenarios, demonstrating the lateral strength and stiffness advantages of cold-formed round-ended CFST columns.

Material innovations have further enriched the field^29,30, investigating the integration of recycled aggregates and aluminium alloys in CFST systems. These studies provided insights into the mechanical and environmental benefits of alternative materials, alongside the development of stress-strain models and performance formulas that accurately reflect confinement and failure behaviours under axial and impact loading. Advancements in multi-chamber CFST configurations^31,32, have revealed significant improvements in energy dissipation and axial performance. Their studies demonstrated the benefits of additional chambers in enhancing confinement effects, especially under seismic and post-fire conditions. In parallel, innovative reinforcement techniques, such as incorporating steel fibres in beams and one-way slabs³³ or using new reinforcement configurations in rectangular squat structural walls³⁴, have also underscored the importance of enhanced ductility and load-bearing capacity across diverse structural applications.

Despite recent advancements in simplified prediction models for estimating the load-bearing capacity of confined concrete columns under axial and eccentric loads, these models continue to face limitations in accuracy and adaptability across varying conditions. To address these gaps, this study employs cutting-edge ML techniques, including Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), and Categorical Boosting (CatBoost), along with deep learning (DL) approaches such as Deep Neural Networks (DNN), Convolutional Neural Networks (CNN), and Long Short-Term Memory (LSTM) networks. These models are designed to leverage an extensive dataset comprising 200 experimental and FEM-generated samples, encompassing key input parameters such as concrete strength ($\:{f}_{c}^{{\prime\:}}$), column length ($\:h$), cross-sectional dimensions ($\:b\:\text{a}\text{n}\text{d}\:d$), steel tube thickness ($\:{t}_{s}$), and steel yield strength ($\:{f}_{ys}$). By efficiently capturing non-linear interactions and handling large or noisy datasets, these advanced methods provide robust and reliable predictions. Moreover, the interpretability of the ML models is evaluated to identify the most influential parameters governing load-carrying capacity, offering actionable insights for structural designers. The primary objectives of this study are to: (i) develop and validate advanced data-driven models for accurately predicting the axial load-carrying capacity of round-ended CFST columns, (ii) benchmark the performance of these models against existing analytical and finite element methods, and (iii) identify and quantify the critical structural parameters that govern load-carrying capacity to guide practical engineering design. Figure 2 presents a flowchart illustrating the workflow of the study conducted.

Fig. 2

Workflow of the present study.

Methodology

This study adopted a comprehensive approach that leverages an extensive dataset derived from existing experimental and FEM simulation studies available in the literature, with certain assumptions guiding the scope of our analysis. Specifically, we focus on round-ended CFST stub columns, treating the steel tube material properties as uniform and the steel–concrete interface as fully bonded. We also do not consider eccentric loading or extreme slenderness ratios, as these factors lie beyond the current study’s scope and will be explored in future work. The primary objective was to develop advanced ML and DL models capable of accurately predicting the axial load-carrying capacity of round-ended CFST stub columns. The dataset incorporated results from 200 columns as presented in Table 1, encompassing a wide range of experimental and FEM-simulated configurations reported in prior research, ensuring robust and diverse data coverage. The dataset was carefully curated by collecting and standardizing data points from multiple studies. Key parameters such as concrete compressive strength ($\:{f}_{c}^{{\prime\:}}$​), column length ($\:h$), cross-sectional dimensions (width ($\:b$) and depth ($\:d$)), steel tube thickness ($\:{t}_{s}$), and yield strength of the steel tube ($\:{f}_{ys}$) were extracted and tabulated in Table 1.

Table 1 Summary of key parameters and experimental configurations for the dataset.

This study utilized three ML models: XGBoost, LightGBM, CatBoost and three DL models: DNN, CNN, and LSTM, all implemented using the Python programming environment within the Anaconda software. When selecting models for a study, it’s crucial to consider the specific requirements and characteristics of your data and problem. XGBoost, LightGBM, and CatBoost are popular machine learning models due to their strengths in handling structured and tabular data. XGBoost is known for its powerful and efficient gradient boosting capabilities, making it suitable for a wide range of tasks. It manages large datasets effectively and is resistant to overfitting, often performing well in competitive environments. LightGBM offers fast training speeds and lower memory usage compared to other gradient boosting methods. It’s designed to handle large datasets and high-dimensional data efficiently, and it supports categorical features directly, which simplifies pre-processing. CatBoost, on the other hand, is specifically designed to handle categorical features with minimal pre-processing. It performs well on noisy data and is effective across various tasks, offering good performance with minimal parameter tuning.

For DL, the choice of models depends on the nature of your data. DNN is versatile and capable of modelling complex relationships in data. They are particularly useful when feature interactions are intricate and not easily captured by simpler models. CNN is highly effective for tasks involving spatial data, such as images or text with spatial components, due to their ability to capture hierarchical patterns. LSTM networks excel in learning from sequential data and capturing long-term dependencies. They are ideal for time series forecasting, natural language processing, and other applications where the order of data points is significant. Using both ML and DL models allows you to leverage the strengths of each approach. ML models like XGBoost, LightGBM, and CatBoost are often simpler to train and perform well on structured data. In contrast, deep learning models such as DNN, CNN, and LSTM are more suited for unstructured data and complex patterns.

Descriptive statistics

The dataset for this study has 70:30 split for training and testing purposes. The adopted models were trained using six input features (X1 to X6​) to predict the load-carrying capacity ($\:{P}_{cc}$) of confined columns. Table 2 summarizes the descriptive statistics for the input parameters and output. These parameters include the concrete strength of standard cylinders ($\:{f}_{c}^{{\prime\:}}$), the overall length of the column (h), the cross-section width (b), the cross-section depth (d), the thickness of the steel tube ($\:{t}_{s}$), and the yield strength of the steel tube ($\:{f}_{ys}$). The output parameter is the load-carrying capacity of the confined column ($\:{P}_{cc}$). Each parameter is described in terms of its unit, symbol, minimum and maximum values, mean, median, and standard deviation (SD).

Table 2 Descriptive statistics of inputs and output.

The concrete strength of standard cylinders ($\:{f}_{c}^{{\prime\:}}$) ranges from 23.91 MPa to 90.16 MPa, with a mean of 39.09 MPa and a median of 40.46 MPa. The standard deviation is 9.92 MPa, indicating a moderate spread around the mean. The overall length of the column (h) varies significantly, from 300 mm to 9600 mm. The mean length is 2455.47 mm, while the median is notably lower at 1600 mm. The standard deviation of 2324.80 mm indicates considerable variability in column lengths. The cross-section width (b) of the columns ranges from 100 mm to 806 mm, with a mean of 388.19 mm and a median of 396 mm. The standard deviation is 161.87 mm, showing moderate variability. The cross-section depth (d) ranges from 30 mm to 264 mm, with a mean of 186.17 mm and a median of 198 mm. The standard deviation is 55.31 mm. The thickness of the steel tube ($\:{t}_{s}$) ranges from 2 to 10 mm. The mean thickness is 4.14 mm, and the median is 3.80 mm, with a standard deviation of 1.27 mm. The yield strength of the steel tube ($\:{f}_{ys}$) varies from 195.20 MPa to 550 MPa, with a mean of 332.17 MPa and a median of 324.60 MPa. The standard deviation is 58.29 MPa. The load-carrying capacity of the confined column ($\:{P}_{cc}$), which is the output parameter, ranges widely from 103.20 kN to 10,143 kN. The mean capacity is 3251.11 kN, and the median is 2713.11 kN, with a standard deviation of 2152.14 kN.

Histograms

Figure 3 illustrates histograms representing the frequency distribution of the input features (X1 to X6​) and the output feature (Y). Each histogram provides a visual summary of how the values for each variable are distributed within specific ranges. For X1​, the majority of data points, approximately 165, are concentrated within the range of 23.91–46.00. The frequency declines sharply in the subsequent ranges, with only 30 data points between 46.00 and 68.08 and a minimal count of 5 in the 68.08–90.16 range. A similar trend is observed for X2, where the highest frequency of 156 occurs within the 300–3400 range, followed by a steep decline to 21 and 23 data points in the ranges of 3400–6500 and 6500–9600, respectively. The histogram for X3 exhibits a slightly different pattern, with the highest frequency of 95 data points in the middle range of 335.3–570.7. This is followed by a notable frequency of 75 in the lower range of 100–335.3, while the higher range of 570.7–806.0 has a lower frequency of 30.

For X4​, the majority of data points, numbering 137, fall within the upper range of 186–264, while the ranges of 30–108 and 108–186 contain 33 and 30 data points, respectively, indicating a distribution favouring higher values. In the case of X5​, the majority of the data points, 144, are concentrated in the lowest range of 2.000–4.667, with a significant drop to 50 in the next range of 4.667–7.333 and only 6 in the range of 7.333–10.000, highlighting the prevalence of smaller values. The histogram for X6 shows a peak frequency of 104 in the middle range of 313.5–431.7, followed by 88 data points in the lower range of 195.2–313.5, while the upper range of 431.7–550.0 has only 8 data points, signifying a skew towards mid-range values. The output feature (Y) exhibits the highest frequency, 120 data points, in the lowest range of 103–3450, with a steady decline to 63 and 17 data points in the ranges of 3450–6796 and 6796–10,143, respectively. This distribution indicates that the majority of the output data is concentrated in the lower value range.

Fig. 3

Histograms of studied features.

Correlation analysis

Figure 4 depicts the correlation matrix in the form of a heatmap, offering a quantitative assessment of the relationships between X1 to X6​ and Y. The intensity of the heatmap’s colours corresponds to the magnitude of the correlation coefficients, with darker red indicating strong positive correlations and darker blue representing strong negative correlations. The diagonal elements naturally show a perfect correlation for each variable with itself.

Fig. 4

Heatmap correlation matrix.

The correlation between X1 (concrete strength of the standard cylinder) and other variables is generally weak. X1 has a slight positive correlation with X3 (cross-section width) at 0.13, X5 (thickness of the steel tube) at 0.08, X6 (yield strength of the steel tube) at 0.14, and Y (load-carrying capacity of the confined column) at 0.24. These positive values, though weak, indicate that as the concrete strength increases, these variables tend to increase slightly as well. The correlation between X1 and X2 (overall length of the column) and X4 (cross-section depth) is close to zero, suggesting little to no linear relationship. X2 shows a range of correlations with other variables. The correlation between X2 and X4 is 0.39, indicating a moderate positive relationship, where an increase in the overall length of the column is associated with an increase in cross-section depth. X2 also has a weak positive correlation with X3 at 0.18 and X5 at 0.20. Interestingly, X2 has a weak negative correlation with X6 at -0.13 and Y at -0.35, indicating that longer columns tend to have slightly lower yield strengths and load-carrying capacities. X3 exhibits moderate to strong correlations with several variables. The correlation with X4 is 0.43, indicating that wider columns tend to have greater depths. The strongest correlation observed is between X3 and Y at 0.72, suggesting that an increase in the cross-section width is strongly associated with an increase in the load-carrying capacity of the confined column. The correlations with X5 and X6 are weaker, at 0.14 and − 0.12 respectively.

X4 shows moderate correlations with a few variables. Besides the already mentioned correlations with X2 and X3, X4 has a moderate positive correlation with X5 at 0.44, indicating that columns with greater depths tend to have thicker steel tubes. The correlation between X4 and X6 is nearly zero at -0.09, suggesting no significant linear relationship. X5, the thickness of the steel tube, shows some noteworthy correlations. In addition to its moderate correlation with X4, X5 has a weak positive correlation with Y at 0.29, indicating that thicker steel tubes are slightly associated with higher load-carrying capacities. The correlation with X6 is very weak at 0.06, suggesting little to no relationship between steel tube thickness and yield strength.

Finally, Y, the load-carrying capacity of the confined column, exhibits various levels of correlation with the input variables. The strongest positive correlation is with X3 at 0.72, highlighting the significant impact of cross-section width on load-carrying capacity. Y also shows moderate correlations with X4 (0.42) and X5 (0.29), indicating that columns with greater depths and thicker steel tubes tend to have higher load-carrying capacities. The correlation with X6 is weak at 0.06, suggesting a minimal relationship between yield strength and load-carrying capacity.

Description of ML/DL models

XGBoost is a highly effective and versatile ML library that excels in handling large datasets and complex predictive modeling tasks⁴⁰. Its ability to handle missing values, regularization techniques, and parallel processing capabilities make it a reliable choice for various applications. With its high accuracy, speed, and scalability, XGBoost is a popular choice for many industries, including finance, computer vision, and natural language processing⁴¹. Overall, XGBoost is a powerful tool for data scientists and machine learning engineers, offering a robust and efficient way to build predictive models that can drive business decisions and improve outcomes.

LightGBM is a fast and efficient gradient-boosting framework designed for large-scale machine learning tasks⁴². It aims to outperform other popular gradient-boosting libraries, such as XGBoost, in terms of speed and scalability while maintaining comparable performance. LightGBM is highly effective at handling large datasets and complex models, making it a preferred choice for applications such as classification, regression, and ranking tasks. The core idea of the histogram algorithm in LightGBM is to convert successive floating-point eigenvalues into k integers and create a histogram of width k. During data traversal, statistics are accumulated in the histogram based on the discretized values as indices. Once the data traversal is complete, the histogram contains the necessary statistics, and the optimal split point is determined according to the discrete histogram values.

CatBoost is a powerful machine learning algorithm designed for handling categorical features and producing accurate predictions^43,44. It is a variant of gradient boosting that can handle both categorical and numerical features without requiring preprocessing like one-hot encoding or label encoding. CatBoost employs its built-in encoding system called “ordered boosting” to process categorical data directly, resulting in faster training and better model performance⁴⁵. It is particularly useful for regression tasks where the goal is to predict a continuous target variable. CatBoost is known for its speed, accuracy, and ease of use, especially in situations involving structured data with many categorical features⁴⁶. It also offers feature relevance rankings that help with feature selection and understanding model choices.

DNNs are a class of artificial neural networks with multiple layers between the input and output layers. They are capable of learning complex patterns in data through a process called backpropagation. DNNs are versatile and can be applied to various regression tasks, such as predicting continuous outcomes based on input features. Their architecture allows them to model non-linear relationships, making them suitable for complex datasets where traditional linear regression may fail⁴⁷.

CNNs are primarily designed for processing grid-like data, such as images. They utilize convolutional layers that apply filters to the input data, capturing spatial hierarchies and patterns⁴⁸. While CNNs are predominantly used in image classification and recognition tasks, they can also be adapted for regression tasks, particularly when dealing with spatial data or time-series data reshaped into a grid format. For instance, CNNs can be combined with LSTMs to handle sequential data, leveraging their ability to extract features while maintaining temporal dependencies.

LSTMs are a specialized type of recurrent neural network (RNN) designed to learn from sequences of data. They are particularly effective for time-series prediction tasks because they can maintain long-term dependencies and remember information over extended sequences. This capability makes LSTMs suitable for regression tasks involving temporal data, such as forecasting stock prices or weather patterns. LSTMs can be used alone or in combination with CNNs to enhance prediction accuracy by capturing both spatial and temporal features⁴⁹.

Hyperparameters tuning

Selecting the right hyperparameters is essential for optimizing machine learning model performance⁵⁰. While grid search (GS) and random search (RS) are commonly used, they can be time-consuming and less efficient due to high variance and lack of integration of previous evaluations⁵¹. In contrast, Bayesian optimization (BO) refines the search using past evaluations, improving efficiency and reducing the number of trials needed⁵². This study adopts BO for hyperparameter optimization. To prevent overfitting and ensure model robustness, a 5-fold cross-validation (CV) integrated with BO (BO + 5CV) is used, ensuring reliable and generalizable predictions.

In ML and DL, hyperparameters are external configurations that control the training process of a model. They are set before the learning process begins and remain constant during training. Unlike model parameters, which are learned from the data, hyperparameters are predefined and play a crucial role in determining the model’s performance and its ability to generalize to new data.

In ML models, several hyperparameters are particularly influential. The number of estimators refers to the count of trees in ensemble methods, directly affecting model complexity and performance. A higher number of estimators can lead to better learning but may also increase the risk of overfitting. The learning rate controls the magnitude of weight adjustments during training; a smaller learning rate can lead to more precise convergence but requires more iterations. Maximum depth sets the deepest level of each tree, influencing the model’s ability to capture data complexity; deeper trees can model more intricate patterns but may also capture noise. Minimum child weight specifies the minimum sum of instance weights needed in a child node, aiding in preventing overfitting by controlling tree splitting. Subsample ratio indicates the fraction of the training data utilized for each tree, introducing randomness to enhance generalization. Column subsample ratio (colsample_bytree) denotes the proportion of features sampled for tree construction, promoting model diversity and reducing overfitting. L2 leaf regularization (l2_leaf_reg) applies L2 regularization to leaf weights, helping to prevent overfitting by penalizing large weights.

In DL models, hyperparameters also play an essential role. The number of units in dense layers determines the count of neurons in fully connected layers, affecting the model’s capacity to learn representations. In CNNs, the number of filters specifies the quantity of filters in convolutional layers, influencing the model’s ability to detect various features in input data, while kernel size defines the dimensions of the convolutional filter, affecting the receptive field and the granularity of feature detection. In LSTM networks, the number of units sets the number of memory cells in LSTM layers, impacting the model’s capability to capture temporal dependencies. The activation function determines the output of neurons, introducing non-linearities that enable the model to learn complex patterns.

Evaluation criteria

Evaluating the effectiveness of machine learning models is pivotal to ensuring their reliability and applicability, particularly when predicting complex phenomena such as the axial load-carrying capacity of CFST stub columns^53,54. While training datasets are instrumental in constructing models by optimizing their parameters, they primarily indicate how well the models fit the given data. However, without testing datasets, the ability of these models to generalize to unseen data remains uncertain. Testing datasets serve as a critical benchmark, enabling the assessment of a model’s capability to make accurate predictions beyond the training set. This validation step ensures that the models are not merely memorizing the training data but are genuinely learning patterns that apply to new inputs. Such generalization is fundamental for real-world deployment, where data variability and uncertainty are inevitable⁴⁵.

To comprehensively evaluate model performance, a dual approach comprising visual and quantitative assessments was adopted. Visual assessments leverage graphical representations to provide intuitive insights into the model’s behaviour. Scatter plots, for instance, are extensively employed in regression tasks to illustrate the correspondence between predicted and actual values. These plots help in identifying trends, patterns, and deviations, thereby highlighting areas where the model may underperform. Violin boxplots were also used to present the distribution of predictions, offering a visual comparison of the central tendencies and variability across models. Additionally, Taylor diagrams⁵⁵ were incorporated to analyse the statistical relationship between predicted and observed values, combining metrics such as correlation coefficient, root mean square error (RMSE), and standard deviation into a single graphical representation. This approach aids in diagnosing discrepancies and refining model predictions⁵⁶. Uncertainty analysis was further performed to evaluate the robustness and consistency of the models, ensuring reliability under varying conditions.

Quantitative assessments complement visual methods by providing objective metrics for performance evaluation^57,58. Among the metrics employed, regression error characteristic (REC) curves played a central role. REC curves are particularly advantageous for regression tasks, as they plot the error tolerance against the percentage of predictions within that tolerance. A higher REC curve indicates superior performance, as it reflects a greater proportion of predictions closely aligned with actual values. To summarize the model’s performance using REC curves, the area over the curve was calculated, with smaller areas signifying better accuracy and tighter error margins. This metric provides a holistic view of model accuracy across varying levels of error tolerance, making it indispensable for comparing different models.

By integrating visual insights with rigorous quantitative metrics, the evaluation framework ensures a balanced and thorough assessment of the models. This comprehensive approach not only validates the scientific reliability of the predictions but also underscores their practical applicability, ensuring the models are robust and effective for real-world scenarios⁵⁹.

Regression metrics

Accurate evaluation of regression models requires robust metrics that provide insight into their predictive performance from various perspectives⁶⁰. Key metrics used in this study include the determination coefficient ($\:{R}^{2}$), RMSE, mean absolute error (MAE), mean absolute percentage error (MAPE), and mean bias error (MBE). Each metric serves a distinct purpose in assessing model accuracy and reliability⁶¹. $\:{R}^{2}$ quantifies the proportion of variance in the dependent variable explained by the independent variables, with values closer to 1 indicating a superior model fit. RMSE measures the average magnitude of prediction errors, emphasizing larger errors due to squaring, making it particularly sensitive to outliers. MAE, on the other hand, provides the mean absolute difference between predicted and actual values, offering a straightforward and robust measure of prediction accuracy unaffected by extreme values. MAPE expresses prediction error as a percentage, enabling comparisons across datasets of varying scales, while MBE identifies systematic bias, indicating whether the model consistently overestimates or underestimates the target variable. Positive MBE values signify overestimation, whereas negative values indicate underestimation. Collectively, these metrics enable a comprehensive evaluation of model performance, balancing fit, accuracy, and error characteristics. The mathematical formulations for these metrics are presented in Table 3.

Table 3 Equations of the chosen regression metrics.

Where n is the dataset number; $\:{y}_{i}$ and $\:\widehat{{y}_{i}}\:$are actual and predicted $\:{i}^{th}$ values, respectively; $\:\stackrel{-}{y}$ is the mean of actual values; $\:\stackrel{-}{\widehat{y}}\:$is the mean of predicted values.

Uncertainty analysis

Uncertainty analysis plays a pivotal role in assessing the reliability of model predictions by quantifying the uncertainties arising from experimental conditions, input predictors, and model outcomes⁶². This study employs the uncertainty measure $\:{U}_{95}$​, which is calculated using Eq. (6):

$$\:{U}_{95}=1.96\times\:\sqrt{{\text{SD}}^{2}+{\text{RMSE}}^{2}}$$

(6)

Here, SD represents the standard deviation of prediction errors, and the constant 1.96 corresponds to a 95% confidence interval in a standard normal distribution. This measure provides a quantitative assessment of prediction reliability, ensuring informed decision-making based on the degree of uncertainty inherent in the model’s outputs.

Feature importance and interpretability

Understanding and interpreting machine learning models is essential for assessing their effectiveness, trustworthiness, and reliability, particularly in engineering applications. To gain insights into how a model makes predictions, it is crucial to understand the significance and influence of different input features. Two advanced methodologies commonly employed for feature sensitivity analysis are SHapley Additive exPlanations (SHAP) and Partial Dependence Plots (PDPs). These tools provide researchers and practitioners with a deeper understanding of the model’s behaviour by illustrating how individual features impact the model’s outputs.

SHAP values are derived from cooperative game theory and offer a unified approach to interpreting machine learning models. The core concept behind SHAP is to fairly distribute the prediction among the input features by assigning an “importance value” to each feature, representing its contribution to the overall prediction⁶³. This is achieved by calculating the marginal contribution of each feature across different subsets of the input features, ensuring a consistent measure of feature importance. One of the key advantages of SHAP is its ability to provide local interpretability, meaning it can explain individual predictions rather than just general trends across the dataset. This allows practitioners to understand why the model made a specific prediction for a given instance, thereby enhancing transparency. Moreover, SHAP values are consistent and additive, making them a reliable tool for feature importance analysis in complex, non-linear models.

PDPs, on the other hand, are graphical representations that help to visualize the relationship between one or more input features and the predicted outcome of a machine learning model⁶⁴. By averaging out the effects of other features, PDPs depict how changes in a specific feature, or a pair of features influence the model’s predictions. This enables researchers to interpret the global behaviour of the model with respect to the selected features. PDPs are particularly useful for understanding the direction and magnitude of feature influence. For example, they can reveal whether an increase in a particular feature value leads to higher or lower predictions, and whether this relationship is linear, monotonic, or more complex. However, PDPs assume feature independence, which can sometimes limit their effectiveness when features are strongly correlated. Despite this, PDPs remain a valuable tool for assessing feature importance and gaining insight into the model’s predictive patterns.

Results and discussions

Best hyperparameters

The BO process successfully identified optimal hyperparameters for each model, significantly enhancing their performance. Table 4 summarizes these parameters. For XGBoost, the best configuration included 822 estimators, a learning rate of 0.148, a maximum depth of 25, a minimum child weight of 9, a subsample ratio of 0.4824, and a column sample by tree value of 1. These parameters ensure a balanced trade-off between model complexity and overfitting, optimizing predictive accuracy. LightGBM achieved its optimal performance with 1000 estimators, a learning rate of 0.413, a maximum of 100 leaves, a maximum depth of 30, a minimum child weight of 16, a subsample ratio of 0.406, and a column sample by tree value of 1. These hyperparameters allow LightGBM to effectively model complex interactions while maintaining robustness. For CatBoost, optimal settings included a learning rate of 0.283, a depth of 3, and an L2 leaf regularization of 7.445, ensuring efficiency and reduced overfitting.

In the DL models, the DNN was tuned with 512 units in the first dense layer, 384 units in the second dense layer, a learning rate of 0.01, and the ReLU activation function. This architecture enables efficient learning and captures intricate patterns within the data. The CNN model, optimized with 256 filters, a kernel size of 3, 256 units in the dense layer, and the ReLU activation function, excels in capturing spatial hierarchies, making it particularly effective for structured data. The LSTM model, tailored with 1024 units in both LSTM layers, 1024 units in the dense layer, and the ReLU activation function, demonstrates robust capabilities in processing sequential data, ideal for time-series predictions. The rigorous optimization of hyperparameters through Bayesian techniques highlights the strength of these models in addressing the challenges of predicting $\:{P}_{cc}$​ with high precision.

Table 4 Best hyperparameters obtained from BO tuning process for the adopted models.

Performance evaluation

Regression error characteristic

The performance evaluation of the adopted models using REC curves, as shown in Fig. 5, provides comprehensive insights into their residual errors during both training and testing phases. The REC curve’s steepness and proximity to the y-axis signify the proportion of predictions with lower residual errors, thus indicating better model accuracy. In the training phase (Fig. 5a), CatBoost displayed a steep, nearly vertical initial curve, reflecting its high predictive precision with minimal residual errors for a significant portion of predictions. LightGBM and XGBoost demonstrated similarly steep curves, though slightly less vertical than CatBoost, indicating strong yet slightly lower accuracy. Meanwhile, DNN and CNN exhibited curves that started steep but flattened out more rapidly, suggesting higher residual errors for a subset of predictions. LSTM’s curve was the least steep, with a gradual slope extending further along the x-axis, highlighting its higher residual errors and lower reliability.

The testing phase (Fig. 5b) reinforced these trends. CatBoost maintained its superior performance with a steep curve close to the y-axis, indicating sustained low residual errors. LightGBM and XGBoost continued to perform well, albeit with marginally flatter curves than CatBoost. CNN and DNN demonstrated moderate reliability, with curves reflecting a mix of low and high residual errors. Conversely, LSTM’s performance remained subpar, with a shallow slope indicating a considerable proportion of high residual errors. These findings reiterate CatBoost position as the top-performing model in both phases, followed closely by LightGBM and XGBoost. The DL models, CNN and DNN, delivered moderate results, while LSTM lagged significantly, emphasizing the disparity in predictive reliability among the models.

Fig. 5

REC curves showing the performance of the adopted models in (a) training and (b) testing stages.

Scatter plots

The scatter plots in Fig. 6 illustrate the correlation between predicted and actual values during the training and testing phases for each model, alongside key statistical metrics. XGBoost (Fig. 6a) achieved an $\:{R}^{2}$ of 0.997 during training, with exceptionally low errors (RMSE: 104.721 kN, MAE: 62.414 kN, MAPE: 3.77%) and a minimal bias (MBE: -5.093 kN). In testing, the $\:{R}^{2}$ dropped to 0.906, and the error metrics increased (RMSE: 741.767 kN, MAE: 499.097 kN, MAPE: 26.78%), reflecting reduced generalization accuracy. LightGBM (Fig. 6b) showed similar training results, with an $\:{R}^{2}$ of 0.997, RMSE of 113.661 kN, and negligible bias. Testing metrics were strong but slightly inferior to training, with an $\:{R}^{2}$ of 0.916, RMSE of 701.885 kN, and MAPE of 25.95%. CatBoost (Fig. 6c) excelled during training, achieving an $\:{R}^{2}$ of 1.000 with negligible errors (RMSE: 25.032 kN, MAE: 19.707 kN, MAPE: 0.94%, MBE: -0.117 kN). Testing results remained robust with an $\:{R}^{2}$ of 0.932, RMSE of 633.066 kN, and MAPE of 23.03%, though errors were higher compared to training.

The DNN model (Fig. 6d) performed well, with training $\:{R}^{2}$ of 0.974, RMSE of 322.515 kN, and MAPE of 9.67%. Testing metrics ($\:{R}^{2}$: 0.958, RMSE: 496.191 kN, MAPE: 12.57%) indicated a slight drop in performance but overall reliable predictions. CNN (Fig. 6e) showed notable training performance ($\:{R}^{2}$: 0.987, RMSE: 230.116 kN, MAPE: 8.89%) and stable testing results ($\:{R}^{2}$: 0.951, RMSE: 536.068 kN, MAPE: 15.38%). LSTM (Fig. 6f), however, struggled across both stages, with an $\:{R}^{2}$ of 0.893 during training (RMSE: 657.952 kN, MAPE: 20.90%) and 0.891 during testing (RMSE: 800.619 kN, MAPE: 31.65%), signifying substantial predictive limitations. CatBoost consistently emerged as the most accurate model, closely followed by LightGBM and XGBoost. While CNN and DNN exhibited moderate performance, LSTM underperformed significantly, highlighting the variability in effectiveness among the adopted models. These results collectively emphasize CatBoost robustness and its suitability for this predictive task.

Fig. 6

Scatter plots between actual and predicted P_cc values in the training and testing stages based on (a) XGBoost, (b) LightGBM, (c) CatBoost, (d) DNN, (e) CNN, and (f) LSTM.

Analyzing the performance metrics of the adopted models reveals that certain models underperformed due to inherent characteristics and potential mismatches with the data’s nature. For instance, the LSTM model exhibited lower predictive accuracy during both training and testing phases. LSTM networks are designed to capture long-term dependencies in sequential data, making them particularly effective for time-series forecasting. However, if the dataset lacks strong temporal dependencies or if the sequential patterns are minimal, LSTMs may struggle to identify meaningful relationships, leading to suboptimal performance. Additionally, LSTMs are computationally intensive and require substantial training data to generalize well. In scenarios where the dataset is limited or not inherently sequential, LSTMs might not perform optimally.

In contrast, models like CatBoost, LightGBM, and XGBoost are gradient boosting algorithms that construct ensembles of decision trees. These models are adept at handling structured, tabular data and can effectively capture complex, non-linear relationships within the data. CatBoost, in particular, has advanced techniques for managing categorical variables and mitigating overfitting, contributing to its superior performance in this context. The robustness of these models in handling diverse data types and their ability to model intricate patterns without requiring sequential data make them more suitable for the given dataset. Therefore, the underperformance of the LSTM model can be attributed to a potential mismatch between the model’s architecture, which is optimized for sequential data, and the characteristics of the dataset, which may not exhibit strong temporal dependencies. Selecting models that align more closely with the data’s inherent structure, such as gradient boosting algorithms for tabular data, results in improved predictive accuracy and generalization.

Violin boxplots

The violin plots in Fig. 7 provide a comprehensive visualization of the model predictions compared to the actual values, focusing on the distribution and spread of data during training and testing stages. These plots not only illustrate the accuracy of each model but also highlight the variability in their predictions. In the training stage (Fig. 7a), the actual data, represented in red, exhibits a median value of approximately 2802.78 kN, with an interquartile range (IQR) extending from 1643.00 kN to 4494.46 kN. The ML models demonstrate remarkable alignment with the actual data distribution. XGBoost predictions, shown in brown, have a median of 2795.45 kN and an IQR from 1624.67 kN to 4616.72 kN, reflecting minimal deviation. LightGBM and CatBoost, both represented in green, also perform consistently, with median values of 2809.44 kN and 2802.54 kN, respectively, and narrow IQRs, further reinforcing their predictive accuracy. Neural network models exhibit more variability. DNN (blue) shows a median of 2931.13 kN with an IQR ranging from 1708.83 kN to 4626.95 kN, while CNN (purple) has a median of 2910.60 kN and an IQR of 1695.39 kN to 4639.57 kN. LSTM (magenta) demonstrates the highest variability, with a median prediction of 3564.3 kN and an IQR spanning 1851.16 kN to 5284.35 kN, indicating reduced accuracy in capturing the data distribution during training.

Fig. 7

Violin boxplots for the actual and predicted $\:{P}_{cc}$ in the (a) training and (b) testing stages.

In the testing stage (Fig. 7b), the actual data maintains a median of 2580.04 kN, with an IQR from 1299.57 kN to 4885.00 kN. XGBoost predictions closely follow this pattern, with a median of 2449.33 kN and an IQR from 1444.09 kN to 5368.77 kN, though slightly more variable than in the training stage. LightGBM and CatBoost continue to show robustness, with medians of 2503.42 kN and 2455.56 kN, respectively, and slightly expanded IQRs. Conversely, the neural network models exhibit greater spread during testing. DNN (blue) has a median of 2751.05 kN and an IQR from 1265.05 kN to 5269.22 kN, while CNN (purple) demonstrates a median of 2784.56 kN with an IQR of 1425.27 kN to 5570.06 kN. LSTM (magenta) continues to show the highest variability, with a median of 3096.1 kN and an IQR from 1798.21 kN to 6179.54 kN, reflecting diminished reliability.

Taylor diagrams

Figure 8 employs Taylor diagrams to evaluate model performance, offering a concise depiction of standard deviation, correlation coefficient, and centred RMSE for the training and testing stages. These diagrams facilitate a detailed comparison of model behaviour relative to the actual data. In the training stage (Fig. 8a), the tree-based models and neural networks display distinct characteristics. DNN and CNN models are positioned closest to the actual data point, reflecting standard deviations and correlations that align closely with the training data. CatBoost and LightGBM demonstrate excellent correlation coefficients, nearing 1.0, which signifies a strong linear relationship between their predictions and the actual data. XGBoost, while slightly further from the actual data point, still achieves commendable performance with low RMSE. LSTM, in contrast, exhibits a higher standard deviation, indicating greater variability in its predictions.

During the testing stage (Fig. 8b), the performance of the models reveals a similar trend. CatBoost emerges as the most robust model, exhibiting a near-perfect correlation coefficient and low RMSE, underscoring its capacity to generalize effectively. LightGBM and XGBoost maintain high performance, with standard deviations close to the actual test data, indicating consistent predictions. DL models, particularly LSTM, show increased variability, with higher standard deviation and a more pronounced deviation from the actual test data point. The Taylor diagrams affirm that CatBoost stands out as the most reliable and accurate model, particularly in the testing stage, where its superior correlation and minimal RMSE reflect its generalization capabilities.

Fig. 8

Taylor diagrams the actual and predicted $\:{P}_{cc}$ in (a) training and (b) testing stage.

Uncertainty analysis

The U₉₅ uncertainty analysis, visualized in Fig. 9 through a spider plot, evaluates the confidence in model predictions during both training and testing stages. Lower U₉₅ values indicate greater reliability and robustness. CatBoost consistently demonstrates the lowest U₉₅ values, with 69.51 kN during training and 1762.19 kN during testing, making it the most reliable model across both stages. In comparison, LightGBM and XGBoost show slightly higher uncertainty, with training values of 315.62 kN and 290.62 kN, respectively, and testing values of 1953.36 kN and 2064.35 kN. While these values indicate good performance, their increased uncertainty during testing suggests a slight reduction in reliability.

DL models exhibit higher uncertainty overall. DNN achieves moderate performance with U₉₅ values of 895.34 kN during training and 1379.25 kN during testing, outperforming CNN, which has U₉₅ values of 631.25 kN and 1492.18 kN for training and testing, respectively. LSTM, however, shows the highest U₉₅ values, at 5263.71 kN during training and 6535.26 kN during testing, highlighting its significant variability and reduced reliability. This analysis emphasizes CatBoost robustness, as its low U₉₅ values indicate high confidence in predictions. The consistently low U₉₅ values for CatBoost provide evidence of minimal overfitting, as the model demonstrates reliability across both training and testing stages.

Fig. 9

Spider plot for estimated U₉₅ values across the training and testing stages of the adopted models.

In structural design, understanding and interpreting these uncertainty metrics are crucial, as they directly influence decision-making processes related to safety and cost. A higher U₉₅ value signifies greater uncertainty in the model’s predictions. In practical terms, this increased uncertainty necessitates the incorporation of higher safety factors into the design to ensure structural integrity under unforeseen conditions. Safety factors are multipliers applied to account for uncertainties in material properties, loading conditions, and modelling inaccuracies. When uncertainty is high, engineers compensate by increasing these factors, which leads to more conservative designs. While this approach enhances safety, it also results in the use of additional materials and resources, thereby escalating construction costs.

Conversely, models exhibiting lower U₉₅ values, such as CatBoost in this analysis, provide predictions with higher confidence. This reliability allows engineers to design structures with optimized safety factors, balancing safety and cost-effectiveness. Accurate models reduce the need for overly conservative designs, leading to efficient material usage and lower construction expenses. Therefore, the U₉₅ metric serves as a critical bridge between predictive modelling and real-world structural design. By quantifying the uncertainty in model outputs, U₉₅ demonstrates that the algorithms, particularly CatBoost, are not overfitted and can reliably generalize to unseen data.

SHAP feature importance analysis

The SHAP analysis provides a comprehensive understanding of the contributions of individual features to the machine learning model’s predictions. Figure 10a presents the SHAP summary dot plot, illustrating the distribution of SHAP values across all test set instances. Each dot represents a single prediction, with its position on the x-axis indicating the SHAP value, or the extent of the feature’s impact on the model output. The colour gradient reflects the feature values, with red signifying higher and blue representing lower values. The analysis highlights that feature X3 exhibits a substantial range of SHAP values, demonstrating its variable influence on the model predictions. This indicates that the impact of X3 is context-dependent, changing based on its value. Features X3 and X2 emerge as the most significant contributors to the predictions, with X4 and X1 also playing notable roles.

Figure 10b complements this analysis with the SHAP summary bar plot, which aggregates the mean absolute SHAP values for each feature. The ranking of feature importance is evident, with X3 being the most influential, followed by X2, X4, and X1. The darker colour intensity of the bars for X3 and X2 underscores their dominant roles in shaping the model outputs. These bar plots succinctly convey the average impact of each feature, enabling an efficient assessment of their relative significance in the predictive model.

Fig. 10

SHAP feature importance summary (a) dot plots and (b) bar plots.

In summary, the relationships captured by the model align with established engineering principles, validating its utility as a tool for enhancing design intuition and practical decision-making. For instance, the positive correlation between concrete strength (X1 = $\:{f}_{c}^{{\prime\:}}$) and load-carrying capacity is consistent with structural theory, as higher-strength concrete inherently supports greater loads before failure. Similarly, the influence of cross-sectional dimensions (X2 = b and X3 = d) on capacity aligns with the role of geometry in determining the column’s moment of inertia and overall resistance to deformation. The significant contribution of steel tube thickness (X4 = $\:{t}_{s}$) and yield strength (X5 = $\:{f}_{ys}$) to the predictions reflects their critical role in confining the concrete core, enhancing both ductility and load resistance, which is well-known in structural engineering practice.

Column length (h), however, exhibits a more complex relationship with capacity. As indicated by the SHAP analysis, for practical ranges, capacity tends to decrease with increasing column length due to higher slenderness ratios and the associated risk of buckling. This trend is physically reasonable, as longer columns are more prone to instability under axial loads. The insights provided by the model regarding these relationships enhance interpretability and offer engineers a deeper understanding of how individual parameters influence structural behavior, ensuring the model serves as more than a ‘black box.’ Instead, it becomes a valuable tool that bridges advanced computation with fundamental engineering principles.

PDP feature interpretability analysis

PDPs offer a complementary approach to understanding the influence of individual features by visualizing their marginal effect on the predicted outcome while holding other features constant. Figure 11 provides the PDPs for features X1 through X6, highlighting distinct trends for each. The PDP for X1 reveals a generally increasing trend, with predictions rising gradually as X1 increases from 30 to around 60. Beyond this range, the predictions stabilize before exhibiting a sharp increase above 90. This indicates that higher values of X1 strongly contribute to enhanced predictions, with a pronounced effect at the upper end of the observed range. For X2, the PDP demonstrates a negative relationship with the target variable. The predicted outcomes are higher when X2 ranges between 1000 and 2000 but decline sharply as X2 increases further. This suggests that lower values of X2 are associated with higher predicted outcomes, with diminishing effects as X2 continues to increase beyond 8000.

Fig. 11

PDPs for input features interpretability (a) X1, (b) X2, (c) X3, (d) X4, (e) X5, and (f) X6.

The PDP for X3 depicts a consistent upward trend, indicating a strong positive relationship with the target variable. Predictions show a slight increase when X3 ranges from 100 to 400, followed by a steeper rise between 400 and 600. The trend becomes even more pronounced as X3 exceeds 600, reaching its peak at the highest observed values. The PDP for X4 exhibits a stepwise increase in predictions, with significant rises occurring beyond 100 and around 200. This pattern indicates that higher values of X4 contribute positively to the predictions, particularly beyond the mid-range values. The PDP for X5 highlights a steep increase in predictions as X5 values exceed 4, suggesting a strong positive correlation between X5 and the target variable. Similarly, X6 shows a steady upward trend, with predictions stabilizing between 200 and 300 before rising sharply beyond 300. The PDPs reveal that X1, X3, X4, X5, and X6 positively influence the predictions, with higher feature values correlating with improved outcomes. Conversely, X2 exhibits a negative relationship, with higher values leading to reduced predictions. These insights enhance the interpretability of the model by illustrating the specific nature of each feature’s impact.

Comparison with existing analytical models

To illustrate the efficacy of the ML/DL models more effectively in computing the axial load-carrying capacity of round ended CFST columns the present study compares the performance of the 6 ML/DL models against the 10 analytical models proposed in 10 different literatures. Analytical models, derived from theoretical and empirical frameworks, provide deterministic predictions but often suffer from limited adaptability to diverse datasets. Conversely, ML/DL models excel in handling complex (Table 5), nonlinear relationships but require extensive data and robust validation processes to ensure reliability. In the 10 literatures the capability of prediction of their respective analytical load-carrying capacity models were quantified based upon their average ratio ($\:{N}_{u}^{original}/{N}_{u}^{analytical})$ and coefficient of variation (CoV), which provide insight into accuracy and variability. In contrast, ML models are assessed using metrics such as $\:{R}^{2}$, RMSE, MAE, and MBE, offering a broader and more detailed evaluation of predictive performance. The 10 analytical models exhibit varying degrees of accuracy and consistency, as summarized in Table 6 with the formulation of the analytical models in Table 5. The comparison is aimed at identifying the relative strengths and limitations of both approaches, highlighting the advancements offered by data-driven methods in terms of predictive accuracy, consistency, and robustness. The comparison is based on the following metrics:

a. Accuracy: Analytical models are evaluated using the $\:{N}_{u}^{original}/{N}_{u}^{analytical}$​ ratio and associated error percentages, while ML models are assessed using metrics such as RMSE, MAE, and MAPE.

b. Precision: CoV or SD is used for analytical models, while RMSE and MAE indicate precision in ML models.

c. Bias: Analytical model biases are inferred from deviations in the $\:{N}_{u}^{original}/{N}_{u}^{analytical}$ ratio, while ML models use MBE.

d. Correlation: Correlation coefficients or $\:{R}^{2}$ values are used to measure the predictive strength of models, where available.

Table 5 Formulation of the analytical models.

Table 6 Evaluation of analytical models for predicting load carrying capacity.

The evaluation of the performance of the 10 analytical models shows a wide range of accuracy, as indicated by the mean error, which varies between 0.0% and 16.0%. Most models maintain error levels below 10%, demonstrating reasonable predictive capabilities for axial load-carrying capacity in CFST columns. However, significant deviations are observed in certain cases, highlighting the limitations of some models in achieving consistent accuracy. Hassanein & Patel²³ and Ren et al.²⁷ exhibit the largest biases among the studied models. The $\:{N}_{u}^{original}/{N}_{u}^{analytical}$​ ratio for Hassanein & Patel²³ is 1.16, reflecting a 16.0% overestimation of the load-carrying capacity by the analytical model. Similarly, Ren et al.²⁷ shows a ratio of 0.905, indicating a 9.5% underestimation. These deviations from unity highlight the inability of these models to generalize effectively across diverse scenarios, potentially due to oversimplifications in their assumptions or limitations in their dataset-specific calibration.

The CoV or SD values for the models provide insights into their consistency and reliability. Models with lower CoV or SD values exhibit less variability in their predictions, indicating better precision. Among the 10 models, Ahmed & Liang³⁵ demonstrates the lowest dispersion with an SD of 0.003, suggesting exceptional consistency in its predictions. In contrast, models with higher CoV or SD values, such as Ren et al.²⁰ (CoV = 0.079), indicate greater variability, which could impact their reliability in practical applications. While most analytical models perform within acceptable error margins, the outliers with higher biases and variability underscore the limitations of traditional analytical methods in capturing the complex behaviour of CFST columns under varying conditions. This variability also emphasizes the need for alternative approaches, such as machine learning models, to address these limitations effectively. The ML models demonstrate high predictive capabilities across multiple metrics, detailed in Table 7.

Table 7 Evaluation of ML/DL models for predicting load carrying capacity.

DNN and CNN models exhibit superior predictive performance compared to other ML models across multiple evaluation metrics. Both DNN and CNN achieve notably lower RMSE (496.191 kN and 536.068 kN, respectively) and MAE (342.409 kN and 384.067 kN, respectively), highlighting their ability to minimize large deviations between predicted and actual axial load-carrying capacities. The low RMSE and MAE of DNN and CNN models also suggest higher precision, indicating that their predictions consistently fall within a narrower range of deviation compared to other models such as LSTM (RMSE = 800.619 kN, MAE = 650.387 kN). This precision makes DNN and CNN particularly reliable for applications requiring stringent predictive performance. DNN achieves an $\:{R}^{2}\:$value of 0.958, and CNN achieves 0.951, both of which are substantially high. This indicates that the predictions by these models strongly correlate with the actual values.

While LightGBM reports the highest $\:{R}^{2}$ (0.916), its higher errors in RMSE (701.885 kN), and MAE (479.503 kN), suggest that despite fitting the data well overall, it lacks the fine precision and consistency achieved by DNN and CNN. CNN exhibits an almost negligible MBE (0.102 kN), indicating that its predictions are unbiased and evenly distributed around the true values. CatBoost also performs well in terms of bias (MBE = 2.088 kN), but DNN exhibits a slightly larger negative bias (MBE = -36.963 kN), which indicates a tendency to slightly underestimate the load-carrying capacity. Nevertheless, this underestimation is within acceptable limits for engineering predictions. The exceptional performance of DNN and CNN can be attributed to their inherent architectures, which excel in learning complex patterns and relationships from data. The deep learning frameworks of these models allow them to process nonlinear interactions between variables, making them highly suitable for predicting the axial load-carrying capacity of CFST stub columns. Their superiority in metrics such as RMSE, and MAE indicates their robustness and adaptability in capturing intricate dependencies in the dataset. Figure 12 presents a comparative analysis of analytical models and ML models based on $\:{N}_{u}^{original}/{N}_{u}^{analytical}$ for analytical models and $\:{R}^{2}$ for ML models.

Fig. 12

Comparative analysis (a) analytical models, (b) ML/DL models.

• a. Accuracy: Analytical models generally achieve acceptable accuracy (error < 10% for most), but ML models, particularly DNN and CNN, demonstrate superior predictive capabilities with higher $\:{R}^{2}$ values.

• b. Precision Analytical models are consistent within their empirical formulations, with CoV and SD values suggesting moderate variability. In contrast, ML models like DNN and CNN achieve better consistency, reflected in their lower RMSE and MAE values.

• c. Bias: Analytical models exhibit a wider range of biases in their $\:{N}_{u}^{original}/{N}_{u}^{analytical}$​ ratios, while ML models like CNN and CatBoost exhibit near-zero biases (MBE).

• d. Correlation: Analytical models with reported correlation coefficients perform comparably to ML models in terms of $\:{R}^{2}$.

The analytical models exhibit performance metrics predominantly centred around a value of 1.0, reflecting the accuracy of their predictions relative to actual results. Similarly, ML models demonstrate superior performance with higher $\:{R}^{2}$ values, indicating their enhanced capability to explain variance in data. This comparison underscores the reliability and predictive strength of ML-based approaches in modelling axial load-carrying capacity of CFST columns.

Interactive graphical user interface

To bridge the gap between the sophisticated machine learning framework and its practical application, a user-friendly interactive graphical user interface (GUI) has been developed. This Python-based web application, implemented using the Tkinter package, simplifies the deployment of the optimized model for end-users such as engineers and designers⁶⁷. The GUI, depicted in Fig. 13, features an intuitive layout where users can input values for the model’s variables and instantly obtain the predicted output ($\:{P}_{cc}$). This tool democratizes access to advanced predictive capabilities by eliminating the complexities of database assembly, model training, and validation. To promote accessibility and foster collaborative refinement, the GUI has been hosted on GitHub, enabling widespread use and adaptation for diverse civil engineering applications. By providing a practical and straightforward interface, this innovation facilitates the seamless integration of machine learning models into real-world design tasks, advancing the field’s technological capabilities. The GUI is available at https://github.com/mkamel24/PCC44.

Fig. 13

GUI model for predicting $\:{P}_{cc}$.

The GUI presented is a prediction tool for estimating the load-carrying capacity of confined columns using specified input parameters. It includes fields for six key inputs related to the structural properties of the column: the concrete strength of the standard cylinder (f_c’, in MPa), the overall length of the column (h, in mm), the cross-sectional width (b, in mm), the cross-sectional depth (d, in mm), the thickness of the steel tube (t_s, in mm), and the yield strength of the steel tube (f_ys, in MPa). After entering these parameters, the user can click the “Predict” button to calculate and display the predicted load-carrying capacity (P_cc, in kN), which appears in the “Prediction Result” section. Additionally, the GUI is equipped with robust input validation mechanisms to ensure reliability. Non-numeric or negative values, as well as parameters outside realistic ranges for structural elements, trigger error messages that guide users to make corrections. For example, inputs such as negative values for dimensions or unrealistic material properties are flagged with error notifications, and the prediction process is disabled until all entries are valid.

For example, if the user inputs a concrete strength of 42.07 MPa, a column length of 800 mm, a cross-sectional width of 400 mm, a depth of 200 mm, a steel tube thickness of 3 mm, and a yield strength of 345 MPa, the GUI calculates a load-carrying capacity of 4121.60 kN. This makes the tool highly efficient for engineers and researchers needing quick and accurate predictions based on predefined column specifications. The output is currently presented numerically, but future versions may include graphical visualizations such as capacity trends or comparative charts for enhanced interpretability. If the user wishes to reset all input fields and clear the result, they can click the “Clear” button to start afresh.

Conclusion

This study thoroughly examined various machine learning models for predicting the load-carrying capacity of confined columns ($\:{P}_{cc}$) based on key structural features including concrete strength of standard cylinders (X1), overall length of the column (X2), cross-section width (X3), cross-section depth (X4), thickness of the steel tube (X5), and yield strength of the steel tube (X6). A comparative analysis of the performance of analytical models and ML/DL models in predicting the axial load-carrying capacity of round-ended CFST columns is also presented. The key findings are summarized as follows:

• 1. The performance evaluation revealed that ML model CatBoost consistently achieved the highest accuracy. It exhibited the lowest RMSE of 396.50 kN and a high $\:{R}^{2}$ value of 0.932 during testing, indicating superior predictive capability and reliability. XGBoost and LightGBM followed with competitive performance, showing RMSE values of 449.57 kN and 449.57 kN, respectively, and R² scores of 0.906 and 0.916.

• 2. Conversely, DL models performed less favorably. The DNN had an RMSE of 496.19 kN and $\:{R}^{2}$ of 0.958, while the CNN had an RMSE of 536.07 kN and $\:{R}^{2}$ of 0.951. The LSTM network showed the least performance with an RMSE of 2010.46 kN and an $\:{R}^{2}$ of 0.891.

• 3. SHAP analysis revealed that X3 was the most influential feature in predicting $\:{P}_{cc}$, with the highest mean absolute SHAP value indicating its significant positive impact. In contrast, the X2 had a notable negative effect, reducing predictions by approximately − 2373.23 kN for specific instances. While other features such as X4, X5, and X6 also played important roles, however, their impact was less significant compared to X3 and X2.

• 4. The PDPs provide a comprehensive view of how each feature influences the predicted load-carrying capacity of the confined column. X1 shows a general increase in predictions, with a sharp rise beyond 60 MPa. X2 exhibits a decreasing trend, with notable declines in predictions when the length exceeds 2000 mm. X3 has a strong positive relationship, with predictions rising steadily from 100 mm to 600 mm. X4 shows a stepwise increase, with significant rises in predictions occurring beyond 100 mm and 200 mm. X5 is associated with a steep positive increase, with predictions rising substantially from 2 mm to 6 mm. Lastly, X6 consistently increases predictions, with a notable rise as values exceed 300 MPa.

• 5. ML models significantly outperformed the 10 analytical models in terms of prediction accuracy. Analytical models, which rely on deterministic formulations, failed to adapt to complex, nonlinear interactions as effectively as data-driven ML models.

• 6. The interactive GUI developed using Python and Tkinter provides an accessible tool for engineers and designers. It allows users to input feature values and receive dynamic predictions of $\:{P}_{cc}.$ This interface simplifies the application of complex machine learning models and is available for public use and development via GitHub.

However, it is important to note that this study primarily focuses on data from stub columns under axial compression, limiting the direct applicability of the proposed ML models to slender columns, eccentric loading, or advanced material configurations. Future work should incorporate a broader range of geometries, loading scenarios, and material properties to further validate and refine these predictive models for practical engineering applications. The results affirm that traditional machine learning models, particularly CatBoost, XGBoost, and LightGBM, provide more accurate and reliable predictions compared to deep learning models in this context. By integrating advanced prediction tools and feature analyses, this research offers a framework for optimizing CFST column designs. The findings encourage broader adoption of ML models in civil engineering, bridging the gap between theoretical models and practical requirements.