Introduction

Natural gas hydrates (NGH) are regarded as the most promising green and clean energy source of the twenty-first century due to their vast reserves and high energy density. They are estimated to contain around twice as much organic carbon as all other known fossil fuels1,2,3,4. More than 99% of the NGH are marine hydrates, so exploration efforts primarily concentrate on methane hydrate5,6. At present, methods for in-situ decomposition and extraction of hydrates mainly encompass the depressurization method, heat injection method, displacement method, and chemical reagent injection method7,8,9,10. However, based on experimental research and global on-site trial production test results, the depressurization method has emerged to be the most economical and effective extraction technique. To date, only Japan (in 2013 and 2017) and China (in 2017 and 2020) have conducted offshore natural gas hydrate production experiments, and all of which have employed depressurization method. In 2013, Japan conducted a 6-day production test of marine NGHs in the Nankai Trough, successfully extracting about 11.95 × 104 m3 of natural gas11. In 2017, Japan’s second trial production utilized two single vertical wells, the best performing well of which was tested for 24 days, with approximately 22.25 × 10 m3 cumulative gas production12. In 2017, China successfully implemented an NGH production test in the Shenhu Sea area of the South China Sea for 60 days, achieving a cumulative gas production of over 3.09 × 10 m3 and setting a record for the longest continuous and stable gas production period13. In 2020, China launched its second gas hydrate trial production test in horizontal well, achieving continuous gas production for 30 days with a total gas output of 86.14 × 104 m3, marking a significant improvement in both daily and total gas production14. Although several successful hydrate production trials have been conducted and the production duration and gas production have continued to increase, the hydrate production has still not reached the threshold for commercial extraction15. More than 90% of NGH are found in the undifferentiated sediments of sandy clay on the seabed, however their development is challenging due to factors such as shallow burial depth, low consolidation strength, nondiagenesis, and low permeability2,13,16. The low permeability of the reservoir limits pressure conduction, heat transfer, the flow of chemical agents or substitutes, and gas permeation after hydrate decomposition, which stimulates hydrate decomposition. Addressing stimulation and transformation of low-permeability hydrate reservoirs is a key issue that must be addressed to achieve commercial development of hydrates.

The successful development of low-permeability shale gas reservoirs facilitated by hydraulic pressure technology has inspired the exploration of using hydraulic fracturing technology to carry out stimulation and transformation of hydrate reservoirs17,18,19,20. Numerous scholars have conducted relevant research employing experiments and numerical simulation methods and proposed innovative mining concepts, such as using horizontal well hydraulic fracturing technology to develop hydrates21,22,23,24,25,26. At present, hydraulic fracturing simulation experiments on hydrate reservoirs show that hydrate reservoirs with a certain saturation can form hydraulic fractures through hydraulic fracturing27,28. However, Due to the heat release from cement cementing hydration, hydrate decomposition can occur, thereby affecting the quality of cementing. Currently, effective cementing completion of hydrate reservoir remains a challenge14, and it is also an inevitable issue in achieving segmented hydraulic fracturing of hydrate reservoirs. Hydraulic jet fracturing technology is the integration of high-pressure hydraulic jet technology and fracturing technology. It uses a high-pressure hydraulic jet to erode and break the formation, creating a jet channel is formed, which further forms a pressure boost in the channel. That is, the pressure inside the channel exceeds the fluid pressure in the annular formation. Once the pressure inside the channel surpasses the fracturing pressure of the formation, hydraulic fractures can are induced by fracturing the reservoir29,30. The hydraulic jet channel pressurization has the advantage of achieving multi-stage fracturing transformation of reservoirs without the need for mechanical segmentation while reducing the secondary damage caused by thermal perforation and compression of reservoirs, resulting in reduced permeability31. Hydraulic jet fracturing technology is widely used for increasing production in low-permeability oil and gas reservoirs, However, there are currently limited reports on research pertaining to hydraulic jet fracturing technology for hydrate reservoirs32,33,34. Given that hydrate reservoirs in marine areas consist of undifferentiated sediments with weak mechanical strength and low permeability, hydraulic jet technology possesses a strong applicability potential. Zhou et al.35,36,37 proposed a solid-state fluidized bed mining technology for hydrates. Wang et al.38,39,40 studied the use of high-pressure water jet to break hydrate ore bodies and fluidize them into slurry. In May 2017, a successful hydrate solid-state fluidization trial production operation was conducted in the Shenhu Sea area of the South China Sea41. Li et al.42 proposed a method of using cavitation jet drilling to extract hydrates in radial horizontal wells. Zhang et al.43,44 conducted experimental research on the fragmentation of hydrates by cavitation jet and rotary jet.

Previous studies have primarily focused on the cutting and fragmentation of hydrate deposits by hydraulic jets, examining the effects of nozzle types, jet parameters, jet processes, and other factors on the effectiveness of this method. Specifically, these studies have addressed the issue of tunnel formation by hydraulic jets45,46,47,48,49,50. However, there remains a gap in the research regarding the pressure distribution pattern within the tunnel formed by hydraulic jets in hydrate reservoirs. In the context of consolidated formations, Huang et al.29,51 utilized the Reynolds Stress Model (RSM), whereas Qu et al.52 and Sheng et al.53 adopted the k − ε turbulence model to investigate the pressure distribution and fluid flow patterns within high-pressure jet tunnel using computational fluid dynamics (CFD) simulation methods. Corresponding laboratory studies were also undertaken to validate these findings51,52,53. The results demonstrated that hydraulic jets have a pressure-increasing effect within these tunnels. Based on this principle, hydraulic jet fracturing technology has been extensively applied for reservoir stimulation. However, these studies were confined to consolidated formations. Since hydrate reservoirs consist of soft, unconsolidated sediments, the formation characteristics differ significantly from those of consolidated formations. These differences lead to variations in the morphology of the tunnel created by the jets. Furthermore, the heat generated during cementing can cause hydrate decomposition, making it currently impossible to achieve satisfactory cementing and completion in hydrate formations. Due to the differences in jet borehole morphology and cementing methods, the previous research findings on the pressure distribution patterns within jet tunnel in consolidated formations cannot be directly applied to hydrate reservoirs. Therefore, it is imperative to conduct further research on the pressure distribution within the hydraulic jet channels of hydrate reservoirs, with the aim of exploring the feasibility of utilizing the pressure-boosting effect of hydraulic jet channels to induce hydraulic fractures in the reservoirs and achieve effective hydraulic jet fracturing stimulation.

This paper pertains to the actual drilling and completion practices of China’s second round of hydrate trial production in the Shenhu Sea area. It employs computational fluid dynamics (CFD) methodologies with the Shear-Stress Transport k − ω turbulence model to investigate the pressure distribution patterns within submerged hydraulic jet channels in hydrate reservoirs. Using the actual channel dimensions acquired from engineering experiments, a two-dimensional axisymmetric channel model, closely mirroring the actual size and shape, is established to explore the pressure distribution within the hydraulic jet channel. The impact of single factors such as well completion, the perforation tunnel root diameter, hole diameter on casing wall, nozzle diameter, nozzle pressure drop, and jet distance on the pressure distribution within the perforation tunnel is analyzed. The innovative findings presented in this study offer theoretical support for the application of hydraulic jet fracturing technology in the process of hydrate extraction.

Numerical simulation method

Geometry model

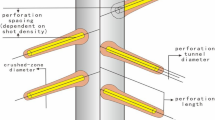
The experimental results of abrasive waterjet erosion on artificial samples of hydrate deposits show that the morphology of the erosion channel is approximately an axisymmetric spindle. Given the axisymmetry of the entire model, it suffices to create a half model to ensure computational accuracy while significantly reducing computational complexity. For easier interpretation of the simulation results, a complete model was generated through axisymmetric mirroring. Due to the heat release caused by cement hydration, it is difficult to cement the wellbore in the hydrate reservoir Section54,55. In China’s second NHG production test, the wellbore was cased but not cemented; however, potential solutions to this challenge are anticipated in the future. The root diameter of the perforation tunnel should exceed the casing hole diameter, owing to the weak strength of the hydrate formation, as illustrated in Fig. 1. Considering three completion scenarios: open-hole wells, uncemented casing completion wells, and cemented casing completion wells, a two-dimensional axisymmetric jet flow field physical model was established based on the experimentally derived orifice morphology. The flow field comprises three regions: the nozzle interior, the jet annulus, and the jet tunnel. As shown in Fig. 2, the nozzle’s internal flow field is simplified to a cylinder, without considering the influence of nozzle type. The centerlines of the nozzle and the erosion tunnel align, forming the axis of symmetry. Key model parameters include Φ (nozzle diameter), d (hole diameter on the casing wall), D (perforation tunnel root diameter), Ljc (distance between the nozzle and the casing), Lc (casing thickness), Lcf (distance between the casing and the formation), and L (jet distance). The tunnel extends 604 mm along the symmetry axis and has a maximum diameter of 110 mm.

Fig. 1
figure 1

Schematic diagram of the hydraulic jet perforation tunnel in hydrate reservoirs with different completion methods.

Full size image
Fig. 2
figure 2

Schematic diagram of the two-dimensional axisymmetric hydraulic jet flow field geometry model.

Full size image

Grid mesh

The jet flow field is divided into quadrilateral grids, with mesh refinement applied to regions experiencing high or abrupt changes in flow velocity to enhance simulation accuracy, as illustrated in Fig. 3. Within the nozzle, the flow rate of the high-pressure fluid is extremely rapid. Upon entering the tunnel, the jet velocity experiences a sharp decrease. Simultaneously, fluid flows both into and out of the tunnel, entering the annulus. Complex fluid motion occurs at the annulus and tunnel inlets. Therefore, mesh refinement is implemented in the core areas of the jet fluid within the nozzle, hole, and annular flow fields. The rough tunnel wall of the formation is a critical area where fluid velocity varies significantly. To address this, the boundary layer is positioned on the wall to increase grid density. The appropriate meshing approach is determined by grid sensitivity analysis. Figure 4 shows the influence of the number of grid cells on the pressurization in the jet erosion tunnel. As the grid cells number increases from 10,799 to 145,527, the relative difference of pressurization is less than 0.4% which indicates that the computational results are grid-independent. A grid cell count of 31,036 is selected to optimize computing time in this study.

Fig. 3
figure 3

Grid division of jet flow field and local region.

Full size image
Fig. 4
figure 4

The influence of grid cells number on the pressurization in the jet erosion tunnel.

Full size image

Control equations

Figure 5 compares several widely used turbulence models, including the k − ε model, k − ω model, and RSM model, with Huang’s experimental results56. The Shear-Stress Transport (SST) k − ω turbulence model and BSL k − ω model were superior consistent with the experimental results. The SST k − ω turbulence model includes all the refinements of the BSL k − ω model, and in addition accounts for the transport of the turbulence shear stress in the definition of the turbulent viscosity57. It is more accurate and reliable for near-wall and vortex flow and is suitable for boundary layer flow, separation, and transition in adverse pressure gradients58. It is better to handle wall-confined flows with high strain rates and large curvature of streamlines than other k − ω models.

Fig. 5
figure 5

Different turbulence models compared with Huang’s experimental results.

Full size image

In this paper, the SST k − ω turbulence model is adopted to solve the pressure distribution inside the hydraulic jet erosion tunnel.

The control equations are:

$${\text{Continuity}}\;{\text{ equation}}:\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial x_{i} }}(\rho {\text{u}}_{i} ) = 0$$
(1)
$${\text{Momentum\,equation}}: \frac{\partial }{{\partial t}}(\rho {\text{u}}_{i} ) + \frac{\partial }{{\partial x_{j} }}(\rho {\text{u}}_{i} {\text{u}}_{j} ) = - \frac{{\partial p}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {{\upmu }\left( {\frac{{\partial {\text{u}}_{i} }}{{\partial x_{j} }} + \frac{{\partial {\text{u}}_{j} }}{{\partial x_{i} }} - \frac{2}{3}\updelta _{{ij}} \frac{{\partial {\text{u}}_{l} }}{{\partial x_{l} }}} \right) - \rho \overline{{{\text{u}}_{i}^{\prime } {\text{u}}_{j}^{\prime } }} } \right]$$
(2)
$${\text{k}}\;{\text{equation}}:\frac{\partial }{{\partial t}}(\rho {\text{k}}) + \frac{\partial }{{\partial x_{i} }}(\rho {\text{ku}}_{i} ) = \frac{\partial }{{\partial x_{j} }}\left( {\Gamma _{{\text{k}}} \frac{{\partial {\text{k}}}}{{\partial x_{j} }}} \right) + G_{{\text{k}}} - Y_{{\text{k}}} + S_{{\text{k}}}$$
(3)
$$\upomega \;{\text{equation}}:\frac{\partial }{\partial t}(\rho\upomega ) + \frac{\partial }{{\partial x_{i} }}(\rho {\upomega u}_{i} ) = \frac{\partial }{{\partial x_{j} }}\left( {\Gamma_{\upomega } \frac{{\partial\upomega }}{{\partial x_{j} }}} \right) + G_{\upomega } - Y_{\upomega } + S_{\upomega }$$
(4)

\(\Gamma_{{\text{k}}}\) and \(\Gamma_{\upomega }\) represent the effective diffusivity of \({\text{k}}\) and \(\upomega\) are given by

$$\Gamma_{{\text{k}}} =\upmu + \frac{{\upmu _{t} }}{{\updelta _{k} }}$$
(5)
$$\Gamma_{\upomega } =\upmu + \frac{{\upmu _{t} }}{{\updelta _{\upomega } }}$$
(6)

where \(\updelta _{k}\) and \(\updelta _{w}\) are the turbulent Prandtl numbers for \({\text{k}}\) and \(\upomega\) ,respectively

$$\updelta _{k} = \frac{1}{{F_{1} /1.176 + (1 - F_{1} )}}$$
(7)
$$\updelta _{\upomega } = \frac{1}{{F_{1} /2 + (1 - F_{1} )/1.168}}$$
(8)

The blending function \(F_{1}\) is given by

$$F_{1} = \tanh (\Phi _{1}^{4} )$$
(9)
$$\Phi _{1} = \min \left[ {\max \left( {\frac{{\sqrt k }}{{0.09{\upomega }y}},\frac{{500{\upmu }}}{{\rho y^{2} {\upomega }}}} \right),\frac{{4\rho k}}{{1.168D_{{\upomega }}^{ + } y^{2} }}} \right]$$
(10)
$$D_{\upomega }^{ + } = \max \left[ {2\rho \frac{1}{1.168}\frac{1}{\upomega }\frac{{\partial {\text{k}}}}{{\partial x_{j} }}\frac{{\partial\upomega }}{{\partial x_{j} }},10^{ - 10} } \right]$$
(11)

where \(y\) is the distance to the next surface and \(D_{\upomega }^{ + }\) is the positive portion of the cross-diffusion term.

The turbulent viscosity \(\upmu _{t}\) is computed by

$$\upmu _{t} = \frac{{\rho {\text{k}}}}{\upomega }\frac{1}{{\max \left[ {\frac{1}{{\upalpha ^{*} }},\frac{{SF_{2} }}{{0.31\upomega }}} \right]}}$$
(12)

\(F_{2}\) is computed by

$$F_{2} = \tanh (\Phi _{2}^{2} )$$
(13)
$$\Phi _{2}^{2} = \max \left[ {2\frac{{\sqrt k }}{{0.09{\upomega }y}},\frac{{500{\upmu }}}{{\rho y^{2} {\upomega }}}} \right]$$
(14)

The coefficient \(\upalpha ^{*}\) damps the turbulent viscosity causing a low-Reynolds number correction. It is given by

$$\upalpha ^{*} = \frac{{\frac{0.072}{3} + {\text{R}}_{et} /6}}{{1 + {\text{R}}_{et} /6}}$$
(15)

where

$${\text{R}}_{et} = \frac{\rho k}{{\upmu \upomega }}$$
(16)

\(G_{{\text{k}}}\) represents the generation of turbulence kinetic energy due to mean velocity gradients, and it is given by

$$G_{k} = - \rho \overline{{{\text{u}}_{i}^{\prime } {\text{u}}_{j}^{\prime } }} \frac{{\partial {\text{u}}_{j} }}{{\partial x_{i} }}$$
(17)

\(G_{\upomega }\) represents the production of ω, it is given by

$$G_{\upomega } = \frac{{\upalpha \upalpha ^{*} }}{{v_{t} }}G_{k}$$
(18)

where

$$v_{t} \equiv\upmu _{t} /\rho$$
(19)
$$\upalpha = \frac{{\upalpha _{\infty } }}{{\upalpha ^{*} }}\left( {\frac{{\frac{{1}}{9} + {\text{R}}_{et} /6}}{{1 + {\text{R}}_{et} /6}}} \right)$$
(20)
$$\upalpha _{\infty } = F_{1} \left( {\frac{0.075}{{0.09}} - \frac{{0.41^{2} }}{{2\sqrt {0.09} }}} \right) + (1 - F_{1} )\left( {\frac{0.0828}{{0.09}} - \frac{{0.41^{2} }}{{1.168\sqrt {0.09} }}} \right)$$
(21)

\(Y_{{\text{k}}}\) represents the dissipation of turbulence kinetic energy, it is given by

$$Y_{k} = \rho\upbeta ^{*} k\upomega$$
(22)

where

$$\upbeta ^{*} = 0.09\left( {\frac{{4/15 + ({\text{R}}_{et} /8)^{4} }}{{1 + ({\text{R}}_{et} /8)^{4} }}} \right)[1 + 1.5F(M_{t} )]$$
(23)
$$F(M_{t} ) = \left\{ {\begin{array}{*{20}l} {0,M_{t} \le 0.25} \hfill \\ {M_{t}^{2} - 0.25^{2} ,M_{t} \rangle 0.25} \hfill \\ \end{array} } \right.$$
(24)
$$M_{t}^{2} \equiv \frac{2k}{{a^{2} }}$$
(25)
$$a = \sqrt {\upgamma RT}$$
(26)

\(Y_{\upomega }\) represents the dissipation of \(\upomega\), it is given by

$$Y_{\upomega } = \rho \upbeta \upomega ^{2}$$
(27)

where

$$\upbeta = 0.0828 - 0.0078F_{1} - 0.135\left( {\frac{{4/15 + ({\text{R}}_{et} /8)^{4} }}{{1 + ({\text{R}}_{et} /8)^{4} }}} \right)F(M_{t} )$$
(28)

where \(\rho\) is the fluid density; \(t\) is time; \({\text{u}}\) is the fluid velocity, \({\text{u}}_{i}\),\({\text{u}}_{j}\) are the velocity components of different coordinate directions, respectively; \(p\) is the pressure; \(\upmu\) is dynamic viscosity; \(\updelta _{ij}\) is Kronecker delta function; \(- \rho {\text{ }}\overline{{{\text{u}}_{i}^{\prime } {\text{u}}_{j}^{\prime } }}\) is Reynolds stress; \(S_{{\text{k}}}\) and \(S_{\upomega }\) are user-defined source terms, and it defined 0 in this paper.

In addition, the following assumptions were made when the pressure distribution inside the perforation tunnel under submerged jet conditions is numerically investigated in this study:

  1. 1.

    Water is a continuous phase and incompressible.

  2. 2.

    There is no heat exchange, and the thermo-physical properties remains constant.

  3. 3.

    The flow is assumed to be turbulent, fully developed and supposed in a steady state.

Boundary conditions and solution settings

In this paper, the pressure distribution law inside the perforation tunnel under submerged jet conditions is numerically investigated using CFD software FLUENT, and the effects of individual factors on the pressure distribution are analyzed. The nozzle inlet, which serves as the computational domain’s inlet, is set to pressure-inlet, while the annulus outlet, serving as the computational domain’s outlet, is set to pressure-outlet. The methane NGH concentration layer is located approximately within 300 m below the seabed, with seawater depths range from 300 to 3000 m59. The static water pressure at the jet position is considered as the confining pressure; therefore, the outlet pressure is assumed to 10 MPa. The centerline of the nozzle and erosion tunnel is set as an axisymmetric boundary condition. The hydraulic jet erosion tunnel boundary, the jet tool, and the pipe column surface are set as the static wall with no slip. The numerical simulation computation employs the shear-stress transport (SST) k − ω turbulence model. The pressure velocity coupling format is the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm. The spatial discretization is performed using the least squares cell-based method. For pressure discretization, a second-order method is used. The momentum equation, turbulence kinetic energy equation, and turbulence dissipation rate equation are measured using a second-order accuracy upwind scheme.

Model validation

The pressure distribution inside the hydraulic jet perforation tunnel in open-hole condition was experimentally measured at a tunnel depth of 120 cm, as shown in Fig. 6. The experimental conditions were as follows: the perforation tunnel root diameter is 5.5 cm, the tunnel depth at the maximum aperture is 48 cm, and the largest aperture is 12.2 cm. Pressure gauges were installed at every 10 cm interval to collect pressure data. The nozzle diameter was 4.5 mm, and the jet distance was set to 30 cm. The water was pressurized by a fracturing pump, resulting in a nozzle pressure drop of 25 MPa. The experimental device was submerged in a water tank to simulate submerged conditions.

Fig. 6
figure 6

Schematic diagram and the physical object of the experimental devices used in this paper.

Full size image

Figure 7a presents a comparison between the numerical and experimental simulations conducted under the same conditions. The results from both simulations and experiments show good agreement. However, owing to the large root diameter of the perforation tunnel, the pressurization within it is relatively low. This finding suggests that, in the context of open-hole wells in hydrate reservoirs, utilizing tunnel pressurization for hydraulic jet fracturing is challenging due to the large perforation tunnel root diameter. Hydraulic jetting gave rise to severe vibrations, leading to the malfunction of the pressure gauge and the incapability of collecting additional experimental data under varying conditions.

Fig. 7
figure 7

Comparison between the numerical and experimental simulations.

Full size image

To further validate the accuracy of the model, the simulation results were compared to Huang’s experimental data58. As shown in Fig. 7b, the simulation results are highly consistent with the experimental results at a jet pressure of 15 MPa. At a jet pressure of 20 MPa, the simulation results were slightly lower, with a deviation of approximately 4%. Overall, this model construction approach is suitable for future studies.

Results and discussion

Fluid flow and pressure distribution characteristics in the erosion tunnel

The fluid flow and pressure distribution characteristics in the erosion tunnel, using a 6 mm nozzle, a 12 mm hole diameter in the casing wall, a 30 mm perforation tunnel root diameter, a 60 mm jet distance, a 10 MPa annular confining pressure, and a 20 MPa nozzle pressure drop, are presented in Figs. 8 and 9, respectively. Figure 8a shows that the length of the constant velocity core is about 10 times the nozzle diameter, and the jet velocity rapidly decreases along the axial direction and diffusing radially, which is consistent with previous research results29. The high-speed jet liquid column exerts a strong suction impact on the formation water in the submerged water jet process, generating turbulence that decreases the kinetic energy and velocity of the jet fluid. As the jet flows through the annulus into the erosion tunnel, fluid exits in the opposite direction between the jet concentration beam and the tunnel wall. Figure 9b illustrates that the high-speed fluid moving in opposite directions at the entrance of the jet erosion tunnel forms a whirlpool, with the shear effect of the fluid further promoting the decay of the jet beam’s velocity and energy.

Fig. 8
figure 8

The hydraulic jet fluid flow characteristics in the erosion tunnel. (a) Velocity contour; (b) Vector contour.

Full size image
Fig. 9
figure 9

The pressure distribution characteristics in the erosion tunnel.

Full size image

The distribution of jet velocity corresponds to the associated pressure distribution. Figure 9a illustrates the pressure distribution within the erosion tunnel. The high-speed fluid at the entrance of the erosion channel creates a zone of relatively low pressure nearby, whereas the annular area experiences relatively higher pressure. Due to the pressure difference and suction effect of the hydraulic jet, fluid from the annulus flows into the erosion tunnel. A net influx of fluid into the erosion tunnel results in an elevated fluid pressure within the tunnel compared to the annulus. Figure 9b shows the fluid pressure curve in the erosion tunnel along the axis of the hydraulic jet. The pressure inside the jet core area is 30 MPa, whereas the fluid pressure outside this area rapidly diminishes. When the fluid pressure in the erosion tunnel reaches a stable state, the pressure at the tunnel axis equates to the pressure on the erosion tunnel wall. Ultimately, the fluid pressure on the inner wall of the erosion tunnel tends to be consistent at 11.15 MPa, which is 1.15 MPa higher than the annular pressure. When the annular pressure is less than the initiation pressure, but the pressure in the tunnel exceeds this threshold due to the pressure increase, the formation can be fractured from the erosion tunnel wall while remaining stable at other points.

Factors influencing the pressurization in the erosion tunnel

Hole inlet diameter

Perforation tunnel root diameter

Figures 10 and 11 shows the effect of perforation tunnel root diameters on the pressure distribution inside the tunnel in three different completion wells. It can be seen from Fig. 11 that the pressurization in the perforation tunnel reduces drastically from about 6 MPa to about 0.5 MPa as the perforation tunnel root diameter increases from 15 to 40 mm in open hole and uncemented casing completion wells. Owever, in cemented casing completion wells, the pressure inside the hole remained almost unchanged as the root diameter of the hole increased. This is because the annular space between the jet liquid column and the tunnel inlet wall is the fluid flow area that flows out of the tunnel during the hydraulic jet process in open hole and uncemented casing completion wells.

Fig. 10
figure 10

Pressure distribution in the erosion tunnel with different the perforation tunnel root diameter under different well completion.

Full size image
Fig. 11
figure 11

The influence of the the perforation tunnel root diameter on pressurization under open hole and un-cemented casing completion.

Full size image

As the perforation tunnel root diameter increases, the expansion of the annular space through which fluid exits the tunnel makes it more challenging to maintain pressure within the tunnel. In cemented casing completion wells, the annular space between the jet liquid column and the hole on the casing wall is the fluid flow area that flows out of the tunnel. The pressurization within the tunnel is solely dependent on the diameter of the hole on the casing wall. The pressurization law of the wellbore in casing cementing completion can be simplified as equivalent to open hole completion, where the equivalent perforation tunnel root diameter corresponds to the hole diameter on the casing wall. Because of the weak reservoir mechanical strength, the perforation tunnel root diameter in the hydrate reservoir is bigger than that in diagenetic formation. The hydraulic jet experiment on artificial hydrate samples demonstrates that the diameter of the perforation tunnel root is often greater than 40 mm, indicating that the pressurization in hydrate reservoirs perforation tunnel might be too small to hydraulic jet fracturing in uncemented casing completion well and open hole completion well. For casing cementing completion wells, the pressurization is sufficient for application of hydraulic jet fracturing in NGH reservoirs.

Hole diameter on casing wall

The diameter of the hole formed by the hydraulic jet on the casing wall is generally 2–3 times that of the nozzle60. When the jet velocity is low, the hole diameter on casing wall may be slightly larger than the nozzle diameter. Figures 12 and 13 show that with a nozzle diameter of 6 mm and a perforation tunnel root diameter of 15 mm, as the hole diameter on the casing wall increases, the tunnel pressure first increases and then decreases, eventually approaching a constant value. When the hole diameter on casing wall is small, it restricts the backflow of fluid in the channel but also hinders fluid entry, resulting in minimal pressurization. As the hole diameter on casing wall increases, the restriction on fluid backflow becomes more significant than that on fluid inflow, leading to a slight increase in pressurization. However, when the diameter of the casing wall perforation further increases, the influence on fluid inflow and outflow becomes negligible. At this point, the pressurization in channel is mainly affected by the perforation tunnel root diameter.

Fig. 12
figure 12

The influence of the hole diameter on casing wall for tunnel pressurization in uncemented casing completion wells.

Full size image
Fig. 13
figure 13

The pressure distribution in tunnel with different hole diameter on the casing wall for uncemented casing completion wells.

Full size image

Nozzle diameter

Figure 14 demonstrates that in an open hole well with a perforation tunnel root diameter of 15 mm, a jet distance of 10 mm, a confining pressure of 10 MPa, and a nozzle pressure drop of 20 MPa, the erosion tunnel pressurization is significantly influenced by nozzle diameter, with this effect becoming more pronounced as the nozzle diameter grows. As the nozzle diameter increases from 4 to 7 mm, the erosion tunnel pressurization increases exponentially from 0.5 to 5.5 MPa.

Fig. 14
figure 14

Effect of nozzle diameter on the pressurization in the jet erosion tunnel for open hole completion.

Full size image

Figure 15 shows that under un-cemented casing completion, keeping the perforation tunnel root diameter in the formation as 24 mm, the nozzle pressure drop as 20 MPa, jet distance as 10 mm and the hole diameter on the casing wall is generally 2 times the nozzle diameter, the erosion tunnel pressurization increases with the increase of nozzle diameter. Using a large-diameter nozzle can achieve higher erosion tunnel pressurization; however, when the nozzle pressure drop is constant, a larger-diameter nozzle requires higher pump injection pressure, thereby imposing greater requirements on the jet equipment’s operational capabilities.

Fig. 15
figure 15

Effect of nozzle diameter on the pressurization in the jet erosion tunnel for uncemented casing completion.

Full size image

Nozzle pressure drop

Figure 16a shows the impact of various nozzle pressure drops on erosion tunnel pressurization in the open hole completion well, with a jet distance of 10 mm, an annular confining pressure of 10 MPa, and an erosion tunnel inlet diameter of 15 mm. The pressure drop of the nozzle determines the speed and energy of the hydraulic jet fluid exiting the nozzle. There is a linear relationship between the erosion tunnel pressure and the nozzle’s pressure drop, and this linearity becomes more pronounced as the nozzle diameter increases. Figure 16b shows that in the scenario of unconsolidated casing completion, the tunnel pressurization increases linearly with the increase of nozzle pressure drop for different casing wall hole diameters. This is also straightforward to comprehend. Under the same jet pressure drop conditions, utilizing a larger diameter nozzle permits more high-pressure fluid to enter the channel within the same timeframe, thus enhancing the pressurization effect. Nevertheless, achieving sufficient jet pressure drop through large-diameter nozzles imposes greater demands on jet pumps. Consequently, it is imperative to select a suitable nozzle diameter, as it is not the case that the larger the diameter, the better the performance.

Fig. 16
figure 16

Effect of nozzle pressure drop on erosion tunnel pressurization. (a) open hole completion, the nozzle diameter changed; (b) uncemented casing completion, the nozzle diameter was 7 mm and the hole diameter on casing changed.

Full size image

Jet distance

Figure 17 shows the pressurization in the erosion tunnel when jetting at different jet distances in a open hole completion well. The pressurization increases first and subsequently declines as the jet distance increases. As the nozzle diameter increases, the jet spacing that achieves the maximum pressurization gradually decreases. At a distance of 100 mm, the pressurization value decreases to 0.29 MPa, which it is quite minimal. When the jetting distance is far, energy attenuation leads to a decrease in fluid velocity, resulting in a relatively small portion of the energy being converted into pressure energy within the tunnel. Conversely, when the distance is close, the high nozzle outlet velocity causes the high-speed fluid to interact with the fluid returning from the tunnel, thereby affecting the pressurization effect. Although this is one possibility for the close condition, the precise mechanism requires further investigation. Nevertheless, in practical applications, a jetting distance of 40–50 mm has been found to be appropriate for nozzles with a diameter of 5–7 mm.

Fig. 17
figure 17

Effect of jet distance on erosion tunnel pressurization with different jet distance for open hole completion.

Full size image

For uncemented casing completion, hydraulic jetting has two annular distances: one is the annular distance between the jetting tool, i.e. nozzle, and the casing, and the other is the distance between the casing and the formation. The diameter of the drilling wellbore, the size of the inserted completion casing, and the outer diameter of the jetting tool all have an impact on these two annular spaces, resulting in varying jet distances (nozzle distance from the formation). The numerical simulation scheme includes two situations: one is that the distance between the casing and the formation remains unchanged, and the distance between the nozzle and the casing wall changes, resulting in a change in the actual jet distance; the other is that the distance between the nozzle and the formation remains unchanged, but the distance between the nozzle and the casing wall changes. The numerical simulation considers that the trial production well is completed using a 9–5/8 "casing14. Figures 18 and 19 show the variation of pressurization with the distance between the nozzle and the casing wall in both cases. As the distance between the nozzle and the casing wall increases, there is a slight increase in pressurization, with an increase of approximately 0.4 MPa. For the scenario depicted in Fig. 18a, as the distance between the nozzle and the casing increases, the actual jetting distance (i.e., the distance from the nozzle to the formation) increases accordingly. Previous analysis indicates that, prior to reaching the optimal jetting distance, tunnel pressure rises with an increase in the injection jetting distance. For the situation illustrated in Fig. 18b, the injection distance remains constant. As the distance between the nozzle and the casing increases, the perforation on the casing reduces the obstruction of the jet entering the channel, while the obstruction of the fluid flowing out of the channel increases. Consequently, the pressurization effect within the channel is slightly enhanced.

Fig. 18
figure 18

Effect of the distance between the nozzle and casing on the pressurization in the jet erosion tunnel. (a) keeping the distance between casing and formation unchanged; (b) keeping the distance between nozzle and formation unchanged.

Full size image
Fig. 19
figure 19

Pressure distribution in the erosion tunnel with different distance between the nozzle and casing. (a) keeping the distance between casing and formation unchanged; (b) keeping the distance between nozzle and formation unchanged.

Full size image

Confining pressure

The confining pressure of a submerged hydraulic jet varies across different positions during hydraulic jet operations, influenced by the formation depth. Multiple confining pressures were set to investigate their influence on erosion tunnel pressurization when jetting with a 6 mm diameter nozzle at a pressure drop of 20 MPa. As illustrated in Fig. 20, the pressure within the erosion tunnel remained constant at 3.01 MPa, despite the formation confining pressure increasing from 5 to 20 MPa, proving that the formation confining pressure had no significant impact on it. The results demonstrate that hydraulic jetting can achieve tunnel pressure enhancement at various locations underground, thereby providing a theoretical foundation for the widespread application of this technology. However, the differences between jet fluid and formation fluid have been overlooked, and further research is required to investigate the pertinent laws.

Fig. 20
figure 20

Effect of confining pressure on erosion tunnel pressurization.

Full size image

Conclusion

In this paper, the (SST) k − ω turbulence model is used to numerically simulate the pressure distribution within the hydraulic jet perforation tunnel under three different well completion in natural gas hydrate reservoirs. The influence of various factors, including well completion, the perforation tunnel root diameter, the hole diameter on casing wall, nozzle diameter, nozzle pressure drop and jet distance on the pressure distribution are analyzed. The main conclusions are summarized as follows:

  1. 1.

    The pressure inside the perforation tunnel in hydrate reservoirs is higher than the confining pressure because of jet flow, that is, a pressurization in the erosion tunnel. The formation confining pressure has no impact on this pressurization; therefore, the pressurization will occur during the progression of the hydraulic jet, regardless of the well depth.

  2. 2.

    For open-hole wells and uncemented casing completion wells, hydraulic fracturing cannot be carried out based on pressurization in hydrate formations due to the large the erosion tunnel root diameter, unless cemented completion is employed. As the perforation tunnel root diameter increases, the pressurization decreases sharply in a parabolic trend under both uncemented casing completion well and open hole completion well. When the perforation tunnel root diameter exceeds 40 mm, the pressurization in the erosion tunnel drops below 0.5 MPa. For cemented casing completion wells, the pressurization depends on the perforation hole diameter on the casing wall, while the the perforation tunnel root diameter has no effect on it.

  3. 3.

    As the nozzle diameter increases, the pressurization in the open-hole well and in the uncemented casing completion well both increases in an exponential trend. For uncemented casing completion, set the hole diameter on the casing wall to be two times the nozzle diameter. Specifically, as the nozzle diameter increases from 4 to 7 mm, the pressurization increases from 0.91 to 2.82 MPa.

  4. 4.

    As the nozzle pressure drop increases, the pressurization increases linearly. For open-hole wells, the larger the nozzle diameter, the more significant the trend of linear increase. For uncemented casing completion well, the rate of linear change increases first and then decreases with the increase of the hole diameter on the casing wall.

  5. 5.

    As the jet distance increases, the pressurization first increases and then decreases. The optimal jet distance in open-hole wells decreases with the increase of nozzle diameter. For uncemented casing completion wells, when maintaining a constant distance from the nozzle to the formation, increasing the distance between the nozzle and the casing will result in a better pressure increase in the wellbore. When the distance between the casing and the formation is constant, the pressurization increases as the nozzle is positioned further away from the casing.