Introduction

Acoustic–structure coupling systems are prevalent in various engineering domains, including buildings and ships. The panel-cavity system is a typical Acoustic–structure coupling system wherein the panels and cavity mutually influence each other: the panels can radiate sound waves, and the acoustic cavity can induce vibrations in the panels. The double-panel configuration offers superior noise control compared to a single-panel system. Therefore, studying the vibro-acoustic characteristics of the double-panel acoustic cavity coupling system is of significant importance for noise control and the acoustic design of equipment structures. With advancements in materials technology, FGMs exhibit excellent mechanical properties and have broad applications in aerospace, construction, and machinery. Given the extensive use of composites in engineering, the integration of FGMs into double-panel acoustic cavity systems is inevitable.

Research into the double plate-acoustic cavity coupling system has an extensive history. Yairia et al.1 analyzed the impact of point force on acoustic radiation in a double-plate system from a theoretical perspective, complementing their study with experimental validation. Utilizing the modal function method and the weighted residual method, Xin et al.2 developed a model of a double-plate system applicable to both infinite and finite domains to examine vibro-acoustic behavior. Garg et al.3 employed glass plates to simulate single, double, and triple panel-cavity structures, exploring the influence of panel thickness and inter-panel spacing on sound transmission loss. Du et al.4 investigated the vibrations of two panels coupled at any angle, extending these findings to configurations involving multiple panels. Li et al.5 employed the modal superposition method to formulate the sound transmission characteristics of the panel-cavity-panel system. Shi et al.6 applied the modified Fourier method and the Rayleigh–Ritz method to analyze the vibro-acoustic properties of the double-elastic panel; subsequently, they7 extended their study to explore the vibro-acoustic behavior of a periodically reinforced double panel-cavity system using the same methods. Anvariyeh et al.8 integrated the Galerkin method with the multiscale method to study the nonlinear vibro-acoustics of a double plate-coupling system under harmonic excitation, thoroughly examining the effects of excitation amplitude, damping coefficients, and cavity depth on frequency and response characteristics. With advances in materials science and the demands of complex operational environments, the use of novel materials has increased significantly. Thus, the double panel-acoustic cavity coupling system employing new composite materials has drawn significant research interest. Innovative composite materials in such systems have captured the focus of numerous researchers. Dozio et al.9 applied Carrera’s unified formula to develop a coupling system for multi-layer composite panels with acoustic cavities. Zhang et al.10 utilized the improved Fourier series method (IFSM) to assess the natural characteristics and responses of single and double composite panels under varying boundary conditions, anisotropy, lamination schemes, and cavity depths.

Composite materials possessing high strength and excellent durability are crucial materials that have garnered significant attention in the research on acoustic properties, such as sandwich panels and laminated structures11,12,13,14,15. FGMs, also as emerging composite materials, possess superior mechanical properties and have been extensively studied in statics, bending, and free vibration contexts16,17,18,19,20,21. FGMs enhance the acoustic and vibration characteristics of structures through the integration of the properties of multiple materials. Similar to the research conducted by Baburaja et al.22 on the vibration and acoustic features of an aluminum–silicon carbide metal matrix composite under temperature loading, adjusting the volume fraction of silicon carbide within the composite material can lead to an improvement in its acoustic performance. Kumar et al.23 employed the LMS SYSNOISE method and the boundary element method (BEM) to investigate the acoustic response of FG elliptical disks. Chandra et al.24 explored the effects of ceramic and metal content on the vibration and response characteristics of FG panels. By employing an improved model of the near-field elemental radiator approach, Chandra et al.25 examined the transmission and radiation properties of FG panels. Yang et al.26 utilized the Hamiltonian principle to assess the impact of temperature fields and material distribution on the acoustic properties of FG panels in thermal environments. Shang et al.27 integrated the pseudo excitation method (PEM) with the improved conventional mode acceleration method (IMAM) to analyze the vibro-acoustic properties of FG shell-coupled structures under steady-state stochastic excitation. Li et al.28 applied the scaled boundary finite element method to address the coupling equation for the implicit high-order time integral in studies of FG shell structures’ vibroacoustic behavior. Masood et al.29 investigated the transmission loss in double-wall constructions featuring FG piezoelectric plates using third-order deformation theory. These findings indicated that the incident angle, depth of the acoustic cavity, and type of gas significantly affect the transmission loss.

The isogeometric analysis (IGA) utilizes shape functions directly from computer-aided design (CAD) as basis functions, which circumvents the errors associated with the reconstruction models typical of traditional finite element analysis30. Owing to its enhanced accuracy and adaptability, IGA has been effectively applied in topology optimizations, fluid mechanics, solid mechanics, and electromagnetics31,32,33,34,35,36. In the context of FGMs and Acoustic–structure coupling, Auad et al.37 employed the Reissner–Mindlin theory with the IGA to investigate the buckling behavior of FG plates. Zhong et al.38 applied the high-order shear deformation theory (HSDT) and the IGA to examine the free vibration of FG round or elliptical plates with variable thickness. Based on the first-order shear deformation theory (FSDT), Chen et al.39 analyzed the natural frequency of FG cylindrical shells with elastic constraints. Xue et al.40 utilized the IGA and the Galerkin method to model acoustic cavities of various shapes and to study their sound transmission loss. Dinachandra et al.41 employed this methodology to explore acoustic fluid–structure interaction, validating the performance IGA with a 2D model for the automotive cavity and beam interaction. Mi et al.42 developed a weak formulation for the steady-state dynamic analysis of vibro-acoustic systems, confirming its accuracy with systems analogous to automotive structures. Employing the combined use of PUFEM/FEM and the direct probability integral method, Ma et al.43 investigated the effects of acoustic impedance and geometric parameters on the response of three-dimensional vibro-acoustic systems. Thus, the application of the IGA in FGMs and Acoustic–structure coupling demonstrates substantial adaptability. In the application of FGMs, components with a high ceramic content are strategically positioned in high-temperature zones, while those with a high metal content are placed in regions demanding superior mechanical properties. The occurrence of harmful load distribution within the plane is a common phenomenon in engineering scenarios44. Therefore, it is necessary to study the effect of in-plane FGMs on the vibro-acoustic characteristics of a double panel- acoustic cavity coupling system. Combining the literature above, research concerning the vibro-acoustic characteristics of double panel-cavity coupling systems that utilize in-plane FGMS remains relatively scarce. On the other hand, the IGA exhibits remarkable accuracy and adaptability when it comes to modeling and analysis FGMs and Acoustic–structure coupling systems. In actual engineering, in addition, the panels of the coupled system are not only limited to rectangular panels.

This manuscript aims to establish a dynamic analysis method for the vibro-acoustic characteristics of a double panel-acoustic cavity coupling system with in-plane functionally graded materials and makes a comprehensive investigation. The system’s acoustic cavity and panels are modeled by using NURBS basis functions combined with classical thin plate theory, then a dynamic model for the double panel-acoustic cavity system with in-plane FGMs is established. The governing equations for the coupling system are derived using the variational method. Numerical examples are presented to validate the convergence and accuracy of the model. The effects of power-law parameters and cavity depths on the system’s free vibration and forced vibration are examined.

Theoretical formulations

Double panel-acoustic cavity coupling system with in-plane FGMs

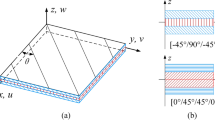
Figure 1 shows the double panel-acoustic cavity coupling system, comprising two thin in-plane FG panels and an acoustic cavity. These panels are situated respectively on the upper and lower surfaces of the acoustic cavity with the same dimensions and material properties. The length and width of the rectangular FG panels are \(Lx \times Ly\); the long axis is Lx and the short axis is Ly of the elliptical FG panels. Their thickness is all t. The FG material is composed of ceramic and metal. The material distribution type adopts the power law rule, the material properties change in the directions of Lx and Ly, which remains unchanged in the thickness direction. This distribution of materials satisfies the following Eqs. (1), (2) and (3):

$$V_{e} (x,y) = \left( \frac{x}{Lx} \right)^{{k_{x} }} \,\left( \frac{y}{Ly} \right)^{{k_{y} }}$$
(1)
$$\quad V_{m} (x,y) = 1 - V_{e} \quad$$
(2)
$$\;\left\{ {\begin{array}{*{20}l} {E(x,y) = E_{m} V_{m} + E_{e} V_{e} } \hfill \\ {\rho (x,y) = \rho_{m} V_{m} + \rho_{e} V_{e} } \hfill \\ {\mu (x,y) = \mu_{m} V_{m} + \mu_{e} V_{e} } \hfill \\ \end{array} } \right.$$
(3)

where V represents the volume fraction; \(E\), \(\rho\) and \(\mu\) correspond to Young’s modulus, density and Poisson’s ratio, respectively; the subscripts e and m respectively denote metal and ceramic; kx and ky are power-law parameters.

Fig. 1
figure 1

Models of a double panel-acoustic cavity coupling system with in-plane FGMs. (a) The coupling system is equipped with rectangular FG panels; (b) The coupling system is equipped with elliptical FG panels.

Full size image

The length (long axis) and width (short axis) of the acoustic cavity are the same as those of panels, and the depth is h. At the contact surface of the acoustic cavity and the panels, two coupling surfaces will be produced due to the interaction of the panels and the acoustic cavity, and except for the two coupling surfaces, the other four faces of the acoustic cavity are rigid. A harmonic force F is applied to the upper panel, and this excitation can cause the panels to vibrate, which affects the variation of sound pressure, which in turn excites the vibration of panels.

Description of the coupling system

Drawing from the principle of the classical thin plate theory, the displacement within the FG panel can be represented as follows

$$u = - z\frac{\partial w(x,y)}{{\partial x}}$$
(4)
$$v = - z\frac{\partial w(x,y)}{{\partial y}}$$
(5)
$$w = w(x,y)$$
(6)

where \(w(x,y)\) is the displacement along the z-direction of the panels.

The relations between strain and displacement within the FG panel can be formulated as follows:

$$\varepsilon_{x} = - z\frac{{\partial^{2} w(x,y)}}{{\partial x^{2} }}$$
(7)
$$\varepsilon_{y} = - z\frac{{\partial^{2} w(x,y)}}{{\partial y^{2} }}$$
(8)
$$\gamma_{xy} = - 2z\frac{{\partial^{2} w(x,y)}}{\partial x\partial y}$$
(9)

The relationship between stress and strain is established according to the generalized Hooke’s law.

$$\left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} C_{11} \quad C_{12} \quad \,\;0 \hfill \\ C_{12} \quad C_{22} \quad \;{\kern 1pt} 0 \hfill \\ 0\quad \quad 0\quad \;\;\;C_{66} \hfill \\ \end{gathered} \right]\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right\}$$
(10)

where \(C_{11} = C_{22} = \frac{E(x.y)}{{1 - \mu (x.y)^{2} }}\); \(C_{12} = \frac{E(x.y)\mu (x.y)}{{1 - \mu (x.y)^{2} }}\); \(C_{66} = \frac{E(x.y)(1 - \mu (x.y))}{{2(1 - \mu (x.y)^{2} )}}\).

The dynamic equation and boundaries of the FG panel are:

$$\nabla \cdot {\varvec{\sigma}} - \rho_{s} \frac{{\partial^{2} {\varvec{u}}_{s} }}{{\partial t^{2} }} = 0\quad {\text{in}}\;{\text{area}}\;{\Omega }_{s}$$
(11)

In boundary \({\Gamma }_{\sigma }\)

$$\sigma \cdot n_{s} = t_{0}$$
(12)

In boundary \({\Gamma }_{u}\)

$$u_{s} = u_{0}$$
(13)

where \(\rho_{s}\) is the density of the panel; \(t_{0}\) is the displacement of \({\Gamma }_{\sigma }\); \(u_{0}\) is the stress on \({\Gamma }_{u}\); \(n_{s}\) is the unit normal vector on the panel.

The Helmholtz equation and boundaries of acoustic cavity are:

$${\Delta }p_{f} - \frac{1}{{c_{f}^{2} }}\frac{{\partial^{2} p_{f} }}{{\partial t^{2} }} = 0\quad \quad {\text{in}}\;{\text{area}}\;{\Omega }_{f} \,$$
(14)

In boundary \({\Gamma }_{p} \,\)

$$p_{f} = p_{0} \,$$
(15)

In boundary \({\Gamma }_{v}\)

$$\,\nabla p_{f} \cdot {\varvec{n}}_{f} = v_{0}$$
(16)

where \(\rho_{f}\) is the density of the acoustic cavity; \(p_{0}\) is the displacement of \({\Gamma }_{p}\); \(v_{0}\) is the stress on \({\Gamma }_{r}\);\({\varvec{n}}_{f}\) is the unit normal vector of the cavity; \(c_{f}\) is the speed of sound.

At the coupling surfaces, both force and velocity exhibit continuity. The weak formula of the governing equations is derived by the variational method:

$$\int_{{\Omega _{{s1}}^{h} }} {\delta \sigma ^{{\text{T}}} \varepsilon {\text{d}}\Omega } + \int_{{\Omega _{{s1}}^{h} }} {\rho _{s} \delta \varvec{u}_{{s1}} \cdot \frac{{\partial ^{2} \varvec{u}_{{s1}} }}{{\partial t^{2} }}{\text{d}}\Omega \;} - \int_{{\Gamma _{{c1}}^{h} }} {p_{f} \left( {\delta \varvec{u}_{{s1}} \cdot \varvec{n}_{f} } \right){\text{d}}\Gamma } = \int_{{\Gamma _{{\sigma 1}}^{h} }} {\delta \varvec{u}_{{s1}} \cdot \varvec{t}_{0} {\text{d}}\Gamma }$$
(17)
$$\int_{{\Omega _{{s2}}^{h} }} {\delta \sigma ^{{\text{T}}} \varepsilon {\text{d}}\Omega } + \int_{{\Omega _{{s2}}^{h} }} {\rho _{s} \delta \varvec{u}_{{s2}} \cdot \frac{{\partial ^{2} \varvec{u}_{{s2}} }}{{\partial t^{2} }}{\text{d}}\Omega \;} - \int_{{\Gamma _{{c2}}^{h} }} {p_{f} \left( {\delta \varvec{u}_{{s2}} \cdot \varvec{n}_{f} } \right){\text{d}}\Gamma } = \int_{{\Gamma _{{\sigma 2}}^{h} }} {\delta \varvec{u}_{{s2}} \cdot \varvec{t}_{0} {\text{d}}\Gamma }$$
(18)
$$\begin{aligned} & \int_{{\Omega _{f}^{h} }} {\nabla \delta p_{f} } \cdot \nabla p_{f} {\text{d}}\Omega + \frac{1}{{c_{f}^{2} }}\int_{{\Omega _{f}^{h} }} {\delta p_{f} \ddot{p}_{f} {\text{d}}\Omega } + \int_{{\Gamma _{{c1}}^{h} }} {\delta p_{f} \left( {\rho _{f} \frac{{\partial ^{2} \varvec{u}_{{s1}} }}{{\partial t^{2} }} \cdot n_{f} } \right){\text{d}}\Gamma } \\ & \quad - \int_{{\Gamma _{{c2}}^{h} }} {\delta p_{f} \left( {\rho _{f} \frac{{\partial ^{2} \varvec{u}_{{s2}} }}{{\partial t^{2} }} \cdot n_{f} } \right){\text{d}}\Gamma } = \int_{{\Gamma _{v}^{h} }} {\delta p_{f} v_{0} d{\kern 1pt} \Gamma } \\ \end{aligned}$$
(19)

where \(\Omega_{s1}\) is the integral domain of the upper panel, \(\Omega_{s2}\) is the integral domain of the lower panel, and \(\Omega_{f}\) is the integral domain of the acoustic cavity. \(\Gamma_{c1}\) and \(\Gamma_{c2}\) are the integral domains of coupling surfaces. \(\Gamma_{\sigma 1}\) and \(\Gamma_{\sigma 2}\) are the areas excited by the force on the panels. \(\Gamma_{v}\) is the area where the acoustic cavity is excited.

Isogeometric analysis

B-splines function as shape function in IGA is obtained from non-negative node vectors \({\mathbf{E}} = \{ \xi_{1} ,\xi_{2} , \cdots ,\xi_{i} , \cdots ,\xi_{n + p + 1} \}\):

$$N_{i,0} (\xi ) = \left\{ {\begin{array}{*{20}c} {1,} & {\xi_{i} \le \xi < \xi_{i + 1} } \\ {0,} & {\text{others}} \\ \end{array} } \right.\quad p = 0$$
(20)
$$N_{i,p} (\xi ) = \frac{{\xi - \xi_{i} }}{{\xi_{i + p} - \xi_{i} }}N_{i,p - 1} (\xi ) + \frac{{\xi_{i + p + 1} - \xi }}{{\xi_{i + p + 1} - \xi_{i + 1} }}N_{i + 1,p - 1} (\xi )\,\,p \ge 0$$
(21)

where n is the total number of basis functions; p is the function order.

In order to accurately represent complex curves such as ellipses and hyperbolas, weights \(\omega_{i}\) are introduced to obtain the non-uniform rational B-splines (NURBS) basis function:

$$R_{i}^{p} (\xi ) = \frac{{\omega_{i} N_{i,p} (\xi )}}{{\mathop \sum \limits_{i = 1}^{n} \omega_{i} N_{i,p} (\xi )}}$$
(22)

NURBS curves are obtained from the NURBS basis function and one-dimensional control points \({\varvec{B}}_{i}\):

$$R(\xi ) = \mathop \sum \limits_{i = 1}^{n} R_{i}^{p} (\xi ){\varvec{B}}_{i}$$
(23)

The double panel-acoustic cavity coupling system is composed of two panels and an acoustic cavity. The panels are represented by the two-dimensional NURBS basis function, and the acoustic cavity is represented by the three-dimensional NURBS basis function. Therefore, the introduction of two-dimensional weights \(\omega_{i,j}\), two-dimensional control points \({\varvec{B}}_{i,j}\), three-dimensional weights \(\omega_{i,j,k}\) and three-dimensional control points \({\varvec{B}}_{i,j,k}\) can obtain the corresponding NURBS basis function:

$$R_{i,j}^{p,q} (\xi ,\eta ) = \frac{{\omega_{i,j} N_{i,p} (\xi )M_{j,q} (\eta )}}{{\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} \omega_{i,j} N_{i,p} (\xi )M_{j,q} (\eta )}}$$
(24)
$$R_{i,j,k}^{p,q,r} (\xi ,\eta ,\zeta ) = \frac{{\omega_{i,j,k} N_{i,p} (\xi )M_{j,q} (\eta )L_{k,r} (\zeta )}}{{\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} \mathop \sum \limits_{k = 1}^{l} \omega_{i,j,k} N_{i,p} (\xi )M_{j,q} (\eta )L_{k,r} (\zeta )}}$$
(25)
$$R\left( {\xi ,\eta } \right) = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} R_{i,j}^{p,q} (\xi ,\eta ){\varvec{B}}_{i,j}$$
(26)
$$R(\xi ,\eta ,\zeta ) = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{k = 1}^{l} {R_{i,j,k}^{p,q,r} (\xi ,\eta ,\zeta ){\varvec{B}}_{i,j,k} } } }$$
(27)

where, p, q, r are the order of the NURBS basis functions in each parameter direction, i. j, k are the sequence of the NURBS basis functions in each parameter direction, and l, n, m are the number of NURBS basis functions in each parameter direction.

Two-dimensional NURBS basis functions are employed to describe the displacement of the FG panel, and three-dimensional NURBS basis functions are utilized to denote the sound pressure within the acoustic cavity:

$$w_{1} (\xi ,\eta ) = R_{1} \left( {\xi ,\eta } \right){\mathbf{u}}_{1} = {\mathbf{R}}_{{s1}} {\mathbf{U}}_{1}$$
(28)
$$w_{2} (\xi ,\eta ) = R_{2} \left( {\xi ,\eta } \right){\mathbf{u}}_{2} = {\mathbf{R}}_{{s2}} {\mathbf{U}}_{2}$$
(29)
$$p_{f} (\xi ,\eta ,\zeta ) = R(\xi ,\eta ,\zeta ){\mathbf{p}} = {\mathbf{R}}_{f} {\mathbf{P}}$$
(30)

where w1 is the displacement of the upper panel; w2 is the displacement of the lower panel; pf is sound pressure inside the cavity.

Taking the upper panel as an example. Substituting Eq. (28) into Eq. (10) obtains:

$${{\varvec{\upvarepsilon}}}_{1} = - z{\mathbf{BU}}_{1}$$
(31)

where \({\mathbf{B}} = \left[ {\frac{{\partial^{2} {\mathbf{R}}_{s1} }}{{\partial x^{2} }},\frac{{\partial^{2} {\mathbf{R}}_{s1} }}{{\partial y^{2} }},2\frac{{\partial^{2} {\mathbf{R}}_{s1} }}{\partial x\partial y}} \right]^{{\text{T}}}\).

By substituting Eq. (31) into the governing equation Eq. (17), the following results are obtained:

$$\int_{{\Omega _{{s1}}^{h} }} {\delta \sigma ^{{\text{T}}} \varepsilon {\text{d}}\Omega } {\text{ = }}\int_{{\Omega _{{s1}}^{h} }} {z^{2} \{ \delta {\mathbf{U}}_{1} \} ^{{\text{T}}} {\mathbf{B}}^{{\text{T}}} {\mathbf{CBU}}_{1} {\text{d}}\Omega }$$
(32)
$${\mathbf{K}}_{{s1}} = \int_{{\Omega _{{s1}}^{h} }} {\frac{{h^{3} }}{{12}}{\mathbf{B}}^{{\text{T}}} {\mathbf{CB}}{\text{d}}\Omega }$$
(33)
$$\int_{{\Omega _{{s1}}^{h} }} {\rho _{s} \delta \varvec{u}_{{s1}} } \cdot \frac{{\partial ^{2} \varvec{u}_{{s1}} }}{{\partial t^{2} }}{\text{d}}\Omega = \int_{{\Omega _{{s1}}^{h} }} {\rho _{{s1}} \delta w_{1} \ddot{w}_{1} {\text{d}}\Omega }$$
(34)
$${\mathbf{M}}_{{s1}} = \int_{{\Omega _{{s1}}^{h} }} {h{\mathbf{R}}_{{s1}}^{{\text{T}}} \rho _{{s1}} {\mathbf{R}}_{{s1}} {\text{d}}\Omega }$$
(35)
$$\int_{{\Gamma _{{\sigma 1}}^{h} }} {\delta \varvec{u}_{{s1}} \cdot \varvec{t}_{0} {\text{d}}\Gamma } = \int_{{\Gamma _{{\sigma 1}}^{h} }} {\delta \varvec{w}_{1} q_{0} {\text{d}}\Omega = \{ \varvec{\delta }{\mathbf{U}}_{1} \} ^{{\text{T}}} \int_{{\Gamma _{{\sigma 1}}^{h} }} {{\mathbf{R}}_{s}^{{\text{T}}} q_{0} {\text{d}}\Omega } }$$
(36)
$${\mathbf{F}}_{{s1}} = \int_{{\Gamma _{\sigma }^{h} }} {{\mathbf{R}}_{s}^{{\text{T}}} q_{0} {\text{d}}\Omega }$$
(37)

where \({\mathbf{K}}_{s1}\),\({\mathbf{M}}_{s1}\) and \({\mathbf{F}}_{s1}\) are the stiffness matrix; mass matrix, and force matrix, respectively. Similarly, a comparable derivation process is carried out for the lower panel to obtain the relevant mass matrix \({\mathbf{M}}_{s2}\), stiffness matrix \({\mathbf{K}}_{s2}\), and force matrix \({\mathbf{F}}_{s2}\).

Substituting Eq. (30) into the governing equation Eq. (19):

$$\int_{{\Omega _{f}^{h} }} {\nabla \delta p_{f} \cdot \nabla p_{f} {\text{d}}\Omega } = \{ \delta {\mathbf{P}}\} ^{{\text{T}}} \left[ {\int_{{\Omega _{f}^{h} }} {[\nabla {\mathbf{R}}_{f} ]^{{\text{T}}} \cdot [\nabla {\mathbf{R}}_{f} ]{\text{d}}\Omega } } \right]\{ {\mathbf{P}}\}$$
(38)
$${\mathbf{K}}_{f} = \int_{{\Omega _{f}^{h} }} {[\nabla {\mathbf{R}}_{f} ]^{{\text{T}}} \cdot \left[ {\nabla {\mathbf{R}}_{f} } \right]{\text{d}}\Omega }$$
(39)
$$\frac{1}{{c_{f}^{2} }}\int_{{\Omega _{f}^{h} }} {\delta p_{f} p_{f} {\text{d}}\Omega = \{ \delta {\mathbf{P}}\} ^{{\text{T}}} } \left[ {\frac{1}{{c_{f}^{2} }}\int_{{\Omega _{f}^{h} }} {{\mathbf{R}}_{f}^{{\text{T}}} {\mathbf{R}}_{f} {\text{d}}\Omega } } \right]\{ {\mathbf{\dot{P}}}\}$$
(40)
$${\mathbf{M}}_{f} = \frac{1}{{c_{f}^{2} }}\int_{{\Omega _{f}^{h} }} {{\mathbf{R}}_{f}^{{\text{T}}} {\mathbf{R}}_{f} {\text{d}}\Omega }$$
(41)
$$\int_{{\Gamma _{v}^{h} }} {\delta p_{f} v_{0} d{\kern 1pt} \Gamma } = \{ \delta {\mathbf{P}}\} ^{{\text{T}}} \left\{ {\int_{{\Gamma _{v}^{h} }} {{\mathbf{R}}_{f}^{{\text{T}}} v_{0} d\Gamma } } \right\}$$
(42)
$${\mathbf{F}}_{f} = \mathop \int \nolimits_{{{\Gamma }_{v}^{h} }} {\mathbf{R}}_{f}^{{\text{T}}} v_{0} d{\kern 1pt} {\Gamma }$$
(43)

where \(\nabla {\mathbf{R}}_{f} = \left[ {{\mathbf{R}}_{f,x} ,{\mathbf{R}}_{f,y} ,{\mathbf{R}}_{f,z} } \right]\); \({\mathbf{K}}_{f}\),\({\mathbf{M}}_{f}\) and \({\mathbf{F}}_{f}\) are the stiffness matrix, mass matrix, and force matrix, respectively.

At the two coupling surfaces, the panels and the acoustic cavity interact with each other:

$$\int_{{\Gamma _{{c1}}^{h} }} {\delta \varvec{u}_{{s1}} \cdot p_{f} \varvec{n}_{f} {\text{d}}\Gamma } = \{ \delta {\mathbf{U}}_{1} \} ^{{\text{T}}} \int_{{\Gamma _{{c1}}^{h} }} {{\mathbf{R}}_{{s_{1} }}^{{\text{T}}} \varvec{n}_{f} {\mathbf{R}}_{f} {\text{d}}\Gamma = \{ \delta {\mathbf{U}}_{1} \} ^{{\text{T}}} {\mathbf{C}}_{{up1}} {\mathbf{P}}}$$
(44)
$$\int_{{\Gamma _{{c2}}^{h} }} {\delta \varvec{u}_{{s2}} \cdot p_{f} \varvec{n}_{f} {\text{d}}\Gamma } = \{ \delta {\mathbf{U}}_{2} \} ^{{\text{T}}} \int_{{\Gamma _{{c2}}^{h} }} {{\mathbf{R}}_{{s_{2} }} ^{{\text{T}}} \varvec{n}_{f} {\mathbf{R}}_{f} {\text{d}}\Gamma = \{ \delta {\mathbf{U}}_{2} \} ^{{\text{T}}} {\mathbf{C}}_{{up2}} {\mathbf{P}}}$$
(45)
$$\int_{{\Gamma _{{c1}}^{h} }} {\delta p_{f} \left( {\rho _{f} \frac{{\partial ^{2} \varvec{u}_{{s1}} }}{{\partial \varvec{t}^{2} }}\varvec{n}_{f} } \right){\text{d}}} \Gamma = \rho _{f} \{ \delta {\mathbf{P}}\} ^{{\text{T}}} \varvec{C}_{{up1}}^{{\text{T}}} {\mathbf{U}}_{1}$$
(46)
$$\int_{{\Gamma _{{c2}}^{h} }} {\delta p_{f} \left( {\rho _{f} \frac{{\partial ^{2} \varvec{u}_{{s2}} }}{{\partial \varvec{t}^{2} }}\varvec{n}_{f} } \right){\text{d}}\Gamma } = \rho _{f} \{ \delta {\mathbf{P}}\} ^{{\text{T}}} \varvec{C}_{{up2}}^{{\text{T}}} {\mathbf{U}}_{2}$$
(47)

where \({\mathbf{C}}_{up1}\) is the coupling matrix between the upper panel and the acoustic cavity; \({\mathbf{C}}_{up2}\) is the coupling matrix between the lower panel and the acoustic cavity.

The coupling equations of the coupling system can be obtained:

$$\{ \delta {\mathbf{U}}_{1} \}^{{\text{T}}} {\mathbf{K}}_{s1} {\mathbf{U}}_{1} + (\delta {\mathbf{U}}_{1} )^{{\text{T}}} {\mathbf{M}}_{s1} {\mathbf{U}}_{1} - \{ \delta {\mathbf{U}}_{1} \}^{{\text{T}}} {\mathbf{C}}_{up1} {\mathbf{P}} = \{ \delta {\mathbf{U}}_{1} \}^{{\text{T}}} {\mathbf{F}}_{s1}$$
(48)
$$\delta {\mathbf{U}}_{2} \}^{{\text{T}}} {\mathbf{K}}_{s2} {\mathbf{U}}_{2} + (\delta {\mathbf{U}}_{2} )^{{\text{T}}} {\mathbf{M}}_{s2} {\mathbf{U}}_{2} - \{ \delta {\mathbf{U}}_{2} \}^{{\text{T}}} {\mathbf{C}}_{up2} {\mathbf{P}} = \{ \delta {\mathbf{U}}_{2} \}^{{\text{T}}} {\mathbf{F}}_{s2}$$
(49)
$$\{ \delta {\mathbf{P}}\}^{{\text{T}}} {\mathbf{K}}_{p} {\mathbf{P}} + \{ \delta {\mathbf{P}}\}^{{\text{T}}} {\mathbf{M}}_{p} {\mathbf{P}} + \rho_{f} \{ \delta {\mathbf{P}}\}^{{\text{T}}} {\mathbf{C}}_{up1}^{{\text{T}}} {\mathbf{U}}_{1} - \rho_{f} \{ \delta {\mathbf{P}}\}^{{\text{T}}} {\mathbf{C}}_{up2}^{{\text{T}}} {\mathbf{U}}_{2} = \{ \delta {\mathbf{P}}\}^{{\text{T}}} {\mathbf{F}}_{f}$$
(50)

Rewrite Eqs. (48)–(50) in the form of a matrix as Eq. (51). If there is no excitation in the coupling system, the right side of the equation is equal to zero, which can be used to solve the free vibration.

$$\left. {\left. {\left\{ {\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{s1} } & {\mathbf{0}} & { - {\mathbf{C}}_{up1} } \\ {\mathbf{0}} & {{\mathbf{K}}_{s2} } & {{\mathbf{C}}_{up2} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{f} } \\ \end{array} } \right.} \right.} \right] - \omega^{2} \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{s1} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{s2} } & {\mathbf{0}} \\ {\rho_{f} {\mathbf{C}}_{up1}^{{\text{T}}} } & { - \rho_{f} {\mathbf{C}}_{up2}^{{\text{T}}} } & {{\mathbf{M}}_{f} } \\ \end{array} } \right]} \right\}\left\{ \begin{gathered} {\mathbf{U}}_{1} \hfill \\ {\mathbf{U}}_{2} \hfill \\ {\mathbf{P}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {\mathbf{F}}_{s1} \hfill \\ {\mathbf{F}}_{s2} \hfill \\ {\mathbf{F}}_{f} \hfill \\ \end{gathered} \right\}$$
(51)

where \(\omega\) is the angular frequency of the coupling system.

Numerical examples

In this section, several numerical examples are used to verify that the established model has good convergence and accuracy, and then the harmonic responses of the coupling system are investigated by applying force on the upper panel. Finally the impact of crucial factors including power-law parameters and acoustic cavity depth on the vibro-acoustic characteristics of the coupling system.

FG panels are composed of ceramic and stainless steel. Stainless steel material properties are: Young’s modulus \(E_{e}\) = 201.04 GPa, density \(\rho_{e}\) = 8166 kg/m3 and Poisson’s ratio \(\mu_{e}\) = 0.3262. Ceramics material properties: Young’s modulus \(E_{m}\) = 348.43 GPa, density \(\rho_{m}\) = 2370 kg/m3 and Poisson’s ratio \(\mu_{m}\) = 0.24. The acoustic cavity is filled with air, and its physical parameters are as follows: density \(\rho_{f}\) = 1.21 kg/m3, sound velocity \(c_{f}\) = 344 m/s. In particular, the boundary conditions of the two panels are the same, and the boundary conditions will be represented by capital letters, C is the clamped boundary, F is the free boundary, S is the simply supported boundary, e.g. CCCC denotes that four edges of the panel are clamped boundary condition. For the geometric parameter of the panels and the cavity, some information about the NURBS and control points should be given. Table 1 shows the Initial control points \({\varvec{B}}_{i,j}\) and related weights \(\omega_{i,j}\) required for rectangular and elliptical panels.

Table 1 Initial control points and related weights of rectangular and elliptical panels.
Full size table

Convergence analysis and result verification

To determinate the appropriate order of the NURBS basis function and number of elements, it is necessary to verify the convergence of the established model. The rectangular panels possess the dimension of \(Lx \times Ly \times t = 1.0{\text{m}} \times 0.6{\text{m}} \times 0.001{\text{m}}\); the power-law parameters are kx = ky = 1 of the FG panels. The acoustic cavity has the dimension of \(Lx \times Ly \times h = 1.0{\text{m}} \times 0.6{\text{m}} \times 0.5{\text{m}}\). Taking the number of elements of the acoustic cavity as an example.

Table 2 presents the convergence analysis of the first eight orders of the coupling system under the CCCC boundary condition. With the increase of the order, the modal frequency gradually converges, and it has basically converged with using the 4th order NURBS. In the case of the same order, the faster the modal frequency converges with the increase of the elements. Therefore, IGA with higher-order NURBS can converge with only a small number of elements. When the order of the NURBS is 4th order and the number of elements is 12 × 12 × 12, the modal frequency satisfies the convergence, and at the same time, the computational effort is smaller than that of the higher-order NURBS basis function or the division of more elements. In the next analysis, 12 × 12 × 12 number of elements and 4th order NURBS basis function will be used.

Table 2 Convergence analysis of the first eight orders of the coupling system.
Full size table

The comparison of modal frequencies with ANSYS results under different boundary conditions is discussed to verify the accuracy of the current method for the coupling system. In ANSYS, the model is established by SHELL63 and FLUID30 elements. The size of the rectangular panels is the same as above. The long axis is 1 m and short axis is 0.6 m of elliptical panels; the power-law parameters are kx = 1 and ky = 0.

Tables 3 and 4 shows the first eight order modal frequencies under different boundary conditions. The relative error is small when the current results are compared to ANSYS, indicating a good agreement with ANSYS, which validates the accuracy of the current method. For the sake of simplicity, the boundary conditions in the subsequent study are assumed to be CCCC.

Table 3 The first eight modal frequencies of the coupling system with rectangular panels.
Full size table
Table 4 The first eight modal frequencies of the coupling system with elliptical panels.
Full size table

Mode shapes can visually express the dynamic characteristics of the system. In the coupling system, both the upper and lower panels possess the same dimensions and physical properties. Consequently, Only the mode shape of the upper panel is analyzed in the analysis below.

Figure 2 shows some mode shapes of the coupling system with rectangular or elliptical panels, which are derived by the current method and ANSYS, respectively. The results are basically consistent with ANSYS results, which still shows that the current method has a good reliability.

Fig. 2
figure 2

Comparison of some mode shapes solved by the current method with ANSYS. (a) The mode shapes of the upper rectangular panel at the 3rd, 4th, 7th, and 9th orders; (b) The modal shapes of the upper elliptical panel at the 3rd, 5th, 7th, and 10th orders.

Full size image

Free vibration analysis

The previous numerical examples verify that the current method is suitable for the double panel-acoustic cavity coupling system with in-plane FGMs, and has good convergence and reliability. This section will make a systematic analysis for the natural characteristics of coupling systems. Because the influence of cavity depth and power-law parameters on the natural characteristics of the coupling system of rectangular and elliptical panels is similar, in order to facilitate research and analysis, only the case of the coupling system with rectangular panels is investigated. The dimension of the acoustic cavity is \(Lx \times Ly \times h = 1.0\;{\text{m}} \times 0.6\;{\text{m}} \times 0.5\;{\text{m}}\); the dimension of the rectangular panels is \(Lx \times Ly \times t = 1.0\;{\text{m}} \times 0.6\;{\text{m}} \times 0.001\;{\text{m}}\).

The effects of power-law parameters kx and ky on the natural characteristics are studied. The kx and ky are the power-law parameters in the x-direction and y-direction respectively, they are related to the volume fraction of the mixed material of the FG panel. The FG panel is composed of ceramic and stainless steel, and the distribution of the two materials adheres to the power law rule.

Table 5 shows the first four modal frequencies with different power-law parameters kx and ky. As evident from the data, within the same order, the modal frequencies exhibit an upward trend with the augmentation of power-law parameters kx and ky. In particular, the magnitude of the modal frequency change is greater in the range of 0 to 1. This is because with the increase of the power-law parameters kx and ky, the stiffness and mass of the element will change, thus the modal frequency will also increase. According to Eqs. (1)–(3) of the power law rule, as the power-law parameters kx and ky transition from 0 to 1, the volume fractions of ceramic and metal undergo the most significant changes, resulting in a significant alteration in modal frequency.

Table 5 The first four modal frequencies with different power-law parameters kx and ky (unit: Hz).
Full size table

The effects of the power-law parameters kx and ky on the mode shapes are studied below. Figures 3 and 4 shows the first two-order mode shapes of the power-law parameters \(k_{x} = \left\{ {0,0.5,2,4} \right\}\), \(k_{y} = \left\{ {0,0.5,2,4} \right\}\).

Fig. 3
figure 3

First-order mode shape with different power-law parameter combinations.

Full size image
Fig. 4
figure 4

Second-order mode shapes with different power-law parameter combinations.

Full size image

The panel of the coupling system has one vibration wave in the first-order mode shapes. To facilitate observation, there are two black lines on panels, which are respectively the middle lines of width and length. It can be seen from Fig. 3 that the valley first appears in the center of the FG panel, and with the ky increase, the valley moves to the left and gradually leans towards the center. As the kx increases, the valley will move to the right, but in the process of kx 2 to 4, the valley will gradually move to the right and will return to the center.

When the power-law parameters are both 0, the range of valley and peak is the same from Fig. 4. The change of the peak is not obvious when the power-law parameters change, but the range of the valley increases with the increase of ky. As kx increases, the range of the valley decreases and then increases until the range of the valley is the same as that of the peak.

The phenomenon of mode shape change is because the power-law parameters are small, then the volume fraction of the metal is larger, which will show the mode shape of the pure metal panel. The ceramic content rises in tandem with the elevation of the power-law parameters, causing the material of the panel to be in an uneven state, and the valley, peak, and ranges will change. When the power-law parameters reach a certain extent, then finally the modes shape of the pure ceramic panels will be displayed.

In addition to the power-law parameters, cavity depth also has effects on the natural frequency. Figure 5 shows the first eight modal frequencies with the change of cavity depths from 0.2 m to 1.0 m when the power-law parameters kx = ky = 1. With the increase of cavity depth, the modal frequency will decrease overall from the figure. The frequencies of the first, third, fifth, and seventh orders change slightly, indicating that the acoustic cavity has little influence on the frequency of the panel-acoustic cavity coupling system, and this part of the frequencies are mainly affected by the panel. Conversely, the second, fourth, sixth, and eighth order frequencies will vary more significantly than those of other orders, so these frequencies have a greater relationship with the depth of the acoustic cavity.

Fig. 5
figure 5

The first eight natural frequencies of the coupling system with different cavity depths.

Full size image

Forced vibration analysis

The preceding section delved into the free vibration analysis of the double panel-acoustic cavity coupling system with in-plane FGMs. The forced vibration analysis of a double panel-acoustic cavity coupling system with in-plane FGMs will be discussed in this subsection. When excitation is applied to the upper panel, it generates vibrations that subsequently alter the sound pressure within the acoustic cavity. This change in sound pressure, in turn, causes the panels to vibrate, and that is a mutual interaction between the panel vibrations and sound pressure variations.

The excitation point is the point (0.2, 0.3, 0.5) on the upper rectangular panel. The harmonic responses of the upper panel, the lower panel, and the acoustic cavity are solved. To validate the accuracy of the current method, the point (0.8, 0.42, 0) on the lower panel, the point (0.7, 0.36, 0.2) in the acoustic cavity, and the point (0.6, 0.48, 0.5) on the upper will be selected. When a harmonic force is applied to the point (0.288,0.427,0.5) on the elliptical panel, the subsequent response points are sequentially chosen as the point (0.785,0.264,0.5) , (0.889,0.3,0) and (0.926,0.414,0.2). When solving the harmonic responses, the references of velocity and sound pressure are respectively \(1 \times 10^{ - 9} \;{\text{m/s}}\) and \(2 \times 10^{ - 5} {\text{Pa}}{.}\) The harmonic force F is 100N. The frequency range is 0~500 Hz and the sweep step is 2 Hz. The damping factors are set as 0.001.

The dimension of the rectangular acoustic cavity is \(Lx \times Ly \times h = 1.0\;{\text{m}} \times 0.6\;{\text{m}} \times 0.5\;{\text{m}}\). The dimensions of rectangular panels are \(Lx \times Ly \times t = 1.0\;{\text{m}} \times 0.6\;{\text{m}} \times 0.005\;{\text{m}}\) and power-law parameters are \(k_{x} = k_{y} = 1\). In the elliptical panels and the acoustic cavity, the long axis is 1.0 m and the short axis is 0.6 m; power-law parameters are \(k_{x} = 1\), \(k_{y} = 0\).

Figures 6 and 7 show the velocity response curves on the upper panel and lower panel, and the sound pressure response curves in the acoustic cavity for the coupling system. Through judgment of the results, the current method solves velocity and sound pressure response curves that are close to those generated by ANSYS, which verifies that the harmonic response analysis using the the current method is reliable again.

Fig. 6
figure 6

Comparison of harmonic response curves of a coupling system with rectangular panels solved using the current method and ANSYS. (a) The velocity response curves at (0.6, 0.48, 0.5) on the upper panel; (b) The velocity response curves at (0.8, 0.42, 0) on the lower panel; (c) The sound pressure response curves at (0.7, 0.36, 0.2) in the cavity.

Full size image
Fig. 7
figure 7

Comparison of harmonic response curves of a coupling system with elliptical panels solved using the current method and ANSYS. (a) The velocity response curves at (0.785, 0.264, 0.5) on the upper panel; (b) The velocity response curves at (0.889, 0.30, 0) on the lower panel; (c) The sound pressure response curves at (0.926, 0.414, 0.2) in the cavity.

Full size image

To investigate the influence of power-law parameters kx and ky on the harmonic response curves of the coupling system, Figs. 8 and 9 respectively illustrate the velocity response curves and sound pressure response curves of the coupling system under varying power-law parameters \((k_{x} = 1;\;k_{y} = 1,2,3)\) and \((k_{y} = 1{;}\;k_{x} = 1,2,3).\) The dimensions of the acoustic cavity and the rectangular panels are the same as that of the reliability verification mentioned above.

Fig. 8
figure 8

Harmonic response curves with different gradient parameters ky. (a) The velocity response curves of the upper panel; (b) The velocity response curves on the lower panel; (c) The sound pressure response curves in the cavity.

Full size image
Fig. 9
figure 9

Harmonic response curves with different gradient parameters kx. (a) The velocity response curves of the upper panel; (b) The velocity response curves on the lower panel; (c) The sound pressure response curves in the cavity.

Full size image

The harmonic response curves in Figs. 8 and 9 are the same due to the identical influence of the power-law parameters kx and ky on the coupling system. These parameters affect the adjustment of the volume fraction of metals and ceramics, resulting in similar harmonic response patterns. In addition, as the power-law parameter increases, the resonance peak shifts to the right, and the resonance peak corresponds to the coupling frequency of the coupling system. That is consistent with the conclusion in the previous section, as the power-law parameters increase, the coupling frequency of the coupling system will increase accordingly, thus the resonance peak here will shift to the right.

In the power-law rule, when the power-law parameters are small, the proportion of metal is relatively large; conversely, when the power-law parameters are large, the content of ceramic is dominant. Ceramics possess a relatively high Young’s modulus and a low Poisson’s ratio. As the power-law parameter increases, the overall stiffness of the panel rises, rendering it less susceptible to deformation. Since the sound pressure within the cavity is generated by the vibration of the upper panel, with the increase of the power-law parameter, the vibration displacement of the upper panel becomes smaller and fails to trigger a peak. Only by increasing the frequency can a peak be produced. Consequently, the first peak of the harmonic response curve of the sound pressure also shifts to the right.

Finally, the cavity depth affects the harmonic responses of the coupling system are explored. Apart from altering cavity depth, the remaining dimensions of both the acoustic cavity and the rectangular panel remain identical to those utilized for verifying the reliability of the coupling system.

Figure 10 illustrates the harmonic response curves with various cavity depths h = {0.2 m, 0.4 m, 0.6 m,0.8 m, 1.0 m} for the coupling system. As can be observed from the figure, the positions of the peaks of the first-order harmonic response curves are very close to each other. This is in line with the conclusion that the depth of the acoustic cavity has an impact on the natural frequency. The harmonic response curves of the upper panel remain basically unchanged. By contrast, significant changes can be seen in the harmonic response curves of the acoustic cavity and the lower panel, especially pronounced in the acoustic cavity. The underlying reason is that the excitation point is situated on the upper panel. The vibration of the upper panel mainly derives from harmonic forces, while the vibration of the lower panel is due to the coupling effect between the panel and the acoustic cavity. Variations in the depth of the acoustic cavity bring about changes in sound pressure, consequently leading to corresponding alterations in the harmonic response curves of the lower panel. Moreover, it can be noted from the variation of the sound pressure response curves that the thinner the cavity depth, the less significant the change in the harmonic response curves. However, as the depth increases, the changes in the curve within the sound cavity become extremely obvious, indicating that a larger depth of the sound cavity exerts a greater influence on sound pressure.

Fig. 10
figure 10

Harmonic response curves with different cavity depth h. (a) The velocity response curves on the upper panel; (b) The velocity response curves on the lower panel; (c) The sound pressure response curves in the cavity.

Full size image

Conclusions

This study presents the vibro-acoustic characteristics of a double panel-cavity coupling system incorporating in-plane FGMs, featuring both rectangular or elliptical panel configurations. The displacement field, sound pressure field, and geometric field of the system are modeled using NURBS basis functions. The governing equations for this coupling system are derived through the application of energy conservation principles and the variational method. The numerical examples are compared with the results obtained from ANSYS to verify the convergence and accuracy of the current method. The findings from the parameter analysis are summarized as follows:

  1. 1.

    The natural frequency of the coupling system varies with different power-law parameters, showing an increasing trend as these parameters are augmented. This results in the resonance peak of the harmonic response curve shifting to the right, and a significant alteration in the peak value. The composition of the ceramic and metal, influenced by the power-law parameters, leads to irregularly distributed mode shapes.

  2. 2.

    The depth of the acoustic cavity also impacts the modal frequency of the coupling system. Typically, as the cavity depth increases, the natural frequency decreases. Certain frequencies are more sensitive to changes in the acoustic cavity, exhibiting a more pronounced decrease. In addition, a larger cavity depth has a greater impact on sound pressure.

  3. 3.

    In the double panel-acoustic cavity coupling system with in-plane FGMs, the vibro-acoustic characteristics are influenced by the material properties of the panels and the dimensions of the acoustic cavity.