Introduction

The P91 steel plates and pipes are commonly welded using arc welding process, Shielded Metal Arc Welding (SMAW), TIG, Laser and EB welding. The SMAW is popular due to its simple, electrode range and its adaptability of equipment. Quality of weld also decided by the experience of welder. TIG welding is popular for thin plate joining with full penetration and for root pass in thick multi-pass welding. Disadvantage of TIG process is the limited penetration in single pass. A variant of the conventional TIG known as flux coated or Active flux TIG welding (A-TIG) process is popular due to increased weld penetration by applying the flux powder coating layer. For P91 steel, few researchers reported the enhancement in penetration twice or more times during the A-TIG. It also eliminates edge preparation requirements and decreases stress. There is minimal reduction in mechanical properties and metallurgical structure of P91steel. It is observed that creep-rupture behavior is enhanced in martensitic steel using the A-TIG welding process1,2,3,4,5,6,7,8.

Arunkumar et al.9 critically observed the A-TIG (P91) welding of P91steel. Author studied the flux coating effect on the weld plate penetration. Compared to the conventional TIG, the tensile strength of the weldment using flux-coated plates is more. Maduraimuthu et al.10 examined the P91steel and the optimization. It was observed from the results that the A-TIG plates have higher hardness, yield strength, and UTS values in comparison with the TIG welded join. The toughness value was lower than the TIG welded joints because of the -ferrite phase formation in A-TIG welding. Stress was tensile in nature in TIG welding, whereas in A-TIG welding, it was compressive. Vasudevan et al.11 have studied the principles of optimizing for the A-TIG process. Input values Voltage, current and weld speed. The response was plotted as HAZ, depth of penetration and size of FZ. The optimization technique that was applied in this work is known as the Genetic Algorithm (GA). The study has shown that the shape and width of the HAZ were calculated through the experimental values of the optimized process parameters achieved using the multi-objective GA optimization, which was well within an acceptable range. Baksha and Vasudevan12 performed the A-TIG experiments on P91 steel. Based on the results, the essence of the hardness is the magnetics of solidification of A-TIG weld joints containing a higher concentration of carbon than standard TIG weld joints. Heat treatment indicated the recution in hardness value was lower in the case of the A-TIG process. Author discussed the A-TIG process, which is become popular in different research area, like nuclear and power plants. Nagaraju et al.13 discussed the optimization of A-TIG for P91 steel material using the RSM Technique. The finite element analysis technique helps predict the pipe or plate’s distortion and stress analysis. The literature shows that SYSWELD, ABAQUS and ANSYS software are famous for studying the thermal and mechanical behavior of P91 steel welding14,19,20. Zubairuddin et al.15,16,17 discussed the thermo-mechanical analysis of P91steel for 3–6 mm thick autogenous and multi-pass welding, considering the preheating welded by the Laser and GTA welding process. Kumar et al.18 discussed the laser welding of 9 mm thick plate stress in different direction in SYSWELD. Kim et al.19 explained the stress and thermal analysis of P91 steel plate in ABAQUS software. Yaghi et al.20 discussed the multi pass welding in P91 steel pipe using ABAQUS software.

In the literature, only a few authors discussed the finite element analysis of A-TIG work. Ganesh et al.21,22. In the literature, only a few authors discussed the finite element analysis of A-TIG work. Ganesh et al.23,24 Studied the 2.25 Cr-1Mo steel plate A-TIG welding analysis, which includes stress, distortion and thermal cycles. Goldak’s double ellipsoidal is used in both papers for Heat Source Fitting analysis (HSF) of the A-TIG welding process. However, a wide range of predicted profile deviations in both cases is observed. Hence, a new model is required to predict more accurately. Based on the literature, limited work is available on comparing TIG and A-TIG welding of Grade 91 steel and limited work on its FEA, which needs to be discussed. The current study aims to conduct a thermo-mechanical simulation of TIG and A-TIG welding of P91 steel using the different heat source models and their experimental validation.

Research plan

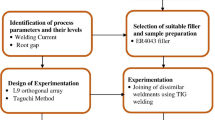
The research plan or approach for the research is shown in the flow chart, as shown in Fig. 1. Two different 4 mm thick P91 steel plates were joined using two different welding techniques, TIG and A-TIG, as shown in Fig. 1. Two different heat source models were used for HSF of the above process. Finite Element Method (FEM) approach helps predict the distortion and residual stress before the actual welding. FEM-based simulation of TIG and A-TIG has been successfully employed using the SYSWELD software. In the FEM-based numerical analysis, the time-dependent field determined the transient analysis based on calculation and then sequentially integrated into the mechanical simulation to obtain density stress and distortion. Further, predicted results were compared with experimental results in each case, as shown in Fig. 1.

Fig. 1
figure 1

Work Plan.

Full size image

Experimental work

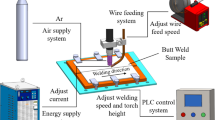
In this investigation, a square butt welded joint was fabricated from thin P91 steel sheets employing TIG and A-TIG welding. Initially, thin sheets of P91 steel with 300 × 250 × 4 mm dimensions were fabricated using TIG welding and later, joined using the A-TIG process. Activating flux was prepared by weighing appropriate quantity of flux in a beaker, which is dried in the furnace for a while. Then, the acetone was mixed activating flux and made it in to past form for coating on plate. Before welding, moisture on plate is removed using the acetone. The activating flux in paste is then applied to the welding surface using a paintbrush and allowed to dry, leaving a flux coating on the welding surface. Once the flux was dried, the plates were welded using TIG welding. K-type thermocouples at different positions were spot-welded for temperature measurement. Figure 2 shows the experimental setup of welding of P91 steel plate for A-TIG and TIG. Distortion in the weld plate is measured before and after the welding on the grids, and the difference is plotted as distortion in the weld plate.

Fig. 2
figure 2

Weld plate for different welding process.

Full size image

The interaction between a heat source and a weld pool is a complex physical phenomenon. Empirical heat input models incorporate various physical factors related to the weld pool, often based on certain assumptions. This approach introduces approximations and necessitates calibration through experimental observations as shown in Fig. 3. A careful examination of a weld’s cross-section reveals that a double ellipsoidal moving heat source is the most suitable model for representing the fusion zone for TIG weld process. Goldak’s double-ellipsoidal heat source model is used to calculate the volumetric heat flux distributions surrounding the weld pool. HSF was computed for bead on plate for both TIG and A-TIG cases, as shown in Fig. 3. Heat input values are given in Table 1–2 for TIG and A-TIG process respectively.

Fig. 3
figure 3

Bead on plate.

Full size image
Table 1 Heat input values.
Full size table
Table 2 Comparison between TIG and A-TIG.
Full size table

Stresses in plates were calculated using sin2ψ method using the XRD process. Distortion in weld plate measured on grid mark position using electronic Vernier height gauge.

Modelling and heat equation

Heat input is the major factor for application of thermal cycle on weld plate. The following equation gives the heat input:

$$Q = \frac{V*I}{{v*1000}} {\text{kJ/mm}}$$
(1)

where V = Voltage (V), I = Current (A), Q = Heat input (kJ /mm), v = Velocity (mm/s),

Heat transfer

The heat distribution due to arc welding has been successfully modelled using a double ellipsoidal configuration. It’s fascinating to note that the heat is distributed through conduction and convection to the surroundings.

Heat transfer in welding depends on several parameters like the geometry of the plate, material properties, atmospheric condition etc. Conduction in weld plate is explained with the 3D equation.

$$\frac{{\partial k{\raise0.7ex\hbox{${\partial T}$} \!\mathord{\left/ {\vphantom {{\partial T} {\partial x}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial x}$}}}}{\partial x} + \frac{{\partial k{\raise0.7ex\hbox{${\partial T}$} \!\mathord{\left/ {\vphantom {{\partial T} {\partial y}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial y}$}}}}{\partial y} + \frac{{\partial k{\raise0.7ex\hbox{${\partial T}$} \!\mathord{\left/ {\vphantom {{\partial T} {\partial z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial z}$}}}}{\partial z} + Q = \rho C_{p} \frac{\partial T}{{\partial t}}$$
(2)

The natural boundary condition can be defined as:

$$k_{n} \frac{\partial T}{{\partial n}} + q + \alpha \left( {T\left( {x,y,z,t} \right) - T_{a} } \right) + \sigma \epsilon \left( {T\left( {x,y,z,t} \right)^{4} - T_{a}^{4} } \right) = 0$$
(3)

y, z, x are points on the boundary for times after t = 0, α = Heat Coefficient (W/m2 °C), kn = Thermal conductivity (W/m °C), Ta = Atmospheric condition (°C), q(x, y, z, t) = Heat flux (W/m2).

Goldak’s double ellipsoidal model

Heat power density (W/m3) in Gaussian distribution with its centre at (0, 0, 0) and semi-axes (a, b, c) is considered.

$$q_{f} (x,y,z,t) = \frac{{6\sqrt[{}]{3}f_{r} Q}}{{a_{r} bc\pi \sqrt[{}]{\pi }}}e^{{ - 3x^{{^{2} }} /a_{r}^{{^{2} }} }} e^{{ - 3y^{2} /b^{2} }} e^{{ - 3\left[ {z + v(\tau - t)} \right]^{2} /c_{1}^{2} }}$$
(4)
$$q_{f} (x,y,z,t) = \frac{{6\sqrt[{}]{3}f_{r} Q}}{{a_{f} bc\pi \sqrt[{}]{\pi }}}e^{{ - 3x^{{^{2} }} /a_{f}^{{^{2} }} }} e^{{ - 3y^{2} /b^{2} }} e^{{ - 3\left[ {z + v(\tau - t)} \right]^{2} /c_{1}^{2} }}$$
(5)

Model parameters are as b = 7 mm, af = 2.5 mm, c = 4 mm, v = 1.67 mm/s, ar = 7.5 mm.

The above parameters help to predict size and shape model, as shown in Fig. 4a. Where ‘f’ represents the heat deposition fraction in rear and front quadrants, where ff + fr = 2. The difference in ellipsoid size is obtained using 'c2' and 'c1' as the semi-axes behind and ahead25,26.

Fig. 4
figure 4

Heat Source models.

Full size image

Heat source considering the conical model

In this model, the reassurance of the peak value in heat being observed at the top is followed by a gradual reduction in a conical shape in thickness direction till the bottom as illustrates in Fig. 4b. This gradual decrease in heat is essential for the conical model, which ensures high penetration, as mentioned in the literature.

Heat input per unit volume is

$${\text{Q}}_{{\text{r}}} = {\text{Q}}_{0} {\text{exp}}\left( {\frac{{ - 3{\text{r}}^{2} }}{{{\text{r}}_{0}^{2} }}} \right)$$
(6)
$$r = \sqrt {x^{2} + y^{2} }$$
(7)
$$r_{o} = r_{e} - \left[ {\frac{{\left( {r_{e} - r_{i} } \right)\left( {z_{e} - z} \right)}}{{\left( {z_{e} - z_{i} } \right)}}} \right]$$
(8)

Q0 is maximum heat input, Qr is the heat input, Ze and Zi respectively, ri and re are radii in plane directions.

Combined double ellipsoidal with 3D conical Gaussian heat source

High energy weld bead cross section shows an elliptical upper portion like a nail head. Conical and double ellipsoidal heat source model is combined to account for that nail head shape. The power for each heat source is then distributed according to HSF as 60–40% of heat input, as shown in Fig. 5.

Fig. 5.
figure 5

3D Conical Gaussian with Cylindrical Gaussian heat source.

Full size image

Meshing and boundary condition

In SYSWELD, Visual mesh tool is preferred for meshing and modelling. In finite element analysis, heating on weld plate is done along all the elements and can be prolonged to include the whole construction. There is another way of describing the weld path is using the weld trajectory and the reference line. Clamping in weld plate was assumed by considering both elastic and rigid clamping at three different location as shown in Fig. 6.

Fig. 6
figure 6

Weld plate skin and clamping.

Full size image

A trajectory line contains all the information on the definition of the motion of weld source space and the path of the centre of the power source, which is equivalent to the local Y-axis, parallel to the weld line element. This line is applied on the skin of the joint and not in the root. The reference line is meshed with one dimensional element and it is parallel with the weld line. It is used similarly to the weld line to specify the standard trajectory and must comprise as many pieces as the weld line. The parameters that should be entered into this group do not differ from the parameters of trajectory, which are the Start node, the End node, and the Start element. If no reference data are to be specified, the source must be axially symmetrical relative to the trajectory. Once more, the start node is just one node that defines a place of the start-point of the trajectory.

The meshing of square and bead on a plate 4 mm thick plate with dimensions 300 mm × 125 mm and 60 mm × 100 mm was carried out, as shown in Fig. 7a–b The model was meshed with eight nodes Hexahedron with varying sizes, with several nodes and elements and nodes 188,689 and 67,321. The weld zone experiences a high-temperature gradient during the welding process. As a result, the weld zone, heat-affected zone (HAZ), and the surrounding areas are meshed with a fine meshing technique. To optimize computational time, the remaining areas are meshed with a coarser approach in both square butt joint plates and bead-on-plate configurations. Fine meshing is applied closer to the fusion zone (FZ), while a coarser mesh is utilized in the HAZ. Clamping conditions are a critical boundary factor in welding simulations. Notably, when clamping is positioned too close to the molten zone, it can lead to significant localized plasticity, potentially resulting in much longer simulation times. This analysis examines two types of clamping conditions, elastic and rigid. Elastic constraints for elements represent the most straight forward approach to modelling realistic clamping conditions. These constraints are applied to elements or nodes with a stiffness of 1000 N/mm, as illustrated in Fig. 6. In the FZ and HAZ region, element size is set to 0.5 mm × 0.5 mm × 0.5 mm. Movement of the weld plate is restricted by clamping the weld plate at the three different corners in different directions, as shown in Fig. 7.

Fig. 7
figure 7

Meshing and Clamping.

Full size image

Result and discussion

The A-TIG affects the shape and size of FZ, HAZ and the boundaries. HSF was initially modelled for full penetration depth using the optimum heat input parameters. Further, the similar heat values were used for the butt plate. FEM-based modelling of the bead on the plate was computed using two different models, double ellipsoidal and combined conical and double ellipsoidal models. Further same values have been used for the thermal and mechanical simulation of butt joints.

Heat source fitting

HSF analysis of a weld profile is calculated based on input model parameters were observed from the weld crater size using bead-on-plate experiment. The experimentally measured size of FZ in case of TIG is 7.44 mm, it is reduced to 6.72 mm in A-TIG. Similarly HAZ size in the TIG welding process is 17 mm, it is reduced to 11.2 mm in A-TIG as shown in Fig. 8.

Fig. 8
figure 8

Weld profile of Bead on Plate.

Full size image

A double ellipsoidal model has been selected for the TIG welding process based on previous numerical analysis on the P91 steel plate welded15,16. Figure 9 shows FEM based analysis of bead on plate weld profile, it is observed closer to experimental profile by considering the combined conical and double ellipsoidal model in A-TIG. The double ellipsoidal model gives wider weld width at top and narrows at bottom with less penetration, whereas the conical model represents deeper penetration. While combining both models, it is observed that there is a reduction in weld width at the top with full depth of penetration, which is closer to the experimental profile. Predicted HAZ in case of TIG welding is18 mm, which is more than A-TIG case 12.1 mm. The predicted FZ size in TIG welding is 7.9 mm, and in the case of A-TIG is 6.9 mm. In both FZ and HAZ values are similar to experimental measured values.

Fig. 9
figure 9

Heat Source Fitting for TIG and A-TIG process (Temperature Value in °C).

Full size image

Thermal analysis

Maximum temperature values in case of FEM analysis for A-TIG and TIG is 1645 °C and 1713 °C, more than 1510 °C the melting point of P91 steel. In predicted thermal analysis the FZ is denoted by pink colour as shown in Figs. 10 and 11. Heat analysis shows wider FZ and HAZ in TIG as compare to A-TIG. Predicted thermal cycle from the weld centre line at 10 and 15 mm distances is validated with experimental values, as shown in Figs. 12 and 13. FEM-based calculated maximum temperature are 653 °C and 721 °C and at 10 mm distance for A-TIG and TIG, respectively. Experimental measured peak temperature values are 689 °C and 621 °C for TIG and A-TIG, closer to predicted values. At 15 mm distance, the maximum predicted temperature values are 522 °C and 438 °C; experimental values at the exact location are 498 °C and 418 °C for the TIG and A-TIG processes, respectively. It is also observed that the material nearer to weld line is heated within a short period and cools rapidly in A-TIG as compared to TIG.

Fig. 10
figure 10

Thermal analysis of TIG considering the double ellipsoidal model (Temperature Value in °C).

Full size image
Fig. 11
figure 11

Thermal analysis of A-TIG considering the combined model (Temperature Value in °C).

Full size image
Fig. 12
figure 12

Thermal cycle validation at 10 mm distance.

Full size image
Fig. 13
figure 13

Thermal cycle validation at 15 mm distance.

Full size image

Mechanical analysis

The significance of accurately predicting temperature distribution during welding has been acknowledged by both scientists and engineers for many years. This importance arises because many phenomena, such as stresses, distortion, and metallurgical changes, stem from uneven temperature distribution and the rapid heating and cooling rates during welding cycles. Residual stress impacts the load-carrying capacity of welded components, potentially leading to failure before reaching their limits. Distortion also affects the design of welded components. Therefore, computational analyses of stress and distortion are essential in minimizing the need for redesign and rework of welded components. The mechanical analysis discussed the stress and distortion induced in both cases in detail. In the welding process, during cooling, the weld plates are subjected to residual stresses due to thermal and plastic deformation.

Stress analysis

In this article, strain were measured and calculated In to stress in a transverse direction at an interval of 5 mm. Figures 14 and 15 compares the predicted and X-ray-based calculated stress values. It is observed that there is a high-stress distribution after HAZ due to material shrinkage during the cooling process and phase transformation, a similar type of stress profile (M Profile) is observed in both cases.

Fig. 14
figure 14

Predicted and measured stress comparison for TIG.

Full size image
Fig. 15
figure 15

Predicted and measured stress comparison for A-TIG.

Full size image

The tensile stress value at the HAZ is gradually transferred into compressive stress. The maximum stress value is 509 MPa, next to HAZ at a 15 mm distance from the centre line. Towards the corner, the stress is compressive in nature. Figures 14 and 15 compares predicted and experimentally observed stress in A-TIG weld joints, showing a high degree of agreement. The material phase transformation and shrinkage during the solidification of the molten zone induced the peak tensile stress close to the interface of the weld and HAZ. The fact that the peak temperature is more than melting point, leading to the induction of plastic strains and solidification tensile stress, further reinforces the reliability of research.

It is noted that maximum stress in A-TIG is reached up to 471 MPa next to HAZ, whereas in the TIG welding, it is 509 MPa. In the simulation, the maximum stress values predicted for the TIG and A-TIG process are 563 MPa and 547 MPa, closer to experimentally measured values. Phase transformation is observed in the stress profile from minimum stress value at the weld line to maximum next to HAZ. A similar type of weld profile is observed for P91 steel in literature for the different welding processes13,14,15,16,17,18,20. The compressive stress value is observed for predicted and measured values for AT-G welding, reaching up to − 240 MPa. The tensile stress was observed as 180 MPa towards the edge of the plate in TIG welding. Minimum tensile stress value and high compressive stress values in A-TIG are beneficial to the weld joint.

Distortion analysis

The welded plates were bowed after releasing the weld clamp. It is dislocated and changes shape after releasing the stresses during the cooling. The weld plates were clamped at the corner. After releasing the weld clamps, the weld plate tends to buckle distortion. The run-in, run-out plate and tack weld restrict the shrinkage in the longitudinal direction. Based on Grid marking on the weld plate, the difference between before and after welding distortion in the plate is measured and plotted. Predicted distortion in the square butt joint plate for the A-TIG case is shown in Fig. 16. Distortion in the TIG and A-TIG welding processes has no symmetric profile. It may be due to the unclamping sequence and the change in the force applied during the weld plate clamping. The A-TIG weld pad’s predicted distortion shape, shown in Fig. 17, exhibits a significant buckling distortion. In FEM analysis, the same force is added for clamping at three corners but is restricted in different directions. Releasing the clamping or sequence of unclamping was not modelled explicitly. Figure 17 shows comparison between numerically calculated and recorded distortion in plate weld plate joined using the Autogenous TIG process. Higher distortion value is observed in case of TIG as compared to the A-TIG due to the broader weld width in the TIG process. In both cases, the FEM based calculated distortion profile looks more similar to the measured profile.

Fig. 16
figure 16

Distortion analysis of A-TIG (mm).

Full size image
Fig. 17
figure 17

Comparison of predicted and experimental distortion.

Full size image

Mechanical analysis shows the maximum distortion in case of TIG is 3.64 mm, for the same location measured value is 3.21 mm. In A-TIG, the peak value of measured distortion is 2.35 mm at the corner, predicted value at the exact position is 2.73 mm as shown in Fig. 17.

Heating and cooling during the welding produces the expansion and contraction induces residual stresses. These stresses exceed the yield value and cause plastic deformation in the form of distortion. Heat input affects both the stress and distortion in the weld plate. More heat input causes a bigger HAZ and a more significant thermal gradient, which enhances thermal stresses and further increases the distortion. In A-TIG the maximum stress is 471 MPa it is increased to 509 MPa in TIG process. Similarly, in the both cases the peak value of distortion is overserved at the corner. In the case of the TIG the peak distortion value is 3.21 mm for the exact location; in the A-TIG cases, it is 2.35, which is 27% less than the TIG welding process.

Conclusion

This paper discussed the FEM-based thermal and mechanical analysis of the A-TIG and TIG process for a 4 mm plate. Welding analysis was carried using two models for heat source distribution modelling. Results comparison of FEM-based calculated temperature values with experimentally verified with error values 10% for the TIG and A-TIG processes. The experimental validation showed that the numerical model has produced results with reasonable accuracy with recorded and calculated values for distortion, stress and thermal cycles for autogenous A-TIG and A-TIG process on 4 mm thick Grade 91 steel. However, some important conclusions are listed below.

  1. 1.

    Full penetration depth is observed in both the cases at heat input values of 659 J/mm for A-TIG case and 792 J/mm for TIG welding.

  2. 2.

    Predicted and measured maximum temperature values at 10 and 15 mm are 689 °C and 621 °C & 498 °C and 418 °C for TIG and A-TIG welding, respectively. It shows the 16–10% reduction in peak temperature value at 15 and 10 mm distance from the centre line is due to the A-TIG welding process.

  3. 3.

    The peak value of the experimental calculated stress is tensile with values 471 MPa and 509 MPa for the A-TIG and TIG cases. The FEM-based calculated stress value is 543 MPa and 563 MPa, with a 6–13% error range.

  4. 4.

    Comparison of predicted and experimental measurements shows the effect of phase transformation is observed in both cases. The stress profile is observed to be broader in the case of TIG due to wider heat distribution.

  5. 5.

    In conventional TIG welding, the distortion in the longitudinal direction is observed 27% more compared to the A-TIG. The FEM-based calculated analysis showed a success similar to the measured distortion values for A-TIG and TIG cases with an error range of 15–12%.