High precision water quality retrieval in Dianchi Lake using Gaofen 5 data and machine learning methods

Abstract

Water quality indicators (WQI) reflect both the current state and the changing trends of water quality. Extracting these indicators from remote sensing data enables rapid and efficient inversion of water quality conditions, providing a key step in predicting water pollution. The low-precision inversion results of WQI limit the understanding of the ecological safety of water resources. In this paper, the Advanced Hyperspectral Imager (AHSI) data from the GF-5 satellite was used to analyze the Dianchi Lake. A spectrum processing method based on the Savitzky-Golay Standard Normal Variate transformation (SG-SNV) was developed, alongside optimal inversion techniques, to enhance the accuracy of predictions for 6 WQI in Dianchi, including CODcr, NH3-N, TP, TN, pH, and Chl. The results indicated that (1) For all inversion models, the determination coefficients (R²) exceeded 0.85. The Back Propagation Nondominated Sorting Genetic Algorithm-II (BP-NGA) model consistently yielded positive results for most WQI. (2) Water quality in Dianchi varied significantly by region and season. (3) It was recommended to build wetlands and ecological parks on the southwest side of Dianchi and improve sewage interception pipelines on the northeast side to lessen the risk of eutrophication by reducing the inflow of nitrogen and phosphorus.

Introduction

Lakes are essential forms of surface coverage and vital resources for the survival of humankind¹. In recent decades, a plethora of water-related environmental challenges have emerged as a consequence of heightened global warming, urbanization, industrialization, and rapid social development². Statistics indicate that the water quality of more than 50% of the world’s lakes and reservoirs is deteriorating, with eutrophication identified as a primary contributing factor³. China, as one of the nation most adversely affected by these algal blooms, particularly with regard to Dianchi, a plateau lake experiencing significant eutrophication pressures⁴. Natural climate, biological resources, social livelihood, and national policies are all significantly impacted by algal blooms^5,6,7. However, remote sensing technology offers a means to conduct real-time and accurate assessments of water quality on a large scale, enabling the detection of pollution sources and the timely evaluation of pollution levels. Consequently, the utilization of high-quality remote sensing data to investigate novel methods of water quality inversion can facilitate advancements in water quality monitoring technology, thereby providing essential technical support for enhancing national environmental management capabilities.

Although traditional manual water quality testing methods can yield accurate results, the incorporation of remotely sensed data more effectively addresses the requirements for high-frequency and large-scale water quality monitoring⁸. For example, Zhu et al.⁹ utilized the extensive and simultaneous monitoring capabilities of remote sensing to establish baselines for the spectral indices of phycocyanin and chlorophyll-a, facilitating the identification of algal blooms and aquatic vegetation across the entire littoral zone of Taihu Lake. Their combined model achieved accuracies of 93% and 95%, respectively. In addition, spaceborne hyperspectral devices provide information that is not limited to specific points or locations, unlike handheld and aircraft-based sensors. Zhang Shouxuan et al.¹⁰ proposed extracting algal blooms using a single-band threshold approach combined with China-Brazil Earth Resources Satellite (CBERS), Moderate-resolution Imaging Spectroradiometer (MODIS), and Enhanced Thematic Mapper (ETM) data. Kong Yuxiang¹¹ analyzed the spatial and temporal distribution of chlorophyll-a concentration in the water column utilizing CBERS data. Hyperspectral satellite imagery has been established as a critical data source supporting water quality assessment, as confirmed by researchers such as Zhang Peng¹² and Zhang Zhijun¹³. The hyperspectral imaging of Gaofen-5 (GF-5) enable the acquisition of hundreds of spectral bands, each with a bandwidth of less than 10 nm, thereby minimizing spectral confusion. The advancements by GF-5 represent significant technological progress in the domain of water quality research, facilitating a transition from qualitative assessments to semi-quantitative or quantitative analyses¹⁴. Currently, there is a limited amount of research on the use of hyperspectral remote sensing to quantify water quality in inland plateau lakes. Liu Yiming¹⁵, Bao Qifan¹⁶ et al. conducted suspended sediment inversion studies of the Yangtze River estuary and coastal waters based on hyperspectral imagery from GF-5. Zhang Yongyong¹⁷ conducted bathymetric inversion of Hengsha, a shoal shallow water area in Shanghai, based on GF-5 remote sensing data. So, most of the current studies using GF-5 data have focused on the oceans and estuaries.

The indicators that reflect water quality, along with the algorithm of the mathematical model, have played a crucial role in achieving an effective inversion of water quality remote sensing models. The physicochemical indicators for assessing water quality commonly include potential of hydrogen, nitrogen, and phosphorus et¹⁸. In prior research on water quality in Dianchi, conventional band combinations¹⁹ or linear models²⁰ are typically employed for inversion; however, these approaches often lack the sensitivity required to adequately address multiple interacting variables, resulting in errors. Machine learning algorithms, by contrast, are adept at analyzing complex multi-dimensional spectral data and can establish non-linear relationships that more accurately represent real-world conditions^21,22. For instance, a study conducted by Hayder et al. in 2020 demonstrated that artificial neural network methods generally yield satisfactory results in predicting and estimating parameters in the Kelantan River Basin²³. Moreover, machine learning facilitates real-time monitoring by utilizing continuously updated data, thus accommodating the dynamic characteristics of diverse water bodies. Sun et al.²⁴ presented a near-remote sensing water quality monitoring model in 2021, aiming to enhance result accuracy by integrating near-ground hyperspectral data. Marta Jemeljanova²⁵ et al. found that back-propagation neural networks, support vector machines, and random forests generally exhibited superior predictive performance, with the random forest model demonstrating the highest consistency. Notably, the random forest model was employed in 66 out of 94 articles, establishing it as the machine learning model with the most reliable results.

Therefore, this study focused on Dianchi, developing inversion models based on actual data and spectral reflectance for 6 Water quality indicator (WQI): chemical oxygen demand (CODcr), ammonia nitrogen (NH3-N), total phosphorus (TP), total nitrogen (TN), potential of hydrogen (pH), and chlorophyll (Chl). There are two improved inversion algorithms, back propagation neural network model based on the NSGA II optimized genetic algorithm and improved support vector machine regression. These are compared to the classical random forest model. The results regarding the spatial and temporal distribution of the 6 WQI obtained from the 6 most effective models were interpolated using full-area kriging to simulate the continuous transitions of WQI across various locations in real-world scenarios. Finally, field surveys were carried out in selected areas, and the experimental results were validated by combining high-resolution satellite imagery with measured data. The study could serve as a robust scientific basis for the accurate monitoring and management of water bodies in areas with karst landforms, as well as for the enhancement of the water environment in Dianchi.

Method

Study area and data collection

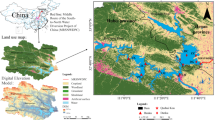
Dianchi Lake, known as the Pearl of the Plateau, lies at an elevation of 1886 m and extending across 24°39′56″ to 25°01′32″N and 102°35′42″ to 102°47′19″E, is located in the heart of the Kunming Basin in southwestern China. It is flanked by DaGuan Park to the north and JinNing County to the south, stretching from the ChengGong District in the east to the foothills of XiShan in the west (Fig. 1). Dianchi, encompassing an area of 311 km² and with a shoreline length of approximately 150 km, is the largest lake in the basin of southwest China. The lake is partitioned into two sections, Caohai (Ch) and Waihai (Wh), by a longitudinal embankment. The Wh encompasses an area of 289.065 km², which constitutes more than 90% of the overall extent of Dianchi. As a fault basin lake, Dianchi is believed to have originated during the transition from the Mesozoic to the Cenozoic eras²⁶. Dianchi has experienced permanent eutrophication throughout the year, primarily due to excessive fertilizer inputs resulting from urban expansion that have surpassed the organic load capacity of this unique geological formation. Changes in land use and the unpredictable impacts of precipitation have further contributed to this condition²⁷. Additionally, due to the recurrent interplay between surface water and groundwater, the Dianchi Lake harbors high concentrations of calcium²⁸. Karst water bodies demonstrate a greater susceptibility to pollution in comparison to other inland water bodies. Consequently, incidents of ‘cyanobacterial water bloom’ and ‘black-odorous water’ frequently occur. Concerns regarding the water quality of Dianchi have escalated in recent years, prompting the implementation of various large-scale engineering projects aimed at expeditiously improving the lake’s water quality.

Fig. 1

Survey Region. ArcGIS 10.8 was used to create the map containing satellite imagery, with the URL: https://www.esri.com, http://www.gscloud.cn/ and https://www.mnr.gov.cn/.

Launched on May 9, 2018, the GF-5 satellite has the world’s first spacecraft to simultaneously and extensively observe the land and atmosphere. Its notable features include a wide coverage area, high resolution, and high load spectral calibration accuracy. GF-5 is equipped with an AHSI that operates in the visible and shortwave infrared regions, with a swath width of 60 km, spatial resolution of 30 m, and spectral precision of 5 nm. In comparison to conventional cameras, it offers more than a 100-fold increase in spectral range and channel number, capturing 330 spectral channels ranging from the visible to the short-wave infrared (400–2500 nm). For this study, high-quality GF-5 data with minimal cloud cover were selected for March 22, 2019, and December 16, 2019. Detailed parameters of the remotely sensed image data can be found in Table 1.

Table 1 AHSI parameters in order to acquire GF-5 satellite synchronous quasi-synchronous measure data for the months of March and December in 2019, a selection was made of ten nationally controlled sampling sites. Among these, two sampling sites were located in Ch, while the remaining eight were situated in Wh, as detailed in Table 2. The monitoring frequency for these sites was set at once per month. Consequently, a total of 20 sets of WQI were obtained. These WQI comprised the biological indicator Chl, as well as five chemical indicators: pH, CODcr, TP, NH3-N, and TN.

Table 2 Sampling point information.

Methodological overview

The methodology employed in this study encompasses the pre-processing of hyperspectral data obtained from the GF-5 satellite, the development of a machine learning-based inversion model, and the subsequent visualization of the inversion results derived from the optimal model (Fig. 2). During the modeling phase, this research contrasts the improved support vector regression model and the improved back propagation neural network against the classical random forest algorithm, which serves as the benchmark. Taking into account the differing areas of the Ch and Wh, as well as the slower rate of water circulation between the two regions. Subsequently, the Ch is divided into about 11,102 grids of 30 m*30m and the Wh is divided into about 35,641 grids of 90 m*90m to improve the computational efficiency. The most effective model for each WQI was applied to the center of each grid. In order to mitigate spatial heterogeneity and facilitate smoother transitions, maps depicting the distribution of WQI were generated utilizing kriging interpolation.

Fig. 2

Technique flow chart.

Preprocessing of satellite image data

The image preprocessing used ENVI software, including radiometric calibration, atmospheric correction, geometric correction, water body extraction, and visual interpretation. Radiometric calibration establishes a correlation between the satellite sensor’s associated field of view and its brightness gray-scale data²⁹. And it is imperative to eliminate strong atmospheric influences as they often constitute more than 80% of the total signals in water remote sensing inversion³⁰. The geometric correction was utilized for the purpose of mitigating geometric distortions present in the remote sensing image, whilst simultaneously providing geographic and projection coordinates. In this study, the files GF5_AHSI_VNIR_Spectralresponse.raw and GF5_AHSI_VNIR_RadCal.raw were utilized as constraining factors for radiometric calibration calculations. The MODTRAN4 + radiation transfer model is employed for pixel-level atmospheric correction³¹. Finally, the discrepancy in reflectance values between the green band within the non-water sensitive region and the near-infrared band within the water-sensitive region was computed by the Normalized Difference Water Index (NDWI) to facilitate the initial extraction of water bodies³². And in order to achieve a more precise delineation of the study area, manual visual interpretation was incorporated to exclude terrestrial regions that may be erroneously classified.

Spectral data processing

In order to mitigate the influence of water movement on the correspondence between WQI and spectral values at the same sampling points, we adopt an improved measurement method. A square buffer with a side length of three image pixels was applied around each measurement point. The hyperspectra at each measurement point are represented by the mean de-trended curve remaining after the removal of anomalous curves. De-trending is a polynomial smoothing technique to eliminate baseline drifts from spectral curves exhibiting similar trends³³. Spectral curves may change dramatically due to various factors, such as abrupt changes in the surrounding environment or human intervention³⁴. These factors can compromise the model’s stability and limit its capacity to respond effectively to different situations. Consequently, it is necessary to remove noise present in the original spectra. In the present study, a combination of various spectral de-noising techniques and spectral variations was utilized. Such as, the spectral curves were filtered using the Savitzky-Golay (SG) filtering method, using weighted values derived from least-squares fitting based on a specified high-order polynomial. All peak points on the spectral curves, identified through polynomial searching, were connected. The trend lines exhibiting the highest slopes were subsequently chosen from the peak lines. These peaks were then subtracted to acquire the continuum-removed reflectance values. As shown in Eqs. (1), (2), and (3).

$$\:\begin{array}{c}y={\text{a}}_{0}+{\text{a}}_{1}*t+{\text{a}}_{2}*{\text{t}}^{2}+\dots\:+{\text{a}}_{\text{k}-1}*{\text{t}}^{\text{k}-1}\end{array}$$

(1)

$$\begin{array}{*{20}c} {A = \left( {X^{T} \cdot X} \right)^{{ - 1}} \cdot X^{T} \cdot Y} \\ \end{array} \begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {y_{{ - n}} } \\ {y_{{ - n - 1}} } \\ \vdots \\ {y_{n} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & { - n} & \cdots & {( - n)^{{k - 1}} } \\ 1 & { - n + 1} & \cdots & {( - n + 1)^{{k - 1}} } \\ \vdots & \vdots & \vdots & \vdots \\ 1 & n & \cdots & {n^{{k - 1}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {a_{0} } \\ {a_{1} } \\ \vdots \\ {a_{{k - 1}} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {e_{{ - n}} } \\ {e_{{ - n + 1}} } \\ \vdots \\ {e_{n} } \\ \end{array} } \right)} \\ \end{array}$$

(2)

$$\begin{array}{*{20}c} {A = \left( {X^{T} \cdot X} \right)^{{ - 1}} \cdot X^{T} \cdot Y} \\ \end{array}$$

(3)

$\:\text{y}$ is the polynomial fitting result; $\:\text{t}$ is the observation point (-n, -n + 1, 0, …, n-1, n); $\:\text{a}$ is the smoothing parameter; $\:\text{A}$ is the fitting parameter determined by the least-square method; $\:\text{Y}$ is the fitting result; $\:\text{X}$ is design matrix that contains the independent variable terms.

In addition, spectral data demonstrating nonlinearity or heteroscedasticity was eliminated through the utilization of the Standard Normal Variate (SNV). In order for the spectra to follow a standard normal distribution, the centralization was divided by the standard deviation, shown as Eq. (4). Furthermore, the Multiplicative Scatter Correction (MSC), resembling SNV, enhanced data stability by calculating MSC factors that corresponded to the sample wavelengths, shown as Eq. (5).

$$\:\begin{array}{c}{\text{Y}}_{\text{i}}={{\Phi\:}}^{-1}\left[\frac{1}{\text{n}}{\sum\:}_{\text{j}=1}^{\text{n}}{\Phi\:}\left({\text{Z}}_{\text{i}\text{j}}\right)\right]\end{array}$$

(4)

$\:\text{n}\:\text{i}\text{s}\:\text{t}\text{h}\text{e}\:\text{t}\text{o}\text{t}\text{a}\text{l}\:\text{n}\text{u}\text{m}\text{b}\text{e}\text{r}\:\text{o}\text{f}\:\text{s}\text{a}\text{m}\text{p}\text{l}\text{e}\text{s}$, $\:{{\Phi\:}}^{-1}$ is the inverse function of the standard normal cumulative distribution function. $\:{\text{Z}}_{\text{i}\text{j}}$ is the data of the jth sample point of the ith wavelength after scale scaling, $\:{\text{Y}}_{\text{i}}$ is the data of the ith wavelength after standard normal transformation, and $\:{\Phi\:}\left({\text{Z}}_{\text{i}\text{j}}\right)$ is the cumulative distribution function value of the scaled data.

$$\:\begin{array}{c}{\text{K}}_{\text{i}}=\frac{{\sum\:}_{\text{j}=1}^{\text{m}}{\text{c}}_{\text{i}\text{j}}{\text{s}}_{\text{j}}}{{\sum\:}_{\text{j}=1}^{\text{m}}{\text{s}}_{\text{j}}^{2}}\end{array}$$

(5)

$\:{\text{K}}_{\text{i}}$ is the MSC factor, $\:{\text{c}}_{\text{i}\text{j}}$ is the MSC standard sample spectral value of the jth sample point at the ith wavelength, $\:{\text{s}}_{\text{j}}$ is the MSC spectral value of the jth standard sample.

The partial least squares regression (PLSR) method is particularly adept at addressing issues of high correlation and colinearity in spectral data, while also identifying latent factors associated with the target variable³⁵. So, compared to other fundamental regression techniques, it is better suited for interpreting the suitability of results obtained from hyperspectral data processing. In this research study, a comparative analysis of the outcomes achieved through the utilization of SG + SNV and SG + MSC techniques was undertaken, employing the method of PLSR.

Previous studies have demonstrated the potential of utilizing a combination of spectral bands and logarithmic derivative transformed bands for pixel-by-pixel inversion^36,37,38. In this study, the spectral dataset was divided into red, green, blue, and yellow bands. These bands were utilized individually or in combination to perform a range of computations, including band addition, band subtraction, first-order derivative of logarithmic bands, and the ratio of band reflectance difference to band reflectance sum. Based on the various spectral bands, a total of 25 spectral combinatorial variables (SCV) were categorized into four groups: 10 location variables (Supplementary Table A1), 4 area variables (Supplementary Table A2), 6 band combination variables (Supplementary Table A3), and 5 common vegetation indices (Supplementary Table A4). Lastly, in order to explore additional potential bands that could be used for inversion, logarithmic and derivative variations were implemented on the spectral data after de-noising process. These variations encompassed first-order derivative (1Der), second-order derivative (2Der), and third-order derivative (3Der), as well as logarithmic first-order derivative (Log + 1Der), logarithmic second-order derivative (Log + 2Der), and logarithmic third-order derivative (Log + 3Der).

To identify variables that are responsive to changes in different WQI, Pearson correlation analyses were conducted the spectral data (both before and after logarithmic derivative transformations) and the 25 SCV. Only those spectral band variables, spectral derivative variables, logarithmic derivative variables, and SCV variables that met the significance requirements (significance level P < 0.001) were selected.

Improved support vector regression models

The Support Vector Machine (SVM) model serves as the basis for Support Vector Regression (SVR). It possesses a distinctive feature where in losses are not computed within the data’s margin. Losses are only computed when the absolute difference between f(x) and y exceeds the margin³⁹. This implied that the function model was solely impacted by the losses incurred by non-boundary support vectors. Consequently, in order to design the widest margin, it was imperative to also fulfill the minimum loss requirement. The function is shown as Eq. (6):

$$\begin{array}{*{20}c} {Z = \mathop {\min }\limits_{{w,b}} \frac{1}{2}\parallel w\parallel ^{2} + C\mathop \sum \limits_{{i = 1}}^{m} l_{\smallint } \left( {f\left( {x_{i} } \right),y_{i} } \right)} \\ \end{array}$$

(6)

where, $\:\text{Z}$ is the optimal model, $\:\text{w}$ is the model coefficients, $\:\text{b}$ is the model intercept, $\:\text{C}$ is the support vector machine loss function, $\:\text{f}\left(\text{x}\right)$ is the model output values, y is the real value, $\:{\text{y}}_{\text{i}}$ is the actual value of the -th sample, $\:{\text{x}}_{\text{i}}$ is the -th sample.

The function’s margin constraints were relaxed by incorporating linear soft interval, allowing certain samples to exceed the boundary⁴⁰. This ensured that every data point follows Eq. (7).

$$\begin{array}{*{20}c} {\left| {y_{i} - \left( {wx_{i} + b} \right)} \right| \le \varepsilon + \zeta ,\forall _{i} } \\ \end{array}$$

(7)

Where,$\:\:{\upepsilon\:}$ is the original margin, $\:{\upzeta\:}$ is the linear soft interval variable, $\:{\forall\:}_{\text{i}}$ is the measure of whether the i-th sample exceeds$\:.$

We achieved improved SVR modeling in MATLAB. The SVM predict function, utilizing the Gaussian radial basis kernel function, was employed for SVR prediction. The gamma parameter within this kernel function governed the data distribution in the novel feature space, consequently impacting both the training process and prediction efficiency. Moreover, the C parameter modulated the model’s generalization capability. We employed a grid search methodology for cross-validation, systematically evaluating each parameter combination. This process identified C = 2 and gamma = 0.0221 as the optimal parameters.

Bp neural network model optimized by NSGA II genetic algorithm

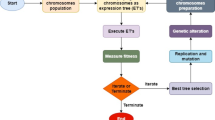
The BP neural network is built upon the Back Propagation technique, which adjusts the weights and biases of the network in response to erroneous values⁴¹. The learning process of the artificial neural network was monitored using gradient descent, which progressively aligned the output values of the network with the actual values (Fig. 3b). In genetic algorithms, three genetic operators were utilized: gene crossover, gene mutation, and gene selection⁴². Genetic crossover introduced various crossover strategies, such as multipoint crossover and even crossover, to enhance the diversity of the population (Fig. 3c).

In this study, we proposed an enhanced BP neural network framework that utilized the NSGA II algorithm for multi-objective optimization. The aim was to improve the adaptive and global advantages of genetic algorithms in efficiently finding the optimal solution. By harnessing the global optimization capabilities of evolutionary algorithms, we could prevent local minima during training and obtain optimal initial weights and thresholds for the BP network. The algorithmic approach is illustrated in Fig. 3. The constructed BP neural network inversion model utilized reflectance data from GF-5 remote sensing satellite as input layer data. The data was split into training and testing sets with a 7:3 ratio for modeling the neural network with five hidden layers. Through 20 iterations, a crossover rate of 0.2 and a mutation probability of 0.001 were identified as the optimal genetic optimization parameters. The use of the NSGA II algorithm for multi-objective optimization resulted in a lower termination mutation rate compared to the unimproved model. Furthermore, the optimized model showed smaller gradient values than the pre-optimization ones, indicating a more stable convergence.

Fig. 3

Flowchart of BP-NGA.

Random forest model

One of the most widely used machine learning algorithms is Random Forest (RF), which employs a recursive feature selection process to segment data from reclassified samples. The predictive reliability of RF could be enhanced by adjusting parameters such as maximum depth, halting condition, feature subset size, and splitting criterion⁴³. In decision tree learning methods, the determination of the maximum depth threshold or the number of samples at a node was influenced by the segmentation criterion. The Gini coefficient was employed as the primary evaluation criterion for splitting decision tree nodes, with a lower Gini coefficient indicating a more effective data segmentation⁴⁴. The function is defined as Eq. (8):

$$\:\begin{array}{c}Gini\left(\text{p}\right)=\sum\:_{\text{n}=1}^{\text{N}}{\text{P}}_{\text{n}}\left(1-{\text{P}}_{\text{n}}\right)=1-\sum\:_{\text{n}=1}^{\text{N}}{{\text{P}}_{\text{n}}}^{2}\end{array}$$

(8)

For binary tree based decision tree can be expressed as Eq. (9) and Eq. (10):

$$\:\begin{array}{c}Gini\left(\text{p}\right)=2p\left(1-\text{p}\right)\end{array}$$

(9)

$$\:\begin{array}{c}Gini\left(\text{D},\text{A}\right)=\frac{\left|{\text{D}}_{1}\right|}{\left|\text{D}\right|}Gini\left({\text{D}}_{1}\right)+\frac{\left|{\text{D}}_{2}\right|}{\left|\text{D}\right|}Gini\left({\text{D}}_{2}\right)\#\left(10\right)\end{array}$$

(10)

Where,$\:\text{G}\text{i}\text{n}\text{i}$ is the coefficient, $\:\text{n}$ is the categories of decision tree, and $\:{\text{P}}_{\text{n}}$ is the probability that the sample belongs to class n. $\:\text{p}$ is the probability of the sample. $\:{\text{D}}_{1}$ is the set of satisfying characteristics, and $\:{\text{D}}_{2}$ is the set of features that do not satisfy.

RF models were built using the R programming language. The optimal parameter, which was identified as the minimum number of decision trees required to stabilize the model error rate at a relatively low level, was determined. When the count of decision trees reaches 130, the out-of-bag error exhibited both small and stable characteristics.

Error metrics

In this paper, k-fold cross-validation is employed to assess the effectiveness of the model. The dataset is partitioned into k subsets, with one subset designated as the validation set during each iteration. The metrics obtained from the k validation processes are averaged to derive a comprehensive performance of the model. The comprehensive performance evaluation metrics include mean square error (MSE), coefficient of determination (R²), root mean square error (RMSE) and mean absolute error (MAE). R², which measured the goodness of fit, exhibited a positive correlation with model accuracy, with higher values indicating better precision. Conversely, lower MAE, MSE, and RMSE values implied higher model accuracy and less variation between predicted and actual values. These indicators are defined as Eq. (11), Eq. (12), Eq. (13), Eq. (14):

$$\:\begin{array}{c}{\text{R}}^{2}=\frac{\sum\:_{\text{i}=1}^{\text{n}}\left({\text{x}}_{\text{i}}-\overline{\text{x}}\right)\left({\text{y}}_{\text{i}}-\overline{\text{y}}\right)}{\sqrt{{\sum\:_{\text{i}=1}^{\text{n}}\left({\text{x}}_{\text{i}}-\overline{\text{x}}\right)}^{2}}{{\sum\:}_{\text{i}=1}^{\text{n}}\left({\text{y}}_{\text{i}}-\overline{\text{y}}\right)}^{2}}\end{array}$$

(11)

$$\:\begin{array}{c}MSE=\frac{1}{\text{n}}\sum\:_{\text{i}=1}^{\text{n}}{{\text{w}}_{\text{i}}\left({\text{y}}_{\text{i}}-\overline{{\text{y}}_{\text{i}}}\right)}^{2}\end{array}$$

(12)

$$\:\begin{array}{c}MAE=\frac{1}{\text{n}}\sum\:_{\text{i}=1}^{\text{n}}\left|\overline{{\text{y}}_{\text{i}}}-{\text{y}}_{\text{i}}\right|\end{array}$$

(13)

$$\:\begin{array}{c}RMSE=\sqrt{\frac{1}{\text{n}}\sum\:_{\text{i}=1}^{\text{n}}{{\text{w}}_{\text{i}}\left({\text{y}}_{\text{i}}-\overline{{\text{y}}_{\text{i}}}\right)}^{2}}\end{array}$$

(14)

where, $\:\text{n}$ is the number of samples, $\:{\text{x}}_{\text{i}}$ is the independent variable, $\:\overline{\text{x}}$ is the average of all independent variables, $\:{\text{y}}_{\text{i}}$ is the value of measured data, $\:\overline{\text{y}}$ is the average of all measured data, and $\:\overline{{\text{y}}_{\text{i}}}$ is the predicted data.

Results

SG with SNV outperforms SG with MSC in spectral processing

The spectral reflectance profile of the Dianchi water body was derived by utilizing the regions of interest (ROIs) from the winter and spring data points. It was observed that the visible to near-infrared wavelength range exhibited the most prominent characteristics of our research subject. So, data within the wavelength range of 400 to 1000 nm were exclusively analyzed. Notably, the yellow-green spectrum corresponding to wavelengths between 560 and 580 nm showed the highest level of light reflection by water. Peaks in the red band between 690 and 710 nm, as well as between 790 and 810 nm, were attributed to the presence of algae and suspended particles in Dianchi. Furthermore, two troughs were identified between these peaks, one between 650 and 700 nm and another between 730 and 790 nm, which could be attributed to water absorption caused by carotenoids and chlorophyll.

Fig 4a shows the spectrogram for each sampling point. Figure 4b presents the plots before and after SG smoothing, SNV transformation, and MSC transformation for the data from the Baiyukou monitoring station. Figure 4c illustrates the results of 1Der, 2Der, 3Der, Log + 1Der, Log + 2Der, and Log + 3Der processing, also using data from the Baiyukou monitoring station as an example. The spectral fluctuations obtained after different treatments showed a similar trend in the range of 400–650 nm, but there was a significant difference in the range of 650–1000 nm. Comparing with the PLSR method, it is evident that the regression outcomes of the SNV transformed hyperspectral data are more robust and possess broader applicability (Fig. 5).

Fig. 4

(a) Original spectrogram. (b) Comparison of spectral pre-processing. Spectrum acquired at point 10 (BaiYuKou). The blue line represents the original spectrum, the orange line represents the spectrum after SG smoothing, the red line represents the spectrum after SNV transformation based on the orange line, the green line represents the spectrum after MSC transformation based on the orange line; (c) Spectral derivative and logarithmic transformations. The spectral changes from top to bottom are first-order derivative, second-order derivative, third-order derivative, logarithmic first-order derivative, logarithmic second-order derivative, and logarithmic third-order derivative. All six spectral variations are based on preprocessed spectra at point 10.

Fig. 5

Comparison of the effects of SNV and MSC when utilized in conjunction with SG. The red dashed line represents the degree of applicability of the spectra obtained by SG + MSC preprocessing in the 6 WQI. The black solid line represents the degree of applicability of the spectra obtained by SG + SNV preprocessing in the 6 WQI.

Development of models for 6 WQI

Screening characteristic bands

The correlation heat maps presented in Supplementary Fig.A1-A6 indicate that there is a correlation between the various WQI and optical properties of Dianchi. The 6 WQI all exhibit more than two significant correlation bands within the original spectral wavelength range of 400 nm to 600 nm (Fig. 6). Significant correlation bands for the 6 WQI were observed decentralize across the wavelength range following the spectral change (Fig. 7). Moreover, as the order of the derivative increases, the number of significant correlation bands obtained diminishes. A limited number of criteria-compliant correlation bands were observed between the 25 SCV and the 6 WQI, with Blue-edge-amplitude ($\:{\text{D}}_{\text{b}}$), Blue-edge-area ($\:{\text{S}\text{D}}_{\text{b}}$), and Perpendicular Vegetation Index (PVI) emerging more frequently as indicators exhibiting high correlations (Fig. 8).

Fig. 6

Correlation diagram of original spectral. The black line represents the correlation between pH and the spectral bands after preprocessing. The red line represents the correlation between CODcr and the spectral bands after preprocessing. The blue line represents the correlation between TP and the spectral bands after preprocessing. The orange line represents the correlation between NH3-N and the spectral bands after preprocessing. The purple line represents the correlation between TN and the spectral bands after preprocessing. The green line represents the correlation between Chl and the spectral bands after preprocessing. Values above the solid line indicate a strong correlation between the band and the WQI. Values above the dashed line indicate a stronger correlation between the band and the WQI.

Fig. 7

Correlation diagram of spectral derivatives and logarithmic transformations. (a) first-order derivative; The black line represents the correlation between pH and the spectral bands after preprocessing and first-order derivative. The red line represents the correlation between CODcr and the spectral bands after preprocessing and first-order derivative. The blue line represents the correlation between TP and the spectral bands after preprocessing and first-order derivative. The orange line represents the correlation between NH3-N and the spectral bands after preprocessing and first-order derivative. The purple line represents the correlation between TN and the spectral bands after preprocessing and first-order derivative. The green line represents the correlation between Chl and the spectral bands after preprocessing and first-order derivative. (b) second-order derivative; The WQI indicated by the line colors are the same, but the spectral bands are preprocessed and second-order derivatived. (c) third-order derivative; The WQI indicated by the line colors are the same, but the spectral bands are preprocessed and third-order derivatived. (d) logarithmic first-order derivative; The WQI indicated by the line colors are the same, but the spectral bands are preprocessed and logarithmic first-order derivatived. (e) logarithmic second-order derivative; The WQI indicated by the line colors are the same, but the spectral bands are preprocessed and logarithmic second-order derivatived. (f) logarithmic third-order derivative. The WQI indicated by the line colors are the same, but the spectral bands are preprocessed and logarithmic third-order derivatived. Values above the solid line indicate a strong correlation between the band and the WQI. Values above the dashed line indicate a stronger correlation between the band and the WQI.

Fig. 8

Correlation diagram of 25 SCV. The black line represents the correlation between pH and the SCV obtained from preprocessed spectra. The red line represents the correlation between CODcr and the SCV obtained from preprocessed spectra. The blue line represents the correlation between TP and the SCV obtained from preprocessed spectra. The orange line represents the correlation between NH3-N and the SCV obtained from preprocessed spectra. The purple line represents the correlation between TN and the SCV obtained from preprocessed spectra. The green line represents the correlation between Chl and the SCV obtained from preprocessed spectra. Values above the solid line indicate a strong correlation between the band and the WQI. Values above the dashed line indicate a stronger correlation between the band and the WQI.

Screening the best model for each 6 WQI

In this study, we carried out a statistical analysis to evaluate the accuracy of WQI models constructed using three different algorithms under 7 spectral variations: 1Der, 2Der, 3Der, Log + 1Der, Log + 2Der, Log + 3Der, and SCV (Fig. 9). After eliminating over fitting models, it was observed that the BP-NGA model demonstrated suitability for the inversion of most WQI with a high degree of accuracy. Conversely, the improved SVR model exhibited instability in the inversion of various WQI, characterized by a substantial discrepancy between the highest and lowest accuracy. In contrast, the RF model maintained stability. The correspondence between the algorithms utilized in the models and the optimal hyperspectral processing methods is delineated, along with a comprehensive enumeration of essential evaluation criteria, specifically the maximum R² (Fig. 10). Where the red curve represents the best inversion model for each WQI and the green and yellow curves are progressively less applicable. Specific model parameters and expressions for each WQI are listed in Supplementary Table A5. For the CODcr, the R² values of the three models all exceed 0.88; however, the improved SVR model exhibits the highest MSE at 15.86. The R² value of the optimal model for NH3-N is 0.99 and the MSE is $\:{2.65\text{e}}^{-3}$. Overall, all three inversion models exhibited relatively high accuracy for NH3-N. Concerning the TN, the minimum R² value for the three inversion models is 0.89, and the maximum MSE is 0.65. As for the TP, the minimum R² value among the three inversion models is 0.94, while the maximum MSE is $\:{2.70\text{e}}^{-4}$. In terms of the pH, the maximum MSE and the the maximum R² of the three inversion models are 0.16 and 0.92, respectively. These values indicate that pH exhibits inferior overall inversion performance in comparison to other WQI. Lastly, for the Chl, the BP-NGA was poor modeling, showing lower R² and higher MSE. In summary, the Log + Der2, Der3, Der1, and Der3 spectrum transformations of the BP-NGA model served as the foundation for the best inversion models for CODcr, NH3-N, TN, and TP, respectively.

Fig. 9

Comparison of precision results based on 126 models. Gray is the accuracy of CODcr modeled based on different spectral features (first-order derivative, second-order derivative, third-order derivative, logarithmic first-order derivative, logarithmic second-order derivative, logarithmic third-order derivative and 25 SCV). Red is the accuracy of NH3-N modeled based on different spectral features. Blue is the accuracy of TP modeled based on different spectral features. Green is the accuracy of TN modeled based on different spectral features. Purple is the accuracy of pH modeled based on different spectral features. Yellow is the accuracy of Chl modeled based on different spectral features.

Fig. 10

Optimal modeling of the 6 WQI. The red color indicates the spectral variation and modelling required for the best inversion model for each WQI. The green color indicates the spectral variation and modelling required for the second best inversion model for each WQI. The yellow color indicates the spectral variation and modelling required for the third best inversion model for each WQI.

Validation of the 6 best inversion models from screening

It illustrates the validation results of the test set for the BP-NGA model (Fig. 11). It is observed that the trend of the fitted line closely adheres to the Y = T axis. The validation results for the RF model demonstrate a strong alignment between the predicted values and the actual values (Fig. 12). And it presents the validation results for the improved SVR model (Fig. 13), indicating minor discrepancies between the predicted and actual values. These findings suggest that the BP-NGA model was effective in simulating the CODcr, NH3-N, TN, and TP. The RF model was suitable for determining the pH, while the improved SVR model could be utilized for simulating the Chl.

Fig. 11

BP-NGA model validation diagram((a) modelling of CODcr (b) modelling of NH3-N (c) modelling of TN (d) modelling of TP). The horizontal and vertical coordinates are the actual and predicted values of the validation set, respectively. The black solid line is the fitted line for the validation set. The red dashed line is the control line, where R² is close to 1.

Fig. 12

Improved SVR model validation diagram. The orange line is the predicted value of the validation set and the black line is the actual value of the validation set.

Fig. 13

RF model validation diagram. The black line is the actual value of the validation set and the orange line is the predicted value of the validation set.

Analysis of spatial and temporal variations in dianchi water quality and validation of results

The winter and spring inversion maps of Dianchi were obtained by kriging the results of the optimal inversion model (Fig. 14). The results revealed significantly lower concentrations of the most WQI in Ch compared to the Wh. Notably, in the normalized water quality map, TP, NH3-N, CODcr, pH and Chl displayed similar correlations, suggesting that the water quality of the Ch was superior to that of the Wh (Fig. 15, 16). In summary, water quality is lower in the edge areas than in the center. And in the seasonal study, the inversion results in March and December were compared. It was observed that the risk of eutrophication was higher in spring than in winter, with both the extent and rate of nutrient enrichment increasing more rapidly. Specifically in the northeastern region, the presence of dominant southerly winds during springtime exacerbates the likelihood of eutrophication.

CODcr concentrations decreased during the winter, particularly in the southwestern region, while new aggregation zones emerged in the northeast. The northeast and southwest coasts of Wh recorded the highest concentrations of NH3-N, while these high-concentration areas gradually diminished from spring to winter, resulting in significantly reduced concentration peaks. Ch exhibited higher levels of TN compared to Wh. Noteworthy high concentrations of TN were observed in the northern regions of Wh, with a declining trend from north to south, and the maximum concentrations were significantly lower during winter. In terms of TP, Ch generally exhibited low concentrations, with a few coastal locations displaying elevated levels. From spring to winter, the high-concentration area on the northeast coast of Wh shifted northward, accompanied by a rapid decline in overall TP concentration across the Dianchi. On the southeastern bank of Ch, there was an arcuate pattern of high pH concentration. Moreover, there was a significant and positive correlation between pH and water temperature⁴⁵. The pH distribution in Wh decreased gradually from winter to spring. Across Ch, the concentrations of the Chl consistently remain low. In spring, the high concentrations of Chl were primarily situated in the central region of Wh and gradually extended to the north and south.

Fig. 14

Inverse Mapping of the 6 WQI of Dianchi for different months. The units of codcr, NH3-N, TP, TN and Chl in this graph are all mg/L. The larger the value, the closer the color is to red.

Fig. 15

Inverse Mapping of Spring (March) normalised WQI in Dianchi: (a) is CODcr, (b) is TN, (c) is TP, (d) is NH3-N, (e) is Chl, (f) is pH. All values of WQI in this figure are normalized to values between 0 and 1. The larger the value, the closer the color is to red.

Fig. 16

Inverse Mapping of winter (December) normalised WQI in Dianchi: (a) is CODcr, (b) is TN, (c) is TP, (d) is NH3-N, (e) is Chl, (f) is pH. All values of WQI in this figure are normalized to values between 0 and 1. The larger the value, the closer the color is to red.

The results from monitoring station observations were compared to the interpolation results of different WQI (Fig. 17). Most of the sites’ inversion results show good precision and strong consistency with the measured values with the R² up to 0.8. However, some indices show significant deviations from the true values. As the R² of pH is only 0.7, indicating that the model or the interpolation method may still need to be improved.

Fig. 17

Inversion result validation plot: (a) CODcr; (b) NH3-N; (c) TN; (d) TP; (e) pH ; (f) Chl. The horizontal and vertical coordinates in the figure are the inverted and true values of all measured points after region-wide interpolation, respectively.

Discussion

In this study, different optimal inversion models were developed for the 6 WQI based on BP-NGA, improved SVR, and RF, which all demonstrates superior accuracy. These models provide a practical option for policymakers, facilitating more sustainable management of water resources. And we conducted a field survey of the conditions surrounding Dianchi to evaluate the efficacy of the proposed predictive model in accurately forecasting various WQI. The primary potential sources of pollution in the study area identified after the field survey (Fig. 18). Anthropogenic pollution, shoreline destruction, and low vegetation coverage contribute to the generation of pollution sources. Anthropogenic pollution sources included river injection pollutants, tertiary industry pollutants, agricultural pollutants, and domestic pollutants. Sporadic factories and numerous waterfront buildings existed. Large-scale agricultural production and free-range animal breeding continued in areas where the “no aquaculture” law was enforced. And in the absence of vegetation cover, nutrients from the land could seep into the river. The results indicate that the spatial and temporal variations in water quality in Dianchi from winter to spring are consistent with findings documented in the existing literature. Niejufen⁴⁶ proposed an evaluation of water quality pollution in Dianchi utilizing the theory of standard curves and set-pair analysis, revealing that the levels of CODcr and TN were significantly higher in January compared to December of that year, while the level of TP was moderately elevated. Zhu et al.⁴⁷ employed a geographical detector to assess the spatial variability of the lake’s ecological health, finding that water quality in the southern lake area, as well as in the northern and eastern bay areas, was considerably inferior to that in the central lake area. So, the inverse model, based on hyperspectral satellite data, achieved effective water quality monitoring results for lakes in karstic landscapes, serving as a valuable complement to macro water quality monitoring efforts.

Fig. 18

Field Survey Results. This map shows the problematic locations identified as a result of the field assessment. The green point is the artificial pollution source. The yellow point is the low vegetative cover. The red point is the low health shoreline.

The results of the analyses indicate that various WQI exhibit distinct fluctuation regularities across different regions of Ch and Wh. Field surveys suggest that the inflowing rivers, specifically the PanLong River and BaoXiang River on the northern coast of Wh, significantly contribute to CODcr burden of the Dianchi Lake basin, accounting for 44% of the total input. This finding is consistent with the observed formation of a CODcr aggregation zone in the northeastern region of Wh. Satellite imagery has identified several areas in the eastern part of Wh with minimal or no vegetation cover, rendering them susceptible to soil erosion and acting as conduits for the entry of phosphate fertilizers, pesticides, and sewage from adjacent lands. Furthermore, research conducted by Wang et al.⁴⁸ indicates that rising temperatures accelerate the degradation rate of organic matter, resulting in an increased outflow of phosphorus. This observation aligns with the documented regional distribution and the spatial and temporal variation of TP in the study. Riparian rocks and soils possess the capacity to neutralize acids, thereby mitigating the influx of pollutants into Dianchi^49,50. Extensive field investigations have demonstrated that the majority of the clay-based shoreline substrate in the northeastern area displays negatively charged surfaces and exhibits greater efficacy in neutralizing acidic cations compared to the rocky soil substrate along the southeastern shoreline. It is consistent with the elevated pH levels proposed for the southeastern shore in the study.

The TP, NH3-N, CODcr, pH, and Chl exhibited a substantial regional pattern of similarity. The findings of the study demonstrated that only TN concentrations were markedly higher in the Ch area compared to the Wh area. Investigations revealed that the silt present in the shallow waters of Ch was rich in nitrogen compounds, thereby contributing to the elevated TN levels observed. Furthermore, significant external TN inputs within the northern region were primarily influenced by urbanization and the development of third-industry infrastructure, such as DaGuan Park. Biological processes, particularly photosynthesis occurring in wetlands like GanGouWei Wetland, facilitated the conversion and release of nitrogen. This biological activity may account for the pronounced disparity in concentration between the TN and the other WQI in the distributions of Ch and Wh. Additionally, a temporal regularity was noted among the 6 WQI, which may be attributed to increased runoff and rainfall during the spring, as well as the influences of sunlight and temperature. These environmental factors not only promoted the release of nutrients that had accumulated throughout the preceding winter but also led to a more uniform distribution of WQI. Research conducted by Guo et al.⁵¹identified that certain cyanobacteria are capable of both fixing nitrogen and absorbing phosphorus from sediments, which can facilitate the co-production and cycling of these nutrients within aquatic ecosystems. Consequently, the observed similarity in the patterns of change among WQI may also result from the fact that these WQI share common sources. This finding aligns with the results reported by Yang et al.⁵².

The application of hyperspectral data in water quality inversion is garnering increasing scholarly attention, primarily due to its high spectral resolution and extensive spectral information. Rallo et al.⁵³ indicated that technological advancements in the industrial production of hyperspectral sensors, characterized by a substantial number of contiguous spectral bands, have prompted scientists to conduct more precise analyses. The study presented in this paper demonstrates that the AHSI sensor onboard the GF-5 is capable of providing reliable spectral data for various band combinations, thereby offering improved options for model construction. However, it is important to note that these results of models may not be entirely accurate, as they are derived from the processing of data obtained from individual satellite images collected in March and December. So, we do not take into account the autumn and summer seasons, nor do they consider the specific optical properties of the atmosphere, both of which may significantly influence the results.

Related studies⁵⁴ have employed machine learning techniques, such as improved SVR and RF, to analyze complex spectral data. Nonetheless, the effective selection and combination of spectral bands that are appropriate for machine learning models in the context of water quality inversion continues to present a significant challenge. This study identifies that the optimal spectral variation for predicting pH and TN using the RF model is SCV, which encompasses a considerable number of yellow-green bands. But, the presence of algae and aquatic plants in the water can influence the spectral response within this spectral region. Carter et al.⁵⁵ reported that leaf health can dictate the variability of spectral response in the yellow region. The spectral response is intrinsically linked to the natural environment of the study object. Consequently, the model developed in this paper may not be generalizable. So, additional studies across other lakes situated in karstic landscapes are necessary to validate or refute our findings.

Due to the impact of the epidemic, this study was unable to acquire a substantial amount of measured hyperspectral data during the specified timeframe. As a result, the training sample for the model was constrained, which hindered the model’s generalizability. To enhance the applicability of the model, future research should consider integrating data from satellites with shorter imaging intervals, such as Sentinel-2, in conjunction with ground-based spectrometer data. Additionally, conducting comprehensive analyses of spectral properties, including the inclusion of additional blue light bands and the expansion of the spectral bands utilized, would improve the overall reliability of these models.

Conclusions

This study presents the improved methodology aimed at acquiring high-precision inversion outcomes based on hyperspectral data. It specifically focused on identifying the most efficient models for the inversion of the 6 WQI (CODcr, NH3-N, TP, TN, pH, and Chl) in Dianchi Lake by utilizing GF-5 AHSI data in combination with improved BP-NGA, improved SVR, and RF models. The spatial and temporal fluctuations of water quality in Dianchi were obtained based on these optimal model results. This confirms that these methodologies can be applied to the study of intricate optical characteristics of karst lakes. The main conclusions of the research are as follows:

(1) The R² values in this study all exceed 0.85, suggesting that the water quality inversion models developed using GF-5 data exhibit a high level of accuracy. And the improved BP-NGA approach provided the most versatile applications. The optimized models for each WQI are as follows: BP-NGA model with Log + Der2 for CODcr; BP-NGA model with Der3 for NH3-N and TP; BP-NGA model with Der1 for TN; RF model based on SCV for pH; improved SVR model with Log + Der1 for Chl.

(2) Water quality is generally better in winter than in spring. During the spring, the extreme values of most WQI increased by more than 10%. And the WQI of polluted areas were relatively high and widely dispersed. Conversely, during the winter, the distinctions in water quality between the coastal and central regions were significantly diminished. In addition, Dianchi Lake’s water quality exhibited spatial differences. Ch consistently demonstrates superior water quality in comparison to Wh. The WQI in Ch displayed greater uniformity. Conversely, the coastal sectors of Wh showcased greater variability, with stable central regions.

(3) Urban development is more concentrated in the eastern region. During winter, there has been a noticeable rise in TP concentrations in the northeastern part, which might suggest the presence of illicit sewage discharges. Therefore, it is crucial to prioritize the improvement of interceptor drains and monitoring systems in this specific zone. Furthermore, the establishment of ecological parks and wetlands as buffer zones could serve as effective measures in mitigating pollutant input.