Introduction

Magnetic targets magnetic field signals contain intrinsic and induced magnetic fields, the intrinsic magnetic field is caused by its magnetic material, and the induced magnetic field is caused by the magnetization of the geomagnetic field. The geomagnetic field around the magnetic target generates local distortion and forms quasi-static magnetic field, i.e., magnetic anomaly signatures (MAD), which is a nonlinear and non-stationary signal1. Compared with radar, laser, infrared and other non-acoustic detection technologies, marine MAD technology has the ability of strong concealment, high reliability, low time delay, shallow sea anti-jamming, etc., and is widely used in marine target detection and identification2. However, the electromagnetic signals in the marine environment are complex and variable, and the magnetic target field signals are susceptible to the interference of a variety of noise signals, such as wave magnetic field, near-shore magnetic field, near-seafloor magnetic field3, industrial frequency magnetic field, shipborne electronic equipment magnetic field4, and solar magnetic storms, which leads to a reduction in the effect of target detection and identification. Therefore, magnetic target field signals denoising has become one of the research hotspots for marine target detection and identification.

In recent years, many scholars have carried out a lot of research on the magnetic target field signals denoising5. Liu et al. proposed an adaptive coherent noise suppression (ACNS) method, which is capable of detecting weak magnetic anomalous signals hidden in geomagnetic background noise, but the denoising effect is dependent on the reference signal6. Shen et al. used the wavelet entropy denoising technique to denoise the magnetic signals of unexploded ordnance in the complex background noise environment, but it is difficult to select the wavelet basis, the noise model dependence is large, and the entropy value calculation uncertainty is large7. Ma et al. used an adaptive filter based on variable-step-size normalized least mean square (NLMS) to suppress the noise interference for the magnetic field measurement system of surface buoys, but it is difficult to converge efficiently8. Cheng et al. used the orthogonal basis function method for denoising the ships magnetic field signal for the problem of aeronautical magnetic detection, but the basis function selection depends on experience, poorly adapts to non-stationary noise, may produce boundary effects, and requires high signal sparsity9. Gao et al. used backpropagation neural network (BPNN) method to eliminate background noise for the magnetic sensor array measurement signals denoising under low signal-to-noise ratio (SNR) conditions10. Xu et al. used convolutional neural network (CNN) to learn the features of magnetic anomaly signals and geomagnetic noise from a large amount of training data based on a deep learning framework, and then carried out denoising experiments on test data, but the data dependence is strong, the model is poorly interpreted, and the risk of overfitting is high11. Raissi et al. designed a physically informed neural network (PINN) to embed partial differential equations into a loss function to solve the denoising problem under the constraints of magnetic diffusion equations, but the simplification of the physical model may lead to errors, relies on the understanding of the physical laws, is more difficult to train, is difficult to deal with noise under extreme conditions, and has a relatively complex model interpretability12.

For nonlinear and non-stationary signals, a single denoising method cannot effectively improve the SNR of the signal, and fusion of multiple methods can further improve the denoising performance. Compared with EMD13, EEMD14, and CEEMDAN15, ICEEMDAN adopts a fine-grained strategy to distinguish intrinsic mode functions (IMFs) and minimize IMFs aliasing, which improves the accuracy and reliability of decomposition16. In the study of joint denoising algorithm based on ICEEMDAN, Zhang et al. used ICEEMDAN to obtain the IMFs, IMFs screening by calculating the permutation entropy (PE) of IMFs, and finally wavelet thresholding denoising (WTD) of signal IMFs, but the wavelet parameters are difficult to be set accurately17. Yang et al. used crested porcupine optimizer (CPO) to optimize the parameter settings of ICEEMDAN, improve the decomposition of IMFs, screen IMFs by calculating the correlation coefficients (CC) between the IMFs and the original signals, and then reconstruct the effective IMFs so as to complete the denoising of the signals, but the complexity of the calculation is high18. Ran et al. used ICEEMDAN for signal decomposition, screened effective IMFs with fuzzy entropy (FE) as a criterion, and then performed adaptive interval threshold denoising (AITD) on the noisy IMFs, but the screening of IMFs was not precise enough19. Yuan et al. classified IMFs into three categories by calculating the consecutive mean square error (CMSE) of IMFs based on ICEEMDAN decomposition and performed AITD on the noisy IMFs, but the classification of IMFs was also not precise enough3. Li et al. introduced hierarchical amplitude-aware permutation entropy (HAAPE) and reverse permutation entropy (RPE) to improve the classification accuracy of IMFs20. Table 1 lists some ICEEMDAN-based joint denoising algorithms in recent years.

Table 1 Signals joint denoising algorithms with ICEEMDAN.
Full size table

To address the challenge of noise reduction in magnetic target field signals more effectively, we propose a novel ICEEMDAN–RPE–AITD algorithm. This method begins by decomposing the raw signal into intrinsic mode functions (IMFs) using ICEEMDAN. Next, the RPE value of each IMF is calculated to establish dual thresholds, enabling the classification of IMFs into three distinct categories: signal IMFs (signal-dominant), noisy IMFs (mixed signal and noise), and noise IMFs (noise-dominant). The signal IMFs are retained directly, while noise IMFs are discarded. For noisy IMFs, an AITD process is applied to suppress residual noise while preserving critical signal features. The final denoised signal is reconstructed by integrating the retained signal IMFs and the processed noisy IMFs. To validate the algorithm’s efficacy, we conducted comprehensive denoising experiments on both scaled ship model magnetic field signals and real-world vessel magnetic field measurements. Comparative analyses with state-of-art denoising techniques. This framework provides a robust solution for enhancing magnetic field signals denoising in complex environments, particularly in maritime applications where weak target signals are obscured by intense ambient noise.

ICEEMDAN–RPE–AITD algorithm

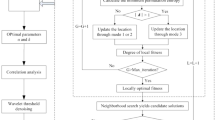
Algorithm flowchart

Magnetic field signals of magnetic targets are first decomposed by ICEEMDAN, after which IMFs are classified by RPE criterion. Finally, AITD is employed to signal denoise and reconstruction. The specific steps are as follows:

  1. (1)

    IMFs decomposition

    Set ICEEMDAN noise amplitude, number of realizations and maximum number of iterations. Magnetic field signals of magnetic targets are decomposed by ICEEMDAN to obtain the IMFs adaptively.

  2. (2)

    IMFs classify

    The RPE value of IMFs are calculated. IMFs are classified by two thresholds Lth and Hth. IMFs whose RPE larger than or equal to Hth are classified as signal IMFs. IMFs whose RPE located between Lth and Hth are classified as noisy IMFs. IMFs whose RPE smaller than Lth are classified as noise IMFs.

  3. (3)

    IMFs denoising and reconstruction

    Signal IMFs are remained, noisy IMFs are employed AITD, noise IMFs are removed and then the three IMFs are added to reconstruct the denoised signal.

    ICEEMDAN–RPE–AITD flowchart is shown in Fig. 1.

Fig. 1
figure 1

ICEEMDAN–RPE–AITD flowchart.

Full size image

ICEEMDAN

ICEEMDAN is an enhancement of CEEMDAN16,30. ICEEMDAN effectively mitigates mode mixing, reduces the spurious modes, and minimizes overlapping scales by screening the kth IMF of the white Gaussian noise (WGN) after EMD. ICEEMDAN accurately decomposes and effectively denoises the signals by incorporating refined strategy and adaptive noise21. ICEEMDAN is employed to decompose magnetic field signals of magnetic targets using following steps31:

  1. (1)

    Signal x is added with a WGN \(w_{{}}^{i} \left( {i = 1,2, \cdots ,K} \right)\) with standard normal distribution as follows:

    $$x_{1}^{i} = x + \beta_{0} E_{1} \left( {w^{i} } \right)$$
    (1)

    where \(x_{1}^{i}\) is the first mixed signal, \(\beta_{0}\) is added noise amplitude, \(E_{1} \left( {w^{i} } \right)\) is the first IMF of WGN achieved by EMD.

  2. (2)

    Decompose the first mixed signal \(x_{1}^{i}\) by EMD over K realizations and calculate the first IMF as follows:

    $${\text{IMF}}_{1} = x - r_{1}$$
    (2)
    $$r_{1} = \left\langle {M\left( {x_{1}^{i} } \right)} \right\rangle$$
    (3)

    where \(r_{1}\) is first residue, \(\left\langle \cdot \right\rangle\) represents the mean operator, \(M\left( \cdot \right)\) denotes the local average.

  3. (3)

    The second mixed signal \(x_{2}^{i}\) is as follows:

    $$x_{2}^{i} = r_{1} + \beta_{1} E_{2} \left( {w^{i} } \right)$$
    (4)

    Decompose the second mixed signal \(x_{2}^{i}\) by EMD over K realizations and calculate the second IMF as follows:

    $${\text{IMF}}_{2} = r_{1} - r_{2}$$
    (5)
    $$r_{2} = \left\langle {M\left( {x_{2}^{i} } \right)} \right\rangle$$
    (6)
  4. (4)

    Repeat the above steps for the kth decomposition and obtain the kth IMF as follows until the stopping criterion is satisfied:

    $${\text{IMF}}_{k} = r_{k - 1} - \left\langle {M\left[ {r_{k - 1} + \beta_{k - 1} E_{k} \left( {w^{i} } \right)} \right]} \right\rangle$$
    (7)

    ICEEMDAN algorithm flowchart is shown in Fig. 2.

Fig. 2
figure 2

ICEEMDAN flowchart.

Full size image

RPE-AITD

Appropriate IMFs for signal reconstruction are classified by the entropy value of the RPE. RPE improves the ability to screen high frequency noise and robustness compared with PE20,32. Smaller RPE indicate stronger signal complexity and nonlinear characteristics. Random noise occurrence within signals can be numerically evaluated by RPE.

Reconstructed phase space X of signal \(\left\{ {x_{1} ,x_{2} , \ldots ,x_{N} } \right\}\) is33

$${\mathbf{X}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{1 + \tau } } & \cdots & {x_{{1 + \left( {m - 1} \right)\tau }} } \\ {x_{2} } & {x_{2 + \tau } } & \cdots & {x_{{2 + \left( {m - 1} \right)\tau }} } \\ \vdots & \vdots & \vdots & \vdots \\ {x_{{N - \left( {m - 1} \right)\tau }} } & {x_{{N - \left( {m - 2} \right)\tau }} } & \cdots & {x_{N} } \\ \end{array} } \right]$$
(8)

where m is embedding dimension, τ is delay time, N is signal length.

Each row of X is a reconstruction component, and the elements of each row in X are sorted in ascending order

$$\left\{ {x_{{i + \left( {j_{1} - 1} \right)\tau }} ,x_{{i + \left( {j_{2} - 1} \right)\tau }} , \cdots ,x_{{i + \left( {j_{m} - 1} \right)\tau }} } \right\}$$
(9)

where i is the column index and \(j_{1} ,j_{2} , \cdots ,j_{m}\) represents the element position of reconstructed component.

Each row of the matrix X is denoted by a symbols sequence:

$$S\left( l \right) = \left\{ {j_{1} ,j_{2} , \cdots ,j_{m} } \right\}$$
(10)

where \(l = 1,2, \cdots ,n\) and \(1 \le n \le m!\).

The probability of occurrence of symbols sequence \(S\left( l \right)\) is \(P_{l}\). RPE of signal is calculated by34

$${\text{RPE}}\left( m \right) = \sum\limits_{l = 1}^{m!} {P_{l}^{2} } - \frac{1}{m!}$$
(11)

When \(P_{l} = {1 \mathord{\left/ {\vphantom {1 {m!}}} \right. \kern-0pt} {m!}}\), the minimum value of \({\text{RPE}}\left( m \right)\) is 0.

Calculate the RPE value of each IMF and determine the two thresholds Lth and Hth. After extensive testing and analysis, Lth and Hth are set to 0.4 and 0.48, respectively. IMFs whose RPE larger than or equal to Hth are classified as signal IMFs. IMFs whose RPE located between Lth and Hth are classified as noisy IMFs. IMFs whose RPE smaller than Lth are classified as noise IMFs. Signal IMFs are remained, noisy IMFs are employed AITD, noise IMFs are removed and then the three IMFs are added to reconstruct the denoised signal.

AITD algorithm gently shrinks the signal by a reasonable value, effectively discards residual noise and adequately preserves the original signal amplitude19. AIT function with shrinkage related to the extreme value is as follows3

$$\hat{g}_{i} \left( {z_{i}^{j} } \right) = \left\{ {\begin{array}{*{20}c} {g_{i} \left( {z_{i}^{j} } \right)\left[ {1 - \lambda^{{{{\left( {\alpha \lambda + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\alpha \lambda + 1} \right)} \lambda }} \right. \kern-0pt} \lambda }}} } \right],} & {\left| {g_{i} \left( {r_{i}^{j} } \right)} \right| > T_{i} } \\ {0,} & {\left| {g_{i} \left( {r_{i}^{j} } \right)} \right| \le T_{i} } \\ \end{array} } \right.$$
(12)

where \(\hat{g}_{i} \left( {z_{i}^{j} } \right)\) is the value of jth interval of the ith IMF that has been processed, \(g_{i} \left( {z_{i}^{j} } \right)\) is the original value of jth interval of the ith IMF, \(g_{i} \left( {r_{i}^{j} } \right)\) is the local single extrema of the corresponding interval. \(\lambda = {{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } {\left| {g_{i} \left( {r_{i}^{j} } \right)} \right|}}} \right. \kern-0pt} {\left| {g_{i} \left( {r_{i}^{j} } \right)} \right|}}\) and \(\alpha = 5\). Threshold \(T_{i}\) is estimated by the noise energy within the IMF, as follows

$$T_{i} = \left\{ {\begin{array}{*{20}c} {C\sqrt {2\left[ {\frac{{{\text{median}}\left( {\left| {{\text{IMF}}_{1} } \right|} \right)}}{0.6745}} \right]^{2} \log \left( L \right)} ,} & {i = 1} \\ {C\sqrt {\frac{{2\rho^{ - i} }}{\beta }\left[ {\frac{{{\text{median}}\left( {\left| {{\text{IMF}}_{1} } \right|} \right)}}{0.6745}} \right]^{2} \log \left( L \right)} ,} & {i \ge 2} \\ \end{array} } \right.$$
(13)

where L is length of the IMF, \({\text{median}}\left( \cdot \right)\) is the median-taking operator. \(C = 0.6\sim 0.8\), \(\beta = 0.719\) and \(\rho = 2.01\).

Evaluation index

Signal-to-noise (SNR) and root mean square error (RMSE) are used for evaluated signals denoising with known true values35

$${\text{SNR}} = 10\log_{10} \frac{{\sum\limits_{n = 1}^{N} {x_{n}^{2} } }}{{\sum\limits_{n = 1}^{N} {\left( {x_{n} - \hat{x}_{n} } \right)^{2} } }}$$
(14)
$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^{N} {\left( {x_{n} - \hat{x}_{n} } \right)^{2} } }$$
(15)

where \(x_{n}\) is pure signal, \(\hat{x}_{n}\) is denoised signal, and N is signal length. SNR represents ratio of signal power and noise power, and the higher the SNR more effective the denoising. RMSE represents discrepancy between pure signal and denoised signal, the lower the RMSE more effective the denoising.

Noise intensity (NI) and correlation dimension (CD) are used for evaluated signals denoising without known true values32

$${\text{NI}} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^{N} {\left( {\hat{x}_{n} - \frac{1}{N}\sum\limits_{k = 1}^{N} {\hat{x}_{k} } } \right)^{2} } }$$
(16)
$${\text{CD}} = \mathop {\lim }\limits_{R \to 0} \frac{\log C\left( R \right)}{{\log R}}$$
(17)

where \(C\left( R \right)\) is the correlation integral, R is the hypersphere radius. The smaller NI the better the denoising. CD represents the fractal self-similarity of the phase diagram, and the smaller the CD the better the denoising.

Signals denoising test

Ship model magnetic field signals test

To validate the proposed algorithm effectiveness, a scaled model test was conducted. Magnetic field signal of the ship model is directly proportional to the real ship36. Depth, departure, and trajectory of ship model are the converted parameters corresponding to the real ship. The bow and stern of the ship model point in a north–south direction. The ship model test conditions and test system are shown in Table 2 and Fig. 3a,b, respectively.

Table 2 Ship model test conditions.
Full size table
Fig. 3
figure 3

Ship model test system.

Full size image

Three components of the magnetic field have similar characteristics, and X component is used as an example for denoising analysis.

Time domain and frequency domain of different types of noise are shown in Fig. 4a,b. Time domain and frequency domain of X component of synthetic ship model magnetic field signals with WGN are shown in Fig. 5a,b. The SNR and sampling frequency of noisy signal are 5dB and 100Hz, respectively.

Fig. 4
figure 4

Time domain and frequency domain of WGN.

Full size image
Fig. 5
figure 5

Time domain and frequency domain of ship model magnetic field signals with WGN.

Full size image

IMFs classify effect of ship model magnetic field signals at SNR = 5dB are shown in Fig. 6a,b. The blue line is the signal IMFs, the pink line is the noisy IMFs, and the red line is the noise IMFs in the Fig. 6b. The signal IMFs are remained, the noisy IMFs are denoised by ICEEMDAN–RPE–AITD, and the noise IMFs are removed. From Fig. 6b, the green line is obviously more chaotic, indicating that it contains a large amount of noise, the blue line is smoother and has a larger amplitude than the green line, indicating that it contains a small amount of noise and useful signals, and the red line is the smoothest, indicating that it contains a large amount of useful signals.

Fig. 6
figure 6

IMFs classify effect of ship model magnetic field signals at SNR = 5 dB.

Full size image

The comparison algorithms use five algorithms such as OWSWATD37, AFD38, ICEEMDAN–PE–WTD17, ICEEMDAN–FE–AITD19 and ICEEMDAN–CMSE–AITD3. Parameters setting of denoise algorithms are shown in Table 3. The test computer processor is Intel(R) Core (TM) i9-14900HX 2.20 GHz with 32.0 GB of RAM.

Table 3 Parameters of denoising algorithms.
Full size table

Time domain and frequency domain of ship model magnetic field signals after denoised are shown in Fig. 7. SNR and RMSE of ship model magnetic field signals after denoised are shown in Table 4. The noisy signal with SNR = 5dB is improved by denoising. OWSWATD, AFD, ICEEMDAN–PE–WTD, ICEEMDAN–FE–AIT, ICEEMDAN–CMSE–AITD and ICEEMDAN–RPE–AITD increase the SNR to 12.11 dB, 20.15 dB, 20.15 dB, 22.49 dB, 24.20dB and 25.08 dB, respectively. The denoising effect of ICEEMDAN–RPE–AITD is most obvious.

Fig. 7
figure 7figure 7

Time domain and frequency domain of ship model magnetic field signals after denoising with WGN at SNR = 5 dB.

Full size image
Table 4 SNR and RMSE of ship model magnetic field signals after denoised at SNR = 5dB.
Full size table

Each denoising algorithm runs independently 100 times at different SNR. A different white Gaussian noise is randomly added for each run. Statistical significance test is performed to validate the differences in performance metrics. Non-parametric Friedman test is used to rank the performance of the six algorithms. The statistical formula is40

$$F_{f} = \frac{12a}{{b\left( {b + 1} \right)}}\left[ {\sum\limits_{s} {R_{s}^{2} } - \frac{{b\left( {b + 1} \right)^{2} }}{4}} \right]$$
(18)

where b is the number of algorithms, a is the number of tests, and Rs is the average ranking of the sth algorithm.

The average SNR and RMSE of 100 denoising tests are shown in Table 5, and the average rank ordering of each algorithm is calculated by Friedman’s test, and the corrected p-value with a significance level of 0.05 is calculated by Hommel’s procedure41. The bolded portion of the table shows the better results. ICEEMDAN–RPE–AITD exhibits a discernible denoising effect on the ship model magnetic field signals. ICEEMDAN–RPE–AITD increases the SNR by 17.22–21.45 dB. ICEEMDAN–RPE–AITD improves by 1.5%, 10.4%, 12.7%, 32.9% and 137.9% in terms of SNR over ICEEMDAN–CMSE–AITD, ICEEMDAN–FE–AITD, ICEEMDAN–PE–WTD, AFD and OWSWATD, respectively. All of adjusted p-values of ICEEMDAN–CMSE–AITD, ICEEMDAN–FE–AITD, ICEEMDAN–PE–WTD, AFD and OWSWATD are less than 0.05, indicating that the statistics are significantly different. ICEEMDAN–RPE–AITD has excellent and stable denoising effect.

Table 5 Comparison of denoising results of ship model magnetic field signals.
Full size table

Ship magnetic field signals test

To validate the effectiveness of the ICEEMDAN–RPE–AITD algorithm, denoising tests were conducted using ship magnetic field signals measured in August 2020 in the Bohai Sea, China, where the measured signals contain complex marine magnetic field noise signals. One of the measurement targets is shown in Fig. 8a–d. The measurement device was deployed on the muddy and sandy seabed around 30 m, and the magnetic field signals were measured using magnetic induction coil rods. The sampling rate is 100 Hz and the measurement time is 100s.

Fig. 8
figure 8

Magnetic targets.

Full size image

Time domain waveform and PSD of ship magnetic field signals before and after denoising are shown in Fig. 9a–d. Ship magnetic field signals waveform is full of noise before denoising and become clearer and smoother after denoising. High frequency noise is deleted after denoising, part of low frequency noise is suppressed, and useful signal is retained. ICEEMDAN–RPE–AITD algorithm can denoise the ship magnetic field signals effectively.

Fig. 9
figure 9

Time domain and frequency domain of ship magnetic field signals before and after denoising.

Full size image

Comparison of denoising results of ship magnetic field signals are shown in Table 6. NI and CD of four types of ship magnetic field signals are reduced one by one after denoising by six algorithms. NI, CD, and AAPE of all the ships reach the lowest after denoising by ICEEMDAN–RPE–AITD. NI and CD of Ship1 were decreased by 12.7% and 64.3%, respectively. NI and CD of Ship2 were decreased by 55.9% and 55.2%, respectively. NI and CD of Ship3 were decreased by 55.4% and 68.9%, respectively. NI and CD of Ship4 were decreased by 5.6% and 67.3%, respectively. ICEEMDAN–RPE–AITD algorithm can denoise the ship magnetic field signals effectively.

Table 6 Comparison of denoising results of ship magnetic field signals.
Full size table

Conclusion

ICEEMDAN–RPE–AITD is proposed based on ICEEMDAN, combined with AITD, and it is applied to the denoising of ship model magnetic field signals and measured ship magnetic field signals, and the following conclusions are obtained.

  1. 1.

    ICEEMDAN–RPE–AITD can be categorized into three steps: IMFs decomposition, IMFs classification, IMFs denoising and reconstruction. ICEEMDAN effectively mitigates mode mixing, reduces the spurious modes, and minimizes overlapping scales. RPE accurately evaluates the random noise occurrence within signals, which can better distinguish the signal IMFs from the non-signal IMFs. AITD algorithm gently shrinks the signal by a reasonable value, effectively discards residual noise and adequately preserves the original signal amplitude and achieves better denoising effect.

  2. 2.

    ICEEMDAN–RPE–AITD has excellent and stable denoising effect for WGN, which obtains the largest SNR and the smallest RMSE. ICEEMDAN–RPE–AITD increases the SNR by 17.22–21.45 dB. ICEEMDAN–RPE–AITD improves by 1.5%, 10.4%, 12.7%, 32.9% and 137.9% in terms of SNR over ICEEMDAN–CMSE–AITD, ICEEMDAN–FE–AITD, ICEEMDAN–PE–WTD, AFD and OWSWATD, respectively.

  3. 3.

    ICEEMDAN–RPE–AITD has excellent and stable denoising effect for measured ship magnetic field signals, which obtains the smallest NI and CD. The denoised measured ship magnetic field signals discard a large amount of noise, the time domain waveform becomes clearer and smoother, the high frequency noise is effectively discarded.

In the next step, the parameters of ICEEMDAN will be optimized with swarm intelligence optimization algorithm to mitigate mode mixing. Secondly, the thresholds of RPE will be calculated adaptively to enhance the denoising robustness. Finally, non-Gaussian noise will be studied for denoising.