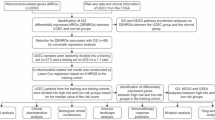
Abstract
Medical costs (MCs) represent a significant burden on household finances and often lead to economic challenges. This study analyzed the data of 8,993 Iranian households from 2021 collected by the Iranian Statistical Center. Using a marginalized two-part model (MTP) with lognormal and gamma distributions, the relationship between MCs and factors such as age, gender, education, and household characteristics was examined. A two-level structure was applied to account for heterogeneity across provinces, with analyzes performed using R software. The mean annual MC was $180 with high variability (SD = $324.39). The main determinants included family size, residence area, education level, and socioeconomic status. Single households and families with more students had lower MCs. Among the models evaluated, the MTP-Lognormal model (MTP-LN) performed better than the MTP-Gamma model (MTP-G), as it provided better predictive accuracy and better reflected cost differences between province. These results highlight the socio-economic and demographic factors that influence household MCs in Iran. The MTP-LN model provides valuable insights for identifying at-risk groups and developing targeted interventions to reduce the financial burden of healthcare, especially for vulnerable populations. This study emphasizes the importance of tailored interventions to address regional inequalities and promote equitable access to healthcare.
Similar content being viewed by others
Introduction
Medical costs (MCs) are an essential but often underestimated component of maintaining and improving one’s health1. These expenses cover many healthcare costs, such as doctor visits, hospitalizations, surgeries, medications, checkups, etc. You must be aware of the significant costs associated with healthcare and actively manage your healthcare. By staying informed and engaged, you can make informed decisions about your healthcare, reduce unnecessary spending and prioritize your well-being2,3. The escalation of medical costs in recent decades reflects the development of living standards and quality of life in different societies4,5. A closer look at the course and extent of this increase reveals considerable differences in the level and development of healthcare expenditure between individual countries6,7,8,9,10. The costs associated with healthcare and medical services are a significant component of household finances and can lead to economic stress and financial challenges. These expenses, known as the costs of health impoverishment, have the potential to drive households into financial instability and jeopardize their economic prosperity11.
In many developing countries, particularly in countries such as Iran, a considerable portion of medical costs is covered by households12. This heavy reliance on out-of-pocket payments for healthcare underscores a critical aspect of the healthcare system in these areas. However, heavy reliance on direct household payments is considered an inadequate method of ensuring financial stability13. When families need healthcare beyond their means, they encounter significant challenges and may resort to measures such as borrowing, selling assets or cutting back on other essential spending to cover the costs14. A study conducted by Meharara in Iran on household health expenditure revealed that a significant proportion of the population, about 5.2%, is affected by catastrophic health expenditure15. Vulnerable groups, including rural households, households with unemployed people, households with young children and elderly people, and people without insurance coverage, are more susceptible to unsustainable healthcare costs A priority objective of a country’s health policy is therefore to reduce direct payments and introduce more equitable financing mechanisms to ensure wider access to health services16.
Chronic diseases, such as diabetes, obesity, and depression, impose a significant economic burden on families and contribute to escalating healthcare costs17,18,19,20. Several studies have shown a positive correlation between a person’s economic status and medical costs21,22,23, with expenses generally increasing with age24. In addition, insurance coverage has been shown to be an important factor influencing medical costs23,25,26,27. Household head characteristics such as gender, education level and urban or rural residence have also been associated with differences in medical expenditure in various studies28,29,30. Although the coefficients associated with these variables may vary from country to country due to different circumstances, overall, they influence healthcare expenditure patterns23,28,29,30,31,32,33. These findings highlight the importance of considering household head characteristics in understanding differences in healthcare spending patterns and emphasize the need for tailored interventions to address inequalities in MC based on these factors.
Modeling medical costs presents challenges due to the unique characteristics of the data, including non-negativity, right skewness, and a substantial percentage of observations equal to zero, defining it as "semi-continuous" data34,35,36. Traditional approaches such as linear models cannot adequately handle this complexity without additional modifications37. Advanced statistical models tailored to semi-continuous healthcare cost data have been shown to be valuable tools for addressing the complexity of cost analysis38. Techniques such as Tweedie distributions in generalized linear models39, two-part mixed-effects models40,41,42, joint models43, machine learning38,43, and Bayesian inference methods41 provide greater insight into healthcare cost patterns and allow researchers to examine the impact of various determinants on medical costs. Marginalized two-part (MTP) models, including commonly used models, are for the structure of mixed semi-continuous data36,43,44,45. In summary, the search results show the importance of using specialized statistical models such as MTP to effectively analyze semi-continuous data, which is a common characteristic of healthcare cost data and other medical variables.
This study aims to investigate the factors associated with MC in Iranian households by using marginalized two-part models in a multilevel framework. By utilizing advanced statistical methods, this study attempts to elucidate the various determinants affecting medical costs and their impact on the level of household health expenditure. Finally, this study attempts to provide valuable insights for health care financing and insurance coverage strategies to ultimately promote a more equitable health care system for Iranian households.
Materials and methods
Study population
This study belongs to the type of analytical, applied and data-oriented epidemiological studies. The data used in this study refer to the information on Iranian households’ medical expenditures obtained from a national project entitled “The Households Income and Expenditure Survey (HIES)” in 2021. The data comes from the Statistical Center of Iran (SCI), which can be found at https://www.amar.org.ir52. This information was provided to the researchers of this project in raw form and as a random sample. The final sample size, after applying entry and exit restrictions, was 8993 household heads in Iranian provinces.
To minimize potential biases that may result from the use of self-reporting, the HIES survey used standardized procedures and strict quality control protocols implemented by SCI to ensure the reliability and validity of the data collected. The nationally representative sampling design of the survey and subsequent data processing further reduced errors and inconsistencies prior to analysis.
The household data was kept confidential throughout the study. The study was conducted after approval from the Research Ethics Committee (REC) of Ahvaz Jundishapur College of Medical Sciences (AJUMS) with project number U-02034 and ethics code IR.AJUMS.REC.1402.064.
Predictor variables
For all and based on the information available, the 19 variables that the researchers believe may have an impact on MC were grouped into two categories: Information related to the household head (five variables) and information related to the household (15 variables).
Information about the household head includes age (young adults; middle-aged adults; older adults), gender (male; female), education level (illiterate and elementary; lower than diploma; diploma and associate; bachelors; MSc or PhD), marital status (married; widowed or divorced; single), employment status (employed; not working; have income without a job; others). Household variables include the number of family members (1; 2; 3; 4 or more persons), residential area (urban, rural), number of employees (noun, one, two or more), number of students in the family (noun; one; two or more), number of educated persons in the family (noun; one; two or more), type of home ownership (have a home; mortgage, rent & other), subsidies (no; yes), internet access (no; yes), car ownership (no; yes), bicycle ownership (no; yes), family income in the year and household expenditure on food (below; above the national average), clothing (below; above the national average) and housing (below; above the national average) in the year were extracted and used in the analysis phase.
Outcome variable
In this study, the total medical costs of a year (such as costs for dental and eye care, medication, addiction treatment, surgery, etc.) for each household were considered as total medical costs and outcomes. The cost variable is a positive amount or zero. Assuming that there is a correlation in the cost of healthcare services within each province and that there are differences and heterogeneity among these cities, the provincial cities in the center of Iran were considered as clusters and random effects were considered to account for heterogeneity.
Semi-continuous data
Data on healthcare costs are often characterized as semi-continuous and exhibit a non-normal distribution with an unbalanced ratio of zeros to positive values34. In health economics and service research, such data are widely used and pose a challenge for analysis due to their unique characteristics. These types of data, known as semi-continuous data with zero inflation, cover a wide range of areas, such as research on healthcare costs, medical care services, health assessments34,37, average daily alcohol consumption37,53, annual car insurance claims, and the relative abundance of the microbiome37,46.
In the context of semi-continuous data with zero inflation, the presence of a significant proportion of zeros alongside positive skewed values requires special treatment in statistical analysis. Failure to account for this peculiarity when running regression models can lead to biased estimates, incorrect conclusions and ultimately misleading results. Taking into account the atypical distribution of semi-continuous data with zeros is crucial for the accuracy and validity of research results in various fields of study.
Two-part models for semi-continuous data
Semi-continuous data usually needs two-part mixture models to effectively capture both the discrete and continuous aspects of the data. In the case of independent observations, the typical format of the two-part model is outlined below:
where \({\pi }_{i}=Pr({Y}_{i}>0)\), \({\mathbb{l}}_{(.)}\) serves as an indicator function, and \(g({y}_{i}|{y}_{i}>0)\) is a function that depends on a specific location parameter \({\mu }_{i}\), a positive scale parameter \(\sigma\), and \(\kappa \in \mathfrak{R}\) that determines the shape or skewness of the distribution. Commonly preferred densities include the gamma (G)54 or generalized gamma (GG)48,55,56, lognormal (LN)57,58, weibull (W)59, and log-skew-normal (LSN)57,60, which will be further elaborated on below.
In above equation, covariates are included in two separate linear predictors, one for \({\pi }_{i}\) and one for \({\mu }_{i}\). An instance of this is the conditional two-part (CTP) model61, where a logit link is utilized for the binary part and a positive continuous distribution is used for \(g({y}_{i}|{y}_{i}>0)\). The model is structured as below:
where \({{\varvec{Z}}}_{{\varvec{i}}}^{\boldsymbol{^{\prime}}}\) is a \(1\times q\) covariate vector and \(\boldsymbol{\alpha }\) a \(q\times 1\) regression coefficient in the binary part. Also, \({{\varvec{X}}}_{{\varvec{i}}}^{\boldsymbol{^{\prime}}}\) is a \(1\times p\) covariate vector and \({\varvec{\beta}}\) a \(p\times 1\) regression coefficient in the continuous part. By disregarding the intercept, the components of \(\boldsymbol{\alpha }\) indicate unit changes in the log-odds of a positive response, while the components of \({\varvec{\beta}}\) represent unit changes on the conditional mean of the logged positive values, \({\mu }_{i}=E\left[\text{ln}({Y}_{i}|{Y}_{i}>0)\right]\). The conditional interpretation of \({\varvec{\beta}}\) suggests that it assesses the effects of covariates on individuals who exhibit a positive response, rather than on the overall population.
In statistical modeling, researchers often focus on examining the effects of certain factors on the transformed marginal means. However, there are cases where it is crucial to examine the impact on the untransformed marginal mean, denoted \(E({Y}_{i})\), in order to draw conclusions about the overall population, which includes both users and non-users of health services44,45,46,50. To address the need for such inferences, Smith and colleagues introduced a marginalized two-part (MTP) model that allows direct parameterization of the effects of covariates on the marginal mean51. The MTP model is characterized by its parameters as:
In this context, \(\boldsymbol{\alpha }\) has the same meaning as in the CTP model and represents a vector of log-odds ratios. The model allows the estimation of covariate effects on the overall marginal mean and standard error by linear combinations of the parameters in the second part. Specifically, \(\text{exp}({\beta }_{k})\) represents the multiplicative effect on the overall mean when the kth covariate increases by one-unit. With utilizing this parameterization, the marginal means and standard errors predicted by the model can be easily determined by calculating \(\text{exp}({{\varvec{X}}}_{i}{\prime}{\varvec{\beta}})\) at the specified values of the covariates.
In this class of models, different distributions can be used to effectively analyze the semi-continuous data. Based on AIC and BIC, we used the Vuong test (V) to determine whether the zero and positive components of the cost variables are generated by different processes62. This non-nested hypothesis test produces a Z statistic, where a value greater than 1.96 supports the alternative assumption that the first model fits the data better, while a value less than − 1.96 indicates that the second model provides a better fit. In our analysis, we evaluated our independent two-equation model against a Tobit model that accounts for interdependence. The calculated test statistic was 69,729.1, and since V is greater than 1.96, we find evidence supporting the hypothesis of independence of process. Although Tobit or Heckman models could account for interdependence, their use is not justified here. The principle of parsimony favors the simpler independent two- equation model, which effectively captures the data and provides more interpretable coefficients without the complexity of interdependence. In particular, the MTP model allows for adaptability by considering a range of distributions and variance structures34,44,50,51,63. To justify the choice of distributions in the marginalized two-part model (MTP), we selected lognormal and gamma distributions based on their theoretical suitability for modeling right-skewed, non-negative medical cost data, their frequent use in related studies, and their applicability to the multilevel structure of the data in the final section of the models.
Multilevel models in cluster analysis
According to Ning Li’s research, data can be organized in a composite or stratified format, where hierarchies signify that observations within identical groups or contexts share commonalities or similarities that imply some degree of uniformity64. Consequently, a mixed framework can be used to describe a model for semi-continuous data with two levels. The first level pertains to observations (\(i=1,\dots ,{n}_{j}\)) nested in two-level units (\(j=1,\dots ,m\)) that refer to center provinces.
The model’s parameterization is divided into two parts that are fitted separately.
In part I, the binary outcome is modeled as:
where \({b}_{1i}\sim N(0,{\sigma }_{b1}^{2})\) represents the random effect that accounts for the correlation within a cluster (level 2) in the zero part.
Assuming that the logarithm for the g link function, the location parameter \({\mu }_{ij}\) for the continuous component in the second part is modeled as:
where \({b}_{2i}\sim N(0,{\sigma }_{b2}^{2})\) represents the random effect that accounts for the correlation within a cluster (level 2) in the continuous part. These random effects capture the unobserved characteristics or factors that may influence the outcome variable within each cluster. By including this random effect in the model, we can account for the clustering of observations within each cluster and better estimate the true relationship between the predictors and the outcome variable. In this context, it is assumed that the random effects \({b}_{1i}\) and \({b}_{2i}\), pertaining to the processes zero and non-zero, are independent and uncorrelated.
\({{\varvec{Z}}}_{{\varvec{i}}{\varvec{j}}}^{\boldsymbol{^{\prime}}}\) represents the covariates for the i-th subject in the j-th cluster for the binary part, and \({{\varvec{X}}}_{{\varvec{i}}{\varvec{j}}}^{\boldsymbol{^{\prime}}}\) represents the covariates for the i-th subject in the j-th cluster used for the continuous part. The two parts may have common or completely different covariates. \(\boldsymbol{\alpha }\) represents the vector of model coefficients for the binary part, while \({\varvec{\beta}}\) represents the vector of coefficients for the continuous part, under the condition that the values are non-zero.
For a TP model, the marginal mean and variance of \({Y}_{ij}\) can be derived as follows:
when lognormal is assumed in the continuous part, the marginal mean is
and when gamma is assumed in the continuous part, the marginal mean is
In binary models, the \(\boldsymbol{\alpha }\) estimates represent the average probabilities of positive values in the population. On an exponential scale, \(\text{exp}(\alpha )\) is the odds ratio for a one-unit increase in the covariate. In continuous models, the \({\varvec{\beta}}\) estimates are only for non-zero positive values, a subset of the data. When a log link is used, \(\text{exp}(\beta )\) shows the multiplicative change in the overall mean as the covariate increases by one unit, assuming the observation is not zero. To summarize, the binary part estimates the probabilities of non-zero values in the population, while the continuous part shows the effects on the population mean when the values are non-zero. Moving forward, to simplify the presentation, we refer to the marginalized two-part lognormal and marginalized two-part gamma models as MTP-LN and MTP-G, respectively.
Parameter estimation and inference for MTP
Let \(n={n}_{j}\times m\) be the total number of subjects and assume that subjects \((i=1,\dots ,{n}_{j})\) on different clusters \((j=1,\dots ,m)\) are independent. Given the random effects \({{\varvec{b}}}_{1{\varvec{i}}}\) and \({{\varvec{b}}}_{2{\varvec{i}}}\), The likelihood function can be described as such:
where \({n}_{j}\) is the number of subjects in the cluster j, \({\pi }_{ij}\) is given (4) if the logit link function is used in Part I, \(g({y}_{ij}|{y}_{ij}>0)\) is depend on the distribution assumption on \({y}_{ij}>0\) (lognormal or gamma), and \(\varphi \left({b}_{1}\right)\) and \(\varphi \left({b}_{2}\right)\) are the normal density of two random effects \({b}_{1}\) and \({b}_{2}\).
The likelihood in Eq. (9) requires the integration of a nonlinear function over the two random effects in the likelihood function. To obtain maximum likelihood estimators for \(\alpha\), \(\beta\), and the random effects, numerical methods combined with integration approximation techniques are essential. Some researchers used a high-order Laplace approximation to estimate the marginal likelihood and employed an approximate Fisher scoring algorithm for maximization65,66,67. Similarly, Tooze et al. used a quasi-Newton algorithm in conjunction with an adaptive Gaussian quadrature for likelihood maximization68. Hubin69 and Wang70 also investigated the Integrated Nested Laplace Approximation (INLA) and a generalized version of the Fisher scoring method for estimating the marginal likelihood and maximizing the likelihood, respectively.
In this article, we use different methods to estimate the parameters in the utilization models. For the MTP-LN model, we use an integration method known as adaptive Gauss-Hermite quadrature and an optimization method that combines hybrid EM and quasi-Newton approaches. For the MTP-G model, on the other hand, we implement the Laplace approximation as the integration method and use maximum likelihood estimation via ‘TMB’ (Template Model Builder) as the optimization method. These different techniques meet the unique requirements of each model and ensure accurate parameter estimation and robust model fitting for both MTP-LN and MTP-G models. This methodology can be easily implemented in widely used standard statistical packages. Data cleaning, statistical analyses, and data visualization were primarily conducted using R 4.3.2 version71. The corresponding codes are included in the Appendix A for reference. Maps were created using the free plan of the Datawrapper site (https://app.datawrapper.de)72.
Model fit assessment
The log-likelihood (\(LL\)) determined by maximum likelihood estimation serves as an indicator of how well a model fits the data, with higher values indicating a stronger fit. However, when comparing different models, it is more appropriate to use information criteria such as Deviance (\(D=-2LL\)), Akaike information criterion (\(AIC=-2LL+2k\)), and Schwarz’s Bayesian information criterion (\(BIC=-2LL+k\text{log}n\)) where n is the sample size or the data point in X’s, and K is the number of estimable parameters73. These criteria are based on the log likelihood function, but include a penalty for the number of parameters in the model, which helps to prevent overfitting. The model with the smallest value of the information criterion is generally preferred, as it represents the best balance between model fit and complexity. Using compliant and large sample data, we perform an evaluation to determine the time to convergence of the models.
To assess the fit of the models used, scatter plots and heat maps were created to compare the actual values with the fitted values for the MTP models. These scatter plots provide a visual representation of how well the models can predict the data, allowing a more comprehensive evaluation of their performance.
Results
The average medical cost of Iranian households (n = 8993) for one year, including dental and eye care, surgery, etc., included as response variables were about $180 with a notable standard deviation of $39,324 (median = $52.32, IQR = $204), indicating a wide range of costs. In addition, the minimum and maximum medical costs in 2021 were zero and over $2000, respectively. The skewness and kurtosis of the response variables were 29.3 and 16.13, respectively.
The histogram of total MCs of Iranian households in 2021 is shown in Fig. 1. This plot shows that medical costs was a semi-continuous variable with 2385 (26.5%) values equal to zero and a continuous right skewed distribution among the positive values. The fitted values extracted from two proposed models, MTP-LN and MTP-G, are also inserted into the histogram.
Table 1 shows the factors associated with MC in Iranian households for the year 2021, broken down by head of family and family variables. This data provides valuable insights into the determinants of medical expenditure in households in Iran. The total number of families included in the study was 8993, out of which 2386 (26.53%) had zero MC and 6607 (73.47%) had nonzero (positive) MC.
The mean age of the head of family was 52.64 years in families with positive MC, which was higher than families with zero MC (51.21 years). There is also a significant association between age groups and MC, with a higher proportion of young adults among those with nonzero MC (P < 0.001). The majority of the heads in Iranian family were male in both groups, with no significant difference between zero and nonzero MC (P = 0.425). In terms of education, heads with higher education levels (bachelor’s degree or higher) had a higher proportion of positive MC compared to family heads with lower education levels (P = 0.034). Married individuals constituted the majority in both groups, but married heads had a higher proportion of nonzero MC compared to widowed/divorced or single heads (P = 0.004). Employed heads had a higher proportion of positive MC compared to families who head were not working or head had income without a job (P < 0.001).
Families with positive MC tend to have a slightly larger family size compared to those with zero MC. The mean family size was 3.32, which was significantly higher in families with positive MC. There is also a significant association between family size categories and MC (P < 0.001). The majority of families resided in urban areas (71.5%), with a significantly higher proportion of families with nonzero MC residing in urban areas (P < 0.001). The mean number of employees was not significantly different between the two groups. The presence of employed members per family also shows a significant difference between the groups based on MC. There is no significant difference in the distribution based on the number of student members (P = 0.575), but there is a significant difference in the distribution based on the number of educated members (P = 0.004). The majority of families owned their homes (70.9%), received subsidies (89.1%), and had internet access (78.3%), with no significant difference between the two groups. While the ownership of a car and a bicycle does show significant differences. Finally, the mean income, feeding cost, clothing cost, and housing cost were all significantly higher in families with positive MC (P < 0.001).
Table 2 shows the estimated coefficients with standard errors for fitting the marginalized two-part lognormal model (MTP-LN) and the two-part gamma model (MTP-G) to Iranian household MC of Iranian households in 2021. Factors considered include various demographic and socioeconomic variables related to family head of the family and family characteristics.
In both models, the zero part evaluates the probability that a household has a positive MC. The MTP-LN model shows that households aged 60 and over are significantly 1.46 times more likely (\({e}^{0.3797}\cong 1.46\)) to have a positive MC than households aged 18 to 39. The MTP-G model also provides comparable results. In addition, households headed by individuals with a bachelor’s degree are approximately 1.38 times less likely (\({1/e}^{-0.3246}\cong 1.38\)) to have positive MC than households with lower or higher levels of education. Notably, rural households are significantly 1.4 times less likely (\({1/e}^{-0.3390}\cong 1.40\)) to have a positive MC than urban households in both models. In addition, households with two or more educated members have a 1.35 times higher probability (\({e}^{0.3030}\cong 1.35\)) of positive MC in both models. Interestingly, households with a mortgage, renting or in alternative forms of living also have a 17% higher probability (\({e}^{0.1572}\cong 1.17\)) of positive MC in the MTP-G model.
The positive part of the two models estimates the amount of MC for households with positive costs. In the MTP-G model, the results are generally consistent with the MTP-LN model. However, there are some additional significant results in MTP-G model. In both models, household heads with a higher level of education and a different employment status have a significantly higher (24% and 43% respectively) amount of MC. Households with a different employment status have significantly higher MC compared to employed households. At the mean of the sample, $180.58, a 43% increase (\({e}^{0.3555}\cong 1.43\)) represents a relatively additional $77.67 spent on MC for Iranian households in one year. In contrast, single household heads have significantly lower (− 35%) MC compared to married, widowed or divorced household heads. At the mean of the sample, a 35% decrease (\({e}^{-0.4317}\cong 0.65\)) represents a relatively lower $63.11 spent on MC for single Iranian households in one year. Among the family characteristics, larger families (4 or more people) (33%) and lower student group membership (20%) were associated with a higher amount of MC in both the MTP-LN and MTP-G models. At the sample mean, the increase of 33% (\({e}^{0.2819}\cong 1.33\)) and 20% (\({1/e}^{-0.1835}\cong 1.20\)) means that Iranian households with larger size and lower student membership, spend relatively $58.62 and $36.25 more on MCs in a year, respectively. Households with two or more educated members were associated with a higher (20%) amount of MC in the MTP-G model. Higher than average income (23−26%) and higher than average food (20%), clothing (4−5%) and housing costs (22−26%) were also associated with a higher amount of MC in both models.
Random effects models estimate variance components at each level. These components quantify the total variability of the dependent variable due to differences between clusters (level 2) and within clusters (level 1). The estimated variance values for the random effects in the two parts of the models can be found at the end of Table 2. The dispersion of the responses in the second part of the log-normal model is significantly larger than in the gamma model, indicating a broader coverage of the responses with this model. The large dispersion of medical costs at the provincial level (78.5%) necessitated the use of the two-part multilevel model [(8.94/(0.77 + 1.66 + 8.94)) × 100 = 78.5%].
Table 3 compares and evaluates the goodness-of-fit statistics for two models. The results show that the MTP-LN model has a better fit compared to the MTP-G model, as evidenced by lower log-likelihood, AIC and BIC values. It is important to note that the MTP-LN model requires more time for estimation than the MTP-G model.
Figure 2A compares the actual values with the fitted values using the MTP-LN model, while Fig. 2B does the same using the MTP-G model for the MC values. The data show a concentration of observations at lower cost levels. Notably, the two-part lognormal model shows a better fit between the actual and fitted values than the two-part gamma model. The lognormal model with random effects captures the dispersion better than the gamma model, which tends to underestimate the data with minimal skewness and low predictive power.
Figure 3 shows the actual values of MC (3A) and the average costs predicted by the MTP-LN (3B) and MTP-G (3C) models, categorized by different provinces in Iran. The results show that, despite possible discrepancies in the estimated figures, the predictions of the MTP-LN model correspond very well with the actual values, with a slight overestimation. In contrast, the MTP-G model tends to significantly underestimate the values. Therefore, it appears that the MTP-LN model performs better than the MTP-G model in terms of predictive accuracy.
Actual (A) and predicted average MC of Iranian households using MTP-LN (B) and MTP-G (C) models, separated by different provinces of Iran in 2021. Maps were created in Datawrapper (https://app.datawrapper.de/) 72.
Discussion
The study on the medical costs of Iranian households in 2021 provide valuable insights into the determinants and patterns of medical expenditure within the population. The average MC for Iranian households was approximately $180 per year, with a notable standard deviation, indicating a wide range of costs. The data exhibited a right-skewed distribution with a significant proportion of households having zero MC. Factors such as age, education level, employment status, family size, urban/rural residence, and income were found to be associated with MC in Iranian households.
Researchers working with semi-continuous data often use two-part models that combine logistic/probit regression for predicting zero values and linear regression for positive values51,74. In more recent studies, these models have been extended to include zero augmented beta prime34, multivariate proportionally restricted models75, random effects models for longitudinal data67, marginalized models51, and quantile regression models76. The MTP model helps to assess the influence of factors on the marginal mean, which improves insight into health outcomes in different populations63. Multilevel models, such as the two-part models introduced by Belotti41, are crucial for dealing with nested data structures with different variables between groups. Understanding hierarchical data structures is essential for accurate modeling, especially in areas of decision making such as business and science. In this study, comparison of the MTP-LN and MTP-G models showed better predictive accuracy, with the MTP-LN model closely approximating actual medical costs in Iranian provinces and outperforming the MTP-G model. This research also shows the importance of understanding the hierarchical structure of data and its impact on modeling by creating scatter plots and mapping diagrams.
Our study provides new insights into the factors influencing medical costs in Iranian households, particularly regarding the role of education, family size, income, and rural versus urban residence. The analysis revealed that older individuals are less likely to have positive MC than younger individuals. Research consistently shows that age is a significant factor in determining MC and access to care. Richman found that both younger and middle-aged adults are vulnerable to burdensome MC, with younger adults particularly at risk even with moderate incomes77. This is further supported by Na, who found that younger medicare beneficiaries are less likely to receive recommended care compared to older age groups78. However, Faraji et al.79, Brockmann80, and Mueller81 provide a different perspective, suggesting that older individuals may actually have lower MC, with the latter study indicating that high medical spending among older households is associated with decreased nonmedical spending. These findings highlight the complex interplay of age, medical costs, and access to care.
Some studies show that, higher education levels among family heads were associated with a less likelihood of incurring MC79,81,82. The results of this study suggest that, holding family income and insurance status constant, higher education has a positive effect on MC in different quantiles, especially for spouses with higher education and in higher quantiles of health care expenditures. In addition, the study showed that having a PhD increases household MC by about $47 per year compared to an illiterate household.
In terms of rural vs. urban differences, our study aligns with findings from Lee83 and Hartley84, who noted that rural populations face more financial barriers in accessing care, despite generally lower medical costs. Our study highlights the importance of improving healthcare access and providing financial subsidies to rural households.
In both models, heads of households with a higher level of education and a different employment status have significantly higher MC, with non-working households spending around 43% more on MC compared to working households, while single heads of households spend around 35% less on MC than married, widowed or divorced heads of households. Larger families (4 or more people) and households with fewer students tend to have higher MC, while households with two or more educated members, above average income and above average expenditure on food, clothing and household costs are also associated with higher MC. Research consistently shows that larger family sizes, lower student group membership, and higher income and spending are associated with higher levels of MC81,82,85,86. These factors can be seen as indicators of increased healthcare needs and utilization, which in turn drive up medical spending. However, the specific mechanisms through which these factors influence MC may vary, and further research is needed to fully understand these relationships.
The study compared statistical models for analyzing MC, focusing on methods for positive skewed healthcare costs. The two-part models, MTP-LN and MTP-G, were utilized to analyze the multilevel MC data. The results indicated that the MTP-LN model provided a better fit compared to the MTP-G model, as evidenced by lower log-likelihood, AIC, and BIC values. Liu and Powers both explore the use of two-part models in analyzing MC data55,87. Liu (2010) specifically focuses on a two-part random effects model, while Powers evaluates the predictive modeling of total healthcare costs using pharmacy claims data. Both studies find that the two-part models are effective in their respective analyses. However, Lin and Crawford present alternative approaches. Lin compares the two-part model with neural networks, finding strong evidence in favor of the latter88. Crawford compares the accuracy of total population and disease-specific neural network models in predicting MC, with the latter proving more effective89. These studies suggest that while the two-part models can be useful, they may not always provide the best fit compared to other modeling techniques59,90.
The MTP-LN model has been found to be more accurate in capturing data dispersion, particularly in the presence of random effects, compared to the MTP-G model. This is supported by Liu, who highlighted the impact of model misspecification on the marginalized models49, and Iddi, who emphasized the importance of considering overdispersion and correlation in modeling91. Voronca further demonstrated the superiority of the MTP-LN model in the context of the Generalized Gamma family of distributions47. However, The search results do not provide direct evidence to support the claim that the MTP-LN model is more accurate in capturing data dispersion, particularly in the presence of random effects, compared to the MTP-G model40,92.
Implications for health policy
The findings of this study offer several important insights that could guide health policy in Iran, especially given the substantial burden of medical costs on households. The wide variability in medical expenditures, with a significant proportion of households having no medical costs while others have much higher expenditures, points to the need for more targeted interventions. Firstly, the relationship between education level and medical costs shows that households with a higher level of education tend to have higher medical costs. This could be due to greater awareness and utilization of healthcare services. Policy makers could consider improving access to preventive measures and health literacy programs, especially for low-income and less educated households, to avoid high medical costs. Second, the finding that rural households tend to have lower medical costs but face greater financial barriers underscores the importance of improving access to health care in these areas. Measures could include improving health infrastructure, providing financial subsidies to rural populations and offering mobile health services to reduce the economic burden of seeking healthcare. Third, the significant relationship between family size and medical costs suggests that larger families are more likely to have higher health care expenditures. Financial support measures such as expanding family-oriented health insurance plans or providing subsidies for larger households could help reduce these costs. Finally, the observed relationship between higher income and higher health care costs underscores the importance of addressing the health care needs of wealthier households, particularly with regard to insurance coverage and out-of-pocket spending. Policymakers could consider expanding coverage to reduce spending for high-income households while ensuring that low-income households continue to receive adequate support. When these factors are taken into account, health policies in Iran can be better tailored to reduce the financial burden on households, especially for the more vulnerable populations who face higher medical costs.
Study limitations
When interpreting the results of this study, it is important to consider that, as with other studies using household data, this is self-reported data that may be influenced by recall bias. This means that patients may have forgotten, underestimated or overestimated some of the information provided. Since the study focuses on 8993 Iranian households, its generalizability to the broader population is limited. The unclear methods of data collection could affect the reliability of the results and lead to bias. Due to the selective inclusion of certain cost determinants, the study could lack depth and robustness. The specificity of the study to Iran in 2021 also limits the broader implications. To address these limitations, future research should consider a broader range of data and statistical approaches to improve the depth and robustness of the analysis. The use of advanced statistical techniques such as multivariate regression analysis, weighted samples, propensity score matching, structural equation modeling, or machine learning algorithms can provide a more comprehensive understanding of the factors influencing healthcare costs in Iran.
Conclusion
In this cross-sectional study, we conducted retrospective reporting on the MCs of Iranian households in 2021. In summary, the study illustrates the complexity of factors influencing MC in Iranian households and demonstrates the utility of MTP models in analyzing such data. The results emphasize the importance of considering demographic, socioeconomic, and geographic variables in understanding and predicting medical expenditure patterns within a population. The results of this study offer several important insights that could guide healthcare policy in Iran, especially in light of the significant medical cost burden faced by households. The wide variability in medical expenditures, with a substantial portion of households incurring zero medical costs, while others face much higher expenses, suggests the need for more targeted interventions. Understanding these factors can help policy makers and healthcare providers develop targeted interventions to reduce the financial burden of healthcare for vulnerable populations. The MTP-LN models provide valuable insights into the factors associated with MCs of Iranian households. The models can be used to identify groups with a higher risk of high MC and to develop targeted measures to reduce the financial burden on the healthcare system for these groups.
Data availability
The data sets utilized and/or analyzed in this study are not publicly accessible due to sensitivity concerns. However, they can be made available upon a reasoned request to the corresponding author. The data originates from the Statistical Center of Iran (SCI), and the sources can be found at https://www.amar.org.ir.
Abbreviations
- MC:
-
Medical cost
- HIES:
-
Households Income and Expenditure Survey
- SCI:
-
Statistical Center of Iran
- MTP-LN:
-
Marginalized two-part lognormal
- MTP-G:
-
Marginalized two-part gamma
- GG:
-
Generalized gamma
- W:
-
Weibull
- LSN:
-
Log skew-normal
- CTP:
-
Conditional two-part
- D:
-
Deviance
- AIC:
-
Akaike information criterion
- BIC:
-
Bayesian information criterion
- IQR:
-
Interquartile range
References
Roebuck, M. C., Liberman, J. N., Gemmill-Toyama, M. & Brennan, T. A. Medication adherence leads to lower health care use and costs despite increased drug spending. Health Affair 30(1), 91–99. https://doi.org/10.1377/hlthaff20091087 (2017).
How Proactive Healthcare Can Save on Costs | Chicago Booth Review. (2024). https://www.chicagobooth.edu/review/how-proactive-healthcare-can-save-costs
Liu, P.-H. et al. Cost-effectiveness of human papillomavirus vaccination for prevention of cervical cancer in Taiwan. BMC Health Serv. Res. 10, 11 (2010).
Hussey, P. S., Wertheimer, S. & Mehrotra, A. The association between health care quality and cost a systematic review. Ann. Intern. Med. 158(1), 27 (2013).
Prioritizing health: A prescription for prosperity|McKinsey. (2024). https://www.mckinsey.com/industries/healthcare/our-insights/prioritizing-health-a-prescription-for-prosperity
Brück, C. C., Wolters, F. J., Ikram, M. A. & de Kok, I. M. C. M. Projections of costs and quality adjusted life years lost due to dementia from 2020 to 2050: A population-based microsimulation study. Alzheimer’s Dement. 19(10), 4532–4541 (2023).
Brück, C. C., Wolters, F. J., Ikram, M. A., de Kok, I. M. C. M. Projections of costs and quality adjusted life years lost due to dementia from 2020 to 2050: A population‐based microsimulation study. Alzheimer’s Dement. (2023).
Galvani, A. P., Parpia, A. S., Foster, E. M., Singer, B. H. & Fitzpatrick, M. C. Improving the prognosis of health care in the USA. Lancet 395(10223), 524–533 (2020).
Odonnell, O. et al. Who pays for health care in Asia?. J. Health Econ. 27(2), 460–475 (2008).
Queenan, J. T. The increasing cost of medical care. Obstet. Gynecol. 100(4), 629–630 (2002).
Doshmangir, L., Yousefi, M., Hasanpoor, E., Eshtiagh, B. & Haghparast-Bidgoli, H. Determinants of catastrophic health expenditures in Iran: A systematic review and meta-analysis. Cost Eff. Resour. Alloc. 18(1), 1–21 (2020).
Pauly, M. V., Zweifel, P., Scheffler, R. M., Preker, A. S. & Bassett, M. Private health insurance in developing countries. NCHS Data Brief 25(2), 369–379. https://doi.org/10.1377/hlthaff252369 (2017).
Health financing. https://www.who.int/health-topics/health-financing#tab=tab_1
Cohen, R. A. & Kirzinger, W. K. Financial burden of medical care: a family perspective. NCHS Data Brief 142, 1–8 (2014).
Mehrara, M. & Fazaeli, A. A. Health finance equity in Iran: An analysis of household survey data (1382–1386). J. Health Adm. 13(40), 51–62 (2010).
Ahmadi, A. M., Nikravan, A., Naseri, A. & Asari, A. Effective determinants in household out of packet payments in health system of Iran, using two part regression model. (2014).
Xu X, Huang X, Zhang X, Chen L. Family economic burden of elderly chronic diseases: evidence from China. In: Healthcare, 99 (MDPI, 2019).
Health and Economic Costs of Chronic Diseases | CDC [Internet]. (2024). https://www.cdc.gov/chronicdisease/about/costs/index.htm
Gambert, S. R. The burden of chronic disease. Mayo Clin. Proc. Innov. Qual. Outcomes 8(1), 112 (2024).
Chronic conditions lead health care spend in the U.S. | Employer | UnitedHealthcare. (2024). https://www.uhc.com/employer/news-strategies/chronic-conditions-lead-health-care-spend-in-the-us
Han, K.-T., Kim, W. & Kim, S. Disparities in healthcare expenditures according to economic status in cancer patients undergoing end-of-life care. BMC Cancer. 22(1), 303 (2022).
Lee, H. J. et al. Association between changes in economic activity and catastrophic health expenditure: Findings from the Korea Health Panel Survey, 2014–2016. Cost Eff. Resour. Alloc. 18, 1–9 (2020).
Okunade, A. A., Suraratdecha, C. & Benson, D. A. Determinants of Thailand household healthcare expenditure: The relevance of permanent resources and other correlates. Health Econ. 19(3), 365–376 (2010).
Polder, J. J., Bonneux, L., Meerding, W. J. & Van Der Maas, P. J. Age-specific increases in health care costs. Eur. J. Public Health 12(1), 57–62 (2002).
Romley, J. A. et al. The relationship between commercial health care prices and medicare spending and utilization. Health Serv. Res. 50(3), 883–896 (2015).
Young, G. J. Do financial barriers to healthcare services affect health status?. Med. Care. 48(2), 1–10 (2010).
Health coverage protects you from high medical costs | HealthCare.gov. (2024). https://www.healthcare.gov/why-coverage-is-important/protection-from-high-medical-costs/
Liu, H. et al. Catastrophic health expenditure incidence and its equity in China: A study on the initial implementation of the medical insurance integration system. BMC Public Health. 19(1), 1–10 (2019).
Fang, K. et al. Illness, medical expenditure and household consumption: Observations from Taiwan. BMC Public Health 13(1), 743 (2013).
Azzani, M., Roslani, A. C. & Su, T. T. Determinants of household catastrophic health expenditure: A systematic review. Malays. J. Med. Sci. 26(1), 15 (2019).
Tur-Sinai, A., Magnezi, R. & Grinvald-Fogel, H. Assessing the determinants of healthcare expenditures in single-person households. Isr. J. Health Policy Res. 7(1), 191996 (2018).
Almalki, Z. S. et al. Original research: Investigating households’ out-of-pocket healthcare expenditures based on number of chronic conditions in Riyadh, Saudi Arabia: a cross-sectional study using quantile regression approach. BMJ Open 12(9), 66145 (2022).
Tur-Sinai, A., Magnezi, R. & Grinvald-Fogel, H. Assessing the determinants of healthcare expenditures in single-person households. Isr. J. Health Policy Res. 7(1), 48. https://doi.org/10.1186/s13584-018-0246-8 (2018).
Kamyari, N., Soltanian, A. R., Mahjub, H., Moghimbeigi, A. & Seyedtabib, M. Zero-augmented beta-prime model for multilevel semi-continuous data: A Bayesian inference. BMC Med. Res. Methodol. 22(1), 283. https://doi.org/10.1186/s12874-022-01736-0 (2022).
Liu, L. Joint modeling longitudinal semi-continuous data and survival, with application to longitudinal medical cost data. Stat. Med. 28(6), 972–986 (2009).
Shahrokhabadi, M. S., Chen, D. G., Mirkamali, S. J., Kazemnejad, A. & Zayeri, F. Marginalized two-part joint modeling of longitudinal semi-continuous responses and survival data: With application to medical costs. Math 9, 2603 (2021).
Liu, L. et al. Statistical analysis of zero-inflated nonnegative continuous data. Stat. Sci. 34(2), 253–279 (2019).
Mazumdar, M. et al. Comparison of statistical and machine learning models for healthcare cost data: A simulation study motivated by Oncology Care Model (OCM) data. BMC Health Serv. Res. 20(1), 7183716 (2020).
Kurz, C. F. Tweedie distributions for fitting semicontinuous health care utilization cost data. BMC Med. Res. Methodol. 17(1), 171. https://doi.org/10.1186/s12874-017-0445-y (2017).
Zero-Inflated and Two-Part Mixed Effects Models • GLMMadaptive. (2024). https://drizopoulos.github.io/GLMMadaptive/articles/ZeroInflated_and_TwoPart_Models.html
Belotti, F., Deb, P., Manning, W. G., Norton, E. C. & Arbor, A. twopm: Two-part models. Stata J. 15(1), 3–20 (2015).
Blozis, S. A. Bayesian two-part multilevel model for longitudinal media use data. J. Mark. Anal. 10(4), 311–328. https://doi.org/10.1057/s41270-022-00172-9 (2022).
Rustand, D., Briollais, L. & Rondeau, V. A marginalized two-part joint model for a longitudinal biomarker and a terminal event with application to advanced head and neck cancers. Pharm. Stat. 23(1), 60–80 (2024).
Smith, V. A., West, B. T. & Zhang, S. Fitting marginalized two-part models to semicontinuous survey data arising from complex samples. Health Serv. Res. 56(3), 558 (2021).
Kamyari, N., Soltanian, A. R., Mahjub, H. & Moghimbeigi, A. Diet, nutrition, obesity, and their implications for COVID-19 mortality: Development of a marginalized two-part model for semicontinuous data. JMIR Public Health Surveill. 7(1), e22717 (2021).
Chai, H., Jiang, H., Lin, L. & Liu, L. A marginalized two-part Beta regression model for microbiome compositional data. PLoS Comput. Biol. 14(7), e1006329 (2018).
Voronca, D. C., Gebregziabher, M., Durkalski, V. L., Liu, L. & Egede L. E. Marginalized two part models for generalized gamma family of distributions. arXiv151105629 (2015).
Jaffa, M. A. et al. Analysis of longitudinal semicontinuous data using marginalized two-part model. J. Transl. Med. 16(1), 1–15 (2018).
Liu, X. et al. Are marginalized two-part models superior to non-marginalized two-part models for count data with excess zeroes? Estimation of marginal effects, model misspecification, and model selection. Health Serv. Outcomes Res. Methodol. 18, 175–214 (2018).
Smith, V. A. & Preisser, J. S. A marginalized two-part model with heterogeneous variance for semicontinuous data. Stat. Methods Med. Res. 28(5), 1412–1426. https://doi.org/10.1177/0962280218758358 (2018).
Smith, V. A., Preisser, J. S., Neelon, B. & Maciejewski, M. L. A marginalized two-part model for semicontinuous data. Stat. Med. 33(28), 4891–4903 (2014).
Statistical Centre of Iran > Metadata > Statistical Survey > Household, Expenditure and Income. https://www.amar.org.ir/english/Metadata/Statistical-Survey/Household-Expenditure-and-Income
Liu, L., Ma, J. Z. & Johnson, B. A. A multi-level two-part random effects model, with application to an alcohol-dependence study. Stat. Med. 27(18), 3528–3539 (2008).
Gebregziabher, M. et al. Joint modeling of multiple longitudinal cost outcomes using multivariate generalized linear mixed models. Health Serv. Outcomes Res. Methodol. 13, 39–57 (2013).
Liu, L., Strawderman, R. L., Cowen, M. E. & Shih, Y.-C.T. A flexible two-part random effects model for correlated medical costs. J. Health Econ. 29(1), 110–123 (2010).
Manning, W. G., Basu, A. & Mullahy, J. Generalized modeling approaches to risk adjustment of skewed outcomes data. J. Health Econ. 24(3), 465–488 (2005).
Neelon, B., O’Malley, A. J. & Smith, V. A. Modeling zero-modified count and semicontinuous data in health services research part 2: Case studies. Stat. Med. 35(27), 5094–5112 (2016).
Li, N., Elashoff, D. A., Robbins, W. A. & Xun, L. A hierarchical zero-inflated log-normal model for skewed responses. Stat. Methods Med. Res. 20(3), 175–189 (2011).
Malehi, A. S., Pourmotahari, F. & Angali, K. A. Statistical models for the analysis of skewed healthcare cost data: A simulation study. Health Econ. Rev. 5, 1–16 (2015).
Chai, H. S. & Bailey, K. R. Use of log-skew-normal distribution in analysis of continuous data with a discrete component at zero. Stat. Med. 27(18), 3643–3655 (2008).
Manning, W. G. et al. A two-part model of the demand for medical care: Preliminary results from the health insurance study. Health Econ. 137, 103–123 (1981).
Vuong, Q. H. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 57(2), 307 (1989).
Smith, V. A., Neelon, B., Maciejewski, M. L. & Preisser, J. S. Two parts are better than one: Modeling marginal means of semicontinuous data. Health. Serv. Outcomes Res. Methodol. 17, 198–218 (2017).
Li, N., Elashoff, D. A., Robbins, W. A. & Xun, L. A hierarchical zero-inflated log-normal model for skewed responses. Stat. Methods Med. Res. 20(3), 175–189. https://doi.org/10.1177/0962280208097372 (2008).
Raudenbush, S. W., Yang, M.-L. & Yosef, M. Maximum likelihood for generalized linear models with nested random effects via high-order, multivariate Laplace approximation. J. Comput. Graph. Stat. 9(1), 141–157 (2000).
Bock, R. D. Maximum Marginal Likelihood Item Factor Analysis By Adaptive Quadrature Stephen Schilling school of Education (University of Michigan, 2005). https://api.semanticscholar.org/CorpusID:58914630
Olsen, M. K. & Schafer, J. L. A two-part random-effects model for semicontinuous longitudinal data. J. Am. Stat. Assoc. 96(454), 730–745 (2001).
Tooze, J. A., Grunwald, G. K. & Jones, R. H. Analysis of repeated measures data with clumping at zero. Stat. Methods Med. Res. 11(4), 341–355 (2002).
Hubin, A. & Storvik, G. Estimating the Marginal Likelihood with Integrated nested Laplace Approximation (INLA). arXiv161101450. (2016).
Wang, Y. Maximum likelihood computation based on the Fisher scoring and Gauss-Newton quadratic approximations. Comput. Stat. Data Anal. 51(8), 3776–3787 (2007).
Team RC. R: A Language and Environment for Statistical Computing. (R Foundation for Statistical Computing, 2013).
Datawrapper: Create charts, maps, and tables. (2024). https://www.datawrapper.de/
Burnham, K. P. & Anderson, D. R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach (Springer, 2002).
Tom, B. D. M., Su, L. & Farewell, V. T. A corrected formulation for marginal inference derived from two-part mixed models for longitudinal semi-continuous data. Stat. Methods Med. Res. 25(5), 2014–2020 (2016).
Xie, Y., Zhang, Z., Rathouz, P. J. & Barrett, B. P. Multivariate semi-continuous proportionally constrained two-part fixed effects models and applications. Stat. Methods Med. Res. 28(12), 3516–3533 (2019).
Merlo, L., Maruotti, A. & Petrella, L. Two-part quantile regression models for semi-continuous longitudinal data: A finite mixture approach. Stat. Model. 22(6), 485–508. https://doi.org/10.1177/1471082X21993603 (2021).
Richman, I. B. & Brodie, M. A national study of burdensome health care costs among non-elderly Americans. BMC Health Serv. Res. 14, 1–7 (2014).
Na, L. et al. Disparities in receipt of recommended care among younger versus older medicare beneficiaries: A cohort study. BMC Health Serv. Res. 17, 1–13 (2017).
Faraji, M. et al. Out-of-pocket pharmaceutical expenditure and its determinants among Iranian households with elderly members: A double-hurdle model. Cost Eff. Resour. Alloc. 22(1), 1–9 (2024).
Brockmann, H. Why is less money spent on health care for the elderly than for the rest of the population? Health care rationing in German hospitals. Soc. Sci. Med. 55(4), 593–608 (2002).
Mueller, C. W., Charron-Chénier, R., Bartlett, B. J. & Brown, T. H. Budgetary consequences of high medical spending across age and social status: evidence from the consumer expenditure surveys. Gerontologist. 60(7), 1322–1331 (2020).
Blackburn, J. & Choi, S. Patterns and factors associated with medical expenses and health insurance premium payments. Financ. Couns. Plan. 29(1), 6–18 (2018).
Lee, W.-C., Jiang, L., Phillips, C. D. & Ohsfeldt, R. L. Rural-Urban differences in health care expenditures: Empirical data from US households. Adv. Public Health. 2014, 1–10 (2014).
Hartley, D., Quam, L. & Lurie, N. Urban and rural differences in health insurance and access to care. J. Rural Health. 10(2), 98–108 (1994).
Lu, S., Zhang, Y., Niu, Y. & Zhang, L. Exploring medical expenditure clustering and the determinants of high-cost populations from the family perspective: A population-based retrospective study from rural China. Int. J. Environ. Res. Public Health. 15(12), 2673 (2018).
Halliday, T. J. & Park, M. Household size, home health care, and medical expenditures. Inst Study Labor (IZA) Univ Hawai’i Manoa. http://www.Economic.hawaii.edu/research/workingpapers/WP_09-16.pdf. (2009).
Powers, C. A., Meyer, C. M., Roebuck, M. C. & Vaziri, B. Predictive modeling of total healthcare costs using pharmacy claims data: A comparison of alternative econometric cost modeling techniques. Med Care. 43(11), 1065–1072 (2005).
Lin, C., Hsu, S. & Takao, A. A review and comparison of medical expenditures models: Two neural networks versus two-part models. J. Risk Res. 11(8), 967–982 (2008).
Crawford, A. G., Fuhr, J. P. Jr., Clarke, J. & Hubbs, B. Comparative effectiveness of total population versus disease-specific neural network models in predicting medical costs. Dis. Manag. 8(5), 277–287 (2005).
Garrido, M. M., Deb, P., Burgess, J. F. Jr. & Penrod, J. D. Choosing models for health care cost analyses: Issues of nonlinearity and endogeneity. Health Serv. Res. 47(6), 2377–2397 (2012).
Iddi, S. & Molenberghs, G. A combined overdispersed and marginalized multilevel model. Comput. Stat. Data Anal. 56(6), 1944–1951 (2012).
Duan, Y., Emir, B., Bell, G. & Cabrera, J. twopartm: Two-part model with marginal effects. CRAN Contrib Packag. (2022). https://cran.r-project.org/package=twopartm
Acknowledgements
The authors would like to thank the Statistical Center of Iran (SCI) for providing the data used in this study. This research is part of the Biostatistics MS thesis of Elham Daghaghele and was supported by Ahvaz Jundishapur University of Medical Sciences (AJUMS). Special thanks to the Research Deputy of Ahwaz Jundishapur University of Medical Sciences for providing financial support for this project.
Funding
This research was supported by project U-02034 from Ahvaz Jundishapur University of Medical Sciences. However, the source of funding had no influence on the study design, data collection, analysis and interpretation, writing of the report, or the decision to publish the article.
Author information
Authors and Affiliations
Contributions
CRediT authorship contribution statement: ED: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Data curation, Writing–original draft, writing—review & editing, Visualization, Project administration. KA-A: Conceptualization, Data curation, Formal analysis, Investigation, Writing–original draft, writing—review & editing. NK: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data curation, Writing–original draft, writing—review & editing, Visualization, Supervision. MS: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Data curation, Writing—original draft, writing—review & editing, Visualization, Project administration.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This study was approved by the Research Ethics Committee (REC) of Ahvaz Jundishapur University of Medical Sciences under the ID number IR.AJUMS.REC.1402.064. Methods used complied with all relevant ethical guidelines and regulations. The Ethics Committee of Ahvaz Jundishapur University of Medical Sciences waived the requirement for written informed consent from study participants.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Daghaghele, E., Angali, K.A., Kamyari, N. et al. Marginalized two part model for analyzing multilevel semicontinuous medical costs in Iranian households. Sci Rep 15, 7491 (2025). https://doi.org/10.1038/s41598-025-91309-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-91309-0