Introduction

The Junggar Basin is the largest coal-bearing basin in the west of China. The coal measure strata are extremely developed with great amount of coalbed methane of nearly 40.1 × 108m3. Nevertheless, it usually has no any direct and effective commercial production capacity, owing to the poor physical properties of tight coal measure reservoirs and extremely low permeability. Currently, large-scale hydraulic fracturing technology is an only critical means to break through this problem1,2,3. Previous studies indicate that in-situ stress is a very key parameter in the process of hydraulic fracturing of coalbed methane reservoir4,5. Moreover, the morphology, scale and extension direction of fracturing fractures are related to in-situ stress6. It could also provide reference for the analysis of borehole stability and the optimization design of borehole. Therefore, aiming at obtaining high-quality pressure fractures and providing effective guidance for the design of hydraulic fracturing and network optimization of horizontal well to improve the stimulation effect of fracturing, it is extremely necessary to accurately evaluate the in-situ stress of coalbed methane reservoir.

Currently, the main methods for obtaining in-situ stress parameters are seismic inversion, acoustic emission of core, stress recovery and hydraulic fracturing7,8,9,10. Acoustic emission and hydraulic fracturing method are commonly used in the development of unconventional resource. The precision of these two methods is relatively higher. While, the acoustic emission method is completed in the laboratory and greatly relies on the number of cores. Hydraulic fracturing is limited by the number of tested point and borehole collapse. Meanwhile, only shallow and discontinuous in-situ stress data could be achieved by these two mentioned methods, moreover are also influenced by geological, equipment and other environmental factors. Thus, these cannot efficiently and accurately estimate the geomechanical properties of deep formations. Logging methods are characterized as the advantages of large measurement depth, low cost and continuous data11,12. This method has been used in the prediction of in-situ stress in carbonate formations. However, the application of logging data to evaluate the in-situ stress of tight reservoir is still rare. Presently, there are uniaxial strain model, anisotropic formation model and Huang’s model for in-situ stress prediction13,14,15. Logging data are required for the latter two models. The first three models have some shortcomings. The uniaxial strain model assumes that there is only vertical strain in the formation, while the horizontal stress is generated by the vertical stress, and the maximum and minimum horizontal principal stress are equal15. It is mainly applicable to the formation with weak strength structure, such as the central abdomen of the basin15. Although the anisotropic formation model considers the non-equality of the horizontal principal stress, the model needs many determined parameters, but it is difficult to obtain these parameters accurately by the current measurement methods15.

Considering the geological condition of Xishanyao Formation in the southern margin of Junggar Basin, the calculation model of in-situ stress is established by using acoustic logging and density logging parameters. The precision correction is conducted by improved differential strain method. The direction of in-situ stress is determined by combining wave velocity anisotropy method and paleomagnetic method.

Geological setting

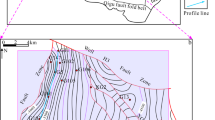
The southern margin of the Junggar Basin is located at the uplift of the basin and Tianshan orogenic belt. Since the late Paleozoic, the basin has experienced multi-stage tectonic movements of Hercynian, Indosinian, Yanshan and Himalayan, and is a superimposed basin composed of multi-stage different types of prototype basins. The region contains Sikeshu depression and Qigu fault-fold belt, and Fukang fault belt developed along Bogda Mountain (Fig. 1a)16,17. The Junggar Basin has experienced three principal stages of evolution in geological history, i.e., foreland, depression and regenerated foreland. The formation period of depression of the basin is mainly Mesozoic Triassic, Jurassic and Cretaceous. The whole western region was in the shallow lacustrine pan-basin sedimentary era during the Jurassic period, and the coal measure strata were extremely developed. The coal measure strata in Junggar Basin are concentrated in Badaowan Formation (J1b) of the Lower Jurassic and Xishanyao Formation (J2x) of the Middle Jurassic, with a wide coal-bearing area and the thickest coal seam up to 300 m. It has several coal-accumulating centers in Xishanyao Formation, and the lithology is composed of gray and gray-green mudstone, sandstone, argillaceous sandstone, pebbly sandstone, and coal seam (Fig. 1(b)). The macroscopic types of coal seams in Xishanyao Formation are semi-bright, bright and dim.

Fig. 1
figure 1

The regional tectonic location and comprehensive histogram of Xishanyao Formation in Southern China.

Full size image

In-situ stress estimation

Vertical stress

The prediction model of vertical principal stress based on density and acoustic logging parameters is as follows7:

$${\sigma _{\text{v}}}=\int_{0}^{H} {\rho (h)} \times g \times dh$$
(1)

Where: \(\:{{\upsigma\:}}_{\text{v}}\)-Vertical principal stress, MPa; \(\:\rho\:\left(h\right)\)- The formation density at different depth, g/cm3; H- The target depth of the formation, m; h- The depth of any position of the formation, m; g-The acceleration of gravity, g/cm3.

Horizontal principal stress

Actually, there are several computational models for horizontal principal stress, including the Mattews & Kelly model, the Anderson model, the Newberry model, and Huang’s model. The models proposed by Mattews & Kelly, Anderson, and Newberry do not consider tectonic movement in the horizontal direction and are therefore unsuitable for regions with significant tectonic activity13,14,15,16. In contrast, Huang’s model was developed based on the assumption of tectonic stress influence15,16. Given that the southeastern margin of the Junggar Basin experiences relatively intense tectonic movement, this study adopts Huang’s model, which is specifically designed for areas with significant tectonic effects, as the horizontal principal stress calculation model. The model is expressed as follows:

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _{\text{H}}}=\frac{v}{{1 - v}}\left( {{\sigma _{\text{v}}} - \alpha {P_p}} \right)+\alpha {P_p}+{\beta _1}\left( {{\sigma _{\text{v}}} - \alpha {P_p}} \right)} \\ {{\sigma _{\text{h}}}=\frac{v}{{1 - v}}\left( {{\sigma _{\text{v}}} - \alpha {P_p}} \right)+\alpha {P_p}+{\beta _2}\left( {{\sigma _{\text{v}}} - \alpha {P_p}} \right)} \end{array}} \right.$$
(2)

Where: \(\:{\sigma\:}_{\text{H}}\),\(\:{\sigma\:}_{\text{h}}\)-The maximum and minimum horizontal principal stresses respectively, MPa; \(\:\alpha\:\)-The porosity coefficient, 0.01; v-Poisson’s ratio, 0.01; \(\:{\beta\:}_{1}\), \(\:{\beta\:}_{2}\)-Tectonic stress coefficient, 0.01; \(\:{P}_{\text{p}}\)- Pore pressure of formation, MPa.

  1. (1)

    Tectonic stress coefficient.

The tectonic stress coefficient in the similar tectonic setting is usually considered as constant, which mainly characterized the magnitude of the tectonic stress in the studied area. The tectonic stress coefficient is generally calculated with the experimental data by substituting the stress obtained in the laboratory into the established horizontal principal stress model.

  1. (2)

    The determination of rock mechanical parameters.

Rock mechanics parameters are the key to calculating in-situ stress18. It is difficult to gain rock mechanics parameters with core measurement in the laboratory, while logging data is relatively easy to acquire and one-dimensional rock mechanics parameter distribution along the wellbore can be obtained. Therefore, logging method is adopted to calculate rock mechanics parameters. It needs acoustic logging parameters, such as longitudinal and shear wave time difference to calculate rock mechanics parameters19,20,21. However, it usually has no shear wave time difference in most mining areas, thus shear wave time difference needs to be calculated by longitudinal wave time difference. The empirical formula is as follows22:

$$\Delta {t_s}=\frac{{\Delta {t_p}}}{{{{\left[ {1 - 1.15\frac{{\left( {1/{\rho _b}} \right)+{{\left( {1/{\rho _b}} \right)}^3}}}{{{e^{1/{\rho _b}}}}}} \right]}^3}}}$$
(3)

The rock mechanical parameters required by the above model can be calculated from the following table (Table 1).

Table 1 The calculation formula of rock mechanics parameters.
Full size table

Where: \(\:{{\uprho\:}}_{\text{b}}\)- Volume density of formation, g/cm3; \(\:{{\uprho\:}}_{\text{m}\text{a}}\)- The density of rock skeleton, g/cm3; \(\:\varDelta\:{\text{t}}_{\text{s}}\)- Shear wave time difference of formation, us/ft; \(\:\varDelta\:{\text{t}}_{\text{m}\text{s}}\)- Shear wave time difference of rock skeleton, us/ft; \(\:\varDelta\:{\text{t}}_{\text{p}}\)- Longitudinal wave time difference of formation, us/ft; \(\:\varDelta\:{\text{t}}_{\text{m}\text{p}}\)- Longitudinal wave time difference of rock skeleton, us/ft; \(\:{v}_{s}\) - Shear wave velocity of formation, m/s; \(\:{v}_{ms}\) - Shear wave velocity of rock skeleton, m/s; \(\:{v}_{\text{p}}\)- Longitudinal wave velocity of formation, m/s; \(\:{v}_{\text{m}\text{p}}\)- Longitudinal wave velocity of rock skeleton, m/s.

Experiment

The coal measures strata of Xishanyao Formation in the southern margin of Junggar Basin are characterized as complex lithology and tightness. It is difficult to drill small core in such formation. These geomechanical properties in the studied area increase the difficulty of test of in-situ stress. Owing to the difficulty to drill larger core, the commonly used acoustic emission test (AE) and inelastic strain recovery test are not applicable to this area. Therefore, methods such as differential strain analysis on the principal direction, wave velocity anisotropy and paleomagnetic method are comprehensively used to measure the values and direction of in-situ stress and direction of the core.

Test of in-situ stress in the laboratory

The differential strain analysis on the principal direction method was used to measure the in-situ stress. The horizontal principal stress direction of the core was determined based on wave velocity anisotropy and paleomagnetic method comprehensively. Then, the required rock sample was processed according to the determined principal stress direction. The rock samples were listed as Fig. 2, i.e., mudstone, sandstone, limestone respectively. As shown in the Fig. 3 below, three strain gauge test channels are used, and three resistance strain gauges (numbered 1,2,3) are pasted according to the direction of in-situ stress.

Fig. 2
figure 2

Rock samples. (a) Mudstone; (b) Sandstone; (c) Limestone.

Full size image
Fig. 3
figure 3

Required rock sample morphology by the differential strain analysis on the principal direction and sticking of the strain gauge.

Full size image

The rock sample is prepared according to Fig. 3, then sealed into the pressure chamber, finally confining the pressure exceeding the formation pressure where the rock sample is located. The strain values in the three directions can be measured from the strain gauge, which are denoted as \(\:{\epsilon\:}_{1}\), \(\:{\epsilon\:}_{2}\) and \(\:{\epsilon\:}_{3}\) respectively. They are corresponding to the vertical, minimum and maximum horizontal principal strain values respectively. By substituting the values of the principal strains in the three directions into Eq. 523, the ratio of the principal stresses in the three directions can be calculated. After the vertical principal stress is calculated with the density logging, the principal stress values of the other two directions are calculated from the stress ratio of the three directions. The actual stress direction of non-oriented core can be determined by combining wave velocity anisotropy and paleomagnetic method.

$${\sigma _1}:{\sigma _2}:{\sigma _3}=\left[ {v\left( {{\varepsilon _2}+{\varepsilon _3}} \right)+\left( {1 - v} \right){\varepsilon _2}} \right]:\left[ {v\left( {{\varepsilon _1}+{\varepsilon _2}} \right)+\left( {1 - v} \right){\varepsilon _3}} \right]:\left[ {v\left( {{\varepsilon _3}+{\varepsilon _1}} \right)+\left( {1 - v} \right){\varepsilon _2}} \right]$$
(4)

Where: \(\:{\epsilon\:}_{1}\),\(\:{\epsilon\:}_{2}\),\(\:{\epsilon\:}_{3}\)-The strain in the direction of principal stress respectively; \(\:{\sigma\:}_{1}\),\(\:{\sigma\:}_{2}\),\(\:{\sigma\:}_{3}\)-The maximum, intermediate and minimum principal stresses (MPa), respectively; v-Poisson’s ratio.

Determination method of in-stress direction in the laboratory

(1) Wave velocity anisotropy analysis.

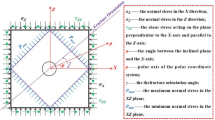
After the rock core is separated from the stratum, it will release its own stress, along with the generation of small-sized cracks. The development of small-sized cracks depends on the magnitude and direction of the in-situ stress. The core relaxation is the largest in the direction of the maximum horizontal principal stress, and the microcracks are mainly perpendicular to the maximum horizontal principal stress (Fig. 4). The wave impedance values of rock and air are significantly different24,25,26. The velocity of acoustic wave propagating in the rock is significantly greater than that in the air, and the micro-fractures make the propagation of acoustic waves in the core have a significant difference. Generally, the direction of the minimum wave velocity is the direction of the maximum horizontal principal stress, while the direction of the maximum wave velocity is the direction of the minimum horizontal principal stress.

Fig. 4
figure 4

Schematic diagram of microcracks and directions of maximum and minimum horizontal principal stress in core.

Full size image
  1. (2)

    The paleomagnetic analysis.

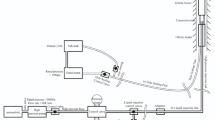
The paleomagnetic experiment is mainly considered as an auxiliary aid of wave velocity anisotropy analysis method to determine the direction of horizontal principal stress. The test device consists of three parts: weak magnetic space system, demagnetization system and magnetic vector system (Fig. 5). As the rock itself contains ferromagnetic minerals and could record the geomagnetic direction, the determination of the direction of in-situ stress with paleomagnetic analysis method is mainly achieved by using geomagnetic instruments to measure the geomagnetic field direction when the rock is magnetized27,28.

If the core is not oriented, only the relative direction of the horizontal principal stress can be obtained through the wave velocity anisotropy experiment. The true direction of the in-situ stress should be combined with the paleomagnetic experiment to orient the core, then restore the initial direction of the core in the formation to finally determine the direction of the horizontal principal stress of the real rock. Specific implementation steps are as follows (Fig. 6) : (1) A north pole line is assumed at the position of the core close to the wellhead section; (2) The sample used to determine the paleomagnetic direction is drilled perpendicular to the rock face; (3) The wave velocity anisotropy of the rock was measured by rotating the sample counterclockwise; (4) The maximum horizontal principal stress orientation is obtained by adding the minimum acoustic propagation orientation measured by wave velocity anisotropy and the paleomagnetic lithology orientation.

Fig. 5
figure 5

The device of paleomagnetism test.

Full size image
Fig. 6
figure 6

Test diagram.

Full size image
  1. (3)

    Determination of maximum horizontal principal stress.

The determination of maximum horizontal principal stress is as follows Eq. 6.

$$\theta =\alpha +\gamma$$
(5)

Where: \(\:\theta\:\)- The azimuth of maximum horizontal principal stress, \(\:^\circ\:\); \(\:{\upalpha\:}\)- The paleomagnetic orientation, \(\:^\circ\:\); \(\:{\upgamma\:}\)- The minimum propagation of acoustic wave, \(\:^\circ\:\).

The distribution of in-situ stress

The upper part of Xishanyao formation is interlayer of sandstone, mudstone and coal seam, and the lower part is interlayer of sandstone and mudstone. The in-situ stress of coal measures in Xishanyao formation of cored well F15 in the southeastern margin of Junggar Basin is calculated by using the logging evaluation method proposed in the paper. Then the calculated result is compared with the coring test. The comparison indicates that the error between the in-situ stress measured in the laboratory and the calculation with logging method is less than 8% (Table 2), which could meet the precision requirements of application in the oilfield. Therefore, the method of in-situ stress prediction with logging parameters can be popularized in the field.

The maximum horizontal principal stress of Xishanyao Formation is 37.5-51.5 MPa. The minimum horizontal principal stress is 28.1-46.3 MPa (Fig. 7). On the whole, the maximum horizontal principal stress, minimum horizontal principal stress and vertical principal stress increase gradually with the depth. The type of in-situ stress is type III principal stress. It is conducive to maintaining good opening state and flow conductivity of natural fractures, and is also conducive to vertical tensile fracture caused by hydraulic fracturing. The generated compressive fracture has strong lateral expansion ability. As it can be seen from Fig. 7, the maximum principal stress distribution of different lithologies are as follows: mudstone is 31.3-51.5 MPa, with mean of 41.9 MPa; sandstone is 30.6 ~ 50.5 MPa, with mean of 38.7 MPa; coal is 29.8-41.8 MPa, with mean of 35.5 MPa. Similarly, the minimum horizontal principal stress distribution is as follows: mudstone is 28.7-36.1 MPa, with mean of 32.1 MPa; sandstone is 28.9-33.4 MPa, with mean of 30.3 MPa; coal is 25.3-33.1 MPa, with mean of 29.2 MPa. Therefore, the in-situ stress of mudstone in coal measure stratum is the highest, while that of coal is the lowest.

The horizontal principal stress distribution diagram of coal measures in Xishanyao formation in the southern margin of Junggar Basin is obtained by comprehensively using the logging evaluation model to calculate the in-situ stress of coal measures in other 12 Wells of Xishanyao formation in the studied area. It can be seen from Fig. 8 that the distribution of the maximum horizontal principal stress is large in the center of the basin and small on both sides. The maximum horizontal principal stress is inversely proportional to the permeability. The greater the maximum horizontal principal stress, the more detrimental it is to the flow of coalbed methane in the pores, resulting in lower daily gas output. As can be seen from Fig. 8, as the maximum horizontal principal stress in the center of the basin is greater than that in the two wings, the daily gas column of coalbed methane wells in the two wings is significantly greater than that in the central area.

Table 2 Derived minimum and maximum horizontal stress magnitude, and orientation with laboratory and wireline logging.
Full size table
Fig. 7
figure 7

Prediction profile of in-situ stress in well F15.

Full size image
Fig. 8
figure 8

Plane distribution of maximum horizontal principal stress in the southern margin of Junggar Basin.

Full size image

Discussion

Relationship between in-situ stress and fracture

In-situ stress is one of the important parameters evaluating the fracability of coal measure strata. It is closely related to the morphology, trend, occurrence and complexity of fracture network. Generally, for the non-compressional basin, the vertical principal stress of the formation is the vertical stress of gravity. It is equal to the overlying formation pressure29,30. The vertical principal stress is mainly estimated by the integral of density logging, which could be referred to Eq. 1. On the basis of calculating the vertical principal stress, a model describing the three-way in-situ stress is deduced based on the generalized Hooke’s law of isotropic bodies and the additional component of stress, and then the maximum and minimum horizontal principal stress could be calculated31,32,33. The maximum and minimum horizontal principal stresses are generated on the condition of vertical principal stress. When the formation is homogeneous, the maximum and minimum horizontal principal stresses are equal, as presented in Eq. 7. However, the actual formation is usually heterogeneous, resulting in the difference between the maximum and minimum horizontal principal stresses, as presented in Eq. 2. It considers horizontal tectonic movement, pore pressure, and formation heterogeneity, and accords with the properties of the actual formation.

$${\sigma _H} - {P_p}={\sigma _h} - {P_p}=\frac{v}{{1 - v}}\left( {{\sigma _V} - {P_p}} \right)$$
(6)

Owing to the strong difference of sedimentary environment, the coal measure strata is characterized as complicated lithology. There are obvious differences in the in-situ stress among different lithologies. The smaller the horizontal principal stress difference is, the more easily complex cracks are formed. The morphology, structure and conductivity of pressure fractures are affected by formation in-situ stress conditions34,35. When the difference of horizontal principal stress is small, fractures are easy to propagate along multiple directions, which is conducive to forming the sufficient fracture network36. With the increase of the horizontal principal stress difference, the control effect of the ground stress on the fracture is gradually enhanced. At this time, the fracture mainly expands along the direction of the maximum horizontal principal stress, and the fracture morphology is relatively simple37,38. The numerical simulation results indicate that3, when the difference coefficient of horizontal principal stress is less than 5 MPa, the more obvious the trend of complex fracture network is, and the greater the difference of horizontal principal stress is, and the more obvious the directivity of compressive fracture extension along the direction of maximum horizontal principal stress is.

Longitudinally, there are bulkhead layers of mudstone and sandstone with larger thickness (greater than 2 m) in the coal measures of Xishanyao Formation. The compressive strength of the bulkhead layers is greater than that of the coal seam. The average compressive strength of mudstone, sandstone and coal seam is 87.5 MPa, 69.2 MPa and 20.1 MPa respectively. It can be seen that the sandstone and mudstone barrier play an important role in hindering the longitudinal extension of fractures in coal seam, which is not conducive to the longitudinal extension of fractures. Therefore, when hydraulic fracturing is conducted in the coal seam of Xishanyao Formation, the fractures are mainly interlayering extension. It is difficult to generate cross-layer extension and interlayer interference in the fracturing process.

It can be seen from Fig. 4 that the difference of horizontal principal stress of strata with different lithologies is significantly different. The horizontal principal stress difference of coal seam of number 3, 4, 5, 6 and 7 is all less than 7 MPa, while the horizontal principal stress difference of mudstone is the largest, with mean of 12.6 MPa, followed by sandstone, with mean of 11.3 MPa.

The morphology of pressure fractures in the strata with three different lithologies is analyzed. Generally, the fracture morphology is commonly characterized by the difference coefficient of horizontal stress Kh, namely:

$${K_h}=\left( {{\sigma _{\hbox{max} }} - {\sigma _{\hbox{min} }}} \right)/{\sigma _{\hbox{min} }}$$
(7)

Taking well location F15 as the example, mudstone formation at 796.0–821.0 m was selected for fracturing. The horizontal principal stress was 49.6-71.3 MPa, elastic modulus was 1.93-3.37GPa, and Poisson’s ratio was 0.196–0.251. The Kh of the formation was calculated to be 0.447, larger than 0.3. When the Kh is greater than 0.3, complex fracture network could not be generated by hydraulic fracturing (Fig. 9).

Fig. 9
figure 9

Relation between the difference coefficient of horizontal stress and fracture network.

Full size image

The sandstone at 928.5–932.1 m is selected for fracturing. The mean of maximum horizontal principal stress of this layer is 56.7 MPa, the mean of minimum horizontal principal stress is 40.6 MPa. The Kh is 0.399 and greater than 0.3. The fracture morphology formed by hydraulic fracturing in the sandstone are mainly single and cannot generate complex fracture network system. When the coal seam of number 3 is selected for fracturing, the mean of the minimum horizontal principal stress is 32.6 MPa, the mean of the maximum horizontal principal stress is 41.7 MPa. The Kh is 0.279, and less than 0.3. Therefore, complex fracture network is easily formed during the fracturing process of the coal seam of number 3. Microseismic monitoring is conducted on the fracturing process of this layer (Fig. 10). The monitoring results can confirm that the fracture network system formed by artificial fracturing in this coal seam has good structure, more microseismic events, and the fracture area can reach 20-38m2.

Fig. 10
figure 10

Microseismic monitoring of hydraulic fracturing.

Full size image

Relation between in-situ stress and the trend of natural fracture

Wang divided the in-situ stress states into three categories39. The type of in-situ stress that is easy to generate vertical tensile cracks is type III (\(\:{{\upsigma\:}}_{\text{H}}>{{\upsigma\:}}_{\text{V}}>{{\upsigma\:}}_{\text{h}}\)), moreover the direction of expansion is consistent with the direction of the maximum horizontal principal stress. But the ability of longitudinal extension of this kind of fracture is relatively weak, and the transverse propagation is relatively strong. The state of Type I is \(\:{{\upsigma\:}}_{\text{V}}>{{\upsigma\:}}_{\text{H}}>{{\upsigma\:}}_{\text{h}}\), and is also easy to generate vertical tensile fracture. The direction of expansion is consistent with the direction of the maximum horizontal principal stress. According to the predicted results, the stress state in the studied area is type III, and the lateral expansion ability of natural fractures is strong.

Tectonic stress is the fundamental driving force for the formation of cracks. When the direction of in-situ stress is consistent with the direction of cracks, in-situ stress has a secondary transformation effect on natural cracks, and has good protection effect on the opening and permeability of natural cracks. When the natural crack is compressed by the in-situ stress, its conduction capacity will be reduced correspondingly, which is not conducive to gas migration40. The formation at the high ground stress area is compressed, and the opening of natural fractures decreases with it41. The permeability decreases exponentially with the increase of the horizontal principal stress42. Moreover, the in-situ stress controls the development of pore and fractures, and then affects the permeability of coal reservoir43. It can be seen from Fig. 11 that the fracture trend in the studied area is basically consistent with the current in-situ stress direction. Although it has some difference, the difference is not large. The current in-situ stress direction is conducive to the secondary transformation of natural fractures, and the fractures maintain good opening. According to the analysis of wave velocity anisotropy and paleomagnetic data, the maximum horizontal principal stress direction in the studied area is near NE56.6°-82.0°. Therefore, the fractures whose trend is more consistent with the in-situ stress direction in the studied area are dominant fractures.

Fig. 11
figure 11

Imaging logging of pressure fracture in well F15 and Well F16. (a) Pressure fracture in well F15 at 900 ~ 911 m, with fracture strike NE75.6°; (b) Pressure fracture in well F16 at 811 ~ 823 m, with fracture strike NE80.7°.

Full size image

Conclusions

The principal stress calculation model is established based on logging parameters, and the in-situ stress characteristics of coal measures in Xishanyao Formation, southern margin of Junggar Basin are concluded by combining differential strain analysis on the principal stress direction, wave velocity anisotropy and paleomagnetic analysis method.

  1. (1)

    The maximum horizontal principal stress of coal measures in Xishanyao formation is 37.5-51.5 MPa. The minimum horizontal principal stress is 28.1-46.3 MPa. The maximum horizontal principal stress direction is NE56.6°-82.0°. It has obvious difference in the in-situ stress and difference of horizontal principal stress between different lithologies. When the horizontal stress difference coefficient of mudstone and sandstone is greater than 0.3, hydraulic fracturing cannot generate complex fracture network. While the horizontal stress difference number of coal seam is less than 0.3, it can form a complex fracture network.

  2. (2)

    Compared with the laboratory test, the error of the in-situ stress predicted by the logging method is less than 8%, thus the model can be applied to the evaluation of in-situ stress in this area;

  3. (3)

    The distribution of horizontal principal stress in the southern margin of Junggar Basin are small on two wings and large in the center. The daily gas column of CBM in the center area is smaller than that on two wings;

  4. (4)

    The stress type in the studied area is type III. It is conducive to maintaining good open state and flow conductivity of natural fractures, and is also conducive to vertical tensile fracture caused by hydraulic fracturing. The generated compressive fracture has strong lateral expansion ability.