Introduction

Many salts, known as ionic liquids (ILs), remain in a liquid state at near-ambient conditions, in contrast to table salt, which maintains its crystalline form up to approximately 1074 K1,2. Ionic liquids (ILs) have garnered considerable scientific and commercial interest due to their numerous advantageous features. As a new class of compounds, ILs have been a prominent research topic for three decades, with a rapidly increasing number of publications3,4. Characteristically, ILs are salts that exist as liquids at or near ambient temperatures, typically exhibiting low melting points, often below 100 °C5,6. These compounds consist entirely of ionic species and can be classified into various categories based on their properties and synthesis methods7,8,9. ILs have high thermal decomposition temperatures, around 473 K, and their boiling points are not commonly recorded. Additionally, their specific gravities range from 1.1 to 1.6, positioning them below the water layer in biphasic extraction7,10,11. ILs can consist of numerous cations and anions, often characterized by significant differences in ionic size and asymmetrical ions, resulting in low melting points. Typically, they are composed of quaternary ammonium cations, such as 1-butyl-3-methylimidazolium or N-butylpyridinium, paired with inorganic anions like tetrachloroaluminate or tetrafluoroborate. ILs can be formed from discrete cation-anion pairs or deep eutectics made from various mixtures. By carefully selecting the cations and anions, numerous ILs can be tailored for specific applications12,13,14. Producing ionic liquids requires organic cations in combination with either inorganic or organic anions15,16,17,18.

ILs serve as eco-friendly solvents for various industrial applications, including chemical synthesis, catalysis, biocatalysts, nanomaterial synthesis, fuel cells, chemical sensors, dye-sensitized solar cells, porous solid production, and separation technologies19,20,21,22. Their properties depend on the nature and size of their cation and anion components. To develop new processes using ILs or their mixtures, a thorough understanding of their transport, physicochemical, and thermodynamic properties is essential23,24. A significant barrier to the industrial adoption of ILs is the limited knowledge of their physicochemical characteristics and structure20,21. Few studies have focused on calculating the critical properties of ILs using Molecular Dynamics (MD) simulations22,23,24,25. ILs begin to decompose as their temperature approaches the normal boiling point. However, some thermodynamics models, such as semi-empirical and cubic equations of state, require these critical properties for modeling processes involving ILs, necessitating their derivation from theoretical models26,27,28,29,30,31,32. For example, Rebelo et al.33 determined the critical normal boiling temperatures of 15 ILs using empirical equations and experimental data on IL density and surface tension. Valderrama et al.34,35,36 calculated the acentric factor, normal boiling point, critical pressure, critical volume, and critical temperature of 250 ILs through the group contribution method, assessing the consistency and accuracy of their results by computing the bubble point pressure of IL-CO2 binary systems and IL density. Bagheri and Mohebbi37, along with Shariati et al.38, employed vapor-liquid equilibrium data of IL-solvent systems with the Patel-Teja and Peng-Robinson equations and genetic algorithms to derive the acentric factor, critical pressure, critical volume, and critical temperature of several ILs. Recently, MD simulations have been applied to calculate various properties of ILs, including liquid density, diffusion coefficient, heat capacity, surface tension, latent heat of vaporization, viscosity, thermal conductivity, and excess properties34,35,36,37,38,39,40,41,42,43,44,45,46,47. Sattari et al.48 estimated the critical temperatures of 106 ILs using the Guggenheim equation, group contribution, and Quantitative Structure-Property Relationship (QSPR) model. They found that the insufficient database for ILs critical temperatures results in models with poor predictive ability. Similarly, Weiss49 examined the molar enthalpy of vaporization and critical temperatures for various fluids, including simple, polar, and ILs, using Guggenheim’s rule. The properties of [C2mim][NTf2], [omim][NTf2], and [hmim][NTf2] were calculated, revealing that while simple fluids align with Guggenheim’s predictions, polar and ionic liquids deviate significantly. Ghatee et al.50 studied IL critical temperatures by analyzing surface tension data between 293 and 393 K. Their use of scaling-law, Guggenheim, and Eötvös approaches indicated that critical temperatures are influenced by cation type, alkyl chain length, and anion type, with anions generally leading to higher critical temperatures. Their research links critical temperatures to interaction energy derived from quantum mechanical density functional theory, offering insights into IL properties for industrial applications.

Weiss51 conducted classical MD simulations to investigate the liquid-vapor equilibrium of [C4mim][PF6], optimizing the OPLS-type force field for particle interactions. The simulations, carried out at temperatures from 300 to 1075 K over 25 ns, yielded critical properties of pc = 3.1 ± 1.4 bar, Tc = 1105 ± 25 K, and ρc = 227 ± 19 kg/m3. Polishuk et al.52 derived critical properties for seven ILs using chain-particle chain-statistical associating fluid theory, which closely matched the Tc and pc values for the solutes. They noted that critical constants influence phase equilibria, with increased asymmetry leading to reduced solubility. Their model effectively predicted solubility trends, emphasizing the relationships among critical constants and phase equilibria while excluding association and polarity effects. Rai and Maginn53 estimated critical pressure, critical temperature, density, compressibility factor, normal boiling point, and enthalpy of vaporization for imidazolium-based ionic liquids ([Cnmim][BF4], n = 1, 2, 4, 6) using Gibbs ensemble Monte Carlo (MC) simulation. Their findings indicated that these properties decreased with longer cation alkyl chains, contrasting with trends observed in other nonionic polar and alkane compounds. MC simulations are generally easier to construct than MD simulations, especially for complex particle models. However, MD simulations offer significant advantages, particularly for studying dynamical features like temporal correlation functions and relaxation to equilibrium. In complex systems, MD is effective for determining the structural and thermodynamics parameters that influence molecular behavior. Properties of ILs, including density, heat capacity, thermal conductivity, and viscosity, have been measured under various experimental conditions.

This study employed MD simulations based on the binary mixture concept to determine the critical temperature, pressure, and density of 1-butyl-3-methylimidazolium tetrafluoroborate ([C4mim][BF4]). First, to validate the method, we calculated the critical properties, density, and heat capacity at constant pressure for pure water, pure ethanol, and their mixture, comparing these results with experimental data. Subsequently, we identified the critical points of [C4mim][BF4] and examined its behavior near the critical point as a binary mixture.

Methodology

Critical region

Systems near the critical point are categorized by universality classes, where systems within the same class share identical scaling functions and critical exponents. Critical behavior is best described using field variables that remain consistent across co-existing phases54,55,56. Near the critical point (CP), minor changes in temperature or pressure can cause significant alterations in density, greatly affecting the substance’s structure due to the transition from sub- to supercritical conditions57,58,59,60. At the CP, the densities of the gas and liquid phases equalize, merging into a single phase known as supercritical fluid (SCF), which exists above the CP in terms of pressure and temperature. SCFs lack surface tension, as there is no liquid/gas interface58,61. Near the CP, density fluctuations due to long-range molecular correlations result in unique properties in both pure and mixed systems. Certain properties, including thermal compressibility, thermal conductivity, isobaric heat capacity, and sound speed, can change rapidly with slight adjustments in conditions. For example, at the CP with ρ = ρc, the heat capacity can approach infinity as the temperature nears the critical value59,62,63,64.

Molecular dynamics details

Fluid properties can be determined through various methods, with a common approach being the establishment of an equation of state (EoS) that includes molecular details. Cubic EoS often accurately represents gas phase data, it may significantly deviate in liquid phase density calculations30,31. Near the critical region, the accuracy of the cubic EoS for thermodynamic properties diminishes27,29, necessitating the use of new methods like molecular dynamics (MD) simulations.

In molecular dynamics (MD) simulations, the NVT and NpT ensembles are frequently used to examine particle behaviour under various conditions. NVT, which stands for Constant Number of particles (N), Volume (V), and Temperature (T), features a fixed simulation box volume, enabling the study of density-invariant systems65,66. Temperature is held constant through thermostats like the Nosé-Hoover or Langevin, making it ideal for investigating thermal equilibrium, phase transitions, and temperature-dependent properties67,68,69,70. Conversely, NpT maintains a Constant Number of particles (N), Pressure (P), and Temperature (T). Here, a barostat, such as the Parrinello-Rahman or Berendsen, regulates pressure, allowing the simulation box volume to adjust accordingly36,71,72. Like the NVT ensemble, the temperature remains constant with a thermostat to ensure thermal equilibrium. NpT is suitable for exploring systems under controlled pressure and temperature, such as liquids, gases, and solids under pressure, and is useful for studying phase behaviour and compressibility39,73,74.

MD simulations employ a detailed model of interatomic interactions to accurately track the movement of atoms within proteins or other molecular systems over time40,70. These simulations effectively illustrate a wide range of important chemical processes and provide precise atomic positions with femtosecond resolution. The core principle of MD simulations is straightforward: by determining the coordinates of all atoms in a molecular system, one can calculate the forces acting on each atom from all others24,69,73. Newton’s equations of motion are then used to update the position and velocity of each atom over time. These simulations are powerful for several reasons. They capture the exact location and movement of each atom at all times, a feat difficult to achieve experimentally. Additionally, the simulation conditions are well-defined and can be carefully controlled. By comparing simulations under different conditions, one can assess the effects of various molecular perturbations49,50,51,69,70,71,72,73,74.

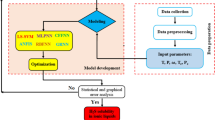
In this study, all MD simulations were run using Nanoscale Molecular Dynamics (NAMD)82 software (version 2.12) (URL link: https://www.ks.uiuc.edu/Research/namd/). To simulate pure water, a box with 3921 H2O molecules was used; for ethanol, a box with 1000 ethanol molecules; and for [C4mim][BF4], a box with 1000 cation-anion pairs. To model a water-ethanol binary mixture at a 0.5 water mole fraction, a 90 × 90 × 90 ų box containing 3921 H2O and 3921 ethanol molecules was employed in NpT ensemble simulations. The critical properties of [C4mim][BF4] were calculated using both NpT and NVT ensembles. For the NVT simulations, a cell with 1000 [C4mim][BF4] molecules (90 × 90 × 90 ų) was placed in a larger box (270 × 90 × 90 ų) and subjected to varying temperatures, constant volume, and periodic boundary conditions. The Chemistry at Harvard Macromolecular Mechanics (CHARMM) force field parameters were used for water and ethanol simulations, while the optimized potentials for liquid simulations (OPLSAA) force field parameters were utilized for [C4mim][BF4], later converted to CHARMM parameters. The simulations were conducted in NpT and NVT ensembles with periodic boundary conditions, using the Langevin dynamics method to maintain the desired temperature and the Langevin Piston method to keep the pressure constant. To enhance comprehension of the study process, the flow-process diagram based on MD simulation for pure component (water or ethanol) and binary mixture (water-ethanol mixture or [C4mim][BF4] IL) is illustrated in Fig. 1 and more details are given in the Supplementary file.

Fig. 1
figure 1

The flow-process diagram of MD simulation for pure component (a) and binary mixture (b).

Full size image

The primary reason for the significantly larger number of water molecules compared to ethanol in the MD simulations lies in the density and molecular structure of these substances. Water molecules are smaller and lighter than ethanol molecules. Water has a molecular weight of about 18 g/mol, while ethanol is around 46 g/mol. This means that, in a given volume, there are more water molecules than ethanol molecules due to their smaller size. In molecular dynamics (MD) simulations, the number of molecules is set to fit a specific volume. Since water is denser (1.0 g/cm³) than ethanol (0.789 g/cm³), more water molecules must match their respective densities in the simulation. A larger number of smaller water molecules ensures better statistical sampling and a more accurate representation of thermodynamics properties in simulations. This is crucial for obtaining reliable results, particularly for properties like radial distribution functions, diffusion coefficients, and heat capacities. Simulating a larger number of smaller molecules (water) can sometimes be computationally more efficient and produce smoother and more accurate results for certain properties. This is because smaller molecules move and interact more frequently within the same simulation time, providing more data points for analysis.

The decision to use both NpT and NVT ensembles for MD simulation of ionic liquids, but not for pure water or ethanol, is due to the distinctive properties of ionic liquids compared to simpler fluids. ILs like [C4mim][BF4] comprise large, complex ions that exhibit strong electrostatic interactions, resulting in unique structural and dynamic characteristics. These substances often show complex phase behaviours, such as varying melting and boiling points and multiple critical points from different ionic species. Consequently, a more thorough simulation approach is required. The NpT ensemble allows for volume fluctuations in the simulation box, which is essential for capturing the pressure-dependent properties and phase behaviours of ILs23,52. This method aids in understanding how ILs respond to pressure changes, which is critical for their industrial applications. Additionally, the NpT ensemble is valuable for identifying phase transitions and critical points by analysing density and volume variations at different pressures and temperatures. The NVT ensemble maintains a constant temperature, crucial for examining the equilibrium properties of ILs at specific temperatures, allowing for insights into structural and dynamic behaviours without the influence of volume changes. It is used to calculate properties like heat capacity and radial distribution function (RDF) at constant temperature, illuminating molecular interactions and thermal properties49,71. Water and ethanol, as simpler molecules, exhibit well-defined phase behaviours and fewer complex interactions, making either the NpT or NVT ensemble suitable depending on the property studied. Researchers may target specific properties such as phase transitions, density, or heat capacity using the ensemble that aligns best with their objectives. Typically, the NpT ensemble suffices for capturing phase behaviours, while the NVT ensemble is reserved for equilibrium studies.

The simulation times were set to 4 ns for water and ethanol in NpT ensembles, 8 ns for the IL in NpT and 16 ns in NVT ensembles, all using a 1 fs time step. The cutoff radius for potential calculations was 16 Å for water and ethanol and 18 Å for the IL. Near the critical point, non-bonded force fluctuations (van der Waals and electrostatic) increase significantly, causing sudden volume changes and intense energy oscillations in constant-pressure simulations, leading to system instability. For ILs, the charged nature of ions exacerbates these fluctuations. To mitigate this, two parameters in the NAMD software were adjusted: the oscillation period (LangevinPistonPeriod) and the oscillation damping (LangevinPistonDecay). Increasing the oscillation period enhances system inertia by effectively increasing piston mass, while the damping parameter reduces fluctuations from non-bonded forces.

The Particle Mesh Ewald (PME) method was used to calculate electrostatic forces beyond the potential cutoff radius. In NAMD simulations, since the software grids the box size at the beginning, any expansion of the box during NpT ensemble simulations increases errors in these calculations, especially in ionic liquids due to cation and anion interactions. To minimize error, the initial box size must be maximized, ensuring that the simulation box size remains smaller throughout the simulation. NpT ensemble simulations were conducted at various constant pressures (e.g., 50 bar) and temperatures ranging from 550 to 750 K. Visual Molecular Dynamics (VMD 1.9.2) software (URL link: http://www.ks.uiuc.edu/Research/vmd/) was utilized to observe results and create energy graphs and radial distribution functions. The heat capacity at constant pressure was calculated using Eq. (1):

$$\:{C}_{P}=(\langle{H}^{2}\rangle-\langle{H}\rangle^{2})/\:{k}_{B}{T}^{2}$$
(1)

where H is enthalpy, kB is Boltzmann constant and T is temperature.

Results and discussion

Pure components: ethanol and water

To identify phase-change and critical points of pure components using MD simulation, we examined variations in the radial distribution function, heat capacity, and density of water and ethanol with respect to temperature and pressure. Figures 2 and 3 show the radial distribution function of water and ethanol at pressures below the critical point, respectively. These figures demonstrate that the radial distribution function reaches a maximum at a specific distance before converging to a stable value as distance increases, with the maximum reflecting the highest local density around the central molecule.

Fig. 2
figure 2

The radial distribution function behavior of water at (a) p = 100 bar and (b) p = 212 bar at different temperatures. Both pressures are lower than pc of water.

Full size image
Fig. 3
figure 3

The radial distribution function behavior of ethanol at (a) p = 50 bar and (b) p = 60 bar at different temperatures. Both pressures are lower than pc of ethanol.

Full size image

Figures 2 and 3 show that, at a constant pressure, the maximum of the radial distribution function and the distance at which this maximum occurs vary with temperature. Below the critical pressure, the maximum value of the radial distribution function decreases with increasing temperature until the phase-change temperature is reached. At this temperature, there is a rapid shift in the radial distribution function, marked by a significant drop in its peak value. As the temperature continues to rise beyond the phase transition, the radial distribution function declines. The radial distribution function is useful for detecting phase transition points. This study generated two types of radial distribution function plots: one with periodic boundary conditions and another with non-periodic boundaries. In the NpT ensemble, the system’s volume fluctuates continuously69. Intense volume fluctuations due to changing boundaries render the radial distribution function plots obtained from periodic boundary conditions less reliable for detecting phase transition points, although they ultimately approach a value of one70. Conversely, the radial distribution function plots from non-periodic boundary conditions offer more accurate phase transition detection, as they do not converge to one71. With non-periodic boundaries, local density at large radii approaches zero due to the absence of mirrored images. Therefore, we focused our analysis on the radial distribution function plots with non-periodic boundary conditions to identify phase transition points.

The heat capacity of a gas is significantly influenced by changes in pressure and temperature. An increase in pressure leads to a rise in the gas’s heat capacity, while a temperature increase results in a decrease in the heat capacity. In contrast, pressure variations have minimal effect on the heat capacity of liquids, which increases with temperature. Near the critical point, heat capacity dramatically rises as pressure approaches critical levels and temperature nears the critical threshold, due to changes in density and enhanced molecular interactions. Additionally, at the phase-change point, the heat capacity of a liquid experiences a discontinuity, reflecting a significant change in the heat required to alter the temperature. This is because the energy supplied is primarily used to break intermolecular bonds rather than to increase temperature. At the critical point, heat capacity diverges, indicating critical fluctuations and limitations of the mean-field approximation75. Figure 4 illustrates the Cp versus T and Cp versus p behaviors of water and ethanol.

Fig. 4
figure 4

The heat capacity behavior of water and ethanol at various pressures and temperatures (water: a-c, ethanol: d, e).

Full size image

If the heat capacity increases with temperature, it indicates that the component behavior is like liquids, namely on the left side of the maximum point. Conversely, a decrease in heat capacity with rising temperature implies gas-like behavior, characteristic of the region beyond the maximum point. Below the critical pressure (Tc = 647.3 K, pc = 220 bar for water; Tc = 516.25 K, pc = 64 bar for ethanol76), the maximum point signifies a phase transition from liquid to vapor; above the critical pressure, it reflects a change in fluid behavior. As pressure rises and moves away from the critical point, the maximum point diminishes until it eventually disappears. The density behavior of water and ethanol with respect to temperature and pressure is depicted in Figs. 5 and 6, respectively.

Fig. 5
figure 5

The density behavior of water at various pressures and temperatures, (a): density versus temperature, (b): density versus pressure.

Full size image
Fig. 6
figure 6

The density behavior of ethanol at various pressures and temperatures, (a): density versus temperature, (b): density versus pressure.

Full size image

At constant pressure, density decreases with increasing temperature (see Figs. 5 and 6). Below the critical pressure, a temperature rise causes a sudden density drop, signaling a phase transition. As pressure approaches the critical point, the density difference between liquid and vapor phases narrows, disappearing entirely at the critical point. Beyond the critical pressure, the density decrease is no longer observable, and with an increase in temperature at constant pressure, the density gradually decreases relative to the vicinity of the critical point. Figures 5 and 6 also show that, at constant temperature, the densities of water and ethanol rise as pressure increases. Below the critical temperature, at constant temperature, an increase in pressure leads to a sudden density rise, indicating a phase change, which is not observed at temperatures above the critical temperature.

As a result, and based on Figs. 2, 3, 4, 5 and 6, it can be observed at the phase-change point, the density and radial distribution function exhibit rapid changes, while heat capacity reaches a maximum. As the critical point is approached, the sharp changes in density and radial distribution function diminish, yet the peak in heat capacity increases, with maximum heat capacity occurring at the critical point. The calculated values for the density and heat capacity of water and ethanol at T = 298 K and p = 1 bar are listed in Table 1, based on MD simulation.

Table 1 Calculated values for density and heat capacity of water and ethanol using MD simulation.
Full size table

As one can see from Table 1, there is a good agreement between the MD simulation results and experimental data. Moreover, the critical properties of water and ethanol were calculated using MD simulation. Table 2 provides the obtained results. As observed in this table, there is a good agreement between the calculated critical properties and those of the experimental data.

Table 2 Calculated critical properties of water and ethanol using MD simulation.
Full size table

Binary mixture: Ethanol-water

The heat capacity at constant pressure and density behavior of a 50 mol% ethanol mixture was analyzed. Figures 7 and 8 display the calculated density and heat capacity of the water-ethanol binary mixture, respectively. Figure 7(a) shows that the density decreases linearly with temperature for T < 500 K. However, beyond 500 K and below 140 bar, a sudden drop in density occurs. In Fig. 7(b), the density versus pressure data, where the mixture density gradually increases for p > 140 bar. The critical points of the water-ethanol mixture appear to fall within the ranges of 500 < T(K) < 600 and 50 < p(bar) < 100. Further investigation was conducted on the heat capacity of the water-ethanol mixture.

Fig. 7
figure 7

(a) The density versus temperature and (b) the density versus pressure for water-ethanol binary mixture (water mole fraction = 0.5).

Full size image
Fig. 8
figure 8

(a) The heat capacity versus temperature and (b) the heat capacity versus pressure for water-ethanol binary mixture (water mole fraction = 0.5).

Full size image

In Fig. 8 (a), the highest peak for the water-ethanol mixture for isobar p = 90 bar is at 550 K, while in Fig. 8 (b), the peak for isotherm T = 550 K occurs at 90 bar pressure. Both figures confirm that the mixture’s critical temperature and pressure are 550 K and 90 bar, respectively. Comparing the temperature and pressure at these peaks with the corresponding values of experimental data reveals that the critical point of the water-ethanol mixture occurs at maximum heat capacity. The observed trends in density and heat capacity provide valuable insights into the thermodynamics behavior of the water-ethanol binary mixture, particularly near its critical point. The linear decrease in density with temperature below 500 K, as shown in Fig. 7(a), is consistent with the typical thermal expansion behavior of liquids. However, the sudden drop in density beyond 500 K and below 140 bar suggests a transition to a critical state, where the distinction between liquid and gas phases becomes less pronounced. This behavior is further supported by the density versus pressure data in Fig. 7(b), where the gradual increase in density for pressures above 140 bar indicates that the mixture becomes more compact under higher pressures, as the molecules are forced closer together. This behavior is typical of liquids under compression and further supports identifying the critical point within the specified ranges. Abdurashidova et al.77 reported these values as 106 bar and 553.15 K. Additionally, the calculated critical density from MD simulations was 400 kg/m³, compared to the experimental value of 293.90 kg/m³77.

Ionic liquid: [C4mim][BF4]

The optimized equilibrium structure of [C4mim][BF4] IL, generated using Gaussian 09 W software (Gaussian, Inc. USA), is shown in Fig. 9. Figure 10 displays the computational cells containing 1000 molecules of [C4mim][BF4] IL before and after the MD simulation.

Fig. 9
figure 9

The equilibrium structure of [C4mim][BF4] IL from Gaussian 09 W software.

Full size image
Fig. 10
figure 10

The computational cell contains 1000 molecules of [C4mim][BF4] IL, (a) before starting the MD simulation, (b) at the end of MD simulation. The pictures of (a) and (b) were generated by VMD 1.9.2 software. URL link: http://www.ks.uiuc.edu/Research/vmd/.

Full size image

For NpT ensemble simulations, the following assumptions are made: (1) Each ionic liquid molecule consists of an anion and a cation held together by a strong ionic bond. (2) In molecular dynamics (MD) simulations, forces are categorized into binding and non-binding; ionic bonds are treated as part of the unconnected electrostatic forces. As a result, each IL is modeled as a binary mixture with equal numbers of cations and anions. (3) In a binary system under pressures below critical pressure, phase changes occur over a range of temperatures rather than at a specific point. High polarity in the components may lead to azeotropic behavior at certain pressures, particularly pronounced in ILs. (4) In a binary system with distinct components, each component has its own critical temperature and pressure, while the binary mixture exhibits unique critical parameters depending on its composition. At the critical point, long-range electrostatic fluctuations are more intense, resulting in abrupt changes in heat capacity. Thus, an IL possesses three critical points: one for the cation, one for the anion, and one for the cation-anion mixture, with noticeable heat capacity changes at each critical transition.

This study assumes a binary system with equal numbers of [C4mim] and [BF4] ions to calculate the critical points of [C4mim][BF4]. The strong electrostatic forces between the cations and anions in [C4mim][BF4] may obscure observable properties of the binary system. Nevertheless, ionic liquids behave like binary systems, with cations and anions remaining paired in the gas phase after a phase change. To determine the critical points of [C4mim][BF4], we examined the variations in the radial distribution function, density, and heat capacity of the ionic liquid with temperature. The behavior of the radial distribution function of [C4mim][BF4] is shown in Fig. 11. This behavior is similar to water and ethanol radial distribution functions.

Fig. 11
figure 11

The radial distribution function behavior of [C4mim][BF4] at (a) p = 8 bar, (b) p = 11 bar and (c) p = 16 bar.

Full size image

Figure 11 (a) demonstrates that below the critical pressure (p = 8 bar), increasing temperature significantly reduces the peak of the radial distribution function (RDF), indicating a phase change. As the temperature approaches the phase change, the RDF shifts, marked by a notable decline in peak value. After surpassing the phase transition, the RDF continues to decrease. At pressures of 11 bar and higher (Fig. 11 (b) and (c)), the distance between RDF curves narrows, and the rapid decline in the RDF is absent. Similar trends were previously observed for water and ethanol (Figs. 2 and 3).

Figure 12 shows the calculated densities of [C4mim][BF4] in both gas and liquid states at various temperatures. It indicates that the critical temperature for [C4mim][BF4] exceeds 1350 K. Additionally, the results of Hernandez et al.78 for this ionic liquid are also included in Fig. 12 for comparison. The data show a good agreement between our findings and those of Hernandez et al.78, who simulated 250 IL molecules. However, due to their smaller system size, they could only observe phases up to approximately 1150 ± 10 K and calculate the corresponding densities. They predicted higher temperature densities through a curve-fitting method.

Fig. 12
figure 12

The calculated densities of [C4mim][BF4] for its gas or liquid state at different temperatures.

Full size image

In this study; however, due to the use of 1000 ionic liquid molecules, the density of each liquid and vapor phase was predicted up to a temperature of 1350 ± 10 K. Based on the density distribution behavior, it can be observed that with an increase in temperature at a constant volume, the volume of the liquid present in the system increases, while the volume of the gas decreases. This indicates that the system transitions from gas to liquid when heated. In thermodynamics processes at constant volume, if the system’s density is below the critical density, heating the system will ultimately lead it to the vapor state, whereas if the system’s density exceeds the critical density, heating it at constant volume will cause the liquid surface to rise until the entire system becomes liquid. Therefore, it can be concluded that the critical density of the [C4mim][BF4] must be less than 210.6 kg/m3.

Figure 13 illustrates the density behavior of [C4mim][BF4] with temperature at various pressures. At low pressures, the phase-change point and the distinctions between liquid and vapor phases are clearly identifiable (Fig. 13(a)). As pressure approaches the critical point, these differences diminish, and at the critical point (around p = 11 bar and above), no phase change is observed (Fig. 13(b)). For pressures greater than the critical pressure, density steadily decreases with temperature and no phase change occurs (Fig. 13(c)).

Fig. 13
figure 13

The density versus temperature for [C4mim][BF4] at various pressures: (a) p = 6–8 bar, (b) p = 10–12 bar and (c) p = 12, 13 and 16 bar.

Full size image

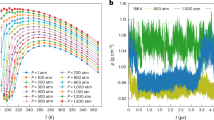
The heat capacity and density behaviors of [C4mim][BF4] against temperature are shown in Fig. 14. According to Fig. 14(a) and (b) and at p = 6 and 7 bar, the heat capacity of the liquid phase shows small fluctuations due to energy fluctuations and the averaging error of energy variations. In contrast, these fluctuations are lesser for the vapor phase. A notable jump in heat capacity occurs at 8 bar and 1370 K (Fig. 14(c)), signifying intense energy fluctuations and potentially indicating the first critical point for [C4mim][BF4], which has a density of 99.209 kg/m³ under these conditions. As pressure increases from 8 to 11 bar (Fig. 14(c)-(f)), the peak of the initial jump diminishes, but a new jump appears at 1400 K, reaching its maximum at approximately 11 bar (Fig. 14(f)). The density of [C4mim][BF4] at the specified pressure and temperature is 147.647 kg/m³ (Fig. 14(f)). With increasing pressure, a new discontinuity is observed at a pressure of 13 bar and temperature of 1425 K and the density increases to 161.874 kg/m3 (Fig. 14(h)). As pressure rises to 21 bar, the peak of the density jump gradually decreases (Fig. 14(n)).

Fig. 14
figure 14figure 14

The heat capacity and density versus temperature for [C4mim][BF4] at various pressures, (a) p = 6 bar, (b) p = 7 bar, (c) p = 8 bar, (d) p = 9 bar, (e) p = 10 bar, (f) p = 11 bar, (g) p = 12 bar, (h) p = 13 bar, (i) p = 14 bar, (j) p = 15 bar, (k) p = 16 bar, (l) p = 17 bar, (m) p = 19 bar and (n) p = 21 bar.

Full size image

The density graphs used to determine Tc and Pc for the IL at pressures up to 11 bar and temperatures up to 1400 K show a phase change. However, this phase change is not visible in the density graphs at pressures and temperatures exceeding the mixture’s critical points. At a pressure of 13 bar and a temperature of 1425 K—conditions that exceed the critical point of the mixture—no phase change occurs. However, the heat capacity at this pressure and temperature reaches its maximum peak beyond 1400 K and 11 bar, which corresponds to the mixture’s critical point. This suggests that the observed point may represent the third critical point. Below the critical points of the mixture, two phase changes were observed: one at the first critical point (p = 8 bar and T = 1370 K) and another at the second critical point (p = 11 bar and T = 1400 K).

The observed behaviors of [C4mim][BF4] in Figs. 11, 12, 13 and 14 highlight the complex interplay between temperature, pressure, and phase transitions in this ionic liquid. The radial distribution function, density and heat capacity trends provide critical insights into the thermodynamics properties of [C4mim][BF4], particularly near its critical points. At pressures below the critical point (p < 11 bar), the liquid-vapor phase transition is well-defined, with distinct density changes and heat capacity jumps corresponding to the phase change. The first critical point, identified at 8 bar and 1370 K, marks a significant transition in the system’s behavior, characterized by a sharp increase in heat capacity and a corresponding density of 99.209 kg/m³. As the pressure increases beyond the first critical point, the system exhibits additional critical-like behavior, with new heat capacity jumps and density discontinuities emerging at higher temperatures and pressures. For instance, at 11 bar and 1400 K, a second critical point is suggested by the peak in heat capacity and a density of 147.647 kg/m³. This trend continues at even higher pressures, such as 13 bar and 1425 K, where another discontinuity is observed, accompanied by a further increase in density to 161.874 kg/m³. These successive critical points indicate that [C4mim][BF4] undergoes multiple phase transitions or critical-like phenomena under varying thermodynamics conditions. At pressures exceeding 21 bar, the density jumps gradually diminish, suggesting that the system is approaching a supercritical state where the liquid and vapor phases are indistinguishable. In this regime, the density decreases smoothly with temperature, and no phase transitions are observed. This behavior aligns with the general characteristics of supercritical fluids, where the system exhibits properties intermediate between those of a liquid and a gas.

Therefore, MD simulations reveal that [C4mim][BF4] behaves like a binary mixture, identifying three critical points for the compound. The first and third critical points correspond to the [C4mim] anion and [BF4] cation, but it is unclear which point pertains to which species. The numerical values are as follows: first point (Tc = 1370 K, pc = 8 bar, ρc = 99.209 kg/m3, from Fig. 14(c)); second point for [C4mim][BF4] (Tc = 1400 K, pc =11 bar, ρc = 147.647 kg/m3, from Fig. 14(d), (e), and (f)); third point (Tc = 1425 K, pc = 13–14 bar, ρc = 161.874 kg/m3, from Fig. 14(g), (h)). Table 3 provides the second critical point obtained from MD simulations. The second critical point; however, is associated with the [C4mim][BF4] ionic liquid and has been chosen as its main critical point. Additionally, Table 3 compares these findings with existing literature. While the 19% error observed in the water-methanol system provides a useful benchmark, it cannot be directly assumed that the same error range applies to ionic liquids due to their unique and complex molecular interactions. Additionally, different simulation approaches can produce varying results for critical properties. Conversely, since experimental data may not be available for all aspects of ionic liquid behavior, validating our method against well-characterized mixtures (e.g., water-ethanol) helps establish its reliability within certain limits. As highlighted in Table 3, different methods can lead to considerable variations in the predicted critical properties, which underscores the need for caution when interpreting these results. Therefore, the critical properties calculated for the ionic liquid will vary considerably depending on the approach used to simulate the properties. To ensure the critical points associated with the anion, cation, and ionic liquid (as a mixture) are accurately identified, several system behaviors at each critical point must be analyzed. Initially, the temperature and pressure at which the heat capacity peaks are determined, as such a peak typically indicates a critical point. The largest peak is often linked to the critical point of the ionic liquid, reflecting significant energy fluctuations from long-range interactions. Subsequently, the radial distribution function (RDF) at various temperatures and pressures surrounding each critical point is evaluated. At the mixture’s critical point, the RDF should reveal distinct changes that signify phase behavior across different conditions, capturing the collective behavior of both cations and anions. Furthermore, the variation in density with temperature and pressure is assessed. At the mixture’s critical point, density changes are more pronounced due to the combined effects of both ionic species, and the difference between liquid and vapor phase densities becomes negligible. Finally, to verify the critical points, results are cross-referenced with existing literature on [C4mim][BF4] or similar ionic liquids, as prior studies provide valuable insights into the correspondence of critical points to specific species, thereby enhancing reliability.

Table 3 Calculated the critical properties of [C4mim][BF4] IL using MD simulations and compared the results with existing studies.
Full size table

The composition of a binary mixture significantly affects its critical properties, including critical temperature, critical pressure, and critical density83. These properties are crucial in understanding phase behavior, fluid dynamics, and thermodynamics interactions within the mixture84. In pure substances, the critical point is well-defined and corresponds to the highest temperature and pressure at which liquid and vapor phases can coexist. For mixtures; however, the critical point becomes more complex due to the interaction between different components. The critical temperature of a binary mixture is influenced by the individual critical temperatures of the pure components and their interaction. In total, as the composition changes, the effective critical temperature of the mixture can either increase or decrease, depending on the nature of the components and their interactions85. For instance, when one component of the mixture is a light gas and the other is a heavy liquid, increasing the amount of the heavier component (which has a higher Tc) can potentially elevate the critical temperature of the mixture. Conversely, if the mixture consists of two components with considerable interaction and similar molecular weights, the critical temperature may decrease due to the dominance of weaker interactions86. The critical pressure of a binary mixture is notably affected by intermolecular interactions and the relative proportions of the components. Mixtures often display critical pressures that do not follow a straightforward linear interpolation between the critical pressures of the pure components. Observed behaviors can be complex due to the presence of strong hydrogen bonds or van der Waals forces that modify how the components interact at the critical point. Increasing the proportion of a component with a higher critical pressure in the mixture tends to shift the critical pressure of the mixture upward. For instance, in mixtures where one component is a polar molecule and the other non-polar, the polar molecules can significantly alter the vapor pressure and hence the critical pressure of the overall mixture5. The Van Konynenburg and Scott theory explains that the critical point of a mixture depends on the composition and interactions between the components. The critical point shifts with changes in composition, leading to phenomena like critical end points and upper critical solution temperatures. The Van Konynenburg and Scott theory provides a comprehensive framework for understanding the phase behavior of binary mixtures, which can be extended to explain how composition affects critical properties in mixtures. This theory is based on a global phase diagram that categorizes different types of phase behavior into six main categories (Types I to VI) depending on the intermolecular interaction parameters between components6. The critical points and lines in binary mixtures are influenced by the composition, as they connect the pure component critical points or terminate at critical endpoints. The van der Waals equation of state, often used in this context, shows that changes in composition can lead to variations in the shape and continuity of these lines87,88,89. Van Konynenburg and Scott classified phase behavior based on the shape and characteristics of the coexistence curves in the phase diagram. In total, the interplay between composition and critical properties in binary mixtures is a multifaceted subject that requires consideration of molecular characteristics, interactions, and thermodynamic principles. The critical behavior of a mixture can be predicted effectively through a combination of experimental data and theoretical models. The composition of a binary mixture plays a crucial role in determining its critical properties. Understanding these relationships is crucial for applications in chemical engineering, materials science, and physical chemistry86,90. This framework is applicable to ionic liquids due to the significant influence of their complex anion-cation interactions on critical properties.

Replacing the anion tetrafluoroborate ([BF₄]⁻) with tetrachloroaluminate ([AlCl₄]⁻) while retaining the same cation ([C4mim]⁺) can significantly affect the ionic liquid’s critical points. [BF₄]⁻, being smaller and more symmetric, generally leads to higher liquid density, while the larger, less symmetric [AlCl₄]⁻ may result in lower density. The smaller size and symmetry of [BF₄]⁻ contribute to a lower heat capacity due to simpler interactions, whereas the larger size and asymmetry of [AlCl₄]⁻ can increase heat capacity from more complex interactions and stronger Coulomb forces81. Additionally, [BF₄]⁻’s symmetry may result in lower compressibility due to a more rigid structure, while the asymmetry and larger size of [AlCl₄]⁻ can enhance compressibility through greater structural flexibility. Consequently, the critical temperature and pressure for [C4mim][BF₄] may be lower, reflecting its more stable and less complex structure, whereas [C4mim][AlCl₄] may exhibit higher critical points due to increased complexity and stronger interactions. The larger, more polarizable [AlCl₄]⁻ anion can also enhance cohesion within the ionic liquid.

Conclusions

This study introduces a novel method using the binary mixture concept to calculate the critical properties of ionic liquids through MD simulations. To validate this approach, we predicted the critical density, critical pressure, and critical temperature of pure water and ethanol by analyzing the radial distribution function, heat capacity, and density near their critical points, and comparing the results with experimental data. Subsequently, we calculated the critical points of a water-ethanol binary mixture with a 0.5 mol fraction of water, revealing the existence of three critical points for the mixture. The first and third critical points correspond to pure water and pure ethanol, respectively, while the second pertains to the water-ethanol mixture. Based on the results of the water-ethanol mixture, the critical points of [C4mim][BF4] ionic liquid were estimated by analyzing the radial distribution function, heat capacity, and density behaviors near the critical points. The analysis showed that [C4mim][BF4] behaves like a binary mixture and has three critical points, with the second one identified as the critical point of the ionic liquid. Finally, the calculated critical properties were compared with existing literature.