Isogeometric modeling and vibroacoustic analysis of a symmetrically laminated thin plate coupled with an acoustic cavity

Abstract

This study presents vibroacoustic modeling and analysis of symmetrically laminated thin plate-cavity coupled systems. The plate, cavity, and their coupling are characterized by classical plate theory, the Helmholtz equation, and a displacement–pressure formulation, respectively. The governing equations for plate-cavity coupled systems are derived using non-uniform rational B-splines (NURBS) and variational formulations. The isogeometric analysis (IGA) approach is employed to construct exact geometric models and solve the discretized governing equations of laminated plate-cavity coupled systems for the first time. Numerical results, validated against other available data, reveal the convergence and accuracy of the present method. The study explores the vibroacoustic characteristics of two specific systems: a rectangular plate-trapezoid cavity coupled system and an elliptical plate-cavity coupled system. Parametric investigations examine the effects of geometric shapes, boundary conditions, acoustic media, and lamination schemes on the vibroacoustic characteristics. These innovative findings provide valuable theoretical guidelines for designing laminated plate-cavity coupled systems and offer benchmark solutions for future research.

Introduction

Structure-cavity coupled systems are widely encountered in many engineering occasions. Ship sonar domes, aircraft fuselage sections, and train cabins and their internal acoustic fields can be abstracted into a class of structure-cavity coupled systems composed of closed acoustic cavities and flexible plates or shells. For these coupled systems, due to the coupling effect, the internal acoustic behaviors are not only related to the sound source characteristics or external excitations, but also related to the acoustic and mechanical properties of the walls. In recent years, besides traditional isotropic structure-cavity coupled systems, laminated structure-cavity coupled systems have also drawn some attention of researchers, because laminated materials typically exhibit superior strength and stiffness-to-weight ratios compared to some traditional isotropic materials, depending on the application and loading conditions.

For isotropic structure-cavity systems, some analytical approaches can be used to obtain the solutions. Li and Cheng¹ presented a vibroacoustic analysis of a trapezoid cavity with a tilted wall and studied the influence of the wall inclination angle on vibroacoustic behaviors by using the combined integro-modal approach. Shi et al.² presented a vibroacoustic model for the flexible plate-partially opened cavity coupled system using an improved Fourier series method (IFSM), in which the structural–acoustic coupling between the plate and interior cavity, and the acoustic coupling between the finite cavity and exterior semi-infinite field are both considered. By using the classical modal coupling method, Wang et al.³ presented a theoretical model of a clamped panel-rectangular cavity coupled system, and analyzed the natural frequency and mode attenuation performance with some key parameters, including geometric parameters and panel damping. Xie et al.⁴ built the vibroacoustic model of a plate-irregularly cavity coupled system by a modified variational method and domain decomposition strategy, in which the vibroacoustic fields are approximated by Chebyshev orthogonal polynomials. Using the Rayleigh–Ritz method integrated with modal interaction approach, Pirnat et al.⁵ provided analytical and experimental results for a mass-loaded plate-air cavity coupled system with an internal acoustic excitation. Du et al.⁶ and Liao et al.⁷ employed the Rayleigh–Ritz method with Fourier series and Legendre series, respectively, to model plate-cavity coupled systems. Xin and Lu⁸ built an analytical model for sound transmission through a triple-panel partition separated by two cavities, and examined the effects of fluid–structure interaction on transmission loss. Henry and Clark⁹ developed a curved panel-cylindrical cavity coupled system by utilizing the modal interaction approach. Although the above analytical methods possess high computational efficiency, they are only suitable for coupled systems with relatively simple geometric features, and it is difficult to solve practical complex problems in engineering.

For most of ship sonar domes and cabins of vehicles like aircraft or cars, these structure-cavity coupled systems generally have irregular geometric shapes. Due to difficulties in getting the analytical solutions, some numerical methods are used to solve this kind of coupled system. Tournour and Atalla¹⁰ studied the forced response of a structure-cavity coupled system by using finite element method (FEM) and a pseudostatic corrections technique, in which the pseudostatic displacement and pressure were expressed using a mode selection technique that retains dominant modes while neglecting negligible ones. Larbi¹¹ presented the coupled FEM–BEM method to reduce the noise and vibration by adopting viscoelastic and passive piezoelectric treatments. A reduced-order FEM was used to model the internal structural–acoustic coupled system, and the direct boundary element method (BEM) was employed for modeling the acoustic scattering/radiation of the plate. Wu et al.¹² studied the dynamic response properties of structural–acoustic systems with uncertain plate parameters by the subinterval perturbation approach and edge-based smoothed FEM. For high-frequency structural–acoustic coupled problems, Dong et al.¹³ presented a design sensitivity analysis using energy FEM, where the interaction between structural-structural junctions and structural–acoustic interfaces were characterized by power transfer coefficients. The wave based method (WBM) was used by Chen et al.¹⁴ to solve the steady-state plate-cavity system under harmonic excitations and thermal environment. While the WBM is effective for analyzing simple plate-cavity systems, its computational efficiency is currently limited when dealing with complex non-convex systems. To enhance computational efficiency, Goo et al.¹⁵ presented the hybrid FE-BEM, which was successfully employed for the topology optimization of vibroacoustic problems. To enhance computational efficiency, a hybrid FE-BEM was introduced, which has been effectively applied to the topology optimization of vibroacoustic problems. Gao et al.¹⁶ developed a hybrid BE-statistical energy analysis (SEA) method for predicting mid-frequency behaviors of a statistical thin plate backed by a deterministic acoustic cavity. Besides theoretical numerical methods, the practical experimental approach used by Liu et al.¹⁷ and Ouisse et al.¹⁸ is also an important way to investigate plate-cavity systems. The study objects of the above research are nearly all isotropic structural–acoustic systems.

During the last decades, with the development of material science and the improvement of manufacturing technology, some new materials have been developed to meet the higher requirements of mechanical and physical properties. Composite laminated material is made by stacking several layers with different material properties. As a typical representative, laminated material has superior properties¹⁹ such as lightweight, high stiffness, and strength-to-weight ratios, so laminated structures are used in various equipment like ships, high-speed railways, and aircraft. Ashour²⁰ investigated the free vibration of elastically supported angle-ply laminated plates employing the finite strip transition matrix method. Wang ²¹ carried out the free vibration analysis of angle-ply symmetric laminated plates by using the Kirchhoff plate theory and discrete singular convolution. Arab and Ganesan²² presented the free vibration analysis of thickness-tapered laminated plates by using an energy formulation, and discussed the influences of internal-taper parameters on the fundamental frequency. Considering general boundary restraints and internal line supports, Ye et al.²³ solved the free vibration problems of moderately thick laminated plates, in which the IFSM and an artificial spring technique were respectively used to describe the displacement field and boundary condition. Focusing on vibration transmission and energy flow characteristics, Zhu and Yang²⁴ studied laminated plates with spatially curvilinear fibers and showed that the dominant energy flow paths can be specifically controlled by the fiber angles. Kim and Park²⁵ conducted the free vibration analysis of a laminated structure with circular holes, whose effective stiffness is described by a continuous orthotropic plate. By using the isogeometric approach and an inverse tangent shear deformation theory, Thai et al.²⁶ studied the mechanical characteristics of laminated composite and sandwich plates.

With the wide application of composite materials, besides composite structures, composite structural–acoustic coupled systems are also fascinating to study. Based on the IFSM, some laminated plate-cavity coupled systems were studied, such as a laminated sector plate-cavity coupled system²⁷, a laminated plate partially coupled with a limited fluid²⁸, and a laminated annular plate-dual cylindrical cavities coupled system²⁹. On the basis of the FEM and different plate theories, like layerwise and equivalent single-layer (ESL) theories³⁰, Mindlin plate theory³¹, and trigonometric sinusoidal shear deformation theory³², dynamic characteristics of composite structure-rectangular cavity coupled systems were analyzed.

From the above research, it can be found that most of the previous studies focused on coupled systems with relatively simple geometric features and isotropic material properties. Traditional FEM can theoretically deal with structural–acoustic coupled models with complex shapes, but it may lead to irreparable geometric errors in the laborious meshing process. Hughes et al.³³ first proposed the isogeometric analysis (IGA) in the framework of non-uniform rational B-splines (NURBS) basis functions, which are used for the accurate representation of complex geometries and improved accuracy of numerical solution. Increasing the order in the IGA requires less effort than traditional FEM. The use of high order basis functions allows the use of fewer elements, which can significantly decrease computational time during analysis. Besides, the IGA simplifies mesh generation by representing geometries using NURBS basis functions, reducing errors in traditional meshing processes, which can typically consume time in the pre-processing stage and expedite the calculation process. In recent years, the IGA approach has worked out very well in the fields of structural dynamics^34,35,36, acoustics^37,38,39, and structural–acoustic interaction^40,41,42.

Studying mathematical modelling is crucial as it provides a framework for understanding complex systems, predicting behaviors, and optimizing solutions across various fields^43,44,45. As mentioned by Animasaun et al.⁴⁶, it enhances decision-making, supports scientific research, and drives innovation by enabling the analysis of real-world phenomena in a structured, quantifiable manner. The mathematical study of IGA was presented by da Veiga et al.⁴⁷ and Bazilevs et al.⁴⁸, in which the mathematical theory and various applications of IGA in engineering fields are introduced.

From the above literature review, it can be found that most of the published literature focused on the dynamic characteristics of isotropic plate-simple cavity coupled systems and laminated plates. So far IGA solution to the vibroacoustic problem of laminated plate-irregular cavity coupled systems has not been developed in the literature. Considering the significance of these coupled problems in engineering applications, this paper is pioneering in building a symmetrically laminated plate-cavity coupled system by coordinated use of IGA, classical plate theory(CPT), Helmholtz equation, and displacement–pressure formulation. In another words, this research presents a novel application of IGA to investigate the vibroacoustic behavior of laminated plate-cavity coupled systems. With the superior capabilities of IGA, such as constructing exact geometries and using higher-order basis functions, the comprehensive parametric study considering various geometric and material parameters provides valuable insights into the behavior of laminated plate-cavity coupled systems. The presented approach can easily model coupled systems with irregular shapes and effectively achieve mesh generation, which provides an alternative solution for investigating the vibroacoustic characteristics and has significant practical applications.

Symmetrically laminated plate model

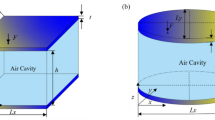
Consider a symmetrically laminated plate illustrated in Fig. 1a. In 3D Cartesian coordinate system, the mid-plane plate displacements in three basic directions (x, y, and z) are respectively denoted by u, v, and w. Symbol θ is used to describe the layering angle between the principal direction of orthotropic layer and x-axis of global coordinate system. In a symmetrically laminated structure, while layers may exhibit different thicknesses, they can also possess varying material properties, including stiffness and density, which significantly influence the overall mechanical behaviour. In this study, each layer of the laminated structure possesses the same material parameters and equal thickness. The examples of two lamination schemes [− 45°/90°/− 45°] and [0°/45°/45°/0°] are illustrated Fig. 1b. The total number of layers for symmetrically laminated plate could be odd or even.

Fig. 1

Schematic illustration of symmetrically laminated plate: (a) global Cartesian coordinates, (b) examples of two lamination schemes.

For a symmetrically laminated structure, in-plane and transverse bending vibrations may exhibit minimal coupling under certain conditions. However, in practice, their interactions can be complex and should be analysed in specific applications. In the present study of the symmetrically laminated plate, based on the classical plate theory (CPT), coupling between transverse bending and in-plane stretching is avoided⁴⁹. In accordance with the CPT, the displacement field of any point (x, y, z) on a symmetrically laminated plate can be described by transverse deflection w and its partial derivatives, written as

$${\mathbf{u}} = \left[ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - z\frac{\partial w(x,y)}{{\partial x}}} \\ { - z\frac{\partial w(x,y)}{{\partial y}}} \\ {w(x,y)} \\ \end{array} } \right]$$

(1)

The CPT is based on the Kirchhoff assumptions, in which transverse normal and shear stresses are neglected. So, the CPT is only suitable for thin plates (the plate thickness h is much smaller than the plate length a, thickness-to-length ratio h/a ≤ 0.05 or smaller). Compared with other plate theories, the CPT has only one independent variable, which implies the advantages of simpler displacement expressions and fewer unknown variables.

Under small strains assumption, the strain components can be obtained as

$${{\varvec{\upvarepsilon}}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ {\frac{\partial v}{{\partial y}}} \\ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \\ \end{array} } \right] = z\left[ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w(x,y)}}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w(x,y)}}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w(x,y)}}{\partial x\partial y}} \\ \end{array} } \right] = z{{\varvec{\upvarepsilon}}}_{p}$$

(2)

where ${{\varvec{\upvarepsilon}}}_{p}$ is pseudo-strain.

Based on the generalized Hooke’s law, the stress components for the k’th layer are given by

$${{\varvec{\upsigma}}}_{k} = \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right]_{k} = \left[ {\begin{array}{*{20}c} {\overline{{Q_{11}^{k} }} } & {\overline{{Q_{12}^{k} }} } & 0 \\ {\overline{{Q_{12}^{k} }} } & {\overline{{Q_{22}^{k} }} } & 0 \\ 0 & 0 & {\overline{{Q_{66}^{k} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right]_{k}$$

(3)

where $\overline{{Q_{ij}^{k} }} (i,j = 1,2,6)$ represent stiffness coefficients of the k’th layer, expressed as

$$\left[ {\begin{array}{*{20}c} {\overline{{Q_{11}^{k} }} } & {\overline{{Q_{12}^{k} }} } & {\overline{{Q_{16}^{k} }} } \\ {\overline{{Q_{12}^{k} }} } & {\overline{{Q_{22}^{k} }} } & {\overline{{Q_{26}^{k} }} } \\ {\overline{{Q_{16}^{k} }} } & {\overline{{Q_{26}^{k} }} } & {\overline{{Q_{66}^{k} }} } \\ \end{array} } \right] = {\mathbf{T}}\left[ {\begin{array}{*{20}c} {Q_{11}^{k} } & {Q_{12}^{k} } & 0 \\ {Q_{12}^{k} } & {Q_{22}^{k} } & 0 \\ 0 & 0 & {Q_{66}^{k} } \\ \end{array} } \right]{\mathbf{T}}^{T}$$

(4)

$${\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta^{k} } & {\sin^{2} \theta^{k} } & { - 2\sin \theta^{k} \cos \theta^{k} } \\ {\sin^{2} \theta^{k} } & {\cos^{2} \theta^{k} } & {2\sin \theta^{k} \cos \theta^{k} } \\ {\sin \theta^{k} \cos \theta^{k} } & { - \sin \theta^{k} \cos \theta^{k} } & {\cos^{2} \theta^{k} - \sin^{2} \theta^{k} } \\ \end{array} } \right]$$

(5)

$$Q_{11}^{k} = \frac{{E_{1}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }},Q_{12}^{k} = \frac{{\mu_{12}^{k} E_{2}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }},Q_{22}^{k} = \frac{{E_{2}^{k} }}{{1 - \mu_{12}^{k} \mu_{21}^{k} }},Q_{66}^{k} = G_{12}^{k}$$

(6)

where θ^k is the layering angle; T is the transformation matrix, and $Q_{ij}^{k} (i,j = 1,2,6)$ are material coefficients defined in material coordinate system; $E_{1}^{k}$ and $E_{2}^{k}$ are Young moduli in the longitudinal and transverse directions respectively; μ₂₁ and μ₁₂ are Poisson’s ratios satisfying $\mu_{12}^{k} E_{2}^{k} = \mu_{21}^{k} E_{1}^{k}$, and $G_{12}^{k}$ is shear modulus. If material parameters of each layer follow $\mu_{12}^{k} = \mu_{21}^{k}$, $E_{2}^{k} = E_{1}^{k}$ and $E_{1}^{k} /G_{12}^{k} = 2(1 + \mu_{12}^{k} )$, the laminated plate becomes an isotropic plate in this particular case.

Integrating the stress ${{\varvec{\upsigma}}}_{k}$ through the plate thickness h, the pseudo-stress ${{\varvec{\upsigma}}}_{p}$ is acquired as

$${{\varvec{\upsigma}}}_{p} = \left[ {\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right] = \int_{ - h/2}^{h/2} {{{\varvec{\upsigma}}}_{k} } z\text{d}z = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{16} } \\ {D_{12} } & {D_{22} } & {D_{26} } \\ {D_{16} } & {D_{26} } & {D_{66} } \\ \end{array} } \right]{{\varvec{\upvarepsilon}}}_{p} = {\mathbf{D\varepsilon }}_{p}$$

(7)

$$D_{ij} = \frac{1}{3}\sum\limits_{k = 1}^{N} {\overline{{Q_{ij}^{k} }} } \left[ {Z_{k + 1}^{3} - Z_{k}^{3} } \right],\;i,j = 1,2,6$$

(8)

where M_x, M_y, and M_xy are bending and twisting moments; D_i,j are flexural rigidities; Z_k and Z_k+1 denote the coordinates of lower surface and upper surface of the k’th layer, and N is the total number of layers. Equation (7) builds the relations between pseudo-strain ${{\varvec{\upvarepsilon}}}_{p}$ and pseudo-stress ${{\varvec{\upsigma}}}_{p}$.

Governing equations of a laminated plate-cavity coupled system

A rectangle laminated plate-cavity coupled system is depicted in Fig. 2. Symbols n_s and n_f represent the unit outward normal vectors with respect to the plate mid-plane and fluid domain, denoted by Ω_s and Ω_f. In addition, subscripts s and f are related to the structure and the fluid in the following descriptions. In the coupled system, the structural vibration and acoustic propagation interact with each other, meaning that the structure displacement and the fluid pressure must be solved simultaneously. The dynamic equation for the structural domain governs the motion of the laminated plate, while the Helmholtz equation for the fluid domain describes acoustic wave propagation, both essential for understanding the coupled vibroacoustic behavior.

Fig. 2

A rectangle laminated plate coupled with a cuboid acoustic cavity.

For the structure domain, considering rotary inertia, the dynamic equation is expressed as¹⁹

$$\frac{{\partial ^{2} M_{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{2} M_{{xy}} }}{{\partial x\partial y}} + \frac{{\partial ^{2} M_{y} }}{{\partial y^{2} }} + I_{0} \frac{{\partial ^{2} w}}{{\partial t^{2} }} + I_{2} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \frac{{\partial ^{2} w}}{{\partial y^{2} }}} \right) = 0\;{\text{in }}\Omega _{s}$$

(9)

where $I_{0} = \rho_{s} h$ is the mass per unit area, $I_{2} = \rho_{s} h^{3} /12$ is the mass moments of inertia per unit area, w(x, y) is the structural transverse deflection, and ρ_s denotes the mass density.

For the fluid domain, the Helmholtz equation is written as

$$\nabla^{2} p_{f} - \frac{1}{{c_{f}^{2} }}\frac{{\partial^{2} p_{f} }}{{\partial t^{2} }} = 0\;{\text{in }}\Omega_{f}$$

(10)

where $\nabla^{2} { = }\frac{{\partial^{2} }}{{\partial x^{2} }}{ + }\frac{{\partial^{2} }}{{\partial y^{2} }}{ + }\frac{{\partial^{2} }}{{\partial z^{2} }}$ is the Laplace operator, and c_f is the sound speed.

At structural-fluid coupling boundary Γ_c, continuous conditions of force and velocity are described by displacement–pressure formulation

$$\begin{array}{*{20}l} {{{\varvec{\upsigma}}} \cdot {\varvec{n}}_{s} = p_{f} {\varvec{n}}_{f} } \hfill \\ {\nabla p_{f} = - \rho_{f} \frac{{\partial^{2} w}}{{\partial t^{2} }} \cdot {\varvec{n}}_{f} } \hfill \\ \end{array}$$

(11)

in which ρ_f denotes the mass density of the acoustic medium.

Based on Eq. (9), the derivation of the weak form can be obtained either by multiplying displacement variation $\delta w$, and integrating by parts (done twice), or more directly by application of the Hamilton’s principle¹⁹. For the laminated plate, the strain energy U_ε, kinetic energy K, and external work W_f are given as

$$U_{\varepsilon } = \frac{1}{2}\int_{V} {{{\varvec{\upsigma}}}_{k}^{T} {{\varvec{\upvarepsilon}}}} \text{d}{\text{V}} = \frac{1}{2}\int_{{\Omega_{f}^{h} }} {\int_{ - h/2}^{h/2} {{{\varvec{\upsigma}}}_{k}^{T} z} } {{\varvec{\upvarepsilon}}}_{p} \text{d}z\text{d}\Omega = \frac{1}{2}\int_{{\Omega_{f}^{h} }} {{{\varvec{\upsigma}}}_{p}^{T} {{\varvec{\upvarepsilon}}}_{p} \text{d}\Omega }$$

(12)

$$K = \frac{1}{2}\int_{{\Omega_{f}^{h} }} {\int_{ - h/2}^{h/2} {\rho_{e} {\dot{\mathbf{u}}}^{T} {\dot{\mathbf{u}}}} } \text{d}z\text{d}\Omega = \frac{1}{2}\int_{{\Omega_{s}^{h} }} {I_{2} } \left( {\frac{{\partial \dot{w}}}{\partial x}} \right)^{2} + I_{2} \left( {\frac{{\partial \dot{w}}}{\partial y}} \right)^{2} + I_{0} \dot{w}^{2} \text{d}\Omega$$

(13)

$$W_{f} = \int_{{\Gamma_{c}^{h} }} {p_{f} } {\varvec{n}}_{f} \cdot w{\text{d}}\Gamma + \int_{{\Gamma_{\sigma }^{h} }} {w \cdot {\varvec{t}}_{0} } {\text{d}}\Gamma$$

(14)

where ${\dot{\mathbf{u}}}$ and $\dot{w}$ respectively denote first order partial derivative of u and w with respect to time, and t₀ denotes the prescribed traction on structure boundary Γ_σ.

Substituting Eqs. (12–14) to the Hamilton’s principle $\delta \int_{{t_{1} }}^{{t_{2} }} {\left( {U_{\varepsilon } + K - W_{f} } \right)dt = 0}$, the weak form of governing equation for structure is obtained

$$\int_{{\Omega_{s}^{h} }} {\delta {{\varvec{\upsigma}}}_{p}^{\text{T}} } {{\varvec{\upvarepsilon}}}_{p} {\text{d}}\Omega + \, \int_{{\Omega_{s}^{h} }} {\delta {\dot{\mathbf{w}}}_{p}^{\text{T}} {\mathbf{m\dot{w}}}_{p} } {\text{d}}\Omega - \int_{{\Gamma_{c}^{h} }} {p_{f} } {\varvec{n}}_{f} \cdot \delta w{\text{d}}\Gamma = \int_{{\Gamma_{\sigma }^{h} }} \delta w \cdot {\varvec{t}}_{0} {\text{d}}\Gamma$$

(15)

where

$${\mathbf{w}}_{p} = \left[ {\begin{array}{*{20}c} w & {\frac{{\partial w}}{{\partial x}}} & {\frac{{\partial w}}{{\partial y}}} \\ \end{array} } \right]^{\text{T}} ,\;{\mathbf{m}} = \left[ {\begin{array}{*{20}c} {I_{0} } & 0 & 0 \\ 0 & {I_{2} } & 0 \\ 0 & 0 & {I_{2} } \\ \end{array} } \right]$$

(16)

The weak form of governing Eq. (10) for fluid domain is obtained by multiplying pressure variation $\delta p_{f}$, integrating by parts and applying the boundary conditions, expressed as

$$\int_{{\Omega_{f}^{h} }} \nabla \delta p_{f} \cdot\nabla p_{f} {\text{d}}\Omega + \frac{1}{{c_{f}^{2} }}\int_{{\Omega_{f}^{h} }} \delta p_{f} \ddot{p}_{f} {\text{d}}\Omega + \int_{{\Gamma_{c}^{h} }} \delta p_{f} \left( {\rho_{f} \frac{{\partial^{2} w}}{{\partial t^{2} }} \cdot {\varvec{n}}_{f} } \right){\text{d}}\Gamma = \int_{{\Gamma_{v}^{h} }} \delta p_{f} v_{0} {\text{d}}\Gamma$$

(17)

where v₀ is the specified velocity respectively on fluid boundary Γ_v.

Isogeometric formulation of a vibroacoustic system

A brief introduction to NURBS

To construct B-spline basis functions, a non-decreasing knot vector E = [ξ₁ = 0, ξ₂,⋯, ξ_i, ⋯, ξ_m+p+1 = 1] should be predefined, as it determines the function’s continuity and smoothness, impacting the accuracy of the geometric representation in CAD applications. The non-negative real number ξ_i is called the knot, and positive integers m, p respectively represent the number and the polynomial degree of the spline functions. An open knot vector is adopted here, meaning that both the beginning knot ξ₁ and the ending knot ξ_m+p+1 repeat p + 1 times, to be in line with CAD standards.

B-spline basis M_i,p(ξ) and NURBS basis $R_{i}^{p} (\xi )$ in 1D parametric space are respectively constructed as³³

$$\begin{gathered} p = 0: \, M_{i,0} (\xi ) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;\xi_{i} \le \xi \le \xi_{i + 1} } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \hfill \\ p \ge 1: \, M_{i,p} (\xi ) = \frac{{\xi - \xi_{i} }}{{\xi_{i + p} - \xi_{i} }}M_{i,p - 1} (\xi ) + \frac{{\xi_{i + p + 1} - \xi }}{{\xi_{i + p + 1} - \xi_{i + 1} }}M_{i + 1,p - 1} (\xi ) \hfill \\ \end{gathered}$$

(18)

$$R_{i}^{p} (\xi ) = \frac{{\omega_{i} M_{i,p} (\xi )}}{{\sum\nolimits_{i = 1}^{m} {\omega_{i} M_{i,p} (\xi )} }}$$

(19)

where ω_i is the positive weight which is associated with each B-spline function.

By employing the tensor product of univariate B-spline basis, multivariate NURBS basis functions in 2D and 3D parametric spaces can be mathematically defined as

$$R_{i,j}^{p,q} (\xi ,\eta ) = \frac{{\omega_{i,j} M_{i,p} (\xi )N_{j,q} (\eta )}}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\omega_{i,j} M_{i,p} (\xi )N_{j,q} (\eta )} } }}$$

(20)

$$R_{i,j,k}^{p,q,r} (\xi ,\eta ,\zeta ) = \frac{{\omega_{i,j,k} M_{i,p} (\xi )N_{j,q} (\eta )L_{k,r} (\zeta )}}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {\omega_{i,j,k} M_{i,p} (\xi )N_{j,q} (\eta )L_{k,r} (\zeta )} } } }}$$

(21)

in which ω_i,j and ω_i,j,k are the 2D and 3D weights; n, l and q, r respectively are numbers and degrees of the other two basis functions N_j,q(η) and L_k,r(ζ). Figure 3 illustrates an example of quadratic 2D B-spline basis, in which solid and dashed lines on the boundaries of 2D basis are 1D B-spline functions rooted on the knot vectors E = [0, 0, 0, 0.5, 1, 1, 1] and H = [0, 0, 0, 0.2, 0.4, 0.6, 1, 1, 1] respectively.

Fig. 3

Bivariate B-spline basis function.

NURBS surface and solid objects are defined via

$${\mathbf{S}}(\xi ,\eta ) = \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {R_{i,j}^{p,q} (\xi ,\eta )} } {\mathbf{B}}_{i,j}$$

(22)

$${\mathbf{S}}(\xi ,\eta ,\zeta ) = \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {R_{i,j,k}^{p,q,r} (\xi ,\eta ,\zeta )} } } {\mathbf{B}}_{i,j,k}$$

(23)

Here, B_i,j and B_i,j,k are control points with respect to the 2D surface and 3D solid, respectively.

Vibroacoustic model based on NURBS

In accordance with the central concept of the isogeometric approach, spline functions which are geometric modeling tools of the plate and acoustic cavity also play a role in describing the numerical solution, so structure displacement and sound pressure of vibroacoustic systems are expressed as

$$\, w(\xi ,\eta ) = \sum\limits_{A = 1}^{m \times n} {R_{A} } (\xi ,\eta )w_{A} = {\mathbf{R}}_{s} {\mathbf{W}}$$

(24)

$$p_{f} (\xi ,\eta ,\zeta ) = \sum\limits_{A = 1}^{m \times n \times l} {R_{A} } (\xi ,\eta ,\zeta )p_{A} = {\mathbf{R}}_{f} {\mathbf{P}}$$

(25)

where $R_{A} (\xi ,\eta )$ and $R_{A} (\xi ,\eta ,\zeta )$ are NURBS basis functions for structure and acoustic cavity respectively; W and P are displacement and sound pressure vectors respectively.

Substituting Eq. (24) into Eqs. (2) and (16), pseudo-strain ${{\varvec{\upvarepsilon}}}_{p}$ and vector ${\mathbf{w}}_{p}$ can be formulated as

$${{\varvec{\upvarepsilon}}}_{p} = \left[ {\begin{array}{*{20}c} { - \frac{{\partial^{2} {\mathbf{R}}_{s} }}{{\partial x^{2} }}} & { - \frac{{\partial^{2} {\mathbf{R}}_{s} }}{{\partial y^{2} }}} & { - 2\frac{{\partial^{2} {\mathbf{R}}_{s} }}{\partial x\partial y}} \\ \end{array} } \right]^{\text{T}} {\mathbf{W}} = - {\mathbf{B}}{\mathbf{W}}$$

(26)

$${\mathbf{w}}_{p} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{{\text{s}}} } & {\frac{{\partial {\mathbf{R}}_{s} }}{\partial x}} & {\frac{{\partial {\mathbf{R}}_{s} }}{\partial y}} \\ \end{array} } \right]^{\text{T}} {\mathbf{W}} = {\mathbf{NW}}$$

(27)

Substituting Eqs. (24) and (25) into Eq. (15), four equations for the structure domain are obtained as

$$\int_{{\Omega_{s}^{h} }} {\delta {{\varvec{\upsigma}}}_{p}^{\text{T}} } {{\varvec{\upvarepsilon}}}_{p} {\text{d}}\Omega = \delta {\mathbf{W}}^{\text{T}} \left( {\int_{{\Omega_{s}^{h} }} {{\mathbf{B}}^{\text{T}} {\mathbf{D}}{\mathbf{B}}} {\text{d}}\Omega } \right){\mathbf{W}} = \delta {\mathbf{W}}^{\text{T}} {\mathbf{K}}_{s} {\mathbf{W}}$$

(28)

$$\int_{{\Omega_{s}^{h} }} {\delta {\dot{\mathbf{w}}}_{p}^{\text{T}} {\mathbf{m\dot{w}}}_{p} } {\text{d}}\Omega = \delta {\dot{\mathbf{W}}}^{\text{T}} \left( {\int_{{\Omega_{s}^{h} }} {{\mathbf{N}}^{\text{T}} {\mathbf{mN}}} {\text{d}}\Omega } \right){\mathbf{\dot{W} = }}\delta {\dot{\mathbf{W}}}^{\text{T}} {\mathbf{M}}_{s} {\dot{\mathbf{W}}}$$

(29)

$$\int_{{\Gamma_{c}^{h} }} {p_{f} {\varvec{n}}_{f} \cdot \delta w} {\text{d}}\Gamma = \delta {\mathbf{W}}^{{\varvec{T}}} \left( {\int_{{\Gamma_{c}^{h} }} {{\mathbf{R}}_{s}^{{\varvec{T}}} } {\varvec{n}}_{f} {\overline{\mathbf{R}}}_{f} {\text{d}}\Gamma } \right){\mathbf{P}} = \delta {\mathbf{W}}^{{\varvec{T}}} {\mathbf{C}}_{up} {\mathbf{P}}$$

(30)

$$\int_{{\Gamma_{\sigma }^{h} }} \delta w\cdot{\mathbf{t}}_{0} {\text{d}}\Gamma = \delta {\mathbf{W}}^{\text{T}} \left( {\int_{{\Gamma_{\sigma }^{h} }} {{\mathbf{R}}_{s}^{\text{T}} } q_{0} {\text{d}}\Omega } \right) = \delta {\mathbf{W}}^{\text{T}} {\mathbf{F}}_{s}$$

(31)

where ${\overline{\mathbf{R}}}_{f}$ is the basis function of acoustic cavity on coupling surface Γ_c; ${\dot{\mathbf{W}}}$ denotes first order partial derivative of W with respect to time t; C_up is the structural–acoustic coupling matrix; K_s, M_s, and F_s represent generalized stiffness matrix, mass matrix, and external force vector of the symmetrically laminated plate.

Similarly, substituting Eq. (25) into Eq. (17), four equations for the acoustic domain are expressed as

$$\int_{{\Omega_{f}^{h} }} \nabla \delta p_{f} \cdot\nabla p_{f} {\text{d}}\Omega = \delta {\mathbf{P}}^{\text{T}} \left( {\int_{{\Omega_{f}^{h} }} {\left( {\nabla {\mathbf{R}}_{f} } \right)^{\text{T}} } \cdot \left( {\nabla {\mathbf{R}}_{f} } \right){\text{d}}\Omega } \right){\mathbf{P}} = \delta {\mathbf{P}}^{\text{T}} {\mathbf{K}}_{f} {\mathbf{P}}$$

(32)

$$\frac{1}{{c_{f}^{2} }}\int_{{\Omega_{f}^{h} }} \delta p_{f} \ddot{p}_{f} {\text{d}}\Omega = \delta {\mathbf{P}}^{\text{T}} \left( {\frac{1}{{c_{f}^{2} }}\int_{{\Omega_{f}^{h} }} {{\mathbf{R}}_{f}^{\text{T}} } {\mathbf{R}}_{f} {\text{d}}\Omega } \right){\mathbf{\ddot{P}}} = \delta {\mathbf{P}}^{\text{T}} {\mathbf{M}}_{f} {\mathbf{\ddot{P}}}$$

(33)

$$\int_{{\Gamma_{c}^{h} }} \delta p_{f} \left( {\rho_{f} \frac{{\partial^{2} w}}{{\partial t^{2} }}\cdot{\varvec{n}}_{f} } \right)d\Gamma = \rho_{f} \delta {\mathbf{P}}^{{\text{T}}} {\mathbf{C}}_{up}^{{\text{T}}} \ddot{W}$$

(34)

$$\int_{{\Gamma_{v}^{h} }} \delta p_{f} v_{0} d\Gamma = \delta {\mathbf{P}}^{{\text{T}}} \left( {\int_{{\Gamma_{v}^{h} }} {{\mathbf{R}}_{f}^{{\text{T}}} } v_{0} } \right)d\Gamma = \delta {\mathbf{P}}^{{\text{T}}} {\mathbf{F}}_{f}$$

(35)

where K_f, M_f, and F_f respectively denote the stiffness matrix, mass matrix, and sound source vector of the acoustic cavity.

Substituting harmonic displacement ${\mathbf{W}} = \overline{{\mathbf{W}}} e^{{{\varvec{j}}\omega t}}$ into Eq. (29), $\delta {\dot{\mathbf{W}}}^{\text{T}} {\mathbf{M}}_{s} {\mathbf{\dot{W} = }}\delta {\mathbf{W}}^{\text{T}} {\mathbf{M}}_{s} {\mathbf{\ddot{W}}}$ is obtained. Organizing Eqs. (12), (17), and (28–35), the variational governing equations of the laminated plate-cavity coupled system can be expressed as

$$\{ \delta {\mathbf{W}}\}^{{\varvec{T}}} \left( {{\mathbf{K}}_{s} {\mathbf{W}} + {\mathbf{M}}_{s} {\mathbf{\ddot{W}}} - {\mathbf{C}}_{up} {\mathbf{P}}} \right) = \{ \delta {\mathbf{W}}\}^{{\varvec{T}}} {\mathbf{F}}_{s}$$

(36)

$$\{ \delta {\mathbf{P}}\}^{{\varvec{T}}} \left( {{\mathbf{K}}_{f} {\mathbf{P}} + {\mathbf{M}}_{f} {\mathbf{\ddot{P}}} + \rho_{f} {\mathbf{C}}_{up}^{{\varvec{T}}} {\mathbf{\ddot{W}}}} \right) = \{ \delta {\mathbf{P}}\}^{{\varvec{T}}} {\mathbf{F}}_{f}$$

(37)

Rewriting them in matrix form

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{s} } & { - {\mathbf{C}}_{up} } \\ {\mathbf{0}} & {{\mathbf{K}}_{f} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\mathbf{W}} \hfill \\ {\mathbf{P}} \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{s} } \hfill & {\mathbf{0}} \hfill \\ {\rho_{f} {\mathbf{C}}_{up}^{{\varvec{T}}} } \hfill & {{\mathbf{M}}_{f} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\mathbf{\ddot{W}}}} \hfill \\ {{\mathbf{\ddot{P}}}} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {{\mathbf{F}}_{s} } \hfill \\ {{\mathbf{F}}_{f} } \hfill \\ \end{array} } \right]$$

(38)

Then, introducing harmonic solutions for sound pressure and external loadings with angular frequency ω, namely ${\mathbf{P}} = {\overline{\mathbf{P}}}e^{{{\varvec{j}}\omega t}}$, ${\mathbf{F}}_{s} = {\overline{\mathbf{F}}}_{s} e^{{{\varvec{j}}\omega t}}$, $\, {\mathbf{F}}_{f} = {\overline{\mathbf{F}}}_{f} e^{{{\varvec{j}}\omega t}}$, the discretized governing equations are obtained

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{s} } & { - {\mathbf{C}}_{up} } \\ {\mathbf{0}} & {{\mathbf{K}}_{f} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\overline{{\mathbf{W}}} } \hfill \\ {{\overline{\mathbf{P}}}} \hfill \\ \end{array} } \right] - \omega^{2} \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{s} } \hfill & {\mathbf{0}} \hfill \\ {\rho_{f} {\mathbf{C}}_{up}^{{\varvec{T}}} } \hfill & {{\mathbf{M}}_{f} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\overline{{\mathbf{W}}} } \hfill \\ {{\overline{\mathbf{P}}}} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{F}}}_{s} } \hfill \\ {{\overline{\mathbf{F}}}_{f} } \hfill \\ \end{array} } \right]$$

(39)

Thus, displacement vector W and sound pressure vector P can be obtained by solving Eq. (39). Inserting them into Eqs. (24) and (25), transverse displacement w and sound pressure p_f of the vibroacoustic system can be further approximated by the aid of NURBS basis functions. In the study of frequency responses, when the acoustic medium is air or water, relative displacement (RD) and sound pressure level (SPL) are always expressed as follows⁵⁰:

$${\text{RD}} = 20\log_{10} \left( {\frac{\left| w \right|}{{w_{ref} }}} \right)$$

(40)

$${\text{SPL}} = 20\log_{10} \left( {\frac{{\left| {p_{f} } \right|}}{{p_{ref} }}} \right)$$

(41)

where w_ref = 1 × 10⁻¹² m and p_ref = 2 × 10⁻⁵ Pa respectively are reference values with respect to the displacement and sound pressure.

Without the external loads, the discretized governing equations of the coupled system are given by

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{s} } & { - {\mathbf{C}}_{up} } \\ {\mathbf{0}} & {{\mathbf{K}}_{f} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\overline{{\mathbf{W}}} } \hfill \\ {{\overline{\mathbf{P}}}} \hfill \\ \end{array} } \right] - \omega^{2} \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{s} } \hfill & {\mathbf{0}} \hfill \\ {\rho_{f} {\mathbf{C}}_{up}^{{\varvec{T}}} } \hfill & {{\mathbf{M}}_{f} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\overline{{\mathbf{W}}} } \hfill \\ {{\overline{\mathbf{P}}}} \hfill \\ \end{array} } \right] = {\mathbf{0}}$$

(42)

in which the total stiffness and mass matrix are obviously asymmetric, so full eigenvalues and eigenvectors solver should be employed to get the vibroacoustic characteristics.

To determine the coupling strength between acoustical and structural modes, the transfer factor was used by Pan and Bies⁵¹. The transfer factor between uncoupled nth acoustical mode and mth structural mode is defined by

$$T_{m,n} = \left[ {1 + \left( {\frac{{\omega_{n} - \omega_{m} }}{2}} \right)^{2} \frac{1}{{B_{m,n}^{2} }}} \right]^{ - 1}$$

(43)

where

$$B_{m,n} = C_{m,n} \left( {\frac{{\rho_{f} c_{f}^{2} }}{{\rho_{s} h\Lambda_{m} \Lambda_{n} }}} \right)^{1/2} ,\;C_{m,n} = \int_{{\Omega_{s}^{h} }} {{\mathbf{W}}_{m} {\mathbf{P}}_{n} {\text{d}}\Omega } ,\;\Lambda_{m} = \int_{{\Omega_{s}^{h} }} {{\mathbf{W}}_{m}^{2} {\text{d}}\Omega } ,\;\Lambda_{n} = \int_{V} {{\mathbf{P}}_{n}^{2} {\text{dV}}}$$

(44)

The coupling coefficient $C_{m,n}$ describes the spatial matching degree between acoustical and structural modes, which determines the possible energy transfer. When the coupling coefficient is 0, the transfer factor is 0, meaning that there is no energy transfer between structure vibration to the acoustic field. When the transfer factor is close to 1, the coupling strength and energy transfer between acoustical and structural modes are large⁵².

Numerical results

In this section, vibroacoustic characteristics of symmetrically laminated thin plate-cavity coupled systems are investigated. The mechanical properties of the laminated plate are described by five parameters {E₁, E₂, G₁₂, μ₁₂, ρ_s} = {400 GPa, 10 GPa, 6 GPa, 0.25, 1600 kg/m³}. Considering the fluid in the acoustic cavity as air or water, typical weak and strong coupled systems are discussed. Unless otherwise specified, the density and sound speed of fluid media are $\rho_{f}^{{{\text{air}}}}$ = 1.21 kg/m³, $\rho_{f}^{{{\text{water}}}}$ = 1000 kg/m³ and $c_{f}^{{{\text{air}}}}$ = 340 m/s, $c_{f}^{{{\text{water}}}}$ = 1480 m/s. Except for the plate-cavity coupling surface, all other boundaries of the cavity are rigid, which means that the velocity is zero at those boundaries.

Verification study

Consider a laminated square plate-cavity coupled system with main parameters: cavity size {L_x, L_y, L_z} = {1 m, 1 m, 0.5 m}, plate thickness h = 5 mm, and lamination scheme [0°/90°/90°/0°]. In this example, the density and sound speed of air are $\rho_{f}^{{{\text{air}}}}$ = 1.225 kg/m³, $c_{f}^{{{\text{air}}}}$ = 344 m/s. For verifying the convergence and reliability of the present model, Table 1 gives the first eight non-dimensional frequencies $\beta_{s} = \omega L_{x}^{2} \sqrt {\rho_{s} /\left( {E_{2} h^{2} } \right)}$ respectively acquired by the IGA and IFSM⁵⁰ in conjunction with a simple first-order shear deformation theory (SFSDT). The boundary conditions of four sides are all simply supported, denoted as SSSS.

Table 1 Convergence of the first eight non-dimensional frequency parameters $\beta_{s} = \omega L_{x}^{2} \sqrt {\rho_{s} /\left( {E_{2} h^{2} } \right)}$ for SSSS [0°/90°/90°/0°] laminated square plate.

As can be seen from Table 1, with the element numbers and orders of NURBS basis increasing, the non-dimensional frequencies gradually converge and have a good agreement with the reference values. To preserve precision and save effort simultaneously during the numerical calculation, p = q = 3 and N_p = 16 are used in the following analysis. Table 2 gives some natural frequencies (Hz) of the rectangular cavity with rigid walls obtained by present method and analytical solution. As can be found, the numerical results match well with the exact analytical values, which are calculated by

$$\left( {f_{f} } \right)_{lmn} = c_{f} \sqrt {\left( {\frac{l}{{2L_{x} }}} \right)^{2} + \left( {\frac{m}{{2L_{y} }}} \right)^{2} + \left( {\frac{n}{{2L_{z} }}} \right)^{2} } { ,}\;l{,}m,n = 0,1,2,3, \cdots$$

(45)

Table 2 Comparison of some natural frequencies (Hz) of the rectangular cavity with rigid walls.

The first four natural frequencies of the coupled system with different plate thicknesses and acoustic medium are given in Table 3. The other geometric parameters used here are the same with Table 1. The boundary condition of the plate is fully free, denoted as FFFF. It is worth addressing that FFFF represents a plate with no translational or rotational constraints at any edge, commonly studied for theoretical insights but rarely seen in practical systems. As can be observed, when the range of thickness h is 1–10 mm, the natural frequencies calculated from one-variable CPT and four-variable SFSDT match well. When the acoustic medium is air, the first four natural frequencies of the coupled system are slightly reduced compared to the in-vacuo plate frequencies. The reduction in natural frequencies is attributed to the added mass effect, quantified by the equivalent inertial contribution of the acoustic medium. For systems with low structural–acoustic interaction strength, the coupled frequencies are primarily influenced by the structural modes or the acoustic medium’s dominant modes, depending on resonance conditions and mass ratios. In this numerical example, the fundamental frequency of cavity filled with air at standard atmospheric pressure and room temperature is 172 Hz, always much higher than the fourth frequencies of the in-vacuo laminated plate, so the first four modes of this plate-cavity coupled system are dominated by the plate vibration. However, for a plate-water cavity strongly coupled system, the natural frequency generally does not match the vibration frequency of structure or heavy fluid, due to the strong coupling effect. Vibroacoustic characteristics of rectangular plate-trapezoid cavity and elliptical plate-cavity coupled systems with various parameters are investigated in the following subsections. After the verification of the corresponding model, the dynamic analysis is presented for symmetric laminated plate-cavity coupled systems to discuss the effects of cross-ply and angle-ply lamination schemes.

Table 3 The natural frequencies (Hz) of FFFF [0°/90°/90°/0°] laminated square plate coupled with a rectangular cavity under different plate thicknesses and acoustic medium.

Rectangular plate-trapezoid cavity coupled system

Consider a coupled system including a rectangular plate and an isosceles trapezoid cavity (ITC) or a right trapezoid cavity (RTC), as illustrated in Fig. 4. The geometric parameters are: cavity size {L_x, L_y, L_z} = {1.5 m, 0.3 m, 0.4 m}, plate thickness h = 5 mm, and the inclination angle of walls of the trapezoid cavity ψ = arctan(1/4).

Fig. 4

Schematic diagram of a laminated plate coupled with the considered trapezoid cavity. (a) Isosceles trapezoid cavity (ITC), (b) right trapezoid cavity (RTC).

To further demonstrate the reliability and convergence of the computational model, the isotropic rectangular plate, four-layer cross-ply [0°/90°/90°/0°] laminated plate, and plate-ITC coupled system are studied using different numbers of cubic elements. The first ten non-zero natural frequencies are listed in Table 4. Material properties of the isotropic plate are {E, ρ, μ} = {71 GPa, 2770 kg/m³, 0.33}. The boundary condition of the plate is SSSS, and the cavity fills with air. It can be noticed that the current solution of isotropic plate-ITC coupled system has a good agreement with the results obtained by Xie et al.⁴. Taking into account computational efficiency and precision, 33 × 11 × 12 cubic elements will be employed in the following numerical calculation.

Table 4 The first ten natural frequencies (Hz) of the isotropic plate, [0°/90°/90°/0°] laminated plate, and plate-ITC coupled system.

Some natural frequencies of the [0°/90°/90°/0°] laminated plate-trapezoid cavity coupled system under SSSS and fully clamped (denoted as CCCC) boundary conditions (BC) are given in Table 5. To observe the changes in frequencies between the coupled and uncoupled systems, the frequency parameters of the in-vacuo plate and the uncoupled trapezoid cavity with rigid walls are also given. For uncoupled acoustic cavities, the isosceles trapezoid cavity generally possesses higher natural frequencies than the right trapezoid cavity, because the former has a smaller volume than the latter. However, the ninth natural frequency of these two cavities is equal. Because every cross-section vertical to x direction has the invariable width L_y = 0.3 m. The ninth acoustic mode (0, 1, 0) indicates that the pressure variation is confined to the y-direction, with uniformity in the x- and z-directions due to geometric constraints. The ninth frequency can be calculated by $\left( {f_{f} } \right)_{010} = 0.5c_{f} /L_{y} = 566.67{\text{Hz}}$.

Table 5 The first ten natural frequencies (Hz) of the [0°/90°/90°/0°] laminated plate, trapezoid cavity, and their coupled system.

It can be noticed from Table 5 that the natural frequencies of the coupled system filled with air or water exhibit significant differences. The plate-air cavity coupled system exhibits a weak coupling effect between the plate and the acoustic medium, so the natural frequencies of the coupled system are slightly higher or lower than those of the in-vacuo plate or rigid cavity. In this case, some natural frequencies of the coupled system can be reasonably matched to those of the uncoupled plate or acoustic cavity one by one. When the medium is water, which has much higher density and added mass than air, a strong coupling effect is caused. So the strongly coupled system demonstrates significantly lower natural frequencies compared to the weakly coupled system. The frequency parameters of uncoupled components and strongly coupled systems are fundamentally different, and there is generally no one-to-one match between them.

Generally, the modal analysis of structure-cavity systems is essential for estimating major contributions in terms of energy, either from the cavity or from the structure. To better understand the coupling effects of light and heavy fluids, some mode shapes of the SSSS laminated plate-ITC coupled system are presented in Fig. 5. The normalized distributions of the displacement and acoustic pressure are both plotted with the colormap limit [− 1, 1].

Fig. 5

The first eight mode shapes of the SSSS laminated plate-ITC coupled system. (a) Air medium, (b) water medium.

Comparing the results shown in Fig. 5a and Table 5, it can be found that the 1st, 5th, and 7th modes of the coupled system are dominated by the air vibration in the cavity. As a result, the structural displacement distribution in these modes aligns closely with the acoustic pressure distribution. However, the other five modes of the plate-cavity coupled system are dominated by the structural vibration, corresponding to the first five modes of the in-vacuo laminated plate. In these cases, the structural displacement distribution has a slight influence on the acoustic pressure distribution especially in the upper region.

In order to have a physical quantity measuring the coupling strength between cavity and plate modes, transfer factors for the SSSS laminated plate-ITC coupled system filled with air are given in Table 6. Some transfer factors are close to 0, suggesting minimal energy transfer between plate and cavity, characteristic of weak coupling regimes. The transfer factor between the 6th plate mode and the 4th cavity mode is 0.9555, approximately close to 1, which means that there is large energy transfer between these two modes. The reason is that the difference between these frequencies is small, determining the large transfer factor.

Table 6 Transfer factors for the SSSS laminated plate-ITC coupled system.

Due to the coupling effects of fluids with varying densities, coupled systems filled with different media may have different mode shapes. When the acoustic medium is water, it can be seen from Fig. 5b that the first eight modes of the strongly coupled system are all dominated by the plate. These mode shapes display similarities with the 2nd–9th plate modes and the (0, 0, 0) cavity mode. Besides, the first order mode (1, 1) of the plate disappears, because water is so dense that the first order structural vibration is not enough to totally disturb the acoustic pressure distribution on the coupling surface. Although the 1st–4th modes of the strongly coupled system and the 3rd, 4th, 6th, and 8th modes of the weakly coupled system are similar as regards structural displacement distributions, they have radically different sound pressure distributions. In strongly coupled systems, cavity mode patterns are significantly altered due to the dominant effect of fluid density and added mass on coupled dynamics.

Consider a plate with three-layer cross-ply [0°/90°/0°] lamination scheme. Table 7 list the corresponding results. Comparing the data in Tables 5 and 7, it can be found that [0°/90°/0°] laminated plate has lower frequencies than [0°/90°/90°/0°] laminated plate under both SSSS and CCCC boundary conditions. Meanwhile, the plate-cavity coupled system with [0°/90°/0°] scheme exhibits lower frequencies than one with four-layer cross-ply [0°/90°/90°/0°] scheme. This difference in frequency is attributed to the distinct layer composition, where the thickness of the 90° layer is reduced and the thickness of the 0° layer is increased in the [0°/90°/0°] scheme compared to the [0°/90°/90°/0°] scheme. Generally, for the mechanical properties of the orthotropic material used in this section, layering angle 90° can provide higher flexural stiffness than 0°. So the total flexural stiffness of [0°/90°/90°/0°] laminated structure is higher than [0°/90°/0°] one.

Table 7 The first ten natural frequencies (Hz) of the [0°/90°/0°] laminated plate-trapezoid cavity coupled system.

Then, the symmetric angle-ply laminated plate-trapezoid cavity coupled system is studied. A three-layer symmetric angle-ply [θ/− θ/θ] lamination scheme is considered in the investigation. For CCCC boundary condition and different layering angles θ = 15°, 30°, and 45°, the numerical results are given in Table 8. It can be noticed that the layering angle has a marked impact on the frequencies of uncoupled plate and coupled system. The frequencies gradually increase with the increase of the layering angle. The laminated structure allows optimization of mechanical and acoustic properties through tailored ply orientation, enhancing performance in specific coupling scenarios. So it is possible to optimize a laminated structure-cavity coupled system by selecting a reasonable laying scheme. Besides, the mode type (structure-controlled or acoustic-controlled) of the coupled system might change under different layering angles. For example, when θ = 15° the second mode of the weakly coupled system is structure-controlled. Nevertheless, it is acoustic-controlled mode when θ = 30°, 45°. The weakly coupled system exhibits more acoustic-controlled modes as layering angle increases.

Table 8 The first ten natural frequencies (Hz) of the CCCC angle-ply [θ/-θ/θ] laminated plate-trapezoid cavity coupled system.

Next, the effect of the inclination angle ψ of the trapezoid cavity is discussed. Take the CCCC laminated plate-ITC coupled system filled with air as an instance. When the inclination angle ψ increases from 0° to 50° with the step size 5°, Fig. 6 describes the variations of the first four frequencies of the coupled system. At ψ = 0°, the trapezoid cavity becomes a rectangular cavity, reducing the structural stiffness contrast and altering resonance conditions. In this case, the coupled system possesses the minimum first natural frequency. As the inclination angle increases, the first mode of the coupled system is always acoustic-controlled and the fundamental natural frequency generally becomes higher.

Fig. 6

The variations of the first four natural frequencies of the laminated plate-ITC coupled system with the inclination angle ψ. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°].

For the angle-ply laminated plate-cavity system, it is observable from Fig. 6a, b, and c that different layering angles and inclination angles lead to different mode types and natural frequencies. The inclination angle has an obvious effect on the acoustic-controlled frequencies. For the coupled system with [45°/− 45°/45°] laminated plate, the first four modes are dominated by acoustic responses due to the fundamental frequency of the plate exceeding cavity frequencies, minimizing structural influence on coupled dynamics. As can be seen from Fig. 6d, for the coupled system with [0°/90°/0°] laminated plate, the mode type of the third mode changes near ψ = 20°. It is controlled by the second mode of the cavity when ψ < 20°. However, it is controlled by the second mode of the plate when ψ > 20°. In addition, the fourth mode of the coupled system is a structure-controlled mode at first, and then changes to an acoustic-controlled mode when ψ > 20°. Because the second frequency of the trapezoid cavity gradually increases with the inclination angle ψ. When it is quite close to the second frequency of the laminated structure, the mode type of the coupled system may change. Different dynamic characteristics can be achieved by various inclination angles and lamination schemes, which can enhance the dynamic performance and mitigate resonance issues during the design of the coupled system. Similarly, other geometric sizes of the coupled system, for example, plate dimensions, can also be design variables for vibration and noise reduction.

Lastly, vibroacoustic responses of the coupled system perturbed by an external harmonic force are studied. To verify the correctness, sound pressure responses of the isotropic plate-rectangular cavity coupled system are calculated and compared with those in Ref. [4], as presented in Fig. 7, which shows a good agreement. The unit excitation force and plate displacement response are located at the same point A (0.65, 0.15, 0). The sound pressure response is measured at point B (0.6, 0.15, 0.2) inside air cavity or point C (0.75, 0.15, 0.2) inside water cavity. The modal loss factor of plate-air cavity coupled system is η = 0.01, which is set by introducing complex elastic modulus and complex sound speed. The frequency step of excitation force is Δf = 1 Hz. Other parameters used here, like boundary conditions, geometric sizes, and material properties, are the same as isotropic plate-ITC coupled system used in Table 4, except ψ = 0.

Fig. 7

Sound pressure responses of the isotropic plate-rectangular cavity coupled system. (a) Point B inside air cavity, (b) point C inside water cavity.

Figure 8 presents the displacement responses for simply supported laminated plate-ITC cavity coupled systems with an inclination angle of ψ = 25°, comparing different acoustic media and lamination schemes. The lamination scheme has a significant effect on displacement responses. The response curves gradually shift to the right as the layering angle increases from 15° to 45°, indicating changes in the natural frequencies. Comparing Fig. 8a with Fig. 8b shows that the displacement response curves are remarkably distinct. The system with a water cavity has denser resonant frequencies and generally smaller displacement response amplitudes than the system with an air cavity. This is because plate-water cavity systems have denser natural frequencies and higher energy absorption ability than plate-air cavity systems.

Fig. 8

Displacement responses of the laminated plate-ITC cavity coupled system. (a) Air cavity, (b) water cavity.

In order to explore how inclination angle and lamination scheme affect sound pressure responses, Fig. 9 illustrates sound pressure responses at point B in the laminated plate-trapezoid air cavity coupled system. When the shape of trapezoid air cavity varies, four displacement response curves for plate-ITC and plate-RTC with ψ = 10° and ψ = 25° exhibit a similar trend. However, the value of the displacement changes, especially when the frequency exceeds 200 Hz. Comparing Fig. 9a–d shows that the lamination scheme has a more pronounced influence on the sound pressure responses than changes in the shape of the trapezoid air cavity. This suggests that optimizing the lamination scheme could be a more effective way to manipulate the sound pressure responses of laminated plate-air cavity coupled systems.

Fig. 9

Sound pressure responses of the laminated plate-trapezoid air cavity coupled system. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°]

Elliptical plate-cavity coupled system

In this section, a laminated elliptical plate-cavity coupled system is investigated. The geometry parameters of the system are described by: the major radius a, minor radius b, plate thickness h, and cavity depth L, as shown in Fig. 10.

Fig. 10

Schematic diagram of a laminated elliptical plate-cavity coupled system.

To re-examine the accuracy of the present method, an isotropic circular plate-cavity weakly coupled system is analyzed first. The corresponding geometric parameters are: cavity size {a, b, L} = {1 m, 1 m, 0.8 m}, plate thickness h = 5 mm. Material properties of the plate are described by three parameters {E, μ, ρ_s} = {105 GPa, 0.35, 8440 kg/m³}. The density and sound speed of air are $\rho_{f}^{{{\text{air}}}}$ = 1.225 kg/m³, $c_{f}^{{{\text{air}}}}$ = 344 m/s. Taking different numbers of the element number and NURBS order, the first eight frequencies of a fully clamped isotropic circular plate-cavity coupled system are given in Table 9. The computational time for solving the Eq. (42) using an inbuilt function eig in MATLAB is also given. The computation is repeated three times, and the average value is taken as the computational time. The computer used in this example is Lenovo Legion Blade 7000 K with 12th Gen Intel^® Core™ i7-12700F 32 GB CPU (2.10 GHz, up to 4.9 GHz). It can be noticed that the present results exhibit satisfactory convergence and match well with the reference values, which are calculated by the IFSM and FEM⁵³. Considering the numerical precision and computational cost, p = q = 3 and N_p = 16 are used in the following calculation.

Table 9 Convergence of the first eight frequencies (Hz) for a fully clamped isotropic circular plate-cavity coupled system.

Next, consider a [0°/90°/90°/0°] laminated plate-elliptical cavity coupled system with geometric parameters: cavity size {a, b, L} = {1.5 m, 1 m, 0.8 m}, plate thickness h = 5 mm. For the laminated plate clamped or simply-supported at four sides, Table 10 presents some natural frequencies of the single plate, cavity, and coupled system filled with air or water. The nonzero fundamental frequency of the rigid elliptical cylindrical cavity is always higher than the first eight frequencies of the elliptical plate. Making a comparison between the frequencies of the laminated plate and coupled system, it can be preliminarily judged from Table 10 that the first eight modes of the weakly coupled system are all structure-controlled. For the fully clamped plate-cavity weakly coupled system, except for the fundamental frequency, other frequencies are slightly decreased compared to those of the corresponding uncoupled plate. For the simply supported plate-air cavity coupled system, the 4th, 5th, 7th, and 8th frequencies are slightly lower than those of the uncoupled plate, whereas the 1st, 2nd, 3rd, and 6th frequencies are slightly higher. Table 11 lists transfer factors for the simply supported laminated plate-elliptical cylindrical cavity coupled system filled with air. As can be seen, most of transfer factors are small, indicating small coupling strength between acoustical and structural modes.

Table 10 The first ten natural frequencies (Hz) of the [0°/90°/90°/0°] laminated plate, elliptical cylindrical cavity, and their coupled system.

Table 11 Transfer factors for the simply supported laminated plate-elliptical cylindrical cavity coupled system.

Figure 11 presents the first eight mode shapes of the laminated plate backed by an elliptical cylindrical cavity. As can be seen, the structural displacement distribution and acoustic pressure distribution are very similar in the upper region. The strong coupling effect between the elliptical plate and the water cavity results in the suppression or disappearance of the first elliptical plate mode (1, 1). Furthermore, the 1st–7th modes of the strongly coupled system exhibit similar shapes to the 3rd, 2nd, 4th, 6th, 5th, 7th, and 8th modes of the weakly coupled system. But for the strongly coupled system, the strong coupling makes a more obvious impact on the distribution of structural displacement and acoustic pressure.

Fig. 11

The first eight mode shapes of the fully clamped [0°/90°/90°/0°] laminated plate-elliptical cylindrical cavity coupled system: (a) air medium, (b) water medium.

The boundary condition and lamination scheme are two important factors in the inherent characteristics of laminated plate-cavity coupled systems. Considering a three-layer symmetric angle-ply [θ/− θ/θ] plate with different layering angles θ = 15°, 30° and 45°, Tables 12 and 13 give the first eight frequencies of the elliptical cylindrical cavity with a laminated flexible wall, respectively under simply supported and fully clamped boundary conditions. As can be obviously seen, the first eight modes of the weakly coupled system are always plate-controlled, namely their mode types are not changed by the fiber orientation in this numerical example. Besides, frequencies of the plate and coupled system generally tend to rise with the layering angle. Because the total stiffness of laminated plate increases when the layering angle varies from 15° to 45°.

Table 12 The first eight natural frequencies (Hz) of the simply supported angle-ply [θ/-θ/θ] laminated plate-elliptical cylindrical cavity coupled system.

Table 13 The first eight natural frequencies (Hz) of the fully clamped angle-ply [θ/-θ/θ] laminated plate-elliptical cylindrical cavity coupled system.

Next, the effects of the geometric sizes including the plate thickness h, aspect ratio a/b, and cavity depth L are investigated. The following discussions focus on the fully clamped laminated plate-air cavity coupled system with four lamination schemes. The relationship between plate thickness and some natural frequencies of the coupled system is graphically represented in Fig. 12. Due to the increasing total stiffness of the coupled system, the frequencies exhibit an upward trend as the plate is thickened from 1 to 8 mm. When the minor radius of elliptical plate is constant b = 1 m, Fig. 13 displays the remarkable changes of the first ten natural frequencies versus the major radius a. The results indicate that the frequencies decrease as the major radius increases for all lamination schemes. Because the elliptical area increases linearly as the major radius grows, the smaller plate stiffness results in the smaller frequencies of the elliptical plate and plate-controlled coupled system. Giving different cavity heights L, some natural frequencies of the coupled system are listed in Table 14. It can be found that the frequency fluctuates relatively slightly when the cavity height ranges from 0.1 m to 0.9 m with the step size 0.2 m. This demonstrates that although the coupling degree between the plate and elliptical cylindrical cavity varies with cavity depth, cavity height plays a weak role in the coupled system in this numerical example.

Fig. 12

The variations of some frequencies of the laminated plate-elliptical cylindrical cavity coupled system with the plate thickness h. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°]

Fig. 13

The variations of some natural frequencies of the laminated plate-elliptical cylindrical cavity coupled system with the major radius a. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°]

Table 14 The first eight natural frequencies (Hz) of the three-layer laminated plate-elliptical cylindrical cavity coupled system with different cavity heights.

Lastly, vibroacoustic responses are investigated. The unit excitation force and plate displacement response point are both located at point A (1, 0, 0), and the sound pressure response is measured at point B (1, 0, 0.2). The modal loss factor of plate-cavity coupled system is η = 0.01 and the frequency step of excitation force is Δf = 1 Hz. Other parameters, like boundary conditions, geometric and material parameters, are identical to those used in Table 13 for the coupled system.

Figures 14 and 15 respectively present displacement responses and sound pressure responses of the laminated plate-elliptical cylindrical coupled system with different acoustic media and lamination schemes. It can be seen that lamination scheme has an obvious impact on vibroacoustic responses. The plate-water cavity system exhibits denser resonant frequencies than the plate-air cavity system because the former has denser natural frequencies. Besides, the system containing water has generally smaller displacement response amplitudes and higher sound pressure levels compared to the system filled with air. Because water has much higher mass and inertia than air, which can help to dampen the vibration displacement of the coupled systems. On the other hand, water also has a higher sound speed than air, meaning more efficient sound transmission, which can lead to higher sound pressure levels.

Fig. 14

Displacement responses of the laminated plate-elliptical cylindrical coupled system. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°]

Fig. 15

Sound pressure responses of the laminated plate-elliptical cylindrical cavity coupled system. (a) [15°/− 15°/15°], (b) [30°/-30°/30°], (c) [45°/− 45°/45°], (d) [0°/90°/0°]

Conclusions

Isogeometric analysis (IGA) approach integrated with variational formulation is utilized in this paper to analyze vibroacoustic behaviors of symmetrically laminated thin plate-cavity coupled systems. The classical plate theory and Helmholtz equation are used to govern the displacement field of plate and acoustic pressure of cavity respectively, which are further described by the non-uniform rational B-splines. Two kinds of coupled systems, namely, the rectangular plate-trapezoid cavity and elliptical plate-cavity are studied systematically, while the effects of some important factors, such as lamination schemes, acoustic medium, geometric shapes, and boundary conditions on vibroacoustic characteristics are explored. Several conclusions can be summarized as:

• (1) A verification study about the plate-cavity coupled systems shows that IGA exhibits satisfactory convergence and accuracy.

• (2) Due to the coupling effects of light or heavy fluids, coupled systems filled with different media may have different mode shapes. Strong coupling has a greater influence than weak coupling on the mode shapes.

• (3) For laminated plate-trapezoid cavity coupled systems, the isosceles trapezoid cavity generally possesses higher natural frequencies than the right trapezoid cavity. Different vibroacoustic characteristics can be achieved by various inclination angles and lamination schemes.

• (4) For laminated plate-elliptical cylindrical cavity coupled systems, frequencies of the plate and coupled system generally increase as the plate thickness increases and the major radius reduces, because the total stiffness of laminated plate increases.

• (5) For vibroacoustic responses,the system filled with water has smaller displacement response amplitudes but higher sound pressure levels and denser resonant frequencies compared to the system filled with air.