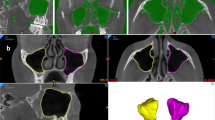
Abstract
Recent advancements in deep learning have revolutionized digital dentistry, highlighting the importance of precise dental segmentation. This study leverages active learning with the three-dimensional (3D) nnU-net and multi-labels to improve segmentation accuracy of dental anatomies, including the maxillary sinuses, maxilla, mandible, and inferior alveolar nerves (IAN), which are important for implant planning, in 3D cone-beam computed tomography (CBCT) scans. Segmentation accuracy was compared using single-label, adjacent pair-label, and multi-label relevant anatomic structures with 60 CBCT scans from Kooalldam Dental Hospital and externally validated using data from Seoul National University Dental Hospital. The dataset was divided into three training stages for active learning. The evaluation metrics were assessed through the Dice similarity coefficient (DSC) and mean absolute difference. The overall internal test set DSCs from the multi-label, single-label, and pair-label models were 95%, 91% (paired t-test; p = 0.01), and 93% (p = 0.03), respectively. The DSC of the IAN in the internal and external datasets increased from 83% to 79%, 87% and 81%, to 90% and 86% for the single-label, pair-label, and multi-label models, respectively (all p = 0.01). Prediction accuracy improved over time, significantly reducing the manual correction time. Our active learning and multi-label strategies facilitated accurate automatic segmentation.
Similar content being viewed by others
Introduction
The field of dentistry has remarkably advanced in recent years, propelled by the integration of cutting-edge technologies such as machine learning and artificial intelligence (AI)1. This advancement has highlighted the rise of digital dentistry as a key field component. The application of emerging technologies such as augmented reality, robotics, and three-dimensional (3D) printing in dentistry has increased2. Among them, 3D printing has facilitated the creation of medical devices such as implant surgery guides, patient-specific implants, and maxillofacial implants3,4. Augmented reality has been leveraged for surgical training, and robots have been incorporated into implant surgery and orthodontics5. Implementing these technologies requires precise 3D information on patients, with accurate segmentation of anatomical structures being crucial6. Ensuring that the implant is inserted with optimal depth and stability is paramount when performing dental implantation. This must be achieved without compromising the integrity of the maxillary sinus (MS) or the inferior alveolar nerves (IAN). Accurate dental segmentation is vital for digital dentistry and the development of patient-specific devices, significantly influencing clinical applications, including diagnosis, treatment planning, and outcome evaluation. However, segmenting dental images, particularly anatomical structures, requires considerable time from anatomical experts and proficiency in dental imaging devices, rendering the segmentation process labor-intensive and expensive7. Including clinically significant structures, such as the MS and IAN, increases the complexity of the labeling process. Thus, deep learning has emerged as a method for automating dental segmentation, reducing the workload of clinicians, and improving both the accuracy and efficiency of the process8,9,10,11.
Therefore, many segmentation studies have been performed on individual dental anatomy structures, including maxillary sinus, condyle, mandible, and maxilla. Morgan et al. used 3D U-Net architecture and achieved 98.4% accuracy on maxillary sinus12. Shaheen et al. developed a model based on 3D U-Net for teeth segmentation and achieved a 90% dice score13. Brosset et al. segmented the mandibular condyle with a dice score of 94%, Jha et al. developed a condyle segmentation model using 3D U-Net with 93% accuracy, and Lo Giudice et al. segmented the mandible with 97% accuracy14,15,16. Many further studies have applied their complex frameworks to segment IAN. Lahoud et al. achieved 77% accuracy at mandibular canal segmentation using 3D U-Net models. Lim et al. achieved a 58% dice score using the nnU-Net architecture, whereas Jeoun et al. derived an 87% dice score using Canal-Net17,18.
However, the effectiveness of deep learning models depends on the availability of extensive, high-quality annotated datasets, which makes labeling these datasets resource-intensive. To overcome this challenge and enhance the accuracy of the training process, active learning has been adopted as an effective solution19,20,21. Moreover, previous studies faced inefficiencies in training because they only focused on individual labels, which required additional models to be created for different label splits when necessary. When predictions were made based on a model that considered only single labels, there were limitations in evaluating the relative positions of other anatomical structures. This study describes an active learning framework to reduce labeling efforts even with limited training data from cone-beam computed tomography (CBCT) scans, aiming to validate the accuracy and efficiency of segmentation using multi-labeled data.
Methods
Overall process of active learning
Figure 1 describes the active learning process of dental segmentation. Initially, an expert manually segmented MS, maxilla, mandible, and IAN in 24 cases of CBCT scans. The 3D nnU-net model was trained on 18 manually segmented CBCT scans using single-label, adjacent pair-label, and multi-label models of relevant structures. In the case of the multi-label model, all labels were made into one image. For the pair-label model, the oral structures were divided into the MS and maxilla for the upper, and mandible and IAN for the lower. Subsequently, the trained model was employed to generate prediction labels of test sets (N = 6). The performance of these segmentations was evaluated using the Dice similarity coefficient (DSC) and mean absolute difference (MAD) metrics. Finally, the segmented outputs from the trained model were manually corrected to serve as additional training data for the next stage. This cycle of utilizing both existing and newly corrected data for further training was repeated to improve the model’s performance.
Image acquisition and segmentation
This study was approved by the Institutional Review Board of Asan Medical Center (IRB no. 2024 − 0485) and performed according to the principles of the Declaration of Helsinki. The requirement for informed consent was waived owing to the retrospective nature of this study. A total of 60 anonymized CBCT scans (i-CAT FLX V17, Imaging Sciences International, Hatfield, PA, USA) were acquired from patients who visited Kooalldam Dental Hospital to diagnose malocclusion and establish a treatment plan between 2017 and 2020 (Table 1). Most patients at the hospital had dental prostheses, and the CT scans were selected explicitly for these individuals. Patients with severe metal artifacts from multiple metal prostheses or restorations were excluded, making segmenting the surrounding anatomical structures difficult. Patients with severe maxillofacial deformities, edentulism, or a significant number of missing teeth were also excluded from the training data.
For external data, a total of 10 computed tomography scans (Somatom Sensation 10, Siemens AG, Erlangen, Germany) were obtained from Seoul National University Hospital (IRB no. ERI20022; Table 1). Key anatomical structures relevant to dental surgery, including the MS, mandible, maxilla, and IAN, were segmented using the Mimics software version 17 (Materialize Inc., Leuven, Belgium). The left maxillary sinus (LMS) and right maxillary sinus (RMS) were segmented using a threshold function (− 1024 to − 400 Hounsfield Units (HU)), with regions manually selected and further refined through manual corrections. The mandible and maxilla were segmented using a threshold function (300 to 3000 HU) and manually corrected. The maxilla was cut from the temporomandibular joint, the highest point in the axial direction from the segmented mandible. The left inferior alveolar nerve (LIAN) and right inferior alveolar nerve (RIAN) were manually segmented, with all segmented structures verified by JWP, an orthodontist with over 25 years of experience.
Preprocessing and training architecture
Most patients had dental prostheses, resulting in high HU values ranging from 2000 to 3000. This situation can affect the normalization process, as the intensity of dental anatomical structures may appear different in patients without dental prostheses. The presence of metal artifacts from these prostheses often leads to higher maximum HU values, which can distort the perceived intensity of anatomical structures unrelated to the disease being studied. In contrast, such discrepancies are not present in cases without dental prostheses, where maximum HU values remain stable. To address this issue and minimize the impact of metal artifacts, we adjusted the HU values in our CBCT scans. The average HU value for the maxillary sinus is −1000. The average HU values for the mandible range from 93 to 1157, while the maxilla has average values between 153 and 1753. Additionally, the mandibular canal has an average HU value of −700in the CBCT scans22,23,24. The clipping range was set from − 500 to 500 to ensure effective differentiation of values. Values below − 500 were adjusted to −500, while values above 500 were capped at 500. This adjustment establishes an ideal window width, creating a consistent threshold that significantly delineates the airway region, extracts metal artifacts, and highlights differences in tissue densities by reducing the impact of extreme values25. Given the variation in average values across anatomical structures, HU values are clipped within the range of −500 to 500 to enhance visibility after normalization. So, these values were normalized between 0 and 1 using min–max normalization to improve convergence during training, activation function compatibility, and avoid numerical instability at deep learning model. We utilized a 3D full-resolution nnU-Net architecture, which is a deep learning-based segmentation method that automatically configures itself, including preprocessing, network architecture, training, and post-processing for medical or dental tasks based on U-Net architecture26.
Active learning
When dividing data into stages for active learning, the number of stages and amount of data entering each stage should be correctly determined. Accordingly, two models with three and four stages were created.
For the three-stage model, in the first stage, 18 datasets (14 training and 4 validation) were employed. These dataset labels were manually segmented by two experts and confirmed by a dentist with over 25 years of experience, establishing a solid gold standard for the initial stage. In the second stage, 36 datasets (28 training and 8 validation) were employed, including the datasets from stage 1 and the predicted labels corrected using the Mimics software. In the third stage, 54 datasets (42 training and 12 validation) were employed, incorporating new patient CBCT datasets and further enhancing the model’s performance (Fig. 2).
For the four-stage model, in the first stage, 14 datasets (10 training and 4 validation) were employed. These initial datasets were manually segmented by experts and confirmed by an experienced dentist to establish a reliable gold standard. In the second stage, 28 datasets (20 training and 8 validation) were employed, including the datasets from stage 1 and new datasets specific to stage 2. The predicted labels were manually corrected using the Mimics software, setting a new gold standard for the subsequent stage. In the third stage, 42 datasets (30 training and 12 validation) were employed, ensuring the model’s robustness and accuracy. In the fourth stage, an additional 12 new patient datasets were added, making a total of 54 datasets (39 training and 15 validation) (Fig. 2).
The model’s performance was evaluated using six test datasets after each training stage. As the training stage progressed, the model’s weights from the previous stage were refined by incorporating additional data for the next stage and existing training data from the last stage. Additionally, the accuracy of the active learning model in dental segmentation was evaluated using 10 external CBCT datasets (Fig. 2).
Training configurations
The model was developed utilizing TensorFlow version 1.14.0 and underwent training on an NVIDIA TITAN RTX 24GB GPU. Each phase of the learning process comprised 500 epochs, with a batch size set to 1. For optimization, the model used the Stochastic Gradient Descent optimizer, featuring a learning rate of 0.01, momentum of 0.99, and a weight decay set at 0.0005 to prevent overfitting of the model27, in addition to employing a random rectified linear unit function. Data augmentation strategies were implemented to enhance model robustness, including scaling within 0.85–1.25, and independent rotations around each axis within − 15° to 15°. The training loss was quantified using the average Dice coefficient loss. Since we separated labels for left and right, the training protocol was designed to exclude axis-based flips to maintain label integrity.
Evaluation and statistical analysis
We used DSC and MAD as evaluation methods for the predicted labels. The DSC primarily focused on the overlap between the predicted and actual segment labels. It is sensitive to the proportion of actual positive results, making it suitable for evaluating the general accuracy of segmentation areas. Segmentation accuracy was evaluated by comparing the DSC between the gold standard and the predicted results. The DSC analysis was conducted using the image analysis metrics package, scikit-learn version 1.3.2, in Python version 3.10.5. To assess improvements across stages, a paired t-test was used to compare DSC between each stage using IBM SPSS Statistics v25.00 (IBM Corp., New York, USA).
The MAD quantifies the spatial accuracy of segmentation boundaries, highlighting the alignment between predicted and actual boundaries. To analyze shape differences of segmentation between manual segmentation and the single-label, pair-label, and multi-label models, each set of labeled data was converted into Standard Triangulated Language (STL) format. A distance map was used to compare each STL file using the 3-matic software (version 9; Materialise, Leuven, Belgium), facilitating a detailed comparison of the segmented outputs. The mean absolute distance was calculated to comprehensively measure the distance between the surfaces of the gold standard and predicted segmentation models.
Labeling efficiency was evaluated by comparing the time between manual segmentation and single-label, pair-label, and multi-label model prediction, each with manual correction. The labeler measured the manual segmentation time using a timer while performing the labeling task, recording the segmentation time for each label separately. The correction time at each stage includes preprocessing time, prediction time, and manual correction time. This correction time was calculated using various models, and the manual segmentation model was compared using a paired t-test. Additional datasets were included at each stage for comparisons between different stages, so the Mann-Whitney U test was employed for reliability testing.
Results
Segmentation accuracy
The DSC results of the three-stage and four-stage models were compared to distribute stages for efficient and high-performance active learning. The overall average DSC of 95.55% (90.05% for IAN) was significantly better than 94.27% (86.95% for IAN) of the four-stage model (Supplementary Table 1). We also compared the DSC results of stage 1 using multi-label between models that used preprocessing and those that did not (Supplementary Table 2). To address the issue of excessively high HU value due to metal artifacts, we clipped the model and confirmed that there was a significant difference in the maxilla compared to the model that did not perform preprocessing. Based on this result, we divided the datasets into three stages with preprocessing of clipping in subsequent comparisons.
Table 2 shows the DSC of models trained with single-label, pair-label, and multi-label across different stages. The average values of DSC for all six classes increased throughout each stage at all of the single-label, pair-label, and multi-label models. The average DSC for the LIAN significantly increased from 78.61% (95% confidence interval (CI): 77.64 to 79.57%) to 84.48% (CI: 81.25 to 87.72%; p = 0.03), 82.02% (CI: 78.83 to 85.20) to 86.48% (CI: 84.43 to 88.54; p < 0.01), and from 86.47% (CI: 84.68 to 88.25) to 89.93% (CI: 88.95 to 90.91; p < 0.01). Meanwhile, the DSC for the RIAN significantly Rose from 79.46% (CI: 75.57 to 83.35) to 82.54% (CI: 79.66 to 85.41; p = 0.24), 80.96% (CI: 76.89 to 85.03) to 86.59% (CI: 85.09 to 88.09; p = 0.03), and from 84.74% (CI: 81.02 to 88.46) to 90.18% (CI: 88.74 to 91.62; p < 0.01) for the single-label, pair-label, and multi-label models, respectively. Segmentation accuracy using external CBCT datasets with a multi-label model achieved an average DSC of 92.53% ± 6.41%, showing the good performance on the overall medical image (Supplementary table 3). Figure 3 displays a distance map illustrating the MAD between the gold standard label and the predictions from the single-label, pair-label, and multi-label models. The root-mean-square values were 0.008 ± 0.234, 0.008 ± 0.237, and 0.007 ± 0.268 mm for the single-label, pair-label, and multi-label models, indicating the accuracy of the segmentation. When comparing the difference between the gold standard and predictions, all values remained < 0.83 mm for the single-label model (0.42 mm for IAN), 0.82 mm for the pair-label model (0.37 mm for IAN), and < 0.9 mm for the multi-label model (0.34 mm for IAN). These results confirm that the model trained using multi-labels makes good predictions at the Spatial boundaries of medical images.
Comparison of the distance map in three-dimensional models from the front view between the gold standard label and (a) single-label, (b) pair-label, and (c) multi-label models. Distance map of the inferior alveolar nerves between the gold standard label and (d) single-label, (e) pair-label, and (f) multi-label models.
Comparison of segmentation time
Segmentation time, a crucial metric for assessing labeling efficiency, was measured. The total time spent on manual segmentation, as well as segmentation using single-label models followed by manual correction, and multi-label models followed by manual correction, was recorded as 285 min 18 s ± 14 min 6 s, 29 min 40 s ± 2 min 17 s, and 20 min 17 s ± 50 s, respectively (Table 3). These data underscore the significant reduction in time required for segmentation when leveraging trained models, especially for the multi-label models, compared with traditional manual segmentation methods (p < 0.01). The time taken to perform manual corrections after predictions from a trained model decreases with the progression of each stage (p < 0.01).
Discussion
Accurate segmentation of anatomical structures in CBCT scans is crucial in digital dentistry, dental implants, and surgical planning. However, the process remains labor-intensive and time-consuming. Our study has successfully and efficiently segmented important dental anatomies, including the MS, maxilla, mandible, and IAN, using 3D nnU-Net in an active learning framework. We found that overall segmentation accuracy improved when adjacent anatomical structures were learned. By simultaneously training the model on these related structures, we enhanced its ability to recognize and understand their locations and relationships. As a result, our approach demonstrated robust performance, even when tested on external datasets. This study utilized active learning, which segments the learning process into discrete stages rather than simultaneously inputting the entire training dataset. The main reason behind this strategy is to enable more efficient AI-coordinated learning by manually correcting only the incorrect parts of the predicted label. Furthermore, even when no solid gold standard label is determined for training the model, automated segmentation is generally performed to create new labels for the entire dataset from labels of small datasets. This way, active learning can effectively reduce the time and labor required to segment anatomical structures from medical images. As the stages progress sequentially through active learning, the model’s segmentation accuracy has increased (Tables 2 and 3). Comparing the DCS of stages 1 and 3, the LIAN label significantly improved in the single-label model; the LMS, mandible, LIAN, and RIAN in the pair-label model; and the LMS, RMS, maxilla, mandible, LIAN, and RIAN label in the multi-label model. Since segmentation accuracy gradually improved as the stage progressed, the time to perform manual correction was significantly reduced to approximately 7% (Table 3).
Moreover, IAN accuracy significantly differed when comparing the three-stage and four-stage models. Labels of the MS, maxilla, and mandible were not significantly different between the two models (Supplementary Table 1). Because the size of the validation dataset of the four-stage model was insufficient, and because the weights from the first stage were received and used again in the next stage, the validation dataset entered into the first stage was used at every stage, thus indicating a high possibility of overfitting. When few datasets are available for learning, despite active learning being beneficial, judging and selecting an appropriately sized dataset per stage are crucial rather than overly subdividing the stages.
Different training methods for dental anatomies were compared, utilizing single-label, pair-label, and multi-label techniques. The segmentation accuracy showed significant differences among predictions from these three learning approaches. Specifically, the RIAN segmentation accuracy significantly differed between the stage 3 single-label model and the pair-label model. Significant differences in the LIAN and RIAN segmentation accuracy were observed between the single-label and multi-label models and between the pair-label and multi-label models. For the IAN, the average DSC improved from 83% with the single-label model and 87% with the pair-label model to 90% with the multi-label model. Thus, the multi-label of relevant structure labels significantly enhanced accuracy, whereas the single-label and pair-label learning may yield suboptimal outcomes.
The maximum distance between the gold standard and predictions was 0.83, 0.82, and 0.9 mm for the single-label, pair-label, and multi-label models, respectively. The discrepancy between the gold standard and single-label, pair-label, and multi-label prediction can be attributed to the over-segmentation of the maxilla. Regarding the maxilla, numerous thin bone segments were observed, and many sections were not unified. Consequently, no additional post-processing was performed after the prediction. This led to errors in the small segments that were not addressed during the manual segmentation process. For the IAN, all values were < 0.42, 0.37, and 0.34 mm for the single-label, pair-label, and multi-label models, respectively. When clinically inserting an implant, the target error is 1.5 to 2 mm28. When inserting an implant in clinical practice, the average and maximum errors are 1.12 and 4.5 mm, respectively29. Thus, our segmentation was within the acceptable error range, indicating a consistent and reliable performance in segmenting the IAN with multi-label training strategies.
Previous studies have documented DSC values for IAN segmentation ranging from 60 to 80% across various architectures18,25,30,31. Lim et al. achieved a DSC of 58% using the nnU-Net architecture with a dataset of 98 cases17. Krishnan et al. developed an encoder model based on the 3D ShuffleNetV2 architecture, achieving a DSC of 92% with 11,000 datasets32. The IAN segmentation in our study demonstrated a similar or slightly higher performance than those of other studies, even with a limited dataset (Table 4).
Our study has several limitations. First, the lack of a multi-center approach limited the diversity of the CBCT data used, thus restricting the generalizability of our results. To overcome this limitation, multi-center and multi-vendor research with more data will be conducted in the future. This will improve segmentation accuracy across various clinical environments, thereby increasing the robustness of the findings. Second, the limited data availability hindered further performance enhancements for specific anatomical structures. Hence, future studies should use larger datasets to assess the stability and efficiency of the segmentation process more comprehensively. This will address current limitations and could reveal new insights into the capabilities and limitations of the methodologies used. Third, since the test sets used in our study differed from those used in other studies, additional validation using a standard dataset was needed. Fourth, our study emphasizes the efficiency gains of segmentation but does not evaluate the ease of use of clinicians regarding our automated method. We are currently conducting further research on segmenting the dental anatomy of the respective model to establish a surgical plan. This research includes the development of a semi-automatic or fully automatic implant insertion robot, as well as treatments utilizing 3D printing. As part of these studies, we plan to conduct a satisfaction survey to evaluate clinicians’ perceptions of the accuracy of the segmentation model, its usefulness in actual clinical practice. Lastly, we only used the 3D nnU-net model for the training model. In further studies, we will compare and analyze the performance of various models.
Conclusion
The findings underscore the importance of utilizing multi-label and active learning strategies to achieve enhanced dental segmentation accuracy, even with small datasets. Deep learning significantly improved accuracy and efficiently reduced labeling time within digital dentistry, particularly in diagnosis and treatment planning. Insights gained from active and multi-label learning methods will pave the way for future advancements in accurately segmenting complex dental anatomies, indicating a promising direction for continued research and application.
Data availability
Datasets in the study are available from the corresponding author upon reasonable request with our IRB allowance.
References
Grischke, J., Johannsmeier, L., Eich, L., Griga, L. & Haddadin, S. Dentronics: towards robotics and artificial intelligence in dentistry. Dent. Mater. 36, 765–778 (2020).
Dutã, M. et al. An overview of virtual and augmented reality in dental education. Oral Health Dent. Manag. 10, 42–49 (2011).
Sheela, U. B. et al. In 3D Printing in Medicine and Surgery83–104 (Elsevier, 2021).
Kim, T. et al. Accuracy of a simplified 3D-printed implant surgical guide. J Prosthet Dent 124, 195–201 .e192 (2020). https://doi.org/10.1016/j.prosdent.2019.06.006
Kivovics, M., Takacs, A., Penzes, D., Nemeth, O. & Mijiritsky, E. Accuracy of dental implant placement using augmented reality-based navigation, static computer assisted implant surgery, and the free-hand method: an in vitro study. J. Dent. 119, 104070. https://doi.org/10.1016/j.jdent.2022.104070 (2022).
Lee, S. et al. Automated CNN-based tooth segmentation in cone-beam CT for dental implant planning. IEEE Access. 8, 50507–50518 (2020).
Xu, J. et al. Automatic mandible segmentation from CT image using 3D fully convolutional neural network based on DenseASPP and attention gates. Int. J. Comput. Assist. Radiol. Surg. 16, 1785–1794 (2021).
Gan, Y., Xia, Z., Xiong, J., Li, G. & Zhao, Q. Tooth and alveolar bone segmentation from dental computed tomography images. IEEE J. Biomedical Health Inf. 22, 196–204 (2017).
Jang, T. J., Kim, K. C., Cho, H. C. & Seo, J. K. A fully automated method for 3D individual tooth identification and segmentation in dental CBCT. IEEE Trans. Pattern Anal. Mach. Intell. 44, 6562–6568 (2021).
Hegazy, M. A., Cho, M. H., Cho, M. H. & Lee, S. Y. U-net based metal segmentation on projection domain for metal artifact reduction in dental CT. Biomed. Eng. Lett. 9, 375–385 (2019).
Hatvani, J. et al. Deep learning-based super-resolution applied to dental computed tomography. IEEE Trans. Radiation Plasma Med. Sci. 3, 120–128 (2018).
Morgan, N. et al. Convolutional neural network for automatic maxillary sinus segmentation on cone-beam computed tomographic images. Sci. Rep. 12, 7523 (2022).
Shaheen, E. et al. A novel deep learning system for multi-class tooth segmentation and classification on cone beam computed tomography. A validation study. J. Dent. 115, 103865 (2021).
Brosset, S. et al. in. 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), pp 1270–1273 (Ieee). (2020).
Jha, N. et al. Fully automated condyle segmentation using 3D convolutional neural networks. Sci. Rep. 12, 20590 (2022).
Lo Giudice, A., Ronsivalle, V., Spampinato, C. & Leonardi, R. Fully automatic segmentation of the mandible based on convolutional neural networks (CNNs). Orthod. Craniofac. Res. 24, 100–107 (2021).
Lim, H. K., Jung, S. K., Kim, S. H., Cho, Y. & Song, I. S. Deep semi-supervised learning for automatic segmentation of inferior alveolar nerve using a convolutional neural network. BMC Oral Health. 21, 1–9 (2021).
Jeoun, B. S. et al. Canal-Net for automatic and robust 3D segmentation of mandibular canals in CBCT images using a continuity-aware contextual network. Sci. Rep. 12, 13460 (2022).
Ren, P. et al. A survey of deep active learning. ACM Comput. Surv. (CSUR). 54, 1–40 (2021).
Kim, T. et al. Active learning for accuracy enhancement of semantic segmentation with CNN-corrected label curations: evaluation on kidney segmentation in abdominal CT. Sci. Rep. 10, 366 (2020).
Ryu, S. M., Shin, K., Shin, S. W., Lee, S. & Kim, N. Enhancement of evaluating Flatfoot on a weight-bearing lateral radiograph of the foot with U-Net based semantic segmentation on the long axis of tarsal and metatarsal bones in an active learning manner. Comput. Biol. Med. 145, 105400 (2022).
Deeb, R. et al. Three-dimensional volumetric measurements and analysis of the maxillary sinus. Am. J. Rhinol. Allergy. 25, 152–156 (2011).
Sande, A. & Ramdurg, P. Comparison of Hounsfield unit of CT with grey scale value of CBCT for hypo and hyperdense structure. Eur. J. Mol. Clin. Med. 7, 4654–4658 (2020).
Aryal, D., Dhami, B., Pokhrel, S. & Regmi, S. Assessment of Hounsfield unit in the maxillary and mandibular ridges using CBCT. J. Kantipur Dent. Coll. 3, 10–13 (2022).
Cipriano, M., Allegretti, S., Bolelli, F., Pollastri, F. & Grana, C. in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 21137–21146.
Isensee, F., Jaeger, P. F., Kohl, S. A., Petersen, J. & Maier-Hein, K. H. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods. 18, 203–211 (2021).
Ying, X. in Journal of physics: Conference series. 022022 (IOP Publishing).
Chen, S. T., Buser, D., Sculean, A. & Belser, U. C. Complications and treatment errors in implant positioning in the aesthetic zone: diagnosis and possible solutions. Periodontology 2000. 92, 220–234 (2023).
Tahmaseb, A., Wismeijer, D., Coucke, W. & Derksen, W. Computer technology applications in surgical implant dentistry: a systematic review. Int. J. Oral Maxillofac. Implants. 29, 25–42 (2014).
Jaskari, J. et al. Deep learning method for mandibular Canal segmentation in dental cone beam computed tomography volumes. Sci. Rep. 10, 5842 (2020).
Lahoud, P. et al. Development and validation of a novel artificial intelligence driven tool for accurate mandibular Canal segmentation on CBCT. J. Dent. 116, 103891 (2022).
Krishnan, V. G. et al. Optimized IANSegNet: Deep Segmentation for the Detection of Inferior Alveolar Nerve Canal. BioMed Res. Int. 2023, 1–10 (2023).
Acknowledgements
This study was supported by a grant from the Technology Innovation Program (20007888) funded By the Ministry of Trade, Industry & Energy (MOTIE, Republic of Korea) and by a grant from the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (HI22C0471).
Author information
Authors and Affiliations
Contributions
S.O. conducted learning through nnU-net, wrote codes according to the desired learning settings, and wrote the main manuscript text, figures, and tables. J.O. performed label segmentation and processed modifying the labels predicted through nnU-net for the next learning stage. M.B., S.B., and S.H. managed the data, and J.P. provided clinical expertise. Based on scientific knowledge and experiences, N.K. supervised this study and the revision of the manuscript. All the authors reviewed and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This study was approved by the Institutional Review Board of the Asan Medical Center (IRB No. 2024 − 0485) and Seoul National University Hospital (IRB no. ERI20022) and performed according to the principles of the Declaration of Helsinki. It was based on a review of retrospective charts of patients at Kooalldam Dental Hospital between 2017 and 2020 and at Seoul National University Dental University Hospital between 2010 and 2017. The IRB Committee waived the requirement for informed consent from both institutions, which approved the study due to retrospective observational studies. We received anonymized head and neck CBCT images of patients who don’t have severe maxillofacial deformities, edentulism, or multiple missing teeth with 0.3 mm slice thickness.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
On, S., Ock, J., Bae, M. et al. Improving accuracy for inferior alveolar nerve segmentation with multi-label of anatomical adjacent structures using active learning in cone-beam computed tomography. Sci Rep 15, 7441 (2025). https://doi.org/10.1038/s41598-025-91725-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-91725-2