Optimization of large-diameter deep-hole stope blasting technology based on numerical simulation: a case study of the Dongguashan copper mine

Abstract

In large-diameter deep-hole blasting operations for mining stopes, optimizing blasting techniques can enhance ore recovery rates while minimizing damage to the surrounding rock mass. To improve blasting efficiency in the large-diameter deep-hole stopes of the Dongguashan Copper Mine, this study employed numerical simulations to evaluate the impact of various bore-hole parameters and charge structures on blasting outcomes. First, by comparing stress wave distributions and peak pressures for boreholes of different diameters, and analyzing crater formation patterns for different row and borehole spacing configurations, the optimal borehole net-work parameters for 165 mm boreholes with non-coupled charge structures were determined. Subsequently, edge-hole blasting models were developed using radial non-coupled and axial spaced charge methods under different blasting schemes. Finally, the damage characteristics of ore pillar rock masses were examined through damage contour maps and stress curves for different edge-hole charge structures. Key findings indicate that increasing the radial non-coupling coefficient reduces peak stress and stabilizes equivalent stress at monitoring points, minimizing damage to ore pillars. Additionally, axial charge structures with optimized charge density and segment length significantly improve boundary control by reducing the damage radius. These results establish optimized borehole and charge configurations, achieving a balance between efficient fragmentation and minimal ore loss.The findings have practical implications for improving blasting designs in underground mines, particularly under high-stress conditions, and provide a basis for future research on advanced blasting techniques with enhanced energy efficiency and minimal environmental impact.

Introduction

Mineral resources are essential raw materials for the processing industry and serve as the foundation for society’s sustainable development. With the rapid economic growth, the demand for these resources has surged, leading to increasing mining depths and larger working faces to address the growing imbalance between supply and demand^1,2,3. For deep mining conditions, characterized by significant ground pressure and the presence of large and extra-large ore bodies, a staged backfilling process is often employed. This involves temporarily isolating pillars in large disk areas, quarries, or large-scale production sites. The backfill mining method consists of three steps: first, mining the chamber and filling it with full tailings cement; second, mining the pillars, where full tailings with non-cemented filling are used, and a low-grade sand-cement fill is applied for safety; third, isolating the pillars in the plate area, which is then filled with either full tailing sand or low-grade sand-cement^4,5,6. However, this method increases the complexity and difficulty of mining pillars. Some mining pillars are affected by factors such as the ore body’s natural joints, fractures, faults, and the impact of blasting, including compression and vibration damage. These factors often lead to issues like flaking of the sidewalls, overbreak, and over-excavation, which present significant safety risks and may even prevent the completion of mining operations, leading to resource wastage^7,8. Therefore, effective control of the blasting boundary during step-by-step mining is critical. It not only impacts mining safety and efficiency but also influences the depletion index, which in turn affects the stability of production and the overall economic viability of the mine.

Scholars have conducted extensive research on axial spaced charge blasting and radial uncoupled charge blasting techniques^9,10,11. Cheng¹², combining numerical simulations with field tests, studied the effect of axial air spacing on peak particle velocity (PPV). His research focused on the different positions of the air layer and the corre-sponding attenuation patterns of PPV. Roy¹³ utilized blasting experiments, neural network modeling, and regression analysis to assess the significance of various charging structures on vibration amplitude, proposing an optimized set of blasting charge parameters through a predictive equation related to PPV. You¹⁴ validated the Riedel-Hiermaier-Thoma (RHT) model for iron-rich ores using Hopkinson’s test and numerical simulations, ultimately identifying a reasonable charging structure and delay time to enhance deep-hole blasting performance. Ma¹⁵ investigated the energy dissipation and crack extension behavior of uncoupled charge structures in blasting. By developing a single-hole 3D model and varying uncoupling coefficients, Ma analyzed the pressure, energy evolution, and crack propagation along the borehole wall. Zhang¹⁶ applied the SPHFEM method, integrated with an image recognition algorithm, to ex-amine the effective stress distribution and damage evolution surrounding the borehole. He further explored the influence of the uncoupling coefficient on blasting effectiveness. Liu¹⁷ used a two-hole planar analysis model to evaluate the impact of different coupling materials on stress transmission, propagation, and superposition, along with the effects of hydrostatic pressure and anisotropic ground stress on crack initiation and extension. Lou¹⁸ measured the blast pressure field around boreholes using a cement mortar model and dynamic pressure testing system. With the assistance of ANSYS/LS-DYNA simulations, he analyzed pressure attenuation and superposition at multiple measurement points. The initial impact pressure on the borehole wall resulting from axial uncoupled charge blasting was then calculated using Starfield superposition theory. Wang¹⁹ proposed advanced active support technology for backfilling and mining faces, aiming to enhance mechanization levels and improve working environments in coal mines. Zhou²⁰ studied the anisotropic strength, deformation, and failure behaviors of gneiss granite under high stress and temperature conditions, providing valuable data for stability analysis in deep underground engineering. Wang²¹ addresses the challenges of high labor intensity in passive advanced support in coal mining. Through theoretical calculations, the supporting force of the surrounding rock and the required reinforcement support strength are determined. The "full-roadway roof anchor cable reinforcement support" technology is introduced and its strength is verified. Numerical simulations reveal the mineral pressure distribution law of the backfilling stope. Ding²² investigated the impact of different bottom cushion media on blasting damage characteristics and strain evolution in rock masses, finding that a combination of fine sand and steel balls effectively reduces blasting damage. Wang²³ addresses the challenges of long curing times and simplified tunneling simulation devices in rock similar materials. The authors propose a new method to prepare rock similar materials with early strength and good brittleness, utilizing a self-developed scaled TBM testing machine for rock-breaking simulations.

In the area of boundary control, scholars have extensively studied the issues of over-excavation and undercutting in tunnels^24,25,26. Mei²⁷ proposed a cutting method known as the "center hole and four wedge-shaped cutting holes," along with an optimized arrangement of blast holes and charging structures based on blasting excavation tests. The results showed that this optimized approach effectively reduced arch separation and step over-excavation. Specifically, the over-excavation area was reduced by 61.1%, and the depth of under-excavation decreased significantly, improving the stability of the sur-rounding rock and accelerating the rate of deformation convergence. Verma²⁸ critically assessed the factors influencing blast damage, including rock properties, blast characteristics, and blast design parameters, to analyze their effects on over-excavation. Through modeling tests, Verma evaluated blast damage and ultimately proposed an optimized arrangement for perimeter blast holes and a suitable charging structure. Wu²⁹ focused on the damage prevention mechanisms in interlayer rock using numerical simulations. He analyzed the process of crack propagation and designed different charging structures tailored to the thickness of the interlayer rock. Wu also implemented microseismic controlled blasting technology, which successfully maintained the stability of the interlayer rock and effectively controlled the blasting boundary.

While tunnel blasting can provide reference for mine blasting, there are notable differences between the two^30,31,32. In terms of boundary control for ore, Zhang³³ investigated the variation of specific charge under different stress conditions through explosion pit tests. He proposed a specific charge correction coefficient that accounts for the influence of ground stress and established a quantitative relationship between this co-efficient, the stress intensity ratio, and the lateral stress coefficient, which helped effectively control the blasting boundary. Yu³⁴ developed a hybrid meta-model based on the sine–cosine algorithm and the random forest heuristic model. Using Monte Carlo simulations, Yu analyzed the probability distribution and parameter sensitivity, enabling more accurate determination of ore boundaries post-blasting. Huo³⁵ evaluated rock damage caused by single-row lateral blasting through measurements of acoustic wave velocity and void zone boundaries. He found that a well-designed combination of loading structure and the number of blasting rows can effectively control rock damage, achieving better boundary control by establishing a numerical model for three-row drilling holes. Kan³⁶ created numerical models to analyze rock damage and blast-induced seismicity in multi-hole blasting under different initiation modes. His findings revealed that simultaneous initiation led to more severe rock damage and in-creased blast seismicity, while preferential initiation of holes with larger explosive charges improved rock damage control.Yin³⁷ proposed a novel method based on ConvLSTM (ConvLong Short Term Memory) for analyzing the behavior patterns of overlying rock layers during underground mining processes.Taking the Yunnan germanium rich lead–zinc ore enrichment area in the northeastern part of the Sichuan Yunnan Guizhou metallogenic belt as an example, Han³⁸ analyzed the oblique distribution patterns of ore bodies at different scales and the underlying mechanical models based on the theory and methods of ore field geomechanics. The research results indicate that in three-dimensional space, the oblique distribution of ore bodies (veins), ore body groups, and mineral deposits is controlled by the mechanical properties, kinematic characteristics, and tectonic stress fields of ore-forming/controlling fault structures during the mineralization period. These findings have important guiding significance for exploration deployment at the ore field scale, evaluation of deep and surrounding mineral exploration, and arrangement of exploration projects.

In summary, many scholars have extensively studied the effects of continuous radial uncoupled charges, radial coupled charges, and axial charging structures on factors such as blasting stress waves, vibration, and the range of blasting damage. However, there has been limited research on the combined impact of radial uncoupled charges, axial spacing charges, and the radial uncoupling coefficient on blasting stress waves. In the context of large-diameter deep-hole blasting quarries, most studies focus on analyzing either the influence of the axial structure of side holes on blasting vibration or the effect of the radial uncoupling coefficient on crack propagation. However, there has been relatively little research comparing these two charging structures and their combined effects.

Using the Dongguashan Copper Mine as a case study, this research aims to optimize large-diameter deep-hole blasting technology through numerical simulation. First, the optimal hole network parameters were determined by comparing stress wave distributions and peak pressures across different hole diameters, along with analyzing blasting patterns with varying row and hole spacing combinations. Next, several side-hole blasting models were developed, incorporating both radial uncoupled loading and axial spaced loading. These models were used to investigate the damage characteristics of the ore pillar rock under different blasting schemes.

Engineering background and intrinsic model for numerical simulation

Engineering background

The main ore body of the Dongguashan Copper Mine is situated at an elevation ranging from − 690 to − 1010 m, making it a typical deep-buried ore deposit. The ore body extends 1820 m in length, with an average width of approximately 500 m and a thickness varying from 20 to 60 m. Its strike direction is NE 35–40°, with an average dip of 20°. The dip reaches a maximum of 40° at both ends of the ore body, while the central section has a gentler dip of less than 15°. The ore body structure is relatively simple, with few joints. The surrounding rock is primarily composed of marble and skarn, while the footwall consists of sandstone and diorite. The ore body mainly contains cop-per-bearing pyrite and chalcopyrite, characterized by high rock strength and strong mechanical properties.

Natural geographical conditions of the mining area

The mining area is located on the south bank of the middle and lower reaches of the Yangtze River, belonging to the low mountain and hilly terrain along the river. Its southern edge is Laoya Ridge, connected to a vast plain to the north, bordered by Baimang Mountain and Boji Mountain to the east, and surrounded by green mountains to the west. The elevation of the terrain ranges from 40 to 220 m, with the highest point being Laoyaling, which has an altitude of 245.6 m and is the highest in the mining area. The Puji River flows on the west side of the mining area, while the Yang River winds through on the east side. The height of the riverbed in the lower reaches of the two rivers is 10 m, which constitutes the lowest erosion baseline in the region. These two rivers eventually merge into the Yangtze River, with a significant increase in water volume during the rainy season and a relative decrease during the dry season. This natural geographical environment has a profound impact on mining activities and ecological protection in mining areas.

Geological structural characteristics

• 1. Fold structure

The most prominent geological feature in the mining area is the Qingshan Anticline, which forms an integral part of the Datong-Shun’an Composite Syncline. The anticline spans approximately 8 km in width and extends nearly 32 km in length. Its axis trends between 40° and 50°, dipping northeastward. The two ends of the anticline exhibit slight eastward and westward offsets in the NE and SW directions, respectively, forming an S-shaped curve. The mining area is specifically located in the northeastern section of the Qingshan Anticline, with a total extension of over 400 m, starting from Bao Village in the north and extending southward to Laoyaling. Its geographical location and regional boundaries are clearly defined.

At different geological depths, the morphology of the Qingshan Anticline varies significantly. Above an elevation of − 400 m, the axial region displays relatively complex features, including typical double-crest folds and localized overturned or inclined folds. However, below − 400 m, the anticline’s structure becomes simpler, with gentler dips on both limbs and a more open configuration overall.

Due to magmatic intrusions and faulting activities, minor folds are prevalent in the axial region of the anticline. Additionally, the Xishizi Mountain Anticline, part of the NE-oriented fold group, is another significant structure controlling ore formation within the region.

• 2. Fault structure

The mining area exhibits well-developed fault systems, primarily trending NE, nearly N–S, and nearly E–W. Most faults are compressional, tensile, or tensile-shear in nature.

• 3. Joints

The primary joint sets in the mining area exhibit a distinct NW–SE orientation, with dip angles ranging from 75° to 85°. Scattered joint sets show a NE–SW orientation, with dip angles varying between 68° and 89°.

In the Qixia Formation marble, the overall dip direction is southwest. The primary joint set aligns with the main joint set of the mining area, exhibiting a NW–SE orientation with dip angles of 73° to 80°. The secondary joint set trends NE to nearly E–W, dipping southeast with dip angles between 68° and 78°. Scattered joints are widely distributed in the Qixia Formation marble, trending NE–SW with dip angles generally ranging from 68° to 89°, though in specific areas, the dip angle is approximately 58°.

For quartz diorite, the joints are primarily filled with calcite and are well-cemented. The primary joint set shows a NE to nearly E–W orientation, with dip angles between 50° and 80°, most of which dip northwest. The secondary joint set trends NW–SE, dipping southwest with dip angles ranging from 70° to 90°. Scattered joints generally trend NE, with dip angles between 50° and 80°, and dip to the southwest.

• 4. Geological structural stress field.

This copper mine is a typical deep-buried mine, where measuring in-situ stress is crucial for stability analysis and for predicting and preventing rockbursts. The mining area is affected by NW-oriented residual structural stress and NE-oriented geological structural stress. The direction of the maximum principal stress within the mining area is NE-oriented.

Hydrological conditions

Based on the hydrogeological characteristics, the aquifers in the mining area can be broadly divided into five groups. The groups and their water abundance levels are shown in Table 1.

Table 1 Comparison table of water rich degree of water bearing rock formations.

Mining method

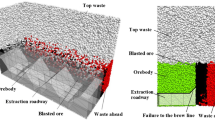
Given the high-stress state of the deep deposit, the Dongguashan Copper Mine employs a mining method that first reserves isolated pillars in the open stope stage, followed by a filling mining approach. Along the strike of the ore body, a disk area is designated every 100 m, with an 18-m-wide isolation pillar placed between adjacent disk areas to ensure the safety and stability of mining operations. Each disk area measures 100 m in width, matches the horizontal length of the ore body, and has a height equal to the thickness of the ore body. Each disk area is further subdivided into mining rooms and pillar quarries, consisting of 20 quarries in total, with the quarry arrangement aligned with the strike of the ore body. The width of each quarry is 18 m, with the mining room quarries extending 82 m in length and the mining pillar quarries extending 78 m. The mine uses the stage-empty field subsequent filling meth-od. The quarry mining sequence involves two steps: first, mining the rooms and filling them with collodion sand, followed by mining the pillars and filling them with either full tailing sand or low-ratio collodion sand. Depending on the actual conditions, the mine adopts an “alternate mining” strategy or a "three mine, one backfills" approach. Figure 1 is the schematic diagram of the Dongguashan Copper Mine quarry layout, showing the arrangement of mining rooms, pillar quarries, and isolation pillars along the strike direction of the ore body. The layout illustrates the mining sequence and the spatial relationship between different mining units.

Fig. 1

Schematic diagram of quarry layout and division.

Numerical simulation of the intrinsic model and parameters

ANSYS/LS-DYNA³⁹ (Livermore Software Technology Corporation—Dynamic Analysis,version R-19.0) is a widely used nonlinear dynamic analysis software, recognized as the best explicit analysis tool. Its reliability and accuracy have been verified through multiple comparisons with experimental results. In addition, LS-DYNA has unique advantages in dealing with complex nonlinear and large deformation problems, and is particularly suitable for simulating high dynamic processes such as blasting. In numerical simulations of blasting processes, the finite element method (FEM) is more suitable for handling the dynamic response of continuous media and can effectively capture the stress wave propagation and material failure process caused by blasting loads. In contrast, other methods such as Discrete Element Method (DEM) are mainly used to simulate particle matter interactions and are suitable for dealing with problems such as particle mixing, fragmentation, and stacking. Therefore, choosing finite element method for numerical simulation of blasting process can provide efficient and accurate analysis results.

The RHT model is now widely used in the numerical analysis of kinetic problems in the fields of concrete intrusion, impact, and explosion, and provides a powerful tool for studying the behavior of brittle materials under extreme loading conditions. The p-α equation of state in this model describes the process of pore space from crushing to compaction when the material is loaded, and the equation of state of the material after compaction is:

$$P=\left\{\begin{array}{c}{A}_{1}\mu +{A}_{2}{\mu }^{2}+{A}_{3}{\mu }^{3}+\left({B}_{0}+{B}_{1}\mu \right){\rho }_{0}e,\mu >0\\ {T}_{1}\mu +{T}_{2}{\mu }^{2}+{B}_{0}{\rho }_{0}e,\mu <0\end{array}\right.$$

(1)

$$\mu =\frac{\rho }{{\rho }_{0}}-1$$

(2)

where, μ is the body strain, the material volume compresses when μ > 0; ρ₀ is the initial density of the material; ρ is the density of the material during compression; A₁, A₂, A₃ are Hugoniot polynomial coefficients; B₀, B₁, T₁, T₂ are the parameters of the equation of state; and e is the initial internal energy of the material.

In ANSYS/LS-DYNA, the intrinsic behavior of explosives is defined using the keyword MAT_HIGH_ EXPLOSIVE_BURN, and the Jones–Wilkins–Lee (JWL) equation of state is employed to describe the relationship between the volume of explosive detonation products and the pressure:

$$P=A\left(1-\frac{\omega }{{R}_{1}V}\right){e}^{-{R}_{1}V}+B\left(1-\frac{\omega }{{R}_{2}V}\right){e}^{-{R}_{2}V}+\frac{\omega {E}_{0}}{V}$$

(3)

where A, B, R1, R2, are material constants; P is the pressure of the detonation products; E0 is the initial internal energy density; and V is the relative volume. I n LS-DYNA, the air material behavior is defined using the keyword MAT_NULL, while the EOS_LINEAR_POLYNOMIAL keyword is used to specify the equation of state:

$$P={C}_{0}+{C}_{1}\mu +{C}_{2}{\mu }^{2}+{C}_{3}{\mu }^{3}+({C}_{4}+{C}_{5}\mu +{C}_{6}{\mu }^{2})$$

(4)

where C₀, C₁, C₂, C₃, C₄, C₅, C₆ are constants; is the specific volume. The keyword used in the numerical simulation for the gun clay filling material is MAT_PLASTIC_KINEMATIC, representing an elastic–plastic model with kinematic hardening. This intrinsic numerical model is currently one of the most widely used in the field of blast impact loading. Its yield condition is described by Eq. (5):

$$\varnothing =\frac{1}{2}{\xi }_{ij}-\frac{{{\sigma }_{y}}^{2}}{3}$$

(5)

According to the actual situation on site, this article chooses the parameters of on-site skarn for simulation. The mechanical parameters of the skarn in the mine are shown in Table 2⁴⁰.

Table 2 Mechanical parameters of siliceous rock.

Where the shear modulus parameter can be calculated as following:

$$G=\frac{E}{2(1+\mu )}$$

(6)

The following parameters were calculated from the Rankine–Hugoniot and Mie–Gruneisen equations:

$${A}_{1}={\rho }_{0}{c}_{0}^{2}$$

(7)

$${A}_{2}={\rho }_{0}{c}_{0}^{2}(2s-1)$$

(8)

$${A}_{3}={\rho }_{0}{c}_{0}^{2}(3{s}^{2}-4s+1)$$

(9)

$${T}_{1}={\rho }_{0}{c}_{0}^{2}$$

(10)

$${B}_{0}={B}_{1}=2s-1$$

(11)

$${T}_{2}=0$$

(12)

where, c₀ is the propagation velocity of sound in the material; s is an empirical parameter, Meyers gives the value of the relevant material parameter, here with reference to the similar rock material, s = 1.11. Then we have A₁ = T₁ = 49.90 GPa, A₂ = 60.88 GPa, A₃ = 11.48 GPa, B₀ = B₁ = 1.22.

$${\beta }_{c}=\frac{4}{20+3{f}_{c}}$$

(13)

$${\beta }_{t}=\frac{2}{20+{f}_{c}}$$

(14)

$${P}_{el}=\frac{2{f}_{c}}{3}$$

(15)

According to Eqs. (13), (14) and (15) calculated: β_c = 0.0106, β_t = 0.0106, P_el = 79.6Mpa, and take α₀ = 1.0, D₁ = 0.04, D₂ = 1, ξ = 0.5, ε_p^m = 0.015, P_co = 6.0 GPa, N_p = 3.0; A, N, fs*, fs*, Q₀, B, A_f, N_f, g_c*, g_t* the way of obtaining is more complicated, here refer to the similar rock parameters values are taken and corrected.

The parameters of explosives are mainly determined directly based on the parameters selected on site, such as density and detonation velocity, while the parameters of the JWL equation of state are selected based on past experience; The parameters of air and blockage are also selected based on previous research.

The parameters related to the silica RHT model, explosives, air, and plugging materials are shown in Table 3.

Table 3 Parameters of silica RHT model, explosives, air, plugging materials.

Optimization study of hole network parameters for large diameter deep hole quarries

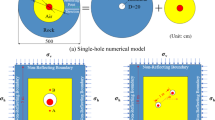
In accordance with the conventional layout of large-diameter parallel deep-hole blasting at the Dongguashan Copper Mine, the holes exhibit a certain symmetry. To reduce the model size and shorten calculation time, two rows of holes can be used to simulate the blasting effects of multiple rows. For each row, two holes are selected for analysis. In this simulation, the rock body is 20 m in length, 20 m in width, and 5 m in height, with a total of two rows and four holes.

Optimization of hole sizes for large diameter deep hole mining

In this study, we selected borehole diameters of 165 mm and 120 mm for analysis based on the actual engineering conditions of the Dongguashan Copper Mine and experiences from similar mining projects. The 165 mm diameter holes are commonly used for large-scale deep-hole blasting operations due to their higher energy output and extensive fragmentation capabilities. In this study, we recommend using 165 mm diameter holes for large blasting volumes. Specifically, we define "large blasting volumes" as operations where the single-blast rock removal volume exceeds 1000 cubic meters (m³). This definition is based on the practical experience from deep-hole blasting operations in large-scale open-pit mines and underground stope mining scenarios, where extensive rock mass needs to be fragmented efficiently. In contrast, the 120 mm diameter holes are considered for scenarios where more precise control of blasting effects is required. By comparing these two diameters, we aim to understand the influence of borehole size on stress wave propagation and rock fragmentation efficiency, thereby providing a basis for optimizing blasting designs in similar mining environments.In this study, an uncoupled charge structure was employed for both the 165 mm and 120 mm boreholes. The uncoupled charge structure, where the explosive charge is smaller than the borehole diameter, allows for a buffering effect through the air gap between the explosive and the borehole wall. This reduces the peak stress on the borehole wall and minimizes excessive damage to the surrounding rock mass, which is critical for maintaining the stability of the ore pillars and reducing ore loss. The use of uncoupled charges also helps in extending the duration of the blasting load, thereby improving the overall fragmentation efficiency.

Figure 2 is the plane sliced stress wave distribution for blast holes of different diameters (165 mm and 120 mm). The figure shows the propagation pattern of stress waves and peak pressure zones in the surrounding rock mass, highlighting the differences in stress distribution between the two hole sizes. The diagram reveals that for both 165 mm and 120 mm holes, the propagation pattern of the blasting stress waves is essentially the same. The waves radiate outward in a columnar fashion from the blasting source, and the pressure is highest near the blast origin. As the distance from the source increases, the peak stress wave rapidly attenuates from several GPa to a few MPa. The high-stress wave distribution extends to a radius of 2 to 3 times the borehole radius.

Fig. 2

Plane sliced stress wave distribution of blast holes of different diameters.

Typically, the shock wave generated by the explosion exceeds the dynamic compressive strength of the rock, forming a crushed cavity. This blasting crushing zone develops quickly, lasting only about 1–2 ms. As shown in Fig. 3, the crushing zone cavity map illustrates that the explosion from the 165 mm uncoupled charging structure creates a crushed zone with a radius of approximately 190 mm—around 2.3 times the borehole radius. The peak pressure at the hole wall is about 5 GPa. For the 120 mm borehole with an uncoupled charge, the explosion forms a crushed zone with a radius of about 120 mm—approximately 2.0 times the hole radius, with a peak pressure of around 3.6 GPa. Both the crushed zone radius and peak pressure increase as the borehole diameter increases.

Fig. 3

Plane sliced stress wave distribution of blast holes of different diameters.

In Fig. 4, the horizontal axis represents time (in milliseconds, s), and the vertical axis represents pressure (in gigapascals, GPa). The text above the curve indicates the peak pressure point, corresponding to the maximum pressure value at the moment of explosion.As shown in Fig. 4, simulations were used to calculate the stress wave distribution patterns for different borehole diameters in a single-hole infinite rock medium. The preset monitoring points near the blast hole walls provided stress decay curves, indicating that, for both the 120 mm and 165 mm single-hole explosions, the area within 2–3 times the borehole diameter experiences a significant impact load. This load greatly exceeds the rock’s compressive strength, forming a pulverized (compression) zone. As the stress wave propagates farther from the blast, the peak stress, wave speed, and frequency begin to attenuate. In these regions, the compressive stress becomes insufficient to cause further rock yield, but the radial and circumferential tensile stresses generate a fissure zone as the rock fractures under tension⁴¹. The size of the fissure zone extends to approximately 40–60 times the borehole diameter. The peak pressure at the wall of the 165 mm borehole is about 5 GPa, while the peak pressure at the 120 mm borehole is around 3.6 GPa. The radius of the crush zone.

Fig. 4

Peak pressure decay curves for the typical rock units near 165 mm and 120 mm diameter boreholes.

As the hole diameter increases, the peak pressure value also rises. To achieve the same blasting effect with 120 mm holes as with 165 mm holes, the distance between holes and the row spacing should be correspondingly reduced, which in turn increases the workload and operating time.

Optimization of large diameter deep hole mining network

To optimize the hole network parameters for large-diameter deep-hole blasting, numerical simulations were conducted under various row spacing and hole spacing conditions. The delay time for blasting was set to 5 ms (ms) based on previous experience from similar blasting operations in deep mining environments. This experience has shown that a delay time of 5 ms effectively balances the propagation of stress waves and the fragmentation efficiency, while minimizing the risk of excessive stress wave superposition and damage to surrounding rock masses. Specifically, this delay time was determined through extensive numerical simulations and field tests in similar geological conditions, which demonstrated that 5 ms is optimal for achieving efficient rock fragmentation while maintaining stability in high-stress environments.

First, based on the experience from similar mining projects, an approximate range of reasonable hole network parameters for the blast holes was estimated. Then, using ANSYS/LS-DYNA, simulations were conducted under various row spacing and hole spacing conditions. The results were analyzed to determine the optimal hole network parameters for each borehole diameter. The propagation and superposition patterns of effective stress in the model were examined, and the shape of the holes post-blasting in the ore rock model was observed. If there is an obvious triangular wedge in the middle of the hole or at the corners, and large ore pieces slide down due to this suspended wedge, it indicates that the hole network parameters are too large. By adjusting these parameters, the optimal choice is the largest hole network where no significant triangular wedges interfere with the blasting effect.

Based on the experience from previous projects, three sets of hole network parameters were selected for analysis and comparison: 2.8 m × 2.8 m, 3.0 m × 3.0 m, and 3.2 m × 3.2 m (row spacing × hole spacing). During blasting, a method of using micro-delays both between rows and within rows was employed. This means the first row of blast holes was detonated first, followed by the second row sequentially. The detonation stress waves for different rows of holes are shown in Fig. 5. Figure 5 shows that stress wave distribution for different rows of blast holes (first row and second row), showing the propagation and superposition effects during sequential detonation. The figure highlights the impact of row spacing on stress wave interaction.To further observe the superposition effect of the stress wave, a node numbered 10,205 was selected as an observation point at the center between the holes. The time history of the vertical vibration velocity at this observation point is illustrated in Fig. 6.

Fig. 5.

Different rows of holes detonation stress wave map.

Fig. 6

Velocity time course in vertical direction of monitoring node.

As shown in Fig. 6, after the first hole in the first row detonates, the monitoring point’s vertical vibration velocity quickly reaches its peak and then begins to decline. The figure shows how vibration velocity changes over time. Each subsequent blast slightly increases the peak velocity, but it never exceeds the initial peak velocity. Overall, the peaks become progressively smaller, and the frequency decreases⁴².Additionally, the z-velocity exhibits a decreasing and stable trend when Time is less than 0.03 s. This initial trend reflects the propagation of stress waves and the initial response of the rock mass to the blasting load. As the stress waves propagate through the rock mass, the z-velocity gradually decreases and stabilizes.However, when Time exceeds 0.03 s, the z-velocity suddenly reaches − 4. This significant change in z-velocity can be attributed to the reflection of stress waves at the free surface or other reflective interfaces within the rock mass. When the stress waves encounter these interfaces, they generate reflected waves that interact with the incident waves, leading to abrupt changes in the vertical velocity.This suggests that the inter-row and intra-row differential blasting effectively prevents stress wave superposition, reduces blasting vibrations, extends the duration of the blasting load, and mitigates the high-stress zones caused by simultaneous blasting. As a result, the stress distribution becomes more uniform and reasonable, leading to a more efficient rock crushing effect. The damage diagrams of the blasting hole shapes for the three different hole network parameters are shown in Fig. 7.

Fig. 7

Explosion hole diagram of model with different pore mesh parameters.

From Fig. 7, it can be seen that with the increase of the hole mesh parameters, the effect of rock breaking is getting worse and worse. The figure illustrates the optimal hole spacing for minimizing damage.When the pore mesh parameter is 2.8 m × 2.8 m, there is basically no obvious triangular spine suspension generated at the corners, indicating that this parameter is appropriate. When the hole mesh parameters for the 3.0 m × 3.0 m, the corners of just a little bit of triangular spine hanging generation, that this parameter can also meet the blasting requirements. When the hole network parameters for 3.2 m × 3.2 m, the corners have obvious triangular spine suspension generated, the blasting effect is relatively poor, easy to produce large blocks, indicating that this time the hole network parameters are too large, the explosion between the holes tends to be independent of the role of the loss of stress waves superimposed on the role of rock fragmentation. In summary, to maximize the utilization rate of explosives, it can be concluded that the optimal hole network parameters for 165 mm uncoupled charge blasting are 3.0 m × 3.0 m (row spacing × hole spacing).

Large diameter deep hole mining side hole blasting damage simulation analysis

In the design of large-diameter deep hole mining sites, the design of blast holes and charge structures is a key step to ensure blasting effectiveness and safety. According to the actual production needs of the mine, the diameter of the blast hole is designed to be 165 mm, and explosive rolls with a diameter of 140 mm and a length of 0.5 m are selected. Bamboo tubes are used to achieve air interval charging to optimize blasting parameters, control energy release, and reduce unnecessary losses. The specific design of the charge structure is as follows: 3 explosive rolls are loaded into each blast hole, and bamboo tubes with a length of 1.5 m are used at axial intervals to enable the explosives to function in sections, further improving the uniformity and efficiency of blasting. After charging to the designed height of the blast hole, the blasting timing is controlled by precise delay detonation, with a selected delay time of 5 ms, to effectively reduce the mutual interference between adjacent blast holes and enhance the effect of rock disintegration. During the research process, the blasting model and the main research area are shown in Fig. 8b. The axial charge structure of the blast hole fully refers to the actual production conditions of the mine, combined with experience and scientific design, and adopts a scheme of three-stage explosives and 4.5 m air interval charge to ensure that it can meet the requirements of ore disintegration while minimizing environmental impacts such as dust and vibration. The specific schematic of its axial charge is shown in Fig. 8c.

Fig. 8

Meshing details of the blasthole and surrounding area.

The model size and grid division in this study follow the actual requirements of blasting simulation, ensuring a balance between model accuracy and computational efficiency. The model is modeled and calculated using the International System of Units (SI). To improve simulation accuracy, the model partitioning method adopts mapping partitioning technology, where the grid size of all areas except for the row and column units where the blast hole is located is uniformly 10 cm × 10 cm × 10 cm, to ensure uniformity and solution efficiency within the calculation area. In response to the particularity of the blast hole area, in order to more accurately describe the propagation of blasting loads and charge effects, the mesh around the blast hole has been finely divided, as shown in Fig. 8e for specific details. At the same time, in response to the modeling requirements of radial uncoupled charges, full consideration is given to the interaction between charges, air gaps, and rock masses. By refining the grid and reasonable charge distribution, accurate simulation of the actual blasting process is achieved. In order to simulate the dynamic response of infinite rock mass more realistically, the model adopts non reflective boundaries in the setting of boundary conditions. Except for the free surface of the model, all other rock surfaces are set as non reflective boundaries to eliminate the interference of boundary reflection waves on the blasting simulation results. This boundary treatment method effectively ensures the natural propagation of blasting waves in the model, avoiding error accumulation caused by wave reflection. By designing the above model and handling the boundary conditions, an accurate and reliable simulation environment can be provided for subsequent blasting dynamics analysis.In this paper’s simulation, the rock units and plugging units are modeled using the Lagrange algorithm, while the bamboo tube spacing is treated as air. The explosive units, air units, and fluid–solid coupling spaces are modeled using the ALE (Arbitrary Lagrangian–Eulerian) algorithm. The calculation simulates a single hole and a single section of detonation. From the damage cloud results, it can be observed that the blasting damage is fully developed within 5.0 ms. Therefore, the time interval between hole detonations is set to 5.0 ms to reduce computational time and cost, and to improve calculation efficiency. Explosives within the same hole are detonated simultaneously⁴³. Since the mine is located at an elevation of − 730 m or below, with no major faults and undeveloped joints and fissures, the discontinuity of the rock body is not considered in the simulation.

Influence of side aperture diameter toward the uncoupling coefficient

The decoupling coefficient is a key parameter for the energy transfer efficiency between the charge and the rock, which directly affects the distribution and transfer of energy during the blasting process. When the decoupling coefficient is too high, energy may be too concentrated, leading to excessive blasting effect and unnecessary damage to the boundary of the ore body; When the decoupling coefficient is too low, energy may not be effectively transmitted, resulting in poor blasting effect and inability to achieve the expected rock fragmentation effect. By optimizing the decoupling coefficient, it is possible to ensure a reasonable allocation of blasting energy, effectively control damage to the boundaries of the ore body, avoid waste and crack formation, and thus improve the resource utilization and safety of mining operations. In addition, a reasonable selection of decoupling coefficients can help improve the accuracy of blasting operations, making boundary control more refined and controllable.

In smooth blasting and pre-fracture blasting, the use of uncoupled charging methods in boreholes has become widespread across various construction sites. Scholars generally agree that in uncoupled charge blasting, the explosive’s impact initially compresses the air in the gap between the borehole and the explosive charge. This air acts as a buffer, reducing the direct impact on the borehole wall before the shock wave refracts into the surrounding rock, forming a shock wave around the borehole⁴⁴. Compared to coupled charging, uncoupled charging reduces the peak shock wave, thereby lessening the damage to the rock at the borehole wall. Additionally, the presence of air, which compresses and expands, prolongs the detonation’s action time, effectively enhancing the utilization of the explosive’s energy.

In the large-diameter deep-hole mining operations at the copper mine, the side holes use explosives with a diameter of 140 mm, corresponding to a radial uncoupling coefficient of k₁ = 1.18. To study the impact of the radial uncoupling coefficient on the damage to the ore pillar, different explosive diameters were selected based on commonly used sizes. These included explosive rolls with diameters of 125 mm, 110 mm, 100 mm, and 90 mm, corresponding to radial uncoupling coefficients k₁ of 1.32, 1.5, 1.65, and 1.83, respectively. The axial loading structure and the effects of these radial uncoupling coefficients are examined. The axial loading structure is shown in Fig. 9, along with the radial modeling details.The decoupling coefficients of borehole 4 are respectively 1.18, 1.32, 1.5, 1.65, and 1.83.

Fig. 9

Radial uncoupling coefficient modeling details.

The calculation parameters for the 4# borehole uncoupled blasting is shown in Table 4. The mine’s original plan uses a 140 mm explosive charge for the side holes, with a radial uncoupling coefficient of 1.18. Keeping other conditions unchanged, Programs 2 through 5 sequentially increase the uncoupling coefficient for the side holes and proportionally reduce the diameter of the explosive charge. Blasting models for each program were established based on these variations.

Table 4 4 # hole diameter to the uncoupled blasting calculation parameters.

The damage cloud diagrams at t = 1.2 ms, 4.2 ms, 5 ms, 6.1 ms, 10.0 ms, 15.0 ms, 20.0 ms, 25.0 ms for the side aperture toward the uncoupling coefficient k1 = 1.18 and the top view of the damage of the ore column at t = 25.0 ms are shown in Fig. 10.The figure shows the development of rock damage and stress wave propagation over time. As seen in Fig. 10, after the detonation of explosives in hole 1# at t = 1.2 ms, the compressive stress wave reflects off the free surface and transforms into a tensile stress wave, causing damage to the rock at the free surface. Axially, the damage is characterized by a larger affected area in the section containing explosives and a smaller one in the air layer. Comparing Fig. 10b,c shows little difference in damage at t = 4.2 ms and t = 5.0 ms, indicating that the damage fully develops by t = 5.0 ms, making this time extension more reasonable. At t = 5.0 ms, significant damage occurs between the free surface and the borehole along the line of minimum resistance. At t = 6.1 ms, after the detonation of explosives in hole 2#, the tensile stress wave generated at the free surface causes further damage to the rock, and the overlapping axial area between holes 1# and 2# experiences greater damage than hole 1# alone. This result is due to two factors: (1) node constraints were applied differently between holes 1# and 2#, and (2) the integrity of the rock after hole 1#’s detonation was better, allowing hole 2#'s explosion to accumulate more damage to the surrounding rock mass. At t = 10.0 ms, the damage from hole 2# is fully developed and merges with the damage area of hole 1#. Due to the "empty hole effect," tensile damage forms between holes 2# and 3#, although the overall damage is lower than 0.2. By t = 15.0 ms, the damage in hole 3# is essentially complete, with surface damage along the line of holes, though again, the damage value remains below 0.2. At t = 20.0 ms, the blast damage from hole 4# is fully established, causing significant damage to the ore column. The largest damage occurs along the line of the holes, with the middle section showing more damage than the two ends, but with values generally lower than 0.2. By t = 25.0 ms, there is no significant change in the damage area compared to t = 20.0 ms.

Fig. 10

Damage cloud at each moment of k₁ = 1.18.

For k₁ = 1.32, the damage clouds at t = 15.0 ms and t = 25.0 ms are shown in Fig. 11, along with the top view of the ore column’s damage at these times. From Fig. 11a, it can be seen that by t = 15.0 ms, the damage range caused by hole 3# is essentially determined. Due to the "empty hole effect," significant damage occurs along the line connecting the holes, with the middle of the damage zone being more extensive than the areas at either end. Compared to k₁ = 1.18, the damage range at k₁ = 1.32 is larger, although the overall damage value remains below 0.2. By t = 25.0 ms, the damage ranges from hole 4# is also fully developed. As shown in Fig. 11b, when k₁ = 1.32, significant damage occurs along the line of minimum resistance for hole 4#. It is evident that as the radial uncoupling coefficient increases, the overall damage range of the ore column decreases at k₁ = 1.32 compared to k₁ = 1.18. By comparing Figs. 10i and 11c, it can be seen that, except for the direction of the blast hole line, the damage range in the x-axis and y-axis directions decreases, but the damage range in the direction of the blast hole line increases.

Fig. 11

Damage cloud at each moment when k₁ = 1.32.

The top views of the damage cloud at t = 15.0 ms and t = 25.0 ms for k₁ = 1.5, along with the damage cloud of the ore column at t = 25.0 ms, are shown in Fig. 12. From Fig. 12a, it can be observed that by t = 15.0 ms, the damage range caused by hole 3# is essentially determined. Due to the "empty hole effect," significant damage occurs along the hole line direction, with the middle of the damage zone being more extensive than at the ends. At k₁ = 1.32, the damage is greater, but the overall damage remains below 0.2. By t = 20.0 ms, the damage caused by hole 4# is fully developed. As seen in Fig. 12b, when k₁ = 1.5, significant damage also occurs along the minimum resistance line of hole 4#. Comparing Figs. 11b and 12b, it is clear that as the radial uncoupling coefficient increases, the overall damage range of the pillar decreases at k₁ = 1.5 compared to k₁ = 1.32. Additionally, comparing Figs. 11c and 12c shows that the damage range decreases along the x-axis and y-axis, except along the direction of the gunnel line, where the damage range increases.

Fig. 12

Damage cloud at each moment when k₁ = 1.5.

For k₁ = 1.65, Fig. 13 shows the top view of the damage cloud diagrams at t = 15.0 ms and t = 25.0 ms, as well as the damage cloud of the ore column at t = 25.0 ms. From Fig. 13a, it can be seen that by t = 15 ms, the damage range caused by hole 3# is essentially determined. Due to the "empty hole effect," significant damage occurs along the hole connecting line, with the damage near the middle being greater than at the ends. The damage range at k₁ = 1.65 is larger than at k₁ = 1.5, although the overall damage remains below 0.2. By t = 20.0 ms, the damage range caused by hole 4# is fully developed. As seen in Fig. 13b, when k₁ = 1.65, the damage along the minimum resistance line of hole 4# is reduced compared to k₁ = 1.5. Comparing Figs. 12b and 13b, it is evident that as the radial uncoupling coefficient increases, the overall damage range of the ore column decreases at k₁ = 1.65 compared to k₁ = 1.5. Similarly, comparing Figs. 12c and 13c shows that the damage range decreases in the x-axis and y-axis directions, except along the gunnel connecting line, where the damage range increases.

Fig. 13

Damage cloud at each moment when k₁ = 1.65.

The top views of the damage cloud at t = 15.0 ms and t = 25.0 ms for k₁ = 1.83, as well as the damage cloud of the ore column at t = 25.0 ms, are shown in Fig. 14. As seen in Fig. 14a, by t = 15.0 ms, the damage range caused by hole 3# is essentially determined. Due to the "empty hole effect," significant damage occurs along the hole connecting line. The damage near the intermediate charging section is larger than near the blocking section, and the damage range is greater than at k₁ = 1.65, although the overall damage remains below 0.2. By t = 25.0 ms, the damage range caused by hole 4# is fully developed. As seen in Fig. 14b, when k₁ = 1.83, the damage along the minimum resistance line of hole 4# is reduced compared to k₁ = 1.65. Comparing Figs. 13b and 14b, it is evident that as the radial uncoupling coefficient increases, the overall damage range of the pillar decreases at k₁ = 1.83 compared to k₁ = 1.65. Similarly, comparing Figs. 13c and 14c shows that the damage range decreases in the x-axis and y-axis directions, except along the gunnel connecting line, where the damage range increases.

Fig. 14

Damage cloud at each moment when k₁ = 1.83.

As the uncoupling coefficient in the diameter direction of the 4# hole increases, the overall damage range of the pillar decreases, while the damage range along the hole connecting line increases. This damage is characterized by a smaller range at the two ends and a larger range in the middle, though the overall damage remains below 0.2. The damage cloud diagrams for the center of the 4# hole connecting line at t = 25.0 ms for uncoupling coefficients k₁ = 1.18, k₁ = 1.32, k₁ = 1.5, k₁ = 1.65, and k₁ = 1.83 are shown in Fig. 15.

Fig. 15

Damage cloud at the center of the borehole with different uncoupling coefficients for 4# borehole.

From Fig. 15a, it can be seen that, due to the accumulation of damage, the severe damage areas (where D ≥ 0.9) caused by holes 2#, 3#, and 4# in the connecting plane are larger than those around hole 1#. There is no severe damage area around the air section in the upper axial part of the hole, but the damage still exceeds 0.5. By t = 25.0 ms, the damage range of hole 4# is fully developed, with the damage near the mouth and bottom of the hole being greater than that near the center of the mine columns. In the middle loading section, the damage range is larger than in the air spacing section, indicating that the loading section sustains more damage. When the uncoupling coefficient k₁ = 1.18 is used for the side hole diameter, some severe damage areas (D ≥ 0.9) also appear at the boundary between the pillars and the mine room near the charging section.

From Fig. 15b, it can be seen that as the uncoupling coefficient increases, the extent of the serious damage area (where D ≥ 0.9D ≥ 0.9) near the explosive section of hole 4# at k₁ = 1.5 is significantly reduced compared to k₁ = 1.18. Additionally, the damage range of the ore column near the opening of hole 4# (where D ≥ 0.5) is also noticeably smaller than at k₁ = 1.18. However, the overall damage range on the connecting surface between the hole’s increases compared to k₁ = 1.18, with smaller damage areas at both ends and larger damage in the middle.

From Fig. 15c, it can be seen that as the uncoupling coefficient increases, the extent of the serious damage area (where D ≥ 0.9) near the explosive section of hole 4# at k₁ = 1.5 is significantly reduced compared to k₁ = 1.32. Additionally, the damage range of the ore column near the mouth and bottom of hole 4# (where D ≥ 0.5) and the intermediate charge section (where D ≥ 0.5) is noticeably reduced compared to k₁ = 1.18 and k₁ = 1.32. However, the overall damage range on the connecting surface of the hole’s increases compared to k₁ = 1.32, with smaller damage ranges at both ends and a larger damage range in the middle.

From Fig. 15d, it can be observed that when k₁ = 1.65, the extent of the serious damage area (where D ≥ 0.9) near the explosive section of hole 4# is significantly reduced compared to k₁ = 1.5. Similarly, the damage range near the mouth and bottom of hole 4# (where D ≥ 0.5) and the middle charging section (where D ≥ 0.5) is also noticeably reduced compared to k₁ = 1.5. However, with k₁ = 1.65, the overall damage range on the connecting surface of the holes increases, and the degree of damage becomes larger. Additionally, at k₁ = 1.65, some areas with damage below 0.2 appear at the boundary of the mine room in the air spacing section of hole 4#, indicating the possibility of under digging. From Fig. 15e, it can be seen that when k₁ = 1.83, the extent of the serious damage area (where D ≥ 0.9) near the explosive section of hole 4# is significantly reduced compared to k₁ = 1.65. Similarly, the damage range of the ore column near the blockage at both ends (where D ≥ 0.5) and near the intermediate loading section (where D ≥ 0.5) is noticeably reduced compared to k₁ = 1.5. However, when k₁ = 1.83, the damage range on the connecting surface of the holes increases compared to k₁ = 1.65. At k₁ = 1.83, some areas with damage below 0.2 appear at the boundary of the mine room in the air spacing section of hole 4#, indicating the potential for underdigging.

To accurately describe the damage and destruction of the pillar’s rock body under different radial uncoupling coefficients, LS-PREPOST post-processing software was used to calculate the volume of units with D ≥ 0.5 at t = 25.0 ms under varying loading conditions for the No. 4# holes. The volume of pillar damage and destruction under different radial uncoupling coefficients for the side holes is presented in Fig. 16. When k₁ = 1.18, the damage volume of the ore column is 11.25 m³; at k₁ = 1.32, the damage volume is 10.40 m³; at k₁ = 1.5, the damage volume is 9.87 m³; at k₁ = 1.65, the damage volume is 9.54 m³; and at k₁ = 1.83, the damage volume decreases to 8.63 m³. As shown in Fig. 16, the damage volume of the ore column decreases as the radial uncoupling coefficient k₁ increases. The figure demonstrates the reduction in damage volume with increasing uncoupling coefficient, highlighting the optimal coefficient for minimizing damage.When k₁ is between 1.18 and 1.65, the rate of reduction in damage volume slows with the increase in the radial uncoupling coefficient.

Fig. 16

Damage volume of ore pillar with different radial uncoupling coefficients in 4# shell hole.

Figure 17 shows the effective stress propagation cloud diagram of the rock body when the uncoupling coefficient k₁ = 1.83 in 4# hole. Observation of explosives from detonation to the end of the rock changes, it can be seen in t = 0.2 ms when the 1 # gun hole detonation of the wave front surface in an elliptical shape to the surrounding area to reach the highest peak stress of 171 MPa after a rapid decline in t = 5.15 ms when the 2 # holes began to detonate the highest peak value of 177 MPa, and then superimposed with the 1 # holes in the subsequent several hundred microseconds of the stress wave generated by the peak stress rises to 204 MPa, to t = 10.0 ms when the peak effective stress dropped to 124 MPa. When t = 10.5 ms when the 3 # holes detonated, the effective stress rose to 192 MPa or so, to t = 15.5 ms 4 # holes began to detonate, the entire mine intersected the stress waves to form a complex wavefront surface, the highest peak stress at this time amounted to 229 MPa, the superposition effect is obvious.

Fig. 17

Effective stress cloud (k₁ = 1.83).

The distribution of measurement points and the locations for effective stress extraction in the unit are shown in Fig. 18. A total of five measurement points, labeled A through E, are set to monitor the effective stress distribution of the column under different loading structures. The effective stress extraction locations for the pillars under different loading conditions are the same as those depicted in Fig. 18.

Fig. 18

Schematic diagram of effective stress monitoring points in the pillar.

The stress-time curves at measurement points A through E under different side hole uncoupled charging coefficients are shown in Fig. 19. The figure displays a total of four stress peaks at the measurement points on the pillar. Over time, the value of the stress peaks shows an increasing trend. The number and size of these stress peaks are determined by the timing and location of the blast holes. The first hole, furthest from the measurement point, detonates first, with the stress wave reaching the pillar stress monitoring point after approximately 2 ms. As the stress wave travels, it attenuates with distance, reaching the measurement point with a peak of about 8 MPa. As the second and third holes detonate sequentially, two higher stress peaks appear at the measurement point, with an interval of about 5 ms, corresponding to the delayed detonation timing of the holes. The greatest impact on the surrounding rock occurs with the detonation of the side hole, due to its proximity to the surrounding rock. The attenuation of the stress wave peak is smaller, resulting in a “jump” in the stress peak compared to the first three detonation events.

Fig. 19

Stress time curves of radial decoupling coefficients at different monitoring points.

Figure 19f illustrates the relationship between peak stress at each measurement point under different uncoupling coefficients. As seen in the Fig. 19f, the uncoupling coefficients of the side-hole loading have a significant impact on the surrounding rock. The peak stress generated, from largest to smallest, follows the loading structure sequence: d2 = 140 mm > d2 = 125 mm > d2 = 110 mm > d2 = 100 mm > d2 = 90 mm. The larger the uncoupling coefficient, the smaller the equivalent stress at the monitoring points of the pillar. When the uncoupling coefficient is k₁ = 1.83, the peak stress is around 50 MPa. As the radial uncoupling coefficient increases from k₁ = 1.18 to k₁ = 1.83, the peak stress decreases gradually, with a variation of about 10 MPa. This indicates a relatively flat trend in the equivalent force at the same monitoring point as the uncoupling coefficient changes. When the loading diameter for hole 4# is 140 mm, the maximum peak stress generated is around 96 MPa. Combined with the data in Fig. 16, this confirms a close correlation between peak stress and the damage to the pillar: the greater the peak stress, the more significant the damage. In practical applications, when considering the blasting effect in the mine room, efforts should be made to maximize the uncoupling coefficient for side holes⁴¹.

Additionally, in our numerical simulations, we observed that the peak stress at point A was higher when the radial decoupling coefficient (k1) was 1.83 compared to when k1 was 1.65. This seemingly counterintuitive result can be attributed to the complex interactions of stress waves and the specific layout of the blast holes.When k1 is 1.83, the larger air gap between the explosive charge and the borehole wall results in a more gradual energy transfer to the surrounding rock mass. This can lead to a more uniform distribution of stress waves, which may result in higher peak stress values at specific monitoring points like point A. In contrast, when k1 is 1.65, the smaller air gap allows for a more direct and concentrated transfer of energy, which can lead to lower peak stress values at point A due to reduced stress wave superposition.

Effect of axial loading structure of side holes

The axial charge structure refers to the arrangement and structural form of the charge inside the blasting hole, which directly affects the direction and mode of propagation of blasting energy along the hole. A reasonable axial charge structure can ensure more uniform transmission of blasting energy in the rock mass, thereby reducing the excessive concentration of energy in certain areas, which helps to avoid uneven damage to the boundaries of the ore body. If the charge structure is unreasonable, energy may be too concentrated in certain areas, resulting in severe damage to the boundaries of the ore body, and may even cause vibration or rock fractures, affecting mining safety. By optimizing the axial charge structure, the direction and distribution of energy release can be better controlled, ensuring the accuracy of blasting effects and the stability of boundaries, thereby achieving effective control of ore body boundaries, reducing ore body losses, and improving mining efficiency.

To reduce the charge density of the side hole line by adjusting the axial charge structure, the following schemes have been designed: (1) Scheme 1: The length of the axial single-stage charge remains unchanged, using 3 rolls of explosives (1.5 m of explosives with a roll diameter of 140 mm). The air interval length is increased from 1.5 to 2.5 m, reducing the axial charge from 5 sections of explosives to 4 sections, resulting in a 20% reduction in explosive volume. The lengths of the bottom plugging and hole mouth plugging remain unchanged at 2 m and 2.5 m, respectively. (2) Scheme 2: The axial single-stage charge length and the use of 3 rolls of explosives (1.5 m, 140 mm diameter) remain the same. However, the air interval length is increased from 1.5 to 4.5 m, reducing the axial charge from 5 sections of explosives to 3 sections, leading to a 40% reduction in explosive volume. The lengths of the bottom plugging and hole mouth plugging remain unchanged at 2 m and 2.5 m, respectively. (3) Scheme 3: The air interval length remains unchanged at 1.5 m, while the axial charge uses 2 rolls of explosives (1 m charge length, 140 mm diameter). This setup uses 6 sections of explosives, reducing the explosive volume by 20%. (4) Scheme 4: Similar to scheme 3, the single-stage charge length remains at 1 m (140 mm diameter), but the air interval length is increased from 1.5 to 2.125 m. This setup uses 5 sections of explosives, reducing the explosive volume by 33.3% compared to the original design of mine. The modeling details for the axial charge structure of the 4# blasthole are shown in Fig. 20.

Fig. 20

Modeling details of axial charging structure of 4# hole.

The blasting calculation parameters of the axial charging structure of 4# holes are shown in Table 5.

Table 5 Parameters for blasting calculations for side aperture diameter-oriented charging structures.

The top view of the damage cloud at t = 15.0 ms and t = 25.0 ms for scheme 1 and the damage cloud of the ore column at t = 25.0 ms are shown in Fig. 21. At t = 15.0 ms, the damage caused by hole 3# is fully developed, and due to the "empty hole effect," damage occurs along the ore column in the direction of the hole line. Comparing Fig. 21a with Fig. 10f, it can be seen that, unlike the changes observed with the radial non-coupling coefficient, there is no significant change in the damage range along the hole line direction between scheme 1 and the original scheme. By t = 25.0 ms, the damage range of hole 4# is fully determined. Comparing Fig. 21b with Fig. 10h, the damage range caused by hole 4# in scheme 1 decreases, but the damage range along the hole connecting line increases slightly. The damage in the middle of the ore column is greater, while the damage at both ends is smaller, though the difference is minimal. Comparing Fig. 21c with Fig. 10h, it can be observed that the overall damage range of the ore column for hole 4# in scheme 1 is reduced compared to the original scheme, particularly in the x-axis direction.

Fig. 21

Damage cloud diagram at each moment of scheme 1.

The top views of the damage cloud diagrams at t = 15.0 ms and t = 25.0 ms, along with the damage cloud diagram at t = 25.0 ms for the ore column in scheme 2, are shown in Fig. 22. At t = 15.0 ms, the damage caused by hole 3# is fully developed, and due to the "empty hole effect," it causes damage to the ore column along the hole connecting line. Comparing Fig. 22a with Figs. 10f and 21a, it can be seen that, unlike the changes associated with the radial non-coupling coefficient, there is no significant change in the damage range along the hole connecting line in scheme 2. By t = 25.0 ms, the damage range caused by hole 4# is fully established. Comparing Fig. 22b with Fig. 10h, the damage range in scheme 2 decreases. This is characterized by a larger damage range near the charge section and a smaller damage range near the air spacing section. However, there is no significant change in the damage range along the hole connecting line, with a larger damage range in the middle and a smaller range at both ends, though the difference is relatively minor. Comparing Fig. 22b with Fig. 21b, it is clear that the damage range near the charge section in scheme 2 is larger than in scheme 1, while the damage range near the air spacing section is reduced. Additionally, comparing Fig. 22c with Fig. 10h shows that the overall damage range in scheme 2 is reduced compared to the original mine design, mainly in the x-axis and y-axis directions. Finally, comparing Fig. 22c with Fig. 21c, it can be observed that the damage range in scheme 2 decreases along the y-axis but increases along the x-axis compared to scheme 1.

Fig. 22

Damage cloud diagram at each moment of scheme 2.

The top views of the damage cloud at t = 15.0 ms and t = 25.0 ms, along with the damage cloud at t = 25.0 ms for scheme 3, are shown in Fig. 23. At t = 15.0 ms, the damage caused by hole 3# is fully developed, and due to the "empty hole effect," it causes damage to the ore column along the hole line. Comparing Fig. 23a with Fig. 10f, it can be seen that, unlike the changes due to the radial non-coupling coefficient, there is no significant difference in the damage range along the hole line between scheme 3 and the original plan. At t = 25.0 ms, the damage caused by hole 4# is fully determined. Comparing Fig. 23b with Fig. 10g, it can be observed that the damage range of the mine pillar in scheme 3 is reduced, but the damage along the hole connecting line is also smaller compared to the original scheme. The damage range is larger in the middle and smaller at both ends, though the difference is minimal. Comparing Fig. 23b with Fig. 21b shows that the damage range of the ore column in scheme 3 is smaller than in scheme 1, indicating that with the same explosive charge, a more uniform distribution of explosives results in a smaller damage range. Comparing Fig. 23c with Fig. 10g, it can be seen that the overall damage range of the mine pillar in scheme 3, particularly for the 4# holes, is reduced compared to the original mine plan, especially in the x-axis and y-axis directions. Finally, comparing Fig. 23c with Fig. 21c reveals that the damage range in scheme 3 is smaller than in scheme 3.

Fig. 23

Damage cloud diagram of scheme III at each moment.

The top view of the damage cloud at t = 15.0 ms and t = 25.0 ms and the damage cloud at t = 25.0 ms for scheme IV is shown in Fig. 24. At t = 15.0 mst = 15.0 ms, the damage caused by hole 3# is fully developed, and due to the "empty hole effect," it causes damage to the ore column along the hole line. Comparing Fig. 24a with Fig. 10f, it can be seen that, despite the change in the radial non-coupling coefficient, there is no significant difference in the scope of damage between scheme 4 and the original scheme in the direction of the hole line. By t = 25.0 ms, the damage caused by hole 4# is fully determined. As shown in Fig. 24b, the damage range of the mine pillar caused by the 4# hole in scheme 1 decreases, but the damage range along the hole connecting line increases significantly. This is characterized by a larger damage range in the middle and smaller damage at both ends, though the difference is minimal. Comparing with Fig. 24c, it is evident that the overall damage range of the ore column in scheme 4, particularly for the 4# shell hole, is reduced. This reduction is mainly observed in the x-axis and y-axis directions.

Fig. 24

Damage cloud diagram of scheme IV at each moment.

The damage cloud diagram for the center of the hole connecting line at t = 25.0 ms for schemes I, II, III, and IV is shown in Fig. 25. Combining Fig. 25a and Fig. 15a, it can be observed that when keeping the radial uncoupling coefficient and the length of single-segment explosives unchanged, and only changing the axial loading structure, the range of serious damage caused by the explosive section of the 4# shell hole (D ≥ 0.9) remains mostly the same. However, the degree of damage in the air section is reduced due to the increased length of the air interval. The damage range greater than 0.5 in the ore column near the mouth and bottom of the 4# hole in scheme 1 is similar to that of the original scheme used in the mine, but the damage range near the middle section of the hole increases. Unlike changing the radial uncoupling coefficient, the overall damage range (D ≥ 0.2) on the connecting surface of the borehole slightly increases.

Fig. 25

Damage cloud of the center of the hole under different charging schemes.

From Fig. 25b, it is evident that in scheme 2, when keeping the radial uncoupling coefficient and the length of single-segment explosives unchanged, and only changing the axial loading structure, the range of serious damage caused by the explosive section of the 4# hole (D ≥ 0.9) is similar to the original scheme, while the degree of damage in the air section decreases due to the increased air spacing length. The damage range greater than 0.5 near the mouth and bottom of the 4# hole is consistent with the original scheme, but the damage range near the middle section of the hole increases. The damage range in the loading section near the mine is significantly larger than in the air spacing section, with the lowest damage occurring near the air spacing center. The overall damage range (D ≥ 0.2) on the connecting surface of the borehole slightly decreases compared to changing the radial uncoupling coefficient.

In Fig. 25c, with the radial uncoupling coefficient and air spacing length kept unchanged, but the length of a single explosive section reduced from 1.5 to 1.0 m in scheme 3, the range of serious damage (D ≥ 0.9) in both axial and radial directions becomes smaller. The damage range greater than 0.5 near the mouth and bottom of the 4# hole is consistent with the original scheme of mine. The overall damage range (D ≥ 0.2) on the connecting surface of the hole is slightly reduced compared to scheme 1. Additionally, the damage range near the center hole and bottom of the pillar is reduced compared to the original scheme. In Fig. 25d, by keeping the radial uncoupling coefficient unchanged and the length of the single explosive section at 1.0 m, but increasing the air spacing length from 1.5 to 2.125 m in scheme 4, the serious damage range of the air section is reduced. However, the damage range in the ore column near the center of the borehole increases compared to scheme 3, with an increase in the degree of damage. The overall damage range (D ≥ 0.2) on the connecting surface of the borehole slightly increases.

To accurately describe the damage and destruction of the ore column rock body under different axial loading structures, LS-PREPOST post-processing software was used to calculate the unit volume with D ≥ 0.5 at t = 20.0 ms for each scheme. The damage and destruction volumes of the ore column for the 4# borehole under different axial loading structures is shown in Fig. 26.

Fig. 26

Damage damage volume of ore column in different axial loading schemes of 4# hole.

As shown in Fig. 26, the damage volume of the ore column (D ≥ 0.5) for scheme 1 is 9.84 m³, for scheme 2 is 7.87 m³, for scheme 3 is 9.30 m³, and for scheme 4 is 8.70 m³. In Scheme 2, the destruction volume is comparatively smaller than other schemes, primarily due to the increased air spacing length and optimized charge structure. The increased air spacing acts as a buffer, reducing the peak stress transmitted to the surrounding rock mass. Additionally, the reduction in single-section charge weight and the total number of charge sections further minimizes the localized stress concentration, resulting in a more uniform distribution of blasting energy. This optimization not only reduces the overall destruction volume but also enhances the efficiency of rock fragmentation.

As the explosive charge volume of the 4# shell hole decreases, the damage volume of the ore column also decreases. Comparing scheme 1 and scheme 3, it is evident that with the same charge, a more uniform distribution of explosives results in less damage to the pillar. For an explosive diameter of 125 mm (radial uncoupling coefficient k₁ = 1.32), reducing the explosive charge by 20.3% results in a damage volume of 10.40 m³. In contrast, with a 20% reduction in explosive charge, schemes 1 and 3 result in damage volumes of 9.84 m³ and 9.30 m³, respectively, which are lower than the damage volume at k₁ = 1.32. For an explosive diameter of 110 mm (radial uncoupling coefficient k₁ = 1.50), a 38.3% reduction in explosive volume leads to a damage volume of 9.54 m³, which is greater than the damage volume in scheme 3. This suggests that adjusting the axial charging structure is more effective in reducing pillar damage, improving explosive energy utilization, and minimizing over-excavation in the mine room quarry.

Figure 27 shows the effective stress propagation cloud diagram of the rock body in scheme 1. At t = 0.2 ms, the detonation of hole 1# produces an elliptical wavefront that propagates outward, reaching a peak stress of 186 MPa before rapidly declining. At t = 5.15 ms, hole 2# begins to detonate, reaching a peak stress of 165 MPa. In the following microseconds, the stress waves from hole 1# and hole 2# superimpose, causing the peak stress to rise to 184 MPa. By t = 10.0 ms, the effective stress drops again. When hole 3# detonates at t = 10.5 ms, the effective stress rises to around 238 MPa. Finally, at t = 15.5 ms, hole 4# begins to detonate, and the intersecting stress waves in the mine room form a complex wavefront, with the highest peak stress reaching 290 MPa.

Fig. 27

Effective stress cloud (scheme I).

Unlike the method of changing the uncoupling coefficient of the holes, Fig. 28 shows that modifying the loading structure has a significant impact on the stress-time curve at the pillar’s stress monitoring point. In Fig. 28a,d, representing scheme 1 and scheme 4, the stress-time curves display three smaller stress peaks before reaching the peak stress of the entire blasting process. The impact of holes 1# to 3# on the pillar is much smaller than that of the side hole 4#. After reaching the peak stress, the curves rapidly decline and then stabilize. In Fig. 28b, due to the increased air column length and reduced explosive charge, the peak stress (53 MPa) of the entire stress-time curve is significantly lower than the peak stress (90 MPa) in scheme 1. In Fig. 28c, when the stress-time curve reaches its peak, the stress development pattern before the peak is similar to the other schemes. However, after reaching the peak, several stress monitoring points show a slower decrease in stress. The effective stress acting on the pillar is higher than in the other schemes, suggesting that reducing the number of explosive segments may be necessary in the actual loading process.

Fig. 28

Stress time curves of radial decoupling coefficients at different monitoring points.

As shown in Fig. 29, the comparison of effective stress generated by different loading structures highlights the impact on the pillar more intuitively. The original plan, with the largest charge, produces the highest stress peak at all five monitoring points (A–E). Although scheme 1 and scheme 3 have the same total charge, scheme 1 uses a larger single-section charge, resulting in a slightly higher stress peak than scheme 3. Similarly, scheme 4, with a reduced charge, has a peak stress close to that of scheme 2. Scheme 4, which has the smallest charge, exerts the least stress on the pillar. To minimize damage to the pillar, it is crucial to control both the maximum charge and the number of explosive segments during loading.

Fig. 29

Peak stress of different axial loading structures in 4# holes.

Discussion on the transition between tensile and compressive failure mechanisms

In the blasting process, rock failure is primarily driven by two mechanisms: compressive failure and tensile failure. The transition between these mechanisms is critical for understanding the overall damage characteristics and optimizing blasting parameters to achieve efficient fragmentation while minimizing damage to surrounding structures.

Compressive failure mechanism

Compressive failure occurs when the stress wave generated by the explosion exceeds the dynamic compressive strength of the rock, leading to the formation of a crushed zone near the blast source. This mechanism is dominant in the immediate vicinity of the blast hole, where the peak pressure is highest. For example, in our simulations, the peak pressure at the wall of the 165 mm borehole reached approximately 5 GPa, while for the 120 mm borehole, it was around 3.6 GPa (Fig. 4). In both cases, the crushed zone extended to about 2 to 3 times the borehole radius, indicating significant compressive damage in this region.

The compressive failure mechanism is characterized by the rapid attenuation of stress waves as they propagate outward from the blast source. Within the crushed zone, the rock is pulverized due to the high compressive stress, resulting in fine fragmentation. This mechanism is crucial for achieving efficient rock disintegration, especially in large-diameter deep-hole blasting operations where high energy output is required.

Tensile failure mechanism

As the stress wave propagates further from the blast source, the compressive stress gradually decreases, and tensile stresses become dominant. Tensile failure occurs when the radial and circumferential tensile stresses exceed the dynamic tensile strength of the rock, leading to the formation of fractures and cracks. This mechanism is responsible for the development of the fracture zone, which extends significantly beyond the crushed zone.

In our study, the tensile failure mechanism was observed to play a significant role in the overall damage profile. For instance, the damage cloud diagrams (Figs. 10, 11, 12, 13, 14) show that significant damage occurs along the line of minimum resistance, particularly in the middle section of the blast hole line. This is attributed to the tensile stresses generated by the stress wave reflection and the "empty hole effect," which enhances the tensile failure in these regions.

The transition from compressive to tensile failure is influenced by several factors, including the borehole diameter, charge structure, and blasting parameters. For example, increasing the radial uncoupling coefficient (k1) was found to reduce the peak stress and stabilize the equivalent stress at monitoring points, thereby minimizing compressive damage and enhancing tensile failure (Fig. 19). This suggests that optimizing the uncoupling coefficient can help achieve a more balanced failure mechanism, reducing the risk of excessive damage to surrounding rock.

Practical implications

Understanding the transition between compressive and tensile failure mechanisms is essential for optimizing blasting designs. By controlling the peak stress and promoting tensile failure, it is possible to achieve more efficient fragmentation while minimizing damage to surrounding structures. For example, our simulations showed that increasing the radial uncoupling coefficient (k1) from 1.18 to 1.83 significantly reduced the damage volume (Fig. 16) and peak stress (Fig. 19), indicating a more favorable failure mechanism transition.

In practical applications, this knowledge can be used to design blasting parameters that maximize fragmentation efficiency while reducing the risk of overbreak and damage to ore pillars. For instance, using larger uncoupling coefficients and optimizing axial charge structures can help achieve a more uniform stress distribution, enhancing tensile failure and reducing compressive damage.

Application of mining site boundary control engineering

The underground mining site of a copper mine in Anhui Province adopts the large-diameter deep hole mining method. The experimental mining site is the mining room mining site of a copper mine in Anhui Province, which is located below the elevation of − 730 m. The mining site is 82 m long, 18 m wide, and the designed length of the side hole is about 23.8 m. Combining "Influence of side aperture diameter toward the uncoupling coefficient" and "Effect of axial loading structure of side holes", under the same charge conditions, adjusting the axial charge structure of the side holes is more conducive to reducing pillar damage. Scheme three has a more uniform distribution of damage and effective stress compared to Scheme two, and the range of blast hole damage is smaller than Scheme four. The middle blast hole in the mining area still adopts the original mining plan, which is 1.5 m explosives and 1.5 m bamboo tubes; Improve construction quality and change the charging scheme for the side holes of the mining site to 1 m explosives and 1.5 m bamboo tubes. Conduct 3D laser scanning of the goaf after mining, and compare and analyze the designed mining unit with the solid model.

Analysis of overexcavation situation

Cut the void model every 5 m from − 725 m to − 755 m along the elevation direction, as shown in Fig. 30. The obtained void profile is shown in Fig. 31.

Fig. 30

Model and section location of goaf in mining area.

Fig. 31

Model and section location of goaf in mining area.

By comparing the void section generated along the elevation direction with the horizontal boundary of the mining site design, it is possible to clearly observe the phenomenon of over excavation or under excavation of the boundary at a specific elevation.Fig. 32 shows the comparison between the actual horizontal boundary and the design boundary of the airspace at an elevation of − 740 m. Among them, the purple solid line represents the actual measured boundary line of the empty space, while the blue solid line represents the designed unit boundary.

Fig. 32

Comparison between the actual boundary and the design boundary of the empty space − 740 m horizontal profile.

From Fig. 32, it can be seen that the − 740 m boundary control effect of the experimental vegetable field is good, and there is no obvious over excavation or under excavation near the boundary of the mining pillar.

Establish a mining design unit model based on the blasting design profile and the horizontal map of the middle section of the mining area, and combine it with the solid model to more intuitively reveal the differences between the actual model boundary and the design model boundary, and conduct comparative analysis. The experimental mining design unit is 82 m long, 18 m wide, and the mining height is the thickness of the ore body. The mining design model volume is 36,031 m³, and the mining design model is shown in Fig. 33.

Fig. 33.

3D model of mining design in the mining area.

The comparison of the boundary between the experimental mining design model and the solid model is shown in Fig. 34.

Fig. 34

Comparison of the boundary between the mining design model and the detection void model in the mining area.

From Fig. 34, it can be seen that there is under excavation around the mining area, with a significant amount of under excavation near the isolated pillars at both ends, and under excavation at the boundary of adjacent pillars in the mining area. There are a small number of over excavation phenomena around the mining area, most of which occur at the boundaries of adjacent pillars and at the corners of the upper part of the mining area where non explosive waste rock is designed. There are many over excavations, and there are no over excavations at both ends of the mining area. The left end of the void model differs significantly from the mining design model, possibly due to the presence of some ore remaining during void detection.

Overlay and composite the solid model of the detection void in the experimental mining area with the solid model of the mining design unit in the mining area, and then create four DTM faces along the boundary line of the mining area and cut them, retaining only the entity of the overexcavation part. Calculate the volume of the over excavation solid model around the boundary of adjacent mining pillars separately, and obtain the over excavation situation around the experimental mining area. There is a phenomenon of over excavation around the mining site, and the amount of over excavation is relatively small. The volume of over excavation near the upper boundary is only 63 m³, indicating a relatively small amount of over excavation; The amount of over excavation near the lower boundary is relatively large, about 512 m³. The total over excavation amount is 575 m³, which is relatively small with an over excavation rate of 1.60%. Compared with before, the over excavation rate has decreased by 7.87%. The boundary control effect of the mining room and mining area is good, and the over excavation and under excavation amounts are relatively small.

Analysis of underexcavation situation

In the process of backfilling in the mining area, the under excavation amount refers to the volume difference between the actual excavation space and the top plate of the mining design model from below the top plate to the bottom pulling space. In order to more accurately evaluate this indicator, models such as the upper ore rock boundary, mining design, measured voids, and bottom space roof will be overlaid and analyzed to reveal the differences between actual excavation conditions and design expectations. The composite diagram is shown in Fig. 35.

Fig. 35

Model composite diagram.

The formula for calculating the amount of underexcavation in the mining area is shown in Eq. (16):

$$W = N + Z - T - W_{1}$$

(16)

In the formula: W is the volume of under excavation; N is the volume of the mining design unit in the mining area; T is the volume of the detection gap between the top plate of the mining design model and the bottom space top plate; Z is the surrounding overexcavation volume between the top plate of the mining design model and the bottom space top plate; W1 is the volume of unmined ore from mining.

The calculation results of underexcavation in the experimental mining site are shown in Table 6.

Table 6 Parameters for blasting calculations for side aperture diameter-oriented charging structures.

Intensify the inspection of the deviation rate of the side holes in the experimental mining site, control the deviation angle of the side holes, improve drilling accuracy, and adjust the axial charge structure of the side holes. Adopt scheme three, which is 1 m explosive and 1.5 m bamboo tube. After analyzing the solid model of the goaf in the mining area and optimizing it, the boundary control of the mining area is better- The 740 m horizontal profile indicates that there is less over excavation or under excavation at the boundary of the mining area. There are a small amount of overexcavation in two directions around the mining site, but the total overexcavation amount is only 575 m³, and the overexcavation rate has decreased to 1.60%, a decrease of 83.10% compared to before. The boundary control of the mining site has been improved.

Conclusion and prospect

Conclusions

In this paper, we employed numerical simulations using the LS-DYNA software to analyze the step-by-step optimization of deep-hole blasting parameters in the Dongguashan copper mine. By comparing different hole diameters, network parameters, and charge structures, we identified the optimal configurations for minimizing damage to surrounding rock while achieving efficient fragmentation. The main conclusions are as follows:

This study employed numerical simulations using the LS-DYNA software to optimize the deep-hole blasting parameters for the Dongguashan copper mine. By analyzing different hole diameters, network parameters, and charge structures, we aimed to minimize damage to surrounding rock while achieving efficient fragmentation. The main findings and recommendations are as follows:

• 1. Optimal Hole Diameter: The simulations showed that 165 mm diameter holes are more effective for large blasting volumes. This diameter provides higher energy output and improved fragmentation efficiency compared to smaller diameters.

• 2. Optimal Hole Network Parameters: For 165 mm diameter holes, the optimal hole network parameter was determined to be 3.0 m × 3.0 m (row spacing × hole spacing). This configuration minimizes stress wave superposition and achieves better rock fragmentation, with a peak stress reduction of approximately 20% compared to a 3.2 m × 3.2 m configuration.

• 3. Effect of Radial Uncoupling Coefficient: Increasing the radial uncoupling coefficient (k1) from 1.18 to 1.83 resulted in a decrease in peak stress and damage volume. Specifically, the damage volume decreased from 11.25 to 8.63 m³, indicating that a higher k1 value effectively reduces the impact on surrounding rock.

• 4. Axial Charge Structure Optimization: Scheme 2, which increased the air spacing length to 4.5 m, resulted in a reduced destruction volume of 7.87 m³. This scheme demonstrated that optimizing the axial charge structure can significantly improve energy distribution and reduce over-excavation.

Prospect

This article mainly studies the boundary control technology of underground deep hole blasting. Through numerical simulation, the damage and effective stress under the decoupling coefficient of the edge hole diameter, axial charge structure, and deflection angle are analyzed. By establishing a three-dimensional solid model of the goaf in the mining area and adjusting the blasting parameters, the over excavation situation in the mining area is analyzed, and good boundary control effect is achieved.The following content is a prospect for the future:

• 1. Field validation: It is recommended to conduct field tests to validate the numerical simulation results and further refine the blasting parameters based on actual mining conditions.

• 2. Energy efficiency: Future research should focus on developing more energy-efficient blasting techniques that minimize environmental impact while maintaining high fragmentation efficiency.

• 3. Advanced monitoring: Implementing advanced monitoring technologies, such as real-time stress wave analysis and microseismic monitoring, can provide valuable data for optimizing blasting designs and improving safety.

• 4. Material properties: Further studies on the mechanical properties of different rock types and their response to blasting can help in developing more tailored blasting strategies for various geological conditions.