Introduction

An unwieldy amount of data overwhelms our surrounding visual world. Therefore, implementing mechanisms enabling robust signal-to-noise ratio enhancement of the incoming input is of key importance for effectively navigating this crowded and often dynamic stream of visual information1,2,3,4,5,6. Such enhancement is implemented through both selective attention7,8 and distractor suppression9,10,11,12,13 mechanisms. While the former boosts fine-tuned perceptual processing of task-relevant targets, the latter aims to prevent attentional capture effects by task-irrelevant or competing distractors14.

The mechanism by which selective attention is deployed across space has been conventionally outlined by models – like the spotlight15,16, the zoom-lens17,18,19,20 or the gradient21,22,23 models – which all collectively agree on predicting an inversely proportional monotonic function characterizing perceptual sensitivity at progressively increasing distances from the center of the attentional focus. In other words, attention-based performance is typically found to be hindered at incrementally farther spatial locations.

Interestingly, converging findings in psychophysics24,25,26,27,28,29,30,31,32,33,34,35,36,37,38, computational modelling4,5,6,39 and neuroscience32,33,36,40,41,42,43,44,45,46, have alternatively and differentially outlined a “center-surround inhibition” (CSI) model of selective attention distribution, characterized by an area of sustained inhibition encircling the focus.

The concept of an “inhibitory attentional beam” was originally outlined by Tsotsos4, who later detailed the underlying mechanism5 and eventually presented the fully integrated model6. Building on this foundational work, the concept has since been differentially taken up by several other authors33,43,45,47. Noteworthy, most of them adopted the term “Mexican-Hat” to denote the shape and the mathematical function describing the data distribution when mapping the spatial extent of the attentional profile31.

Notably, while agreeing with classical models on predicting optimal processing of stimuli located within the focus15,16,17,18,21,22,23, the center-surround inhibition model diverges by predicting a performance gain at most distal spatial positions31, with both the center and the shape of the focus being flexibly variable4,5,6.

More specifically, the “Selective Tuning Model” (STM) proposed by Tsotsos states that attentional selection is realized recursively through a feedforward bottom-up winner-take-all mechanism, with the inhibitory ring arising around the focus of attention engendered by a top-down pruning of all irrelevant-distracting connections, namely the ones related to items spatially located around the winning element4,5,6,32. Remarkably, the above account has proven effective in explaining a variety of empirical observations30,32,33,43,45.

Noteworthy, the unfolding of the inhibitory ring has a functional role as it optimizes the signal-to-noise ratio of the incoming stimuli. It achieves this by maximizing the processing of relevant targets while simultaneously minimizing the disruptive effects of irrelevant distractors and maintaining at the same time a good processing at the peripheral locations. At the neural level, the above mechanism lies in top-down frontal and parietal modulations exerted over lower-level visual areas42,46. Furthermore, extending beyond the visuo-spatial domain, evidence of center-surround inhibition has also been gathered in feature-based attention48,49,50,51,52, working memory53,54,55,56, and grasping movement planning57, thus suggesting that it is a domain-general principle of cognition.

Critically, within the visuo-spatial domain, a number of cognitive factors, such as perceptual34 and cognitive load35, as well as working memory load and capacity58, have been found to be capable of modulating the spatial extension of the attentional focus by shifting or dragging the inhibitory ring away or proximal to it.

Beyond the above-mentioned cognitive factors, it has been shown that experience-dependent mechanisms can likewise modulate the way attentional resources are allocated in space59. Among them, selection history mechanisms have been characterized by the fact of (a) being dependent upon prior experience, whose effects (b) cannot be confined to direct modulation of current goals, and (c) being applicable to arbitrary stimuli60. Among such mechanisms, reward history61,62,63 and statistical learning64 have been extensively investigated. Indeed, it has been consistently found that – in visual search tasks – reward-associated stimuli features65,66,67 – being either targets or distractors – or spatial positions68,69 are characterized by greater attentional priority, thus modulating deployment of attentional resources and entailing both costs and benefits in visual search efficiency. Similarly, statistical learning has been widely demonstrated to implicitly orient the allocation of attention resources in the immediate future64. More specifically, within the domain of visuo-spatial attention, there is a consistent observation that implicit learning of spatial probabilities – namely the likelihood of a given event or stimulus to occur at a specific location in space – can shape search efficiency in subsequent trials64. Its effects tend to emerge very rapidly in time, thus necessitating exposure to relatively few trials to occur70,71,72,73,74,75, and can be quickly and dynamically adjusted when new statistical regularities are introduced76. Of paramount importance, statistical learning effects markedly differ between target stimuli and distractors, that is, by enhancing the processing of task-relevant targets70,71,72,77,78,79 in frequently attended spatial positions and/or by optimizing distractor filtering mechanisms in frequently inhibited positions70,71,72,78,79,80,81,82,83,84. Furthermore, it has also been demonstrated that the two learning processes operate at different timeframes, with the learning of target spatial contingencies having long-lasting effects while the learning of distractor spatial contingencies having – instead – more transient, short-lasting ones72. However, it has also been established that statistical learning of target and of distractor spatial contingencies are nonetheless characterized by interactive effects of cross-talk. Specifically, distractor spatial probability alters search efficiency by hampering target selection when the latter is displayed at high distractor probability locations. Conversely, target spatial probability can influence distractor filtering mechanisms by enhancing distractors’ attentional capture effect when they are displayed at high target probability locations70,79.

Interestingly, both reward history69 and statistical learning70 are thought to unveil through plastic changes, over time, of spatial hubs within a priority map.

This map acts as a topographical representation, where peaks and hollows represent different levels of attentional priority. These priorities arise from the combined effect of perceptual salience, goal-relevance, and selection history85,86,87, modulating covert attentional guidance and predicting fixation sequences in the context of eye-movements88,89.

Interestingly, it has been hypothesized that the priority landscape undergoes a dynamic and flexible process of attentional reweighting through experience-dependent mechanisms, thus biasing the allocation of attentional resources in the immediate future69,70.

To the best of our knowledge, only two studies have specifically looked into the effects of experience-dependent mechanisms on the center-surround inhibition of the attentional focus90,91, showing that stimuli-reward associations were capable of cancelling the inhibitory ring encircling the focus of attention. In other words, a distractor that would normally be suppressed when near the attentional focus can still capture attention and disrupt target processing when associated with a high reward but not when associated with a low reward91. However, whether statistical learning of spatial contingencies has an effect on visuo-spatial center-surround inhibition and – if that holds true – through which mechanism it occurs are hitherto unexplored questions.

In the current study, we addressed the above gap by employing a visual search psychophysical task – enabling us to comprehensively map the visuospatial attentional profile – wherein we asked subjects to report the gap orientation of a ‘C’ letter when appearing as a salient color singleton (Baseline Condition) or as a non-salient probe (Probe Condition) at progressively increasing probe-to-singleton distances. It is important to note that, while in the Baseline Condition, the color singleton is truly a goal-relevant object (i.e., the one to which the response has to be made), in the Probe Condition, it becomes an interfering distractor that needs instead to be ignored. Critically, we manipulated singleton spatial contingency to make it occur more frequently adjacent to the probe, so that, by allocating attention the color singleton, inhibition is engendered in the nearby spatial position – i.e., where the probe is then displayed and performance tested – and where a reduction in accuracy is eventually expected.

Even more importantly, we systematically applied the spatial contingency manipulation to the color singleton of both Baseline and Probe Conditions. In this way – and because of the mixed design – we engendered the maximum level of uncertainty (chance level = 0.5) concerning the real identity of the color singleton when it appears on-screen, as it was equally likely to be either a target (Baseline Condition) or a distractor (Probe Condition).

Following attentional guidance differences consistently observed in the statistical learning of spatial probability between target and distractors70,71,72,77,78,79,80,81,82,83,84,92, we anticipated our results to be dependent on how spatial position of the color singleton is represented within the associated priority map. In other words, we aimed to disentangle if, following statistical learning, the spatial position of the color singleton is coded as a high priority target spatial location or, conversely, as a low priority distractor spatial location. Specifically, we tested two alternative and mutually exclusive hypotheses: In the (H1) Distractor – Weakened Attentional Capture Hypothesis, the spatial position of the color singleton is coded as a high probability distractor spatial position. Accordingly, a priority loss is expected to follow statistical learning at this spatial position, which will no longer exert attentional capture effects, thus preventing surround-inhibition to hinder attentional performance at nearby locations in the Probe Condition. Given the mixed design, the priority loss effect should also manifest in the Baseline Condition where, being here the color singleton the target to which a response must be made, a performance reduction is expected. In the (H2) Target – Enhanced Inhibition Hypothesis, the spatial position of the color singleton is coded as a high probability target spatial position. Consequently, an attentional priority gain is expected over there, following statistical learning, increasing the signal’s strength and facilitating attentional capture. Accordingly, we predict that the greater the attentional capture, the greater the center-surround inhibition projected in nearby locations. We also predict that the priority gain effect will bias performance in the Baseline Condition, where increased accuracy is expected for the color singleton.

Methods

Participants

A sample of 27 neurologically healthy young adults (4 males, MAge = 24.5 ± 3.2 years) took part in the experiment voluntarily. The study’s inclusion criteria encompassed being aged between 18 and 35, having normal or corrected-to-normal visual acuity, and unimpaired colour vision. One subject had to be excluded from statistical analyses because of technical issues in data recording. Accordingly, our final sample consisted of 26 subjects (4 males, MAge = 24.6 ± 3.3 years; handedness: NRight = 24 (92.3%)). Each participant underwent the experimental procedure after giving written informed consent. The experimental protocol was reviewed and approved by the ethical committee of the Department of Psychology of the University of Milano-Bicocca (Ethical Committee Prot. RM-2023–704), and all participants were treated in accordance with the Declaration of Helsinki. We ran a power analysis through the GPower software (GPower 3.1.793). The sample size estimation was computed based on prior experimental works70,71,72,73, which employed visual search paradigms similar to ours and where a significant main effect of spatial probability (high vs. low) was reported with large or very large effect sizes. However, given the exploratory nature of the current study, we opted to adopt a safeguard power approach94, thus considering a medium-to-large effect size of d = 0.6. We thus estimated a minimum sample of 24 subjects for a Dependent Samples t-test with a conventional α = 0.05 and Power = 0.80. The choice of estimating the sample size using a two-tailed t-test is justified by the a priori assumption that the hypothesized effect of SL would alternatively weaken vs. enhance accuracy performance within spatial positions proximal to the attentional focus.

Apparatus and stimuli

We adapted the experimental paradigm previously used by our research group36,38,46, which brings the specific advantage of mapping in a finely-grained way the entire spatial range of the attentional focus. All the stimuli have been presented superimposed on a gray background (RGB = 128, 128, 128). The fixation point consisted of a black ring displayed centrally to the computer monitor’s vertical and horizontal axes. The visual search array, presented either in the right vs. left visual hemifield with respect to the central fixation point, encompassed nine blue ‘C’ capital letters (RGB: 4, 52, 255) iso-eccentrically displayed at a distance of 8.5° of visual angle from the central fixation point. All the stimuli were arranged with a gap of 0.6° of visual angle between each other. The central ‘C’ was spatially aligned to the horizontal axis, while all the other ‘C’ were spatially arranged upward (4) and downward (4) with respect to it, thus defining an upward quadrant and a downward quadrant, with the midline ‘C’ letter shared between them. The color singleton consisted of a red-colored ‘C’ letter (RGB: 255, 37, 0), while the probe stimulus was realized by means of a white-colored ring encircling the central ‘C’ letter. All the ‘C’ stimuli have been rendered by removing a portion subtending 45° of angle from a ring-shaped figure. The gap orientation for each ‘C’ of the stimulus array was displayed randomly (chance level = 0.25) and independently from the others in one of four possible directions: upward vs. downward vs. rightward vs. leftward. Ultimately, the mask consisted of complete ring-shaped figures.

Procedure

Participants were seated centrally at a distance of 67 cm from the computer monitor (1920 × 1080 pixels, 60 Hz refresh rate) in a darkened laboratory room and with their heads resting over a chinrest. They were explicitly asked to maintain their gaze at the central fixation point throughout the running of each trial. Accordingly, trial onset was controlled by an EyeLink® 1000 Plus, which continuously tracked participants’ gaze so that each trial started only when the gaze at fixation condition criterion was met within a time window of 3 s. If the criterion was not satisfied, the script stepped into the next trial. At the end of the trial list, all the trials eventually skipped were run again until all of them were correctly executed.

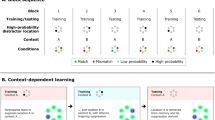
After checking the gaze at fixation condition, the stimulus array, made of all blue ‘C’ letters, was displayed onscreen for 50 ms (3 refresh cycles), with stimuli appearing either in the left or the right visual hemifield in a randomized, counterbalanced order. The task consisted of a mixed design encompassing two counterbalanced conditions randomly presented across the experiment (see Fig. 1a). In the Baseline Condition, one of the ‘C’ letters – i.e., the color singleton – turned red, remaining onscreen for 100 ms (6 refresh cycles). To minimize aftereffects, a mask was then presented for ~ 17 ms (1 refresh cycle). Lastly, a response screen displaying all four possible C-gap orientations, each associated with one keyboard button (1, 2, 3 or 4) was presented until a response was given. Participants were asked to indicate the gap orientation of the color singleton ‘C’, by pressing the corresponding keyboard button. Accordingly, as the onset of response provision was timely-constrained, only accuracy was stressed. Differently, the Probe Condition – otherwise equal in structure to the Baseline one – was characterized by the appearance, ~ 17 ms (1 refresh cycle) after the color singleton onset, of the probe stimulus, which remained onscreen for 83 ms (5 refresh cycles). The probe always appeared over the central ‘C’ letter, i.e., the one aligned with the horizontal midline. Crucially, the color singleton remained onscreen throughout the entire presentation of the probe stimulus. In the above condition participants were asked to indicate, by pressing the corresponding keyboard button, the gap orientation of the ‘C’ letter encircled by the probe stimulus, irrespective of whether it was the color singleton or a non-singleton object. In other words, in the Probe Condition, the red ‘C’ singleton had to be ignored, except when it was displayed in the horizontal midline, where the probe would then appear, thus making it the stimulus to which a response had to be made.

Fig. 1
figure 1

(a) The Task Procedure encompassed a Baseline Condition where participants were asked to indicate – among other non-target stimuli – the gap orientation of a task-relevant salient red ‘C’ capital letter target and a Probe Condition where the instruction was, instead, to indicate the gap orientation of the ‘C’ letter inside a withe circle probe. (b) The experimental paradigm encompassed a Training Block followed by a Balanced Block – characterized by an even distribution of singleton occurrence across spatial positions. Immediately afterwards, there were 4 Statistical Learning Blocks, characterized by an uneven distribution of singleton occurrence across spatial positions, with a higher probability over PD1 spatial position. Lastly, a post-experiment survey was administered to assess explicit awareness of the SL manipulation. (c) The center-surround inhibition (Mexican-Hat) visuospatial attentional profile is characterized by an inhibitory ring encircling the attentional focus, which hinders perceptual processing over stimuli lying in adjacent spatial positions. In the current experiment, the red ‘C’ singleton is characterized by high attentional priority owing to both its goal-relevance and its perceptual salience, thus increasing the likelihood of the center of the attentional focus being allocated over there. As a function of probe-to-target distances (PDs), the model predicts attentional performance at the probe to be the highest at PD0, systematically impaired at PD1 and progressively better at increasing distances (e.g., PD2, PD3 and PD4). The image shows the expected attentional priority when the probe and the singleton fall proximal to each other (i.e., PD1). (d) In the Balanced Block, the spatial contingency manipulation was equally applied to all of the visual quadrants of the two visual hemifields. In Statistical Learning Blocks, the spatial contingency manipulation was applied in crossed visual quadrants relative to each of the two visual hemifields by enhancing the probability of the red ‘C’ singleton appearing in the PD1 spatial position while maintaining it unaltered in the other visual quadrants.

Full size image

Therefore, determining to which stimulus making a response was a function of the presence or absence of the probe: if the probe was on, the response had to be made to the ‘C’ letter inside it; if the probe was off, the response had to be made to the color ‘C’ singleton.

To ensure perceptual processing in covert attention, the timings of the experimental task were specifically set to prevent eye movements made toward the periphery of the visual field, thus adhering to methodological recommendations from prior psychophysical experiments on attentional center-surround inhibition31 and in line with the timing of attentional allocation during visual search95.

Of utmost importance, within the Probe Condition, the spatial relationship between the probe and the color singleton is intended to be the key factor in investigating center-surround inhibition processes. Indeed, while the probe position was always kept constant over the central ‘C’ letter aligned with the horizontal midline, the color singleton could appear at any of the nine spatial positions constituting the stimulus array. Accordingly, five “probe-to-target” distances (PDs) could be defined for each quadrant of each visual hemifield of the stimulus array, ranging from PD0 – where both the probe and the color singleton appeared aligned to the horizontal midline – to PD4 – where the color singleton appears at the most distal position from the probe – and with all other PDs defining intermediate and progressively increasing distances (see Fig. 1c). Similarly, the PDs logic was applied to the Baseline Condition, but with the horizontal midline adopted as the spatial point of reference with respect to the color singleton position. The rationale of the task is the following: while the Baseline Condition is aimed at providing the color singleton with goal-relevance, in the Probe Condition the color singleton is intended to be irrelevant or even distracting. Furthermore, in the Probe Condition, the color singleton is always temporally antecedent to the probe. Accordingly, when it appears onscreen, the uncertainty linked to its role would likely recruit both top-down and attentional capture effects, owing to its goal-relevance (possibly) and perceptual salience, respectively. As a consequence, in both Baseline and Probe Conditions, the attentional focus will be established in first instance over the color singleton spatial position and, in line with the center-surround inhibition framework, when the color singleton in the Probe Condition appears over PD1 position – i.e., the one immediately proximal to the probe – an inhibitory ring will likely extend over the ‘C’ letter encircled by the probe, thus hindering its perceptual processing and consequently determining an impaired attentional performance (see Fig. 1c).

In the original version of the experimental paradigm, PDs were uniformly counterbalanced yet randomized across all spatial positions constituting the stimulus array. In the present version, we manipulated the probability of the color singleton ‘C’ letter to appear over the PD1 spatial position of each visual quadrant – upper vs. lower – and of each visual hemifield – right vs. left – of the stimulus array in both Baseline and Probe Conditions. More specifically, the upper and lower visual quadrants are defined by all spatial positions above and below the horizontal midline, respectively, with the PD0 spatial position located at midline, and thus shared by both upper and lower quadrants. Given that the color ‘C’ singleton can appear in any of the nine possible positions within the stimulus array, and that the probe is spatially-fixed at PD0, the two stimuli always appear within the same quadrant of space on a single trial.

Indeed, we defined a Balanced Block comprising 180 trials (90 Baseline and 90 Probe) characterized by an equal probability (5.5%—5 trials) of color singleton occurrence across all of the spatial positions of the stimulus array, and a Statistical Learning Block comprising 180 trials (90 Baseline and 90 Probe) characterized by an uneven probability of the color singleton across all the spatial positions of the stimulus array. More specifically, we set PD1 as a high-probability spatial position (23.33%—21 trials), while all the other PDs had been set as low-probability spatial positions (3.33%—3 trials). Crucially, the counterbalancing of the SL manipulation had been operated as follows: for half of the sample, the manipulation had been applied on the upper visual quadrant of the stimulus array within the right visual hemifield and in the lower visual quadrant of the left one; on the other side, for the remaining half of the sample, the manipulation had been applied on the lower visual quadrant of the stimulus array within the right visual hemifield and in the upper visual quadrant of the left one (see Fig. 1d). A schematic representation of the overall experimental paradigm is shown in Fig. 1b. At the beginning of the protocol, participants underwent a short-lasting Training Block of 24 trials (12 Baseline and 12 Probe) aimed at familiarizing them with the task and checking for proper instruction comprehension. The Training was followed by a single Balanced Block (180 trials), subsequently succeeded by four Statistical Learning Blocks (180 trials each), for a total of 900 trials. Ultimately, participants were asked to fill in a post-experiment survey aimed at evaluating their explicit awareness of spatial probability manipulation. More specifically, they were asked to indicate if there was a disproportion in the probability of the color singleton occurrence across all spatial positions of the stimulus array. If this was the case, they were then presented with an image of the stimulus array (both left and right visual hemifields), and they were specifically asked to indicate which spatial location(s) was/were subjected to probability manipulation and to what extent (i.e., high vs. low probability). The experiment was run, and data were collected through the E-Prime 3.0 Software (Psychology Software Tools, Pittsburgh, PA). The entire procedure had an overall duration of about 1 h.

Results

Statistical analyses have been conducted within the R environment (Version 4.3.2) (R Development Core Team, 2023), focusing on the Probe Condition, which is the critical one. Statistical analyses on the Baseline Condition are reported in the Supplementary Materials.

Accuracy

Firstly, we analyzed subjects’ accuracy in both the Baseline and Probe Conditions of the Balanced Block. On average, attentional performance was considerably high, and all subjects performed well above chance level in both Baseline (MAccuracy Baseline = 0.916, SDAccuracy Baseline = 0.069, all accuracies ≥ 0.7) and Probe (MAccuracy Probe = 0.831, SDAccuracy Probe = 0.091, all accuracies ≥ 0.66) Conditions.

Probe condition

Secondly, we analyzed data on the Probe Condition, with independent analyses for Balanced and Statistical Learning Blocks. The analysis was specifically aimed at predicting accuracy performance based on two independent variables (IVs): Probe-to-Target Distance (five PDs levels: PD0, PD1, PD2, PD3 and PD4) and Quadrant Spatial Probability (two levels: Equal Spatial Probability vs. Unequal Spatial Probability). To take account of the binary nature of the dependent variable (DV) and of the nested (within subjects) structure of the data, multilevel logistic regression models have been chosen as the main statistical procedure96. Data have been analyzed through the “glmer” function of the “lme4” R package (Version 1.1.35.21)97. The model has been fitted by entering “Probe-to-Target Distance”, “Quadrant Spatial Probability”, as well as the “Probe-to-Target Distance” by “Quadrant Spatial Probability” interaction as fixed effects, while the “Subject” identifier was entered as the random intercept. Marginal and Conditional R2 have been estimated throughout the R package “performance” (Version 0.10.8)98,99.

Balanced block

The summary statistics of the fitted model (R2 Marginal = 0.051; R2 Conditional = 0.159) are reported in Table 1a. Considering the main effects of Probe-to-Target Distance, results indicate that PD1 (b = -1.322, z = -4.91, p < 0.001), PD2 (b = -1.089, z = -3.97, p < 0.001) and PD3 (b = -0.671, z = -2.35, p = 0.019) all significantly differed when contrasted to the PD0 reference level. The data nicely fit with the expected center-surround inhibition profile (see Fig. 2a). Indeed, attentional performance is at its highest value when both probe and the color singleton overlap in PD0 (MPD0 = 0.927, SEPD0 = 0.260), while it gets sustainedly hindered in PD1 (MPD1 = 0.773, SEPD1 = 0.197). Finally, a performance gain is progressively observed in PD2 (MPD2 = 0.811, SEPD2 = 0.203) and PD3 (MPD3 = 0.867, SEPD3 = 0.220). Neither the main effect of Quadrant Spatial Probability nor the interactions of Probe-to-Target Distances by Quadrant Spatial Probability turned out to be statistically significant (all p > 0.05).

Table 1 (a) Summary statistics (fixed effects) of the Balanced Block of the Probe Condition. (b) Summary statistics (fixed effects) of the Statistical Learning Blocks of the Probe Condition. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Full size table
Fig. 2
figure 2

(a) Predicted Marginal Means of Accuracy as a function of Probe-to-Target Distance (PDs) in the Balanced Block of the Probe Condition. (b) Predicted Marginal Means of Accuracy as a function of Probe-to-Target Distance (PDs) and Quadrant Spatial Probability in the Statistical Learning Blocks of the Probe Condition.

Full size image

Statistical learning blocks

The summary statistics of the fitted model (R2 Marginal = 0.032; R2 Conditional = 0.167) are reported in Table 1b. Results showed a non-significant main effect of Quadrant Spatial Probability (b = 0, z = 0, p = 1). However, interestingly, a significant interaction emerged between PD1 spatial position and Quadrant Spatial Probability (b = 0.540, z = 2.17, p = 0.030), indexing that attentional performance tends to increase over PD1 position in the manipulated Unequal Spatial Probability Quadrant (MPD1-Unequal Spatial Probability = 0.877, SEPD1-Unequal Spatial Probability = 0.151) as contrasted to the control Equal Spatial Probability Quadrant (MPD1-Equal Spatial Probability = 0.805, SEPD1-Unequal Spatial Probability = 0.176). Consistently to the above result, no significant Probe-to-Target Distance by Quadrant Spatial Probability interactions turned out to be statistically significant in the other unmanipulated PDs (all p > 0.05) (see Fig. 2b).

To explore the learning process across Blocks, we plotted predicted marginal means of Accuracy by splitting the Statistical Learning Block into its four component sub-blocks. At a visual graph inspection, it appears that an uneven dynamic may probably underpin the learning process across Blocks (see Fig. 3).

Fig. 3
figure 3

Predicted Marginal Means (Accuracy) as a function of Probe-to-Target Distances (PDs) and Quadrant Spatial Probability across the four Statistical Learning Blocks of the Probe Condition. Dashed boxes highlight differences in the probability of accurate response in PD1 between Equal vs. Unequal Spatial Probability Quadrants across Blocks.

Full size image

Temporal dynamics

To quantitatively characterize this learning process and to reduce model complexity, we thus opted to fit two independent simplified multilevel logistic regression models – one for Equal Spatial Probability Quadrants and one for Unequal Spatial Probability Quadrants – where data have been subsetted to include only PD1 Probe-to-Target Distance, and by entering Block Type as the only fixed effect predictor, along with Subject as the random intercept. The analysis of the Equal Spatial Probability Quadrants revealed that accuracy performance in none of SL2 (b = -0.121, z = -0.43, p = 0.670), SL3 (b = 0.041, z = 0.15, p = 0.880), and SL4 (b = -0.081, z = -0.29, p = 0.770) significantly differ from the one of reference level SL1, thus indexing that in Equal Spatial Probability Quadrants no temporal learning is actually occurring (MPD1-Equal Spatial Probability-SL1 = 0.810, SEPD1-Equal Spatial Probability-SL1 = 0.038; MPD1-Equal Spatial Probability-SL2 = 0.790, SEPD1-Equal Spatial Probability-SL2 = 0.040; MPD1-Equal Spatial Probability-SL3 = 0.816, SEPD1-Equal Spatial Probability-SL3 = 0.037; MPD1-Equal Spatial Probability-SL4 = 0.797, SEPD1-Equal Spatial Probability-SL4 = 0.039). On the contrary, the analysis of the Unequal Spatial Probability Quadrants showed that, while accuracy performance in both SL2 (b = 0.334, z = 2.71, p = 0.007) and SL4 (b = 0.377, z = 3.03, p = 0.002) significantly differs from the one of reference level SL1, accuracy performance of SL3 was not different (b = 0.113, z = 0.960, p = 0.339) from SL1 one, thus suggesting that – overall – dynamic learning is actually occurring across Blocks, yet possibly in an uneven way (MPD1-Unequal Spatial Probability-SL1 = 0.848, SEPD1-Unequal Spatial Probability-SL1 = 0.019; MPD1-Unequal Spatial Probability-SL2 = 0.887, SEPD1-Unequal Spatial Probability-SL2 = 0.016; MPD1-Unequal Spatial Probability-SL3 = 0.862, SEPD1-Unequal Spatial Probability-SL3 = 0.018; MPD1-Unequal Spatial Probability-SL4 = 0.891, SEPD1-Unequal Spatial Probability-SL1 = 0.015).

To delve deeper into such temporal dynamics, we subsequently run two independent multilevel logistic regression models on PD1 trials of Equal and Unequal Spatial Probability Quadrants across all Blocks. The main scope of this analysis was to assess if the probability of responding accurately to the probe was predicted by gradually increasing PD1 Trials and finely characterize the above process by adding to the function orthogonal polynomials up to the cubic one. We thus entered orthogonal polynomials – up to the cubic – of the “Trial” variable as a fixed predictor. The above variable was also entered in the model as the random intercept to account for the nested data structure. The analysis for Unequal Spatial Probability Quadrants revealed both linear (b = 11.212, z = 3.81, p < 0.001) and cubic (b = 8.237, z = 2.947, p = 0.005) significant trends, thus indexing a temporal learning effect of PD1 from the beginning to the end of the task. On the contrary, the analysis for Equal Spatial Probability Quadrants showed that none of the linear, quadratic, and cubic trends significantly predict Accuracy across PD1 Trials (all p > 0.05), thus attaining that in unmanipulated visual quadrants, no learning process is actually occurring (see Fig. 4).

Fig. 4
figure 4

(a) Predicted Probability of Accurate Response as a function of progressively increasing PD1 Trials in Unequal Spatial Probability Quadrants of both Balanced and SL Blocks (from SL1 to SL4). The function is described by both a linear and a cubic trend. (b) Predicted Probability of Accurate Response as a function of progressively increasing PD1 Trials in Equal Spatial Probability Quadrants of both Balanced and SL Blocks (from SL1 to SL4). The function is not statistically significant, namely no learning process is actually at play.

Full size image

Trend analysis with polynomial contrasts

By analyzing the temporal dynamic of the statistical learning process, we observed a non-linear function. Accordingly, in the subsequent analysis, we opted to concentrate only on the last Statistical Learning Block (SL4), namely the one over which the effect of our spatial contingency manipulation appears to stabilize. Accordingly, to look over how the visuospatial attentional profile has been reshaped from the Balanced Block to the SL4 Block (see Fig. 5), we performed a trend analysis with polynomial contrasts by running three independent multilevel logistic regressions for each unique combination of Quadrant Spatial Probability (Equal vs. Unequal) and Block Type (Balanced vs. SL4). The focus of this analysis was to assess whether adding non-linear terms (i.e., quadratic and cubic) to the Probe-to-Target Distance fixed predictor, along with the by-Subject random intercept, improves the model’s fit compared to the standard linear one. The three models have been contrasted through likelihood ratio tests to account for their nested structure. The best model choice had been primarily based on statistical significance and, secondly, on a trade-off between goodness of fit and model complexity through the Akaike Information Criterion (AIC). A summary of each model output is reported in Table 2. The analysis indicates that for all unmanipulated Quadrants, the best model describing data distribution is the one including a cubic polynomial contrast, i.e., the one typically describing the visuospatial center-surround inhibition. Interestingly, only for the manipulated Quadrant neither the linear nor the cubic polynomial contrast functions turned out to be statistically significant, therefore indexing that the function incorporating the quadratic trend was the one that better fitted data distribution. Comprehensively, data suggests that SL has transformed the visuospatial attentional profile from having a center-surround inhibition pattern to a non-linear gradient. Crucially, the above modulation appears to be asymmetric as it occurred only on manipulated Quadrants, leaving unaltered the unmanipulated ones (see Fig. 5).

Fig. 5
figure 5

Predicted Accuracy as a function of Block Type, Quadrant Spatial Probability and Probe-to-Target Distance. Each unique Block Type and Quadrant Spatial Probability combination has been plotted based on its best-fitting model. While in the Balanced Block, both Equal and Unequal Spatial Probability Quadrants are better described by a cubic term of the Probe-to-Target Distance variable – thus determining a symmetric Mexican-Hat profile –, in the Statistical Learning Block 4, only the Equal Spatial Probability Quadrant is better described by a cubic term, as the Unequal Spatial Probability Quadrant is – instead – better described by a quadratic term – thus determining an asymmetrical Mexican-Hat profile. Note that in the Balanced Block, the distinction between Equal vs. Unequal Spatial Probability Quadrants is meaningless, as both quadrant types have an equal probability of target occurrence. However, for the sake of the current analysis, we believe it might be useful to graphically visualize how attentional performance has changed between Blocks over identical Quadrants.

Full size image
Table 2 Summary of the trend analysis models for each unique Block Type and Quadrant Spatial Probability combination. Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Full size table

Attentional suppression index

To look closer at how attentional priority has been plastically changed across Probe-to-Target Distances as a result of the spatial contingency manipulation, we computed an Attentional Suppression Index (ASI)38, which is given by the difference in accuracy between Baseline and Probe Conditions across Blocks, Quadrants, and Probe-to-Target Distances. This measure is expected to be higher in spatial position characterized by sustained attentional inhibition. We, therefore, run two independent repeated measure ANOVAs – Balanced vs. Statistical Learning Blocks – through the “aov” function of the “stats” R package (Version 4.3.2) by entering Probe-To-Target Distance and Quadrant Spatial Probability as the within predictor variables. Effect sizes (partial eta-squared \({\eta }_{p}^{2}\)) have been computed through the “eta_squared” function of the “rstatix” R package (Version 0.7.2). The computation of estimated marginal means has been run through the “emmeans” R package (Version 1.8.9). When needed, post-hoc contrasts have been carried out through the “pairs” R function and applying Bonferroni correction. Results for the Balanced Block indicate a statistically significant main effect of Probe-to-Target Distance (F(4, 100) = 7.68, p < 0.001, \({\eta }_{p}^{2}\) = 0.24). Post-hoc contrasts indeed indicate that ASI at PD1 (MPD1 = 0.156, SEPD1 = 0.026) is statistically higher as compared to ASI at PD0 (MPD0 = 0.035, SEPD0 = 0.026) (t(100) = -3.880, p = 0.002), PD3 (MPD3 = 0.042, SEPD3 = 0.026) (t(100) = 3.630 , p = 0.004) and PD4 (MPD4 = 0.044, SEPD4 = 0.026) (t(100) = 3.570, p = 0.006), see Fig. 6a. Data, therefore, are nicely consistent with the visuospatial center-surround inhibition framework, with the spatial position characterized by the highest ASI being the one immediately proximal to the center of the attentional focus. On the other hand, results for the Statistical Learning Blocks showed a statistically significant interaction between Probe-to-Target Distance and Quadrant Spatial Probability (F(4, 100) = 3.84, p = 0.006, \({\eta }_{p}^{2}\) = 0.13). Post-hoc contrasts indicate that ASI at PD1 was significantly higher in the Equal Spatial Probability Quadrant (MPD1-Equal Spatial Probability Quadrant = 0.189, SEPD1-Equal Spatial Probability Quadrant = 0.022) as contrasted to the Unequal Spatial Probability Quadrant (MPD1-Unequal Spatial Probability Quadrant = 0.110, SEPD1-Unequal Spatial Probability Quadrant = 0.025) (t(125) = 4, p < 0.001). All other contrasts did not reach the significance (all p > 0.05). Data are therefore indicative of the selectivity of the SL effect, which indeed unfolds as a priority gain only over the manipulated spatial position, leaving all the unmanipulated ones unaltered, see Fig. 6b,c and d.

Fig. 6
figure 6

(a) Attentional Suppression Index (ASI) in the Balanced Block as a function of Probe-to-Target distances. Bars represent Estimated ASI, while dots represent individual average ASI (b) Attentional Suppression Index in the Statistical Learning Blocks as a function of Probe-to-Target distances and Quadrant Spatial Probability. Bars represent Estimated ASI, while dots represent individual average ASI (c) 2D Priority Map of PD0 spatial position in Equal Spatial Probability Quadrants of the Statistical Learning Blocks as a function of Probe-to-Target Distance (d) 2D Priority Map of PD0 spatial position in Unequal Spatial Probability Quadrants of the Statistical Learning Blocks as a function of Probe-to-Target Distance.

Full size image

Post-experiment survey

In the Baseline Condition, only one out of the 26 subjects (3.8%) reported having noticed a higher probability of the color singleton appearing across spatial positions of the stimulus array. While correctly identifying the PD1 position of the Unequal Spatial Probability Quadrants of both visual hemifields, this subject – however – also reported the PD1 position of the Equal Spatial Probability Quadrants, along with the PD0 position. In the Probe Condition, four out of the 26 subjects (15,4%) reported having noticed a higher probability of the color singleton appearing across spatial positions of the stimulus array. Two of these subjects correctly identified the PD1 position of the Unequal Spatial Probability Quadrants of both visual hemifields, but – however – also reported the PD1 position of Equal Spatial Probability Quadrants and, for one of them, other unmanipulated spatial positions. Finally, the remaining two subjects reported all unmanipulated spatial positions. Accordingly, the results of the post-experiment survey led us to reliably rule out the possibility that the present results were driven by subjects who were explicitly aware of the applied spatial contingency manipulation.

Discussion

The primary objective of the current study was to explore whether statistical learning of spatial contingencies modulated the visuo-spatial center-surround inhibition (CSI) of the attentional focus. CSI is indeed a mechanism enabling search efficiency optimization through an enhancement of the signal-to-noise ratio of the attended spatial regions at the expense of surrounding – and thus possibly interfering – ones6,31,32. Our findings showed that statistical learning markedly reshaped the spatial extent of attentional focus, transforming the center-surround inhibition profile into a non-linear gradient one, specifically through a localized performance gain over the high probability probe-to-target distance. Interestingly, such a reshaping occurred unevenly in time and asymmetrically, as it specifically affected manipulated visual quadrants, whilst leaving unaltered the unmanipulated ones. These results are novel and demonstrate for the first time that statistical learning mechanisms can modulate the spatial attentional profile. They complement previous findings by showing the impact of other experience-dependent mechanisms on selective spatial attentional processes.

Notably, in our experimental paradigm, the color singleton is inherently uncertain in its identity. Indeed, while in the Baseline Condition the color singleton is actually a task-relevant item, in the Probe Condition, conversely, it serves as a distractor. Critically, by equally applying the spatial contingency manipulation on both Baseline and Probe Conditions, we engendered the maximum level of uncertainty regarding the stimulus identity (i.e., chance level = 0.5). Moreover, given intermixing and randomization throughout the experiment, it becomes unfeasible to proactively anticipate the upcoming trial’s category. As widely supported by a substantial body of evidence, the effect of statistical learning of spatial probability – alongside its underlying mechanisms and the temporal dynamics through which it plastically modulates the priority map landscape – robustly differs between target and distractors70,71,72,77,78,79,80,81,82,83,84,92. Hence, to deeply understand the performance gain we observed – and its underlying mechanism – it becomes of pivotal importance to elucidate whether the spatial position over which we applied the spatial contingency manipulation had been up-prioritized as a high target spatial probability location or, conversely, de-prioritized as a high distractor spatial probability location.

On the one hand, our results in the Balanced Block of the Probe Condition nicely replicated those from prior psychophysical experiments32,33,36,38,43,45,46, which systematically observed that the signal-to-noise ratio of the spatial attentional focus is enhanced through a ring of sustained inhibition encircling it. Hence, beside optimal performance in reporting probe orientation at an overlapping spatial position (PD0), we found that accuracy at the same position was robustly hindered when the probe was flaked at short-range (PD1) by the color singleton, whilst not at wider spatial gaps (PD2, PD3 and PD4). On the other hand, in Statistical Learning Blocks of the Probe Condition, the inhibitory ring appears to be disrupted when learning that the color singleton is more likely to appear in the PD1 spatial position of Unequal Spatial Probability Quadrants. This results nicely align with our initial H1 hypothesis (Distractor – Weakened Attentional Capture Hypothesis) wherein we specifically predicted that, if coded as a high distractor probability location, the effect of statistical learning would have engendered an attentional priority down-weighting of the manipulated PD1 spatial position70,71,72,78,79,80,81,82,83,84. As a consequence of such a down-weighting, the color singleton, now prevented from inducing any further attentional capture effects, would have impeded the attentional focus to be spatially established over there. Consequently, this would have hampered the inhibitory ring from being projected over the probe at the adjacent PD0 which, ultimately, would have thus gained attentional priority, as indeed observed. However, it would have also logically followed that the effects of PD1 down-weighting should have been observed as well in the Baseline Condition, where the color singleton is actually task-relevant. Indeed, if coded as a high distractor probability location, it would have been likely to expect a hindered performance at PD1 spatial position of Unequal as compared to Equal Spatial Probability Quadrants. Nonetheless, our data strikingly contrast with this prediction, as we did not observe such a difference (see Supplementary Materials, S1.2).

However, and unexpectedly, our data strikingly contrast also with our H2 hypothesis (Target – Enhanced Inhibition Hypothesis), wherein we specifically predicted that, through statistical learning of spatial contingencies, we would have engendered a ring of inhibition of greater magnitude. Accordingly, to better frame our findings, we thus propose an alternative hypothesis (H3): Target – Attentional Focus Zooming-Out (see Fig. 7). With this hypothesis we posit that, while maintaining high attentional priority at PD1, the performance gain observed at PD0 would have been the result of a zooming-out of the attentional focus, which has extended up to enfold also the PD0 spatial position. Notably, this possibility does not come at odds, as it well resonates with prior findings indexing an adjustment of the spatial extent of the focus of attention to optimize visual search17,18,19,20,47. Additionally, it neatly aligns with data probing both bottom-up and top-down modulations of the center-surround inhibition of the attentional focus34,35,58. Building upon these assumptions, beyond a performance improvement at the PD0 spatial position of the Probe Condition, this hypothesis also predict a nearly optimal performance in the PD1 spatial position of the Baseline Condition, as indeed strongly indexed by our data (see Supplementary Materials, S1.2).

Fig. 7
figure 7

Expected Accuracy on PD0 of Probe and Baseline Conditions as a function of alternative hypotheses (H1) Distractor – Weakened Attentional Capture Hypothesis (H2) Target – Enhanced Inhibition Hypothesis (H3) Target – Attentional Focus Zooming-Out Hypothesis.

Full size image

While offering a conceivable framework to interpret our data, the rationale underlying why this should constitute the most functional mechanism throughout which statistical learning has operated remains hitherto an object of speculation. Within this regard, valuable insight might be garnered from the concept of attentional template as thoroughly operationalized in feature-based attention domain. The attentional template is indeed conceptualized as a mental representation of target features, which is actively maintained in working memory or long-term memory amidst the execution of a visual search task100,101,102. Notably, a substantial body of evidence has consistently reported that attentional guidance does not necessitate a finely-grained veridical attentional template to maximize search efficiency, but it suffices – instead – of a representation which is “good-enough”101,102. Critically, it is widely recognized that the attentional template content might be biased – either adaptively or inflexibly – by visual distractors103 e.g., through top-down modulations intended to enhance target-to-distractor distinctiveness101,102,104,105. Moreover, even experience-dependent mechanisms – e.g., reward feedback106 and statistical learning107,108,109 – have proved capable of biasing working memory content. What clearly emerges from this evidence is that attentional template biases are tightly linked to the specific context wherein visual search unveils, especially if under conditions marked by heightened uncertainty: more specifically, evidence have proved that uncertain target features are tracked as pattern of statistical regularities, wherein the likelihood of such features is adaptively used to adjust attentional priority in guiding search behaviour110,111. All things considered, we advocate a similar explanation in interpreting our findings: indeed, we hypothesized that the unpredictable identity of the color singleton in our paradigm has entailed – thorough statistical learning – a conflict in its encoding within the associated attentional template. As uncertainty is at its highest level, thus hampering the possibility of univocally leaning toward a unique outcome, the conflict is resolved throughout a zooming-out of the attentional focus, in a way that both the color singleton in the Baseline Condition and the probe in the Probe Condition have gained attentional priority. Additionally, such an adjustment came along with the elimination of the inhibitory area: it is plausible that through the zooming-out of the attentional focus, having all task-relevant items under the same spatial attentional lens, the interfering effect of non-target elements within the array becomes negligible, thereby making the inhibitory ring unnecessary.

Consistently to prior literature, we claim that the effect of statistical learning we observed has unveiled consequently to processes of plastic reweighting within a priority map coding for the spatial attentional priority of the visual array locations70,85,86,87,88,108, as indexed by our data of the Attentional Suppression Index (ASI).

Overall, we believe such a mechanism to be conceivable as a “good-enough” strategy orienting attentional guidance, as it does not rely upon a finely-grained veridical representation of the priority landscape, but rather it uses plastic and adaptive templates to guarantee an overall optimal search performance across task conditions.

We consider what exposed above to be still consistent with the STM account. Indeed, we might speculate that introducing statistical regularities into the search context have biased the initial feedforward bottom-up selection as postulated by the STM model4,5,6, impacting on the following backward, top-down pruning and – ultimately – influencing attentional selection. This notion also aligns with the recent proposal that preparatory spatial tuning, following statistical learning, occurs proactively before visual search onset, with its effects on spatial priority maps becoming evident – also at the neural, oscillatory level – if pinged by bottom-up sensory input112.

While the exact direction of the effect was expected to be dependent on the type of learning – specifically, suppression vs. selection history – we unexpectedly observed that under conditions of uncertainty, control mechanisms may flexibly and adaptively adjust the attentional focusing, preventing performance disruption across different task conditions.

Interestingly, recent findings47 have shown evidence of a similar zooming-in mechanism driven by a spatiotemporal coarse-to-fine progression along the visual cortex hierarchy. This mechanism is responsible for more efficient selection when covertly shifting attention, especially when scrutiny and spatial precision are required. Indeed, under those conditions, covert attention has been found to originate at low-levels of the visual hierarchy where spatial resolution of receptive fields (RFs) is finer. Additionally, this top-down pass determines the surrounding inhibitory beam, which contributes to increment the signal-to-noise ratio of the incoming input. We therefore consider this account to resonate with our observation in the Balanced Block. However, when statistical regularities introduce uncertainty into the task, a zoom-out of the focus, incorporating all task-relevant items, may be more efficient rather than implementing two different mechanisms. In this case, selection may originate at a mid-level of the visual hierarchy, where spatial resolution of RFs is coarser. Being scrutiny and spatial precision less demanding following the expansion of the attentional window, the inhibitory beam may become unnecessary, which would explain why, in the unbalanced visual quadrants of the Probe Condition, we did find the inhibitory beam to be eliminated.

An alternative to the zoom-out account is a proactive reorientation strategy with short-range landing. Indeed, after learning the new spatial regularities, participants may have adapted to quickly shift their attention to PD0 after initially focusing on PD1. Assuming that, in the zoom-out account, the expanded attentional window remains constant in its eccentricity across the entire peripheral visual field, then the proactive reorientation strategy could likely explain why we observed the disappearance of the center-surround inhibition, rather than simply having it shifted further away in space.

Whilst we cannot draw firm conclusions in this regard, thus leaving the proposed explanations only speculative, we nonetheless highlight the importance, for future studies, of exploring whether the concept of a good-enough attentional template, as gathered in feature-based attention domain, do also extend to the spatial dimension in shaping priority maps for attentional guidance.

Interestingly, by breaking down into the temporal dynamic of the learning process, we observed that it unveiled unevenly across blocks. Many studies have observed that statistical learning effects – either related to target or distractors – tend to robustly emerge very rapidly in time70,71,72,73,74,75, yet having differential extinction time frameworks, with long-lasting target effects vs. short-lasting distractor effects72,74,113 and with the possibility to flexibly and dynamically re-adjustment to new statistical regularities76. Notably, we build upon these findings by specifically focusing on the temporal course of the ongoing learning process. We probed that, in accordance with prior studies, the effect of statistical learning tends to emerge quite earlier in time (i.e., already at SL2 Block). Still, we additionally showed that the performance gain fluctuates over time, as indexed by both significant linear and cubic functions fitting. Interestingly, this observation aligns with the current proposal of statistical learning as a continuous, stochastic, and dynamic process, unfolding from an initial exploratory mode to a more accurate error-correction mode118. Therefore, the uneven temporal unfolding of SL in our task may be accounted for by a progressive shift from an exploratory strategy (SL1, 2 and 4 Blocks) to a more accurate, error-correction-based one (SL4 Block).

Crucially, our findings revealed that learning occurred specifically at PD1 position within Unequal Spatial Probability Quadrants, whilst leaving Equal Spatial Probability ones unchanged. The confined effect within Unequal Spatial Probability Quadrants nicely fit with prior studies showing that statistical learning of spatial contingencies – at least for distractor learning – operate at a local scale114. Furthermore, it has been consistently observed that the effect of statistical learning of distractor location scales up with distance, namely through a gradient of progressively decreased suppression as one moves further away from the high distractor probability location81,115,116. Notably, in Exp. 1 of Ferrante et al.70 it has been observed that target statistical learning is outlined by high spatial specificity, with the effect remaining confined to the individual location without spreading to nearby spatial positions. While, on the one hand, they argue for the need to further explore the spatial specificity of this effect through ad hoc spatial denser arrays, on the other hand, by finely-grain mapping the spatial extent of the attentional profile, we have shown that this effect does not extend beyond the high probability location. Whether the existence of asymmetries in the spatial gradient of target vs. distractor statistical learning requires further investigation, we nonetheless believe that our observation supports the H3 hypothesis. Ultimately, a notable asymmetry in the center-surround inhibition attentional profile has emerged due to the localized effect of statistical learning within Unequal Spatial Probability Quadrants. While, on the one hand, the zoom-lens model predicts an iso-eccentric adjustment of the attentional focus17,18,19,20, on the other hand a biased modulation of the spatial gradient across blocks has been observed in the study by Wang & Theeuwes117, yet employing a different search paradigm than ours, wherein the high probability distractor location changed across the task. Therefore, to our knowledge, our findings represent a first empirical demonstration of an asymmetrical modulation of the spatial profile of the attentional focus.

In summary, in our psychophysical experiment we demonstrated that statistical learning of spatial patterns, when occurring within spatial locations engendering sustained surrounding inhibition, alters the spatial profile of the attentional focus, re-shaping it into a gradient pattern. Such a learning effect is spatially localized and thus asymmetrical, and it unfolds unevenly in time across blocks. We propose this re-shaping mechanism to arise from a plastic re-weighting of the spatial priority map, resulting in an enlargement of the attentional focus. This mechanism might indeed serve as a good-enough principle of attentional guidance allowing to mitigate performance disruption due to the uncertainty of stimulus identity. In future research, it would be thus valuable to further explore how statistical learning differentially modulates the spatial attentional focus at varying levels of uncertainty. Ultimately, for a more comprehensive understanding of the phenomenon, it would be worthy to further investigate its implication in center-surround inhibition in feature-based attention and in working memory representation.