Granular soil particle breakage prediction model based on population evolution theory

Abstract

A novel particle breakage model for granular soils was developed based on population evolution theory. The relationship between population evolution and particle breakage was first established, introducing key parameters such as the migration rate k, comprehensive environmental impact coefficient r_ij, energy dissipation ratio m_ij, and effective constraint coefficient β, with detailed explanations of their physical significance and calculation methods. The model’s characteristics were analyzed, highlighting its ability to account for monodispersity, the equilibrium of extreme grain groups, and the inclusivity of over-limit particle groups. Parameters including fractal dimension and crushing coefficient were derived to further quantify the breakage process. Validation was conducted using experimental data from single-particle and multi-particle size group tests under varying soil conditions and stress states, demonstrating the model’s capability to accurately describe the evolution of particle breakage across diverse scenarios.

Introduction

Granular soil, encompassing materials such as gravel, macadam, and other granular substances with minimal viscosity, serves as a crucial filler in civil engineering projects¹. Its applications span a wide range, including large earth-rock dams, port riprap foundations, gravel roadbeds, and railway ballast. The point-to-point contact between granular particles renders them prone to fragmentation under external loads, which significantly affects the soil’s strength and deformation behavior. Consequently, extensive research has been dedicated to understanding the breakage behavior of granular soils. Key focus areas include quantifying particle breakage degrees, identifying factors influencing breakage, examining its impact on soil strength and deformation characteristics, developing numerical simulations of particle breakage, and formulating constitutive models to describe the underlying mechanisms^2,3.

Due to the significant impact of soil particle crushing on soil structural deformation, many scholars have conducted experimental studies to explore the engineering characteristics of particle breakage. Kong Xianjing et al.⁴ conducted large-scale triaxial tests to examine the effects of stress path and wet/dry conditions on rockfill particle breakage during storage. Results showed that while the breakage rate varies with stress path, particle gradation evolves consistently. Higher water content increases the breakage rate, but gradation evolution remains similar under wet and dry conditions. Liu Jie et al.⁵conducted triaxial tests to study the crushing behavior of coral sand under varying relative density, water content, and confining pressure. Results showed that particle breakage increased with relative density and confining pressure, while it initially rose with water content before decreasing at higher levels. Fine particles from crushing filled pores, improving gradation and slightly enhancing coral sand strength. Jin Aibing et al.⁶ used compression tests and 3D scanning to analyze the crushing characteristics of ore particles at macro and micro scales. Results identified four fracture modes: edge wear, middle breakage (dominant), through fracture, and random cracking. Liu Yang et al.⁷ used an impact load tester to study ballast crushing under varying shapes, sizes, and loads. Results showed flaky and needle-like particles had higher mass loss, while block-shaped particles mainly experienced wear. The crushing process comprised three stages: spatial adjustment, contact crushing, and equilibrium stabilization. Li Tao et al.⁸ used ring shear tests to study the strength and crushing behavior of calcareous mixed sand. Results showed that the crushing rate decreases with higher roundness and width-to-length ratio but increases with axial pressure. Additionally, more fine particles reduce the extent of particle breakage. Meng Minqiang et al.^9,10 conducted surface vibration compaction tests on gravel with different gradations, finding that a higher uniformity coefficient lowers the void ratio and raises the coordination number until stabilization.

The particle size distribution of soil is a fundamental aspect of soil mechanics, serving as the basis for soil classification, mechanical strength calculations, and targeted engineering applications. The essence of particle fragmentation lies in the alteration of soil particle size distribution. A predictive model for the gradation curve of granular soil under particle breakage conditions is crucial for understanding the evolution of particle gradation. To date, several scholars have investigated the evolution of particle breakage. McDowell et al.¹¹ conducted uniaxial compression tests on fine sand with a single particle size and found that the relationship between the “survival probability” of particles and applied load followed a Weibull distribution. Tong Chenxi et al.¹² combined the Weibull distribution and Markov chain models to statistically calculate the crushing limit of single-particle size groups. Their work, focusing on the simpler fragmentation behavior of single-particle groups, offers valuable insights for multi-particle size group studies. Long Yao et al.¹³ investigated the dynamic crushing behavior of red sandstone coarse-grained soil, developing a probability density function for crushing and a particle breakage model. This model describes the evolution of particle fragmentation under varying stress states, though its predictive accuracy requires further improvement.Tong Chenxi et al.¹⁴ examined the breakage behavior of multi-particle size groups, assuming that the effective breakage probability was the same for each particle size group breaking into smaller sizes. They developed a Markov chain model to describe multi-particle size groups, but the Weibull parameters used in the model are based on single-particle size groups transitioning to the current particle size, rather than reflecting the true crushing parameters for multi-particle size groups. Xiong Haibin et al.¹⁵ proposed that in the e-lnp space, the critical state line of granular soil shifts downward with crushing. They introduced the particle crushing parameter e_B to modify the UH model for sandy soil, resulting in the RIGA-MUH model. This model accounts for particle breakage in deriving the critical state line, offering a new approach for constitutive equations incorporating particle fragmentation.Okzan et al.¹⁶ proposed that the particle breakage process is random and follows a Markov process. They assumed that the probability of a particle breaking into smaller sizes of different particle sizes is equal, and developed a Markov model to describe the gradation evolution. Their model provides a reasonable prediction of the evolution of multi-particle size groups in real-world conditions. Zhang et al.¹⁷introduced a state parameter for particle fragmentation and anisotropy, based on fragmentation stress and spatial sliding surfaces, specifically for rockfill. They enhanced the MPZ model with this parameter, developing a generalized plastic model that captures the stress and deformation characteristics of rockfill materials.

The research above highlights that the evolution of particle breakage in multi-particle size groups remains a challenging area in the study of particle fragmentation, and serves as the foundation for understanding the mechanisms of particle breakage. Especially, a particle breakage model enables the prediction of strength degradation, settlement deformation, and other performance changes under prolonged loading or extreme working conditions, offering reliable guidance for engineering design. Therefore, in this paper, a fragmentation evolution model for multi-particle size granular soil is proposed, based on the fragmentation characteristics of multi-particle groups and the theory of population evolution. The model parameters are discussed, and the effectiveness of the fragmentation model is validated.

Evolution of particle fragmentation in multi-particle size group

In nature, a multi-particle group consists of multiple single-particle groups, where particles of different sizes experience varying contact stresses due to differences in their contact areas. Although the fragmentation of both single-particle and multi-particle groups can be described using fractal models, the fragmentation behavior of multi-particle groups exhibits distinct characteristics. Unlike single-particle breakage, the fragmentation of multi-particle groups is not merely a linear combination of individual particle breakage events; it also encompasses interactions among different particle size groups and the influence of internal constraints. To better understand the evolution of particle fragmentation within multi-particle groups, an organizational population model is introduced.

The organizational population model

The organizational population model is developed within a shared environment where diverse populations compete for finite resources. The size and dynamics of each population influence and constrain one another, ultimately stabilizing at an equilibrium state of coexistence. As outlined in the study referenced¹⁸, the organizational population model is founded on three primary assumptions:

• (1) The organizational population comprises numerous similar organizations, with the total population size representing the aggregate production capacity of these organizations. The growth in population size is influenced by two primary factors: the current population size and the productivity of the organizations.

• (2) Over a given period, environmental resources remain constant, limiting the indefinite expansion of the population size. As the population size increases, its growth rate progressively declines until it stabilizes. Under constant environmental conditions, each population has a maximum size, N_i, that it can achieve within the specified timeframe.

• (3) Within the organizational network, populations exhibit differing growth rates, shaped by their unique characteristics and inherent attributes.

Here’s a revised version incorporating the Logistic model for population growth^18,19 :

$$\frac{{dE(t)}}{{dt}}=rE(t)(1 - \frac{{E(t)}}{N})$$

(1)

In the Equation, r is the growth rate of a population. E(t) represents the sizes of a population at a given point in time. N denotes the maximum size that a population can achieve in a constant environment over a specific time period. 1-E(t)/N represents the inhibition of population growth caused by resource consumption under specific resource conditions.

A competitive relationship exists between populations, wherein the growth in size of population B inhibits the growth of population A, ultimately leading to a reduction in the size of population A. The dynamics of population A’s size can be expressed as:

$$\frac{{dE_{A} (t)}}{{dt}} = r_{A} E_{A} (1 - \frac{{E_{A} }}{{N_{A} }} - \omega _{{BA}} \frac{{E_{B} }}{{N_{B} }}) (\omega _{{BA}}>0)$$

(2)

Where E_A and E_B represent the sizes of two populations A and B at a given point in time, respectively. N_A and N_B denote the maximum sizes that populations A and B can achieve in a constant environment over a specific time period. ω_BA represents the degree of influence that population B exerts on the growth of population A. r_A is the growth rate of population A.

Similarly, as a result of the inhibitory effect from population A, the size of population B will also experience a decline. The size evolution of population B can be expressed as:

$$\frac{{dE_{B} (t)}}{{dt}} = r_{B} E_{B} (1 - \frac{{E_{B} }}{{N_{B} }} - \omega _{{AB}} \frac{{E_{A} }}{{N_{A} }}) (\omega _{{AB}}>0)$$

(3)

Where ω_AB represents the degree of influence that population A exerts on population B.

The mathematical model describing the symbiosis between populations A and B is as follows:

$$\left\{ {_{{\frac{{dE_{B} (t)}}{{dt}} = r_{B} E_{B} (1 - \frac{{E_{B} }}{{N_{B} }} - \omega _{{AB}} \frac{{E_{A} }}{{N_{A} }})}}^{{\frac{{dE_{A} (t)}}{{dt}} = r_{A} E_{A} (1 - \frac{{E_{A} }}{{N_{A} }} - \omega _{{BA}} \frac{{E_{B} }}{{N_{B} }})}} } \right. (\omega _{{BA}}>0, \omega _{{AB}}>0)$$

(4)

Multi-particle group fragmentation occurs under specific spatial and external conditions, where different particle size groups are subjected to crushing. The fragmented particles migrate to other particle groups, leading to an increase or decrease in the content of these groups. After fragmentation, a final grading is achieved, and each particle size group reaches its respective limit. Therefore, it is theoretically valid to consider the interactions between different particle size groups during the fragmentation process, drawing an analogy to the organizational population model.

Let’s consider i pseudo-bounded particle sizes of rock and soil particles, ordered from smallest to largest, as d₁, d₂, ., d_i. Based on the organizational population theory^19,20, it can be proposed that for a given particle size group, the following conditions apply:

$${x_i}_{i}^{\prime}={x_i}_{i}+(\sum\limits_{{}} {{k_{jj}}} \cdot {x_j}_{j} - {x_i}_{i}) \cdot \left[ {1 - (\frac{{{x_i}_{i}}}{{{N_i}_{i}}}+\sum\limits_{{j \ne i}} {{m_i}_{j}} \frac{{{x_j}_{j}}}{{{N_j}_{j}}}) \cdot \beta } \right]$$

(5)

Where x_ii’ represents the final content of the i-th particle group; x_ii is the initial content of the i-th particle group; k_jj denotes the migration rate of the j-th particle group; x_jj is the initial content of the j-th particle group. N_ii and N_jj are the final contents of i-th and j-th particle groups, respectively. m_ij represents the ratio of crushing energy consumption between the i-th particle group and the j-th particle groups. β is the effective constraint coefficient, which characterizes the internal constraint relationship among the multi-particle size groups.

Due to the fact that multi-particle size groups are not merely linear combinations of single particle sizes, it is essential to account for the influence of other particle groups, which can either increase or decrease the size of a given particle group. r_ij can be defined as the comprehensive environmental impact coefficient for each particle group, as expressed in Eq. (6):

$${r_i}_{j}=1 - (\frac{{{x_i}_{i}}}{{{N_i}_{i}}}+\sum\limits_{{j \ne i}} {{m_i}_{j}} \frac{{{x_j}_{j}}}{{{N_j}_{j}}}) \cdot \beta$$

(6)

Formula (7) can be derived from formula (5) and formula (6) :

$${x_{ii}}^{\prime}={x_i}_{i} \cdot [1+({k_{ii}} - 1) \cdot {r_i}_{i}]+\sum\limits_{{j \ne i}} {{x_i}_{j} \cdot {k_i}_{j}} \cdot {r_i}_{j}$$

(7)

In the formula, x_ij represents the content of crushed i-th particle group to j-th particle group.

The literature^13,14,16 asserts that multi-grain crushing should follow Markov chain with a one-step transition. The fragmentation matrix can be derived as follows:

$$P=\left[ {\begin{array}{*{20}{c}} {1+({k_{11}} - 1) \cdot {r_{11}}}&0&0&0&0&0 \\ {{k_{21}} \cdot {r_{21}}}&{1+({k_{22}} - 1) \cdot {r_{22}}}&0&0&0&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{k_{t1}} \cdot {r_{t1}}}&{{k_{t2}} \cdot {r_{t2}}}&{{k_{t3}} \cdot {r_{t3}}}& \cdots &{1+({k_{tt}} - 1) \cdot {r_{tt}}}&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{k_{i1}} \cdot {r_{i1}}}&{{k_{i2}} \cdot {r_{i2}}}&{{k_{i3}} \cdot {r_{i3}}}& \cdots &{{k_{ii - 1}} \cdot {r_{ii - 1}}}&{1+({k_{ii}} - 1) \cdot {r_{ii}}} \end{array}} \right]$$

(8)

Model parameters

Migration rate (k)

The migration rate,k,quantitatively represents the processes of self-survival and fragmentation within one particle size group and its transition to another. While the crushing rate reflects the total amount of fragmentation occurring within a given particle size group, it does not provide a detailed quantitative explanation of how much fragmentation leads to particles migrating into other size groups. In contrast, the migration rate refines this concept by explicitly quantifying the amount of material from a specific particle size group that fragments and transitions into another specific particle size group.

The migration rate varies across different particle size groups and can be determined based on the crushing behavior of a single particle size group.For a specific particle size group, with a maximum particle size of D_i and an initial percentage content of 1, the percentage content of each particle size group after one crushing event can be calculated. These resulting percentage contents represent the migration rates associated with the fragmentation of the original particle size group. For a specific grain group d_i-d_j, the migration rate kis described in the literature^21,22,23 as follows:

$$k_{{ij}} = \frac{{\int_{{d_{j} }}^{{d_{i} }} {d^{{2 - \alpha }} dd} }}{{\int_{0}^{{D_{i} }} {d^{{2 - \alpha }} dd} }} = \frac{{d_{i}^{{3 - \alpha }} - d_{j}^{{3 - \alpha }} }}{{D_{i}^{{3 - \alpha }} }} = F_{{d_{i} }} - F_{{d_{j} }}$$

(9)

$$\text{and}\, \sum {k_{{ij}} } = 1$$

(10)

Here, k_ij represents the migration rate from particle size d_j to particle size d_i; and αdenotes the fractal dimension. According to the literature^24,25, soil particle size distributions typically follow a fractal distribution, with the fractal dimension generally being less than 3.0.

Comprehensive environmental impact coefficient (r _ij)

The comprehensive environmental impact coefficient (r_ij) is introduced based on the following assumptions:

• (1) Particle fragmentation is influenced solely by its intrinsic development behavior and the interactions between different particle sizes.

• (2) The fragmentation behavior and the interactions among particle groups are continuous processes over time.

• (3) The impact coefficient between the two particle groups is determined by heir interaction, quantified by the energy dissipation ratio (m_ij);

• (4) Each particle group is constrained by its internal factors, which are uniformly described using the restriction coefficient (β) .

The comprehensive environmental impact coefficient (r_ij) is serves as a correction factor for the instantaneous growth rate, and its value decreases as the content of the grain group increases. This coefficient represents the unused space available for the growth of a particle size group.In Eq. (6), the term x_ii/N_ii reflects the effect of the grain group content on its own growth, representing the retarding effect caused by the consumption of limited resources within the group.

When multiple particle size groups are present, the influence of other groups must be considered, captured by the term m_ij·x_jj/N_jj. This term indicates that the j-th particle group, by consuming external input energy to break itself, impacts the growth of the i-th particle group. The energy dissipation ratio (m_ij) quantifies the ability of different particle groups to consume external input energy.

Additionally, as the content of a grain group increases from a smaller to a larger value, m_ij decreases from 1 to 0.This progression reflects the diminishing space available for further growth of the grain group. Consequently, an inhibitory effect, termed environmental resistance, emerges as the grain group content approaches its limit.

Energy dissipation ratio (m _ij)

According to population evolution theory, the fragmentation energy dissipation ratio represents the proportional relationship between the amount of resources consumed per unit of supply A by unit quantity B. Extending this concept to particle crushing, it is defined as the energy dissipation ratio (m_ij) for each particle size group, representing the relative energy dissipation required for the fragmentation process between different particle groups.

The essence of particle fragmentation lies in the process of energy conversion. The work done by external forces is transformed into the new surface energy created during particle breakage. Specifically, the work exerted by volumetric stress and shear stress is converted into various forms of energy, including the elastic deformation energy of the soil, frictional energy dissipation between soil particles, external work due to soil dilatancy, and the energy dissipation associated with soil particle interactions.

Einav extended Hardin’s fragmentation theory by incorporating fractal theory, suggesting that particle fragmentation reaches a final gradation where particle sizes exhibit self-similar distribution characteristics. The gradation curves before, during, and after loading can thus be described using mass percentage functions. Based on this insight, Einav proposed a modified Hardin crushing index grounded in fractal theory²⁶:

$${B_r}=\frac{{{B_t}}}{{{B_p}}}=\frac{{\int_{{{d_m}}}^{{{d_M}}} {(F(d) - {F_0}(d)){\text{d}}(\lg d)} }}{{\int_{{{d_m}}}^{{{d_M}}} {({F_u}(d) - {F_0}(d)){\text{d}}(\lg d)} }}$$

(11)

$$\text{and}\, F_{u} (d) = \left| {\frac{d}{{d_{M} }}} \right|^{{3 - \alpha }}$$

(12)

Where d_m is the minimum particle size of the sample, and d_M is the maximum particle size of the sample. F₀(d), F (d), and F_u(d) represent the mass percentage functions before, during and after loading, respectively.

Jia²⁷ suggests that there exists a specific relationship between the crushing parameter B_r and the crushing energy consumption:

$${B_r}=c \cdot \frac{{{{({E_B})}^b}}}{{a+{{({E_B})}^b}}}$$

(13)

Here, a, b and c are the crushing parameter coefficients.

From Eq. (13), the following can be derived:

$${E_B}={\left( {\frac{{a \cdot {B_r}}}{{c - {B_r}}}} \right)^{ - b}}$$

(14)

Then the energy dissipation ratio m_ji is:

$${m_{ji}}=\frac{{{E_{bj}}}}{{{E_{bi}}}}={(\frac{{{B_{rj}}}}{{{B_{ri}}}} \cdot \frac{{c - {B_{ri}}}}{{c - {B_{rj}}}})^{ - b}}$$

(15)

In the formula, B_ri and B_rj are the crushing parameters corresponding to the particle group d_i and d_j, respectively.

Effective constraint coefficient (β)

The effective constraint coefficient (β) quantifies the internal restriction relationship among multiple particle groups based on crushing energy consumption. The percentage content vector of the actual composite after crushing is:

$${g^T}(1)=[{G_1}(1),{G_2}(1) \cdots \cdots {G_i}(1)]$$

(16)

The corresponding calculated value, derived from the crushing matrix of the multi-particle group, is as follows::

$${g^T}({1_t})=[{G_1}({1_t}),{G_2}({1_t}) \cdots \cdots {G_i}({1_t})]$$

(17)

The following objective function is constructed using the least square method:

$$g={[{G_1}(1) - {G_1}({1_t})]^2}+{[{G_2}(1) - {G_2}({1_t})]^2}+ \cdots \cdots +{[{G_i}(1) - {G_i}({1_t})]^2}$$

(18)

Here, g is a function of β, and taking the derivative of this function yields the corresponding value of β.

Considering that the density of a certain grain group is not uniform, with the density increasing from small to large and potentially exceeding the limit value, the restraining influence of the density also increases. This transition is reflected in the shift from under-compensation to over-compensation. Therefore, we assume that, due to this mechanism, for the superabundant grain group, the influence of other grain groups diminishes, meaning the constraint coefficient β approaches 0. Conversely, for non-superabundant grain groups, the influence of other grain groups is more significant, so the constraint coefficient β is close to 1.

Model feature discussion

Monodisperse property of the multi-particle group model

The monodisperse property of the multi-particle group model dictates that when only a single particle group exists, with the content of all other particle groups being zero, the model must comply with the breakage law associated with that specific particle size. In this scenario, the model simplifies to a monodisperse state, where the effective interaction constraint coefficient β between different particle groups is zero.

Under these conditions, the following relationships hold:

• (1) β = 0: No interaction exists between particle groups.

• (2) x_ii≠0, x_jj=0: The non-zero content is confined to the single existing particle group, while all others remain absent.

• (3) k_ij≠0: Interaction parameters between the groups do not apply in this state.

$$\begin{gathered} {x_{ii}}^{\prime}={x_i}_{i}+(\sum {{k_i}_{j} \cdot {x_j}_{j}} - {x_i}_{i}) \cdot \left[ {1 - ( \frac{{{x_i}_{i}}}{{{N_i}_{i}}}+\sum\limits_{{j \ne i}} {{m_{ij}}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right] \hfill \\ \quad ={x_i}_{i}+({k_{ii}} \cdot {x_i}_{i} - {x_i}_{i}) \cdot \left[ {1 - (\frac{{{x_i}_{i}}}{{{N_i}_{i}}}+0) \cdot 0} \right] \hfill \\ \quad ={k_{ii}} \cdot {x_i}_{i} \hfill \\ \end{gathered}$$

(19)

$$\begin{gathered} {x_j}_{j}^{\prime }={x_j}_{j}+({\sum {{k_i}_{j} \cdot x} _{ii}} - {x_j}_{j}) \cdot \left[ {1 - ( \frac{{{x_j}_{j}}}{{{N_j}_{j}}}+\sum\limits_{{i \ne j}} {{m_{ij}} \cdot } \frac{{{x_{ii}}}}{{{N_{ii}}}}) \cdot \beta } \right] \hfill \\ \quad =0+({k_{ij}} \cdot {x_{ii}} - 0) \cdot \left[ {1 - ( 0+{m_{ij}} \cdot \frac{{{x_i}_{i}}}{{{N_i}_{i}}}) \cdot 0} \right] \hfill \\ \quad ={k_{ij}} \cdot {x_{ii}} \hfill \\ \end{gathered}$$

(20)

Here, x_ii' and x_jj' represent the mass percentage of the specific grain group and other grain groups, respectively, after the model calculation. This alignment with the fractal model of particle fragmentation within a single particle group confirms that the multi-particle group model can be simplified under these conditions.

Consistency of extreme grain groups

Extreme particle groups are defined as the smallest particle group that can no longer undergo further breakage and the largest particle group that cannot be replenished through the crushing process.These groups represent the physical boundaries of particle fragmentation and play a critical role in accurately modeling particle size distributions.A population model for particle breakage in geotechnical applications must be sufficiently generic to account for these extreme cases. It should accurately capture the mechanical behavior and interactions of extreme particle groups, ensuring that the model remains consistent with both theoretical principles and observed behavior across the entire particle size spectrum.

For the minimum particle size group, fragmentation ceases due to the inherent lower limit of particle breakage. Particles within this group can no longer undergo further size reduction. As a result, the survival rate of particles within their own group is 1, while the migration rate of particles to other groups is zero. The only source of increment for this particle group comes from the fragmentation of larger particle groups.

Mathematically, the migration rates for the smallest particle size group are expressed as:

• (1) k₁₁ = 1: Full survival within the group.

• (2) k_1j = 0 (j ≠ 1): No migration to other particle groups.

These conditions reflect the physical constraints of fragmentation processes and ensure that the model adheres to the principles of particle conservation and realistic behavior at the lower size limit.

$$\begin{gathered} {x_1}_{1}^{{\prime\prime}}={x_1}_{1}+({\sum {{k_{jj}} \cdot x} _{jj}} - {x_{11}}) \cdot \left[ {1 - ( \frac{{{x_1}_{1}}}{{{N_1}_{1}}}+\sum\limits_{{j \ne 1}} {{m_{jj}}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right] \hfill \\ \quad ={x_{11}}+(\sum\limits_{{j \ne 1}} {{k_{1j}} \cdot {x_j}_{j}} +{k_{11}} \cdot {x_1}_{1} - {x_1}_{1}) \cdot \left[ {1 - ( \frac{{{x_1}_{1}}}{{{N_1}_{1}}}+\sum\limits_{{j \ne 1}} {{m_{jj}}} \frac{{{x_j}_{j}}}{{{N_{jj}}}}) \cdot \beta } \right] \hfill \\ \quad ={x_1}_{1}+(\sum\limits_{{j \ne 1}} {{k_{1j}} \cdot {x_j}_{j}} ) \cdot \left[ {1 - ( \frac{{{x_{11}}}}{{{N_{11}}}}+\sum\limits_{{j \ne 1}} {{m_{jj}}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right] \hfill \\ \end{gathered}$$

(21)

Here, x₁₁" represents the mass percentage of the smallest particle group after the crushing process.

For the largest grain group, particles can only fragment into smaller sizes, and no particles from other groups can migrate into this group. As a result, any changes in the mass of this group are solely due to its own fragmentation, which leads to a non-positive increment.

The migration rates for the largest grain group are defined as follows:

• (1) k_timax=0, where t ≠ i_max: No migration from other groups into the largest grain group occurs.

$$\begin{gathered} x_{{{i_{\hbox{max} }}}}^{{\prime}}={x_{{i_{\hbox{max} }}}}+(\sum {{k_{jj}} \cdot {x_{jj}}} - {x_{{i_{\hbox{max} }}}}) \cdot \left[ {1 - ( \frac{{{x_i}_{i}}}{{{N_i}_{i}}}+\sum\limits_{{j \ne {i_{\hbox{max} }}}} {{m_j}_{j}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right] \hfill \\ \quad =\{ 1+({k_i}_{{_{{\hbox{max} }}}} - 1) \cdot \left[ {1 - ( \frac{{{x_{{i_{\hbox{max} }}}}_{{}}}}{{{N_{{i_{\hbox{max} }}}}_{{}}}}+\sum\limits_{{j \ne {i_{\hbox{max} }}}} {{m_j}_{j}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right]\} \cdot {x_i}_{{_{{\hbox{max} }}}} \hfill \\ ={k_{{i_{\hbox{max} }}}} \cdot \left[ {1 - ( \frac{{{x_{i{m_{ax}}}}}}{{{N_{{i_{\hbox{max} }}}}}}+\sum\limits_{{j \ne {i_{\hbox{max} }}}} {{m_j}_{j}} \frac{{{x_{jj}}}}{{{N_{jj}}}}) \cdot \beta } \right]\} \cdot {x_{{i_{\hbox{max} }}}} \hfill \\ \hfill \\ \end{gathered}$$

(22)

Here, x_imax' represents the mass percentage of the largest particle group after crushing. It is evident that the crushing model effectively determines the crushing amount of the extreme grain group, ensuring that the changes in the mass distribution accurately reflect the constraints and behavior of the largest particle group during the fragmentation process. This approach maintains consistency with the physical principles governing particle breakage and migration.

Inclusivity of the excess content group

The actual crushing process is inherently uncertain, as the content of any given grain group may either increase or decrease due to fragmentation. When the content of a grain group increases, it is possible for the group’s content to temporarily exceed its defined limit. Such transient exceedances are acceptable, provided that the overall trend of the system remains stable.

This stability can be characterized by a stable equilibrium point, where the system reaches a state where further significant changes in the distribution of particle sizes are minimal. Under these conditions, particle breakage will eventually reach a stable state, meaning the following equations are satisfied:

$$\left\{ {\begin{array}{*{20}{c}} {{x_1}(t)={f_1}({x_1},{x_2} \cdots {x_i})={g_1} \cdot {x_1} \cdot [1 - (\frac{{{x_1}}}{{{N_1}}}+\sum {{m_j}\frac{{{x_j}}}{{{N_j}}}} ) \cdot \beta ]} \\ {{x_2}(t)={f_2}({x_1},{x_2} \cdots {x_i})={g_2} \cdot {x_2} \cdot [1 - (\frac{{{x_2}}}{{{N_2}}}+\sum {{m_j}\frac{{{x_j}}}{{{N_j}}}} ) \cdot \beta ]} \\ \vdots \\ {{x_i}(t)={f_i}({x_1},{x_2} \cdots {x_i})={g_i} \cdot {x_i} \cdot [1 - (\frac{{{x_i}}}{{{N_i}}}+\sum {{m_j}\frac{{{x_j}}}{{{N_j}}}} ) \cdot \beta ]} \end{array}} \right.$$

(23)

Where g₁, g_2,, …, g_i represent the instantaneous growth rates of each grain group. By solving these equations, the corresponding equilibrium points can be determined, reflecting the stable state of the system where the particle size distribution no longer undergoes significant changes. These equilibrium points indicate the balance between fragmentation and the redistribution of particle mass, ensuring that the system achieves a steady state despite the inherent uncertainties in the crushing process.

Determination of model parameters

Fractal dimension α

In reference¹², a one-dimensional compression test of calcareous sand with a single particle size was conducted, resulting in the compression and crushing grading curve of the calcareous sand.Using Tyler’s formula²¹for calculating the fractal dimension, we obtain the following Eq. (24) :

$$\frac{{{M_{(r<d)}}}}{{{M_{\text{T}}}}}={(\frac{d}{{{d_{\hbox{max} }}}})^{3 - \alpha }}$$

(24)

Where: M(r < d) is the mass of particles with a size smaller than d; M_T is the total mass corresponding to the maximum particle size; d_max is the maximum particle size. By using Eq. (24), the formula for the shape dimension can be derived, leading to following Eq. (25) :

$$\log (\frac{{{M_{(r<d)}}}}{{{M_{\text{T}}}}})=(3 - \alpha ) \cdot \log (\frac{d}{{{d_{\hbox{max} }}}})$$

(25)

Fig. 1

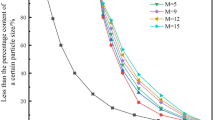
Compression and Crushing Grading Curve of Calcareous Sand with a Single Particle Size (Ref¹²).

Based on Fig. 1 and formula (25), the corresponding fractal dimension α values under different compressive stress conditions can be calculated. The fitting relationship curve between the fractal dimension α and compressive stress σ then obtained, as shown in Fig. 2.

Fig. 2

Relation Curve Between Compressive Stress σ and Fractal Dimension α.

The fitting formula for the fractal dimension α and compressive stress σ is given by Eq. (26):

$$\alpha {\text{=}}e \cdot \ln (\sigma )+f$$

(26)

Where e = 0.268, f = 1.3653, and the correlation coefficient R² = 0.973.

Crushing parameter coefficients a, b and c

According to the relationship curve between crushing energy dissipation E_B and crushing parameter B_rin literature²⁷ (see Fig. 3), the crushing parameter coefficients a, b and c can be obtained by fitting the data using formula (13). The fitting process yields the following coefficients: a = 0.9813, b = 0.2665, c = 0.1412, with a correlation coefficient R² = 0.9694.

Fig. 3

Relationship Curve Between Crushing energy dissipation E_B and crushing parameters B_r(Ref²⁷).

Model validation

Single particle size group crushing demonstration

Tong¹²conducted one-dimensional compression experiments on the fragmentation of 2.5 mm calcareous sand, with axial stresses ranging from 0.8 to 51.2 MPa, the average moisture content of calcareous sand is 11%, and the test temperature is 24 °C. In this paper, the data from reference¹² are used to demonstrate the single particle size group fragmentation model. The results are presented in Fig. 4.

Fig. 4

The literature and calculated values uniaxial compression of calcareous with a single particle size.

Figure 4 shows the literature values and calculated values for the percentage content of each particle size in the failure state corresponding to axial stresses of 1.6 MPa, 3.2 MPa, and 51.2 MPa, with a single particle size of calcareous sand as the initial gradation before crushing. Relevant parameters are provided in the figure, where R² represents the correlation coefficient.

It can be seen from Fig. 4 that the model effectively predicts the fragmentation evolution of a single particle size under different axial stress levels. At relatively low axial stresses, the predicted correlation coefficient exceeds 0.950. However, at an axial stress of 51.2 MPa, the correlation coefficient drops to 0.912, indicating that the crushing state is primarily influenced by stress at higher stress levels. Therefore, it is essential to introduce stress parameters to further optimize the model, improving its accuracy under high-stress conditions.

Multi-particle size group fragmentation demonstration

Bard²⁸ conducted a one-dimensional compression test on a single particle size of 10 mm petroleum coke, the experimental temperature was 20–25 °C, and the moisture content was 1–3%. In this study, the crushing gradation at an initial load of 7.5 MPa is used as the baseline, with further fragmentation occurring under loads of 10 MPa, 20 MPa, and 40 MPa, respectively. Figure 5 presents a comparison between the literature values and the calculated values of the percentage content of each particle size under different stress states, where R² represents the correlation coefficient.

Figure 6(a) and 6 (b) show the comparison between literature values and calculated values of the percentage content of each particle size under different crushing states, as the shear strain of a biogenic carbonate sand increases from 285 to 1180% and from 285 to 13,280%, respectively, as reported in reference²⁹. Shearing was conducted at a rate of about 1.9 mm/min, and the tests were conducted on carbonate sand from the sieve interval 300–425 μm, samples were created in five layers using gentle hand-tamping of each layer after pluviation.

Fig. 5

Experimental values and calculated broken state of petroleum coke in reference²⁸

Fig. 6

The literature and calculated values of ring shear of multi-particle size group calcareous sand in reference²⁹.

The figures illustrate the comparison between literature values and the calculated values, showcasing the model’s capability to accurately predict the fragmentation behavior of multi-particle size groups under varying stress conditions. The correlation coefficients displayed in the figures emphasize the high level of agreement between the model’s predictions and the literature data, further validating the model’s effectiveness in simulating the fragmentation process across different particle sizes and stress levels. This demonstrates the model’s robustness and reliability in addressing complex fragmentation behaviors in geotechnical applications.

In engineering practice, the organizational group model is first used to define objectives and set initial conditions and interaction mechanisms of granular materials. Then, the model simulates material evolution under actual conditions, tracking key parameters like stress path and gradation distribution. Finally, by comparing with experimental data, the model is calibrated to guide material behavior prediction, structural stability analysis, and material optimization.

Applicability and limitations of the model

Applicability:

This model is suitable for predicting the particle breakage process of both single and multi-particle size groups. It effectively describes the particle fragmentation of different soil types under various stress paths, considering both extreme and over limit particle groups.

• (1) Granular Materials: Simulating particle breakage and rearrangement under mechanical loads, such as in soils, aggregates, and ballast materials.

• (2) Dynamic Systems: Modeling systems with evolving conditions, like progressive failure in slopes or cyclic loading in rail tracks.

• (3) Material Design: Optimizing the composition and arrangement of granular materials to enhance performance in engineering applications.

Limitations:

• (1) Certain simplifications, such as neglecting particle shape or chemical interactions, may limit its applicability in highly complex scenarios.

• (2) The accuracy of the model depends on the precise calibration of its parameters, which may require extensive experimental data.

• (3) The model’s reliance on detailed interaction rules and evolutionary processes may lead to high computational demands, especially for large-scale simulations.

Improvements:

• (1) Adding a parameter to represent particle shape would enhance the model’s realism, particularly for granular systems with irregular geometries.

• (2) Developing advanced methods, such as machine learning-based optimization, to calibrate parameters against experimental or field data more effectively.

• (3) Implementing a mechanism for parameters to evolve during simulations, allowing the model to adapt to unforeseen changes in the environment or system behavior.

Highlight of the model

The organizational population model is a theoretical framework that draws from principles of population dynamics and evolutionary theory to describe how groups or populations of individuals evolve and interact over time. This model is often used to capture the complex behaviors of a system of interacting particles by considering factors such as competition, cooperation, and adaptation. The key idea is that particles within a system evolve through mechanisms similar to natural selection, allowing the model to simulate how different particle populations adjust based on their interactions and environmental conditions.

Additionally, the differences between the organizational population model and two widely used models—the Weibull model and the Markov chain model—have been outlined. The comparison highlights the following distinctions:

Interaction Dynamics: The organizational population model accounts for complex interactions among particles, which are not considered in the Weibull model or the state-based transitions of the Markov chain model.

Adaptability: Unlike the fixed distributions in the Weibull model and static probabilities in the Markov chain model, the proposed model adapts to changing environmental conditions by simulating evolutionary processes.

Multiscale Interaction: The organizational population model uniquely addresses interactions between particles of different sizes, which are often overlooked in the other two models.

Dynamic System Evolution: The proposed model captures the dynamic evolution of particle systems over time, surpassing the static nature of the Weibull model and the predefined states of the Markov chain model.

Conclusions

A prediction model for particle breakage based on population evolution theory is proposed by comparing the characteristics of granular soil particle fragmentation and the evolution of the particle population. This model introduces key factors such as the migration rate, comprehensive environmental impact coefficient, crushing energy dissipation ratio, and effective constraint coefficient. The model’s characteristics are discussed, highlighting the monodisperse property of the multi-particle size group, the consistency of the extreme particle size group, and the inclusivity of the over-limit particle size group. The validity of the model is verified through single and multi-particle size particle breakage tests. The key features of the model are as follows:

• (1) Comprehensive Fragmentation Description: The proposed fragmentation model, based on population evolution theory, effectively describes both the breakage law of single particle sizes and the fragmentation behavior of multi-particle size groups.

• (2) Migration Rate (k): The model introduces the migration rate k, which accounts for the migration between particle sizes during the fragmentation process. The migration rate quantifies how a particle size group transitions into another particle size group and describes the survival and fragmentation dynamics of the particle size group.

• (3) Effective Restriction Coefficient (β): To characterize the inter-group constraints during the crushing process, the effective restriction coefficient β is introduced. This coefficient accounts for both insufficient compensation and transition compensation during fragmentation, with values ranging from 0 to 1.

• (4) Comprehensive Environmental Impact Coefficient (r_ij): The coefficient r_ij considers the impact of other particle size groups on the content variation of a specific particle size group. It incorporates the internal restriction coefficient and the energy consumption ratio of particle group interactions.

• (5) Monodisperse Property: The population fragmentation model exhibits the monodisperse property, which allows it to describe the fragmentation behavior of both single and multi-particle size groups. This feature makes the model suitable for analyzing the fragmentation evolution of extreme and over-limit particle groups during the fragmentation process.

• (6) Model Parameters Determination: A logarithmic relationship is observed between the fractal dimension α and compressive stress σ. The crushing parameter coefficients a, b and c were determined through empirical tests.

The proposed model provides a comprehensive framework for predicting particle breakage, incorporating key factors influencing fragmentation, and is validated by empirical tests. However, further research is needed to improve parameter accuracy and extend the model’s applicability to dynamic crushing scenarios.