A novel simultaneous monitoring method for surface roughness and tool wear in milling process

Abstract

Quality prediction and condition monitoring are crucial for realizing zero-defect intelligent manufacturing. Surface roughness is an important technical indicator to measure the surface quality of parts. In the cutting process, tool wear is directly related to the dynamic change of the surface roughness and the machining efficiency. To enhance data utilization and reduce computational costs, this paper develops a novel two-task simultaneous monitoring method for surface roughness and tool wear. First, the enhancement layer corresponding to each sub-task in the broad learning system is replaced with a reservoir with echo state characteristics, and through information sharing between sub-tasks and the capture of their respective dynamic characteristics, a broad echo state two-task learning system with incremental learning is constructed. Then, an end-face milling machining experiment was conducted on a vertical machining center, and the feasibility of the developed method for two-task simultaneous monitoring of surface roughness and tool wear was verified through feature extraction and nonlinear dimensionality reduction of the monitoring signals during the machining process. The experimental results indicate that the developed two-task simultaneous monitoring method is superior to other two-task learning methods in terms of comprehensive performance, and it lays a solid foundation for the high-quality and efficient machining of CNC machine tools.

Introduction

The rise and rapid development of the new generation of artificial intelligence (AI) and sensor technology has provided a good opportunity for applying condition monitoring to manufacturing. To weigh the relationship between quality, cost, and efficiency, it needs to establish an AI model based on computer numerical control (CNC) machine tool machining process information to monitor part machining quality and equipment status while reducing costs and increasing efficiency. Numerous theoretical and experimental studies suggest that surface roughness is closely related to various properties of parts, including wear resistance, corrosion resistance, fatigue strength, sealing effectiveness, contact stiffness, and fitting accuracy¹. Generally, surface roughness is maintained within the desired threshold range by selecting an appropriate combination of cutting parameters, and this process usually relies on time-consuming and labor-intensive tests based on manual experience. In the metal cutting process, the tool, as the actual executor, constantly removes excessive materials on the workpiece surface according to needs, which inevitably results in different degrees of wear, and tool wear will also directly affect the dimensional accuracy and surface integrity of the parts. Additionally, when the tool is severely worn, it will cause the workpiece to be scrapped, and even damage the machine tool and lead to unplanned downtime. Hence, machining process monitoring is a promising development direction in the manufacturing industry. Process monitoring is in close relation with AI tools to extract information from sensor signals that may uncover important hidden information². Currently, data-driven technology has shown great potential in process monitoring and control³.

Surface roughness and tool wear are the two main factors of concern in the cutting process, and extensive studies have been conducted on them. However, due to the dynamic and time-varying characteristics of the CNC machine tool-cutting process, it is difficult to establish a more accurate mathematical model, and data-driven methods are increasingly popular among researchers and engineers⁴. He et al.⁵ provide a systematic review of soft computing techniques for predicting surface roughness in hard turning, covering three key aspects: data acquisition, feature selection, and prediction models. Tool condition monitoring (TCM) is a crucial task in machining processes because it allows for effective diagnosis of cutting tool health by exploiting information gathered from the machining process and its various elements⁶. TCM methods are mainly categorized into two groups: direct techniques and indirect techniques⁷. Among them, direct techniques are usually less ideal due to the unnecessary downtime they require, while indirect techniques infer tool conditions from measurements of various parameters or signals. Commonly measured physical quantities and the sensors used to capture them include accelerometers^8,9, current sensors¹⁰, force sensors¹¹, acoustic emission sensors^12,13, and sound sensors¹⁴, etc.

In recent years, some scholars have tried to leverage the correlation between tool wear and surface roughness to predict these two key factors simultaneously. For example, Matsumura et al.¹⁵ considered both tool wear and surface roughness to minimize costs by optimizing machining operations. This was achieved by analytically predicting flank wear following metal cutting theory and predicting surface roughness with a neural network. To maximize the benefits of hard turning, manufacturers need to develop accurate prediction models for both surface roughness and tool wear. Özel and Karpat¹⁶ employed a neural network to predict surface roughness and tool flank wear throughout machining time under various cutting conditions in finish hard turning. Rao et al.¹⁷ took the nose radius, cutting speed, feed rate, and volume of material removed as input parameters of a multilayer perceptron model to predict surface roughness, tool wear, and workpiece vibration amplitude. The experimental results were highly consistent with the values predicted by the model. Huang and Lee¹⁸ developed a deep learning and sensor fusion method to estimate tool wear and surface roughness, but the two factors were predicted separately. In contrast, Nguyen et al.¹⁹ combined an adaptive neural fuzzy inference system with Gaussian process regression and Taguchi analysis to monitor grinding wheel wear and surface roughness during the grinding process. The experimental results indicate that this method can accurately predict both grinding wheel wear and surface roughness when working with Ti-6Al-4V alloy. Panda et al.²⁰ proposed a method for online monitoring of material machining quality, which simultaneously predicts the remaining useful life of the cutting tool and the surface quality of the workpiece. However, due to uncontrollable factors such as tool wear, accurately predicting surface roughness in complex machining processes is a great challenge. To address this issue, Cheng et al.²¹ introduced a hybrid kernel extreme learning machine model using Gaussian and arc-cosine kernel functions to better predict surface roughness. Meanwhile, Cheng et al.²¹ devised a novel tool wear monitoring framework that integrates an attention mechanism, weighted feature averaging, and deep learning models, with a consideration of tool wear. In addition, Cheng et al.²² introduced a multi-task learning model with shared layers and two task-specific layers to achieve simultaneous prediction of surface roughness and tool wear. Wang et al.²³ put forward a multi-task learning method based on a deep belief network to predict tool wear and part surface quality simultaneously by analyzing vibration signals from the machine tool spindle during milling. The model obtained a prediction accuracy of 99% for tool wear and 92.86% for part surface quality. However, this method categorizes surface roughness as either qualified or not based on specific requirements. Additionally, to address the negative effects of conventional mineral-based cutting fluids, the minimum quantity lubrication with nanofluids (NF-MQL) was used to significantly reduce tool wear and improve surface finish quality²⁴.

To sum up, some scholars have attempted to achieve parallel monitoring of surface roughness and tool wear, but these efforts remain in their early stages and have limited effectiveness. Our work proposes a novel method for simultaneous monitoring of two tasks and designs an end-face milling experiment to evaluate the effectiveness of this method for parallel monitoring of surface roughness and tool wear. Additionally, the monitoring results are compared with those obtained from other two-task monitoring models.

The main contributions of this study are summarized as follows:

• A novel broad echo state two-task learning system (BESTTLS) is designed to capture the dynamic characteristics of each sub-task.

• To simultaneously monitor surface roughness and tool wear, an end-face milling experiment was conducted, and signals including vibration, current, and cutting force were collected during the machining process.

• To validate the superiority of the proposed model, the monitoring signals were subjected to feature extraction and dimensionality reduction, and the results were compared with those from other two-task monitoring models.

Methodology

BLS is an effective and efficient incremental learning system based on the random vector functional link neural network (RVFLNN)²⁵. It is constructed in the form of a flat network structure, rather than a deep architecture, and it is favored in industrial applications²⁶. As shown in Fig. 1, the typical architecture of BLS consists of four main components: the input layer, feature layer, enhancement layer, and output layer.

Fig. 1

The architecture of the typical broad learning system (BLS).

In the BLS training process, the original input data is first mapped to the feature layer nodes through a linear transformation. Then, the outputs from the feature layer nodes are mapped to the enhancement layer nodes through a nonlinear transformation. At last, the outputs of both the feature and enhancement layer nodes are combined and connected to the final output layer. The connection weights from the input layer to the feature layer and from the feature layer to the enhancement layer are randomly generated and kept unchanged throughout the training process. Only the weights of the final output layer are computed using pseudo-inverse or ridge regression methods. Moreover, when BLS performance is insufficient, it can be enhanced via incremental learning. In this process, only the weights of the new components are recalculated, so there is no need to retrain the entire network or use gradient descent for iterations. Attributed to this, BLS is highly scalable and efficient, particularly advantageous for small training sample sizes.

As a typical recurrent neural network, the echo state network (ESN) mainly consists of an input layer, a hidden layer, and an output layer, with the hidden layer being replaced by a dynamic reservoir. The basic structure of ESN is demonstrated in Fig. 2. In ESN, the neuron nodes inside the reservoir are randomly connected and sparse. To ensure the echo state properties and stability of the reservoir, the spectral radius of the internal connection weight matrix $W_{res}$ needs to be less than 1. Therefore, $W_{res}$ is usually scaled as follows:

Fig. 2

The structure of the typical echo state network (ESN).

$$\begin{aligned} W_{res} \leftarrow \frac{\rho }{\left| \lambda _{max}\right| } W_{res} \end{aligned}$$

(1)

where $\left| \lambda _{max}\right|$ denotes the spectral radius of $W_{res}$, and $\rho \in \left( 0,1\right)$ is a scaling factor.

Let the number of neuron nodes in the input layer, reservoir, and output layer of the ESN be D, K, and L, respectively. Meanwhile, let $W_{in} \in \mathbb {R}^{K \times D}$, $W_{res} \in \mathbb {R}^{K \times K}$, and $W_{out} \in \mathbb {R}^{L \times (D+K)}$ denote the connection weights from the input layer to the reservoir, within the reservoir, and from the input layer and the reservoir to the output layer, respectively. Given the input vector $\varvec{u}(t)$ at time t, the reservoir state $\varvec{x}(t)$ and the final output $\hat{\varvec{y}}(t)$ are updated as follows:

$$\begin{aligned} \left\{ \begin{aligned} \varvec{x}(t)&= f \left( W_{in} \varvec{u}(t)+W_{res} \varvec{x}(t-1)\right) \\ \hat{\varvec{y}}(t)&= g \left( W_{out}[\varvec{u}(t), \varvec{x}(t)]\right) \\ \end{aligned} \right. \end{aligned}$$

(2)

where f and g represent the activation functions of the reservoir and the output layer respectively, and g is typically the identity function.

In the training process of ESN, $W_{in}$ and $W_{res}$ remain unchanged after random generation, and only the output weight matrix $W_{out}$ is adjusted through linear regression. Compared with traditional recurrent neural networks, ESN has a significantly simpler network training process.

BLS and ESN have similar training methods, and the CNC machine tool-cutting process has dynamic time-varying characteristics. Considering this, to enable simultaneous monitoring of surface roughness and tool wear, this work proposes a novel broad echo state two-task learning system (BESTTLS) that employs a reservoir with echo state characteristics instead of the enhancement layer for each sub-task in the BLS. The system architecture is shown in Fig. 3. During the training process of BESTTLS, when the system performance fails to meet the requirements, the reservoir can be added one by one through incremental learning to quickly update the connection weights and achieve higher system performance. The specific modeling process of the proposed BESTTLS is outlined below:

Fig. 3

The architecture of the proposed broad echo state two-task learning system (BESTTLS).

In this study, the training sample data set is denoted as $\varvec{S}=\left\{ \varvec{X}, \varvec{Y} \right\}$, where $\varvec{X} = \left( \varvec{x}_{1}, \varvec{x}_{2}, \cdots , \varvec{x}_{N} \right) ^{\textrm{T}} \in \mathbb {R}^{N \times M}$ represents the input data and $\varvec{Y} = \left( y_{1}, y_{2}, \cdots , y_{N} \right) ^{\textrm{T}} \in \mathbb {R}^{N \times L}$ represents the output labels. Here, N denotes the number of samples, M denotes the number of attributes or features contained in each sample, and $L = 2$ denotes the number of tasks. For simplicity, both the feature layer and enhancement layer in BLS are treated as hidden layers.

Additionally, assume that the feature layer of the BLS consists of n feature groups, and each group contains m feature nodes. The output of the ith feature group can be calculated as follows:

$$\begin{aligned} \varvec{F}_i=\varphi _i\left( \varvec{X} \varvec{W}_{F_i}+\varvec{\beta }_{F_i}\right) \in \mathbb {R}^{N \times m}, i = 1,2, \cdots , n \end{aligned}$$

(3)

where $\varphi _i$ stands for a linear transformation, while $\varvec{W}_{F_i}$ and $\varvec{\beta }_{F_i}$ are randomly generated weight matrix and threshold term with appropriate dimensions, respectively.

Then, the outputs from all feature group nodes are combined:

$$\begin{aligned} \varvec{F}=\left[ \varvec{F}_1, \varvec{F}_2, \cdots , \varvec{F}_n\right] \in \mathbb {R}^{N \times n m} \end{aligned}$$

(4)

Subsequently, the output $\varvec{F}$ from the feature layer is mapped to the reservoir for each sub-task through a nonlinear transformation to better capture the dynamic characteristics of each sub-task. The state update equation of the reservoir is given by:

$$\begin{aligned} \varvec{E}_{r}(n)=\psi \left( W_{in} \varvec{F}(n)+W_{res} \varvec{E}_{r}(n-1)\right) \end{aligned}$$

(5)

where $\varvec{E}_{r}$ denotes the state of the reservoir in the rth task, $W_{in}$ denotes the weight matrix connecting the feature layer output to the reservoir, and $W_{res}$ represents the weight matrix within the reservoir. Here, the activation function $\psi$ used is the tanh function.

Finally, the outputs from the feature layer and the reservoir for each sub-task are concatenated and mapped to the final output layer. At this time, the final output of BESTTLS is represented as:

$$\begin{aligned} \widehat{\varvec{Y}}_r=\left( \begin{array}{ll} \varvec{F}&\varvec{E_r} \end{array}\right) \left( \begin{array}{c} \varvec{W}_r^F \\ \varvec{W}_r^E \end{array}\right) \end{aligned}$$

(6)

where $\varvec{W}_r^F$ and $\varvec{W}_r^E$ denote the weight matrices connecting the feature layer to the output layer and the reservoir to the output layer in the rth task, respectively.

Let $\varvec{H}_r=\left( \varvec{F}, \varvec{E_r}\right)$ and $\varvec{W}_r=\left( \varvec{W}_r^F, \varvec{W}_r^E\right) ^{\textrm{T}}$, then $\varvec{H}_r$ can be considered the hidden layer output for the rth task. Thus, $\widehat{\varvec{Y}}_r$ can be abbreviated as:

$$\begin{aligned} \widehat{\varvec{Y}}_r=\varvec{H}_r \varvec{W}_r \end{aligned}$$

(7)

Given the actual training sample label $\varvec{Y}_r$, the output weight matrix $\varvec{W}_r$ can be solved quickly by pseudo-inverse as follows:

$$\begin{aligned} \varvec{H}_r^{+}= & \left( \lambda \varvec{I}+\varvec{H}_r^{\textrm{T}} \varvec{H}_r\right) ^{-\textbf{1}} \varvec{H}_r^{\textrm{T}} \end{aligned}$$

(8)

$$\begin{aligned} \varvec{W}_r= & \left( \lambda \varvec{I}+\varvec{H}_r^{\textrm{T}} \varvec{H}_r\right) ^{-\textbf{1}} \varvec{H}_r^{\textrm{T}} \varvec{Y}_r \end{aligned}$$

(9)

where $\lambda$ and $\varvec{I}$ represent the regularization parameter and the identity matrix, respectively.

If the prediction performance of the model is unsatisfactory, the prediction accuracy can be improved by expanding the reservoir as follows:

Assume that K reservoirs are added one by one to the enhancement layer for each sub-task in BESTTLS. For simplicity, let $\varvec{H}_r^1=\varvec{H}_r$, $\varvec{W}_r^1=\varvec{W}_r$, $W_{in}^1=W_{in}$, $W_{res}^1=W_{res}$. When adding the kth reservoir, the update for the entire enhancement layer in the rth sub-task is expressed as follows:

$$\begin{aligned} \varvec{H}_r^{k+1}=\left[ \varvec{H}_r^{k} \mid \psi \left( W_{in}^{k+1} \varvec{F}+W_{res}^{k+1} \varvec{E}_r\right) \right] , k=1,2,\cdots , K \end{aligned}$$

(10)

where $W_{in}^{k+1}$ denotes the input weight matrix connecting the feature layer to the $(k+1)$th reservoir, $W_{res}^{k+1}$ denotes the connection weight matrix within the $(k+1)$th reservoir, and $\psi$ is the activation function.

After the kth reservoir is added, the pseudo-inverse of $\varvec{H}_r^{k+1}$ can be updated incrementally as follows:

$$\begin{aligned} \left( \varvec{H}_r^{k+1}\right) ^{+}=\left[ \begin{array}{c} \left( \varvec{H}_r^k\right) ^{+}-\varvec{D} \varvec{B}^{\textrm{T}} \\ \varvec{B}^{\textrm{T}} \end{array}\right] \end{aligned}$$

(11)

where $\varvec{D}=\left( \varvec{H}_r^{k}\right) ^{+} \psi \left( W_{in}^{k+1} \varvec{F}+W_{res}^{k+1} \varvec{E}_r\right)$.

$$\begin{aligned} \varvec{B}^{\textrm{T}}={\left\{ \begin{array}{ll} \varvec{\left( C\right) ^{+}}, & \varvec{C} \ne 0 \\ \left( \varvec{I}+\varvec{D}^{\textrm{T}} \varvec{D}\right) ^{-1} \varvec{D}^{\textrm{T}} \left( \varvec{H}_r^{k}\right) ^{+}, & \varvec{C} = 0 \end{array}\right. } \end{aligned}$$

(12)

where $\varvec{C}=\psi \left( W_{in}^{k+1} \varvec{F}+W_{res}^{k+1} \varvec{E}_r\right) -\varvec{H}_r^{k} \varvec{D}$.

Therefore, the new output weight matrix of the rth sub-task is given by:

$$\begin{aligned} \varvec{W}_r^{k+1}=\left[ \begin{array}{c} \left( \varvec{H}_r^k\right) ^{+}-\varvec{D} \varvec{B}^{\textrm{T}} \\ \varvec{B}^{\textrm{T}} \end{array}\right] \varvec{Y}_r=\left[ \begin{array}{c} \varvec{W}_r^k-\varvec{D} \varvec{B}^{\textrm{T}} \varvec{Y}_r \\ \varvec{B}^{\textrm{T}} \varvec{Y}_r \end{array}\right] \end{aligned}$$

(13)

During the training process of BESTTLS, the loss function is defined as the weighted sum of the loss functions for multiple sub-tasks. Generally, the goal is to minimize the value of the loss function for each sub-task as much as possible, which is expressed as follows:

$$\begin{aligned} Loss=\sum _{r=1}^L \lambda _r Loss_r \end{aligned}$$

(14)

where $\lambda _r$ is the weighting coefficient, and $Loss_r$ is the loss function of the rth sub-task.

During the incremental learning process of the BESTTLS enhancement layer, reservoirs for each sub-task are added simultaneously. In this process, only the pseudo-inverse of the newly added reservoir’s connection weight matrix needs to be computed, and there is no need to retrain the entire network model, which significantly improves the training speed of BESTTLS.

Fig. 4

Installation location of each sensor.

Experimental design

Experimental setup

To validate the effectiveness of the proposed BESTTLS for simultaneous monitoring of surface roughness and tool wear, an end-face milling experiment was carried out using a vertical three-axis machining center (VMC850B). The workpiece material was 45 steel with a dimension of $\mathrm 125~mm \times 125~mm \times 120~mm$. The cutting tool was a four-flute flat end mill (UP210-S4-10025) with a diameter of $\mathrm 10~mm$, and the overhang length of the tool during milling was $\mathrm 32~mm$. In the end milling process, the milling depth $a_p$ was $\mathrm 1.2~mm$, the milling width $a_e$ was $\mathrm 10~mm$, the spindle speed n was $\mathrm 3800~r/min$, the feed speed $V_f$ was $\mathrm 600~mm/min$, and air cooling was applied.

Data collection

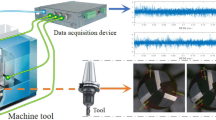
The workpiece was fixed with four bolts directly above the 3-component force sensor (Kistler 9377C), and the sensor was bolted to the CNC machine table. Meanwhile, a three-axis accelerometer (Kistler 8763B050BB) was deployed by magnetic attraction near the tool handle of the machine spindle, and three current clamps (Fluke i200s) were clamped on the U, V, and W three-phase output wires of the machine spindle servo motor drive unit. Then, a new tool was employed to perform back-and-forth end milling operations on the upper surface of the workpiece. The installation location of each sensor is illustrated in Fig. 4.

In this experiment, acquisition software was developed using the LabVIEW environment, and a National Instruments cDAQ-9185 (CompactDAQ chassis) was used, which was equipped with NI-9232, NI-9215, and NI-9234 input modules. These modules were utilized to synchronously acquire vibration, current, and cutting force signals during the cutting process at a sampling frequency of 20 kHz. The waveforms of the raw signals collected by each sensor are exhibited in Fig. 5.

Fig. 5

The original signal waveform diagram collected by each sensor.

To simultaneously monitor tool wear and part surface roughness, measurements were performed at intervals during the end milling process according to on-site conditions. Tool wear was measured off-machine using a ViTiny UM06 microscope, while surface roughness was measured on-machine using a portable roughness meter. The $R_a$ value was taken as the surface roughness index. For each measurement, surface roughness was recorded three times at different positions at the last walking tool end-face and averaged to obtain the final result. The measurement process for both tool wear and surface roughness is illustrated in Fig. 6.

Fig. 6

The measurement process of tool wear and surface roughness in the milling process.

Results and discussion

In this end milling experiment, a total of 816 tool strokes were performed until the milling cutter exhibited severe wear. During this period, 63 measurements were taken at irregular intervals, and 63 sets of valid sample data were obtained. To evaluate the effectiveness of the proposed method for simultaneous monitoring of two tasks, 48 sets of data were randomly selected from these sample data for model training, while the remaining 15 sets were reserved for model testing.

As indicated by the green dotted rectangle in Fig. 5, by manually capturing the signals from the final tool pass before each measurement and removing the unstable portions that occur during tool cutting in and out, the vibration, current, and cutting force signals during the milling process are effectively segmented. Meanwhile, eight time-domain features²⁷ and five frequency-domain features (as listed in Table 1) are extracted from each valid signal channel, leading to a total of 117 features per sample. All simulations were carried out on a 64-bit Windows 11 computer equipped with an Intel(R) Core(TM) i9-13900H 2.60 GHz processor and 32.0 GB of memory, using the MATLAB R2023a software.

Table 1 Frequency-domain feature extraction.

Considering that some of the extracted signal features are irrelevant or redundant and may affect model performance, this study employs kernel principal component analysis (KPCA)²⁸ for nonlinear dimensionality reduction and selects the first 12 principal components as the input for BESTTLS. The cumulative contribution rate reaches 95.11%. Meanwhile, according to the VB value, the milling cutter status is divided into two categories (normal and worn) and is encoded using the one-heat method. The specific status classification is presented in Table 2.

Table 2 The classification of milling cutter wear status.

Before performing the two-task modeling, all variables need to be normalized to the range [0, 1] by

$$\begin{aligned} \overline{x}=\frac{x-min(\varvec{x})}{max(\varvec{x})-min(\varvec{x})} \end{aligned}$$

(15)

where x and $\overline{x}$ denote the original and standardized data, respectively. $max(\varvec{x})$ and $min(\varvec{x})$ represent the maximum and minimum values of the variable $\varvec{x}$, respectively.

Fig. 7

Simultaneous monitoring results of surface roughness and tool wear based on BESTTLS.

In our study, the following loss function is used to evaluate the simultaneous monitoring performance of surface roughness and tool wear status:

$$\begin{aligned} \mathrm{Loss = MAPE + ErrorRate} \end{aligned}$$

(16)

where $\mathrm MAPE$ denotes the evaluation index for surface roughness prediction; $\mathrm ErrorRate$ represents the error rate for the classification of tool wear status, which is calculated as follows:

$$\begin{aligned} \textrm{ErrorRate} = 1 - \frac{n_{correct}}{n_{total}} \times 100\% \end{aligned}$$

(17)

where $n_{correct}$ denotes the number of correctly classified samples, and $n_{total}$ represents the total number of samples.

The mean absolute percentage error (MAPE) is computed as follows:

$$\begin{aligned} \textrm{MAPE} = \frac{1}{N} \sum _{i=1}^{N} \vert \frac{y_{i}-\hat{y}_{i}}{y_{i}} \vert \times 100 \% \end{aligned}$$

(18)

where N denotes the total number of samples, $y_{i}$ and $\hat{y}_{i}$ represent the actual measurement results and the model predicted results for the ith sample, respectively.

Fig. 8

The prediction results of surface roughness by different models.

Fig. 9

The monitoring results of tool wear status using different models.

Fig. 7 shows the results of using the proposed BESTTLS to simultaneously monitor surface roughness and tool condition. The results indicate that the predictions made by BESTTLS are highly consistent with the actual measurement results. Specifically, the model achieves a MAPE of 5.75% for surface roughness prediction, demonstrating its robustness in predicting surface roughness with minimal deviation from actual values. Furthermore, the tool condition monitoring of the system displays excellent performance, with a prediction accuracy of 100%.

To further validate the superiority of the proposed BESTTLS in simultaneously monitoring surface roughness and tool wear, a broad two-task learning system (BTTLS) and a fuzzy broad two-task learning system (FBTTLS) were developed for comparison. These two models are two-task monitoring models designed based on BLS and fuzzy broad learning system (FBLS)²⁹ respectively. Figs. 8 and 9 present the results obtained from the various models. Specifically, Fig. 8 shows the predictions for surface roughness, while Fig. 9 displays the results of tool condition monitoring. Through comparative analysis, it can be clearly seen that the proposed method BESTTLS has significant advantages.

In addition, Fig. 10 shows a comprehensive performance comparison of several two-task models for surface roughness prediction and tool wear condition monitoring. The results indicate that both of the above two-task monitoring methods can accurately predict the tool wear condition, demonstrating their effectiveness in evaluating tool health status. The MAPE of BTTLS, FBTTLS, and BESTTLS in predicting surface roughness are 7.57%, 10.14%, and 5.75%, respectively. The performance of BESTTLS is obviously better than that of the other models. In conclusion, BESTTLS outperforms other models significantly in simultaneous monitoring of surface roughness and tool wear.

Fig. 10

Comparison of model performance for surface roughness prediction and tool wear condition monitoring.

Conclusion

To fully exploit experimental data and avoid time-consuming and laborious repetitive work, this paper constructs a novel broad echo state two-task learning system (BESTTLS), which uses the reservoir with echo state characteristics for each sub-task to capture their respective dynamic characteristics while sharing information. When the system performance does not meet the requirements, incremental learning is performed to achieve higher system performance. Finally, an end-face milling experiment was conducted on a vertical three-axis machining center to validate the effectiveness of the proposed BESTTLS in simultaneously monitoring surface roughness and tool wear. During the milling process, vibration, current, and cutting force signals were collected, followed by feature extraction and nonlinear dimensionality reduction. To further validate the superiority of BESTTLS, its prediction results were compared with those of the BTTLS and FBTTLS two-task learning methods. The results indicate that BESTTLS significantly outperforms the other methods in simultaneously monitoring surface roughness and tool wear.