Assessment of the performances and limitations of spacetime convective corrections for acoustic metacontinua design

Abstract

The acoustic metamaterial extension to aeroacoustic applications is still an open issue principally due to the lack of a reliable methodology for the meta-devices design when they have to operate in a non-quiescent medium. One suitable strategy is to use spacetime coordinate transformations that include the background flow features to tune the meta-device design parameters analytically, and, therefore, the phenomenon must be reinterpreted into the spacetime. However, a change of coordinates capable of including all the convective effects is not known for general flow conditions and analytical approximations are inevitably introduced. This work validates the spacetime framework numerically, providing a better comprehension of the approximation effects on the spacetime-corrected acoustic metacontinuum and its cautious interpretation both from the mathematical and physical points of view.

Introduction

The acoustic metamaterial concept has interested many scientific research fields in the last decades: their attractive feature relies on their potentiality for breakthrough technologies’ development. Firstly thought for electromagnetic applications^1,2, their implementation also reached other branches of physics and engineering (e.g., thermodynamic, acoustic). The advent of the transformation optics technique^3,4,5 facilitated this step forward making exotic behaviours a consequence of the specific application aimed through the meta-device properties adequate characterization. This new degree of freedom reduced the problem of the meta-devices design’s definition into finding a suitable coordinate transformation able to provide the desired specific exotic wave manipulation. With a focus on acoustic applications, the promising results obtained in the electromagnetic field were extended thanks to the similarity between the single-polarization Maxwell equation and the two-dimensional acoustic equation in a fluid⁶. Following this path, Norris developed an acoustic theory where exotic behaviours and unconventional properties definitions go under an extended concept of continuum model called metacontinuum⁷. Specifically, the author identifies the inertia and bulk modulus as the fundamental ingredients for extraordinary acoustic waves manipulations’ achievement (e.g., steering of incident waves with atypical reflection and refraction angles⁸, acoustic cloaking⁹ and perfect absorption¹⁰). These improvements opened up the possibility of dealing with one of the aeronautical community problems of the last decades: aircraft acoustic pollution and community noise reduction requests¹¹. Specifically, with the spread of the concept of drones for civilian applications, the topic gained more importance and the concentration of the research efforts¹². However, the extendibility of acoustic meta-devices’ properties to aeronautical problems immediately showed many difficulties: the coordinate transformation approach (Standard Transformation Acoustics (STA)) works by transforming the Euclidean metric and modifying the space differential operator, meaning that the governing equations’ formal invariance under coordinate change has to be guaranteed. In the optic of introducing acoustic metamaterials into aeronautics, it is necessary to consider that the meta-device has to work within a non-quiescent medium. From the physical point of view, this means that the background flow carries out the acoustic perturbation, leading to a governing equation that manifests the presence of mixed space and time derivatives. Consequently, the governing equation formal invariance property fails, making the STA approach no longer valid and leading to a performance decay of statically designed acoustic meta-devices as the final result. This misbehaviour has interested many authors who tried to overcome the problem: Huang et al.^13,14, and Ryoo et al.¹⁵ investigate new possible metamaterial design through optimization techniques; Huang et al.¹⁶ and Iemma¹⁷ introduced a Doppler factor in the metamaterial design for planar and non-planar incoming wavefronts, respectively. Nevertheless, this task remains an open issue. Finally, with the Analogue Transformation Acoustics (ATA) proposed by García-Meca et al.¹⁸, a proper mathematical structure was defined where mixed space and time derivatives presence no longer influence the governing equation formal invariance under the coordinate transformation (that is now re-ensured). The approach relies on considering the relativistic structure upon which the acoustic perturbation propagates (as already observed by Visser¹⁹) and reinterpreting into the spacetime the phenomenon under investigation. The combination of ATA and STA makes again meta-devices a suitable strategy for aircraft noise emission abatement. Even its generality, the ATA approach revealed itself to be too limited for aeronautical applications: it is applicable only for simple geometries with unfeasible solutions concerning the aeronautical constructive elements constraints^17,20. Despite those limitations, some authors tried to exploit the spacetime formalism by combining the ATA method with the metacontinuum concept: in Iemma and Palma^21,22 appears the possibility of defining meta-devices properties suited for convective applications. In this new approach, the authors rewrite the metacontinuum governing equation into the spacetime domain and introduce a spacetime mapping capable of embedding the convective terms that characterize the background flow. Therefore, the idea is to retrieve the static meta-device properties through STA, derive the associated metric into a $(3+1)$-dimensional pseudo-Riemannian manifold and analytically correct those properties through spacetime coordinate transformation. Therefore, starting from this point, exotic behaviours in flowing media are seen as the result of a specific spacetime mapping finding. Specifically, the authors propose the method using two analytical corrections based on Prandtl-Glauert’s²³ and Taylor’s²⁴ coordinate transformations and different works tried to validate the approach by disclosing its potentialities and limits. Despite the promising results, the adapted meta-device performance recovery is evident but partial, and to correctly attribute the origin of such discrepancy, it is necessary to consider two fundamental aspects. The first is the high complexity of the phenomenon under investigation: the information exchange between conventional and unconventional continuum models is a tricky aspect to deal with. Some steps in this direction are in²⁵ where the boundary conditions’ imposition revealed itself as a crucial and non-trivial task. The second concerns the limited capacity of each analytical correction to capture convective effects with the consequent and inevitable introduction of analytical error^26,27,28. In this context, the present work represents one of the last steps of an incremental process for the validation of the methodology initially proposed in²². The aim is to reveal the potentiality of the spacetime aeroacoustic framework for the adaptation of acoustic meta-devices to convective applications. Therefore, by giving a careful mathematical and physical interpretation of its limitations through numerical simulations, we aim to gain a greater awareness of the methodology to achieve greater control over the performances of an acoustic metacontinuum able to work in non-quiescent conditions. To pursue this goal, the spurious effects that appear with the analytical correction introduction are assessed through Lighthill’s acoustic analogy concept: all the terms that do not contribute to the specific convected wave operator definition are moved to the right-hand side of the equation and reinterpreted as equivalent acoustic sources²⁹. The forcing terms could derive from both the wave equation manipulation in the classical Euclidean form and in terms of spacetime metric tensors differences. Numerical results regard both formalisms through a set-up that aims at the problem complexity minimization: the spacetime-corrected metacontinuum is used as a mathematical model for the acoustic behaviour of a conventional fluid mimicking. This choice allows disregarding the specific acoustic mirage aimed and concentrating solely on the aeroacoustic spacetime framework effectiveness in including convective effects (as in^26,27,28). In this way, the fictitious flow introduction in a region where a static wave equation is originally defined highlights the solely coordinate change capability in capturing the convective features of the background flow. Finally, a sensitivity analysis is used to disclose the analytical approximation influences on the metacontinuum performances.

Analytic convective corrections

In relativistic theory³⁰, it is possible to describe the generic scalar field $\psi (\pmb {\xi })$ propagation into a $(3+1)$-dimensional variety, being $\pmb {\xi }$ the fourth-dimensional vector that represents an event into the spacetime. Disregarding the specific physical meaning of $\psi (\pmb {\xi })$, any wave propagation follows the differential equation in the form

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \nu }\partial _{\nu }\psi \right) = 0, \end{aligned}$$

(1)

where $g^{\mu \nu }$ represents the contravariant metric tensor component, 1/g is its determinant and $\partial _{\alpha }$ indicates the four-dimensional nabla operator, being $\pmb {\partial }=(\partial _{0},\partial _{1},\partial _{2},\partial _{3})$, with the subscript “0” indicating derivation over time, the others indicating derivation over the space variables. Therefore, the information embedded by the metric tensor is the factor that characterizes Eq. (1): any wave propagation is obtainable through the specific $\pmb {g}$ definition. An equivalent form could be obtained following Visser’s work¹⁹, by defining $\pmb {W}=\sqrt{-g}\pmb {g}^{-1}$, with $\pmb {W}$ a second order tensor containing the same metric information of the propagating phenomenon and that derives naturally from the governing equations direct manipulation in their euclidean form. Regarding acoustic propagations, the metric tensor form is diagonal, indicating a Minkowskian spacetime flat metric; whereas, in the presence of convection, the off-diagonal terms appear and embed the background flow information indicating a curved spacetime metric. In the context of the present work, the assumptions of a potential background flow and the small perturbation hypothesis lead to the propagation of an acoustic perturbation convected by an aerodynamic background velocity field $\pmb {\text {v}}$ governed by the convective d’Alembertian for the acoustic potential $\varphi$, that in Euclidean formalism assumes the form

$$\begin{aligned} -\partial _{t}\left[ \frac{\rho _{0}}{c^2_{0}}\left( \partial _{t}\varphi + {\bf {v}}\cdot \nabla \varphi \right) \right] +\nabla \cdot \left[ \rho _{0}\nabla \varphi -\frac{\rho _0}{c^2_{0}}\left( \partial _{t}\varphi + {\bf {v}}\cdot \nabla \varphi \right) {\bf {v}}\right] = 0, \end{aligned}$$

(2)

with $\rho _{0}$ and $c_{0}$ the referenced values of density and speed of sound for the acoustic problem, ${\bf {v}}=\nabla \Phi$, being $\Phi$ the aerodynamic potential enclosing the information of the superposition of a uniform stream (${\bf {v}}_{\infty }$) and the aerodynamic behaviour of an impermeable body ($\pmb {{\textbf {v}}}'$). Here, any source term on the right-hand side recollects all the noise sources excluding any sound induced by vorticity or entropy fluctuations. Exploiting the Lorentzian structure of Eq. (2), it is possible to rewrite it into a ($3D+1$)-dimensional pseudo-Riemannian manifold obtaining the generalized spacetime d’Alembertian operator¹⁹ whose associated metric is represented by the following non-diagonal tensors

$$\begin{aligned} \pmb {g}_{C} = \frac{\rho _{0}}{c_{0}}\begin{pmatrix} -(c_{0}^{2}-\text {v}^{2}) & \vdots & -\pmb {\text {v}}^{T} \\ \cdots & \cdot & \cdots \\ - \pmb {\text {v}} & \vdots & \pmb {I} \end{pmatrix}, \quad \pmb {g}^{-1}_{C} = \frac{1}{\rho _{0}c_{0}}\begin{pmatrix} -1 & \vdots & -\pmb {\text {v}}^{T} \\ \cdots & \cdot & \cdots \\ -\pmb {\text {v}} & \vdots & c_{0}^{2}\pmb {I}-\pmb {\text {v}}\pmb {\text {v}}^{T} \end{pmatrix}, \end{aligned}$$

(3)

as expected. It is worth noting that Eq. (1) is in a conservative form and it is formally invariant under spacetime coordinate transformations: it guarantees the introduction of spacetime mapping while preserving its own mathematical structure. This means the possibility of moving from convective propagations to static ones just by providing a suitable spacetime coordinate change that acts on the metric of the propagating phenomenon as shown in Fig. 1. Naming $\pmb {\Lambda }$ the generic Jacobian matrix that performs such association, the event in the transformed space is $\xi ^{\alpha }=\Lambda ^{\alpha }_{\beta }\xi ^{\beta }$ and the corresponding metric becomes

$$\begin{aligned} \pmb {g}_{S}=\pmb {\Lambda }\pmb {g}_{C}\pmb {\Lambda }^{T}, \end{aligned}$$

(4)

where $\pmb {g}_{S}$ is the metric tensor representative of the static propagation. Recalling that the objective is to find a way to extend acoustic metamaterials to convective applications, the inverse transformation of Eq. (4) is used to extract the convected metric starting from the static one²². However, a change of coordinates capable of exactly including all the convective effects is not known for general flow conditions, therefore, the approach limitation relies on the $\pmb {\Lambda }$ capability in capturing the convective terms with the inevitable introduction of analytical errors as a consequence. In Iemma and Palma²² specific reference is made to Prandltl-Glauert’s²³ and Taylor’s²⁴ coordinate transformations since their inverse applications could be used for the purpose. Each coordinate change is representative of a specific acoustic wave convective phenomenon: Prandtl-Glauert transformation considers a uniform subsonic flow, here assumed aligned with the $x_{1}$-axis, and can be represented in a spacetime form as

$$\begin{aligned} \xi ^{'}_0=\beta \xi _0+M_{\infty }\frac{\xi _1}{\beta }, \quad \xi ^{'}_1=\frac{\xi _1}{\beta }, \quad \xi ^{'}_2=\xi _2,\quad \xi ^{'}_3=\xi _3, \end{aligned}$$

(5)

with $\beta =\sqrt{1-M_{\infty }^2}$, whereas Taylor coordinates change takes into account the non-uniformity of the flow induced by the presence of an obstacle, in the low Mach number limit, and for a potential aerodynamic perturbation ${\bf {v}}'=\nabla \Phi$. Its spacetime form is

$$\begin{aligned} \xi ^{'}_0=\xi _0+M_{\infty }\hat{\Phi }(\pmb {\xi })=\xi _0+M_{\infty }(\xi _1+\hat{\phi }), \quad \xi ^{'}_i=\xi _i, \end{aligned}$$

(6)

where $\hat{\Phi }$ is the adimensionalized velocity potential ($\hat{\Phi }=\Phi /||{\bf {v}}_{\infty }||$) and the transformation holds in the limitation of the O(M)-terms. Recasting Eqs. (5) and (6) in a matrix form, the Jacobian matrix $\pmb {\Lambda }$ associated with each coordinate mapping appears, and the assumed forms are

$$\begin{aligned} \pmb {\Lambda }_{PG}=\left( \begin{array} {cccc} \beta & M_{\infty }/\beta & 0 & 0 \\ 0 & 1/\beta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \quad ;\quad \pmb {\Lambda }_{T}=\left( \begin{array} {ccc} 1 & \vdots & M_{\infty }\nabla \hat{\Phi }(\pmb {\text {x}}) \\ \cdots & \cdot & \cdots \\ 0 & \vdots & \pmb {I} \end{array} \right) , \end{aligned}$$

(7)

where the subscripts “PG” and “T” indicate Prandtl-Glauert’s and Taylor’s coordinate transformation respectively. As said, their application allows describing only partially the aeroacoustic phenomenon, and to better understand how these approximations could affect the performances of a spacetime-adapted meta-device, an assessment of the neglected terms is required.

Fig. 1

Spacetime mapping - $\pmb {\Lambda }$ associates convective propagation into static ones; the vice versa is done by its inverse $\pmb {\Lambda }^{-1}$.

Analysis of analytic transformation defect

The key aspect to consider when analytical corrections are used is precisely the analytical error involved: the spacetime transformation approach relies on the characteristics of the aeroacoustic phenomenon that $\pmb {\Lambda }$ can capture. To isolate the sole analytical error contribution is convenient to refer to the convected d’Alembertian as the reference wave operator with the benchmark represented by the correct representation of a convected phenomenon described by the differential operator in Eq. (2). The fictitious introduction of flow through $\pmb {\Lambda }^{-1}$ corresponds to a partial wave operator implementation concerning the one in Eq. (2). Hence, to quantify such analytical error effects, the acoustic analogy theory is applied to isolate the resulting wave operator on the left-hand side (LHS) of the equations and to bring to the right-hand side (RHS) all the other terms that, from now on, will have the meaning of equivalent acoustic sources²⁹. Such a result could be achieved both by splitting step by step the governing equation in its classic Euclidean formulation, stating from Eq. (2), or by using the associated metric tensor $\pmb {g}$.

Spurious terms: Prandtl-Glauert’s transformation

When Prandtl-Glauert’s coordinate change acts on a static wave equation, the assumptions of uniform and steady stream are made, and the following governing equation results

$$\begin{aligned} -\frac{\rho _{\infty }}{c^2_{\infty }}\partial _{t}\left( \partial _{t}\varphi +{\bf {v}}_{\infty }\cdot \nabla \varphi \right) +\nabla \cdot \left[ \rho _{\infty }\nabla \varphi -\frac{\rho _{\infty }}{c^2_{\infty }}\left( \partial _{t}\varphi +{\bf {v}}_{\infty }\cdot \nabla \varphi \right) {\bf {v}}_{\infty }\right] =0, \end{aligned}$$

(8)

where in this case all the background flow quantities are reduced to the ones associated with the free stream (${\bf {v}}={\bf {v}}_{\infty }, \rho _{0}=\rho _{\infty }$, and $c_{0}=c_{\infty }$). To restore the phenomenon description as Eq. (2), it is necessary to define the source term as:

$$\begin{aligned} \sigma _{PG}=\frac{\rho _{\infty }}{c^2_{\infty }}\sigma _{PG1}+\frac{\rho _{\infty }c^2_{0}}{\rho _{0}c^2_{\infty }}\sigma _{PG2}, \end{aligned}$$

(9)

with

$$\begin{aligned} & \sigma _{PG1}=2{\bf {v}}'\cdot \partial _{t}\nabla \varphi +{\bf {v}}_{\infty }\cdot \nabla \left( {\bf {v}}'\cdot \nabla \varphi \right) +{\bf {v}}'\cdot \nabla \left({\bf {v}}\cdot \nabla \varphi \right) +\nabla ^2\varphi \left( c^2_{\infty }-c^2_{0}\right) +\text {D}_{t}\varphi \left( \nabla \cdot {\bf {v}}'\right) , \end{aligned}$$

(10)

$$\begin{aligned} & \sigma _{PG2}={\bf {v}}\cdot \nabla \left( \frac{\rho _{0}}{c^2_{0}}\right) \text {D}_{t}\varphi -\nabla \varphi \cdot \nabla \rho _{0}, \end{aligned}$$

(11)

with the total derivative $D_{t}=\partial _{t}+{\bf {v}}\cdot \nabla$. In this case, the term $\sigma _{PG}$ considers all aerodynamic perturbations’ effects (as compressibility a non-uniformity of the background velocity field) derived from the presence of a sound-hard obstacle not considered from the uniform convective d’Alembertian in the LHS in Eq. (8).

Spurious terms: Taylor’s transformation

When Taylor’s coordinate transformation is applied to a static wave equation, the presence of a steady but non-uniform aerodynamic stream is accepted. However, a low subsonic Mach regime constraint is introduced and the resulting $O(M_{\infty })$ governing equation assumes the following form

$$\begin{aligned} -\frac{\rho _{\infty }}{c^2_{\infty }}\left( \partial _{tt}\varphi +2{\bf {v}}\cdot \partial _{t}\nabla \varphi \right) +\nabla ^2\varphi =0. \end{aligned}$$

(12)

In this case, the full description of a convected propagation as in Eq. (2) requires the redefinition of the RHS of Eq. (12) as

$$\begin{aligned} \sigma _T=\frac{\rho _{\infty }}{c^2_{\infty }}\sigma _{T1}+\frac{\rho _{\infty }c^2_{0}}{\rho _{0}c^2_{\infty }}\sigma _{T2}, \end{aligned}$$

(13)

with

$$\begin{aligned} & \sigma _{T1}=\left( c^2_{\infty }-c^2_{0}\right) \nabla ^2\varphi +{\bf {v}}\cdot \nabla \left({\bf {v}}\cdot \nabla \varphi \right) , \end{aligned}$$

(14)

$$\begin{aligned} & \sigma _{T2}=\text {D}_{t}\varphi \left[ \nabla \cdot \left( \frac{\rho _{0}}{c^2_{0}}{\bf {v}}\right) \right] -\nabla \varphi \cdot \nabla \rho _{0}, \end{aligned}$$

(15)

where the equivalent source $\sigma _{T}$ takes into account all the compressibility effects and the $O(M^2_{\infty })$-terms not captured by the $O(M_{\infty })$ Taylor’s wave operator. The terms $\sigma _{PG}$ and $\sigma _{T}$ are the analytical representations in a Euclidean space of the approximations committed with the implementation of $\pmb {\Lambda }_{PG}^{-1}$ and $\pmb {\Lambda }_{T}^{-1}$, respectively.

Spurious terms: metrics’ difference in the spacetime domain

The results obtained in a Euclidean formulation are attainable in a spacetime formalism using the metric tensor linked to the resulting governing equation related to the fictitious flow introduction. Compared to previous works^22,27, the equivalent sources are still obtained by exploiting the problem linearity but, in this case, the way in which they are gained is the result of a mathematical manipulation having a corresponding physical meaning: wave propagations that maintain the same structure as the generalized d’Alembertian are added and subtracted with the following equation as a result

$$\begin{aligned} \frac{1}{\sqrt{-g}}\pmb {\partial }\cdot \left( \sqrt{-g}\pmb {g}^{-1}\pmb {\partial }\varphi \right) =\frac{1}{\sqrt{-g}}\pmb {\partial }\cdot \left[ \left( \sqrt{-g}\pmb {g}^{-1}-\sqrt{-g_{\Lambda }}\pmb {g}^{-1}_{\Lambda }\right) \pmb {\partial }\varphi \right] + \boxed {\frac{1}{\sqrt{-g}}\pmb {\partial }\cdot \left( \sqrt{-g_{\Lambda }}\pmb {g}^{-1}_{\Lambda }\pmb {\partial }\varphi \right) }, \end{aligned}$$

(16)

with $\pmb {g}_{\Lambda }$ referring to the generic metric tensor associated with the specific $\pmb {\Lambda }^{-1}$. It is necessary to specify that the four-dimensional nabla operator $\pmb {\partial }=(\partial _{0},\partial _{1},\partial _{2},\partial _{3})$ can be related to the Euclidean derivatives as $\pmb {\partial }=(1/c_{ref}\partial _{t},\partial _{x},\partial _{y},\partial _{z})$, being $c_{ref}$ the referenced propagation velocity that, in the aeroacoustic case, will coincide with the speed of sound equilibrium value for the acoustic propagation phenomenon $c_{0}$. Therefore, the boxed term in Eq.  (16) needs further mathematical manipulations to extract the approximated wave operator whose referenced speed of sound velocity is $c_{\infty }$ both for Prandtl-Glauert’s and Taylor’s differential operators. The resulting equation will have to form

$$\begin{aligned} \pmb {\partial }^{\infty }\cdot \left( \sqrt{-g_{\Lambda }}\pmb {g}^{-1}_{\Lambda }\pmb {\partial }^{\infty }\varphi \right) =S_{\Lambda } \end{aligned}$$

(17)

with $\pmb {\partial }^{\infty }=(1/c_{\infty }\partial _{t},\partial _{x},\partial _{y},\partial _{z})$ and being $S_{\Lambda }$ representative of the analytical approximation in analogy to Eq. (8) forced by $\sigma _{PG}$ and Eq. (12) forced by $\sigma _{T}$.

Convective metacontinuum model

Following Norris’ theory in⁷, the behaviour of atypical acoustic materials, i.e., materials exhibiting behaviours not achievable in nature, is modelled by the characterization of anisotropic inertia and anisotropic stiffness. The governing equation that describes the propagation of the acoustic information within such a medium is written in terms of pseudo-pressure and has the form

$$\begin{aligned} -\partial _{tt}p + K\pmb {S} : \nabla \left( \pmb {\rho }^{-1}\pmb {S}\nabla p\right) =0. \end{aligned}$$

(18)

being $K=\hat{K}K_{ref}$, with $\hat{K}$ the non-dimensional bulk modulus function and $K_{ref}=c_{ref}^{2}\rho _{ref}$ the reference value for the impedance matching that guarantees the acoustic mirage achievement. The inertia and stiffness anisotropy are embedded in the second-order tensors $\pmb {\rho }=\hat{\pmb {\rho }}\rho _{ref}$ and $\pmb {S}$ respectively, with $\pmb {S}$ being non-dimensional, divergence-free and used to define the tensorial basis of the associated elasticity tensor as $\pmb {C}=K\pmb {S}\otimes \pmb {S}$. The metacontinuum model gives freedom in choosing the device’s anisotropic property distribution (that can be attributed to the inertia, the stiffness or both) by focusing on a coordinate change definition that describes how the incoming wave must be modified by the meta-device. Therefore, for the specific application, there are multiple solutions. However, the present work’s aim is not to the metamaterial designs testing but rather to validate the method for acoustic metacontinuum model adaptation to convective applications. Equation  (18) describes only non-convected acoustic propagation within metacontinua, therefore the fictitious flow introduction in the model is provided in the spacetime reformulation of the problem by the $\pmb {\Lambda }^{-1}$, obtaining a spacetime-adapted metacontinuum model for aeroacoustic applications. Since the interest of the present paper is in the approximation effects assessment, the metacontinuum is used as the mathematical tool for the spacetime coordinate transformation approach testing: it is thought to mimic the acoustic behaviour of a domain filled with air (as done in^25,26,27,28). Hence, the quantities $K, \pmb {S}$ and $\pmb {\rho }$ are here defined through an identity transformation and Eq. (18) is simplified setting $K=K_{0}$, $\pmb {S}=\pmb {I}$ and $\pmb {\rho }=\rho _{0}\pmb {I}$. By doing this, the problem complexity is minimized reducing the numerical error sources in the simulations and highlighting the solely analytical errors’ contribution. Moreover, due to the dependence of $\pmb {\Lambda }_{PG}$ and $\pmb {\Lambda }_{T}$ only to the background flow characteristics, all considerations derived by numerical results are easily extendable to actual acoustic meta-designs by just modifying the definition of $K,\pmb {S}$ and $\pmb {\rho }$ (e.g.,^6,7).

Numerical simulations

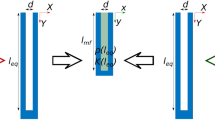
The present work aims at the analytical approximations effect assessment. To this purpose, the test case chosen sees a circular domain, depicted in green in Fig. 2, of radius $R_{in}$, and filled with an acoustic metacontinuum within which acoustic perturbations propagate according to Eq. (18). Since the purpose of this work is to test the possibility of inducing convective–like propagation patterns in a region where a static wave equation was originally defined, Eq. (18) is simplified by setting $K=K_{0}, \pmb {S}=\pmb {I}$ and $\pmb {\rho }=\rho _{0}\pmb {I}$, and the acoustic metacontinuum model is used as a mathematical tool to mimic the acoustic behaviour of a homogeneous, isotropic medium (air, in our case). Hence, the fictitious background flow is introduced into the spacetime reformulation using the inverse of Eq. (6). The specific spacetime mapping implemented is denoted as $\pmb {\Lambda }_{PG}$ or $\pmb {\Lambda }_{T}$, where the subscript “PG” or “T” refer to the Prandtl-Glauert transformation of Eq. (5) or Taylor transformation in Eq. (6), respectively. The spacetime-corrected acoustic metacontinuum communicates with the external conventional medium (hosting fluid), having a domain outer radius $R_{out}=30R_{in}$, in which the green domain is embedded (Fig. 2a). The hosting fluid is air, modelled as a potential fluid, and with the propagation of the acoustic perturbation governed by Eq. (2). Within this outer region, lives a background flow with characteristic free stream Mach that varies its intensity from 0.1 up to 0.3 and a monopole source emitting a monochromatic wave of unit intensity and located at ${\bf {x}}=(0;7.5R_{in})$, which corresponds to fixing $\theta =\pi$, being $\theta$ the angle taken from the negative horizontal axis as shown in Fig. 2b. A radiation condition to the outer boundary ensures no spurious reflections, and a cautious, non-trivial selection of the boundary conditions at the interface between the two media ensures the correct information exchange between the conventional and the unconventional models, with normal vectors at the interface defined as in Fig. 2c. The expression of the boundary conditions used at the interface between the hosting fluid and the acoustic metacontinuum is given in the following (Eqs. (20) to (23)) after the discussion of the critical aspects deriving from the peculiarity of the present application. Indeed, the requirement of ensuring a smooth propagation of the acoustic perturbation across the matching boundary imposes a careful definition of the normal acceleration, taking into account the different natures of the media involved, and the fact that the propagation pattern inside the metacontinuum at rest must match the convected incoming one. It will be shown that the effects of this difference are strictly correlated to the different levels of accuracy of the differential operators involved in the analyses. As said, the analytical error assessment aims to quantify the representation lack of an aeroacoustic propagation given by an approximated convective propagation within the metacontinuum. Therefore, to see the effects of the equivalent sources explained in the previous sections that appear in Eqs. (9) and (13), the introduction of a sound-hard obstacle (SHO) is needed due to their strong dependence of the aerodynamic background flow velocity field. A cylindrical object of radius $R_{SHO}=R_{in}/2$ is introduced in the simulations to give rise to the flow’s non-uniformities and with the total aerodynamic field, generated by the impingement of the free stream on the SHO, that is used as the convected velocity field $\pmb {\text {v}}$ of the aeroacoustic propagation. All simulations are performed in the frequency domain through the commercial FEM solver COMSOL Multiphysics with a working frequency that corresponds to a Helmholtz number of $kR_{in}=4$.

Fig. 2

Geometry sketch: parameters set-up and domains definition in (a); Source location angle $\theta$ definition in (b); definition of the normals to the interface between hosting fluid ($\Omega _{h}$) and metacontinuum ($\Omega _{m}$) in (c).

To give proof of the equivalent sources contribution, both the Euclidean formalism and its spacetime counterpart are implemented: the resulting scattered fields comparison intends to highlight the role of $\sigma _{PG}$ and $\sigma _{T}$ (or equivalently $S_{\Lambda }$) as the missing information not captured by the associated coordinate mapping. For both approaches, forcing the approximated operators with their associated equivalent sources will correspond in restoring the acoustic propagation governed by the convective d’Alembertian. Therefore, Eq. (2) represents the benchmark of the numerical results in the current section where the pressure field comparison is provided in terms of polar plots in Figs. 3 and 4, and sensitivity analysis in Fig. 5: if $\sigma _{\Lambda }$ (or equivalently $S_{\Lambda }$) is considered, there should be a null difference to the referenced case quantified in terms of near-field insertion loss (IL) as

$$\begin{aligned} IL = 20log_{10}\left( \frac{|p_{i}|}{|p_{t}|}\right) , \end{aligned}$$

(19)

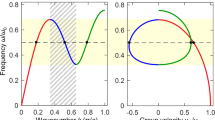
obtained disposing virtual microphones along a circumferential line, concentric to the obstacle and the fluid domains, with an outer radius of $R_{mic}=1.5R_{in}$. In the present case, $p_{i}$ represents the scattered field obtained solving Eq. (2) everywhere: if the missing information is considered as an equivalent source, it should lead to a case where $p_{t}$ is equal to $p_{i}$ meaning that the IL is null. The polar plot results qualitatively assess the analytical error contribution for Prandlt-Glauert’s (see Fig. 3) and Taylor’s (see Fig. 4) coordinate mapping for $M_{\infty }=[0.1;0.3]$ and, for both cases where the blue curve deviations from the benchmark represent the correction lack, it is proved the analytical error sensitivity to the Mach intensity. This behaviour matches the equivalent sources analytical definition given in the previous section, and, as it is possible to see in Fig. 3, there are deviations from the benchmark even at low Mach when $\pmb {\Lambda }_{PG}^{-1}$ is implemented. These effects are due to the inability of Prantl-Glauert’s transformation to take into account the effects of a non-uniform low. This outcome becomes more evident the higher the background flow intensity is, due, as said, to the sensitivity to the Mach number of the correction defect. The fact that this specific test case might not be suited for $\pmb {\Lambda }_{PG}$ testing is further indicated by the results in Fig. 4 where, on the other hand, Taylor’s mapping gives back coherent results with what is expected, with minor errors for the highest Mach. However, this effect is not so surprising since $M_{\infty }=0.3$ test case represents its validity range which is locally overcome by the additional aerodynamic perturbations produced by the SHO. However, it could be considered an acceptable result since $M_{\infty }=0.35$ is the representative Mach of commercial aircraft’s take-off phase. Moreover, it has to be considered that even if from an analytical point of view the Eq. (8), Eq. (12) forced by $\sigma _{\Lambda }$ and Eq. (16) are restoring the full convective d’Alembertian, still the propagation of the acoustic perturbation is governed by the operator on the LHS of each equation, forced by source terms that depend on the same field that the FEM solver is trying to find. These aspects could explain both the strong limitations of the $\pmb {\Lambda }_{PG}^{-1}$ implementation on reaching the reference case and the different results obtained with the two formalisms. Finally, they could also explain the little deviations observed in the $\pmb {\Lambda }_{T}^{-1}$ case that are slightly different from the classical Euclidean description to the spacetime one. These deviations indicate that whenever a spacetime framework of this kind involves the introduction of an approximated wave operator concerning the one in the hosting fluid, there is also the sensitivity to the source location to consider (as pointed out in^26,28).

Fig. 3

Polar dB diagram of the scattered field at $r=1.5R_{in}$ for $M_\infty = 0.1, 0.3$ , with $\Delta r=1dB$. Effect of $\sigma _{PG}$: comparison between Prandl-Glauert’s operator isolation method in Eqs. (8) and (9), and the metric tensors formulation in Eq. (16).

Fig. 4

Polar dB diagram of the scattered field at $r=1.5R_{in}$ for $M_\infty = 0.1$ with $\Delta r=0.5dB$, and $M_\infty = 0.3$ with $\Delta r=1dB$. Effect of $\sigma _{T}$: comparison between Taylor’s operator isolation method in Eqs. (12) and (13), and the metric tensors formulation in Eq. (16).

Naming $\eta$ the overall value of the normalized IL over the circumference of the near-field, it is possible to obtain its sensitivity to the variation of the source position indicated by the angle $\theta$, with $\theta \in [0,\pi ]$. Given the considerations made about the total inability of $\pmb {\Lambda }_{PG}^{-1}$ to capture the convective phenomena in this specific test case even when the convected d’Alembertian is restored, it is reasonable to test the sensitivity effects to the variation of $\theta$ and $M_{\infty }$ solely for Taylor’s wave operator forced by $\sigma _{T}$ or $S_{\Lambda _{T}}$. The results related to this kind of analysis in Fig. 5 show all the aforementioned effects: the $\eta$ trends behave differently from one formulation to another, and this difference is higher the higher the Mach, which corresponds to more relevance of the equivalent sources on the LHS of the governing equation. As in^26,28, a $\theta$ value minimising the residual scattering appears and it corresponds to the acoustic metacontinuum performance recovery maximization. Therefore, the relative position between the source, the treated zone and the free stream is a relevant parameter to consider in this kind of application. In Fig. 5, the minimum is reached for different source locations depending on the formulation used only for $M_{\infty }=0.3$: in the classic formalism, the $\eta _{min}$ is reached at $\theta =\pi /2$ whereas, for the spacetime one, the source is at $\theta =\pi /3$. However, this could only be an effect due to the coarse sampling of the $\theta$ range that has a sampling step of $\Delta \theta =\pi /3$.

Fig. 5

Sensitivity analysis of the reconstructed convected wave operator starting from the O(M)-equation - $\eta$ value for $M_{\infty }\in [0.1;0.3]$ and $\theta \in [0,\pi ]$.

Another way to prove the limited capability of an approximated wave operator in capturing perfectly all the convective aspects is to perform a direct comparison between differential operators’ levels. To do that, the SHO is removed and all the domain for $r<R_{in}$ is filled by air modelled through the spacetime-corrected metacontinuum: for Taylor’s coordinate change, this choice leads to the analytical error minimization resulting in a $\sigma _{T}$ reduced to the $O(M^2)$-terms. Therefore, any deviation from the benchmark will be representative of the correction’s lack and, in the following analyses, the description of the phenomenon in the metacontinuum is given by Eq. (12). In this case, while in the metacontinuum lives Eq. (12), the hosting fluid model is changing being addressed to Eq. (2) or to Eq. (12). Here, the correct communication between the hosting fluid and the metacontinuum is tested and compared: Fig. 6 shows the polar plot results and proves that whenever the convected differential operators are not of the same accuracy, some deviations from the benchmark appear (a discrepancy that becomes more evident the higher the intensity of the background flow). Moreover, since the metacontinuum model is provided only in terms of pseudo-pressure, it is interesting to see what happens when the static wave equation set in motion is written in terms of acoustic pressure. When no SHO is present and $\sigma _{T}$ is only due to the $O(M^2)$-terms, it is possible to show the additional error that appears even when the differential operators have the same accuracy everywhere: there is a further analytical approximation due to the linearization of the Bernoulli equation that links the velocity potential to the acoustic pressure. Both these effects can be recollected in the boundary conditions definition at the interface that plays a fundamental role in these analyses and that, in this case, following the convention indicated in Fig. 2c, assume the following form for the potential-potential problem.

$$\begin{aligned} & \varphi _{m} = \varphi _{h} \end{aligned}$$

(20)

$$\begin{aligned} & \hat{\pmb {n}}_{m}\cdot \left( \nabla \varphi _{m}-\frac{1}{c_{\infty }^{2}}{\bf {v}}\partial _{t}\varphi _{m}\right) = \hat{\pmb {n}}_{h}\cdot \left( \nabla \varphi _{h}-\frac{1}{c_{0}^{2}}D_{t}\varphi _{h}{\bf {v}}\right) , \end{aligned}$$

(21)

whereas, for the potential-pressure case they assume the form of

$$\begin{aligned} & p_{m} = - D_{t}\varphi _{h}/\rho _{0}, \end{aligned}$$

(22)

$$\begin{aligned} & \hat{\pmb {n}}_{m}\cdot \left( \frac{1}{\rho _{\infty }}\nabla p_{m}-\frac{1}{c_{\infty }^{2}\rho _{\infty }}{\bf {v}}\partial _{t}p_{m}\right) = \hat{\pmb {n}}_{h}\cdot \left( \partial _{t}\left( \nabla \varphi _{h}-\frac{1}{c_{0}^{2}}D_{t}\varphi _{h}{\bf {v}}\right) \right) . \end{aligned}$$

(23)

with $\hat{\pmb {n}}_{m}=-\hat{\pmb {n}}_{h}$ and where the subscript “m” refers to the quantities related to the metacontinuum while “h” refers to those related to the hosting fluid. As it is possible to see, the first set of boundary conditions Eq. (20) and Eq. (21), encompass the effect of considering approximated characteristics of the background flow in the Neumann condition. On the other hand, the second set Eqs. (22) and (23), also shows the further approximation degree introduced in the Dirichlet boundary condition. It appears again that in the SHO absence only the $O(M^2)$-terms are representative of Taylor’s coordinate change approximation since $c_{0}=c_{\infty }$ and $\rho _{0}=\rho _{\infty }$.Therefore, when the hosting fluid is addressed to Taylor’s wave operator, the RHS of Eqs. (21) and (23) is simplified leading to the same convective propagation description both inside and outside the metacontinuum. These effects are minimal for low Mach but not negligible for a higher intensity as shown in Fig. 6 where the polar plots are obtained for $\theta =\pi /2$ and $M_{\infty }=[0.1;0.3]$. However, it also shows that the linearized Bernoulli equation brings further analytical error that, together with the different differential operators’ levels involved, have to be considered in the spacetime framework application on actual metamaterial designs. This also means that if a spacetime mapping able to include all the convective effects for general flow conditions is provided, then the adapted metacontinuum performances will reach the desired benchmark.

Fig. 6

Differential operators level testing in the hosting fluid for $M_{\infty }=0.1,0.3$ at $r=1.5R_{in}$, with $\Delta r=0.5dB$; pressure and potential formulations in the metacontinuum.

Again, a sensitivity analysis is performed for the mentioned test cases resulting in Figs. 7 and 8: the former is associated with $M_{\infty }\in [0.1,0.3]$ whereas the latter refers to the static case ($M_{\infty }=0.0$). Figure 7a shows how in a problem that involves differential operators of the same level and where the boundary conditions do not introduce additional approximation ($\varphi _{h-Tay}-\varphi _{m}$ case), the residual $\eta$ is null for all $M_{\infty }$ and $\theta$ values. This proves that if the chosen mapping captures the hosting fluid’s flow conditions, the adapted metacontinuum performance recovery can be total. However, deviations will be inevitable if the communication between the two media is not a direct one ($\varphi _{h-Tay}-p_{m}$ case). On the other hand, in Fig. 7b the $\eta$ values are non-null for both combinations ($\varphi _{h-Eq.(2)}-\varphi _{m}$ and $\varphi _{h-Eq.(2)}-p_{m}$) case since the hosting fluid has Eq. (2) as governing equation. Nevertheless, it is possible to see that the residual is higher in the $\varphi _{h-Eq.(2)}-p_{m}$ due to the additional analytical approximation introduced through the boundary conditions. The results in Fig. 8 testify that the deviations seen in all the previous analyses are indeed linked to the background flow presence and vanish when $M_{\infty }=0.0$ since, for static propagations, the differential operator has the same level in both media and the Bernoulli equation does not require additional linearization anymore.

Fig. 7

$\eta$ sensitivity: $\theta \in [0,\pi ]$ and $M_{\infty }\in [0.1,0.3]$; $\varphi _{h}-\varphi _{m}$ and $\varphi _{h}-p_{m}$ combination evaluation for an adapted metacontinuum communicating with a hosting fluid modelled through Eq. (12) in (a) or Eq. (2) in (b).

Fig. 8

$\eta$ sensitivity: $\theta \in [0,\pi ]$ and $M_{\infty }=0.0$; $\varphi _{h}-\varphi _{m}$ and $\varphi _{h}-p_{m}$ combination evaluation for an adapted metacontinuum communicating with a hosting fluid modelled through Eq. (12) in Fig. 7a or Eq. (2) in Fig. 7b.

Concluding remarks

This work focuses on the assessment of the analytical error that arises when spacetime coordinate transformations represent the building block of the methodology for acoustic metacontinua adaptation to aeronautical application. The fictitious flow introduction inside Norris’ metacontinuum inevitably brings analytical approximations that depend on the flow condition that the specific coordinate change can capture. The identification and evaluation of the analytical error effect on the acoustic metacontinua performance require the simplification of the problem: Norris’ model is seen as the mathematical tool to mimic the acoustic behaviour of air. This approach does not alter the spacetime framework’s validity on applications that involve actual acoustic mirages since the spacetime mappings considered depend solely on the background flow characteristics. However, the first part of the numerical results aim at verifying the equivalence between a Euclidean formulation and its spacetime counterpart: although the results related to Taylor’s transformation (see Fig. 4) are more than satisfactory concerning the benchmark represented by Eq. (2), for Prandtl-Glauert’s one (see Fig. 3) some anomalies were found which, however, are common for both formulations and thus guarantee the equivalence between the two approaches in every case. Having said this, the rest of the results focus on Taylor’s coordinate change exclusively: the sensitivity analysis that followed in Fig. 5 shows that the spacetime-corrected acoustic metacontinua performances are affected both by the relative position between the source, the scatterer and the free stream and by the Mach intensity. These effects are independent of the specific formulation used and indicate a mismatch between the convected behaviour of the metacontinua and the hosting fluid: it gets more evident the higher the background flow intensity since the more relevant the convective terms and the higher the difference between the differential operators addressed to the two media. Focusing on this concept, further analyses are performed in the second part of the numerical results demonstrate that these effects are directly linked to the approximation degree introduced in the problem not only in terms of the differential operators’ different accuracy, but also in the boundary conditions chosen (see Figs. 6, 7 and 8). In fact, whenever it is possible to establish a communication between conventional and unconventional media that involves differential operators of the same level and direct boundary conditions, then the residual factor $\eta$ is null meaning that the total recovery of acoustic metacontinua performance decay can be feasible if a coordinate change comprehensive of general flow conditions is provided. The results obtained in the present work are relevant to understanding the design performance and limitations of an analytically corrected metamaterial and to correctly assess the performance recovery that was lacking in previous studies. However, more steps forward are needed concerning the testing of this approach with a more complex modelling of the external aeroacoustics that includes viscosity and the boundary layer presence that could alter the meta-device performances.