Introduction

Radon (222Rn) is a radioactive gas produced from the disintegration of uranium (238U) and radium (226Ra). Due to its favourable migration properties in gas and liquid phases, it accumulates in the ground atmosphere, particularly in enclosed or inadequately ventilated spaces1. Uranium tailings contain large amounts of radium and uranium; alpha particles from radon decay can cause radiation damage to the respiratory system. The risk of lung cancer is substantially increased by prolonged exposure to elevated radon levels2,3. Cover methods are commonly employed for radon reduction in decommissioning uranium mill tailings pond (UMTs)4. The physical and mechanical properties and the moisture content of the cover layer are essential elements affecting its efficacy in mitigating radon levels and ensuring long-term stability.

Radon exhalation from the covering layer is primarily influenced by soil properties, layer thickness, porosity, and moisture content5,6,7,8,9. Research has indicated a positive correlation between radon exhalation rate and soil porosity10,11,12,13. Additionally, moisture content influences both radon emission and the pore structure of the soil, thereby affecting radon exhalation from the covering layer14,15. Menetrez et al.16 found that the exhalation coefficient and radon concentration increased with rising moisture content in the gas bag experiment. Chen et al.17 found that the radon exhalation rate in the topsoil of UMTs increased rapidly before slowing down as moisture content decreased. At the same dry density, the radon exhalation rate initially increased slightly and then decreased with rising moisture content18. Beyond moisture content and porosity, the thickness of the cover soil significantly influences radon exhalation19. Well-designed cover measures can significantly reduce radon exhalation. As cover thickness increases, the migration path for radon gas extends, effectively lowering the exhalation rate20. Ye et al.21 developed a mathematical model based on seepage-diffusion theory, demonstrating that greater cover thickness correlates with reduced radon exhalation rates, approaching zero. Additionally, Dai et al.22 found that radon reduction efficiency improved with increased cover soil thickness, particularly showing significant enhancements in radon reduction efficiency when thickness reached 10 cm, after which the growth rate of efficiency slowed. Thus, rational design and optimization of covering layer thickness are crucial for controlling radon exhalation in radioactive pollution management projects, such as those involving UMTs.

Clay is an effective cover material for UMTs due to its low permeability. This property prevents the migration of radioactive substances and mitigates the impact of radon on the surrounding environment and populations23. Clay involves various components, including illite, montmorillonite, kaolinite, and chlorite24,25. Ota et al.26 discovered that bentonite mixed soil functions as an effective cover material, effectively preventing the release of radon gas from contaminated soil. Xie et al.27 reported that the radon exhalation rate of red clay-bentonite covers is only 0.32 times that of red clay alone, indicating a significant reduction in radon exhalation. Tan et al.4 evaluated waste rock and laterite mixtures at 0.4 m, 0.8 m, 1.2 m, 1.6 m, and 2.0 m, indicating that these materials in the cover layer substantially diminish radon exhalation rates. Furthermore, Li et al.28 discovered that increasing the density of laterite can reduce its radon diffusion coefficient, implying that choosing the proper density is critical for covering uranium tailings or developing radon-suppression building materials. Due to their superior barrier characteristics, clay materials demonstrate significant potential in radon mitigation applications. By adjusting the moisture content and thickness of the soil, these materials can effectively reduce the diffusion and release of radon gas.

Clay, as a cover material, demonstrates significant potential for radon control applications. Its low permeability coefficient and unique mineral composition are crucial for blocking the diffusion of radioactive materials. By adjusting clay’s moisture content and thickness, these materials can effectively reduce radon gas diffusion and release. Utilizing a self-developed multi-field coupled seepage test system and radon exhalation test device, this study provides valuable experimental data and a theoretical foundation for the cover disposal strategy of decommissioned UMTs. It explores the radon control mechanisms of covering layer and their influencing factors under varying pressure gradients, thickness gradients, and moisture content gradients.

Materials and methods

Experimental materials

Red clay

In this experiment, commonly found red soil from southern China was selected as the base material for the cover layer. The primary performance parameters were tested in accordance with the Standard for Geotechnical Test Methods (GBT 50123 − 2019), and the results are summarized in Table 1.

In this study, a Mastersizer 2000 laser particle size analyzer was used to examine the particle size distribution of the residual soil (RC). The results are illustrated in Fig. 1. Based on the Soil Classification Standard (GB/T 50145 − 2007), the soil sample is predominantly comprised of fine sand particles (75 μm < d ≤ 250 μm), silt particles (5 μm < d ≤ 75 μm), and clay particles (d ≤ 5 μm). Additionally, we conducted a mineralogical analysis of the RC using X-ray diffraction (XRD), with the findings illustrated in Fig. 2. The secondary soil minerals identified include montmorillonite, illite, kaolinite, and chlorite, with kaolinite and montmorillonite being the predominant clay minerals in the lateritic soil.

Fig. 1
figure 1

Particle size distribution of red clay.

Full size image
Fig. 2
figure 2

X-ray diffraction pattern of red clay.

Full size image

Red clay had the characteristics of high plasticity, low permeability, medium compressibility and high strength29,30. The physical and chemical properties of red clay make it had good adsorption and low permeability, and had good barrier property to radon migration. Red clay was easy to obtain and was an ideal material for covering uranium tailings.

Table 1 Main performance parameters of red clay.
Full size table

Uranium mill tailings

The uranium tailings utilized in this experiment were collected from a depth of 1.5 m in a tailings pond. Following a 5 mm sieve to remove debris and impurities, the samples were air-dried under ambient conditions and then stored for later analysis. The mineral composition of the tailings, as determined by X-ray fluorescence (XRF) analysis, is detailed in Table 2.

Table 2 Mineral composition of tailings.
Full size table

Permeability test experiment

Experimental apparatus

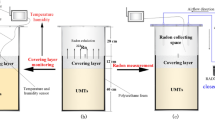
To evaluate the gas permeability of the soil covering layer under varying pressures, moisture levels, and soil depths, we employed a custom-designed multi-field coupling seepage testing apparatus developed explicitly to assess uranium mine tailings. This integrated system comprises several key components: a high-precision injection mechanism, a vacuum evacuation setup, a temperature-regulated heating module, an effluent measurement subsystem, a terminal flow monitoring unit, and an integrated data acquisition and analysis suite. Figure 3 shows a schematic representation of the experimental apparatus.

Fig. 3
figure 3

Multi-field coupled seepage testing apparatus.

Full size image

Sample preparation

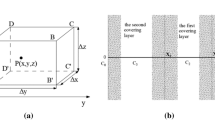
The specific test method was as follows: Different tailing sand and red soil masses were weighed, and water was added to achieve varying moisture content for both materials. The mixture was thoroughly combined and loaded into a sealed plastic box, where it was allowed to cure for over 12 h. The outlet end of the sample tube (Fig. 4) was secured, and the tube was positioned diagonally. Tailing sand was then added in layers from the inlet end, with each layer compacted using a mallet every 2–3 centimeters until the desired thickness was reached. Any excess tailing sand on the inner wall of the tube was wiped clean. The prepared soil specimen was filled as described, and the inlet of the sand-filling tube was tightened. Finally, the sand-filled tube was placed on the experimental bench with the inlet on the left and the outlet on the right, and the pressure was adjusted to calculate the gas permeability (kg) according to Eq. (1) and the measured data.

$$K_{g} = \frac{{2Q_{0} p_{0} \mu _{g} L}}{{A\left( {p_{1} ^{2} - p_{2} ^{2} } \right)}}$$
(1)
Fig. 4
figure 4

Sample tube for seepage testing.

Full size image

where Kg is the gas permeability (×10− 3µm2); Q0 is the gas volume flow rate (mL·s− 1); p0 is the atmospheric pressure (MPa); µg is the gas viscosity (MPa·s); L is the effective length of the specimen (cm); A is the cross-sectional area of the specimen (A); p1 and p2 are the inlet and outlet pressures (MPa).

Experimental methods

To investigate the effects of moisture content and cover soil thickness on gas permeability, the experimental protocol was designed with test pressure gradients set as follows: 0.15 MPa, 0.25 MPa, 0.35 MPa, 0.45 MPa, and 0.55 MPa. These parameters remained unchanged during the testing process. Steady-state gas volumetric flow rates under these varying pressure gradients were achieved using a three-stage pressure regulation system in the multi-field coupled seepage meter, allowing for adjustments in test pressure to measure gas flow rates across different gradients.

To investigate the influence of moisture content on gas permeability, experiments were conducted using uranium tailings sand and laterite samples, with four distinct moisture content gradients set at 5%, 10%, 15%, and 20%. These tests aimed to investigate the effects of varying pressures on the samples’ gas permeability.

Red soil was selected for this investigation to ascertain the influence of cover soil depth on gas permeability. The soil was applied in four varying thicknesses: 0 cm, 5 cm, 10 cm, and 15 cm. During the sample loading process, the red soil cover layer was strategically positioned at the gas inlet end to evaluate its impact on gas permeability under these conditions. Since the aim was to explore the effects under different conditions, no control group was included in the experiment. Additionally, all experimental groups were tested with three replicate trials to ensure the reliability of the results.

Experiment on radon reduction by soil covering

The experimental protocol was carefully designed to explore the influence of covering layer thickness (h) and moisture content (w) on radon exhalation. Soil samples were prepared according to the guidelines for varying moisture content outlined in Sect. 1.2. These samples were stratified and loaded following the procedures detailed in the same section, resulting in four distinct groups. A visual representation of the specimen model after loading is provided in Fig. 5. To make sure the experiment was both comparable and valid, all the samples were given the same resting period before starting. This helped the radon distribution within the tailings-soil cover system reach a nearly balanced state. After 7 days of undisturbed settling for the soil specimens, radon accumulation measurements were conducted using a RAD7 detector. For significant radon exhalation, the measurement duration was 10 min per cycle, with a total of 24 cycles. If the radon exhalation rate is small, the measurement is extended to 72 cycles to ensure the accuracy of the radon exhalation rate measurement.

Fig. 5
figure 5

Experimental modeling of different covering layer thicknesses.

Full size image

To assess the impact of soil depth on the radon exhalation rate, experiments were designed with a fixed radon source depth set at 15 cm for the tailings layer. The overlying soil thickness was systematically varied at 0 cm, 5 cm, 10 cm, and 15 cm. The red soil was prepared in advance, sealed, and allowed to stand for at least 12 h to ensure uniformity. Additionally, to determine the effect of moisture content on radon exhalation from the covering layer, the moisture gradients of the tailings sand and red soil samples were meticulously adjusted to 5%, 10%, 15%, and 20%. This controlled approach facilitated a precise evaluation of how moisture content affects radon exhalation rates.

Results and discussion

Sample permeability characteristic

Based on the principles outlined in Eq. (1), the permeability coefficient for each specimen was determined. The results, illustrating how permeability varies under different covering layer thicknesses at moisture content levels of 5%, 10%, 15%, and 20%, were graphically represented in Fig. 6a–d. Upon examination of Fig. 6, it was evident that the permeability coefficient for each specimen declines with increasing pressure. This decline was initially steep, then levels off gradually. At pressures exceeding 0.35 MPa, the influence of pressure on permeability was markedly reduced, with the permeability curves tending to flatten and most values falling below 1 × 10− 11 m². Additionally, the variability in permeability among different covering layer specimens was minimal under these conditions. Conversely, when the pressure was below 0.35 MPa, the impact of pressure on permeability was more pronounced, as the curves exhibit a steeper gradient, showing a notable difference in permeability between specimens with varying covering layer thicknesses.

Fig. 6
figure 6

Gas permeability of covering layer specimens with different moisture contents. (a) 5% moisture content, (a) 5% moisture content, (c) 15% moisture content, (d) 20% moisture content.

Full size image

The distribution range of gas permeability for each specimen was from 4.29 × 10− 12 m²~3.87 × 10− 11 m².The correlation between the permeability coefficient K(m2)and P(MPa) conformed to the mathematical model presented in Eq. (2), with most fitted R2 values exceeding 0.990.

$$K = \frac{1}{{a + bP}}$$
(2)

Where a represents the initial value of permeability; b reflects the degree to which pressure influences gas permeability.

The fitted model aligns well with the established model used for calculating the permeability coefficient. Variability was observed in the permeability characteristics of both the covering layer and tailings across the tests. This variability could be attributed to differences in the thickness of the covering layer and tailings in the test specimens, as well as inconsistencies in moisture content. These factors collectively contributed to the differences in coefficients a and b in the fitted models for each specimen.

Effect of covering layer thickness and moisture content on permeability

Figure 7 illustrated the average permeability of specimens with covering layer thicknesses of 0 cm, 5 cm, 10 cm, and 15 cm, while Fig. 8 depictd the average permeability of specimens with moisture content of 5%, 10%, 15%, and 20%. The difference in gas permeability between 0 cm and 15 cm covering layer thickness at 0.15 MPa(\(\Delta {K_{0.15}}\)) was 1.88 × 10− 11 m². In contrast, the difference at 0.55 MPa(\(\Delta {K_{0.55}}\)) was 2.40 × 10− 12 m², resulting in a total difference of 16.4 × 10− 12 m² between \(\Delta {K_{0.15}}\) and \(\Delta {K_{0.55}}\). Additionally, the difference in gas permeability between 5% and 20% water content at 0.15 MPa (\(\Delta {K_{0.15}}\)) was 5.59 × 10− 12 m². At 0.55 MPa (\(\Delta {K_{0.55}}\)), the difference was 1.51 × 10− 12 m², leading to a total difference of 4.08 × 10− 12 m². These results indicated that the effect of covering layer thickness on soil infiltration rates was significantly greater than that of soil water content, particularly under low-pressure conditions. Therefore, in the practical application of radon control using soil covers, increasing the thickness of the soil cover could more effectively reduce soil permeability and enhance its radon prevention performance. While increasing soil water content could also reduce permeability, its impact on radon prevention performance was comparatively limited.

Fig. 7
figure 7

Average permeability of specimens with different covering layer thicknesses.

Full size image
Fig. 8
figure 8

Average permeability of specimens with different moisture content.

Full size image

Samples of radon exhalation characteristic

Radon exhalation rate

The relationship between radon exhalation and cover thickness was often approximated using an empirical formula with the covering layer measurement method31. This relationship suggested that covering layer thickness was linearly correlated with the natural logarithm of the ratio of radon exhalation rates measured before and after the application of the cover. The equation representing this relationship was as follows:

$$X_{c} = B\ln \frac{{J_{0} }}{{J_{x} }} + A$$
(3)

where\(X_{c}\)is the thickness of the covering layer (cm); \(J_{0}\)is the radon exhalation rate when it is not covered (Bq·m− 2·s− 10);\(J_{x}\)is the radon exhalation rate of the covering layer layer after being covered (Bq·m− 2·s− 1); A reflects the degree to which the cover layer thickness affects the radon exhalation rate; B represents the initial value of the radon exhalation rate when there is no cover layer.

Substituting the covering layer thickness and the calculated radon exhalation rate into the above expression, the values of slope B and intercept A could be obtained after linear fitting, and the fitting results were shown in Fig. 9.

Fig. 9
figure 9

Fit of covering layer thickness to ln(J0/Jx).

Full size image

The R² values of the linear fit depicted in Fig. 10 are 0.975, 0.903, 0.937, and 0.940, respectively, demonstrating a pronounced linear correlation. The results shown that the physical simulation test of radon control with soil covering layer conformed to the basic law of radon reduction. The coefficients A and B in the fitting model were.

Fig. 10
figure 10

Effect of covering layer thickness on radon exhalation rate.

Full size image

different under different cover soil moisture content, and the fitting lines were obviously separated. It also shown that the moisture content had a significant effect on the radon exhalation rate.

Effect of covering layer thickness and moisture content on radon exhalation

The radon exhalation rates were calculated and categorized using cumulative radon concentrations based on varying cover thicknesses and moisture contents. This process facilitated the generation of graphs illustrating how the radon exhalation rate fluctuates with changes in cover thickness and moisture content, as shown in Fig. 11.

Fig. 11
figure 11

Covering layer properties for different covering layer thicknesses, a is the variation curve of radon exhalation rate and permeability coefficient under the covering layer thickness, and b is the variation curve of radon exhalation rate versus gas permeability.

Full size image

Figure 10 demonstrated the significant influence of both moisture content and soil thickness on the radon exhalation rate. The data indicated a diminishing radon exhalation rate as soil thickness and moisture content increase, following a non-linear relationship. Specifically, with a moisture content of 15% and a soil thickness of 5 cm, the radon exhalation rate approaches zero. Additionally, at a soil thickness of 15 cm, the radon exhalation rate remains nearly minimal, indicating that the effect of moisture content on radon exhalation was minimal under these conditions.

As the cover layer thickens, the path for radon gas to travel becomes longer, increasing the distance over which it diffuses and reducing the permeability, which significantly lowers the radon exhalation rate. Meanwhile, higher water content improves the cover layer’s seal by filling the pores, further reducing radon gas release. However, when the cover layer is thicker, the effect of increasing water content on radon exhalation diminishes, illustrating the combined impact of thickness and moisture content working together.

Radon control law of covering layer

Upon examining Figs. 11 and 12, it becomed evident that radon exhalation in the surface of the covering layer shown a negative correlation with moisture content and covering layer thickness. Conversely, the radon exhalation rate shown a positive correlation with the permeability coefficient. The radon exhalation rates and infiltration coefficients, determined under varying moisture contents and thicknesses in this experiment and presented in Fig. 12b, conform to a natural exponential function model. These relationships were expressed by Eqs. (4) and (5), respectively.

$$y=17.84 - 9.36{e^{ - 19.07}}^{x}$$
(4)
$$y=13.98 - 7{e^{ - 63.42}}^{x}$$
(5)
Fig. 12
figure 12

Properties of covering layer with different moisture content, a is the curve of radon exhalation rate and permeability coefficient change with different moisture content, and b is the curve of radon exhalation rate versus gas permeability.

Full size image

Figure 11a illustrated that both the gas permeability coefficient and the radon exhalation rate of the covering layer clay decrease as water content increases within the range of 5–20%. Notably, the radon exhalation rate decreased rapidly between 5% and 10% water content, while the reduction slows down in the range of 10–20%. The covering layer clay swells upon absorbing water, constricting the soil’s pore spaces. As water content increases, the free water further occupies these pore spaces32,33,34, leading to a decrease in the gas permeability of the soil. Consequently, the blocking effect of the covering layer on radon transport was enhanced, resulting in a reduced quantity of free radon in the tailings that can migrate through the covering layer’s pore space to the surface. This ultimately decreased the radon exhalation from the surface layer of the covering layer.

Figure 12a illustrated that both the permeability coefficient and the radon exhalation rate of the covering layer decrease as thickness increases from 0 cm to 15 cm. A linear relationship existed between gas permeability and covering layer thickness. The radon exhalation rate decreased rapidly in the interval from 0 cm to 5 cm, while the decline becomes more gradual from 5 cm to 15 cm. When free radon in tailings exhalants from the surface of the overlying layer, the migration path of radon in the overlying soil becomed longer with the increase of the thickness of the soil coverlying. At the same time, the gas permeability of soil overlying decreases, and the radon control performance of soil covering layer was enhanced20,35,36. This improvement in radon control properties was significantly influenced by the soil’s water absorption characteristics, covering layer thickness, and pore structure. Therefore, these parameters should be comprehensively considered when designing cover disposal strategies for UMTs to achieve a more economical and effective treatment solution.

In addition to gas permeability, diffusion coefficients played a critical role in understanding the migration of gases like radon through soil. The diffusion coefficient D describeed the rate at which a gas diffuses through a medium due to concentration gradients. According to Fick’s first law of diffusion, the diffusion flux J was directly proportional to the negative of the concentration gradient, as expressed by the Eq. (6):

$$J= - D\frac{{dC}}{{dx}}$$
(6)

Where J is the diffusion flux, Bq/(m2·s) ; D is the diffusion coefficient, (m2/s); is the concentration gradient, Bq/(m4).

For steady-state conditions, assuming a linear concentration gradient of radon C within the covering layer, the relationship between the radon exhalation rate J and the diffusion coefficient D could be described as Eq. (7):

$$D=\frac{{J \cdot h}}{{{C_0}}}$$
(7)

Where C0 is the radon concentration at the bottom of the covering layer, Bq/m³;h is the thickness of the covering layer, m;

The value of C0, the radon concentration at the bottom of the covering layer, was kept consistent across all experiments. This uniformity ensured that the observed variations in the diffusion coefficient and radon exhalation rate were primarily influenced by changes in the cover layer thickness and moisture conten, rather than by differences in initial radon concentration. By standardizing C0, the results could more accurately reflect the impact of the cover layer properties on radon diffusion and exhalation.

According to the results in Fig. 13, the diffusion coefficient decreased as the thickness of the cover layer increased, with a notable drop when the thickness reached 15 cm. This suggested that a thicker cover layer forced radon gas to travel a longer path, which increased flow resistance and reduced the diffusion rate. A positive correlation between gas permeability and the radon diffusion coefficient was observed, implying that higher permeability generally led to a higher diffusion coefficient. This could be attributed to diffusion being primarily driven by concentration gradients, with greater permeability facilitating gas flow and thereby enhancing radon diffusion. Furthermore, the diffusion coefficient decreased as soil moisture content, pressure, and thickness increased. This was due to higher moisture, pressure, and thickness increasing the resistance to gas migration, which ultimately reduced the diffusion coefficient.

Fig. 13
figure 13

Variation of radon diffusion coefficient with covering Layer thickness and moisture content.

Full size image

Conclusion

Gas permeability in soils is profoundly affected by pressure, covering layer thickness, and moisture content. The gas permeability coefficient diminishes as pressure increases, especially below 0.35 MPa, where the effect is more significant. At reduced pressures, the impact of covering layer thickness on soil permeability surpasses that of moisture content. Furthermore, moisture content and covering layer thickness significantly influence the radon exhalation rate, which exhibits a nonlinear decline as these factors increase. The correlation between the radon exhalation rate and permeability follows an exponential function model. Additionally, a positive correlation between gas permeability and the radon diffusion coefficient was also observed, indicating that higher permeability generally leads to a higher diffusion coefficient. This can be attributed to the fact that diffusion is primarily driven by concentration gradients, and greater permeability facilitates gas flow, thereby enhancing radon diffusion. Consequently, in managing cover disposal for UMTs, it is crucial to thoroughly evaluate the soil’s water absorption properties, covering layer thickness, permeability, diffusion coefficient and other pertinent factors to develop an effective and economical cover management strategy.

Future research should explore the use of low-permeability materials, such as bentonite and sandy soils, in radon control, particularly under different environmental conditions. Additionally, optimizing cover layer design, including thickness and moisture content, will be key to improving radon control efficiency in practical applications.