Introduction

Trajectory data loss, frequently caused by environmental factors such as adverse weather, tunnel obstructions, or sensor failures, introduces temporal gaps that critically compromise data integrity. Such incompleteness undermines downstream spatiotemporal analytics, leading to biased conclusions or rendering advanced modeling impractical. Missingness mechanisms are categorized into three types: Missing Completely at Random (MCAR), where missingness is independent of observed and unobserved variables; Missing at Random (MAR), where it correlates with observed variables; and Missing Not at Random (MNAR), where dependencies on unobserved factors exist. Temporal autocorrelation in missingness patterns may further manifest as isolated or cascading gaps.

Conventional approaches to address missing data include deletion (discarding incomplete entries) and imputation (estimating missing values). While deletion risks information loss and temporal discontinuity—particularly detrimental to time-series analysis—imputation preserves dataset utility by reconstructing coherent sequences. Effective management of missing data is therefore essential for robust spatiotemporal analytics.

Imputation methods span statistical techniques (e.g., mean/median substitution, Lagrange interpolation1) to model-driven approaches. While basic methods offer computational efficiency, they lack contextual awareness and precision in complex scenarios2. Algorithmic strategies include regression-based imputation (prone to covariate bias3), expectation–maximization (EM4, scalable but memory-intensive), and k-nearest neighbors (KNN5, reliant on similarity metrics with optimization challenges). Missing Value Completion (MVC6) achieves high accuracy at the expense of throughput, while multiple imputation (MI) trades computational overhead for robustness. Model-based predictions risk overfitting with limited training data.

Ride-hailing trajectories exhibit strong spatiotemporal dependencies that simplistic imputation fails to capture, while their low feature dimensionality restricts comprehensive pattern characterization. To address these limitations, we propose a hybrid feature-driven imputation framework combining LightGBM (gradient-boosted feature engineering), SARIMA (temporal decomposition), and GRU (nonlinear sequence modeling)—the LG-SG model—to enable high-fidelity data recovery for downstream analytical tasks.

Theoretical basis

The proposed LG-SG framework integrates two synergistic modules: (1) a LightGBM-GRU architecture for feature generation and (2) a SARIMA-GRU hybrid model for spatiotemporal prediction.

In the feature generation stage, LightGBM addresses sparse feature representation by learning hierarchical interactions from limited input data (e.g., temporal intervals, velocity), enhancing discriminative capacity through gradient-boosted tree ensembles. Its memory-efficient design accelerates large-scale training while generating enriched feature vectors. These outputs are further refined via GRU’s gated recurrent layers, which capture nonlinear temporal dependencies to mitigate oversimplification in traditional tree-based methods.

For spatiotemporal prediction, SARIMA decomposes trajectory data into cyclical and trend components, while GRU models residual nonlinear patterns through its simplified gating mechanisms. This hybrid architecture synergizes SARIMA’s interpretable temporal decomposition with GRU’s ability to handle vanishing/exploding gradients, enabling robust imputation of missing values in complex time-series applications.

Light gradient boosting machine

Ensemble learning improves model robustness by integrating diverse machine learning algorithms, mitigating the inherent limitations of individual models in classification and anomaly detection tasks. Its operational framework involves training multiple weak learners and aggregating their outputs through context-specific fusion strategies: averaging is optimal for learners with comparable performance metrics, voting achieves superior accuracy in classification scenarios, and stacking employs meta-learning to refine predictions through secondary training.

Prominent methodologies—Bagging, Boosting, and Stacking—target distinct performance dimensions. Boosting algorithms demonstrate exceptional efficacy by iteratively constructing strong learners through error correction, systematically balancing the bias-variance trade-off. The methodological evolution of ensemble techniques has propelled transformative advancements in machine learning applications. The following Table 1 is the Boosting Algorithm Development History.

Table 1 Boosting algorithm development history.
Full size table

Xinran He et al. pioneered GBDT application in CTR prediction, automating feature extraction and interaction discovery to enhance linear classifier performance10.

The Lightweight Gradient Boosting Machine (LightGBM), developed through continuous refinement, achieves comparable accuracy to XGBoost while reducing computation time by approximately tenfold and memory usage by around threefold. These distinct performance advantages over other methods are primarily enabled by the following strategies.

  1. 1.

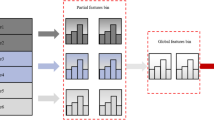
    LightGBM utilizes a histogram-based algorithm11 that discretizes features through value binning, using bin medians as histogram indices for split point selection (Fig. 1). This approach reduces memory usage and computational costs while providing implicit regularization to enhance model robustness.

Fig. 1
figure 1

Histogram Algorithm Principle of Light Gradient Boosting Machine.

Full size image
  1. 2.

    GOSS prioritizes under-trained instances through gradient-based sampling while preserving data distribution. It intelligently groups features while maintaining exclusivity through greedy optimization.

  2. 3.

    EFB compresses sparse features into dense representations via mutualexclusion analysis, employing graph-based optimization to solve feature bundling12.

LightGBM operates on standard Boosting frameworks, with implementation specifics visualized in Figs. 2 and 3.

Fig. 2
figure 2

Boosting algorithm flow.

Full size image
Fig. 3
figure 3

LightGBM flow chart.

Full size image

In the LightGBM algorithm, the expression of the loss function is critically important as it is closely related to the results of the decision tree. Let the loss function be denoted as R, representing the gradient boosting tree after t iterations. In the t-th iteration, the negative gradient of the loss function with respect to the predicted value from the \(\text{t}-1\)-th iteration is equal to the residual of the model in the \(\text{t}-1\)-th iteration, as shown in Eq. (1):

$$-{\nabla }_{{\text{H}}_{\text{t}-1-(\text{x})}}\text{L}\left(\text{y},{\text{H}}_{\text{t}-1}(\text{x})\right)=-\frac{\partial {\text{L}}_{\text{MSE}}\left(\text{y},{\text{H}}_{\text{t}-1}(\text{x})\right)}{\partial {\text{H}}_{\text{t}-1}(\text{x})}$$
(1)
$$\text{c }{\text{H}}_{\text{t}}(\text{x})={\text{H}}_{\text{t}-1}(\text{x})-\upeta {\nabla }_{{\text{H}}_{\text{t}-1-(\text{x})}}\text{L}\left(\text{y},{\text{H}}_{\text{t}-1}(\text{x})\right)$$
(2)

In this context, \(h\left(\text{x},{\uptheta }_{\text{t}}\right)\) represents the prediction result obtained after training a regression tree, i.e., the output of the decision tree model with input \(\text{x}\). \({\uptheta }_{\text{t}}\) denotes the parameters of decision tree \(\text{t}\). In each iteration, the parameters of the decision tree, \({\uptheta }_{\text{t}}\), are optimized using Eq. (3).

$${\text{H}}_{\text{t}}(\text{x})=\underset{{\text{H}}_{\text{t}}^{{^{\prime}}}}{\text{argmin}}\text{L}\left(\text{y},{\text{H}}_{\text{t}}^{{^{\prime}}}(\text{x})\right)\iff \underset{{\uptheta }_{\text{t}}^{{^{\prime}}}}{\text{argmin}}\text{L}\left(\text{y},{\text{H}}_{\text{t}-1}(\text{x})+h\left(\text{x};{\uptheta }_{\text{t}}^{{^{\prime}}}\right)\right)$$
(3)

The final prediction result, \({\text{H}}_{\text{T}}(\text{x})\), is the linear sum of the prediction results from each iteration, \(h\left(\text{x},{\uptheta }_{\text{t}}\right)\), as shown in Eq. (4).

$${\text{H}}_{\text{T}}(\text{x})=\sum_{\text{t}=1}^{\text{T}} h\left(\text{x},{\uptheta }_{\text{t}}\right)$$
(4)

Seasonal auto-regressive integrated moving average model

SARIMA (Seasonal Autoregressive Integrated Moving Average), an extension of ARIMA incorporating seasonal differencing, is designed for time-series data with pronounced periodic patterns (e.g., traffic flow). Following the Box-Jenkins framework, it integrates historical data, decomposes seasonal trends via STL filtering, and transforms non-stationary sequences into stationary components for robust forecasting13.

The workflow involves stabilizing non-stationary data through differencing to remove seasonal/local trends, followed by predictive equation construction. Implementation includes preprocessing, stationarity testing, differencing, Bayesian Information Criterion(BIC)-based model order selection, parameter estimation, and residual diagnostics14. Formally expressed as SARIMA(p,d,q)(P,D,Q,S), the model employs multiplicative seasonality: non-seasonal parameters (p,d,q) govern short-term dynamics, while (P,D,Q,S) capture periodic trends, with S defining seasonal cycle length. This dual architecture concurrently models transient and cyclical patterns, as mathematically defined below15:

$$\varphi (B)\phi \left({B}^{(S)}\right){\nabla }^{(d)}{\nabla }^{(D)}{ }_{S}{Y}_{t}=\theta (B)\Theta \left({B}^{(S)}\right){\varepsilon }_{t}$$
(5)
$$\varphi (B)=1-{\varphi }_{1}B-{\varphi }_{2}{B}^{(2)}-\dots -{\varphi }_{p}{B}^{(p)}$$
(6)
$$\theta \left(B\right)=1-{\theta }_{1}B-{\theta }_{2}{B}^{\left(2\right)}-\dots -{\theta }_{q}{B}^{\left(q\right)}$$
(7)
$$\phi \left({B}^{(S)}\right)=1-{\phi }_{1}{B}^{(S)}-{\phi }_{2}{B}^{(2S)}-\dots -{\phi }_{P}{B}^{(PS)}$$
(8)
$$\Theta \left({B}^{(S)}\right)=1-{\Theta }_{1}{B}^{(S)}-{\Theta }_{2}{B}^{(2S)}-\dots -{\Theta }_{Q}{B}^{(QS)}$$
(9)

In the equation:\({\varphi }(\text{B})\) represents the non-seasonal autoregressive polynomial, \(\uptheta (\text{B})\) denotes the non-seasonal moving average polynomial, and \(\upphi (\text{B}\) is the lag operator.

Gated recurrent neural network

The rise of deep learning has revolutionized predictive analytics, with gated architectures like LSTM and GRU becoming mainstream for time series forecasting. LSTM excels in modeling nonlinear, non-stationary sequences, while GRU (Cho et al.16) simplifies the architecture using two gating mechanisms, achieving comparable performance with reduced computational complexity.

These architectures are particularly effective for traffic prediction tasks due to their ability to model spatiotemporal dependencies through recurrent neural connections. GRU’s update and reset gates address recurrent neural network (RNN) limitations by regulating gradient flow, thereby enhancing stability and enabling efficient real-time forecasting. Figure 4 schematically illustrates GRU’s operational framework, highlighting its streamlined architecture optimized for sequential data analysis.

Fig. 4
figure 4

Illustrates the logical structure of the GRU algorithm.

Full size image

The operation process of GRU is described by Eqs. (10) to (13) 16:

$${r}_{t}=\sigma \left({W}_{r}*\left[{h}_{t-1},{x}_{t}\right]+{b}_{r}\right)$$
(10)
$${z}_{t}=\sigma \left({W}_{t}*\left[{h}_{t-1},{x}_{t}\right]+{b}_{z}\right)$$
(11)
$$\tilde{{h}_{t}}=\text{tanh}\left({W}_{\tilde{{h}_{t}}}*\left[{r}_{t}\cdot {h}_{t-1},{x}_{t}\right]+{b}_{{\tilde{h}}_{t}}\right)$$
(12)
$${h}_{t}=\left(1-{z}_{t}\right)\cdot {h}_{t-1}+{z}_{t}\cdot \tilde{h}$$
(13)

In the equation: '*' represents matrix multiplication, and ':' represents element-wise multiplication. \({\text{z}}_{\text{t}}\) denotes the update gate, \({\text{r}}_{\text{t}}\) is the reset gate, \({\text{x}}_{\text{t}}\) represents the input information at time step \(\text{t}\), \({h}_{\text{t}-1}\) is the input information at time step \(\text{t}-1\), \({\tilde{h}}_{\text{t}}\) refers to the retained input information at the current time step, \(\upsigma\) is the Sigmoid activation function, \(\text{tanh}\) is the hyperbolic tangent activation function, \({\text{W}}_{\text{XZ}},{\text{W}}_{\text{HZ}},{\text{W}}_{\text{XR}},{\text{W}}_{\text{HR}}\) represents the weight matrix, and \({\text{r}}_{\text{t}}, {\text{z}}_{\text{t}}\) is the bias vector. The iterative process of GRU is as follows17: After the current input information \({\text{x}}_{\text{t}}\) enters the gated unit, the input data at time step \({\text{x}}_{\text{t}}\) is fused with the output data at time step \(\text{t}-1\), producing the reset gate output signal \({\text{r}}_{\text{t}}\). The update gate generates the output signal \({\text{z}}_{\text{t}}\), and the input signal is reset according to Eq. (12), yielding the modified data \({\tilde{h}}_{\text{t}}\) . Finally, the output result is \({h}_{\text{t}}\). Through continuous iterations of the GRU neural network, historical information is processed efficiently, allowing it to capture and output important time-series information, thereby reflecting correlations within the data.

Based on LG-SG data filling method

Model construction

This study introduces a feature generation-based hybrid prediction framework (hereafter abbreviated as LG-SG) for robust data imputation18. The framework comprises two synergistic components: (1) a LightGBM-GRU integration for feature generation and (2) a SARIMA-GRU hybrid architecture for spatiotemporal prediction. Traditional decision tree algorithms exhibit inherent limitations in learning rare feature combinations from sparse training data, while deep learning methods—despite their capacity to derive high-level interactions through hidden vector operations—remain constrained in capturing low-order feature relationships19. To address these gaps, we develop a hybrid feature generation framework that synergizes tree-based and deep learning paradigms. This dual-strategy approach not only augments the representational capacity of input features but also generates discriminative feature expressions, thereby improving imputation accuracy.

The feature selection protocol incorporates the spatiotemporal attributes of ride-hailing datasets, prioritizing three critical dimensions: temporal intervals, velocity profiles, and travel distances. These features collectively characterize traffic dynamics across temporal, spatial, and behavioral domains, providing a robust foundation for identifying discriminative patterns to address missing data. The LightGBM-GRU feature generation workflow is implemented through the following sequential steps:

  1. 1.

    Data preprocessing: Address anomalies and missing values in raw datasets through noise filtering and outlier removal.

  2. 2.

    Temporal feature engineering: Transform temporal data into timestamp formats to enable time-window partitioning and differencing operations.

  3. 3.

    Numerical feature normalization: Standardize numerical features (e.g., time-series velocities) via z-score normalization, ensuring dimensional homogeneity across the input feature matrix.

$${\text{X}}_{\text{fe}}=\left[\begin{array}{ccc}{\text{T}}_{1}& {\text{V}}_{1}& {\text{S}}_{\text{d},1}\\ {\text{T}}_{2}& {\text{V}}_{2}& {\text{S}}_{\text{d},2}\\ \vdots & \vdots & \vdots \\ {\text{T}}_{\text{n}}& {\text{V}}_{\text{n}}& {\text{S}}_{\text{d},\text{n}}\end{array}\right]$$
(14)
  1. 4.

    Categorical feature embedding: Apply one-hot encoding to convert categorical variables into high-dimensional sparse vectors, followed by dimensionality reduction using feature embedding techniques.

  2. 5.

    LightGBM configuration: Initialize LightGBM with core hyperparameters (boosting type, learning rate, and tree complexity metrics). Partition datasets into training/validation subsets (70:30 ratio), then train the model to derive interaction-enhanced feature representations.

$${\text{X}}_{{\text{fe}}_{-}\text{LGB}}=\left[\begin{array}{ccc}{\text{T}}_{1}^{{^{\prime}}}& {\text{V}}_{1}^{{^{\prime}}}& {\text{S}}_{\text{d},1}^{{^{\prime}}}\\ {\text{T}}_{2}^{{^{\prime}}}& {\text{V}}_{2}^{{^{\prime}}}& {\text{S}}_{\text{d},2}^{{^{\prime}}}\\ \vdots & \vdots & \vdots \\ {\text{T}}_{\text{n}}^{{^{\prime}}}& {\text{V}}_{\text{n}}^{{^{\prime}}}& {\text{S}}_{\text{d},\text{n}}^{{^{\prime}}}\end{array}\right]$$
(15)
  1. 6.

    GRU input preparation: Integrate LightGBM-generated features with initial features as composite inputs for the GRU network.

$${\text{X}}_{\text{fe}}^{{^{\prime}}}=\left[\begin{array}{cc}& {\text{T}}_{1}{\text{V}}_{1}{\text{S}}_{\text{d},1}{\text{T}}_{1}^{{^{\prime}}}{\text{V}}_{1}^{{^{\prime}}}{\text{S}}_{\text{d},1}^{{^{\prime}}}\\ & {\text{T}}_{2}{\text{V}}_{2}{\text{S}}_{\text{d},2}{\text{T}}_{2}^{{^{\prime}}}{\text{V}}_{2}^{{^{\prime}}}{\text{S}}_{\text{d},2}^{{^{\prime}}} \\ & \vdots \vdots \vdots \vdots \vdots \vdots \\ & {\text{T}}_{\text{n}}{\text{V}}_{\text{n}}{\text{S}}_{\text{d},\text{n}}{\text{T}}_{\text{n}}^{{^{\prime}}}{\text{V}}_{\text{n}}^{{^{\prime}}}{\text{S}}_{\text{d},\text{n}}^{{^{\prime}}}\\ & \end{array}\right]$$
(16)
  1. 7.

    GRU architecture optimization: Optimize GRU hyperparameters (hidden units, time steps, and activation functions) through grid search, minimizing mean squared error (MSE) via backpropagation through time (BPTT).

$${\text{X}}_{{\text{fe}}_{-}\text{GRU}}^{{^{\prime}}}=\left[\begin{array}{ccc}{\text{T}}_{1}^{{^{\prime}}{^{\prime}}}& {\text{V}}_{1}^{{^{\prime}}{^{\prime}}}& {\text{S}}_{\text{d},1}^{{^{\prime}}{^{\prime}}}\\ {\text{T}}_{2}^{{^{\prime}}{^{\prime}}}& {\text{V}}_{2}^{{^{\prime}}{^{\prime}}}& {\text{S}}_{\text{d},2}^{{^{\prime}}{^{\prime}}}\\ \vdots & \vdots & \vdots \\ {\text{T}}_{\text{n}}^{{^{\prime}}{^{\prime}}}& {\text{V}}_{\text{n}}^{{^{\prime}}{^{\prime}}}& {\text{S}}_{\text{d},\text{n}}^{{^{\prime}}{^{\prime}}}\end{array}\right]$$
(17)
  1. 8.

    Feature fusion via stacking: Perform hierarchical fusion of original and generated features using stacking ensembles, yielding an enhanced feature matrix. The workflow is schematically summarized in Fig. 5.

Fig. 5
figure 5

Flowchart of the feature generation model based on LightGBM-GRU.

Full size image

To address missing data imputation, we develop a hybrid SARIMA-GRU prediction model by integrating combined spatiotemporal feature vectors. The workflow initiates with an Augmented Dickey-Fuller (ADF) test to assess the stationarity of raw traffic data. Subsequently, core SARIMA parameters (p,d,q)(P,D,Q,S) are identified through autocorrelation function (ACF)/partial autocorrelation function (PACF) analysis and iterative grid search. The SARIMA component applies Seasonal-Trend decomposition using LOESS (STL) to isolate cyclical trends and generate preliminary forecasts, with model validity rigorously validated through residual diagnostics. Prediction residuals are then channeled into a GRU network to produce error-correction terms, which are iteratively refined via backpropagation. Final predictions are derived by synergizing SARIMA outputs with GRU-corrected residuals. The workflow is systematically illustrated in Fig. 6.

Fig. 6
figure 6

SARIMA-GRU model construction flow chart.

Full size image

Model evaluation

To comprehensively assess the performance of the proposed model, four complementary evaluation metrics were selected: Mean Squared Error (MSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Accuracy (ACC). These criteria quantify prediction errors and classification reliability from distinct perspectives, with their mathematical formulations detailed in20.

$$\text{MSE}\left(\text{y},{{\hat{\text{y}}}}\right)=\frac{1}{\text{n}}\sum_{\text{i}=0}^{\text{n}-1} {\left({\text{y}}_{\text{i}}-{{{\hat{\text{y}}}}}_{\text{i}}\right)}^{2}$$
(18)
$$\text{MAE}(\text{y},{{\hat{\text{y}}}})=\frac{1}{\text{n}}\sum_{\text{i}=0}^{\text{n}-1} \left|{\text{y}}_{\text{i}}-{{{\hat{\text{y}}}}}_{\text{i}}\right|$$
(19)
$$\text{MAPE}(\text{y},{{\hat{\text{y}}}})=\frac{1}{\text{n}}\sum_{\text{i}=1}^{\text{n}-1} \left|\frac{{\text{y}}_{\text{i}}-{{{\hat{\text{y}}}}}_{\text{i}}}{{\text{y}}_{\text{i}}}\right|$$
(20)
$$\text{ACC}=\left(\left.1-\frac{1}{\text{n}}\sum_{\text{i}=1}^{\text{n}} \frac{\mid {{{\hat{\text{y}}}}}_{\text{i}}-{\text{y}}_{\text{i}}}{{\text{y}}_{\text{i}}}\right| \right)*100\text{\%}$$
(21)

where \(\text{y}\) represents the actual value, \({{\hat{\text{y}}}}\) denotes the predicted value, and \(\text{n}\) refers to the number of data points.

Case verification

Experimental data

This study evaluates the proposed LG-SG framework using ride-hailing GPS trajectory data from Chengdu’s primary urban corridors. Post-preprocessing, we focus on weekday (7 November 2018) and weekend (10 November 2018) datasets, analyzing road-segment velocity fluctuations at 5-min intervals over 24-h periods (00:00–24:00), yielding 288 temporal intervals. To simulate real-world data loss scenarios, artificial gaps are introduced into the complete dataset, and the LG-SG model is applied for imputation. Model efficacy is validated by comparing imputed values against ground-truth missing data.

The experimental protocol targets the north–south corridor of Xinhua Avenue, inducing both single-point and full-segment missing data patterns for the selected dates. Detailed classifications of missing data types and their morphological representations are provided in Tables 2 and 3.

Table 2 Single point missing data on the north to south section of Xinhua Avenue.
Full size table
Table 3 Missing data for the entire section of Xinhua Avenue North to South.
Full size table

Result analysis

The LG-SG framework operates through two sequential modules. The first module implements a LightGBM-GRU hybrid architecture for feature generation.

Step 1: Ingest preprocessed raw data, where the initial feature matrix \({\text{X}}_{\text{fe}}\) comprises temporal intervals, average velocity, and travel distance.

$${\text{X}}_{\text{fe}}=\left[\begin{array}{lll}\text{T}& \text{V}& {\text{S}}_{\text{d}}\end{array}\right]=\left[\begin{array}{ccc}{\text{t}}_{1}& {\text{v}}_{1}& {\text{s}}_{\text{d},1}\\ {\text{t}}_{2}& {\text{v}}_{2}& {\text{s}}_{\text{d},2}\\ \vdots & \vdots & \vdots \\ {\text{t}}_{\text{n}}& {\text{v}}_{\text{n}}& {\text{s}}_{\text{d},\text{n}}\end{array}\right]$$

To ensure the comparability of the features, the three features in matrix \({\text{X}}_{\text{fe}}\) need to undergo normalization. After this step, the model construction and computation can begin. First, the initial parameters for the LightGBM algorithm are set. While some parameters of the decision tree model use default values, certain hyperparameters need to be optimized to find the best combination, thereby reducing model error. Tuning the parameters improves accuracy and prevents overfitting. Grid search and cross-validation (GridSearch CV) are employed for hyperparameter tuning, with the final parameters shown in Table 4.

Table 4 LightGBM algorithm parameter setting.
Full size table

Based on the parameter settings above, input \({\text{X}}_{\text{fe}}\) into the LightGBM model to generate a new feature column, \({\text{X}}_{{\text{fe}}_{-}\text{LGB}}\), using the existing time, speed, and travel distance features.

Step 2: A GRU architecture with dual hidden layers is implemented. The model employs mean squared error (MSE) as the loss function, hyperbolic tangent (tanh) for hidden state activation, and a piecewise linear approximation of the sigmoid function for recurrent gate operations. Training is conducted via the RMSProp optimizer over 1000 epochs to optimize the candidate network topology. Hyperparameter configurations for the GRU are summarized in Table 5.

Table 5 GRU algorithm parameter setting.
Full size table

Using \({\text{X}}_{\text{fe}}^{{^{\prime}}}=\left[\begin{array}{llll}\text{T}& \text{V}& {\text{S}}_{\text{d}}& {\text{X}}_{{\text{fe}}_{-}\text{LGB}}\end{array}\right]\) as the input, it is fed into the model for computation, resulting in the generation of the new feature \({\text{X}}_{{\text{fe}}_{-}\text{GRU}}\).

Step 3: The Stacking method is then applied to merge the features generated by the base classifiers, LightGBM and GRU, to form the fused feature matrix \({\text{X}}_{\text{fe\_saccing}}\),. The final data matrix used for prediction is \({\text{X}}_{\text{fe}}^{{^{\prime}}{^{\prime}}}=\left[\begin{array}{llll}\text{T}& \text{V}& {\text{S}}_{\text{d}}& {\text{X}}_{\text{fe\_stacking}}\end{array}\right]\).

The second part involves constructing a prediction model based on SARIMA-GRU.

Step 1: Construct the SARIMA(p, d, q) (P, D, Q, s) model with the following steps.

  1. 1.

    The stationarity test was performed on the original data, and the results of ADF stationarity test were shown in Table 6:

Table 6 Original data source ADF stability test.
Full size table

The augmented Dickey–Fuller (ADF) test results demonstrate statistical significance at the 1%, 5%, and 10% levels. The calculated test statistic (\({\text{T}}_{\text{ADF}}\)) exceeds critical values at all three significance thresholds (∣\({\text{T}}_{\text{ADF}}\)∣ > CV), rejecting the null hypothesis of non-stationarity. Further corroboration is provided by the near-zero p-value (p ≈ 0), which is substantially smaller than the conventional 0.05 significance level. These findings confirm the stationarity of the processed dataset.

  1. 2.

    Determine parameters p, q, d.

From (1), the data series is stationary with the order of differencing d = 0. Based on the autocorrelation function (ACF) and partial autocorrelation function (PACF) plots (as shown in Fig. 7), determine the values of the non-seasonal autoregressive order p and the non-seasonal moving average order q.

Fig. 7
figure 7

ACF and PACF curves for trajectory data.

Full size image

As shown in the figure above, both the ACF and PACF plots of the stationary trajectory data series exhibit a trailing-off pattern. The ACF coefficients become zero after lag 3, while the PACF coefficients become zero after lag 1. This suggests selecting p = 1 for the non-seasonal autoregressive order and q = 3 for the non-seasonal moving average order. Consequently, the model is identified as SARIMA(1, 0, 3)(P, D, Q).

  1. 3.

    Determine parameters P, Q.

Using the Bayesian Information Criterion (BIC), the seasonal autoregressive order P and seasonal moving average order Q were determined. Combined with a grid search approach, 18 combinations of P,Q ∈ {0,1,2} and seasonal differencing order D ∈ {0,1} were evaluated. The combination with the minimum BIC value was selected as the final parameters. The resulting model is identified as SARIMA(1, 0, 3)(0, 1, 1).

  1. 4.

    Bring the confirmed SARIMA model to the test.

The validity was assessed using the Ljung-Box statistic. The final test results show that all p-values are greater than 0.05, which demonstrates that the SARIMA model has successfully captured the essential information in the trajectory data. This confirms that the residuals contain no significant autocorrelation, and the model can be reliably applied to subsequent applications.

  1. 5.

    Stepwise prediction.

Through the aforementioned four steps, a fully specified SARIMA model is obtained. This model is then used to forecast the input data X, and the residuals (prediction errors) are extracted for further analysis.

Step 2: Build the GRU model.

The error data extracted from SARIMA predictions is used as input to train a GRU model, which outputs predicted error values. The final predicted values are obtained by combining the SARIMA forecasted values with the error compensation values derived from the GRU model. These predicted values are then used to fill in missing data. Figure 8 compares the true values with the imputed values, demonstrating the effectiveness of the hybrid approach.

Fig. 8
figure 8

Comparison of filled value and actual value.

Full size image

As shown in Fig. 8, the LG-SG-based data imputation model struggles to achieve precise predictions for abrupt changes in speed values, but its overall trend aligns well with the true values. Tables 7 and 8 summarize the imputation errors across different time periods. The results indicate that the LG-SG method achieves higher accuracy under stable traffic conditions (e.g., off-peak hours) but lower accuracy during periods of high volatility (e.g., peak hours). Specifically:

  1. 1.

    On November 7 (weekday), frequent traffic fluctuations during morning and evening peak hours led to reduced imputation accuracy compared to off-peak periods.

  2. 2.

    On November 11 (weekend), the morning peak saw significantly lower commuting demand, resulting in higher imputation accuracy during both the morning peak and mid-morning off-peak period. However, accuracy declined during the evening peak due to increased travel demand and road condition volatility.

Table 7 Comparison of the error interval between the filled value and the true value on November 7.
Full size table
Table 8 Comparison of the error interval between the filled value and the true value on November 11.
Full size table

To evaluate the model’s performance, multiple metrics were employed, including Mean Squared Error (MSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). The results are detailed in Table 9.

Table 9 Comparison of algorithm evaluation indicators.
Full size table

The results demonstrate that, compared to several commonly used forecasting methods, the model proposed in this study achieves superior imputation performance. Therefore, when processing ride-hailing trajectory data, adopting the LG-SG model proposed in this paper for data imputation yields significantly more accurate results.

Ablation experiments

This section will validate the contribution of each module in the LG-SG model through systematic ablation experiments, including component removal and combination analysis, to test the prediction accuracy and effectiveness of the LG-SG model. The specific test data is shown in Table 10 and Fig. 9 below.

Table 10 Comparison of algorithm evaluation indicators.
Full size table
Fig. 9
figure 9

Data comparison.

Full size image

Ablation experiments systematically validate the interdependent roles of SARIMA, GRU, and LightGBM modules in the LG-SG framework for time series imputation. The full model achieves optimal performance (MSE: 32.332, MAE: 3.698, MAPE: 0.096, ACC: 90.4%), significantly outperforming both standalone and dual-module configurations. When components are isolated, critical limitations emerge: SARIMA maintains periodicity modeling (MSE = 38.523) but fails to capture nonlinear dynamics (ACC = 88.2%); GRU exhibits pronounced error accumulation in long-sequence gaps (MAPE = 0.125); LightGBM processes static features effectively (MAE = 3.937) but ignores temporal dependencies (MSE = 42.318). These results confirm that individual modules only partially address the multidimensional challenges of spatiotemporal data imputation.

Dual-module combinations reveal compensatory but incomplete synergies. LightGBM-SARIMA integrates static-temporal patterns (MSE = 34.515, ACC = 89.4%) yet incurs localized errors (MAPE = 0.106) due to missing dynamic correction. Conversely, SARIMA-GRU combines linear decomposition with nonlinear residuals (MSE = 36.258, MAPE = 0.104) but sacrifices robustness (ACC = 89.6%) without contextual feature fusion. The LightGBM-GRU configuration (MSE = 36.493, ACC = 88.7%) demonstrates SARIMA’s essential role in suppressing error propagation through explicit trend modeling. Notably, SARIMA-GRU’s superior MAPE (0.104 vs. LightGBM-SARIMA’s 0.106) coupled with lower ACC (89.6% vs. 89.4%) highlights a critical trade-off between local error reduction and global consistency.

The LG-SG architecture overcomes these limitations through staged integration: SARIMA first decomposes trends/seasonality via differencing and moving averages; GRU then corrects residual nonlinearities through gated memory units; finally, LightGBM enhances generalization by fusing exogenous static features. This hierarchical workflow reduces MSE by 6.3%, increases ACC by 1.0%, and lowers MAPE by 9.4% compared to LightGBM-SARIMA. Component ablation quantifies their contributions: SARIMA prevents 13.2% MSE degradation in long-term sequences, GRU reduces localized MAPE errors by 10.4%, and LightGBM improves ACC by 1.2% through contextual awareness. The framework achieves Pareto-optimal balance between precision (MSE/MAE) and robustness (ACC), establishing a replicable paradigm for multimodal temporal modeling that synergizes statistical decomposition, deep sequence learning, and ensemble feature engineering.

Discussion

When compared to global studies, the findings of this research demonstrate both alignment and innovation. For instance, Wang14 and Yan17 have shown the effectiveness of combining LightGBM with neural networks for time series forecasting, which resonates with the strengths of the LG-SG framework. Similarly, Zhang15 highlighted the benefits of hybrid models in short-term traffic flow prediction, reinforcing the notion that integrating multiple modeling techniques enhances accuracy and robustness. However, this study distinguishes itself by introducing a multi-layered architecture that combines SARIMA, LightGBM, and GRU, effectively capturing both static and dynamic patterns in shared mobility trajectory data. This unique integration not only improves the model’s interpretability but also enhances its predictive power in complex scenarios.

Despite these advancements, certain limitations persist. The LG-SG model’s performance during high volatility periods remains a challenge, as it struggles to maintain high accuracy in the face of sudden or irregular data fluctuations. This issue aligns with findings from Zhou22, who noted that hybrid models often face difficulties in handling abrupt changes in data. Additionally, the study relied on a dataset that did not incorporate external factors such as weather conditions or event information, which could have provided valuable context for improving predictions. These limitations underscore the need for further refinement and expansion of the model.

Future studies could focus on enhancing the LG-SG model’s robustness in extreme spatiotemporal fluctuations by incorporating advanced techniques such as attention mechanisms or Transformer architectures. Exploring the integration of external data sources, such as weather forecasts or event schedules, could also improve the model’s predictive accuracy. Furthermore, extending the applicability of the LG-SG model to different domains, such as urban planning or logistics, would provide insights into its adaptability across diverse contexts. Incorporating dynamic and multi-modal data, such as real-time traffic conditions or public transit information, could further validate the model’s scalability and effectiveness in handling complex, real-world scenarios. By addressing these areas, the LG-SG model could continue to serve as a valuable benchmark, demonstrating the potential of hybrid approaches in advancing time series analysis and its applications.

Conclusion

This study proposes a novel data imputation framework, LG-SG, which integrates LightGBM, SARIMA, and GRU models to effectively address missing data challenges. By leveraging the complementary strengths of these algorithms, the proposed framework constructs an enhanced feature generation mechanism, significantly improving the comprehensiveness and accuracy of imputed data. Specifically, SARIMA is utilized for initial prediction and error extraction, while GRU refines these predictions through error compensation. The integration of SARIMA predictions with GRU-based error correction yields highly accurate imputed values. Extensive simulation experiments on complete datasets validate the model’s robustness and superior performance across diverse data conditions, demonstrating its efficacy in handling missing data scenarios.

Building on these technical advantages, this study further explores the practical application value of the model in traffic management and provides critical policy recommendations for decision-makers. First, the establishment of data standardization and sharing frameworks is identified as a key measure to enhance the availability and quality of traffic data, thereby supporting more efficient and accurate traffic management. Second, integrating advanced data imputation methods, such as LG-SG, into real-time traffic prediction systems could significantly improve the accuracy of traffic forecasting while optimizing decision-making processes and facilitating the rational allocation of resources for infrastructure development and maintenance.

The implementation of these recommendations is expected to deliver substantial benefits to key stakeholders. Government agencies involved in urban planning and traffic management would gain access to more accurate data-driven insights, enabling improved traffic flow management, optimized signal control, and enhanced responsiveness during peak or disrupted traffic conditions. Transport service providers, including ride-hailing platforms, could leverage the LG-SG model to predict demand more accurately, optimize routes, and enhance operational efficiency. Additionally, end-users, such as commuters and drivers, would experience reduced travel times, decreased congestion, and an overall improvement in transportation experiences. Furthermore, the research findings provide valuable insights for data scientists and researchers, fostering further innovation in spatiotemporal data analysis and contributing to the development of smarter and more sustainable transportation systems.

By combining the LG-SG data imputation model with policy recommendations, this study not only deepens the understanding of advanced data imputation techniques but also offers actionable insights to guide the development of smarter, more sustainable, and efficient urban transportation systems.