Introduction

With the progress of economy, new energy vehicles have become a global research hotspot1. While vigorously promoting the development of new energy vehicles industry, the development of charging piles can not be ignored. Compared with other topologies, LLC isolated topology has the advantages of high power density, simple structure and good soft switching characteristics2, which is widely used in DC charging pile after stage.

Due to its unique advantages, LLC has been studied by scholars at home and abroad. In reference3, a hybrid clamp type three-level half-bridge LLC topology was used, and a two-stage hybrid control of Pulse Frequency Modulation (PFM) was used in step-up and Phase Shift Modulation (PSM) was used in step-down. However, the Zero Voltage Switch (ZVS) of the switch tube in the original edge cannot be realized at low voltage output. A off-time control strategy has been proposed in the literature4, and the proposed method reduces the switching and conduction losses in the low-voltage output case by skipping several pairs of switching control pulses and changes the switching frequency less than the normal control method. However, its practical control is complicated and it is difficult to design an accurate turn-off control ratio. In reference5, the new Burst control based on the highest efficiency phase plane trajectory was introduced into the two-level variable structure LLC topology to effectively improve the working efficiency and realize ZVS at low voltage. In reference6, PWM control was introduced into the bidirectional LLC topology, and the system voltage gain reached 4 times by using the switching coordination between the full bridge and half bridge of the primary side. However, there are many switches in this topology and the control is relatively complex. In reference7, asymmetric LLC topology is used to obtain high voltage gain in different operating modes by using the interaction of two resonators. However, the voltage gain depends on the choice of voltage mode, and the calculation of key parameters is relatively complex. Literature8 introduces variable PWM control in the Burst control mode with fixed frequency, so that the system can achieve ZVS while obtaining a wide voltage output range. In reference9, a half-bridge LLC topology with controllable resonant inductance is proposed, which can adjust the resonant inductance according to the output current to affect the parameters of the resonator, and has good dynamic performance. However, this topology requires additional magnetic adjustment structure, which leads to complex system structure and high cost. The LLC resonant converter is a nonlinear circuit, so it is necessary to simplify the circuit model when analyzing the converter. Therefore, scholars have conducted in-depth research on the solution of dynamic nonlinear equations10 and the suppression of harmonic noise11,12.

For the three-level LLC topology, the inner tube is turned off later than the outer tube, so the resonant cavity current of the inner tube is less than the outer tube when the inner tube is turned off, which leads to the conditions for the soft switching of the inner tube being more stringent than the outer tube13. At low voltage output, the outer tube achieves ZVS but the inner tube cannot. In summary, in order to further optimize the control of LLC topology applied to the rear stage of charging pile at the low-voltage output, this paper analyzes the realization conditions of ZVS and the switching points of each mode based on the hybrid clamp half-bridge three-level LLC resonant converter, and introduces the frequency conversion burst control at the low-voltage output to realize the inner tube ZVS at the low-voltage output. Combined with PFM and PSM to form a three-stage hybrid optimization control, the latter stage of the charging pile obtains a wide output voltage range while the former stage stably supplies power and solves the problem that the inner tube can not achieve ZVS when the low voltage is output, so that the latter stage system is stable, efficient and safe.

This research can be used to reduce the energy loss in the case of low voltage output at the rear stage of DC charging piles for electric vehicles and improve the efficiency of energy transmission. This can not only reduce the use of electric energy, but also reduce the heating and wear of the internal components of the charging pile, extend the service life of the equipment, and thus reduce the operating cost of the enterprise.

Working principle of three-level half-bridge LLC resonant converter

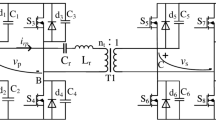
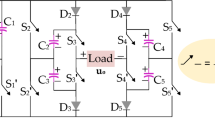
Topology structure

The hybrid clamp topology is easier to achieve automatic midpoint voltage equalization than the topology with only clamp diodes and flying capacitors. Its circuit topology is shown Fig. 1.

Fig. 1
figure 1

Three-level half-bridge hybrid clamp type LLC topology.

Full size image

In the Figure, \({U_{\text{i}}}\)is the prestage output stable DC bus voltage;\({C_1}\)and\({C_2}\)are DC bus capacitors;\({D_{11}}\)and\({D_{12}}\)are clamp diodes;\({C_{\text{S}}}\)is the flying capacitance; \({Q_1}\)~\({Q_4}\)are the primary edge switch tubes, among which\({Q_2}\)and\({Q_3}\)are the inner tubes, and the conditions for achieving ZVS are more demanding.\({L_{\text{r}}}\),\({L_{\text{m}}}\)and\({C_{\text{r}}}\)are resonant inductors, excitation inductors and resonant capacitors, which together form a resonant cavity. T is high frequency transformer;\({D_{21}}\)~\({D_{24}}\)are secondary side rectifier diodes;\({C_{\text{o}}}\)is the output filter capacitor;\({R_{\text{L}}}\)is the load resistance.

Principle of operation

The resonant frequencies of\({L_{\text{r}}}\)and\({C_{\text{r}}}\)are defined as\({f_{{\text{r1}}}}\). The common resonant frequency of\({L_{\text{r}}}\),\({L_{\text{m}}}\)and\({C_{\text{r}}}\)is defined as\({f_{{\text{r2}}}}\).The operating frequency of the system is defined as\({f_{\text{r}}}\). In this paper, the hybrid control method of VFBM, PSM and PFM is adopted, in which the operating frequency of the system is always within\({f_{{\text{r1}}}}\) ~ \({f_{{\text{r2}}}}\)when using PSM and PFM control. It is assumed that all components are ideal devices and the pressure bearing of the primary edge switch tube is constant at 0.5\({U_{\text{i}}}\).The working principle and mode are analyzed with the system working in the subresonant state(\({f_{{\text{r2}}}}{\text{<}}{f_{\text{r}}}{\text{<}}{f_{{\text{r1}}}}\)), and the main waveform is shown in Fig. 2.

In the Figure, \({Q_{{\text{g1}}}}\)~\({Q_{{\text{g4}}}}\)are the driving signals,\({i_{\text{r}}}\)and\({i_{\text{m}}}\)are the current values flowing through the resonant inductor and excitation inductor,\({i_{{\text{D21}}}}\)~\({i_{{\text{D24}}}}\)are the secondary side diode current. The converter has eight operating modes in one cycle, and only the first half cycle is analyzed in this paper because the resonant state is the same before and after half cycle.

Working mode 1: Working phase (\({{\text{t}}_{\text{0}}}\)~\({{\text{t}}_{\text{1}}}\)).\({Q_1}\)is conducting at the same time as\({Q_2}\)at time\({{\text{t}}_{\text{0}}}\), and since\({D_{21}}\)and\({D_{24}}\)are already conducting at this time, the voltage will clamp the\({L_{\text{m}}}\)at this time, and the\({L_{\text{m}}}\)will not participate in the resonance. At this time,\({L_{\text{r}}}\)and\({C_{\text{r}}}\)participate in the resonance, and the current flows through\({Q_1}\),\({Q_2}\),\({L_{\text{r}}}\),\({C_{\text{r}}}\)and\({C_1}\), and\({i_{\text{m}}}\)rises linearly.

Working mode 2: Working phase (\({{\text{t}}_{\text{1}}}\)~\({{\text{t}}_{\text{2}}}\)).\({i_{\text{r}}}\)is equal to\({i_{\text{m}}}\)at time\({{\text{t}}_{\text{1}}}\), at which time\({D_{21}}\)and\({D_{24}}\)achieve zero-current turn-off. At this time, the primary edge of the converter enters the reactive power circulation phase, and the\({L_{\text{m}}}\)is no longer clamped and resonates with\({L_{\text{r}}}\)and\({C_{\text{r}}}\). Since\({L_{\text{m}}}\)is generally 5 to 7 times larger than\({L_{\text{r}}}\), the current\({i_{\text{r}}}\)flowing through the resonant inductor can be approximately considered constant.

Fig. 2
figure 2

Subresonant waveform.

Full size image

Working mode 3: Working phase (\({{\text{t}}_{\text{2}}}\)~\({{\text{t}}_{\text{3}}}\)).\({Q_1}\)is turned off at time\({{\text{t}}_{\text{2}}}\), and the\({i_{\text{r}}}\)will charge the parasitic capacitance to\({Q_1}\)to 0.5\({U_{\text{i}}}\). At the same time\({i_{\text{r}}}\)discharges the parasitic capacitor voltage of\({Q_4}\)to 0 through\({C_{\text{S}}}\)to prepare for\({Q_4}\)’s ZVS. Finally, the upper clamp diode\({D_{11}}\)clamps the\({Q_1}\)voltage to 0.5\({U_{\text{i}}}\), at which point the loop through which the resonant inductor\({i_{\text{r}}}\)flows is\({D_{11}}\)、\({Q_2}\)、\({L_{\text{m}}}\)and\({C_{\text{r}}}\).

Working mode 4: Working phase (\({{\text{t}}_{\text{3}}}\)~\({{\text{t}}_4}\)).\({Q_2}\)is turned off at time\({{\text{t}}_{\text{3}}}\), and the\({i_{\text{r}}}\)will charge the parasitic capacitance of\({Q_2}\)to 0.5\({U_{\text{i}}}\). At the same time\({i_{\text{r}}}\)discharges the parasitic capacitor voltage of\({Q_3}\)to 0, creating conditions for the ZVS of\({Q_3}\). Eventually, the inductor current\({i_{\text{r}}}\)flows through\({D_{24}}\)、\({D_{23}}\)、\({L_{\text{r}}}\)、\({L_{\text{m}}}\)and\({C_{\text{r}}}\). After\({Q_2}\)is turned off, the secondary side diodes\({D_{22}}\)and\({D_{23}}\)conduction,\({L_{\text{m}}}\)reverse clamp,\({i_{\text{m}}}\)starts to linearly decrease. ZVS is realized simultaneously at time\({Q_3}\)and\({Q_4}\)of\({{\text{t}}_4}\).

Here, the other state of the system is working in the resonant state (\({f_{\text{r}}}{\text{=}}{f_{{\text{r1}}}}\)), and the main waveform is shown in Fig. 3.

Fig. 3
figure 3

Resonant state waveform.

Full size image

As can be seen from Fig. 3, the resonant cavity current is a standard sine wave, \({L_{\text{m}}}\)does not participate in the resonance,\({i_{\text{m}}}\)waveform is a triangle wave, secondary side diode is in the critical state of ZCS, At this time, the switching frequency\({f_{\text{r}}}\)is consistent with the resonant frequency\({f_{{\text{r1}}}}\)of\({L_{\text{r}}}\)and\({C_{\text{r}}}\), the output voltage is only determined by the input and the number of transformer turns, and the efficiency of the converter is the highest.

Effective duty cycle is the ratio of the time that the periodic signal is in effective state to the entire cycle time in a cycle. PSM control controls the actual effective duty cycle D of the inverter output voltage by controlling the phase shift Angle between the leading tube and the lagging tube, so as to change the actual effective value of the inverter output voltage. The system is in the PSM control working waveform as shown in Fig. 4.

Fig. 4
figure 4

PSM working waveform.

Full size image

Analysis of limitations of two-stage hybrid control ZVS

Dead time is a period of safety interval set to prevent the phenomenon of short-circuiting caused by the simultaneous conduction of two switching elements (e.g., MOSFETs or IGBTs) on the same bridge arm. In other words, dead time means that after one tube is closed, a certain amount of time must be waited before the other tube can be opened. In light load and low voltage output state, too short dead time may cause ZVS to fail, while too long dead time will cause the resonant current to reverse resonance to re-charge the parasitic capacitor and cause ZVS to fail. According to the analysis in Sect. 2.2, the system should work in the sub-resonant region to ensure the primary edge ZVS and secondary edge ZCS, so the PSM should be switched during the step-down output. In the PSM working state, the system operating frequency should always meet\({f_{\text{r}}}={f_{{\text{r1}}}}\)while achieving ZVS, and reasonable dead time\({T_\text{d} }\)and effective duty cycle D should be calculated. In the following, the derivation of the dead time when the switching frequency is equal to the resonant frequency is first carried out, and the resonant frequency current waveform is shown in Fig. 5.

Fig. 5
figure 5

Resonant frequency current waveform.

Full size image

Let the time interval for the resonant current to change from reverse to 0 be\(\theta\), then the expression of the dead time\({T_\text{d} }\)at this time can be expressed as:

$${T_{\text{d}}}=\frac{\theta }{{{\omega _{\text{s}}}}}$$
(1)

Where\({\omega _{\text{s}}}\)is the system resonant frequency angular velocity. The instantaneous values of resonant current and excitation current in the Figure can be expressed as:

$${i_{\text{r}}}(t)=\sqrt 2 {i_{{\text{r\_rms}}}}\sin (\omega t - \theta )$$
(2)
$${i_m}(t)=\left\{ {\begin{array}{*{20}{c}} {\frac{{{n_2} \cdot {U_{\text{o}}}t}}{{{L_{\text{m}}}}} - {i_{{\text{m\_max}}}}\quad \quad 0<t<0.5{T_{\text{s}}}} \\ { - (\frac{{{n_2} \cdot {U_{\text{o}}}t}}{{{L_{\text{m}}}}} - {i_{{\text{m\_max}}}})\quad 0.5{T_{\text{s}}}<t<{T_{\text{s}}}} \end{array}} \right.$$
(3)

Where\({n_2}=1/n\)is the conversion ratio to the original edge and\({T_{\text{s}}}\)is the system period. Suppose that the expression\({i_{{\text{m\_max}}}}\)is given by:

$${i_{{\text{m\_max}}}}=\frac{{{n_2} \cdot {U_{\text{o}}}}}{{4{f_{\text{r}}}{L_{\text{m}}}}}$$
(4)

Since the resonant energy of the secondary edge comes from the integral of the difference between the resonant current of the primary edge and the excitation current, the effective value of the resonant current can be obtained as:

$${i_{{\text{r\_rms}}}}=\sqrt {\frac{{(4L_{{\text{m}}}^{2}{\pi ^2}f_{{\text{r}}}^{2}+n_{2}^{4}R_{{\text{L}}}^{2})U_{{\text{o}}}^{2}}}{{8n_{2}^{2}R_{{\text{L}}}^{2}f_{{\text{r}}}^{2}L_{{\text{m}}}^{2}}}}$$
(5)

According Fig. 5, the initial value expression of the resonant current is:

$${i_{\text{r}}}{(t)_{t=0}}=\sqrt 2 {i_{{\text{r\_rms}}}}\sin ( - \theta )= - \frac{{{n_2} \cdot {U_{\text{o}}}}}{{4{f_{\text{r}}}{L_{\text{m}}}}}$$
(6)

By substituting Eq. (5) into Eq. (6), the expression of time interval\(\theta\)can be obtained as:

$$\theta =\arcsin (\frac{{{n_2}{U_{\text{o}}}}}{{\sqrt {\frac{{4U_{{\text{o}}}^{2}(4L_{{\text{m}}}^{2}{\pi ^2}f_{{\text{r}}}^{2}+n_{2}^{4}R_{{\text{L}}}^{2})}}{{n_{2}^{2}R_{{\text{L}}}^{2}}}} }})$$
(7)

The maximum value of the dead time\({T_\text{d} }\)can be obtained by substituting Eq. (7) into Eq. (1), which is denoted as\({T_{{\text{d\_max}}}}\). In theory, ZVS can be achieved if the dead time can satisfy one charge and discharge of the parasitic capacitance\({C_{{\text{oss}}}}\)of the switch tube, denoted as\({T_{{\text{d\_min}}}}\), and its expression is:

$${T_{{\text{d\_min}}}}=\frac{{0.5{U_{\text{i}}}{C_{{\text{oss}}}}}}{{{i_{{\text{m\_max}}}}}}$$
(8)

In conclusion, when the switching frequency of the system is the resonant frequency point, the dead time should meet Eqs. (1) and (7). However, when the PSM control is used, not only the dead time should be considered, but also the ZVS condition is related to the effective duty cycle. In order to ensure that the resonant current of the inner tube\({Q_2}\)and\({Q_3}\)can still charge and discharge the parasitic capacitance in the dead time, The minimum effective duty cycle must be calculated.

Figure 4 shows that the dead time\({T_\text{d} }\)is within\({{\text{t}}_{\text{2}}}\)~\({{\text{t}}_{\text{3}}}\), but the mathematical expression of\({i_{\text{r}}}\)is complicated to solve. Since\({i_{\text{r}}}={i_{\text{m}}}\)when \({{\text{t}}_{\text{2}}}\)~\({{\text{t}}_{\text{3}}}\),\({i_{\text{r}}}\)can be represented by\({i_{\text{m}}}\)in the dead time, where the rate of change of\({i_{\text{m}}}\)can be expressed as:

$$\Delta i=\frac{{n{U_{\text{o}}}D}}{{2{f_{\text{r}}}{L_{\text{m}}}}}$$
(9)

The amplitude of\({i_{\text{m}}}\)at the maximum point is given by:

$${i_{\text{m}}}=0.5\Delta i \geqslant \frac{{2{C_{{\text{oss}}}}{U_{{\text{C1}}}}}}{{{T_{\text{d}}}}}$$
(10)

Combined with Eqs. (9) and (10), the minimum effective duty cycle can be obtained as:

$${D_{\hbox{min} }} \geqslant \frac{{8{C_{{\text{oss}}}}{U_{{\text{C1}}}}{f_{\text{r}}}{L_{\text{m}}}}}{{n{U_{\text{o}}}{T_{\text{d}}}}}$$
(11)

In summary, in the PFM and PSM (PFM-PSM) hybrid control, Eqs. (1), (7), and (11) need to be satisfied at the same time to make the original edge switch tube ZVS. The key parameters of the existing converter are shown in Table 1.

Table 1 Key parameters of the converter.
Full size table

Substitute the parameters into Eqs. (1) and (7), and the dead time range is \(2.7{\text{e-9s}} \leqslant {T_\text{d} } \leqslant 6.73{\text{e-7s}}\). When the dead time is less than the minimum value, the parasitic capacitor cannot achieve primary charge and discharge, resulting in the inability to achieve inner tube ZVS. When the dead time is greater than the maximum value, the resonant current will reverse resonance after zero-crossing, resulting in reverse charging of the parasitic capacitor that has been discharged. ZVS could not be implemented. In summary, the dead time \({T_\text{d} }=3{\text{e-8s}}\) is selected in this paper, and the minimum output voltage value of 150 V is substituted into Eq. (11) to obtain the minimum effective duty cycle \({D_{\hbox{min} }} \geqslant 0.44\), and the gain is \({M_{{\text{PSM}}}}=0.637\) at this time, that is, ZVS cannot be realized below this gain. Combined with Table 1, it can be seen that the minimum ZVS voltage achieved under this gain is 299.6 V, not the minimum output voltage of 150 V, and the full output voltage range of ZVS cannot be achieved. Taking the output of 250 V under the condition of Table 1 as an example, the main waveform is shown in Fig. 6. It can be seen that in the PFM-PSM hybrid control, The phenomenon of ZVS failure in PSM operation mode, so it is necessary to optimize the voltage interval from 150 V to 300 V.

Fig. 6
figure 6

The main waveform diagram of output 250 V in PSM operating mode.

Full size image

Three-stage hybrid optimization control strategy

In order to solve the problem that ZVS cannot be realized and work efficiency is low at low voltage, some scholars have proposed burst mode to reduce energy loss by blocking the driving signal of the switch tube. Literature14 proposed a hybrid control method based on PFM-burst to improve the working efficiency of the LLC converter in the full voltage range, aiming at the problem that the LLC converter is difficult to adjust under the condition of very light load and no load. In reference15, a phase-shift burst modulation (PS-burst) method for two-level half-bridge LCC resonant converter was proposed and applied in photovoltaic system to achieve maximum power tracking while achieving full voltage range ZVS. In reference16, the charge is normalized by the switching frequency to obtain the approximate linear relationship between the charge and the load current, and the current sensorless burst control of the half-bridge LLC converter is proposed. Literature17 proposed a PSM-burst hybrid control mode based on two-level full-bridge LLC converter, which achieved wide output voltage range, low resonant current and zero-voltage turn-on of all switches, and optimized resonant parameters and maximum phase shift Angle. Literature18 combined with adaptive theory on the basis of burst control, so that the burst frequency was kept at the preset frequency and the resonant tank operated at the preset optimal load point during the burst time, which solved the problems of current overshoot and low efficiency in traditional burst mode. Drawing on the above control ideas, this paper proposes a burst control of continuous frequency conversion, namely VFBM, which adjusts the output voltage and current of the converter through closed-loop control of the burst period. As the output voltage increases, the burst period also increases. The main working waveform is shown Fig. 7.

Fig. 7
figure 7

VFBM working waveform.

Full size image

It can be seen from Fig. 7 that the driving state in the VFBM is high and low alternately at this time. When the first pulse ends, the switch tube can still be charged and discharged in the dead time, which meets the ZVS condition. Combined with the previous analysis, the minimum effective duty cycle is introduced on this basis to prevent the output voltage fluctuation at the switching point. The three-stage hybrid optimization control was composed by VFBM and PSM and PFM. The switching point between VFBM and PSM was defined as the first switching point and set to 300 V, the switching point between PSM and PFM was defined as the second switching point and set to 470 V, and the system operating frequency under VFBM mode was defined as \({f_{{\text{burst}}}}\). The gain curve of the three-stage hybrid optimization control is shown in Fig. 8. Since the system needs to judge different voltage ranges according to the charging demand of the power battery in the actual work, the frequency conversion burst control is recorded as Mode1, PSM control as Mode2, and PFM mode as Mode3.

Fig. 8
figure 8

Three stage gain curve.

Full size image

When the output voltage increases, \({f_{{\text{burst}}}}\)increases, and the output gain also increases. When the gain is 0.637, that is, the output voltage is 300 V, the system switches to PSM control. At this time, the system works at the resonant frequency, and the effective duty cycle increases with the increase of the output voltage. When the output voltage is 470 V, that is, when the gain is 1, the maximum effective duty cycle is also 1. The system is in the resonant frequency state, and the excitation current is independent of the load. When the output voltage continues to increase, the system works under the control of PFM, and the normalized frequency continues to decrease. When the output voltage is 650 V, the system reaches the maximum gain, which is 1.383, less than the maximum gain of 1.58 when\({L_{\text{r}}}\),\({L_{\text{m}}}\),\({C_{\text{r}}}\), and common resonance\({f_{\text{r}}}={f_{{\text{r2}}}}\).Since different voltage intervals need to be judged in the actual work of the system, the VFBM is denoted as Mode1, PSM control as Mode2, and PFM mode as Mode3. The working flow of the system is shown in Fig. 9.

Fig. 9
figure 9

System flow chart.

Full size image

Simulation experiment verification

In order to verify the correctness of the proposed three-stage hybrid optimization control strategy, this paper builds a simulation model in Matlab/Simulink, and the key parameters of the system are given in Table 1. 300 V and 470 V are selected as the mode switching points, and the three modes of Mode1, 2 and 3 are simulated and analyzed respectively.

Verification by Mode1 simulation

In Mode1, the system starts working with an output voltage of 150 V and a gain of 0.319, and the maximum output voltage in this mode is 300 V. The main waveforms of the system at the output voltage of 150 V and 300 V are shown in Figs. 10 and 11. Figure 10 shows that\(\Delta u=0.7{\text{V}}\), and the minimum effective duty cycle of\({Q_2}\),\({Q_3}\),\({Q_1}\),\({Q_4}\)is\({D_{\hbox{min} }}\), at this time\({f_{{\text{burst}}}}\)is 14.3 kHz. Figure 11 shows that the system still maintains the minimum effective duty cycle, at this time\({f_{{\text{burst}}}}\)is 54.1 kHz,\(\Delta u=0.45{\text{V}}\). In this state, taking inner tube\({Q_2}\)as an example, the ZVS waveform at 150 V and 300 V output is shown in Figs. 12 and 13, where the drain-source voltage of\({Q_2}\)has been reduced by 300 times in equal proportion for convenient display.

Fig. 10
figure 10

Main waveform diagram of output 150 V in VFBM.

Full size image
Fig. 11
figure 11

Main waveform diagram of output 300 V in VFBM.

Full size image
Fig. 12
figure 12

Q2 tube ZVS waveform at output voltage of 150 V.

Full size image
Fig. 13
figure 13

Q2 tube ZVS waveform at output voltage of 300 V.

Full size image

In conclusion, it can be seen that under the control of VFBM,\({f_{{\text{burst}}}}\)of the system increases with the increase of output voltage, and\({Q_2}\),\({Q_3}\),\({Q_1}\)and\({Q_4}\) always maintain the minimum effective duty cycle\({D_{\hbox{min} }}\). Simulation experiments show that the control strategy can achieve stable output while meeting the\({Q_2}\)ZVS of the inner tube, which verifies the correctness of the VFBM strategy.

Verification by Mode2 simulation

In Mode2, the output voltage of the system ranges from 300 V to 470 V, and the system starts to work with gain 0.637 until gain 1. In this mode, the system resonant frequency\({f_{\text{r}}}={f_{{\text{r1}}}}\). The main waveform is shown in Fig. 14, and it can be seen that the\({Q_2}\)is in the critical ZVS state at this time.

Fig. 14
figure 14

Main waveform diagram of output 300 V in PSM.

Full size image

In this paper, the output voltage is 470 V and the gain is 1, so the system works at the resonant frequency point, and the main waveform is shown in Fig. 15.

Verification by Mode3 simulation

In Mode3, the system starts working with\({f_{\text{n}}}=1\)with output voltage ranging from 470 V to 650 V.

Fig. 15
figure 15

The main waveform of the resonant frequency point.

Full size image

Figure 15 shows that the resonant current is approximately a sine wave, the excitation current is approximately a triangle wave, the output voltage is stable, and\({Q_2}\)can achieve ZVS. In summary, the correctness of the PSM control strategy is verified, and the simulation results show that the control strategy can achieve stable output and meet the ZVS of the inner tube.

In order to verify the working characteristics of the resonant frequency point under PFM, it is merged into\({R_{\text{L}}}\)when it is stable, and the total resistance is 28.015Ω. The waveform after loading at the resonant frequency point is shown in Fig. 16. When the output voltage exceeds 470 V, the system resonant frequency\({f_{{\text{r2}}}}{\text{<}}{f_{\text{r}}}{\text{<}}{f_{{\text{r1}}}}\), working in subresonant mode, the full-voltage output waveform of the system is shown in Fig. 17.

Fig. 16
figure 16

Main waveform diagram of PFM at resonant frequency.

Full size image
Fig. 17
figure 17

Main waveform diagram of output 650 V in PFM.

Full size image
Fig. 18
figure 18

Total output voltage waveform of three-stage hybrid control.

Full size image

Figure 16 shows that the resonant current and excitation current only change in amplitude after the load is cut, and the working waveform is similar to that without load cut. The stable output is achieved and the inner switching tube ZVS is satisfied, which verifies that the resonant and excitation current will not be distorted by the load when the system works at the resonant frequency. Figure 17 shows that the system operating frequency \({f_{\text{r}}}\) is 75 kHz and the internal switching tube ZVS, and the output voltage is stable. In conclusion, the correctness of PFM modulation strategy is verified. Finally, the total output voltage waveform diagram of the three-stage hybrid optimization control is shown in Fig. 18.

As can be seen from Fig. 18, the system starts in the mode of Mode1 and enters the VFBM mode, reaches 150 V in 0.06s and remains stable, changes the output voltage command to 300 V in 0.1s and reaches stability in 0.12s. Combined with Figs. 10, 11 and 12, and 13, it can be seen that in this working mode, the system output remains stable and the inner switch tube achieves ZVS, and the minimum effective duty cycle D derived in Subsection 2.3 is maintained to enter the Mode2-PSM working mode at 0.14s. Since Figure (a) maintains the minimum duty cycle in the mode switching, Figure (a) maintains the minimum duty cycle in the mode switching. During mode switching, the voltage fluctuation is only 1.7 V, while the voltage fluctuation in Figure (b) is 43.16 V. At 0.15s, the system completely enters PSM working mode and remains stable. At this time, the system working frequency is equal to the resonant frequency of the two components. At 0.18s, the output voltage command is changed to 470 V and reaches stability at 0.19s, until it enters Mode3-PFM working mode at 0.24s. According to Figs. 14 and 15, ZVS can be realized by switching the tube within the PSM operating mode and resonant frequency point. The system carries out the load cut experiment at 0.245s, and the load is 28.015Ω at this time, and the load cut experiment restores 58Ω at 0.3s. The working characteristics of the LLC converter at the resonant frequency point are verified, and the output voltage instruction is changed to 650 V to maintain a stable output at 0.35s. Figures 16 and 17 show that ZVS is achieved by inner switching tube in PFM operating mode.

Finally, through the simulation verification of the three modes, it is proved that the three-stage hybrid optimization control strategy can achieve the full output voltage ZVS while meeting the wide output voltage range, and strictly meet the gain curve of Fig. 8.

Conclusions

Aiming at the problem that the PFM-PSM hybrid control can not meet the ZVS of the inner tube at the low voltage output, the minimum effective duty cycle and dead time are calculated on the basis of PFM-PSM, and the VFBM is introduced at the low voltage output to form a three-stage hybrid optimization control.

Theoretical and simulation results show that the three-stage hybrid optimization control can make the charging pile back stage output stable DC voltage when the front stage power supply is stable and solve the problem that the inner tube can not achieve ZVS when the low voltage output is under the PFM-PSM hybrid control. Because of the dead time and the minimum effective duty cycle in the VFBM, The voltage oscillation between VFBM and PSM is effectively suppressed. Finally, the system can realize the full range of 150 V ~ 650 V ZVS. By reasonably selecting the mode switching point and system parameters, the system can select the working mode through the required output voltage, so that the charging pile is stable, efficient and safe.