Introduction

Since the first polymeric artificial, which contracts upon heating and expands upon cooling, was developed by Haines et al.1 through twist insertion in precursor fibers with negative coefficient of thermal expansion, enormous progress has been made over the past 10 years2,3,4,5. Polymeric artificial muscles have found applications in many high-tech fields such as in soft robotics6,7,8,9. It also has potential for shock absorption because shape memory polymer fibers have been proved to damp vibration, similar to spider silk10. Various types of precursor fibers have been used to prepare this type of tensile actuators, such as polymeric fibers with negative coefficient of thermal expansion, for instance nylon or polyethylene1,11, or polymeric fibers with two-way shape memory effect, for instance poly(ethylene-co-vinyl acetate)12,13. However, one limitation with these fibrous polymeric muscles is that they cannot reversibly actuate without the application of an external tensile load14,15,16. It is noted that under a small compression load of 0.398 N, heterochiral artificial muscle from twisted and coiled Nylon 6 fiber can expand upon cooling, but the nominal stress was only 0.078 MPa1. Even if they can actuate in bulk form under external pressure, fibrous artificial muscles buckle and crush under certain external compression load due to their large slenderness ratio. This is why a wire or mandrel was used in the heterochiral muscle to prevent the muscle from buckling when it was actuated under external compression (Video S2 in1). Therefore, twisted and coiled fibrous artificial muscles, although they show outstanding reversible actuation under external tensile load, they are very limited in applications where free-standing (actuates without external tensile load) or beyond free-standing (actuates under external compression) are needed, in particular, when a large external compression load is applied.

Over the years, quite a few polymers or polymer blends or polymer composites have been designed and synthesized, which exhibit reversible actuation without the external tensile load17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42, i.e., free-standing, or even under external compressive load43,44, i.e., beyond free-standing. Although it seems that these polymers or polymer blends or polymer composites can serve as free-standing artificial muscles and beyond free-standing artificial muscles, they cannot actuate in fibrous form. The reason is that the specimens used in testing these polymers are in the form of thin film or bulk with small slenderness ratio, not fibers with much larger slenderness ratios. With larger slenderness ratio, these polymers fibers cannot actuate under external compression because the fibers will buckle and crush. Furthermore, the actuation is small and the actuation load is very low. For example, cis Polybutadiene (cPBD) thin film only shows an actuation strain of 6.2% with a very small external compression load of 0.5 N or 0.05 MPa compressive stress43. Therefore, it is highly desired to develop new fibrous artificial muscles that can reversibly actuate without the external tensile load (free-standing) or even under external compression load (beyond free-standing).

It is noted that several types of actuators that can actuate under a compression load have been widely studied, including, but are not limited to, dielectric elastomer actuator and ionic active polymeric actuator45,46,47,48. The mechanism for actuation has been well understood. For example, dielectric electroactive polymers (DEPs) are actuated by electrostatic forces. They can be regarded as capacitors with a compliant polymer film as the dielectric and compliant electrodes. When a strong electric field is applied across such film or stacked films, the attractive forces of the opposing charges compress the dielectric film in the thickness or transverse or out-of-plane direction, and, at the same time causing lateral or in-plane expansion of the dielectric film and the compliant electrodes, due to Poisson’s ratio effect. Both the thickness direction contraction and in-plane expansion can be utilized as actuation strain49. For an ionic active polymeric actuator (IAPC), it operates based on the principle of ion exchange and electrochemical reactions. IAPC consists of an ion exchange polymer matrix and an electrode material. In the ion exchange polymer matrix, numerous ion exchange sites that can adsorb and release metal cations exist. When an external electric field or voltage is applied to the actuator, the metal cations migrate, which are driven by the electric field, moving from one ion exchange site to another. The ion exchange process causes a change in the volume of the ion exchange polymer matrix, leading to deformation of the entire assembly. This volume change can be utilized as an actuation strain45.

As examples, Zhang et al.50 fabricated new all-organic field-type electroactive polymer (EP) composites. As compared to traditional EPs, which needs at least 70 × 106 V/m to actuate, their EPs can be actuated at 13 × 106 V/m. Ma et al.51 developed a water-responsive polymer film, which combines a rigid matrix (polypyrrole) and a dynamic network (polyol-borate) that can exchange water with the environment to induce film expansion and contraction. The film actuator can generate contractile stress up to 27 MPa. In order to enhance the actuation of this type of film actuators, the film can be fabricated into certain structures. To do this, usually a bias element such as springs is used. For example, Feng and Zhan52 fabricated parylene-patterned helical ionic polymer-metal composite spring actuator. The results show that the actuator produced a force of 300 mN. Ghazaryan et al.53 designed a spring-roll actuator using commercially available silicone. Electrodes were deposited on a pre-strained silicone film, coated with functional organosilicone polymer composite, and rolled around a metal spring. The coating enhanced the interfacial adhesion between silicone and compliant electrodes, preserving the integrity and electro-mechanical properties of the fabricated spring-roll actuator. The silicone-based spring-roll actuator could bear 200 times its own weight and displace it by 6% at the applied electric field of 90 V/µm. Rizzello et al.54 prepared dielectric electroactive polymer membrane biased with a linear spring. The motion was generated by the deformation of the membrane caused by the electrostatic compressive force between two compliant electrodes applied on the surface of the polymer film. A mass and a linear spring were used to pre-load the membrane, allowing actuation in the out-of-plane direction. Hau et al.55 fabricated silicone-based strip-in-plane dielectric elastomer actuators with screen printed electrodes. An actuation strain of up to 45% and a force output of 0.38 N were obtained. Hodgins et al.56 developed a diaphragm dielectric electro-active polymer (DEAP) actuator with three different biasing elements to produce out-of-plane actuation. A hanging mass, a linear coil spring, and a nonlinear bistable mechanism were individually paired with an unloaded DEAP actuator. The maximum hanging weight used was 100 g. Goswami et al.57 prepared a redox-controlled gel actuator. By using a mechanical biasing element such as a spring doubling as the electrode, one-dimensional linear actuation was realized, with strains over 40% and a force of 30 kPa at potentials less than 1 V. Hodgins et al.58 also prepared an actuator system consisting of a bi-stable mechanism (a negative-rate bias spring, or NBS) coupled with an out-of-plane dielectric electro-active polymer (DEAP). As compared with conventional linear springs, the NBS-biased actuator exhibits a considerably larger displacement stroke. Based on the test results, the force produced is about 1.5 N in the thickness direction. In addition to studies using electrostatic force to drive actuation, biased actuators driven by forces other than electrostatic force have also been developed. For example, Zhang et al.59 developed a spring-reinforced pneumatic actuator by embedding a spring constraint layer around each single air chamber. Under 50 kPa tension, the linear expansion is 16 mm when the cavity is inflated by air.

Based on the above literature survey, although some of the biased actuators can actuate under compression, they are basically in the form of thin films or stacked films, and the compression is in the transverse or film thickness direction. Therefore, buckling is not a big concern. Also, these electroactive film actuators usually need high voltage to actuate. Therefore, the challenge to prepare linear actuators or fibrous actuators that can reversibly actuate under compression still exists.

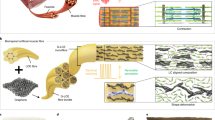
Our idea is to develop hybrid fibrous artificial muscles. In this design, conventional helical metallic springs are combined with two-way shape memory polymer fibers or polymeric artificial muscles. In particular, we propose to insert pre-tensioned two-way shape memory polymer wire or twisted and coiled polymeric fiber into a pre-compressed helical spring. In this assembly, the compressed spring provides the much-needed tensile load to the polymeric actuator, and thus convert the non-free-standing polymer actuator into a free-standing muscle and beyond free-standing muscle. On the other hand, the tensioned fibrous polymeric actuator provides compression to the spring, making repeated reversible actuation of the hybrid muscle possible. In other words, the helical metallic spring is transformed into an artificial muscle. The fabrication process, together with the reversible actuation under compression, is schematically shown in Fig. 1. In Fig. 1, the actuation of a conventional polymeric artificial muscle under tension is also shown.

To prove this new design, two types of two-way shape memory polymers, one type of polymeric artificial muscles, and seven types of helical metallic springs were used to prepare the hybrid artificial muscles. The actuation under tensile load, zero load, and compressive load was evaluated. A theory based on linear elasticity was also developed to help understand this type of hybrid artificial muscles. The test results show that the hybrid fibrous actuators can actuate reversibly under tension, without any load, and particularly, under compression, which is very challenging for other fibrous actuators such as twisted and coiled polymeric fibers because they buckle under compression.

Experimentation

Materials

Two-way shape memory polymer cis poly(1,4-butadiene)

Cis poly(1,4-butadiene) (PBD) under trade name Budene® 1208 from Goodyear Chemical (Akron, OH, USA) was used as the reagent. The viscosity is 40 (Mooney ML 1 + 4 @ 100 °C). The onset glass transition temperature is − 104 °C. The solvent, chloroform, from Sigma-Aldrich (St. Louis, MO, USA), was used to dissolve cis polybutadiene. The preparation of the cis polybutadiene based two-way shape memory polymer follows the previous studies by Lu et al.43. In short, a sticky homogeneous solution was acquired after overnight stirring. The ratio of PBD to chloroform is roughly 1 to 10. The curing agent, dicumyl peroxide (DCP), from Sigma-Aldrich, at the amount of 3 wt% of cis polybutadiene, was added into the solution. After well mixing of the dicumyl peroxide with cis polybutadiene solution, chloroform was removed by simple evaporation overnight in a hood at ambient temperature. The dried cis polybutadiene and dicumyl peroxide mixture was then clamped in a Teflon mold and cured for 30 min in a 150 °C oven. The crosslinked semi-transparent cis polybutadiene (cPBD) was obtained. The sheet was then wrapped and rubbed into a cylinder for use. The stiffness of the cPBD wire, as determined based on Hooke’s law by using a spring balance, was found to be 0.127 N/mm; see Fig. S1. The cPDB cylinder, after 200% stretch during assembling the hybrid muscle, has a dimeter about 1.18 mm.

Fig. 1
figure 1

(Left) Reversible actuation of a conventional polymeric muscle under a constant tensile load. When the temperature drops, it extends, and when the temperature rises, it contracts. This is due to the uncoiling of twisted and coiled muscles or due to the rubbery elasticity and melt/crystallization transition in semicrystalline two-way shape memory polymer muscles. (Right) The fabrication process of the hybrid fibrous actuator and its reversible actuation under a compression load. During the fabrication, the spring is compressed, and the polymeric muscle is stretched. After assembling the hybrid actuator, the spring is under compression, and the muscle is under tension. Under an external compression load, the spring is further compressed, and the pre-stretch in the muscle is reduced, but does not disappear. Therefore, in the fibrous actuator, the muscle is still under tension. As a result, when temperature cycles, the muscle actuates reversibly, causing the hybrid actuator to actuate reversibly, even under a constant external compressive load.

Full size image

Two-way shape memory polymer Polycaprolactone

The polycaprolactone (PCL) with an average Mn 45,000, benzoyl peroxide (BPO) as initiator, and Tetrahydrofuran (THF) as solvent were purchased from Sigma-Aldrich and used without further purifications. The synthesis procedure referred to our previous study44. 18 g PCL powder was firstly dissolved in 50 mL THF by mechanically stirring at room temperature for 6 h. 2 g initiator BPO was then added into the solution and mixed well. The mixture was then poured onto a polytetrafluoroethylene (PTFE) sheet and placed in a hood to allow air dry for 1 day. The obtained PCL was further dried at room temperature in a vacuum oven for 6 h to completely remove the solvent THF. The fully dried PCL was cut into small pieces and put into a PTFE mold to crosslink at 130 °C for 20 min under pressure of 20 MPa through a hot press machine. The thickness of the obtained cross-linked PCL (cPCL) sheet is about 1 mm. The slender cPCL bar with size of 30 mm × 3 mm × 1 mm can be cut from the cPCL sheet for two-way shape memory test and for preparing the hybrid artificial muscle. The stiffness of the thin stripe is about 8.5 N/mm.

Twisted and coiled polyethylene artificial muscle

Commercial Polyethylene (PE) fishing line with a diameter of 533 μm (ZEBCO OMNIFLEX30LBA), was used to fabricate polymer artificial muscles. The artificial muscle was prepared through twist insertion by following a previous study60. In short, the PE copolymer monofilament fishing line was twisted by a commercial reversible rotor with the bottom end fixed while the upper end attached to the rotor. The bottom end was loaded by 360 g of load, which is 16 MPa when normalized to the PE fiber cross-sectional area. The PE fiber was twisted by the manually controlled rotor counterclockwisely at room temperature. The twisting number for coiling is determined by the effective length of fishing line from the bottom end to the upper end. It is found that the slope between the twisting number and effective fiber length is 0.43 twists/mm, which is a critical value for the PE fiber from twist to coil. For example, with an effective length of 100 mm, the critical number of twisting is 43. When the value is larger than 43, it begins to coil; otherwise, it needs more twists. Prior to being coiled, a steel wire with a diameter of 0.75 mm was used as mandrel and wrapped by the twisted PE fiber in the counterclockwise direction. In order to keep the bias angle constant, the wrapping rate must be the same as the twisting rate. The coiled configuration was maintained by fixing both muscle ends once the fiber is coiled completely. It was then put into an oven and maintained for at least 95 min under 80 °C for annealing. The mandrel was removed after being cooled down to room temperature. After annealing, the PE artificial muscle was obtained with a spring index of C = 2.4. After twist insertion and annealing, the precursor fiber, i.e., fishing line, behaves like two-way shape memory polymer, i.e., expansion upon cooling, and contraction upon heating, again, under a constant tensile load. The length of the fishing line artificial muscle used was 30 mm and the stiffness of the artificial muscle was 1.497 N/mm.

Helical springs and pairing of polymeric muscle and helical spring

Seven types of helical metallic springs were purchased from McMaster-Carr. Each type of springs was combined with a polymeric actuator to assemble hybrid artificial muscles. The dimension and stiffness of each spring are summarized in Table 1. From Table 1, two types of two-way shape memory polymers, one type of twisted and coiled polymeric fiber, and seven types of helical springs were selected based on the polymers that have good reversible actuation and springs that are commercially available. The reason that we paired the polymeric muscle and the helical spring randomly was that this was a proof-of-concept study. We realized that there was a large design space for this type of fibrous actuators. Our objective was to prepare samples that were scattered in the design space so that the concept can be validated in a larger design subspace.

Table 1 Details of the assembled hybrid artificial muscles.
Full size table

It is interesting to note that, based on Harings61, if the original spring length over the mean spring diameter is greater than 2.62, the spring buckles. From Table 1, the ratio is 3.38, 2.26, 4.52, 3.31, 4.79, 4.67, and 3.48, for Muscles 1–7, respectively. It is seen that, except for Muscle 2, for the helical springs used to fabricate other Muscles, the ratios are greater than 2.62, therefore, they buckle (It is noted that for Muscles 1–3, two springs were stacked in series for each Muscle.). However, as proved in this study, when the springs were used to fabricate hybrid fibrous actuators, the fibrous actuators did not buckle under axial compression.

Fabrication of the hybrid artificial muscles

A total of seven types of hybrid artificial muscles were assembled, which are named as Muscle 1 to Muscle 7. All of them were fabricated by following a similar procedure. The details of each assembled hybrid muscle are given in Table 1. Therefore, in the following, we only use Muscle 1 as an example. In Fig. 1, the fabrication process has been schematically shown. In this study, assembling the hybrid muscle was made concurrently with testing the actuation using dynamic mechanical analysis (DMA). To assemble Muscle 1, we took two springs (HS1 in Table 1), aligned them, fully compressed them, and held them together with tweezers (for Muscles 4–7, only one spring was used, thus there was no need for this step. However, we still fully compressed the spring and used copper wire to fix the compression.). We then used a copper wire to tie them together to secure them such that the springs did not come apart. Using a scissor, we cut the cPBD cylinder into a wire with dimensions 18.58 mm as the length and 2.18 mm as the diameter and then inserted it into the compressed spring assembly. We inserted one end of the cPBD wire into the upper tension clamp of the dynamic mechanical analysis (DMA) machine and clamped it. Afterwards, we took the opposite end of the cPBD wire, stretched it to 200% of its original length, and inserted and fixed it into the lower tension clamp of the DMA machine. Once the cPBD wire is secured, we cut the copper wire securing the spring assembly and obtained the hybrid artificial muscle. In this hybrid muscle, the spring was compressed, and the cPBD actuator was tensioned. Figure S2a shows the helical spring and the polymeric artificial muscle and their assembly, and Figure S2b shows a cPCL based hybrid muscle clamped by the DMA fixture. Fabrications of other hybrid muscles followed the same procedure. The only change is that the cPBD wire is replaced either by a cPCL stripe or by a PE fishing line artificial muscle.

Testing of the hybrid artificial muscles

To evaluate the actuation of the hybrid muscles, Q800 DMA was used. Using the built-in software from the DMA machine, one can program the test setup, including the heating and cooling rate, the lowest temperature and the highest temperature, and the external load applied (tension, compression, or zero load). In this study, the heating and cooling rate were the same for all the seven types of muscles, 5 °C/min. Depending on the polymer, the temperature range changed. For cPBD based hybrid muscles (Muscles 1–3), the temperature range was from − 50 °C to 40 °C; for cPCL based hybrid muscle (Muscle 5), the temperature range was from − 10 °C to 70 °C; for twisted and coiled PE fishing line-based hybrid muscles (Muscles 5–7), the temperature range was from 50 °C to 100 °C. These temperature ranges were used based on their glass transitions temperature ranges determined previously43,44,60. In the test, positive force represents tension and negative force stands for compression. With each constant load, we set the hybrid muscle to perform several cycles of heating and cooling to trigger muscle action and to observe the possible creep. The DMA machine recorded the load or stress, displacement or strain, and temperature change with respect to time.

Results and discussions

cPBD based hybrid artificial muscles

As shown in Table 1, one cPBD wire and three types of springs are chosen to validate the proposed concept. The actuations of the three hybrid muscles (Muscles 1–3) are shown in Figs. 2, 3 and 4, respectively. One can see that each hybrid muscle is subjected to three types of loads: under tension (conventional muscle), under zero external load (free-standing muscle), and under compression (beyond free-standing muscle).

From Figs. 2, 3 and 4, all hybrid muscles exhibited similar patterns throughout all test runs at varying static force loads. As the temperature within the DMA reached − 50 °C, a maximum output in strain was observed (expansion), and when the temperature reached 40 °C, there was a minimum output in strain, leading to contraction.

Observing the pattern at the crest of the strain graph in the cooling branch, it is seen that there is a peak followed by a dip which is then followed by the ‘true maximum’ of the graph. There was such an occurrence throughout all graphs in all muscles. This behavior has been well understood in the literature on two-way shape memory polymers. At temperatures above the crystallization temperature, the expansion upon cooling is driven by rubber elasticity; at temperature below the crystallization temperature, however, the muscle behavior is driven by melting/crystallization transition62.

Fig. 2
figure 2

Muscle 1 actuation strain changes with temperature and applied static force.

Full size image
Fig. 3
figure 3

Muscle 2 actuation strain changes with temperature and applied static force.

Full size image
Fig. 4
figure 4

Muscle 3 actuation strain changes with temperature and applied static force.

Full size image

As discussed previously, the cPBD developed by Lu et al.43 is one of the two-way shape memory polymers that demonstrated muscle behavior beyond free-standing. Based on Lu et al.43, the PBD exhibited 6.2% expansion when it is subjected to 0.05 MPa compressive stress. Muscles 1–3 performed better than the bulk cPBD two-way shape memory polymer under compression in terms of the compressive stress and actuation strain. Using Muscle 3 as an example. From Fig. 4, Muscle 3 exhibits about 8.4% expansion when it is subjected to 1 N of compression load. To estimate the compressive stress in the cPBD wire, let’s covert the spring to an equivalent cPBD (equal modulus and equal stress). Assuming the cross-sectional area of the cPBD wire is A1 and the area of the equivalent cPBD converted from the spring is A2, we can find that A2 = (K2A1)/K1. Here, A1 = 0.25 × 3.14 × (1.18)2 = 1.09 mm2; Since K1 = 0.127 N/mm and K2 = 0.665 N/mm, we can find A2 = 6.81 mm2. Therefore, the total cross-sectional area in the equivalent hybrid muscle is 1.09 mm2 + 6.81 mm2 = 7.9 mm2. With 1 N compression load, the stress is estimated to be 0.13 MPa, which well exceeds the bulk cPBD which only carried a compressive stress of 0.05 MPa43.

cPCL based hybrid artificial muscles

As given in Table 1, cPCL based hybrid muscle is Muscle 4. Figure S3 shows the two-way shape memory effect of the pure cPCL. From Figure S3, it is seen that, under an external tensile load, the pure PCL exhibits a good two-way shape memory effect as the temperature cycles. As the external tensile load increases, the actuation strain also increases. However, the pure cPCL cannot exhibit two-way shape memory effect if the external tensile load is removed. However, when the cPCL stripe is combined with the metallic spring, the hybrid muscle exhibits reversible actuation, even under an external compressive load; see Fig. 5. From Fig. 5, the hybrid muscle exhibits reversible actuation without external load (free-standing), with external compression (beyond free-standing), and with external tension (normal actuation). For example, the muscle contracts by about 8.3% when it is heated up from − 10 °C to 70 °C, under a compression force of 0.3 N. Similar to the calculation in Muscle 3, we can estimate the compressive stress applied to the hybrid muscle is about 0.085 MPa. Although this muscle is not as good as Muscle 3 in terms of the applied compressive stress, which is 0.13 MPa, it is better than the bulk cPBD, which is 0.05 MPa, and with smaller actuation strain. It is seen that the actuation strain is the smallest under compression and is the largest under external tension. This again validates the concept of the hybrid muscle. It is noted that the cross-sectional shape of the cPCL is rectangular, instead of circular as did in the case of cPBD based hybrid muscles, suggesting that the geometrical shape of the polymeric wire is not a factor in determining the reversible actuation of the hybrid muscles.

Twisted and coiled PE artificial muscle-based hybrid artificial muscles

Figure S4 shows the behavior of the pure fishing line artificial muscle. It is seen that the muscle shows reversible actuation under external tensile load. For such wire, it cannot bear compression, and thus it cannot exhibit beyond free-standing actuation.

Figures 6, 7 and 8 show the actuation test results of the hybrid artificial muscles (Muscle 5, Muscle 6, and Muscle 7 in Table 1). It is seen that, for the hybrid muscles, they demonstrate reversible actuation under either an external tensile load, or zero external load, or external compressive load. Therefore, these three hybrid muscles have free-standing and beyond free-standing behaviors. It is also seen that, with the highest stiffness of the metallic spring (Fig. 7), the hybrid artificial muscle shows higher actuation strain even under higher external compressive load. It is also found that the reversible actuation strain of the hybrid artificial muscles is the highest under external tensile load, followed by zero external load, and the lowest is under external compression load, which further validated the concept in this study.

Fig. 5
figure 5

Reversible actuation of the cPCL (Muscle 4) based hybrid muscle under different stress states.

Full size image

For Muscle 6, it is seen that under 10 N of compression load, the hybrid muscle still has about 2% reversible actuation. Now if we convert the metallic spring to equivalent PE muscle, we can estimate the compressive stress applied to the hybrid muscle. Assuming the cross-sectional area of the PE muscle is A1 and the area of the equivalent PE muscle converted by the spring is A2, we can find that A2 = (K2A1)/K1. Here, A1 = 0.25 × 3.14 × (0.533)2 = 0.223 mm2. Since K1 = 1.497 N/mm and K2 = 1.300 N/mm for Muscle 6, we can find A2 = 0.194 mm2. Therefore, the total cross-sectional area in the equivalent hybrid muscle is 0.417 mm2. With 10 N compression load, the stress is estimated to be 23.98 MPa, which well exceeds the bulk cPBD which only carried a compressive stress of 0.05 MPa43.

Fig. 6
figure 6

Muscle 5 actuation strain changes with temperature and applied static force.

Full size image

The good reversible actuation behavior of Muscles 5–7 comes from the reversible actuation of the twisted and coiled PE fiber. The mechanism for the reversible actuation of such twisted and coiled fibers has been well understood. For the PE fibers with negative coefficient of thermal expansion (NCTE), the driving force is primarily due to the uncoiling of the coiled fiber driven by NCTE1,15,16. For polymeric muscles made of two-way shape memory polymers, it can be understood as the uncoiling of twisted fiber driven by the two-way shape memory effect (2W-SME). The reason is that, although with different mechanisms, 2W-SME behaves similarly to NCTE, i.e., contraction upon heating and expansion upon cooling12,13.

Fig. 7
figure 7

Muscle 6 actuation strain changes with temperature and applied static force.

Full size image
Fig. 8
figure 8

Muscle 7 actuation strain changes with temperature and applied static force.

Full size image

Modeling and analysis

From the above experimental test results, it is seen that several factors affect the actuation strain. To better understand the underlying mechanisms and parameters controlling the muscle performance, this section provides theoretical models for the hybrid muscle. To simplify the formulation, the following assumptions are made. (1) Both the metallic spring and the polymeric actuator are linear elastic materials and obey the Hooke’s law. (2) The spring will be pre-compressed to its maximum deformation, i.e., the coils are in close contact before assembling the hybrid muscle. (3) After assembling the hybrid muscle, the spring is in compression and the polymeric wire is in tension. (4) The stiffness of the spring and polymeric wire is independent of the deformation, i.e., constant. (5) Compression and compressive force are negative and tension and tensile force are positive. (6) While the stiffness of the polymeric wires depends on temperature, the stiffness of the metallic spring is independent of temperature in the range of actuation temperature considered. (7) Deformation or strain is measured with respect to the original length of the spring or the polymeric wire. The formulation consists of two stages. The first stage is to assemble the hybrid muscle, and the second stage is to actuate the hybrid muscle under different external loading conditions, including external tensile load, zero external load, and external compressive load; see a schematic in Fig. 9.

Fig. 9
figure 9

Schematic of (a) the metallic spring and polymeric actuator, (b) Stage 1: assembling the hybrid muscle, and (c) Stage 2: actuation of the hybrid muscle by cycling temperatures.

Full size image

Stage 1: modeling of the hybrid muscle assembling process

To assemble the polymeric wire or actuator and the helical metallic spring into a hybrid muscle, let’s assume the original length, prestrain immediately before tying the polymeric wire and spring together, strain during the process after hooking them together until the assembly or hybrid muscle is in equilibrium, total strain after fabrication, and the stiffness of the polymeric wire and the spring are L1, L2, ε11, ε21, ε12, ε22, Ψ1, Ψ2, K1, and K2 for the polymeric wire and spring, respectively. For those parameters with one subscript, subscript “1” means polymeric wire, and subscript “2” suggests spring. For those parameters with double subscripts, the first subscript represents the material, i.e., “1” for polymer and “2” for spring.

We require that the spring and the polymeric wire have the same length immediately before hooking them together:

$$\:{L}_{1}\left(1+{\epsilon\:}_{11}\right)={L}_{2}(1+{\epsilon\:}_{21})$$
(1)

The displacement or deformation of the polymeric wire and spring from immediately after hooking them together to equilibrium must be equal:

$$\:{L}_{1}{\epsilon\:}_{12}={L}_{2}{\epsilon\:}_{22}$$
(2)

Force equilibrium requires:

$$\:{L}_{1}{K}_{1}\left({\epsilon\:}_{11}+{\epsilon\:}_{12}\right)=-{L}_{2}{K}_{2}({\epsilon\:}_{21}+{\epsilon\:}_{22})$$
(3)

Solving the simultaneous equations, we have:

$$\:{\epsilon\:}_{12}=-\frac{{K}_{1}{\epsilon\:}_{11}\left(1+{\epsilon\:}_{21}\right)+{K}_{2}{\epsilon\:}_{21}(1+{\epsilon\:}_{11})}{({K}_{1}+{K}_{2})(1+{\epsilon\:}_{21})}$$
(4)
$$\:{\epsilon\:}_{22}=-\frac{{K}_{1}{\epsilon\:}_{11}\left(1+{\epsilon\:}_{21}\right)+{K}_{2}{\epsilon\:}_{21}(1+{\epsilon\:}_{11})}{({K}_{1}+{K}_{2})(1+{\epsilon\:}_{11})}$$
(5)

The strain after assembling the hybrid muscle is:

$$\:{\psi\:}_{1}={\epsilon\:}_{11}+{\epsilon\:}_{12}=\frac{{K}_{2\:}({\epsilon\:}_{11}-{\epsilon\:}_{21})}{({K}_{1}+{K}_{2})(1+{\epsilon\:}_{21})}$$
(6)
$$\:{\psi\:}_{2}={\epsilon\:}_{21}+{\epsilon\:}_{22}=\frac{{K}_{1}({\epsilon\:}_{21}-{\epsilon\:}_{11})}{({K}_{1}+{K}_{2})(1+{\epsilon\:}_{11})}$$
(7)

Because ε11 > 0 and − 1 < ε21 < 0, it is clear that after assembling the hybrid muscle, the polymeric wire is in tension (ψ1 > 0) and the spring is in compression (ψ2 < 0).

Stage 2: modeling of the actuation process

Now the hybrid muscle is assembled and is ready for modeling the actuation stage. We have three cases.

Free-standing hybrid muscle (with zero external load under temperature cycling)

In this case, there is no external load. The muscle actuates by simply cycling the temperatures. To solve the actuation strain of the muscle, we need to figure out why and how the muscle actuates. When temperature drops, the polymeric actuator first experiences expansion due to rubber elasticity, followed by melt/crystallization transition for cPBD and cPCL62, and due to uncoiling of the coiled PE artificial muscle1,15,16. This can be clearly seen from the actuation test of the pure cPBD43. Under a constant external load, the cPBD expands as temperature drops. This is impossible for conventional polymers because as temperature drops, the polymer stiffens and under the same external load, it must contract, intend of expansion. Therefore, we can treat the expansion as “softening” of the polymeric wire, and use equivalent stiffness to represent this softening behavior. On the other hand, we can treat the contraction as “stiffening” of the polymeric wire during heating. For convenience, our following discussion will focus on the cooling branch. Assuming a polymeric wire at the hybrid muscle assembling temperature with a length of L. With a tensile force F, the wire is stretched to (L + ΔL), thus the stiffness of the polymeric wire is K1 = F/ΔL. Now we start cooling, the polymeric wire expands by ΔD, which is positive and can be found from DMA test under the same external tensile force F within the designed temperature range. The total expansion of the polymeric wire under the same force F becomes (ΔL + ΔD). Although ΔD is induced by cooling, we treat it as an isothermal event, i.e., the temperature maintains the same, but the polymeric wire “softens”. Assuming the equivalent stiffness of the polymeric wire is Keq, we have the following relationship:

$$\:{K}_{eq}=\frac{F}{\varDelta\:L+\varDelta\:D}$$
(8)

where F is the applied tensile load when determining the stiffness of the polymeric wire, ΔL is the displacement during the stiffness testing of the polymeric wire, and ΔD is the actuation strain of the polymeric actuator during the actuation test under the force F and the designed temperature range. Obviously, ΔD depends on the actuation temperature range. It is clear that in the cooling branch (“softening”), ΔD > 0, thus Keq < K1; in the heating branch (“stiffening”), ΔD < 0, thus Keq > K1.

During temperature induced actuation process of the hybrid muscle, the polymeric actuator and the spring must actuate the same displacement, and must keep force equilibrium:

$$\:{L}_{1}{\epsilon\:}_{13}={L}_{2}{\epsilon\:}_{23}$$
(9)
$$\:{K}_{eq}{L}_{1}\left({\epsilon\:}_{11}+{\epsilon\:}_{12}+{\epsilon\:}_{13}\right)=-{K}_{2}{L}_{2}({\epsilon\:}_{21}+{\epsilon\:}_{22}+{\epsilon\:}_{23})$$
(10)

where ε13 and ε23 are the actuation strain of the polymeric wire and spring, respectively.

Using Eqs. (1), (2), (4), (5), (9), and (10), the actuation strain can be solved as:

$$\:{\epsilon\:}_{13}=\frac{{K}_{2}({K}_{1}-{K}_{eq})({\epsilon\:}_{11}-{\epsilon\:}_{21})}{({K}_{eq}+{K}_{2})({K}_{1}+{K}_{2})(1+{\epsilon\:}_{21})}$$
(11)
$$\:{\epsilon\:}_{23}=\frac{{K}_{2}({K}_{1}-{K}_{eq})({\epsilon\:}_{11}-{\epsilon\:}_{21})}{({K}_{eq}+{K}_{2})({K}_{1}+{K}_{2})(1+{\epsilon\:}_{11})}$$
(12)

Because Keq< K1, ε11 > 0, and − 1 < ε21 < 0, it is obvious that both ε13 and ε23 are positive, i.e., they expand when temperature drops. From Eq. (8), it is seen that the higher the actuation strain ΔD, the lower the Keq is. From Eqs. (11) and (12), it is seen that, when other parameters maintain the same, the lower the Keq, the higher the actuation of the hybrid muscle. However, the relationship is nonlinear. More analysis will be done in “Model analysis”.

The purpose for artificial muscle is to maximize ε13 and ε23. It is seen from Eqs. (11) and (12) that, it is a multi-variable function. It depends on the stiffness of the spring and polymeric wire at muscle assembling temperature (usually room temperature), the pre-strain before hooking them together, and the equivalent stiffness of the “softened” or “stiffened” polymeric wire, which depends on the applied tensile load and tensile actuation capability of the pure polymeric wire, as demonstrated in Eq. (8).

Hybrid muscle subjected to a constant external tensile load (normal actuation)

The effect of the tensile load is to create additional tensile strain in the polymeric wire and reduce the compressive prestrain in the spring. Therefore, we only need to find the additional strain due to the external tensile load to the polymeric wire and to the spring. Once this is done, we can still use Eqs. (11) and (12) to calculate the actuation strain when temperature cycles.

Assuming the external load FT is applied at temperature T, and the stiffness of the polymeric actuator is thus K1T (If we apply the load at the same temperature as assembling the hybrid muscle, then K1T = K1), we can calculate the additional strain in the polymeric actuator and spring as ε14 and ε24 based on force equilibrium and equal displacement as follows:

$$\:{F}_{T}={K}_{1T}{L}_{1}{\epsilon\:}_{14}+{K}_{2}{L}_{2}{\epsilon\:}_{24}$$
(13)
$$\:{L}_{1}{\epsilon\:}_{14}={L}_{2}{\epsilon\:}_{24}$$
(14)

Solving the simultaneous Eqs. (13) and (14), we have:

$$\:{\epsilon\:}_{14}=\frac{{F}_{T}}{({K}_{1T}+{K}_{2}){L}_{1}}$$
(15)
$$\:{\epsilon\:}_{24}=\frac{{F}_{T}}{({K}_{1T}+{K}_{2}){L}_{2}}$$
(16)

In Eqs. (11) and (12), we need to replace strain during assembling the hybrid muscle ε11 by (ε11 + ε14) and ε21 by (ε21 + ε24) in order to calculate the actuation upon cooling. Because ε14 and ε24 are positive, they tend to increase the muscle actuation. This is understandable because an external tensile load further stretches the polymeric wire and thus triggers higher actuation strain.

Hybrid muscle subjected to constant external compressive load (beyond free-standing)

Assuming the external compressive load FC is applied at temperature T, which is negative, and the stiffness of the polymeric actuator is K1c (If we apply the load at the same temperature as assembling the hybrid muscle, then K1c = K1), we can find the additional prestrain in the polymeric wire (ε15) and spring (ε25) using similar procedure, and obtain:

$$\:{\epsilon\:}_{15}=\frac{{F}_{C}}{({K}_{1c}+{K}_{2}){L}_{1}}$$
(17)
$$\:{\epsilon\:}_{25}=\frac{{F}_{C}}{({K}_{1c}+{K}_{2}){L}_{2}}$$
(18)

Again, in Eqs. (11) and (12), we need to replace ε11 by (ε11 + ε15) and ε21 by (ε21 + ε25) in order to calculate the actuation upon cooling. Because ε15 and ε25 are negative, they tend to decrease the muscle actuation. This again is understandable because an external compressive load reduces the pre-stretch in the polymeric wire, decreasing its actuation strain.

Model analysis

It is seen from Eqs. (11) and (12) that there are several parameters that affect the actuation of the hybrid muscles, mainly factors related to the polymeric wire (K1 and Keq), the spring (K2), and the strain during assembling the hybrid muscle (ε11 and ε21). Of course, these are for the condition without external load. With external load, their effect is on ε11 and ε21. With external tensile load, ε11 increases and ε12 decreases; with external compression load ε11 decreases and ε21 increases. Therefore, analysis of the Eqs. (11) and (12) also applies to the cases with external tensile load and external compressive load.

First, we look at the effect of each individual parameter on the actuation. For simplicity, we consider ε13 in Eq. (11) as an example. The results will be similar for ε23 in Eq. (12). To do this, we find the first derivative of ε13 with respect to each individual parameter, while keeping other parameters constant. The results are as follows:

$$\:\frac{{d\epsilon\:}_{13}}{{dK}_{1}}=\frac{{K}_{2}({\epsilon\:}_{11}-{\epsilon\:}_{21})}{(1+{\epsilon\:}_{21}){({K}_{1}+{K}_{2})}^{2}}$$
(19)
$$\:\frac{{d\epsilon\:}_{13}}{{dK}_{2}}=\frac{{(K}_{1}-{K}_{eq}\left)\right({\epsilon\:}_{11}-{\epsilon\:}_{21}\left)\right({K}_{1}{K}_{eq}-{{K}_{2}}^{2})}{(1+{\epsilon\:}_{21}){\left[\left({K}_{1}+{K}_{2}\right)\left({K}_{eq}+{K}_{2}\right)\right]}^{2}}$$
(20)
$$\:\frac{{d\epsilon\:}_{13}}{{dK}_{eq}}=\frac{{-K}_{2}({\epsilon\:}_{11}-{\epsilon\:}_{21})}{(1+{\epsilon\:}_{21}){({K}_{eq}+{K}_{2})}^{2}}$$
(21)
$$\:\frac{{d\epsilon\:}_{13}}{{d\epsilon\:}_{11}}=\frac{{K}_{2}({K}_{1}-{K}_{eq})}{({K}_{eq}+{K}_{2})({K}_{1}+{K}_{2})(1+{\epsilon\:}_{21})}$$
(22)
$$\:\frac{{d\epsilon\:}_{13}}{{d\epsilon\:}_{21}}=\frac{-{K}_{2}({K}_{1}-{K}_{eq})(1+{\epsilon\:}_{11})}{({K}_{eq}+{K}_{2})({K}_{1}+{K}_{2})({1+{\epsilon\:}_{21})}^{2}}$$
(23)

Because K1 > 0, K2 > 0, Keq>0, ε11 > 0, and − 1 < ε21 < 0, it is seen from Eq. (19) that the first derivative is always positive, thus the actuation strain of the hybrid muscle ε13 increases as K1 increases. From Eq. (21), the first derivative is always negative, thus the actuation strain of the hybrid muscle increases as Keq decreases. In other words, when the polymeric wire has larger actuation strain, the hybrid muscle also has larger actuation strain, which makes sense. From Eq. (22), in the cooling branch, K1 > Keq, thus the first derivative is positive and the actuation strain of the hybrid muscle increases as the ε11 increases; in the heating branch, K1 < Keq, thus the first derivative is negative, suggesting that the actuation strain of the hybrid muscle decreases as ε11 increases. From Eq. (23), the effect of ε21 on the actuation strain of the hybrid muscle in the cooling and heating branches is opposite to the effect of ε11 on the actuation strain of the hybrid muscle due to the negative sign in the numerator. The effect of K2 on the actuation strain is more complex in Eq. (20). To visualize the effect, we draw Eq. (20) as shown in Fig. 10. From Fig. 10, in the range of the parameters considered (K1/K2 = 0.1 ~ 10; Keq/K1 = 0.1 ~ 10), the first derivative of the actuation strain ε13 of the hybrid muscle with respect to K2 is negative, suggesting that using stiffer spring leads to smaller actuation strain. This conclusion is supported by the test results. From Figs. 6, 7 and 8, it is seen that Muscle 6 (Fig. 7) has the lowest actuation strain because the spring used in Muscle 6 has the highest stiffness.

Fig. 10
figure 10

Effect of the ratio Keq/K1 and K1/K2 on the normalized first derivative. Here A = [K1(1 + ε21)]/[(ε11-ε21)].

Full size image

In the above analysis, we treat all other parameters constant and only consider one parameter as a variable in finding the first derivative. While this is helpfully in understanding the effect of each parameter on the actuation strain of the hybrid muscle, it is better to consider the case that more than one parameter is changing.

Figure 11 shows the change of the normalized actuation strain Bε13 of the hybrid muscle with the change of ε11 and the ratio ε21/ε11. We set the range of the pre-strain ε11 = 50–200%, or 1/ε11 = 0.5 ~ 2; the ratio ε21/ε11 = − 0.1 ~ − 0.4, or ε21 = − 5% ~ − 80%. It is seen that the effect of the strain during assembling the hybrid muscle on the actuation strain of the hybrid muscle has a fast-increasing region, suggesting that the pre-strain of both the polymeric wire and the spring has a significant impact on the actuation strain of the hybrid muscle. The existence of the peak suggests that the system can be optimized in terms of the pre-strain during assembling the hybrid muscle. It is interesting to note that the graph represents both cooling and heating. During cooling, Keq < K1, thus B > 0. Therefore ε13 is actually positive in the graph, suggesting expansion. On the other hand, during heating, Keq > K1, thus B < 0. Therefore, ε13 is actually negative in the graph, suggesting contraction.

Fig. 11
figure 11

Normalized actuation strain changes with strain ε11 and strain ratio ε21/ε11. Here B = [(Keq+K2)(K1 + K2)]/[K2(K1-Keq)].

Full size image

Figure 12 shows the change of the normalized actuation strain Cε13 with the change of the ratios K2/K1 and Keq/K1. We set the range as K2/K1 = 0.1 ~ 10; Keq/K1 = 0.1 ~ 10. Because ε11 > 0, − 1 < ε21 < 0, parameter C in the graph is positive. It is seen that, again the effect of the stiffness of the polymeric wire and the spring on the actuation strain of the hybrid muscle is very complex. However, it shows that the normalized actuation strain has a certain extremum, which allows potential optimization of the hybrid muscle. It is also seen that when Keq/K1 < 1, the Cε13 value is positive, suggesting expansion; when Keq/K1 > 1, the Cε13 value is negative, suggesting contraction. It is noted that here we have taken ε11 and ε21 as constants. Otherwise, the effect will be much more complex.

Fig. 12
figure 12

Normalized actuation strain changes with the ratio of K2/K1 and Keq/K1. Here C = (1 + ε21)/(ε11-ε21).

Full size image

Conclusions

In this study, we proposed a new concept of fabricating fibrous artificial muscle which can reversibly actuate under external compression load. While some polymers can reversibly actuate without external tensile load or even under small compressive stress, they are in films or bulk forms. They cannot actuate in the fibrous form under external compression due to buckling and crushing of slender fibrous actuators. In this study, we fabricated seven types of hybrid muscles based on three polymers with reversible actuation and seven helical metallic springs with different lengths, diameters, and stiffnesses. Although the combination of the springs and polymeric wires are random in order to explore a larger design space, all the hybrid muscles exhibit reversible actuations under different external loading conditions: external tension (normal actuation), zero external load (free-standing actuation), and external compression (beyond free-standing actuation). We also developed a structural mechanics model to better understand the actuation behavior of the hybrid muscle. It is seen that at least five parameters affect the actuation of the hybrid muscles: stiffness of the polymeric wire and the spring, equivalent stiffness of the polymeric wire (which is related to its own actuation under external tensile load), as well as the pre-strain applied to the polymeric wire and the spring during assembling the hybrid muscles. The model analysis shows that each individual parameter has a different effect on the actuation of the hybrid muscle (positive or negative). We also considered the cases when more than one parameter is changing. The results show that the design can be optimized because there is a certain extremum point. We expect that this study will open new opportunities for applications of fibrous artificial muscles as actuators in engineering structures and devices under different loading conditions.

It is noted that this study is limited in that we only used existing polymers with good reversible actuations and commercially available springs to serve as a proof-of-concept study. Based on the theoretical model predictions, there is a large design space for this type of hybrid fibrous actuators. It is likely that hybrid fibrous actuators with better performance exist. It is expected that optimized polymeric muscles and helical springs will be fabricated based on the model predictions, and better fibrous actuators will be available. This will be a topic for future studies. It is also noted that several assumptions were made in the theoretical modeling. While the assumptions led to closed-form solutions, it may have overlooked the nonlinear behavior of polymers. Again, this will be an interesting topic for future studies.