Introduction

The global energy expansion strategy increasingly focuses on renewable energy sources (RES) to address climate change and achieve sustainable energy objectives1. The swift reduction in renewable energy costs, enhanced energy efficiency, and widespread electrification position RES as a better substitute to fossil fuel-based systems2. Generating electrical energy from RES in islanded or remote areas not only cuts operational expenses but also boosts social and economic development in these regions3. Islanded power systems hold considerable promise for lowering grid operation costs and enabling electrification in remote areas3. Integrating RES with a sustainable storage system offers a strong solution, ensuring reliable power generation and mitigating the intermittency of RES. Effective planning of optimal and reliable islanded power systems necessitates appropriate component sizing, economic assessment, and reliability evaluation4.

Among various RES, solar photovoltaic power stations (SPPS) and wind-driven power stations (WDPS) are the most commonly used technologies due to the widespread availability of solar and wind resources and their efficient systems5. This makes them ideal for islanded power generation. In terms of storage technologies, battery storage is the most prevalent. However, challenges such as self-discharge rates, limited lifespans, and long-term environmental impacts make battery storage systems (BSSs) less suitable for large-scale applications6. Recently, Hydrogen storage systems (HSS) have emerged as a highly attractive alternative to battery storage for grid-level applications due to their higher energy density, scalability, and long storage life. While advanced batteries, such as lithium-ion, are well-suited for short-term energy storage with high round-trip efficiency, their scalability and storage duration are limited compared to HSS. The trade-offs include lower round-trip efficiency for HSS, as energy losses occur during electrolysis, storage, and reconversion. However, hydrogen’s ability to provide long-term storage and address seasonal energy balancing needs makes it a superior choice for large-scale and grid-level storage. Additionally, HSS offers the potential to generate green hydrogen, which can be used across multiple sectors, enhancing its overall utility and eco-technical benefits6. Integrating HSS with SPPS and WDPS offers a promising solution for islanded grid-scale electrification7. Consequently, there has been growing interest in the combined analysis of HSS with distributed RESs, as evidenced by the recent proliferation of articles exploring this topic.

Le et al.8 analyzed the optimal dimension of a BSS, HSS and RES based system using the MPMFA optimization technique, considering component degradation. In9, the optimal planning of an HSS-RES based system, including the mobility system, was determined. Aslani et al.10 presented a model using MCS and optimization techniques for the optimal design of a SPPS, WDPS, HSS and EV charging system-based microgrid, focusing on reliability constraints. Tzamalis et al.11 analyzed the optimal sizing of an SPPS-HSS system based on eco-techno parameters and provided a comparative analysis between an SPPS-HSS and an SPPS-diesel generator-based system. Babatunde et al.12 studied the adaptability and feasibility of HSS for various region-specific energy systems across sub-Saharan Africa using the HOMER software. Moghaddam et al.13 presented an optimal sizing framework considering reliability parameters for an SPPS-WDPS-HSS islanded system using the flower pollination algorithm. Vahid et al.14 determined and analyzed the optimal sizing of different SPPS-WDPS-HSS-BSS configurations using the salp swarm optimization technique for commercial applications. Liu et al.15 integrated and analyzed different combinations of HSS/BSS/thermal storage with an SPPS-WDPS system and performed an eco-technical analysis for a reliability system. Sharafi et al.16 determined the per-unit LCOE of hydrogen production based on optimal component configuration in various locations of installed RES capacity. Qolipour et al.17 presented a case study on the eco-technical feasibility of an SPPS-WDPS-HSS power system using HOMER for the southwest region of Iran. Cappitters et al.18 analyzed the stochastic performance of an optimized SPPS-WDPS-HSS-BSS system. He et al.19 optimized the capacity of different RES and storage combinations based on eco-technical considerations. Zhang et al.20 performed a comparative analysis of RES-grid combination with the RES-storage system using a multi-objective optimization algorithm. Mahmoudi et al.21 conducted an eco-technical analysis of an HSS-RES-nuclear configuration based on optimal sizing. Li et al.22 presented a two-level framework based on a stochastic approach for the optimal configuration of an SPPS-WDPS-Electric heater system using an evolutionary algorithm. A summarized overview of all discussed literature is further presented in Table 1 as follows:

A review of the existing literature reveals that numerous studies have focused on optimal sizing or configuration planning while considering various eco-technical parameters. Additionally, most of these studies employ different optimization methods to determine the optimal system configuration. However, only a limited number of studies have incorporated uncertainty modeling of renewable energy sources into their analyses. Furthermore, even fewer have conducted a comprehensive sensitivity analysis. Among the existing studies that incorporate sensitivity analysis, none have provided a comprehensive examination of the per-unit impact of individual system components. In particular, there has been a notable lack of focus on the influence of hydrogen storage system (HSS) tank size on the eco-technical performance of the overall system. This oversight leaves a critical gap in understanding how variations in HSS tank size can affect system efficiency, cost-effectiveness, and environmental impact. Addressing this deficiency, the current research offers a detailed analysis of these interactions, thereby contributing novel insights to understanding of HSS based system. This gap in the literature underscores the unique aspects addressed in the current research.

This paper presents a single framework for optimal configuration sizing including optimization technique, uncertainty modelling, and sensitivity analysis for reliable and cost-effective configuration for SPPS-WDPS-HSS based power system. The major contribution of this work is as follows:

  • To determine the optimum sizing variation of the same optimization algorithm, the analysis of optimal sizing is performed based on two different and most adoptive economic objective functions.

  • This paper presents the sensitivity analysis along with the optimal sizing of SPPS-WDPS-HSS configuration into the Montle Carlo Simulation (MCS) framework for reliability evaluation under uncertainty.

  • In this paper, 36 different configurations of SPPS-WDPS-HSS with different component capacities are analyzed and compared under the sensitivity study.

  • To determine the percentage impact of reliability and economic variation of different components three different scenario of each component unit variation is performed in this work.

This remaining paper is planned as follows: In “Methodology and formulation” Section detailed problem devising along with methodology and component description is presented. “System modelling” Section elaborates case study wherein analysis of component sizing and sensitivity analyses are performed for SPPS-WDPS-HSS power system. In “Result and discussion” Section, the result analysis of optimal sizing (both cases), and sensitivity analysis in different scenarios of per unit capacity variation of all three components are presented and discussed. In “Conclusion” section, the conclusion of the analysis is summarized.

Table 1 A summarized overview of all discussed literature.
Full size table

Methodology and formulation

This section delivers exhaustive description of mythology and framework formulation. The key objective of this work is to determine the impact of changes in the objective function and the per-unit eco-technical variation of each component of the SPPS-WDPS-HSS configuration. Accordingly, this paper aims to determine the optimum.

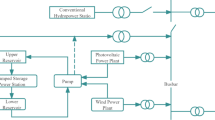
configuration sizing of SPPS-WDPS-HSS using two different objective functions: Case 1 - Minimization of LCOE (levelized cost of electricity) and Case 2 - Minimization of TLCC (Total life cycle cost), based on reliability and capacity constraints. The proposed framework for this work consists of three main stages: optimal sizing assessment, reliability assessment, and sensitivity analysis, as illustrated in Fig. 1 and discussed in the following subsections.

Fig. 1
figure 1

Schematic of planning framework.

Full size image

Optimal sizing assessment

Optimal component sizing of SPPS-WDPS-HSS is determined using Butterfly Particle Swarm Optimization (B-PSO) optimization algorithm. B-PSO, an enhanced version of the classic PSO algorithm, is a metaheuristic approach that offers improved performance. A detailed description of B-PSO can be found in the authors’ previous work23.

Objective function

As discussed in “Methodology and formulation” Section, two different case of different objective function are analysed in this paper as follows:

• case 1

$$\:Min\:of\:\text{T}\text{L}\text{C}\text{C}$$
(1)

wherein, TLCC exhibited the sum of all expenses sustained over the venture life24. TLCC calculation can be expressed as in Eq. (2):

$$\:TLCC\:=\:\:\left(\sum\:_{x\:=0}^{T}\frac{{k}_{x}}{{\left(1+r\right)}^{x}}\right)-P\text{r}\text{e}\text{s}\text{e}\text{n}\text{t}\:\text{w}\text{o}\text{r}\text{t}\text{h}\:\text{o}\text{f}\:\text{r}\text{e}\text{t}\text{r}\text{i}\text{e}\text{v}\text{e}\:\text{v}\text{a}\text{l}\text{v}\text{e}\:$$
(2)

where, kx is the sum of all different costs of system incurred in xth year and “r” denotes the discount rate.

• case 2

$$\:Min\:of\:\text{L}\text{C}\text{O}\text{E}$$
(3)

wherein, LCOE exhibited the cost value to every unit of energy system during the entire project lifespan equals the TLCC when discounted back to base year24. LCOE calculation can be expressed as in Eq. (4):

$$\:\text{LCOE\:}\text{=\:}\frac{\text{TLCC}}{\sum\:_{\text{m=1}}^{\text{T}}\frac{{O}_{x}}{{\left(\text{1+r}\right)}^{\text{x}}}}$$
(4)

where, “Ox” denotes the output energy of configuration in xth year in kWh.

Optimization constraint

The optimum sizing algorithm (B-PSO) is subject to the following constraints

  • Reliability constraints – In this paper, system reliability is constrained by the two most widely used reliability indices, Loss of load expectancy (LOLE) and Energy not supplied (ENS), evaluated through MCS, as follows:

$$\:{LOLE\:\le\:LOLE}_{max}{\prime\:}$$
(5)
$$\:{ENS\:\le\:\:ENS}_{max}$$
(6)

wherein LOLE represents the total number of hours when generation capacity is unable to meet the demand25 and ENS represents the measure of energy that is not supplied during the study period (kWh)25.

  • Component unit constraints – By this constraint, minimum and maximum number limit or range of number of component (SPPS/WDPS/HSS) are limited as follows:

$$N_{\min }^{SPPS}\; \le \;N_{}^{SPPS}\; \le \;N_{\max }^{SPPS}$$
(7)
$$N_{\min }^{WTPS}\; \le \;N_{}^{WDPS}\; \le \;N_{\max }^{WDPS}$$
(8)
$$N_{\min }^{HSS}\; \le \;N_{}^{HSS}\; \le \;N_{\max }^{HSS}$$
(9)

where \(N_{\min}^{SPPS}\)and\(N_{\max}^{SPPS}\) represents number minimum and maximum number of units of SPPS, \(N_{\min}^{WDPS}\)and\(N_{\max}^{WDPS}\)minimum and maximum unit of WDPS and \(N_{\min}^{HSS}\), \(N_{\max}^{HSS}\)presents minimum and maximum units of HSS.

  • Storage constraints – In this paper HSS is used as a storage element. The SOH in the HSS’s tank and maximum and minimum per hour hydrogen supply rate as follows:

$$SOH_{\min }^{HSS}\; \le \;SOH_{}^{HSS}\; \le \;SOH_{\max }^{HSS}$$
(10)

where \(SOH_{\min }^{HSS}\)and \(SOH_{\max }^{HSS}\)represents minimum and maximum limit of SOH in hydrogen tank.

Reliability and economic assessment

For reliability assessment and uncertainty modelling, this work employs MCS framework. The schematic of MCS framework is illustrated in Fig. 2. In this framework the study period is discretized into number of time segments after that the study of power availability of storage and/or generation unit and load availability are analyzed for each time segment as follows:

Generation modelling

The generation modelling involves the sequential power generation modeled data of employed generating unit26 and hardware availability modelled27 data of similar particular unit. The modelling of power generation utilized the modelling techniques and historical data. Wherein hardware availability model employs FOR (force outage rate)27. In this paper beta probability density function (PDF)28 is used for output power modelling of SPPS unit and Weibull PDF28 is used for WDPS output power modelling.

Load modelling

Similar to generation model, sequential data of load is required in MCS framework. In this paper, the constant load is assumed for a particular time slot with step changes occurring between consecutive time slots.

Based on the output from the generating unit and the load, the power flow of the storage unit (HSS) is assessed. When the load exceeds the generation output, the HSS enters emptying mode to supply the load. Conversely, if the load is less than the generation output, the HSS enters filling mode during that time slot. The emptying and filling operations of the HSS are constrained by the SOH of HSS from the previous time slot, which is successively updated in each subsequent time slot. This chronology is repeated across all time slots and planning years. A more detailed discussion of the MCS framework can be found in the authors’ previous work26.

Fig. 2
figure 2

MCS framework26,29.

Full size image

Sensitivity analysis

Following the determination of optimal component sizes in both cases, sensitivity analysis is conducted by changing the component sizes around the attained optimal values. This analysis evaluates the specific impacts of each component unit on system economy and reliability. Therefore, this study includes sensitivity analysis in three scenarios involving unit addition/removal of SPPS, WDPS, and HSS as follows:

  • Scenario I – Per unit increment and decrement of SPPS.

  • Scenario II – Per unit increment and decrement of WDPS.

  • Scenario III – Per unit increment and decrement of HSS.

The analysis of each scenario aims to deliver an understanding of sensitivity of the system’s reliability and economic metrics to changes in the respective component’s capacity. thereby informing optimal sizing strategies for integrating renewable energy.

System modelling

The yielding of electricity from solar and wind energy is greatly affected by weather-related elements like velocity of wind and illumination level of solar. Therefore, in this study, velocity of wind and illumination level of solar are modeled using Weibull and Beta distributions, respectively28. The HSS comprises of three parts viz. electrolyser-hydrogen tank-fuel cell. The modelling of the HSS involves evaluating the SOH characteristics and lifespan by analyzing the excess and shortage of power from RES.

Modelling of solar irradiance

For the modelling of solar power, probabilistic solar irradiance is considered as beta function28. The expression of beta function for taken time “n” is as follows –

$$\:F\left(S\right)=\:\left\{\begin{array}{c}\frac{\beth\:\left({\alpha\:}^{n}+{\beta\:}^{n}\right)}{\beth\:\left({\alpha\:}^{n}\right)\beth\:\left({\beta\:}^{n}\right)}{S}^{\left({\alpha\:}^{n}-1\right)}{S}^{\left({\beta\:}^{n}-1\right)}\:\:\:\:\:0\le\:S\le\:1,\:\:\:\alpha\:,\beta\:\ge\:0\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:Otherwise\end{array}\right.$$
(11)

where, \(\:\alpha\:\) and \(\:\beta\:\) signifies Beta-Distribution-Function for “n” time-segment; and \(\:\beth\:,\:s\) signifies gamma function and solar irradiance intensity respectively.

After irradiance modelling and based on I-V traits of PV30, the yield power is calculated using Eq. (12)

$${O_{PV}}(S)\;=N.v.i.\left[ {\frac{{{v_{mpp}}{i_{mpp}}}}{{{v_{oc}}{i_{sc}}}}} \right]$$
(12)

The correlation between voltage (v), current (i) and cell-temperature (\({t_{PV}}\)) is articulated as follows:

$${t_{PV}}={t_a}+S\,\left[ {\frac{{N - 20}}{{0.8}}} \right]$$
(13)
$$v\; = \;{v_{oc}} - {k_v}\cdot{t_{PV}}$$
(14)
$$i = \;S\,[{i_{sc}} - {k_i}({t_{PV}} - 25)]$$
(15)

where,\({v_{oc}}\)is open-circuit voltage, \({k_v}\) is voltage coefficient, vmpp is voltage at max. powerpoint \({i_{sc}}\) is short-circuit current, \({k_i}\) is current coefficient and impp is current at max. powerpoint.

Modelling of wind generator

The power generation throughout the wind turbine depends upon the design restriction and wind speed as well. In this paper Weibull distribution28 is used for the study of wind speed. The wind generator output power can be expressed as given in Eq. (16).

$$\:{O}_{w}\left(s\right)=\:\left\{\begin{array}{c}x+y{s}^{n}\:\:{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:s}_{in\_cut}\:\le\:\:s\:\le\:\:{s}_{rated}\\\:{p}_{rated}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{s}_{rated}\:\le\:\:s\:\le\:\:{s}_{off\_cut}\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:s\:\ge\:\:{s}_{off\_cut}\:\:,\:\:\:0\:\le\:\:s\:\le\:\:{s}_{in\_cut}\:\end{array}\right.\:\:\:\:\:\:$$
(16)

where, \(\:{p}_{rated}\), \(\:{s}_{rated},\:\:{s}_{in\_dut},\:{\:}_{off\_cut}\) and m denotes wind generator output power in kW, rated speed, cut in speed, cut off speed and order of power curve respectively.

Modelling of HSS

The HSS accumulates excess power generated by renewable sources like SPPS and WDPS by converting it into hydrogen for future use. This system comprises three key components viz. electrolyser, hydrogen storage tank, and fuel cell, each of which is detailed below:

Electrolyser

The electrolyser functions by converting water into hydrogen through electrolysis31, operating specifically when RES generates surplus power beyond current load demand. This excess power is channeled to the electrolyser to produce hydrogen. The maximum rate at which hydrogen flows through the electrolyser is determined from Ref32. The hydrogen generated from surplus power can be computed using Eq. (17)32.

$${H_{el}}\, = \frac{{{P_{excess}}*{\delta _{{H_2}}}}}{{HH{V_{{H_2}}}*{\eta _{el}}}}$$
(17)

where \(HH{V_{{H_2}}}\)is Hydrogen heat value (kWh/m3) that is 3.4 kWh/m3 and \({\delta _{{H_2}}}\)is density of hydrogen that is around 0.09 kg/m3. The \({\eta _{el}}\) presents efficiency of electrolyser that is considered as 90%32.

Hydrogen tank

There have various hydrogen storage technologies are reported in different literature such as physical (liquid and compressed gas) and material-based methods7. In this paper, A highly cost-effective and advanced method for physically storing hydrogen is employed, known as compressed gas technology at 350 bars. The energy needed for compressing hydrogen at this pressure (1.05 kWh/kg) is sourced from Ref33.

Fuel cell

The fuel cell is among the most alluring and appealing solutions for electric power generation from hydrogen. The functioning of the fuel cell operates in contrast to the electrolyser. In this paper, efficiency and the electricity output factor (per unit) are integrated into the program to assess hydrogen consumption by the fuel cell and determine the tank’s SOH. The maximum allowable hydrogen flow rate through the fuel cell is referenced from Ref32. The electric power generated (Pfc) by the fuel cell per kilogram of hydrogen can be derived using Eq. (18).

$${P_{fc}}\, = \left[ {\frac{{H{V_{{H_2}}}}}{{{\delta _{{H_2}}}}}} \right]*{\eta _{fc}}*Hydrogen\;\;(kg.)$$
(18)

where, \({\eta _{fc}}\)is the fuel cell efficiency and in this study, it is considered as 50%32.

Case study

The current study examines two distinct cases (as discussed in “Objective function” Section) to optimize the sizing of SPPS-WDPS-HSS based power system in a hypothetical island situated in Jaisalmer, Rajasthan. With average wind speeds ranging from 3 to 5 m/s and solar irradiance levels between 5 and 6 kWh/m²/day, Jaisalmer is an ideal location for renewable energy projects34,35. Data on solar irradiance and wind speeds for this location were gathered from36] and [37, respectively. As discussed in “System modelling” Section, the variability of solar irradiance in SPPS and wind speed in WDPS are modeled using Beta and Weibull PDFs respectively. The load data has been taken from38 and peak load is assumed to be 100 kW. The study period is taken as one year. In this analysis, the year is broken down into twelve months, and the data from the first day of each month is used to project the trends for that entire month. The annual variations in solar irradiance, wind speed, and load are illustrated across 8,760 time periods (365 days × 24 h).

The per unit capacity of SPPS is 15 kW, WDPS is 10 kW and HSS is 10 kg. is assumed. The electrolyser’s capacity is determined by the maximum generation limit of the specific component combination, while the fuel cell rating is fixed at 100 kW to match the maximum load demand.

The assessment of economic criteria, including their respective measurements and sources, is detailed in Table 2. The reliability criteria viz. LOLE and ENS are derived through life cycle analysis, accounting for uncertainties associated with RES and the availability of backup technologies using MCS as discussed in “Reliability and economic assessment” Section. Optimal component sizing in each case is determined based on identical constraint limits using BF-PSO, as specified in Table 3. The optimal sizing of the system is constrained by a maximum allowable LOLE of 0.2%, ensuring a highly reliable energy supply. Additionally, the system is designed to achieve at least 95% reliability, meaning no more than 5% of ENS.

In this work, 500 iterations were employed for the MCS, and 100 iterations were used for the BF-PSO technique. The BFPSO particle size was set to 25, with constant values referenced from23. The constraint limits for reliability and SOH are referenced from39] and [33, respectively.

Table 2 Economic description of components.
Full size table
Table 3 Constraints for component optimal sizing.
Full size table

Result and discussion

As outlined in “Methodology and formulation” Section, this study explores the optimal sizing of the SPPS-WDPS-HSS system across two distinct cases, each governed by a different objective function. In Case 1, the sizing is optimized by minimizing the TLCC, while in Case 2, the focus shifts to minimizing the LCOE within a BFPSO-MCS framework, taking into account specific reliability and capacity constraints. Table 4 exhibited the results of the optimal component sizing for both cases including the percentage contribution of all components in the complete power supply. The reliability indices corresponding to the optimal component sizes of both cases are accessible in Table 5.

Table 4 Optimal sizing and percentage sharing in all cases.
Full size table
Table 5 Reliability indices value in both case.
Full size table

As indicated in Table 4, Case 1 involves optimal sizing of 360 kW for SPPS, 80 kW for WDPS, and a 120 kg HSS Tank, whereas Case 2 optimally sizes to 300 kW for SPPS, 100 kW for WDPS, and also uses a 120 kg HSS Tank. The analysis of both cases, detailed in Tables 4 and 5, confirms that the obtained sizing meets the specified reliability indices limit. Table 4 additionally displays the percentage contribution of SPPS, WDPS, and HSS to total power supply. The analysis of percentage power supply in both cases reveals that the HSS contributes more than 20% in both scenarios, indicating a positive impact on system reliability. During periods without sunlight, WDPS and HSS step in to supply power, with HSS effectively smoothing out wind intermittency. To provide deeper insights into the role of each component in power distribution, Fig. 3 (a-b) and Fig. 4 (a-b) present power supply graphs and percentage power sharing bar graphs for both cases, respectively.

Fig. 3
figure 3

(a) Contribution of SPPS, WDPS and HSS in power supply to load (Case 1 (min TLCC)). (b) Percentage share of SPPS, WDPS and HSS in power supply (Case 1 (min TLCC)).

Full size image
Fig. 4
figure 4

(a) Contribution of SPPS, WDPS and HSS in power supply to load (Case 2 (min LCOE)). (b) Percentage share of SPPS, WDPS and HSS in power supply (Case 2 (min LCOE)).

Full size image

In this study, sensitivity analysis is performed to investigate how changes in component sizes affect system reliability in the context of optimal system planning across two distinct cases. The main goal is to assess how adjustments in the sizes of the system components—SPPS, WDPS, and HSS—affect overall system reliability. The analysis includes systematically varying these component sizes around their optimal configurations and assessing their impact on key reliability metrics such as ENS and LOLE. All three scenarios of sensitivity analysis conduction are discussed in “Sensitivity analysis” Section. The obtained result of sensitivity analysis corresponding to SPPS, WDPS and HSS unit addition/removal of Case 1 and Case 2 are presented in Figs. 5, 6, 7 and 8. In Figs. 5, 6, 7 and 8, the negative values show the removal of a single unit and positive values show the addition of a single unit of component (SPPS/WDPS/HSS) unit. In this work the per unit value of SPPS is 15 kW, WDPS is 10 kW and HSS is 10 kg. is assumed.

Fig. 5
figure 5

(a) ENS of both cases (based on SPPS variation). (b) ENS of both cases (based on WDPS variation). (c) ENS of both cases (based on HSS variation).

Full size image
Fig. 6
figure 6

(a) LOLE of both cases (based on SPPS variation). (b) LOLE of both cases (based on WDPS variation). (c) LOLE of both cases (based on HSS variation).

Full size image
Fig. 7
figure 7

(a) LCOE of both cases (based on SPPS variation). (b) LCOE of both cases (based on WDPS variation). (c) LCOE of both cases (based on WDPS variation).

Full size image
Fig. 8
figure 8

(a) TLCC of both cases (based on SPPS variation). (b) TLCC of both cases (based on WDPS variation). (c) TLCC of both cases (based on HSS variation).

Full size image

The sensitivity analysis conducted on both cases reveals consistent percentage variations in reliability and economic indices per unit change in the system components. Analysis of Figs. 5, 6, 7 and 8 indicates that adjusting the capacity of the SPPS by one unit leads to an average change of approximately 13% in LOLE, 14% in ENS and 1% in LCOE and TLCC. Similarly, varying the capacity of the WDPS unit, affects LOLE by an average of 16%, ENS by an average 19%, TLCC by an average 3.3%, and LCOE by 1.4% per unit change. On the other hand, adjusting the size of the HSS tank by one unit impacts LOLE by around 2%, ENS by around 2.6% and TLCC and LCOE by approximately 0.02%. Also, the analysis of Figs. 5, 6, 7 and 8 demonstrates that the optimal sizing achieved for case 1 (Min of TLCC) provides the more reliable solution with lower TLCC compared to case 2.

Figure 9 (a-d) and 10 (a-d) present the comparative analysis of ENS, LOLE, LCOE, and TLCC for Case 1 and Case 2, respectively. LOLE measures the number of hours through the study period when generation power is lacking to meet the load demand, while ENS quantifies the sum of unsupplied power. These metrics, LOLE and ENS, serve as robust indicators of reliability when assessing the impact of component unit variations. On the economic side, LCOE represents the per-unit levelized energy cost, and TLCC reflects the total lifecycle system cost, both of which provide a comprehensive analysis of economic variations.

Fig. 9
figure 9

(a) Comparison of the effects of unit variation on ENS in Case 1. (b) Comparison of the effects of unit variation on LOLE in Case 1. (c) Comparison of the effects of unit variation on LCOE in Case 1. (d) Comparison of the effects of unit variation on TLCC in Case 1.

Full size image
Fig. 10
figure 10

(a) Comparison of the effects of unit variation on ENS in Case 2. (b) Comparison of the effects of unit variation on LOLE in Case 2. (c) Comparison of the effects of unit variation on LCOE in Case 2. (d) Comparison of the effects of unit variation on TLCC in Case 2.

Full size image

The analysis of Figs. 9 and 10 for both Case 1 and Case 2 reveals a consistent pattern in the impact of unit variation on reliability (ENS and LOLE) and economic indices (LCOE and TLCC). As shown in both figures, increasing the capacity of any system component enhances system reliability, evidenced by reductions in ENS and the number of LOLE hours. However, the extent of reliability improvement varies across different renewable energy sources (RES) and storage systems. Additionally, Figs. 9 and 10 illustrate a nearly linear relationship between changes in component capacity and economic performance metrics (LCOE and TLCC) for all three components. Despite this linear trend, the degree of economic impact differs among the components. The analysis indicates that variations in WDPS capacity have the most significant effect, followed by SPPS and HSS.

Overall, these figures underscore that while increasing component capacity generally enhances system reliability and affects economic indices linearly, the magnitude of these effects varies, highlighting the distinct roles and contributions of each component within the system.

Conclusion

This paper presents the planning and analysis of a SPPS-WDPS-HSS based islanded power system for Jaisalmer, India under site metrological condition consideration. In this work, two different cases of optimal component size is determined using B-PSO based on the two different and most important economic indices namely TLCC and LCOE under the constrained reliability limit. Apart from the optimal sizing in different cases, this work focuses on the sensitivity analysis of all three different component per unit variation on the system reliability and economy. Based on the performed investigation in this work, following conclusions are drawn:

  • The objective function of the planning framework slightly affects the optimal configuration component size.

  • The storage technologies can highly improve the system reliability and also diminish the operational cost.

  • The sensitivity analysis exhibited that the per unit reliability effect of different components is different.

  • Among all three used technologies, WDPS imposed highest impact on the system reliability, because of the all-day availability of the wind flow.

  • The analysis of HSS tank size variation exhibited that, the small variation in HSS tank’s size exhibited around 15 to 20% reliability impact of the generating unit size variation.

  • The HSS has higher potential of reliability improvement in autonomous RES systems along with hydrogen production because of the uncertainty of the RES power generation.

This work presents an effective analysis of different component sizes on the system’s reliability and economy. Nevertheless, the analysis further extended with incorporation of different storage technologies and/or with different load models.

This paper explores the planning and study of a standalone power system based on SPPS, WDPS, and HSS for Jaisalmer, India, taking into account local meteorological conditions. Two distinct cases are considered to determine the optimal sizes of the components using B-PSO, focusing on the key economic indices viz. TLCC and LCOE, within constrained reliability limits. In addition to identifying optimal sizes, the paper emphasizes sensitivity analysis to evaluate how variations in the sizes of the three components affect system reliability and economic performance. The key findings from the analysis are:

  • The optimal component sizes are slightly influenced by the chosen objective function in the planning framework.

  • Storage technologies greatly enhance system reliability and reduce operational costs.

  • Sensitivity analysis indicates that each component’s impact on reliability varies.

  • WDPS has the most significant effect on structure reliability due to the constant availability of wind.

  • Small changes in HSS tank size can result in a 15 to 20% impact on system reliability, relative to changes in generating unit size.

  • HSS has a high potential for improving reliability in autonomous RES systems and supports hydrogen production, addressing the variability of RES power generation.

This paper delivers an in-depth examination of how component sizes affect system reliability and economic performance. Future research could expand this analysis by incorporating different storage technologies or load models.