Study on the mechanical mechanism and control optimization of station subsurface excavation by pile-beam-arch method

Abstract

This paper is based on the construction of the underground Pile-Beam-Arch station at Beitaipingzhuang Station of Beijing Metro Line 12. It employs finite element software for three-dimensional numerical modeling, faithfully reproducing the entire station construction process. The results indicate that the excavation of the pilot tunnel and the stage of the secondary lining buckle arch are the main causes of surface deformation. Additionally, the construction of the secondary lining buckle arch is the primary factor inducing deformation in the middle column and side pile. On this basis, the paper investigates the influence of four crucial factors: the stagger distance of the pilot tunnel excavation, the sequence of the secondary lining buckle arch, the excavation sequence of the lower soil, and the excavation depth on the stress and deformation characteristics of the stratum and the station structure. The results suggest that when the distance between adjacent pilot tunnel faces is 1.5 to 3 times the diameter of the pilot tunnel, it has the greatest influence on surface settlement. When the first side is followed by the middle, closely aligning the second lining with the initial support, and simultaneously installing buckle arches on both sides minimizes deformation of the stratum and station structure. During excavation of the lower soil in the station, reducing the single excavation depth and prioritizing excavation on both sides help control deformation of the vertical bearing structure. The optimal construction scheme is derived through multi-criteria optimization and implemented in the field. Field monitoring results are in good agreement with simulation outcomes, offering valuable reference for the construction of stations under similar geological conditions.

Introduction

With the rapid rise of urban agglomerations and metropolitan areas, the development of underground urban space has become a crucial strategy for addressing the challenges of “urban syndromes” faced by various countries. The scale of subway lines under construction and planning continues to expand, demonstrating robust growth momentum. At the same time, construction methods for subway stations are continuously innovating and improving^1,2. In China, subway stations are generally constructed at shallow depths, and the geological conditions in most cities, such as Guangzhou and Shanghai, primarily consist of soft rock strata. Consequently, conservative construction techniques such as the CRD method, double side-drift method, and step excavation method are commonly employed to ensure construction safety and structural stability³. However, the selection of construction methods for different geological conditions and the study of the applicability of various methods have become research hotspots in recent years. The underground excavation method, due to its fully subterranean construction characteristics, has minimal impact on surface buildings and traffic, effectively addressing the shortcomings of the open excavation method, and has therefore been widely adopted. Northern Chinese cities are predominantly characterized by Quaternary clay soil, silty soil, sand, pebbles, and various interlayers of clay and silt. In the construction process, the self-stability is low, making it prone to stratum deformation^4,5,6. The pile-beam-arch method is based on traditional shallow-buried excavation methods and incorporates characteristics of cover excavation methods. It forms an arch support system by excavating a smaller guide hole to reduce the height and span of one-time excavation, incorporating the side pile, middle column, longitudinal beam, and top arch. This method has been successfully implemented in numerous subway stations including those in Beijing^7,8, Shijiazhuang, Guangzhou⁹, and Shenyang¹⁰.

The core concept of the pile-beam-arch method involves breaking down the large excavation section into several smaller sections. Excavation occurs under the support of each small section, eventually forming a large section. This method is characterized by high section utilization and effective control of surface settlement^11,12,13,14. However, due to its numerous construction steps, its influence mechanism on surrounding strata differs from that of the general shallow-buried excavation method. Concurrently, deformation and collapse have occurred in subway projects that are either completed or under construction nationwide. For instance, after construction, Guangximen Station of Beijing Metro Line 12 experienced significant deformation, as depicted in Fig. 1. Fortunately, due to timely detection, no major accidents occurred. Similarly, as depicted in Fig. 2, a collapse took place at Shengliqiao Station of Qingdao Metro Line 1, resulting in one casualty and significant losses to human life. Therefore, significant attention should be given to ground settlement and the stability of support structures during the construction of PBA stations.

Fig. 1

Deformation of the primary support reinforcement on the side wall of the pilot tunnel.

Fig. 2

The scene of the accident at Shengliqiao Station of Qingdao.

To more effectively control surface settlement during the construction of subway stations using the pile-beam-arch method, various measures have been implemented. Li et al.¹¹ compared construction methods between eight-pilot tunnels and six-pilot tunnels, highlighting the superiority of the latter. Liu and Bai^15,16,17 proposed that prioritizing excavation of the lower side guide hole can effectively mitigate surface subsidence. Fang et al.¹⁸ suggested methods such as advanced grouting to mitigate surface subsidence in adverse geological conditions surrounding the station. Lu et al.¹⁹ introduced a prediction method for surface subsidence resulting from tunnel construction using a Gaussian function. This method is based on monitoring data from 25 subway stations and the findings of 10 model tests.

In the construction process of subway stations, the stress on the supporting structure is equally crucial^20,21. The middle column, side piles, and upper arch structure are the primary load-bearing components during the excavation of the lower part of a subway station. Serving as the primary load-bearing elements, the load at the top of the station is transmitted through the middle column, side piles, and upper arch structure. Moreover, these components effectively isolate the subway structure from surface engineering and other infrastructure. Qu and Liu^22,23 conducted a detailed study on the lateral deformation of side piles to enhance deformation control. They found that pile diameter and spacing are the primary factors influencing lateral deformation.

It is not difficult to find that the stability of the station caused by the construction of the PBA method has attracted the attention of some scholars. However, existing research mainly focuses on predicting and controlling ground settlement caused by station construction^24,25, with limited attention given to the mechanical mechanisms of excavation. Furthermore, the pilot tunnel excavation stage and the buckle arching stage are both important stages of force conversion during the construction process. The construction sequence of these stages undoubtedly influences the stress system transformation of the station structure. To address the limitations of existing research, this paper examines the Beitaipingzhuang Station of Beijing Rail Transit Line 12 as a case study. Finite element numerical simulation software is employed to establish a three-dimensional strata-structure model. The aim is to elucidate the deformation mechanism in the excavation project of the pile-beam-arch station and discuss the impact of construction factors on the deformation characteristics of strata and station structures. Additionally, a construction optimization plan is proposed and compared with field measurements to verify the reliability of the calculations and provide a reference for similar projects.

Engineering background

Project overview

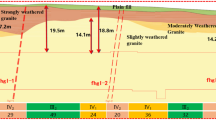
Beitaipingzhuang Station of Line 12 is located on the north side of Beitaiping Bridge in Haidian District, Beijing and is oriented east-west. The building environment around the station is complex, and a T-shaped transfer was constructed simultaneously with the Beitaipingzhuang Station of Line 19 Therefore, the hole pile method was adopted for construction. The main body of the station is a two-story underground structure with four pilot tunnels, two columns, and three span arches. The standard section width of the station is 23.5 m, and the height is 16.7 m. The overburden thickness is approximately 13.7 m. Within the station area, the phreatic level is 0.6 m on the top of the station, and the confined water level is approximately 0.8 m below the bottom of the station. The geographical position and standard section structure of the station are shown in Fig. 3.

Fig. 3

Geographical location of Beitaipingzhuang Station.

Construction method

The excavation area of Beitaipingzhuang Station of Line 12 is large and the surrounding environment is complex. Therefore, the four-pilot hole PBA method is used in the construction process. The structure is shown in Fig. 4, and the detailed construction steps are shown in Fig. 5.

Fig. 4

Schematic diagram of the standard cross-section of a PBA station.

Fig. 5

Construction step.

Considering the complexity of the construction, this paper only studies the influence of the main construction of the station on the stratum and the vertical support structure. Therefore, the construction steps in Fig. 5 is simplified into four stages: Stage I pilot tunnel excavation (stage 1); Stage II pile beam and column formation (stage 2–3); Stage III arch construction (stage 4–5); Stage IV soil excavation and structural construction in the lower part of the station (stage 6–7), as shown in Fig. 6.

Fig. 6

The key steps involved in constructing a PBA station.

Numerical simulation and analysis

Model establishment and parameter selection

Based on the preceding construction sequence, a three-dimensional calculation model using the stratum-structure method is developed. To mitigate boundary effects and consider spatial influence, the entire model spans 35 m along the Z direction of the station (equivalent to the length of the station’s five spans). The X direction has a width of 120 m, corresponding to five times the span of the station. The Y direction extends to the surface, with the lower boundary positioned 50 m below the surface, as illustrated in Fig. 7. The upper surface of the model remains unconstrained, while normal constraints are applied to the remaining surfaces. The stratum employs the modified Mohr-Coulomb constitutive model, whereas the station structure utilizes the linear elastic constitutive model. Side piles and middle columns are modeled using beam elements, while primary support and secondary lining are simulated using solid elements. Table 1 displays the physical and mechanical parameters of the materials in the model.

Fig. 7

Numerical model of station structure.

In the process of numerical simulation, the mixed material of reinforced concrete is simplified according to the principle of equivalence. The elastic modulus of reinforced concrete can be calculated by the following formula:

$${E_{{\text{sc}}}}={E_{\text{c}}}+\frac{{{S_{\text{s}}} \cdot {E_{\text{s}}}}}{{{S_{\text{c}}}}}$$

Where E_sc is the converted elastic modulus of concrete; E_c is the elastic modulus of shotcrete; E_s is the elastic modulus of steel; S_s is the cross-sectional area of the steel grille; S_c is the section area of concrete.

Table 1 The physical and mechanical parameters of the materials in the model.

Simulated results

The PBA method involves a complex construction process with various parameters. The excavation sequence for the pilot tunnel is 1,4 → 2,3, with a synchronous interval of 10 m. Construction of the buckle arch follows a sequence of completing the two sides first, followed by the middle. Additionally, the two sides and the middle buckle arch are staggered by 12 m simultaneously. These parameters are utilized to simulate the excavation construction of the station.

Analysis of vertical displacement of stratum

Figure 8 illustrates the vertical displacement cloud map of the stratum during the primary construction stage. The diagram reveals that following the excavation of the pilot tunnel (stage I), ground settlement on both sides of the station exhibits an axisymmetric pattern. The maximum displacement, reaching 55.39 mm, occurs at the middle line of the station, representing approximately 62.72% of the total displacement. Subsequent to the completion of the buckle arch (stage III), the cumulative stratum displacement reached 88.32 mm, marking an increase of 32.93 mm compared to the pilot tunnel excavation stage, constituting roughly 37.28% of the total displacement. Upon completion of the buckle arch, excavation commences on the lower part of the station (stage IV), resulting in surface settlement rebounding due to unloading effects. Ultimately, the surface settlement decreases to 82.16 mm, indicating a reduction of 6.16 mm. At this stage, surface settlement rebound becomes evident.

Fig. 8

Vertical displacement cloud diagram of stratum in main construction stage.

The strength of the station’s upper structure improves upon the completion of the secondary lining structure of the arch. Simultaneously, a relatively stable arch support structure is formed, and a system is formed together with the internal soil. With the reduction of the soil in the station, the self-weight of the system is reduced, which makes the station appear floating phenomenon, which leads to the rebound of surface settlement. The load transfer mechanism under this construction stage is shown in Fig. 9. From the perspective of the whole construction process, the excavation of the pilot tunnel is the main reason for the change of the ground displacement, followed by the buckle arch construction.

Fig. 9

Load transfer mechanism.

Analysis of axial force variation law of middle column and side pile

The middle column and side pile of the middle section of the model are selected as the research object, and the axial force curve of the middle column and side pile under each construction stage is obtained. Because the default pressure in the software is negative, in order to facilitate the analysis, the axial force is absoluted.

It can be seen from Fig. 10 that the axial force of the middle column shows an increasing trend with the construction step. Among them, the variation of the axial force of the middle column during the construction stage of the top longitudinal beam is relatively small. The primary factor influencing the change in internal force of the middle column is the construction stage of the buckle arch (Stage III), followed by the excavation of the lower soil in the station and the construction of the structure (Stage IV). After the completion of the construction of the buckle arch, the axial force reaches 14,300 kN, which reaches 89.66% of the maximum axial force value. The axial force increment caused by the excavation of the lower soil and the construction of the structure accounts for about 10.34% of the maximum axial force value, indicating that the construction of the buckle arch and the excavation of the lower soil are the main reasons for the change of the axial force of the middle column.

Fig. 10

Variation curve of axial force from top to bottom of middle column in key construction stages.

Numerical simulation results reveal that the construction process significantly impacts the deformation patterns of both the stratum and the station structure. Construction stages I and III primarily induce stratum deformation, while stages III and IV predominantly affect the internal force changes within the station structure. Hence, it is imperative to consider the influence of four crucial factors: the stagger distance of the pilot tunnel excavation, the sequence of the buckle arch, the excavation sequence of the lower soil, and the excavation depth, on the stress and deformation patterns of both the stratum and the station structure.

Study on the influence of construction factors on the stress and deformation law of stratum and station structure

Influence of stagger distance of pilot tunnel excavation

The PBA station is equipped with four pilot tunnels. Owing to their relatively high number and close proximity, adjacent soil disturbance during excavation can easily trigger the group tunnel effect. To mitigate the mutual influence of adjacent pilot tunnel construction, excavation of the side and middle pilot tunnels should be conducted in stages. In practice, the side pilot tunnel is excavated initially, followed by excavation of the middle pilot tunnel. A specific distance separates the front and back of the tunnel face. This paper investigates four pilot tunnel stagger distance schemes, with the specific excavation scheme detailed in Table 2.

Table 2 Construction scheme of pilot tunnel stagger distance.

The vertical displacement nephogram of the stratum at the center line of the model under different tunnel face spacings of the side pilot tunnel and the middle pilot tunnel is shown in Fig. 11. Analysis of the vertical displacement diagrams for the four schemes reveals that with side pilot tunnel and middle pilot tunnel spacings of 6 m, 8 m, 10 m, and 12 m, the maximum vertical displacement of the stratum measures 55.62 mm, 55.59 mm, 55.47 mm, and 55.39 mm respectively following pilot tunnel excavation. As the distance between the faces of the two pilot tunnels increases, there is a decreasing trend in the maximum vertical displacement of the stratum. After the excavation of the pilot tunnel is completed, the maximum displacement of the displacement is located at the top of the middle pilot tunnel. Analysis results indicate that increasing the spacing between tunnel faces of pilot tunnels can mitigate the superposition effect of pilot tunnel excavation on surrounding stratum disturbance.

Simulation calculation results reveal that mutual influence occurs between the step-by-step excavation processes of the side and middle pilot tunnels. The most significant influence occurs when the distance between tunnel faces is approximately 1.5 to 3 times the diameter of the pilot tunnel. Owing to the proximity of the side pilot tunnel to the middle pilot tunnel, excavation of the former induces stratum disturbance in the upper part of the latter. Excavation of the middle pilot tunnel, besides inducing its own stratum disturbance, is also influenced by the excavation of the side pilot tunnel. Consequently, settlement at the top of the middle pilot tunnel is notably greater than that of the side pilot tunnel. Based on the actual construction scenario and the pilot tunnel’s dimensions, the distance between the excavation faces of the side and middle pilot tunnels can be maintained at approximately 10 to 12 m.

Fig. 11

Stratum vertical displacement diagram of the longitudinal section of the pilot tunnel.

The influence of buckle arch sequence

Simulation results indicate that the middle column and side pile not only withstand a portion of the thrust from the secondary lining of the arch but also endure the formation pressure from the top stratum, which constitutes the primary force component of the entire station. To determine the optimal buckle arch scheme, variations in the order of different buckle arches are investigated using surface settlement of the station, axial force, bending moment, and horizontal displacement of the steel pipe column as evaluation indices for assessing their impact on construction mechanical effects.

The construction of the arch of the PBA station includes the initial support arch and the secondary lining arch. In order to facilitate the research, the station vault is numbered. As shown in Fig. 12, according to the different buckle arch order (Table 3), the different mechanical effects brought by the five buckle arch methods are analyzed, as shown in Fig. 13.

Fig. 12

Schematic diagram of buckle arch numbering.

Table 3 Construction scheme of buckle arch.

Fig. 13

Construction scheme of buckle arch.

Analysis of surface settlement

In order to better analyze the influence of different buckle arch order on surface settlement, 23 monitoring points are set up at the surface of the middle position of the calculation model. All the measuring points are set at the model nodes, and the specific layout position of the observation points is shown in Fig. 14.

Fig. 14

Surface settlement observation point.

It can be seen that after the completion of the main construction of the station, the maximum surface settlement caused by the five different buckle arch sequences is 69.79 mm, 67.19 mm, 67.23 mm, 73.71 mm, and 65.96 mm, respectively, as shown in Fig. 15. The surface settlement curves caused by the five arch schemes are basically the same, which are symmetrically distributed along the center of the model, and the surface settlement value at the center is the largest, and the overall numerical difference is small. In the range of 0–50 m from the center of the model, the surface settlement changes greatly. It can be considered that the station has a great influence on the surface within 1 time of the station span in the left and right edges of the station during the excavation construction process, and the influence range outside 1 time is small. Among the five schemes of buckle arch sequence, the surface settlement value caused by staggered buckle arch in scheme five is the smallest, and the surface settlement value caused by scheme four is the largest. The maximum surface settlement values caused by schemes one, two, three and five are 5.32%, 8.85%, 8.79% and 10.51% lower than those caused by scheme four respectively.

Fig. 15

The ground subsidence curve after completion of the station.

Analysis of horizontal displacement of middle column

It can be seen that the horizontal displacement direction of the middle column after the completion of the secondary lining buckle arch points inward to the central line of the station is shown in Fig. 16. The average values of the maximum displacement of the left and right middle columns are 3.45 mm, 3.68 mm, 3.36 mm, 3.20 mm and 3.43 mm, respectively. Among them, the horizontal displacement caused by the fourth scheme is the smallest. This is because after the excavation of the soil under the middle arch is completed, the soil on both sides produces a large horizontal thrust to the center of the station. At this time, the middle column needs to bear the horizontal thrust generated by the soil on both sides.

Fig. 16

After the completion of the secondary lining arch, the top-down transverse displacement curve of the middle column.

Axial force analysis of middle column and side pile

In order to more intuitively understand the axial force of the middle column and the side pile under the 5 schemes, the axial force data of the middle column and the side pile on the left and right sides of the center of the model are extracted, and the axial force curve is drawn. The top-down axial force curve of the middle column and the side pile is shown in Fig. 17. Bending moment is shown in Fig. 18.

Fig. 17

The top-down axial force curve of the middle column and side pile after the completion of the secondary lining arching.

Fig. 18

Internal force diagram of middle column and side pile after completion of secondary lining arching.

After the completion of the second lining buckle arch, the average value of the maximum axial force of the middle column in the five buckle arch schemes is 14398.96 kN, 14485.75 kN, 14421.60 kN, 14310.43 kN and 14872.26 kN, respectively. The average values of the maximum bending moment are 143.48 kN·m, 101.11 kN·m, 32.08 kN·m, 41.96 kN·m and 47.2 kN·m, respectively. The average values of the maximum axial forces of the side piles are 1924.15 kN, 1904.47 kN, 1892.45 kN, 1912.04 kN and 1989.28 kN, respectively. The absolute values of the maximum bending moments of the side piles are 21.67 kN·m, 18.69 kN·m, 13.98 kN·m, 14.12 kN·m and 19.34 kN·m, respectively. For the five schemes, the axial force variation law of the middle column and the side pile from top to bottom is basically the same, which is the law that the axial force at the top is the largest and the axial force at the bottom is the smallest. The bending moment of the middle column caused by the priority excavation of the side span is greater than the corresponding value of the priority excavation of the mid-span. This is because the span of side span is greater than the mid-span. When the side span is completed first, the thrust of the secondary lining structure of the side span on the middle column is greater than that of the mid-span. Therefore, the bending moment of the middle column is larger when the side span is excavated first. When the excavation sequence is the same, the bending moment caused by the immediate construction of the second lining arch after the completion of the initial support arch is smaller than that of the later construction, timely construction of the second lining arch is beneficial to the stability of the central column.

The best buckle arch construction scheme

When comparing the advantages and disadvantages of different arch schemes, six key indices should be prioritized: final surface settlement of the stratum, horizontal displacement of the middle column, axial force and bending moment of the middle column, axial force and bending moment of the side pile post-completion of the secondary lining arch. The analytic hierarchy process (AHP) is employed to systematically divide the construction scheme into three tiers. The optimal station buckle arch scheme is designated as the objective layer. The six indices of final surface settlement, horizontal displacement of middle column, axial force and bending moment of middle column, axial force and bending moment of side pile serve as the criterion layer, while five types of buckle arch schemes constitute the plan layer. The hierarchical structure model for comparing and selecting the station’s arch construction scheme is illustrated in Fig. 19.

Fig. 19

Optimal hierarchical structure model of buckle arch scheme.

Table 4 enumerates the evaluation criteria, which are assessed pairwise using the 1–9 scale method. The pairwise discriminant matrix for each layer regarding the factors influencing the preceding layer is constructed based on the importance ratio between the two factors. Values are assigned according to their relative significance through comparison of the influence degree of the two elements.

Table 4 Evaluation criteria.

Discriminant matrix establishment

There are six criteria: B₁ surface settlement, B₂ middle column horizontal displacement, B₃ middle column axial force, B₄ middle column bending moment, B₅ side pile axial force, B₆ side pile bending moment. The six criteria are compared in pairs, and the scaling method in Table 4 is used to assign values. A 6-order matrix is constructed to solve the priority weight of the objective layer about a criterion, and the importance discriminant matrix of the criterion layer to the objective layer A is shown in Table 5.

Table 5 Criterion layer indicator importance judgment result.

In order to determine the influence degree of each scheme in the plan layer C on the criterion layer B, a pairwise comparison discriminant matrix is established. The discriminant matrix is constructed from the six factors of the surface settlement B₁ caused by the completion of the station construction, the lateral displacement of the middle column B₂ after the completion of the second lining buckle arch, the axial force of the middle column B₃, the bending moment of the middle column B₄, the axial force of the side pile B₅, and the bending moment of the side pile B₆, as shown in Tables 6, 7, 8, 9, 10 and 11.

Table 6 Surface subsidence index discriminant matrix.

Table 7 Transverse displacement index discriminant matrix.

Table 8 Middle column axial force index discriminant matrix.

Table 9 Middle column bending moment index discriminant matrix.

Table 10 Side pile axial force index discriminant matrix.

Table 11 Side pile bending moment index discriminant matrix.

Each criterion contains some factors that belong to it. For each criterion and the factors it belongs to, it can be written as a judgment matrix D = (d_ij)_k×k, and it needs to satisfy d_ij > 0, d_ij = 1 and d_ij = 1/d_ji. Using D·W = λ·W, the corresponding maximum eigenvalue and the corresponding eigenvector are obtained. Then the feature vector is normalized to calculate the weight of each target.

When calculating the weight, it is necessary to use some test methods to detect whether the consistency difference meets the requirements. It is necessary to calculate the maximum eigenvalue λ_max and consistency index CI of each evaluation index, CI = (λ_max-k)/(k-1). In order to measure the size of CI, a random consistency index RI (Query Table 12) is introduced, where CR = CI/RI. In order to avoid the error caused by human factors, it is necessary to check the consistency of the judgment matrix of each index. When the consistency ratio CR < 0.1, the judgment matrix of each evaluation index can be ensured to meet the consistency. The consistency test results of the discriminant matrix of each evaluation index are shown in Table 13.

Table 12 Random index RI value table.

Table 13 The consistency test results of each evaluation index.

Election of the best buckle arch order

The analysis reveals that the consistency ratio of each evaluation index is less than 0.1. Consequently, employing the analytic hierarchy process to compare and select the buckle arch scheme is deemed reasonable.

Using the aforementioned six indicators as the focus of research, the relative weight vector is derived using the weight coefficient calculation formula. Subsequently, the relative weight vector of the criterion layer to the objective layer is determined. Table 14 presents the comprehensive ranking results of each buckle arch scheme, where C_i represents five buckle arch schemes, B_i represents six evaluation indexes, and B_i/A denotes the relative value of evaluation indexes to the target layer.

Table 14 The total sorting results of the AHP of buckle arch scheme.

The analysis indicates that, considering factors such as surface settlement after excavation, horizontal displacement of the middle column following completion of the secondary lining arch, axial force and bending moment of the middle column, axial force and bending moment of the side pile, the fourth construction scheme holds the highest priority, followed by the third, second, first, and fifth schemes. Notably, the weight difference between the third and fourth schemes is a mere 0.021, rendering both viable for implementation. However, the total weight of evaluation indices for the fifth scheme is the lowest, warranting its exclusion. While the order of arch buckling sequence can be adjusted based on site conditions, safety considerations remain paramount. It should be emphasized that regardless of the sequence, whether middle first and then side or side first and then middle, buckling must occur simultaneously on both sides.

The influence of excavation sequence and depth of soil under the station

Based on previous construction experience, it was assumed that the internal force of the steel pipe column would remain relatively stable after completing the secondary lining buckle arch. However, actual monitoring and numerical simulations have revealed fluctuations in the internal force of the middle column during the soil excavation phase. This section primarily examines the impact of two critical factors—the excavation sequence and depth of lower soil—on the stress experienced by the middle column. Internal forces of the middle column corresponding to the five schemes (Table 15) are analyzed based on the excavation order and depth of the lower soil.

Table 15 Excavation scheme of lower soil of station.

Excavation sequence

To investigate the impact of the excavation sequence of the lower soil on the axial force of the middle column, only the sequence of lower soil excavation is altered in the model, while other construction sequences remain constant. The middle column at the station’s center is chosen as the monitoring section. The axial force and bending moment curves of the middle column under various excavation sequences are depicted in Figs. 20 and 21.

Fig. 20

Comparison curve of middle column axial force in two excavation sequences.

Fig. 21

Comparison curve of middle column bending moment in two excavation sequences.

The alteration of the excavation sequence of the lower soil minimally impacts the change in axial force, yet it noticeably affects the bending moment. Upon completion of station excavation, the maximum bending moment resulting from prioritized excavation of the middle soil amounts to 148.98 kN·m, while the maximum bending moment resulting from simultaneous excavation of soil on both sides is 129.53 kN·m, yielding a bending moment difference of 29.45 kN·m between the two excavation methods.

Excavation depth

The preceding analysis reveals that the bending moment value of the soil on both sides of the priority excavation is relatively small. To investigate the impact of each excavation depth of the lower soil on the axial force of the middle column, only the excavation depth of the lower soil is altered while maintaining the model of the soil on both sides of the priority excavation unchanged. The axial force and bending moment curves of the lower middle column under varying excavation depths are depicted in Figs. 22 and 23. Due to identical excavation depths of schemes B and E, and schemes C and D in the negative first layer, only the internal force curves of schemes C and E can be illustrated.

Fig. 22

Axial force comparison curve of middle column in different excavation depth.

Fig. 23

Bending moment comparison curve of middle column in different excavation depth.

According to the diagram, the maximum axial force of the middle column for the four excavation schemes B, C, D, and E is 16727.41 kN, 15915.97 kN, 16392.85 kN, and 16196.92 kN respectively, while the maximum bending moment is − 131.71 kN·m, − 109.49 kN·m, − 119.11 kN·m, and − 110.24 kN·m respectively. Overall, when the excavation depth of the negative first layer remains consistent, the internal force of the middle column increases with the deepening of the negative second layer excavation, thereby heightening the risk of increased internal column force due to single excavation. The impact of the single excavation depth of the negative first layer on the middle column’s internal force is less pronounced than that of the negative second layer. Among the five soil excavation schemes at the station’s lower section, scheme C exhibits the smallest change in middle column internal force, rendering it the most favorable option.

The best construction scheme

According to the analysis of the previous simulation results, the scheme is optimized from the following aspects.

(1) Excavation stagger distance of pilot tunnel.

Initially, deep hole grouting is performed to enhance the stratum’s strength, followed by the excavation of the small pilot tunnel using the step method. The side pilot tunnels on both sides are excavated first, with a staggered step distance of 12 m between adjacent pilot tunnels. During construction, the distance between adjacent pilot tunnels may be adjusted as necessary based on monitoring results, but it must not be less than 10 m.

(2) Buckle arch construction sequence.

First, the middle span primary support buckle arch is carried out, and the leading side span is not less than 12 m. When the primary support buckle arch is carried out, the side wall of the guide hole is prohibited from breaking. When the secondary lining buckle arch is carried out, the side wall of the guide hole is broken in sections, and then the secondary lining buckle arch is carried out. The middle span should lead the side span to no less than two spans, and then the two side span buckle arch should be carried out, and the two side spans should be excavated simultaneously.

(3) Lower soil excavation.

Upon completion of pouring the second lining of the upper arch, excavation of the soil above the middle plate is permissible. Excavation of the lower soil must be conducted in layers. The soil above the middle plate of the negative layer can be divided into two layers, with the first layer excavated to a height of 1 m and the second layer to a height of 2 m, while the remaining soil can be excavated manually. For the soil above the negative second floor, it can be divided into four layers, each with an excavation height of 2 m, with the remaining soil excavated manually. The excavation height of each layer may be adjusted based on site conditions, but must not exceed 3 m per layer.

Construction monitoring analysis and verification

The surface settlement and the change of the internal force of the middle column are important references for understanding the mechanical mechanism of the excavation of the subway station. In order to verify the validity of the discussion results and the feasibility of the construction scheme, we monitored the ground subsidence and the stress of the middle column during the excavation of the PBA station (Fig. 24).

Fig. 24

Installation diagram of measuring points.

Surface settlement monitoring

Surface settlement data from monitoring points in the middle of the station model are selected and compared with settlement monitoring points at the top of the standard section (Fig. 25). Analysis reveals that the model’s calculation results closely resemble field-measured data in terms of surface settlement variation, both exhibiting axial symmetry along the central line with the maximum settlement value situated there. However, the maximum surface settlement value in the simulation results is slightly smaller than the actual monitoring results. This discrepancy can be attributed primarily to the uneven distribution of soil layers in the actual stratum, as opposed to the even distribution assumed for each layer during the simulation process. Nonetheless, overall, the simulation results closely approximate the actual monitoring results.

Fig. 25

Surface settlement curve (DB-14-01–DB-14-13).

Axial force of middle column

Because the installation of the field sensor is carried out with the excavation of the station soil, in order to compare the data across the construction stage as comprehensive as possible, the monitoring point at the top of the standard section of the station and the measuring point data of the same part in the model are selected for analysis (Fig. 26). The axial force data of the middle column in each construction stage are shown in Table 16.

Table 16 The axial force simulation data of the middle column is compared with the measured data.

Fig. 26

Time-axial force curve of middle column.

It can be seen that the overall trend of on-site monitoring data and numerical calculation results is basically the same as the proportion of each stage in Fig. 26. The similarity between the axial force of the middle column in each construction stage obtained by numerical calculation and the on-site monitoring results is greater than 80%. At the same time, the relationship curve between the axial force of the middle column and the construction time obtained by numerical calculation is in good agreement with the curve obtained by on-site monitoring. Therefore, the numerical calculation model established in this paper can accurately reflect the actual construction situation of the station, and the results obtained have certain guiding significance.

Conclusion

This paper adopts the actual underground excavation PBA station as a prototype, utilizing finite element software to simulate the station’s construction process. It investigates the primary causes for variations in stratum displacement and internal forces of the vertical support structure, while analyzing the impact of construction factors on both. Subsequently, the optimal construction scheme for the PBA station is determined and validated through field monitoring. The research findings are outlined as follows:

(1) The primary cause of ground displacement change is attributed to the excavation of the pilot tunnel, accounting for 62.72% of the maximum displacement. Meanwhile, the construction of the secondary lining buckle arch predominantly affects the axial force of the middle column and side pile, contributing to approximately 89% of the total axial force. Both the excavation of the pilot tunnel and the construction of the buckle arch represent pivotal stages for managing surface settlement and structural internal force changes.

(2) Excavating adjacent pilot tunnels exerts a superimposed effect on ground disturbance, particularly pronounced within a range of 1.5 to 3 times the diameter of the pilot tunnel. Concurrently, widening the excavation intervals between adjacent pilot tunnel faces can mitigate the overlapping ground disturbance resulting from excavating two adjacent pilot tunnels.

(3) The sequence of the buckle arch affects surface settlement control to some extent, while significantly impacting the internal force dynamics of the station’s middle columns and side piles. Utilizing the AHP, we comprehensively analyze five different buckle arch schemes. Among these schemes, the fourth, with the side span preceding the middle span, exhibits the least impact on the station’s stratum and structure.

(4) Upon completing the upper arch structure construction, the internal force on the middle column within the station notably rises with increased excavation depth of the lower soil. The impact of excavating the negative second layer on the middle column’s internal force surpasses that of the negative first layer. Simultaneously, excavating soil on both sides preferentially results in minimal horizontal thrust on the middle column.

(5) Multi-criteria optimization analysis concludes that pilot tunnel excavation adheres to the principle of first side and then middle, with adjacent pilot tunnels staggered at 12 m apart. Buckle arch construction follows the principle of first side and then middle, with the second lining closely following the initial support, and simultaneous execution of the two side spans. Lower soil excavation adheres to layered excavation principles, with a single depth of 2 m (adjustable based on-site conditions, with a maximum excavation height of 3 m per layer), and has been implemented on-site. Field monitoring results largely align with numerical simulation, with an error margin of approximately 20%. This indicates that the simulation process accurately mirrors the dynamic evolution of station construction, offering valuable insights for constructing PBA stations in comparable geological settings.