Introduction

As the development of autonomous driving technology keeps advancing, the proportion of intelligent vehicles on the road will incrementally rise, yet the coexistence of human-driven and intelligent driving will endure for a considerable duration prior to the advent of the era of fully intelligent connected vehicles. Among different intelligent vehicles, vehicle information can be exchanged and shared, and the principal influencing factors during driving originate from the uncertainty of human-driven vehicles. Autonomous vehicles are required to identify potential risks from surrounding vehicles and make correct decisions to avert collisions1, which demands precise prediction of the future trajectories of human-driven vehicles in the vicinity of intelligent vehicles. This is conducive to enhancing the efficiency and safety of vehicle operation in heterogeneous traffic flow environments.

Traditional trajectory prediction methods develop models grounded in the principles of vehicle kinematics or dynamics. Lytrivis2 and BERTHELOT3 have formulated a constant angular velocity and acceleration (CTRA) vehicle kinematics model for predicting vehicle states. Li et al.4 introduce a hybrid Kalman filter approach for vehicle state estimation that leverages a nonlinear vehicle dynamics model. Furthermore, Wang et al.5 initially employed Monte Carlo methods to predict the vehicle’s trajectory and subsequently utilized MPC to optimize these trajectories. Although these methodologies demonstrate high computational efficiency and perform well in short-term trajectory forecasting, they fail to take into account the latent information embedded within historical trajectory data, thereby resulting in significant long-term prediction errors.

In recent years, advancements in big data technology have significantly propelled the adoption of data-driven models. Long Short-Term Memory (LSTM) networks6 and Gated Recurrent Units (GRU), along with various adaptations of Recurrent Neural Networks (RNNs)7, have been extensively employed for processing and forecasting time series data. Wang et al.8 utilized a gated recurrent unit neural network to model vehicle-following behavior, incorporating speed, speed difference, and position difference as inputs while predicting speed as the output. They conducted a comparative analysis of prediction accuracy against other network architectures. Ji et al.9 implemented the Softmax function to discern driving intentions of vehicles and employed an LSTM-based encoding-decoding framework to forecast trajectories corresponding to different driving intentions. While these models have demonstrated high accuracy in short-term predictions, challenges remain in effectively extracting long-term information from time series datasets. Transformer models, marked by their distinctive attention mechanism, have the ability to capture the global dependencies throughout the entire sequence and expertly overcome the aforesaid limitations10. Lian et al.11 integrated the geometric and position information of lanes into graph networks, and used an improved residual structure Transformer network to effectively extract and fuse vehicle motion and lane target point features, thus significantly improving the trajectory prediction accuracy and quality in complex traffic environments. The Transformer model’s encoding and decoding structure is relatively complex, and in practical applications often requires a large amount of computing resources. How to balance efficiency and accuracy is the key to using the Transformer model.

Time series models frequently fall short in taking into full account the spatial characteristics and interactions among vehicles when addressing complex trajectory prediction tasks. Scholars employ graph neural networks (GNN), graph convolutional networks (GCN), and graph attention networks (GAT) to forge spatial interaction relationships between vehicles. Graph neural networks regard vehicles as nodes, and vehicle information constitutes the feature of the node. Edges denote the interaction between vehicles12. Moreover, researchers have advanced temporal neural network models that leverage graph neural networks to handle the interactions among vehicles, concurrently integrating neural network models that demonstrate superiority in time series13,14. The model put forth by Huang et al.15 exploits the temporal feature output of LSTM as the input for the GAT module and subsequently yields the spatial interaction feature subsequent to LSTM time-series encoding. Eventually, it integrates temporal and spatial information to fulfill pedestrian trajectory prediction.

This paper presents a vehicle trajectory prediction model that integrates spatial-temporal features by employing Graph Attention Networks (GAT) to extract the spatial interaction characteristics of vehicles, while simultaneously leveraging Long Short-Term Memory (LSTM) and Transformer architectures to comprehensively capture temporal features from both local and global perspectives. The GAT framework exploits high-dimensional data inputs to convey more granular information, thereby strengthening the model’s ability to analyze the complex interactions among vehicles.

The primary contributions of this study are outlined as follows:

  1. (1)

    This neural network architecture seamlessly integrates temporal and spatial features through a composite model known as GAT-TR-LSTM, which synergistically combines Graph Attention Networks (GAT), Transformer encoder, LSTM encoder and decoder. This framework adeptly processes both temporal dependencies and spatial relationships, facilitating efficient predictions of vehicle trajectory information in complex traffic environments.

  2. (2)

    Dual mechanisms for the extraction of local and global temporal features. The Transformer encoder proficiently captures global dependencies within temporal sequences, while the original input data undergoes residual processing to enhance feature representation capabilities. Both outputs are subsequently fed into the LSTM encoder to decode local temporal features, thereby achieving a comprehensive extraction of temporal characteristics.

  3. (3)

    Through the actual validation conducted on the dataset, the model proposed in this paper demonstrates superior accuracy and robustness in predictions compared to both the baseline model and other spatio-temporal neural network architectures.

Related work

Both domestic and international scholars have carried out extensive and comprehensive research on the modeling methods for vehicle trajectory prediction, which has led to remarkable progress in this field. Based on the methodologies adopted, these models can be classified into three distinct types: physics-based models, time series-based models, and neural network models integrating spatial and temporal dimensions.

The physical modeling approach endeavors to employ rigorous formulas for specifying the model, providing stronger theoretical underpinnings, and predicting the vehicle’s trajectory through modeling its kinematic variables. For instance, the classic car following model and the trajectory planning model are included in this category of methods. The microscopic behavioral trajectories of vehicles primarily encompass lane changes and following behaviors. Yang et al.16 have systematically summarized and categorized various branches and advancements in theoretical following models, elucidating research hotspots and developmental directions within this domain. Ding et al.17 investigated the following and lane-changing behaviors of human-driven vehicles (HVs) alongside autonomous vehicles (AVs) under mixed driving conditions, employing the Intelligent Driver Model (IDM) and CACC for following behavior analysis and utilizing the MOBIL model for lane-changing behavior assessment. Wang et al.18 established stability conditions for both human-driven and intelligent vehicles operating in mixed traffic environments, characterizing their following behaviors through an optimal speed model as well as an enhanced adaptive cruise control model tailored for following scenarios. Qi et al.19 developed an improved Following Vehicle Dynamics (FVD) model that accounts for interactions between vehicles in both same-lane and adjacent-lane contexts to investigate driver-following behavior in multi-lane situations; they validated the efficacy of their model via numerical simulations. Adam Houenou et al.20 introduced a comprehensive prediction framework based on constant yaw rate and acceleration parameters combined with polynomial trajectory fitting techniques, significantly enhancing accuracy in short-term as well as long-term trajectory predictions.

Methods utilizing time series models are capable of extracting effective feature representations from extensive datasets, thereby enhancing predictive performance. Huang et al.21 developed a vehicle-following model grounded in a long short-term memory (LSTM) neural network, validated the proposed framework using the NGSIM dataset, and demonstrated its superiority in analyzing asymmetric driving behavior. Sun et al.22 established an LSTM-based vehicle-following model leveraging real-world driving data, exhibiting commendable stability and resilience to interference; furthermore, the prediction outcomes align more closely with actual driving behaviors. Ma et al.23 proposed a seq2seq model based on following behavior, which takes into account historical information memory and reaction delay in driving process and can better reproduce different degrees of lagging driving trajectories compared to IDM and LSTM models. Lin et al.24 integrated an enhanced sampling mechanism in conjunction with a traditional LSTM-based vehicle following model, which predicts vehicle trajectories from the platoon-level perspective to alleviate the propagation of temporal and spatial errors. Wang et al.25 developed an attention-based data fusion vehicle tracking (ABF-CF) model that demonstrated superior performance compared to both single theory-driven and data-driven models in vehicle trajectory prediction, exhibiting improved stability and accuracy. Xu et al.26 proposed a CF model utilizing TransGAN that addresses data incompleteness by extracting latent features from original vehicular data through a Transformer Network, subsequently generating the future state of the target vehicle via a generative adversarial network; this approach was experimentally validated using the NGSIM I-80 dataset. Messaoud et al.27 incorporated an attention mechanism into LSTM to capture inter-vehicle interactions, employing an LSTM encoder-decoder for trajectory prediction. Geng et al.28 presented a hierarchical Transformer network (HTN) and established a transfer learning framework capable of accurately predicting trajectories of heterogeneous intelligent entities even in scenarios with missing data. Xing et al.29 combined the historical trajectory data and driving behavior features of each vehicle, using time-series models to capture the temporal dependencies of vehicle trajectories, thereby improving prediction performance in complex traffic environments.

Temporal and spatial information fusion neural network models effectively account for the influence of surrounding vehicles on a target vehicle. Liu et al.30 incorporated map and vehicle data, utilizing an LSTM encoder-decoder framework while introducing graph query mechanisms to enhance vehicle trajectory prediction. Wang et al.31 employed two distinct LSTM encoders to separately process vehicle positional and status information, complemented by two GAT encoders for spatial position analysis, ultimately generating trajectory outputs via an LSTM decoder. Zhang32 leveraged convolutional neural networks (CNNs) to extract spatial features among vehicles and constructed interactions using GAT; the trajectory was subsequently predicted through a transformer model. Xie et al.33 integrated CNN and LSTM architectures, optimizing hyperparameters to satisfy both spatial and temporal accuracy requirements in predicting surrounding vehicles’ trajectories. Gao34 proposed a trajectory prediction methodology based on graph attention networks (GAT), combining it with a GRU encoder-decoder model for effective temporal sequence feature processing, which significantly reduced prediction errors. Li35 introduced an intentional convolution and hybrid attention neural network (IH-Net) that synergizes driver lane-changing intentions with vehicle interactions for enhanced trajectory predictions, incorporating a hybrid attention mechanism to bolster long-term predictive capabilities. An et al.36 proposed a dynamic graph and interactive perception neural network model called DGInet, which demonstrated superior performance and faster computational efficiency than existing methods on the NGSIM and Apollo datasets. Shi et al.37 combined attention mechanisms with bidirectional LSTMs and temporal convolutional networks (TCN) to predict vehicular behaviors such as following dynamics and lane changes; results indicated exceptional performance in both short-term and long-term forecasting. Meng38 introduced a vehicle trajectory prediction model grounded in LSTM that integrates spatial and temporal attention mechanisms to differentiate the impacts of various spatial locations and extract critical historical trajectory data. Guo39 proposed a dual attention mechanism trajectory prediction model based on LSTM encoding, where the temporal attention mechanism processes historical trajectory information, and the spatial attention mechanism combines the self-vehicle movement trend with the free space of surrounding vehicles, achieving higher trajectory prediction accuracy. Cai et al.40 proposed an Environment-Attention Network (EA-Net) model that more accurately captures the interaction between vehicles and their environment, combining environmental information with vehicle behavior for trajectory prediction. Zhang41 combines the Graph Attention Network (GAT) and the Convolutional Gate Recurrent Unit (ConvGRU) to propose an attention-based automatic driving vehicle surroundings traffic subject interaction perception trajectory prediction (AI-TP) method.

Current research indicates that while physical models possess substantial explanatory power, they are inadequate for long-term predictive tasks due to their failure to account for the temporal and spatial correlations among vehicles. Although single time series models effectively capture temporal dependencies, they often struggle to represent the intricate interactions between vehicles and diverse driving behaviors. Existing spatio-temporal neural network architectures have attempted to integrate these dimensions; however, they frequently encounter performance limitations when addressing complex traffic scenarios. Furthermore, in feature extraction processes, obtaining high-quality and effective features remains a significant challenge. Therefore, there is a pressing need for an innovative neural network architecture specifically designed to efficiently integrate temporal and spatial features, capturing the full dynamic evolution of vehicle behavior over time, to effectively handle complex multi-vehicle interaction scenarios.

Problem description

The vehicle trajectory prediction examined in this paper entails the utilization of historical feature information of the target vehicle and surrounding vehicles for predicting the trajectory of the target vehicle within a future time period via the established model. Six vehicles within a 100-meter range in front and behind the target vehicle are defined as “surrounding vehicles,” as shown in Fig. 1. If there are more than six vehicles within the range, they are selected based on their relative positions to the target vehicle (such as front, front-left, front-right, etc.), and the six closest vehicles to the target vehicle are chosen from them. The historical features for each vehicle comprise position, speed, and acceleration metrics. The model’s input consists of the historical trajectory data from both the surrounding and target vehicles, while its output is the predicted positional coordinates of the target vehicle at designated future time points, encompassing both x and y directional components.

The input vehicle history feature states:

$$X=\left\{ {d_{0}^{t},d_{N}^{t}{\text{|}}t \in \left( {1, \ldots ,{t_{obs}}} \right)} \right\}$$
(1)

Specifically, \(d_{0}^{t}\) represents the feature information of the target vehicle at time \({t_{obs}}\) in the past, and \(d_{N}^{t}\) represents the historical feature information of N nearby vehicles.

$$d_{0}^{t}=\left\{ {x_{0}^{t},y_{0}^{t},v_{x}^{t},v_{y}^{t},a_{x}^{t},a_{y}^{t}{\text{|}}t \in \left( {1, \ldots ,{t_{obs}}} \right)} \right\}$$
(2)
$$d_{N}^{t}=\left\{ {\Delta x_{{i~}}^{t},\Delta y_{{i~}}^{t},v_{x}^{{t,i~}},v_{y}^{{t,i~}},a_{x}^{{t,i~}},a_{y}^{{t,i~}}{\text{|}}i \in \left( {1, \ldots ,N} \right),t \in \left( {1, \ldots ,{t_{obs}}} \right)} \right\}$$
(3)

The output vehicle trajectory information is:

$$\hat {Y}=\left\{ {{{\hat {x}}^t},{{\hat {y}}^t}{\text{|}}t \in \left( {{t_{obs}}+1,{t_{obs}}+2 \ldots ,T} \right)} \right\}$$
(4)

Present the input and output parameters in tabular form for a lucid explanation. The subsequent Table 1 offers a summary of the principal parameters employed in this model along with their respective meanings:

Table 1 Parameter description.
Full size table
Fig. 1
figure 1

Distribution of vehicles around.

Full size image

Methodology

Model architecture

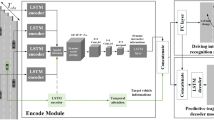
To lucidly represent the neural network structure of the model, a comprehensive and elaborate neural network structure diagram was created, as shown in Fig. 2. This diagram elaborates on the entire processing procedure from the input data to the ultimate output, along with the interconnection relations among submodules.

The neural network architecture predominantly comprises the GAT encoder, Transformer encoder, and LSTM encoder-decoder. Firstly, the three-layer graph attention layer within GAT is employed to handle the input data and extract the spatial characteristics of the vehicle. The output of GAT is placed into the Transformer encoder, in which the self-attention mechanism is utilized to capture the long-term temporal features. The residual processing is capable of enhancing the features of the original data. By combining the outputs of the Transformer encoder and the residual processing, the relevant information is input into the LSTM encoder to extract the short-term temporal sequence features. Eventually, the LSTM decoder produces the future trajectory information of the target vehicle within the next 3 s, relying on the historical trajectory information of the vehicle and the surrounding vehicles during the past 5 s.

Fig. 2
figure 2

Comprehensive diagram of neural network architecture.

Full size image

GAT encoder

Graph Attention Network (GAT) is employed to model the spatial interactions among vehicles. By applying self-attention mechanisms to the nodes, GAT is capable of learning the weights between the nodes and accomplishing effective information interaction and feature extraction in the spatial dimension.

Firstly, a spatial map \({G_t}=\left( {{A_t},{E_t}} \right)\) is constructed. Specifically, \({A_t}\) represents the set of vertices, forming a collection of node feature vectors:

$${A_t}=\left\{ {d_{0}^{{t~}}, \cdots ,d_{{i~}}^{{t~}}, \cdots d_{{n~}}^{{t~}}} \right\}$$
(5)

Where, \(d_{{i~}}^{t} \in {R^F}\), F represents the dimensionality of the input features for each node, and n denotes the total quantity of nodes.

\({E_t}\) denotes the set of edges among nodes, and the mutual influence between vehicles is correlated with the distance between them, which is typically proportional and can be defined through the size of the adjacency matrix based on the distance. When the distance between two nodes surpasses a certain threshold value, it indicates that the nodes are uncorrelated, with the value being 0. On the contrary, it indicates that the nodes are correlated, and the value is 1. The definition of the adjacency matrix \(E \in {R^{N \times N}}\) is presented as follows:

$$E\left( {i,j} \right)=\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{if~s\left( {d_{{i~}}^{{t~}},d_{{j~~}}^{{t~}}} \right) \leqslant \psi ,i \ne j} \end{array}} \\ {\begin{array}{*{20}{c}} 0&{~otherwise~~~~~~~~~~~~~~~~~~~} \end{array}} \end{array}} \right.$$
(6)

Where, \(d_{{i~}}^{{t~}}\) and \(d_{{j~}}^{{t~}}\) respectively represent the nodes corresponding to vehicle i and vehicle j at time t. \(s\left( {d_{{i~}}^{{t~}},d_{{j~~}}^{{t~}}} \right)\) represents the Euclidean distance. \(\psi\) represents the selected threshold, \(\psi = 80\;{\text{m}}\) is chosen after verification.

When conducting vehicle trajectory prediction, the target vehicle and six surrounding vehicles are chosen as the research subjects, and these vehicles are abstracted into the structure depicted in Fig. 3. The adjacency matrix E delineates the connection relationships among these nodes. The core concept of GAT lies in assigning distinct weights to each edge via a multi-head attention mechanism, thereby capturing the diverse influences between nodes.

Fig. 3
figure 3

Graphical structure of the research subject.

Full size image

The following presents the calculation process of the attention coefficient. Firstly, the node features are linearly transformed into higher-dimensional ones. Subsequently, the original attention value \(\left( {i,j} \right)\) of each node to \({e_{ij}}\) is computed, and the ultimate attention coefficient \({\alpha _{ij~}}\) is attained through normalization. The weighted summation of the transformed features and the attention coefficient is employed to acquire a new feature representation for each node.

$${e_{ij~}}=LeakyReLU\left( {{a^T}\left[ {W{d_i}\parallel W{d_j}} \right]} \right)$$
(7)
$${\alpha _{ij}}=\frac{{exp\left( {{e_{ij}}} \right)~}}{{\mathop \sum \nolimits_{{k \in {\mathcal{N}_{\left( i \right)}}}} exp\left( {{e_{ik}}} \right)}}$$
(8)

Where, a constitutes a learnable parameter vector, W represents a weight matrix, \(\parallel\) represents the vector concatenation operation, \(LeakyReLU\) denotes an activation function, and \(\mathcal{N}\left( i \right)\) refers to the set of neighbors of node i.

Fig. 4
figure 4

Overall structure diagram of GAT.

Full size image

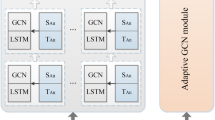
The GAT network used in this paper is shown in Fig. 4, where the nodes and edges are input into the GATblock, which is first processed by BatchNorm. The input features are processed by two parallel graph attention layers att1 and att2, which produce two outputs \({G_1}\) and \({G_2}\). These outputs are stacked and averaged to integrate information from both layers, and then input into the graph attention layer \(at{t_{out}}\) in head2 for further feature fusion to generate the output feature \({G_{out}}\).

The GAT network admits four-dimensional data input (B, T, N, F) and generates output (B, T, N, H), thereby preserving the original and complete spatial information of each vehicle and capturing the spatial relationships and individual characteristics between vehicles more effectively.

Transformer encoder

The Transformer architecture processes time-series data via its self-attention layer, resolving the issue of incomplete feature extraction that is induced by the difficulty of traditional RNN models (such as LSTM) in learning long-term temporal dependencies. Nevertheless, the entire Transformer encoding-decoding structure is overly complex and demands more computing resources. Therefore, in this model, merely the transformer encoder portion is chosen, which can leverage its characteristic of extracting global dependencies and concurrently enhance the speed of training and prediction. The structure of this component is presented in Fig. 5.

Fig. 5
figure 5

Transformer encoder architecture.

Full size image

The input data of the Transformer is mapped onto a high-dimensional space through the Embedding Layer, furnishing the requisite input complexity and space for the subsequent profound processing. These inputs are handled by the Multi-Head Self-Attention mechanism and the feedforward neural network within the Encoder Layer, effectively extracting long-term dependency relationships. The core component is the Self-Attention mechanism.

The essence of the self-attention layer lies in the automatic capture of significant features within the time series by computing the weighted relationship between each time step and other time steps in the sequence. The weight is produced by three matrices: the query matrix Q, the key matrix K, and the value matrix V, which are derived through linear transformation of the input feature matrix X. The calculation formula of self-attention is presented as follows:

$$Attention\left( {Q,K,V} \right)=softmax~\left( {\frac{{Q{K^T}}}{{\sqrt {{d_K}} }}} \right)V$$
(9)

Where, \({d_k}\) represents the dimension of the vector.

Generally, a multi-head attention mechanism is employed, which boosts the expressive capacity of feature representations through multiple parallel attention heads. All output matrices are concatenated and passed through a linear layer to acquire the ultimate output. In this model, nhead = 2.

The output features of GAT are subjected to processing by an MLP (multi-layer perceptron) and subsequently fed into the Transformer encoder (\(T{R_{input}}\)). The dimensional size is (B, T, \(F^{\prime}\)), and the scale size remains invariant after being processed by the encoder part.

Concurrently, to improve the information integrity during the feature transmission process, ResNet is incorporated to extract valid features and conduct residual processing on the original input data to augment the expressive capability of features. The structure of ResNet is illustrated in Fig. 6. Generally, ResNet achieves residual connection via convolutional layers and batch normalization layers, and the processed features preserve the original temporal structure. The output of the Transformer encoder is concatenated with the original input features that have passed through the residual block, integrating the global dependence and enhanced original data features, and the resulting final output is denoted as \({X^{TR}}.\)

Fig. 6
figure 6

Architecture of the residual network.

Full size image

LSTM encoder

The Transformer encoder exhibits excellent performance in handling long-term dependencies; however, LSTM proves to be more efficacious in dealing with finer-grained temporal sequence variations. LSTM is capable of further elaborating features and capturing short-term temporal dependencies via its internal memory units and gate mechanisms, thereby furnishing the decoder with abundant context information.

The LSTM encoder accepts the input and recursively processes each time step through a sequence of LSTM units, with its internal state (hidden state and cell state) being updated at each step. These states are conveyed to the decoder, offering crucial information for generating precise predictions of future trajectories.

The internal architecture of the LSTM encoder predominantly comprises input gate \({i_t}\), forget gate \({f_t}\), output gate \({o_t}\), and a memory cell \({c_t}\). The update computations for time step t are presented as follows:

$${i_t}=\sigma \left( {{W_i}{x_t}+{U_i}{h_{t - 1}}+{b_i}} \right)$$
(10)
$${f_t}=\sigma \left( {{W_f}{x_t}+{U_f}{h_{t - 1}}+{b_f}} \right)$$
(11)
$${o_t}=\sigma \left( {{W_o}{x_t}+{U_o}{h_{t - 1}}+{b_o}} \right)$$
(12)
$${\tilde {c}_t}=\tan h({W_C}{x_t}+{U_c}{h_{t - 1}})$$
(13)
$${c_t}={f_t} \odot {c_{t - 1}}+{i_t} \odot {\tilde {c}_t}$$
(14)
$${h_t}={o_t} \odot \tan h\left( {{c_t}} \right)$$
(15)

Where, \(\sigma\) represents the sigmoid activation function. W, U and b represents the parameters of each structure, \({x_t}\) and \({h_{t - 1}}\) respectively representing the input and the output of the previous hidden layer.

The input of the LSTM encoder constitutes the fused output of the Transformer encoder and the residual block. After traversing this encoder, the ultimate hidden state features are acquired, which are respectively designated as \({h^{lstm}}\) and \({C^{lstm}}\) are utilized to initialize the hidden state of the decoder.

LSTM decoder

The LSTM decoder is employed to generate the future trajectory of the target vehicle, generating the predicted sequence progressively from the final hidden state, \({h^{lstm}}\) and \({C^{lstm}}\) acquired from the encoder.

To enhance the prediction performance of the model, during the training procedure, the LSTM decoder adopts a mixed teaching force modality, that is, at each time step, it determines with a specific probability whether to utilize real data or model prediction as the input for the subsequent step. This strategy proficiently strikes a balance between the training efficiency and the model’s prediction capability. Reference42 selects the optimum teaching rate as 0.5. The specific structure is depicted in Fig. 7.

The operational formula for the decoder at each time step t is given as:

$${h_t},{C_t}=f\left( {{y_{t - 1}},{h_{t - 1}},{C_{t - 1}}} \right)$$
(16)
$${\hat {y}_t}=g\left( {{W_y}{h_t}+{b_y}} \right)$$
(17)

Where, \({y_{t - 1}}\) represents the output of the previous time step, \({h_t}\) constitutes the hidden state at time step t, \(f\left( \cdot \right)\) is a nonlinear activation function, \(g\left( \cdot \right)\) represents the softmax function, \({W_y}\) is the weight matrix of the output layer, and \({b_y}\) is the bias term.

The output of the decoder constitutes a prediction of magnitude\(\left( {{\text{B}},{\text{target}}\_{\text{len}},{{\hat{F}}}} \right)\), where \({\text{target}}\_{\text{len}}\) represents the predicted time step, and \({{\hat {F}}}\) refers to the output trajectory information, encompassing the positions in the x and y directions.

Fig. 7
figure 7

LSTM encoder-decoder architecture.

Full size image

Handling complex multi-vehicle interaction scenarios

In response to complex multi-vehicle interaction scenarios, this study proposes a model architecture that integrates Graph Attention Networks (GAT), Transformer, and Long Short-Term Memory Networks (LSTM) to comprehensively capture the interactions between vehicles and their impact on trajectory prediction.

For spatial interaction modeling, GAT uses a self-attention mechanism to assign weights to the interactions between each pair of vehicles, dynamically adjusting the influence of surrounding vehicles on the target vehicle. This mechanism allows the model to flexibly highlight the interactions of key vehicles based on their relative distance and importance, thereby accurately characterizing the spatial relationships between vehicles.

For time-series feature handling, this study combines Transformer and LSTM. Transformer, with its self-attention mechanism, captures long-range dependencies within the sequence, making it suitable for long-term trajectory prediction tasks. LSTM, on the other hand, focuses on extracting short-term temporal features, accurately capturing the dynamic changes of vehicles in short time intervals, thus improving the accuracy of short-term trajectory predictions. The combination of these two models enables excellent performance in both long-term and short-term prediction tasks.

By integrating GAT, Transformer, and LSTM, the model effectively combines spatial and temporal features, fully exploiting long-term and short-term dependencies in the time series. In complex traffic environments with multi-vehicle interactions, the model can accurately predict the target vehicle’s trajectory by incorporating spatial-temporal features. Subsequent experiments will validate the superiority of this model in multi-vehicle interaction scenarios and demonstrate its significant advantages compared to other models.

Experiment and analysis

Dataset

In the verification of the model experiment, the data set encompassing NGSIM and I-80 sections within the open NGSIM dataset of the United States was chosen. This dataset chronicles the actual driving trajectories of vehicles on highways. Through the execution of operations like filtering, noise handling, and sliding window processing on the original data, a sequence of trajectory sets was acquired. The dataset encompasses information such as vehicle position, speed, and acceleration. Each data sample lasts for 8 s, with the initial 5 s serving as historical observational data and predicting the vehicle trajectory for the subsequent 3 s. Regarding data allocation, 60% is utilized for training, 20% for testing, and the remaining 20% as a validation set. The raw data was first processed using wavelet denoising, followed by the removal of irrelevant features and the addition of new features. Trajectory sequences were extracted using a sliding window method, with a window length of 8 s and a stride of 0.1 s. All input features were normalized to the range [0,1] to ensure stable training, and the data was further subjected to differencing operations.

Evaluation metrics

When assessing the prediction performance of the model, the following evaluation indicators were employed:

MSE (Mean Square Error): It computes the average of the squared errors between the predicted position \(\left( {{{\hat {x}}^t},{{\hat {y}}^t}} \right)\) of the vehicle and the actual position \(\left( {{x_t},{y_t}} \right)\), reflecting the precision of the prediction outcome. Its calculation formula is:

$$MSE=\frac{1}{N}\mathop \sum \limits_{{i=1}}^{n} \left( {{{\left( {{x_t}\left( i \right) - {{\hat {x}}^t}\left( i \right)} \right)}^2}+{{\left( {{y_t}\left( i \right) - {{\hat {y}}^t}\left( i \right)} \right)}^2}} \right)$$
(18)

RMSE (Root Mean Squared Error): It is the square root of the Mean Squared Error and is commonly utilized for assessing the standard deviation of predicted values. The smaller the RMSE, the greater the precision of the predicted speed value. The formula is presented as follows:

$$RMSE=\sqrt {\frac{1}{N}\mathop \sum \limits_{{i=1}}^{n} \left( {{{\left( {{x_t}\left( i \right) - {{\hat {x}}^t}\left( i \right)} \right)}^2}+{{\left( {{y_t}\left( i \right) - {{\hat {y}}^t}\left( i \right)} \right)}^2}} \right)}$$
(19)

AE (Absolute Error): It measures the absolute difference between the predicted value and the actual value, reflecting the magnitude of the error. The formula is:

$$AE=\frac{1}{N}\mathop \sum \limits_{{i=1}}^{n} \left( {\left| {{x_t}\left( i \right) - {{\hat {x}}^t}\left( i \right)} \right|+\left| {{y_t}\left( i \right) - {{\hat {y}}^t}\left( i \right)} \right|} \right)$$
(20)

Results

The experiments were conducted in the PyTorch framework, utilizing an NVIDIA GeForce RTX 4080 GPU for all computational tasks. The Adam optimizer was employed with the mean squared error (MSE) as the loss function. The training process used a batch size of 1024, an initial learning rate of 0.001, and a weight decay of 0.0001. The model was trained for 150 epochs.

The proposed model integrates three main components with carefully tuned hyperparameters. The Graph Attention Network (GAT) consists of three layers. The Transformer encoder is configured with one layer, two attention heads (nheads = 2), and a dropout rate of (0.1) Finally, the LSTM encoder-decoder structure comprises four layers with a hidden size of 256 and a dropout rate of (0.2) These settings were chosen to balance model complexity and performance.

The following Fig. 8 presents the variations of the training loss and the testing loss throughout the model training process. The MSE value of the training error drops rapidly in the initial stage of training, subsequently stabilizes and remains at a low level with fluctuations, demonstrating excellent convergence. The error curves of training and testing are closely interrelated throughout the epoch, without any overfitting issues, indicating strong generalization ability.

Using this model to predict the driving trajectory of the target vehicle in the next 3 s, Table 2 presents the error values at different times. All three error indicators assume small values in the short-term prediction stage, and RMSE and AE gradually increase as the prediction time lengthens. However, the overall increase rate is controlled within a reasonable scope, and the model is capable of providing accurate prediction results.

Table 2 The predictive efficacy of the model on the NGSIM dataset.
Full size table
Fig. 8
figure 8

Loss curve.

Full size image

Moreover, for the purpose of comprehensively assessing the prediction ability of the model in dealing with various vehicle behaviors, the study exhibited comparisons between the predicted vehicle trajectories and the actual ones under three distinct driving conditions: straight driving, right-turning, and left-turning, respectively depicted in Fig. 9. The outcomes reveal that the predicted trajectories of the model are highly in line with the actual trajectories. Under the straight-driving condition, the predicted trajectory is highly congruent with the actual trajectory, demonstrating the high precision of the model in handling straight-driving trajectories. In the scenarios of right-turning and left-turning, although turning elevates the complexity of the prediction, the model is still capable of effectively tracing the overall trend of the trajectory and precisely identifying the starting and ending points of the turn. Particularly, in the left-turning scenario, despite a minor deviation, the model still manifests excellent trajectory tracking performance, which emphasizes its strong robustness and high adaptability in handling non-linear trajectories.

Fig. 9
figure 9

Predictive effects under different operating conditions: (a) straight operation, (b) right-turn operation, (c) left-turn operation.

Full size image

Compare existing research

To more effectively verify the predictive performance of the model proposed in this paper, the error indicators RMSE and AE are employed for comparison with other models. The following models are selected for the comparison:

MTF-LSTM42: A mixed teaching force LSTM encoding-decoding model integrating information of surrounding vehicles and roads.

STGACN43: A spatial-temporal graph attention convolutional neural network (STGACN) model.

AI-TP41: A model combining the graph attention network (GAT) and the convolutional gate-controlled recurrent unit (ConvGRU).

GRIP++44: A model integrating GCNs and GRU.

STI-GCN14: A spatial-temporal interaction graph convolutional network (STI-GCN) that considers road structures and predicts future trajectories by obtaining the spatial-temporal features of vehicles.

STQformer45: A scenario-aware multimodal vehicle trajectory prediction model fusing spatial-temporal queries (STQformer).

GSAN46: An LSTM trajectory prediction model embedding graph self-attention layers to extract the spatial-temporal interaction effects of vehicles.

Table 3 Performance among different models on the NGSIM dataset.
Full size table

Based on the data presented in the Table 3, the GAT-TR-LSTM-LSTM model proposed in this paper demonstrates significantly superior prediction performance compared to the other benchmarked models at diverse time steps. In contrast to the MTF-LSTM, this model reduces the RMSE by 44.82%, 51.4%, and 53.33% respectively at different prediction intervals. Despite the fact that MTF-LSTM integrates information from surrounding vehicles and roads, its LSTM network exhibits certain constraints in handling long-term dependencies, leading to a relatively high error of 1.50 for 3-second predictions. Similarly, the AI-TP model has restricted capability in capturing nonlinear features through its ConvGRU unit, resulting in an RMSE of 1.53 for 3-second predictions. STGACN and GRIP + + display strong competence in processing spatial and temporal information and perform commendably in short-term and medium-term predictions (with 1-second RMSE of 0.40 and 0.38 respectively), yet their accuracy deteriorates in long-term predictions. STI-GCN achieves the best performance in 1-second prediction by considering the spatial and temporal interaction between roads and vehicles (with an RMSE of 0.31), and GSAN attains an AE of 0.11 in 1-second prediction, also indicating favorable short-term prediction outcomes. Nevertheless, the GAT-TR-LSTM-LSTM model proposed in this paper showcases stronger stability and higher accuracy in long-term predictions. It is notable that STQformer, a model constructed based on the Transformer architecture, performs well in medium-to-long-term predictions, with an RMSE of 1.28 for 3-second predictions. The model put forward in this paper employs GAT to extract the spatial relationships among vehicles, utilizes Transformer to capture global sequence dependencies, and adopts an LSTM encoder-decoder to handle multi-scale temporal features information. Thus, it can capture the temporal and spatial dynamic characteristics in complex traffic environments more effectively. Especially, with an RMSE of merely 0.70 in the 3-second prediction, it fully showcases its remarkable superiority in long-term prediction tasks.

To further validate the reliability of the reported RMSE results, 95% confidence intervals (CIs) for RMSE at each time step using bootstrapping was calculated. The results indicate that the confidence intervals for the proposed GAT-TR-LSTM-LSTM model are significantly narrower than those of baseline models, demonstrating the robustness of its performance. For example, at 1 s, the RMSE for GAT-TR-LSTM-LSTM is 0.32 with a 95% CI of (0.25, 0.39), while the RMSE for MTF-LSTM is 0.58 with a wider 95% CI of (0.45, 0.71). The RMSE of GRIP + + is 0.38 and 95% CI is (0.31,0.45). Similarly, the confidence intervals for GAT-TR-LSTM-LSTM at 2 s and 3 s are (0.42,0.62) and (0.58,0.82), respectively. These results confirm that performance improvements of the proposed model are statistically robust and not due to chance.

Ablation study

To conduct a comprehensive assessment of the performance of the proposed model in vehicle trajectory prediction, this study carried out a series of ablation experiments. These experiments disclose the contributions of each component by comparing the performances of different network structures and guarantee that, except for the ablated portion, each group of experiments is executed under the identical structure configuration:

LSTM-LSTM: Served as the baseline model, trajectory prediction is accomplished using an LSTM encoder-decoder structure. The experiment adopts a mixed teaching force strategy, setting the teaching rate at 0.5, to evaluate the fundamental ability of LSTM in processing time series data.

GAT-Transformer: The model captures the graph structure relationship between vehicles through GAT, uses Transformer encoder to extract global time features, and gradually generates future trajectories through decoder.

TR-LSTM-LSTM: In this architecture, a Transformer encoder is introduced to enhance the time series processing capacity, while the LSTM configuration remains consistent with the baseline model.

TR(Res)-LSTM-LSTM: The Residual connection is appended to the TR-LSTM-LSTM model.

GAT-LSTM-LSTM: In this model, a Graph Attention Network (GAT) is incorporated to handle spatial relationships, followed by LSTM for the encoding and decoding of time series.

GATTR-LSTM-LSTM: A sophisticated network architecture that processes input data concurrently by employing GAT and Transformer.

GAT-TR-LSTM-LSTM: The model selected for this study, integrating GAT, Transformer encoder, and LSTM encoder-decoder, aims to achieve high-precision trajectory prediction in complex environments.

Table 4 depicts the error values of the ablation experiments for each model, and Fig. 10 illustrate the RMSE and AE comparisons of each model at diverse prediction times. When conducting an analysis of the error performance of each model at various prediction time points, the following observations can be formulated:

Overall, the GAT-TR-LSTM-LSTM model proposed in this study showcases the optimum performance across all evaluation indicators. In comparison with the GATTR-LSTM-LSTM model, the GAT-TR-LSTM-LSTM model realizes a reduction of approximately 9.5% in the mean square error (MSE), and the disparity is particularly substantial at the 2s prediction time, with RMSE and AE decreasing by 8.77% and 6.66% respectively. The GATTR-LSTM-LSTM model adopts a parallel structure of GAT and Transformer, which enhances the model’s response speed; however, it is marginally inadequate in integrating information profoundly, thereby resulting in higher error indicators.

Furthermore, when contrasted with the GAT-LSTM-LSTM model, the GAT-TR-LSTM-LSTM model decreases the mean square error (MSE) by approximately 32.14%, and the RMSE at the 3s prediction time reduces from 0.93 to 0.70, representing a decrease of 24.73%, while the AE decreases from 0.50 to 0.39, a reduction of 22%. This significant disparity is primarily attributed to the fact that the GAT-LSTM-LSTM model does not incorporate the Transformer encoder, thus manifesting insufficiency in long-term prediction accuracy, which also substantiates the effectiveness of the Transformer encoder in enhancing the accuracy of long-term vehicle trajectory prediction.

With respect to the TR(Res)-LSTM-LSTM and TR-LSTM-LSTM models, the GAT-TR-LSTM-LSTM attained respective reductions of 24.00% and 38.71% in the mean squared error (MSE). Regarding the root mean squared error (RMSE) at diverse prediction time points, it accomplished reductions of 13.51%, 13.33%, 17.65%, 23.81%, 24.64%, and 23.08%. These two models did not incorporate the GAT structure, thereby leading to subpar performance throughout the prediction period. Particularly, the TR(Res)-LSTM-LSTM model featuring residual connections decreased MSE from 0.31 to 0.25, representing a reduction of approximately 19.35%.

In contrast to the baseline LSTM-LSTM model, GAT-TR-LSTM-LSTM manifested pronounced superiority, with MSE descending from 0.47 to 0.19, representing a 59.57% decrease. In the 1-second short-term prediction, RMSE and AE were respectively reduced by approximately 21.95% and 23.81%; in the 3-second long-term prediction, RMSE and AE were respectively decreased by approximately 48.15% and 48.00%. Compared with the better performance of LSTM-LSTM model in short-term prediction, GAT-Transformer has higher stability and accuracy in long-term prediction with Transformer’s global dependence modeling capability for long-term time series. These outcomes not merely validate the accuracy of the GAT-TR-LSTM-LSTM model in both short-term and long-term predictions but also accentuate the significance of considering spatial and multi-scale temporal features in vehicle trajectory prediction.

Table 4 Error values for the ablation experiment models on the NGSIM dataset.
Full size table
Fig. 10
figure 10

Comparative analysis chart of evaluation metrics for ablation study models: (a) comparison of RMSE values. (b) Comparison of AE values.

Full size image

Figure 11 depicts the contrast of predicted and actual trajectories among diverse models under three operational circumstances in the ablation investigation. The figure additionally corroborates the exceptional predictive capacity of the model put forward in this paper, which is manifestly superior to that of other models in the ablation experiments.

Fig. 11
figure 11

Predictive performance of each model in the ablation study: (a) straight operation. (b) Right-turn operation. (c) Left-turn operation.

Full size image

Experiments on the highD dataset

To further validate the generalization and stability of the proposed model, experiments were conducted using the highD dataset. This dataset was collected via drones on German highways at a sampling frequency of 25 Hz. A subset of 56_tracks was selected, and after applying preprocessing steps such as denoising and sliding window processing, a trajectory dataset that meets the experimental requirements was constructed.

Some advanced vehicle trajectory prediction methods are selected, and the specific models are shown as follows:

HSTA-Traj47: A Hybrid Trajectory Prediction Framework for Automated Vehicles With Attention Mechanisms.

Dual Transformer48: A Dual Transformer framework that integrates lane change intention prediction and trajectory prediction.

GRANP49: A vehicle trajectory prediction model called Graph Recursive Attention Neural Process.

GIMTP50: Graph-based Interaction-aware Multi-modal Trajectory Prediction framework.

As shown in Table 5, the proposed GAT-TR-LSTM-LSTM model demonstrates significantly better performance on the highD dataset compared to other advanced trajectory prediction methods. Specifically, compared to the Dual Transformer model, the proposed model achieves reductions in RMSE by 63.4%, 53.2%, and 40.5% for RMSE1s, RMSE2s, and RMSE3s, respectively, highlighting its exceptional prediction accuracy. Furthermore, when compared with the GRANP model, the proposed model reduces RMSE for long-term prediction (3 s) by 5.7%, further validating its applicability in complex traffic scenarios.

It is worth noting that, compared to the model’s performance on the NGSIM dataset, the prediction accuracy on the highD dataset is further improved. This improvement can be attributed to the highD dataset’s higher sampling frequency (25 Hz), larger data volume, and higher data quality. The highD dataset provides richer and more diverse traffic scene features, enabling the model to learn more accurate feature representations.

In summary, the proposed GAT-TR-LSTM-LSTM model not only exhibits outstanding performance across different datasets but also achieves stable and accurate trajectory predictions at various time scales, fully validating its transferability and robustness. These results demonstrate the model’s potential for application in real-world traffic scenarios.

Table 5 RMSE of various models on the highd dataset.
Full size table

Conclusion

This paper delves into the trajectory prediction issue of intelligent connected vehicles surrounded by human-driven vehicles in the heterogeneous traffic flow on highways and puts forward a deep neural network model that takes into account both the spatial interaction information of vehicles and the long-term and short-term characteristics of the time series. The model adopts an encoding-decoding architecture, encompassing a GAT encoder employed to encode the spatial interaction features of vehicles, a Transformer encoder utilized to extract global time-dependent relations, an LSTM encoder used for capturing the short-term characteristics of the time series, and an LSTM decoder for generating the future trajectory of the target vehicle. The NGSIM dataset was utilized as the base data to assess the performance of the proposed model in this paper. Each component (GAT, Transformer, LSTM) operates independently within this framework, rendering the overall model highly modular while facilitating debugging and optimization processes—thereby enhancing its maintainability and scalability. The outcomes of the comparative experimentation with other extant methods suggest that the proposed model achieves significant improvements over other models. Several future research directions can be identified: Firstly, more practical constraints, such as lane lines and traffic signal constraints, could be taken into account during the modeling process. Secondly, future studies might contemplate on how to address the influence of anomalous and missing data within the input data during the modeling phase, so as to fulfill the real-time requirements of the algorithm application.