Introduction

A special category of rock slopes, characterized by the presence of rock bridges exhibiting a locking effect governed by joint arrangement, is commonly observed within diverse geological formations under specific environmental conditions. Importantly, the failure evolution and initiation mechanism are influenced by the cracking behavior of key rock bridges. These key rock bridges, which exist between joints, are often referred to as locked sections1,2. In many instances of rockslides containing locked sections, the mechanical cause of locking failure is attributed to direct shear forces. Therefore, investigating the fracture of rock bridges is essential for comprehending the instability processes of slopes.

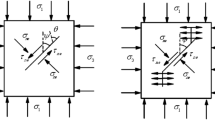
Depending on the positional arrangement of locked sections within the slope, common failure types include middle-locked rockslides, end-locked rockslides, linear-locked rockslides, and stepped-locked rockslides (Fig. 1a–d). In these rockslides, locked sections fail under direct shear force. The middle-locked rockslide represents a failure behavior primarily influenced by a single rock bridge strategically located within the central portion of the slope. Examples of middle-locked rockslides include incidents like the Yanchihe Phosphate Mine rockslide in Hubei, China3, the Zhana rockslide in Longyangxia, China, and the Saleshan rockslide in Gansu, China4. These events are characterized by the direct shearing of the rock bridge. The end-locked rockslide exemplifies a failure behavior predominantly influenced by a singular rock bridge strategically positioned at the back edge of the slope. End-locked rockslides, like the Jiweishan rockslide in Wulong, Chongqing, China5, also involve the direct shearing of the rock bridge. The linear-locked rockslide demonstrates a failure behavior predominantly influenced by multiple rock bridges linearly distributed in the slope. Linear-locked rockslides, such as the Qianjiangping rockslide in Hubei, China6, and the Jipazi rockslide in Sichuan, China7, form a planar failure plane due to the direct shearing of the rock bridge. Similarly, the stepped-locked rockslide demonstrates a failure behavior predominantly influenced by multiple rock bridges arranged in the slope in steps. Stepped-locked rockslides, like the IV# deformation body on the left bank of Xiaowan Hydropower Station in Yunnan, China8, and the Layue rockslide in Tibet, China9, are characterized by the formation of a stepped failure plane due to the direct shearing of the rock bridge. To investigate the initiation mechanism of these locked rockslides, numerous scholars have conducted rock bridge experiments by simplifying rock bridges based on the existing stress state (Fig. 1a–c). Therefore, the progressive fracture process of rock bridges under direct shear force should be studied.

To achieve compressive shear stress, the rock bridge experiments mentioned above mainly involve direct shear tests and uniaxial compression tests. In the aforementioned rockslides, direct shear tests have been conducted on middle rock bridges10, end rock bridges11, and linear rock bridges12. These researches analyze the cracking behaviors of the locked section. However, as shown in Fig. 1d, there is a lack of direct shear tests on stepped rock bridges. Stepped-locked rockslide exhibits a stepped failure mode, controlled by a group of low-inclination joints or two groups of low-inclination joints and high-inclination joints. The failure of the slope is a process in which rock bridges from bottom to top lose their locking effect. The failure of in-situ rock bridges typically shows a tensile fracture due to the low stress level13. Many scholars have simplified the study of failure mechanisms of stepped rock bridges into uniaxial compression tests, focusing on the influence of rock bridge angle on fracture14,15,16,17. A common understanding has emerged from these studies: shear fracture occurs at low angles, tension-shear fracture occurs at medium angles, and tensile fracture occurs at high angles. However, the fracture mode observed in uniaxial compression tests differs from in-situ rock mass failure, making it challenging to gain insights into the mechanism of rockslides solely through rock bridge experiments. In uniaxial compression tests, rock bridges are mediately subjected to shear stress by applying a vertical force. The increasing vertical force raises the normal stress on the rock bridge. This leads to varied fracture modes as stress levels change. Direct shear tests intuitively demonstrate the influence of shear stress on rock bridges while maintaining constant normal stress. Conducting such tests is essential to examine the mechanism of stepped-locked rockslides. Previous research by Sarfarazi et al.18 focused on the tensile fracture mode of rock bridges under the direct shear test. However, The mechanism behind the fracture evolution behavior needs further study.

Fig. 1
figure 1

Schematic diagrams of the simplified rock bridge experiments showing a middle-locked section, b end-locked section, c linear-locked section, and d stepped-locked section, respectively.

Full size image

This study conducts direct shear tests under low normal stress on samples with stepped joints. The cracking behavior of rock bridges, including deformation, strength, fracture mode, and damage, is analyzed. By performing rock bridge experiments, slope bottom friction tests, and slope numerical simulations, the experimental approach proposed in this paper is validated for deducing the shear behavior of small-scale rock bridges to the failure of large-scale slopes. The displacement deflection effect in the rock bridge area elucidates the evolution mechanism of stress on the fracture plane, providing insights into the tensile fracture mechanism of actual rock masses from a rock mechanics perspective. The findings of this study have significant implications for understanding the stepped failure mechanism of slopes.

Experiment methodology

Sample materials and preparation

Red sandstone samples sourced from Ezhou City, Hubei Province, China, were utilized in rock bridge experiments. These samples consisted of clastic minerals and clay minerals, predominantly quartz, feldspar, and illite, along with traces of mica, magnetite, and hematite. The specific mechanical parameters of red sandstone samples could be found in previous research conducted by research group19. The samples were designed as cubes with dimensions of 100 × 100 × 100 mm3 to match the test equipment specifications. The samples were categorized into two types according to the distribution of in-site rock bridges (Fig. 2). The first type of sample only considered the control effect of low-inclination joints, while the second type considered the control effect of both low-inclination joints and high-inclination joints. As shown in Table 1, the length b of the low-inclination joints was set to 40, 50, and 56 mm, corresponding to rock bridge angles of 45°, 90°, and 120°, respectively. The length of the high-inclination joints was set to 10 mm, with angles of 20°, 50°, and 80°. To ensure that the joint could be cut at one time, these joints were created using the wire-cutting method, with a controlled width of 0.6 mm.

Fig. 2
figure 2

Diagram of the red sandstone sample size used in the rock bridge experiments

Full size image

Test equipment and setup

The test equipment utilized in this study employed a static direct shear system (Fig. 3) comprising an acquisition system, a loading system, and a control system. The loading system was capable of applying a maximum normal loading force of 1000 kN and a maximum horizontal loading force of 1500 kN. The testing methodology adhered to the guidelines recommended by the International Society for Rock Mechanics20. A high-speed camera was positioned in front of the sample to capture the fracture evolution process of the rock bridge. The high-speed camera operated at a frame rate of 210 frames per second. Additionally, two acoustic emission Nano30 probes were utilized, with a frequency band ranging from 75 to 750 kHz, a maximum signal amplitude of 100 dB, a threshold set at 40 dB, and a data collection frequency of 1 MSPS. To achieve a tensile fracture mode consistent with the in-site rock mass, it was important to avoid applying excessive normal stress21. As shown in Table 1, direct shear tests were carried out on the first type of samples at normal stresses of 2, 3, and 4 MPa, totaling nine samples. For the second type of sample, a direct shear test was conducted at a normal stress of 2 MPa, involving three samples. To prevent secondary failure along with the middle shear plane, the test would be stopped immediately once the rock bridge failed.

Fig. 3
figure 3

Static direct shear system for rock bridge experiments showing test equipment and red sandstone sample

Full size image
Table 1 Sample information of rock Bridge experiments (N represents the normal stress value)
Full size table

Results

Deformation and strength properties

The mechanical behavior of rock bridges primarily involves deformation and shear strength. The shear force-shear displacement curves of samples under different joint types and normal stress are illustrated in Fig. 4. The blue-shaded area in the figure represents the coalescence of the rock bridge. All curves exhibit microcrack compaction, elastic deformation, plastic deformation, and brittle failure. These curves can be categorized into two types based on the amount of deformation in the plastic stage. Plastic deformation is determined based on the nonlinear characteristics of the curve. The plastic stage of the curve for type A with a 45° rock bridge and type B shows minimal deformation and lacks clear nonlinear characteristics. The increase in shear force during the plastic stage is only 1.12–5.27% of the peak shear force. This indicates a sudden failure of the rock bridge. Type A with 90° and 120° rock bridges exhibit significant nonlinear characteristics in the plastic stage. The increment of shear force in this stage represents 3.34–14.01% of the peak shear force. This indicates obvious precursors (namely the Macroscopic crack evolution process) to the failure of the rock bridge. The deformation law of the curve reflects the fracture mode of the rock bridge, and this deformation law remains consistent within the same fracture mode. Samples with overlapping joint projections in the horizontal direction exhibit more severe shear behavior. This phenomenon may be attributed to the fact that the crack initiation direction deviates from the extension direction of the rock bridge length, and the increased lengths of the two joints have altered the optimal propagation path of the crack. The difference in the curves between the two types can be attributed to the arrangement of joints. The peak shear force represents the coalescence strength of the rock bridge. The curve experiences a rapid drop during the failure stage, indicating strong brittle. Additionally, the appearance of a step in the curve of type B is due to the compression of the high-inclination joint.

Fig. 4
figure 4

Shear force-shear displacement curves of samples showing a 45° rock bridge, b 90° rock bridge, c 120° rock bridge, and d type B

Full size image

The study demonstrates the impact of joint arrangement and normal stress on the shear strength of rock bridges (Fig. 5). It is observed that both the rock bridge angle and high-inclination joint angle exhibit a negative correlation with shear strength under the same normal stress. This is attributed to the lengthening of low-inclination joints and counterclockwise rotation of high-inclination joints, which elevate the stress level at the joint front. Conversely, the normal stress shows a positive correlation with shear strength under the same joint arrangement. Notably, compared to a 45° rock bridge, the internal friction angle shows an increasing trend, while the cohesion exhibits a decreasing trend in 90° and 120° rock bridges due to greater plastic damage before coalescence. This plastic damage, a tensile fracture described in the subsequent section, results in degraded cohesion and increased roughness of the fracture plane.

Fig. 5
figure 5

Coalescence strength of rock bridges showing a type A and b type B

Full size image

Fracture mode and mechanism

The fracture evolution process of a rock bridge is analyzed using high-speed cameras, revealing that the normal stress level does not impact the fracture property. This phenomenon can be attributed to the lower stress level. Specifically, the macroscopic fracture behavior of type A is detailed using a normal stress of 3 MPa as an example. For sample 45-3 (Fig. 6a), initial tensile superficial cracks form on the left and right sides, representing a shear dilatancy phenomenon localized on the sample surface. These superficial cracks are exclusively induced by tensile stress and develop without shear-induced debris. A tensile coalescence crack develops in the middle of the sample as shear stress increases, producing a single-path extension. This coalescence crack is also caused by tensile stress with a rough fracture plane. Samples 90-3 and 120-3 exhibited similar extension paths (Fig. 6b and c), with two oblique tensile coalescence cracks originating from joint tips and eventually forming diamond-shaped blocks. Samples 20-3 and 50-3 display consistent crack growth behavior, with initial superficial cracks due to shear dilatancy (Fig. 7a, b). Subsequently, two coalescence cracks occur in the intact rock between joints. In contrast, sample 80-3 experiences first the occurrence of two tensile coalescence cracks, followed by superficial cracks (Fig. 7c). This is attributed to the inverse relationship between rock bridge length and high-inclination joint angles. Shorter rock bridges are found to have weaker resistance to tensile failure.

Fig. 6
figure 6

Crack evolution process under different rock bridge angles showing a sample 45-3, b sample 90-3, and c sample 120-3

Full size image
Fig. 7
figure 7

Crack evolution process under different high-inclination joint angles showing a sample 20-2, b sample 50-2, and c sample 80-2

Full size image

The analysis of the fracture evolution process reveals that the rock bridge fracture mode consists of tensile single-step mode, tensile diamond-shaped block mode, and tensile double-step mode. The tensile single-step mode corresponds to type A with a 45° rock bridge, while the tensile diamond-shaped block mode encompasses type A with a 90° rock bridge and 120° rock bridge. The tensile double-step mode corresponds to type B. The characteristics of the fracture plane in these modes for the two joint types are depicted in Fig. 8. The presence of polishes and scratches on the fracture plane indicates a typical tensile fracture. This polished scratch area correlates with the internal friction angle of the sample, where a rougher fracture plane suggests a greater internal friction angle. The polished scratch area of the fracture plane of the 90° rock bridge is observed to be larger than that of the 45° rock bridge, supporting the conclusion drawn in Fig. 5a regarding shear strength.

Fig. 8
figure 8

Fracture plane under different fracture modes (U represents the upper part of the sample, and L represents the lower part of the sample)

Full size image

To further elucidate the reasons for the tensile fracture, an analysis of the mechanical mechanism of rock bridge fracture is conducted. Focusing on the force characteristics in the direct shear test, the upper portion of the sample is selected for investigation. Stress analysis of micro-element points along the fracture plane is performed. The stress analysis results are illustrated in Fig. 9, with the fracture plane denoted by a white curved line. The stress components of the micro-element point on the fracture plane are expressed as follows:

$$\left\{ \begin{gathered} {\sigma _x}=x{\sigma _{\text{m}}}{\text{ / }}l (0<x<l - b) \hfill \\ {\sigma _y}={\sigma _{\text{n}}} \hfill \\ {\tau _{xy}}=y{\sigma _{\text{m}}}/l (0.4 L<y<0.5 L) \hfill \\ \end{gathered} \right.$$
(1)

where l is the side length of the sample, b is the length of the low-inclination joint, σn is the normal stress, and σm is the horizontal stress.

Fig. 9
figure 9

Stress analysis of the micro-element point on the fracture plane

Full size image

In the stress analysis schematic diagram, the extension path is influenced by the arrangement of cracks. Macroscopic fracture planes extend obliquely downward from the crack tip. It is noted that compressive stress is considered positive while tensile stress is negative. The normal stress and shear stress on the fracture plane are expressed as follows:

$$\left\{ \begin{gathered} {\sigma _\alpha }=\frac{{\text{1}}}{{\text{2}}}({\sigma _y}+{\sigma _x}{\text{)+}}\frac{{\text{1}}}{{\text{2}}}({\sigma _y}{\text{-}}{\sigma _x}{\text{)cos2}}\alpha - {\tau _{xy}}\sin {\text{2}}\alpha \hfill \\ {\tau _\alpha }=\frac{{\text{1}}}{{\text{2}}}({\sigma _y}{\text{-}}{\sigma _x})\sin {\text{2}}\alpha {\text{+}}{\tau _{xy}}\cos {\text{2}}\alpha \hfill \\ \end{gathered} \right.$$
(2)

where α is the angle between the macroscopic fracture plane and the horizontal direction.

By substituting relevant parameters into Eqs. (1) and (2), the normal stress on the fracture plane can be calculated. The normal stress on the fracture plane in type A and type B is expressed as follows:

$$\left\{ \begin{gathered} {\text{4}}{{\text{5}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.50}}{\sigma _{\text{n}}} ({\text{0}}{\text{0.30}} <a<0.{\text{45}}) \hfill \\ {\text{9}}{{\text{0}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.86}}{\sigma _{\text{n}}} (0.{\text{35}} <a<0.{\text{45}}) \hfill \\ {\text{12}}{{\text{0}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.82}}{\sigma _{\text{n}}} (0.{\text{38}} <a<0.{\text{50}}) \hfill \\ \end{gathered} \right.$$
(3)
$$\left\{ \begin{gathered} {\text{2}}{{\text{0}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.29}}{\sigma _{\text{n}}} ({\text{0}}{\text{0.26}} <a<0.{\text{35}}) \hfill \\ {\text{5}}{{\text{0}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.55}}{\sigma _{\text{n}}} (0.{\text{33}} <a<0.{\text{62}}) \hfill \\ {\text{8}}{{\text{0}}^ \circ }:{\sigma _\alpha }= - a{\sigma _{\text{m}}}{\text{+0}}{\text{0.77}}{\sigma _{\text{n}}} (0.{\text{37}} <a<0.{\text{49}}) \hfill \\ \end{gathered} \right.$$
(4)

where a is a coefficient in the derivation process of equations (its value is related to the position of the micro-element point on the fracture plane).

The relationship between normal stress and horizontal stress is highlighted in Eqs. (3) and (4). Specifically, under the conditions of tensile fracture of rock bridges, an increasing trend in peak shear force is observed with higher normal stress. This is because the higher normal stress increases the shear strength of the sample. Additionally, The a value is negatively correlated with horizontal stress under the same normal stress. Importantly, the a value exhibits an increasing trend with higher rock bridge angle and high-inclination joint angle. Consequently, the horizontal stress decreases as the rock bridge angle and high-inclination joint angle increase. The normal stress on the fracture plane can be determined by substituting the critical value a into Eqs. (3) and (4). The calculated normal stress values on the fracture plane are all tensile stresses, exceeding the tensile strength of the rock bridge (Fig. 10), thus providing mechanical insight into the formation mechanism of tensile coalescence cracks.

Fig. 10
figure 10

Fracture properties showing a different rock bridge angles with 3 MPa normal stress and b different high-inclination joint angles with 2 MPa normal stress

Full size image

Damage evolution behaviors

AE count rate and AE cumulative count rate are indicators of damage evolution within rocks22,23,24,25. AE count rate reflects the activity level of microcracks in two states: quiet period and active period. The quiet period signifies the initiation of microcracks, while the active period represents the growth of microcracks leading to macrocrack formation. AE cumulative count rate demonstrates the speed of microcrack development, with a stable period and an increasing period. The stable period indicates no damage within the rock bridge, while the increasing period shows gradual damage accumulation. A sudden change in the curve of the AE cumulative count rate indicates significant microcrack generation. The damage evolution of type A and type B samples under 3 MPa normal stress is analyzed. The 45° rock bridge has a short active period nearing failure (Fig. 11a), whereas the 90° and 120° rock bridges exhibit longer active periods (Fig. 11b, c), suggesting more damage before failure. The damage inside rock bridges correlates with deteriorating mechanical properties. The stable period of AE cumulative count rate for the 45° rock bridge lags compared to the 90° and 120° rock bridges. The curve transitions to the increasing period only after the shear force reaches 39.24 kN. This implies that a certain level of damage accumulation is necessary before microcracks emerge.

For type B, the changing trend of the AE count rate is consistent with that of the 45° rock bridge (Fig. 11d–f). The curves all exhibit a prolonged quiet period, followed by a brief active period that occurs rapidly as the peak shear force is approached. This suggests a similar damage evolution behavior among them. However, the AE cumulative count rate displays a longer stable period with lower values and shows an increasing period when failure occurs. This difference can be attributed to the short length of the rock bridge. The presence of high-inclination joints weakens the locking effect of the rock bridge.

Fig. 11
figure 11

AE characteristics showing a sample 45-3, b sample 90-3, c sample 120-3, d sample 20-2, e sample 50-2, and f sample 80-2

Full size image

Stress field characteristics

The time series photos captured by the high-speed camera are imported into the flow field processing system to obtain the displacement field on the sample surface. Subsequently, the stress field is derived through algorithm programming. Stress calculation is based on elastic mechanics theory and finite element principle, and the specific equations are as follows:

$$\left\{ \sigma \right\}=\frac{E}{{{\text{2}}A{\text{(1-}}{\mu ^{\text{2}}})}}\left[ \begin{gathered} {\text{1 }}\mu {\text{ 0}} \hfill \\ \mu {\text{ 1 0}} \hfill \\ {\text{0 0 (1-}}\mu ){\text{/2}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {b_i} 0 {b_j}{\text{ 0 }}{b_m}{\text{ 0}} \hfill \\ 0 {c_i}{\text{ 0 }}{c_j}{\text{ 0 }}{c_m} \hfill \\ {c_i} {b_i} {c_j} {b_j} {c_m} {b_m} \hfill \\ \end{gathered} \right]\left\{ \begin{gathered} {u_i} \hfill \\ {v_i} \hfill \\ {u_j} \hfill \\ {v_j} \hfill \\ {u_m} \hfill \\ {v_m} \hfill \\ \end{gathered} \right\}$$
(5)

where E and µ represent the elastic modulus and the Poisson’s ratio, respectively. ci, cj, and cm denote the differences in the x-coordinates of any two points within the triangular mesh nodes in the flow field, while bi, bj, and bm correspond to differences in the y-coordinates. ui, uj, and um indicate the displacement increments in the x-direction of any two points within the triangular mesh nodes in the flow field, while vi, vj, and vm correspond to displacement increments in the y-direction.

To mitigate the impact of boundary conditions, the stress field area is defined as 30 to 70 mm horizontally and 38 to 62 mm vertically. Within this specified region, the shear behavior of the rock bridge is effectively shown. Based on previous analysis, all samples exhibit three fracture modes (see Fig. 8). Hence, samples 45-3, 90-3, and 20-2 are taken as case studies to analyze the stress field before rock bridge coalescence (Fig. 12). The white lines in the figure depict joints.

In sample 45-3 (Fig. 12a), stress concentration bands are observed on the rock bridge fracture plane in the horizontal stress cloud diagram and shear stress cloud diagram. However, the stress concentration band in the vertical stress cloud diagram is discontinuous. This discrepancy is attributed to the gradual increase in horizontal shear force. The joint tip in the horizontal stress cloud diagram experiences compressive stress, while the joint tip in the vertical stress cloud diagram undergoes tensile stress, suggesting a compression-tension-shear mechanical mode for the rock bridge fracture. Stress concentration bands are also visible on the left and right sides of the sample in the vertical stress and shear stress cloud diagrams, indicating the occurrence of tensile superficiality cracks and highlighting a compression-shear mechanical mode due to shear dilatancy.

Stress concentration bands are observed in the horizontal stress, vertical stress, and shear stress cloud diagrams for sample 90-3 (Fig. 12b). The compressive stress states of both horizontal and vertical stresses at the joint tip suggest that the fracture of the rock bridge follows a compression-shear mechanical mode. A comparison with the 45° rock bridge reveals differences in stress concentration bands, indicating distinct failure modes. In the case of the 90° rock bridge, stress concentration bands do not appear at the connection between adjacent joint tips, implying an alternative crack propagation path. Instead, stress concentration bands are visible on the left and right sides of the sample. With increasing joint length, the rock bridge angle also increases, leading to a change in the fracture path. These stress concentration bands extend from the joint tips to adjacent joints at a specific angle, indicating a diamond-shaped block failure.

For sample 20-2 (Fig. 12c), the high-inclination joint tip experiences compressive stress in the horizontal stress cloud diagram and tensile stress in the vertical stress cloud diagram. This suggests that the stress concentration band shares similarities with a 45° rock bridge, indicating a compression-tension-shear mechanical mode for rock bridge fracture. Shear dilatancy also follows a compression-shear mechanical mode. The crack propagation occurs from the high-inclination joint tip to the low-inclination joint tip due to the higher stress level at the former.

Fig. 12
figure 12

Stress cloud diagrams in horizontal, vertical, and tangential directions. a sample 45-3, b sample 90-3, and c sample 20-2 represent different fracture modes, respectively

Full size image

Interpretation of tensile fracture of the locked section

In rock bridge experiments, the direct shear force acts on the rock bridge along the extension direction of low-inclination joints, leading to eventual tensile fracture under low normal stress. The displacement field of the rock bridge before failure is obtained through a particle image velocity processing system (Fig. 13a–c). As the shear force increases, the displacement of the rock bridge area and the left area deflect noticeably, while the displacement direction of the right area becomes parallel to the extension direction of the low-inclination joints. This indicates that the displacement of the rock bridge changes with increasing shear force, deflecting from vertical to horizontal. Furthermore, normal displacement in the rock bridge area decreases while horizontal displacement increases. The reduction of normal displacement must overcome the action of the applied normal stress. The lower the normal stress, the stronger the displacement deflection ability. During the displacement deflection process, the stress state on the fracture plane exhibits two distinct phases. In the initial phase, the displacement vector progressively rotates from the vertical direction towards the normal direction of the rock bridge, resulting in a gradual increase in tensile stress and a concomitant decrease in shear stress on the fracture plane. Subsequently, in the second phase, the displacement vector continues its rotation from the normal direction of the rock bridge towards the horizontal orientation, leading to a progressive reduction in tensile stress accompanied by a corresponding increase in shear stress. The displacement deflection phenomenon reveals a competitive mechanism between tensile fracture and shear fracture in rock bridges. A progressive increase in shear force induces an initial predisposition towards tensile fracture, followed by a subsequent transition to shear fracture behavior. The rock bridge is more likely to undergo a tensile fracture than a shear fracture under low normal stress.

To validate the applicability of the shear behavior observed in rock bridge experiments to real-life slopes, a series of physical model tests and numerical simulations are conducted. The consistent finding in these studies is that the fracture of the rock bridges is tensile. The physical model test is based on a previous study by Chen et al.26 on bottom friction tests. The slope model, measuring 400 × 400 mm² (length×height), features a slope angle of 60°. It incorporates two distinct joint sets: a low-inclination set inclined at 35° with a length of 70 mm and (2) a high-inclination set inclined at 80° with a length of 10 mm. The model is constructed from simulated materials with a mass ratio of barite powder, quartz sand, and paraffin oil of 60:31.6:9. The established similarity relationships from the model tests are presented in Table 2. The displacement field of a slope containing a group of low-inclination joints and the displacement field of a slope containing two groups of low-inclination joints and high-inclination joints are shown (Fig. 13d, e). The displacement of the rock bridge area undergoes obvious deflection and tends to deflect in the extension direction of the low-inclination joints. Near the low-inclination joint zone, the displacement direction was found to be parallel to the joint extension direction. These findings from the physical model test closely resemble the displacement field observed in rock bridge experiments. The 2D Particle Flow Code is utilized in the numerical simulation to analyze the slope. The slope is categorized into low-inclination joints with 45° and 90° rock bridges, as well as a combination of low-inclination joints and high-inclination joints. The methodology for slope numerical modeling is derived from previous research conducted by research group21. Previous studies, such as the analysis of the Xiaowan Hydropower Station, have successfully replicated the stepped mesoscopic progressive failure process of the slope. The simulated slope has a length of 60 m, with a foot length of 12 m and a height of 48 m. The slope angle measures 60°, while the low-inclination joint is at an angle of 35°, and the high-inclination joint is at 70°. In the numerical model, the particle radius ranges from 4 to 10 cm, and the microscopic parameters utilized are presented in Table 3. Observations of displacement fields (Fig. 13f–h) show deflection in the displacement direction within the rock bridge area, while the displacement direction above the joints aligns roughly parallel to the joint extension direction. These findings in the numerical simulation closely resemble the displacement fields observed in rock bridge experiments, suggesting that the shear behavior of rock bridges in direct shear tests can mirror the mechanical behavior of actual slopes. Specifically, direct shear forces are more likely to induce tensile fractures in rock bridges under low normal stress, providing a reasonable mechanical explanation based on the evolution characteristics of displacement fields.

Fig. 13
figure 13

Displacement field of locked sections showing a–c rock bridge experiments, d, e physical model tests, and f–h numerical simulations

Full size image
Table 2 Similarity relationship between slope model and prototype26.
Full size table
Table 3 Mesoscopic parameters used in numerical simulations21
Full size table

The stress intensity factor, commonly used in linear elastic fracture mechanics27, is ideal for characterizing the propagation of defects and is particularly effective in describing the brittle failure of the fractured rock mass. According to Eq. (1), the stress state at the joint tip is as follows:

$$\left\{ \begin{gathered} {\sigma _x}={\sigma _{\text{m}}}{\text{ (}}l - b{\text{)/ }}l \hfill \\ {\sigma _y}={\sigma _{\text{n}}} \hfill \\ {\tau _{xy}}=0.4{\sigma _{\text{m}}}/l \hfill \\ \end{gathered} \right.$$
(6)

Therefore, the stress intensity factor at the joint tip is expressed as follows:

$${K_{{\text{II}}}}=0.4{\sigma _{\text{m}}}\sqrt {\pi b} /l$$
(7)

The fracture criterion for crack initiation is KII = KIIc since the rock bridge shows a tensile fracture, where KIIc is the fracture toughness. Furthermore, the critical horizontal stress causing a tensile fracture is as follows:

$${\sigma _{{\text{mc}}}}=1.25\sqrt {\frac{3}{{\pi b}}} {K_{{\text{Ic}}}}$$
(8)

Discussion

To understand the failure evolution and initiation mechanism of prototype slopes, conducting rock bridge experiments is crucial. This study examines the fracture of locked sections in slopes with stepped joints using direct shear tests under low normal stress. However, previous research has primarily utilized uniaxial compression tests to investigate crack initiation, propagation, and coalescence in rock masses with stepped joints. Park and Bobet28 observed that when the rock bridge angle is less than 90°, the fracture type in the single-stepped mode is tension-shear (Fig. 14a), while angles greater than 90° result in a shear fracture in the single-stepped mode (Fig. 14b) and a tensile and tension-shear fracture in the diamond-shaped block mode (Fig. 14c, d). Conversely, Zhao et al.29 found that angles less than 90° produce both shear and tensile fractures (Fig. 14e, f), while angles greater than 90° lead to a tension-shear fracture (Fig. 14g). Other studies by Bobet30, Li et al.31, Xu et al.32, and Chen et al.33 have also identified similar fracture types in rock bridges, including shear, tensile, and tension-shear, albeit with slight variations in fracture modes. These investigations highlight the complexity of cracking behavior in rock bridges under uniaxial compression tests, making it challenging to deduce the tensile fracture mechanism of real rock masses. This complexity is attributed to low compressive shear stress levels occurring in real rock masses with stepped joints21,34. In comparison to the aforementioned studies, our research offers several advantages: (1) The direct shear tests conducted under low normal stress more accurately reflect the stress conditions present in actual slopes. (2) The tensile fracture behavior observed in rock bridges closely resembles the failure process experienced by real rock masses. (3) Understanding the fracture mechanism of rock bridges enhances our comprehension of the initiation mechanism associated with large slopes. Therefore, this paper focuses on the impact of low compressive shear stress on the cracking behavior of rock bridges, shedding light on the tensile fracture mechanism of locked sections in slopes with stepped joints through rock bridge experiments.

Fig. 14
figure 14

Various forms of fracture modes in uniaxial compression tests (T represents tensile fracture, and S represents shear fracture)

Full size image

It is very effective in understanding the inherent instability mechanism of slopes based on insights from rock bridge experiments. Tang et al.10 conducted direct shear tests on samples with a middle rock bridge. The impact of the locked section length on shear resistance was investigated, highlighting the interplay between cohesion and internal friction. Wu et al.35 proposed a critical load calculation model for overhanging rock instability based on vertical loading tests on samples with an end rock bridge. Qin et al.11 discovered that block spalling in samples with an end rock bridge under direct shear tests is a precursor of Jiweishan rockslide, attributing to tensile crack propagation. Tang et al.36 conducted direct shear tests on samples with linear rock bridges. The influence of the number of rock bridges on slope failure is studied under the same discontinuity persistence, offering a modified stability calculation equation. By comparing displacement fields from rock bridge experiments, slope physical model tests, and slope numerical simulations, the study confirms that the cracking behavior observed in rock bridge experiments can reflect real slopes. In the obtained results, tensile damage on the fracture plane is identified as the primary cause for the reduction in cohesion and the increase in the internal friction angle of rock bridges. The mechanism of rock bridge angle and high-inclination joint angle inversely proportional to peak shear strength is revealed based on the mechanism of tensile fracture. This study also highlights the essential reason contributing to tensile fracture in rock bridges under low compressive shear stress levels. These findings offer valuable insights into understanding the failure evolution process of locked sections. In future research, establishing a quantitative relationship between rock bridge angle and peak shear strength is essential, which is essential for slope stability analysis.

Conclusion

This paper focuses on the fracture of samples containing stepped joints under low normal stress. The obtained results reveal the mechanical mechanism of the tensile failure. The following conclusions are drawn:

  1. 1.

    The deformation behavior of rock bridges exhibits strong brittle characteristics. Plastic damage serves as a precursor to rock bridge failure, with its severity being impacted by the rock bridge angle. High-angle rock bridges, as opposed to low-angle ones, display lower cohesion and higher internal friction angles. Acoustic emission parameters suggest significant tensile damage occurs in high-angle rock bridges.

  2. 2.

    The fracture modes of the rock bridge include single-step mode, double-step mode, and diamond-shaped block mode. Shear dilatancy occurs on both sides of the sample, leading to the formation of tensile superficial cracks. The tensile fracture plane of the rock bridge typically exhibits a certain degree of polishing and scratching. The normal stress value on the fracture plane is determined, and the mechanical causes of tensile fracture are analyzed.

  3. 3.

    The stress concentration zone represents the mechanical mode of fracture. The fracture of low-angle rock bridges involves a compression-tension-shear mechanical mode, while high-angle rock bridges experience a compression-shear mechanical mode. Fractures in samples with a high-inclination joint also exhibit a compression-tension-shear mechanical mode. The displacement deflection effect in the rock bridge area elucidates the stress evolution mechanism that leads to tensile fractures.