Failure control of large-scale exposed tunnels under the combined effects of excavation damage and dynamic disturbance at a depth of 1240 m

Abstract

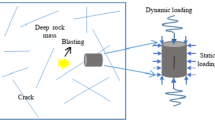
The stability of deeply buried tunnels is significantly influenced by the combined effects of primary joint fissures, blasting-induced damage, high-stress environments, and dynamic disturbances, all of which are key contributors to rock instability. The instability characteristics of rock masses under varying disturbance frequencies and amplitudes remain unclear, making it difficult to establish a reliable basis for tunnel management. This study measured the distribution of joint fissures on the tunnel surface at a burial depth of 1240 m, investigated rock failure characteristics through low-frequency perturbation true triaxial experiments, and analyzed support designs incorporating various combinations of metal mesh, bolts, anchor cables, and shotcrete. The results indicate that as the amplitude and frequency of disturbances increase, the number of cracks in the rock rises significantly and irregularly, while the fractal dimension of the rock’s fracture direction decreases. When the disturbance reaches 10 MPa and 10 Hz, the fractal dimension decreases to a minimum value of 0.62. Additionally, the frequency of pore orientation at angles between 80° and 120° peaks at 52% of its maximum value, approximately 1.68 times that of the original rock. This suggests that the stress experienced by the particles within the rock becomes uneven after disturbance, leading to stress concentration and a pronounced fracture direction. Furthermore, as the amplitude and frequency of disturbances increase, the micropore area observed in scanning electron microscope (SEM) images initially increases rapidly, then continues to grow at a slower rate, with the rate of increase progressively diminishing. Simulations reveal that standard bolts in tunnels subject to dynamic disturbances can effectively resist disturbances with strengths below 40 MPa. However, when the disturbance intensity exceeds 70 MPa, the anchor’s bearing capacity reaches its limit. In the case of bolt-supported tunnels subjected to dynamic disturbances, characteristics such as shallow anchoring depth, low preload force, significant separation of deep surrounding rock, and poor anti-damage ability of the bolts are observed. The use of highly prestressed anchor cable support can resist dynamic disturbances up to 100 MPa and enhance the tunnel’s damage resistance. By combining stress and peak ground acceleration (PGA), the tunnel is classified into five potential risk levels (I to V). Based on this classification, a tunnel support strategy under high-stress disturbances is proposed. Practical applications demonstrate that implementing this strategy reduces the deformation of the surrounding rock by 42.47% to 51.07%, significantly improving the tunnel’s stability.

Introduction

The quality of deep underground tunnels is impacted by various factors such as the overlapping of primary joint fissures, damage from blasting, high stress conditions, and dynamic disturbances ^1,2,3. Blasting damage can worsen the expansion of primary joint fissures and lead to significant loosening around the tunnel, particularly in high-stress environments ^4,5,6. Additionally, dynamic disturbances from afar can cause ground movement around the tunnel, setting the minimum stability requirements. Over time, factors like weathering, repeated dynamic disturbances, and rock creep can also affect tunnel stability ^7,8,9,10. Deep rocks differ from shallow rocks in terms of strength, brittleness, and ductility, with increasing burial depth leading to stronger rock that transitions from brittle to ductile properties. However, external stress can cause the rock to shift back from ductile to brittle, increasing the risk of dynamic disasters like rock bursts ^{11,12,13,14,15}. The Sanshandao Gold Mine, the largest seabed gold mine in Asia, has mining depths exceeding 1100 m in 2022, with current development reaching 1240 m and tunnel lengths exceeding 20 km. The mine has experienced frequent instability and damage accidents in recent years, significantly impacting safe and efficient mining operations.

Figure 1 illustrates the various types of disturbances and damages that high-stress tunnels may experience, including rock collapse, fragmentation, extrusion deformation, and roof fall. Managing tunnels in deep mines affected by both dynamic and static stresses poses challenges. Current methods to address tunnel disasters caused by high static loads include pressure relief support ¹⁶, hydraulic fracturing ¹⁷, borehole pressure relief ¹⁸, and stress transfer. For disasters caused by dynamic load stress ^19,20, techniques such as highly prestressed anchor cables, energy-absorbing brackets, and anti-collision components are utilized to enhance tunnel support capacity and absorb dynamic loads while ensuring tunnel stability ^{10,21,22,23,24}. Aldannawy H A et al. ²⁵ conducted simulations on the dynamic interaction between drill bits and rocks to analyze rock damage from different impact forces. He Manchao et al. ²⁶ introduced high prestress compensation technology for tunnels based on various dynamic disaster mechanisms. Zhao S et al. ²⁷ studied the impact damage mechanism of extra-thick coal seam roadways, identifying key factors in top coal damage and analyzing dynamic load stress wave propagation and response characteristics of rock support systems. Feng Xiating et al. ^28,29 used true triaxial testing to determine threshold values for rock bursts under axial low-frequency periodic dynamic disturbance loads. Minaeian V et al. ³⁰ conducted experimental research on sandstone’s mechanical properties under three-dimensional dynamic and static combined loading using a modified Hopkinson rod test device. Although the above experts have done a lot of research on rock damage under dynamic disturbance, few scholars have systematically studied rock disturbance damage at a depth of more than 1200 m through true triaxial tests. And there are few equipments that can complete this test.

Fig.1

Deformation and damage of deep tunnel: (a) rock collapse, (b) fragmentation (c) extrusion deformation (d) roof fall.

The effects of high stress on destabilizing damage to tunnel perimeter rock during large exposed tunnelling under excavation damage and dynamic disturbance at greater depths (exceeding 1200 m) are not well understood. The impact of static load versus dynamic loads on perimeter rock damage and the specific damage modes remain unclear. This lack of clarity hinders the development of accurate support and disaster prevention measures. To address this, it is crucial to conduct true triaxial static load and dynamic-static combined loading tests to analyze the damage mechanism and key influencing factors. By studying the time evolution of surrounding rock and anchor cable stress under varying dynamic loading intensities, it will be possible to classify the potential risk level of the roadway. Based on this classification, a support strategy can be devised to mitigate high stress disturbances according to the identified risk level. This research will offer valuable insights for designing support systems for similar tunnelling projects affected by disturbances.

True triaxial cyclic dynamic disturbance experiment

The Sanshandao Gold Mine has reached an excavation depth of -1240 m, where the deep rockmass is subjected to substantial self-gravity and tectonic stress fields. Coupled with elevated temperatures and coastal environmental conditions, these factors create a challenging “three high” environment—high stress, high temperature, and high humidity—for the rock mass. Deep rock masses face complex multi-field and multi-phase interactions, with their responses to disturbances being notably severe and intricate. Consequently, studying the joints and fissures within the deep rock mass and conducting disturbance experiments are essential steps in establishing a foundation for preventing and mitigating deep mining disasters.

Quality classification of joints and fissures on the surface of rock mass

The rock mass characteristics at the selected investigation site are representative, with a sufficiently large exposure scale. Analyzing the structural planes through measurement statistics and probabilistic analysis effectively captures the distribution patterns of the ore rock mass’s structural planes. To investigate the joints and fissures within the rock mass, the -1240 m middle section of the tunnel was divided into four investigation zones. Joint data from each zone were individually analyzed, after which the primary joint data from all zones were compiled and statistically examined to identify the key joints influencing rock mass stability across the region. Figure 2 illustrates the distribution of joints and fissures on the rock mass surface at measuring point M3.

Fig.2

Distribution of joints and fissures on the rock mass surface at M3 measuring point.

By systematically analyzing joint inclination, inclination angle, trace length, and spacing, it was determined that the joint inclination angles in the M3 measurement zone predominantly range between 50° and 70°, while the structural plane inclinations are mostly within the 100° to 120° range (refer to Fig. 3). This suggests that the structural planes of the rock mass in this area are generally inclined or steeply inclined. Based on these findings and rock mechanics data, the rock mass quality will be categorized accordingly.

Fig.3

Statistics of joint and crack parameters:(a) Inclination distribution law (b) Inclination angle distribution law (c) Trace length distribution law (d) Spacing distribution law.

The Q-classification method, developed by Barton and colleagues in Norway, utilizes six parameters to evaluate rock mass quality. It emphasizes rock block size, frictional strength, water conditions, and stress levels. The specific details of this method are provided in Eq. (1).

$$Q = \frac{RQD}{{J_{n} }}\frac{{J_{r} }}{{J_{a} }}\frac{{J_{w} }}{SRF}$$

(1)

where RQD is the rock quality designation; ${J}_{n}$ is the number of joint groups; ${J}_{r}$ is the joint roughness; ${J}_{a}$ is the degree of joint alteration; ${J}_{w}$ is the joint water reduction coefficient; and $SRF$ is the in-situ stress reduction coefficient.

The pairwise combinations of the above six parameters in the $Q$ system classification reflect three aspects of rock mass quality and classify the surrounding rock according to the size of the $Q$ value. The classification results are shown in Table 1.

Table 1 Q classification results.

Based on the Q system classification findings, the ore bodies and adjacent rocks in the Sanshandao gold mine study region are categorized as Class IV and V rock masses, with a lower scoring value within Class IV. Specifically, a portion of the M3 survey zone falls under Class V rock mass, indicating poor quality. It is crucial to be vigilant about potential rock mass instability during construction. The support system for fractured areas should be robust and utilize a variety of support methods.

Experimental plan and equipment introduction

Specimen preparation

The rock samples used in this experiment were monzogranite sourced from the Sanshandao Gold Mine. Four sampling points were selected, with three located in the -1240 m tunnel and one in the -1240 m contact tunnel, as illustrated in Fig. 4a. Sampling point M1 was taken from both sides of the tunnel, while M2, M3, and M4 were collected from the top, two sides, and bottom of the tunnel, respectively. A total of 10 cores were drilled, and each core was processed into a standard sample measuring 100 mm × 50 mm × 50 mm, as depicted in Fig. 4c. In this study, 45 standard test blocks were prepared, as depicted in Fig. 4b. All rock samples were precisely cut and processed to ensure that they can present consistent geometry and physical properties in the experiment. The processing accuracy strictly adhered to the International Society for Rock Mechanics (ISRM) standards. During the processing, we used standardized tools to ensure that the dimensional error is controlled within ± 0.1 mm. Additionally, adjacent end faces were perpendicular, opposite end faces were parallel, and the maximum angular deviation was limited to 0.25 degrees.

Fig.4

Standard test piece: (a) Sampling location (b) All processed test pieces (c) Standard sample size.

Test equipment

This study utilized the true triaxial testing machine at the Deep Well Mining Laboratory of Shandong Gold Group. The testing system consists of multiple components, including the equipment host, control console, pressurization and heating system, pore fluid system, electrical system, hydraulic system, and pressure chamber. It employs dynamic hydraulic servo synchronous centering loading control technology to apply low-frequency dynamic disturbances along a specific principal stress direction during the stress–strain process. These disturbances, applied in the direction of the maximum principal stress, are carefully controlled to avoid damaging the rock specimens. The system accommodates centimeter-scale rock sample failures and replicates the failure evolution characteristics of rock masses under stress conditions equivalent to a burial depth of 3000 m. The physical and conceptual diagrams of the testing system are shown in Fig. 5a and b, respectively.

Fig.5

Chamber rock true triaxial testing system:(a) Physical picture of the test system (b) Overall conceptual picture of the test system (c) Loading system.

The high-voltage servo dynamic triaxial testing machine features three independent loading systems: two horizontal systems and one vertical loading/unloading system, as shown in Fig. 5c. The pressure chamber flexibly applies loads in the direction of the minimum principal stress. The machine delivers a maximum load of at least 2000 kN in the first principal stress direction, 4000 kN in the second, and a maximum pressure of 80 MPa in the third principal stress direction. The disturbance load ranges from 0 to 20 kN, with frequencies varying between 0 and 20 Hz. It supports multiple waveforms, including sine waves, shock waves, triangle waves, square waves, and ramp waves. This experiment primarily focused on sine wave disturbances.

True triaxial disturbance test schemes

To investigate the failure behavior of rocks under various low-frequency dynamic disturbances, researchers conducted experiments using a true triaxial testing machine. The disturbances were applied at a frequency of 20 Hz with intensities of 8 MPa, 14 MPa, and 20 MPa. The dynamic perturbation true triaxial test consisted of two stages: static loading and dynamic perturbation loading, with the perturbation force applied along the σ1 direction.

• 1. The sample was loaded in the σ₁ and σ₂ directions to 1 MPa using the displacement control method at a rate of 0.01 mm/s, while the σ₃ direction was loaded to 0.1 MPa.

• 2. The specimen was simultaneously loaded in all three directions to the initial in-situ stress state using the load control method at a rate of 0.5 MPa/s. When the stress reached 80% of the average peak strength, a sinusoidal dynamic disturbance load was introduced.

• 3. The sinusoidal dynamic disturbance load, controlled by displacement, ranged from the σ1 static stress to just below the average peak strength observed in the static true triaxial test. The cyclic perturbation was repeated 3000 times. If the sample did not fail after 3000 cycles, it was further loaded using the deformation control method at a rate of 0.015 mm/min until failure. The stress path of the experiment is illustrated in Fig. 6.

Fig.6

Stress path.

Mechanical properties and damage characteristics

Stress–strain curve and mechanical property analysis

The stress–strain curve of the rock, as shown in Fig. 7(a), demonstrates distinct characteristics during static loading, consisting of a pore compaction phase and a linear elastic phase. In the compaction phase, compression occurs in all three principal stress directions. In contrast, during the elastic phase, compression primarily occurs in the σ1 direction, while expansion is observed in the σ₂ and σ₃ directions, leading to a decrease in volumetric strain. The stress–strain curve from perturbation experiments closely resembles the static curve before dynamic loading.

Fig.7

Rock full stress–strain curve: (a) unperturbed total stress-force-strain curve (b) stress–strain of 8 MPa curve disturbance (c) stress–strain curve of 14 MPa disturbance (d) stress–strain curve of 20 MPa disturbance.

When dynamic disturbance loads are applied, a disturbance ring appears, inducing compression in the σ₁ direction and expansion in the σ₂ and σ₃ directions, with volumetric strain increasing as disturbances accumulate. Repeated cycles of dynamic loading further compress the σ1 direction and expand the other directions, ultimately causing rock failure due to damage accumulation and crack propagation. This failure is accompanied by a substantial stress drop. The observed expansion behavior preceding rock failure and seismic events provides critical insights into the failure mechanisms of brittle rocks. Volumetric strain or minimum principal strain effectively captures the rock’s expansion behavior prior to failure, offering valuable indicators for predicting instability.

During the application of dynamic perturbations, the maximum principal strain of the specimen increases progressively with the number of cycles until it reaches the failure limit. The intensity of rock failure decreases as disturbance stress amplitudes increase, provided that σ₂, σ₃, and vibration frequency remain constant. For example, specimens 1240–1 and 1240–2 experienced disturbance intensities of 8 MPa and 14 MPa, respectively, as shown in Fig. 7b and c. Although no visible damage occurred during the tests with these disturbance loads, the peak strength of the rock declined as the disturbance amplitude increased. In contrast, specimen 1240–3, subjected to a disturbance amplitude of 20 MPa, suffered rock failure during the disturbance process.

At low disturbance stress levels, the maximum principal strain of the specimen increases slowly under dynamic disturbance loads, remaining below the rock’s failure threshold and preventing damage. Conversely, high disturbance stress results in a more significant increase in maximum principal strain, which eventually surpasses the rock’s failure threshold, leading to specimen failure. This behavior highlights the existence of a strain threshold for rock failure under dynamic disturbance loads.

The strain behavior during cyclic loading can be categorized into three stages: initial deformation, constant velocity deformation, and accelerated deformation. In the initial deformation stage, the axial strain rate and accumulated strain per cycle are relatively high. The constant velocity deformation stage is characterized by slow and steady axial strain development over a prolonged period, accounting for a significant portion of the specimen’s fatigue life. Finally, the accelerated deformation stage features a rapid increase in strain rate, resulting in specimen failure. The accumulation of axial deformation across these stages ultimately leads to the specimen’s final failure, as depicted in the enlarged view in Fig. 7d.

The data presented in Table 2 illustrate the peak strength of rocks under static tests and disturbance tests conducted at varying frequencies. The average peak strength of rocks in static tests is recorded at 325.11 MPa. Under a disturbance amplitude of 8 MPa, the average peak strength decreases to 297.43 MPa. At disturbance amplitudes of 14 MPa and 20 MPa, the average peak strengths further decrease to 276.34 MPa and 252.57 MPa, respectively. The transition from static testing to an 8 MPa disturbance results in an average peak strength reduction of 8.51%. Subsequently, a 7.09% decrease is observed as the disturbance amplitude increases from 8 to 14 MPa, followed by an 8.60% decrease when the disturbance amplitude rises from 14 to 20 MPa. Overall, the average rate of decline in rock peak strength is 8.06% as the disturbance amplitude increases. Additionally, the decline rate slows down with higher disturbance amplitudes. Notably, at a disturbance amplitude of 20 MPa, rock damage occurs during the disturbance process, suggesting that higher amplitudes lead to increased internal damage in rocks.

Table 2 Physical and mechanical properties of rock.

Rock failure characteristics

The failure mechanism of rock is characterized by the propagation and expansion of internal cracks when subjected to external loads. This failure mode serves as an indicator of stress distribution within the rock during failure, providing valuable insights into the dynamic instability and failure processes in rock formations, particularly in deep underground engineering applications. To analyze and compare the failure modes of specimens under static loading and three different types of dynamic disturbance loads, post-damage specimens were examined. As shown in Fig. 8, the failure modes of the specimen under static force and three low strain rate dynamic disturbances are compared.

Fig.8

Rock failure pattern: (a) Undisturbed rock failure form (b) 8 MPa disturbed rock failure form (c) 14 MPa disturbed rock failure form (d) 20 MPa disturbed rock failure form.

The static test failure pattern in Fig. 8a reveals predominantly shear failure in the rock. Notably, cracks aligned with the σ₁ loading direction are observed near both sides in the σ₃ direction. Additionally, splitting cracks parallel to the loading direction are visible near the sample’s sides in the σ₃ direction, while shear cracks are evident in the central region of the sample. Localized fragmentation failure is observed, accompanied by noticeable expansion of the sample. The failure exhibits a multi-zonal failure mode, with a certain level of load-bearing capacity retained even after failure.

The analysis presented in Fig. 8 illustrates that the failure characteristics of specimens subjected to static loading and dynamic disturbance loading exhibit similar multi-partitioned patterns. Specifically, splitting cracks aligned parallel to the loading direction are observed near the surfaces on both sides of σ₃, while shear cracks manifest in the central region. The number of cracks increases gradually with the escalation of disturbance intensity, with no discernible cracks evident in the rock under an 8 MPa disturbance. This absence of cracks may be attributed to the low dynamic disturbance effect, impeding crack development. Notably, crack width is smallest under static monotonic loading conditions. Conversely, dynamic disturbance loading induces significant sample expansion and localized fragmentation damage as disturbance intensity rises, resulting in more pronounced damage compared to static loading. At a stress disturbance level of 20 MPa, rock damage cracks cover approximately 65% of the rock surface area, indicating severe internal damage and highlighting the substantial impact of dynamic disturbance on high-stress rock damage near excavation boundaries.

Microscopic fracture morphology characteristics of rocks

The primary cause of strength reduction in rocks due to the propagation of microcracks is the alteration of the rock’s microstructure by external disturbances. Scanning Electron Microscopy (SEM) can be employed to observe changes in the microstructure of rock surfaces under various disturbances. Figure 9 shows the surface microstructure of a sample under disturbances of 8 MPa, 14 MPa, and 20 MPa at a magnification of 5000 times. The figure reveals that with increasing disturbance frequency and amplitude, the microstructure becomes less compact, the surface becomes more irregular, and microcracks begin to form and widen. This leads to pore enlargement and the transformation of isolated pores into interconnected microcracks, resulting in pore aggregation. As the disturbance reaches a critical level, the rock’s surface crystals become exposed, mineral particles loosen, and are only supported by the mineral skeleton. At this stage, pore expansion ceases, and the surface of the rock mass undergoes minimal further changes.

Fig.9

Schematic diagram of the microstructure of the fracture surface of the specimen.

Based on the observed changes in porosity, it can be inferred that the predominant types of cracks in rocks following triaxial disturbance experiments are tensile cracks and compressive shear cracks. Over time, crack fracture models are established based on the evolution of crack development. Tensile stress induces the formation of tensile cracks within crystals, resulting in transgranular fracture. Moreover, due to the uneven expansion of adjacent minerals, varying stresses are generated, leading to forces acting between minerals. When these forces exceed a certain threshold, dislocations occur between different crystals, causing intergranular fracture.

Directional frequency can be used to characterize the spatial distribution properties of pores. By defining the directional angle as the angle between the long axis of the pore and the X or Y axis, this angle can be categorized using a binary method, where the count in each interval represents the directional frequency. To account for the symmetry of pore orientation between 0° and 180°, and between 180° and 360°, the orientation angle is divided into nine 20° intervals. The frequency of pore occurrences within each directional angle interval is denoted as F(a).

The variations in the directional frequency of rock fractures under different disturbance amplitudes and frequencies are shown in Fig. 10. The data reveal that in the original rock, cracks are uniformly distributed across different azimuth intervals, exhibiting no distinct directional preference. However, following disturbances, the distribution of rock fractures changes. For instance, at an 8 MPa disturbance, the frequency of crack orientations increases in the 60° ~ 120° range, while it decreases in the 160° ~ 180° range. At a 14 MPa disturbance, the frequency of crack orientation within the 60° ~ 120° range increases further. At a 20 MPa disturbance, the maximum orientation frequency of pores within the 60° ~ 120° range reaches 50%, approximately 1.72 times that of the original sandstone. Conversely, the minimum orientation frequency of fractures within the 120° ~ 180° range is 22%, about 66.7% of the original rock.

Fig.10

Spatial distribution of cracks.

The original rock exhibits an orientation frequency fractal dimension of 0.88. With escalating amplitude and frequency of disturbances, the directional fractal dimension of rock fractures diminishes, as shown in Fig. 11. At a disturbance level of 20 MPa, the fractal dimension reaches its minimum value of 0.63, suggesting uneven stress distribution among rock particles post-disturbance, resulting in stress concentration and pronounced fracture orientation. Furthermore, distinct rock structures display differing susceptibilities to disturbances, collectively compromising rock continuity and integrity while enhancing heterogeneity and anisotropy.

Fig.11

Frequency fractal dimension.

Tunnel disturbance and damage mechanism

Following tunnel excavation in the mining process, the tunnel roof is enveloped by surrounding rock to create a rock slab configuration. This configuration assumes the surrounding rock to be a consistent and unbroken elastic medium. The rock plate buckling model, which only accounts for a singular direction, is limited in its ability to accurately depict the bottom plate failure process. Since the failure of the rock slab is influenced by both axial and tangential forces, it is more effectively represented as a two-dimensional rock beam structure model, as illustrated in Fig. 12.

$$D\nabla^{4} \omega \left( x \right) - F_{x} \frac{{\partial^{2} \omega \left( x \right)}}{{\partial x^{2} }} = 0$$

(2)

Fig.12

Deeply disturbed surrounding rock stress structure model.

In the formula, $D$ is the bending stiffness of the plate; $\omega \left(x\right)$ is the deflection equation of the plate; ${F}_{x}$ is the force in the X direction of the plate, kN. The boundary of the travertine is a simply supported structure, and the boundary condition is.

$$x = 0,\,a\omega \left( x \right) = 0, \frac{{\partial^{2} \omega \left( x \right)}}{{\partial x^{2} }} = 0$$

(3)

The deflection expression that satisfies this boundary condition is

$$\omega \left(x\right)=\sum_{m=i}^{+\infty }A\mathit{sin}(\frac{m\Pi x}{a})$$

(4)

In the formula, $A$ is a constant; $a$ is the length of the roof rockmass, that is, the tunnel span, m; $m$ is a positive number, $m$≥1.

(4) Bring into (2)

$$\mathop \sum \limits_{m = i}^{ + \infty } A\left( {\frac{{Dm^{4} \Pi^{4} }}{{a^{2} }} - \frac{{F_{x} m^{2} \Pi^{2} }}{{a^{2} }}} \right)\sin \left( {\frac{m\Pi x}{a}} \right) = 0$$

(5)

Well organized

$$F_{x} = \frac{{Dm^{4} \Pi^{4} }}{{a^{2} }}$$

(6)

$$D=\frac{E{h}^{3}}{12(1-{\mu }^{2})}$$

(7)

In the formula, $E$ is the elastic modulus of the roof travertine, GPa; $\mu$ is the Poisson’s ratio of the roof travertine; h is the thickness of the overlying travertine, m.

Let m = 1, then the minimum critical stress for failure of the overlying travertine is

$$\sigma_{cr} = \frac{{F_{x} }}{h} - \frac{{Eh^{2} \Pi^{2} }}{{12a^{2} \left( {1 - \mu^{2} } \right)}}$$

(8)

The roadway is affected by impact dynamic load, and the transmission and reflection effect of the dynamic load stress wave on the rock layer interface is ignored, then the stress ${\upsigma }_{s}$ around the roof rockmass of the roadway superimposed by the dynamic and static load is:

$$\sigma_{s} = \sigma_{j} + \sigma_{d} e^{ - \eta l}$$

(9)

In the formula, ${\upsigma }_{j}$ is the static load stress around the tunnel, MPa; ${\upsigma }_{d}$ is the dynamic load source intensity, MPa; ${\upeta }$ is the dynamic load stress wave energy attenuation coefficient.

$$\sigma_{j} + \sigma_{d} e^{ - \eta l} - \frac{{Eh^{2} \Pi^{2} }}{{12a^{2} \left( {1 - \mu^{2} } \right)}} \ge 0$$

(10)

The travertine layer above the roadway is susceptible to dynamic impact damage. Equation (10) illustrates that the impact damage on the travertine is directly related to the concentrated stress from the static load on the surrounding rock, the intensity of the impact source, and the length of the travertine layer. Conversely, it is inversely related to the distance of stress wave propagation, the thickness, and the strength of the travertine layer. To enhance the resistance to impact in the rockmass above the tunnel, technology such as bolt and cable support can be employed to reduce the load on the rockmass layer, increase its strength and thickness, and improve the overall impact resistance of the surrounding rock. Therefore, investigating the dynamic response characteristics of the tunnel’s surrounding rock and support system under the influence of dynamic impact loads is crucial for enhancing the stability of the tunnel surroundings.

Optimization of tunnel support parameters

Tunnel support program

The through-passage tunnel at the Sanshandao Gold Mine is buried at a depth of 1240 m, with a maximum horizontal principal stress of 27.5 MPa. Located deep underground, the tunnel is situated beneath a hard granite rock layer. The surrounding rock experiences high static load concentration and is frequently subjected to dynamic loads. To analyze the support methods for deeply buried tunnels, a three-dimensional geological model measuring 40.4 × 20 × 40.2 m was created using FLAC 3D numerical simulation software, incorporating the actual stratigraphic conditions. The numerical simulation model is the Coulomb-Moore model. The bottom surface of the entire model is fixed, stress constraints are applied in the X and Y directions, and the upper part of the model is a free surface. The tunnel, designed in a round arch shape with dimensions of 4 × 4 m, is supported by a shotcrete layer. Simulation studies were conducted to investigate the impact of different support methods and dynamic wave conditions on tunnel stability. Cross-simulation was performed based on the mine’s proposal and three stress wave loadings. Stress waves with loads of 100 MPa, 70 MPa, and 40 MPa were applied 15 m from the tunnel’s top to assess the influence of dynamic effects on surrounding rock stability, with a dynamic calculation time of 0.5 s. The specific dynamic loads applied are detailed in Table 3.

Table 3 Dynamic load parameters.

Based on the actual conditions of the mine and the calculation conclusions in the previous chapter, four support schemes are initially proposed. The specific support parameters are shown in Table 4. Due to limited space, only the calculation results of Scheme I and Scheme II are comparatively analyzed below.

Table 4 Support optimization plan.

Analysis of stability of tunnel surrounding rocks under the action of different stress waves

Analysis of roof particle acceleration

Measuring points are placed at various locations on the surface of the surrounding rock in the tunnel to monitor the vibration velocity, displacement, plastic zone, and stress of the supporting components under the influence of different stress waves. The dynamic response characteristics of the surrounding rock in the tunnel are then analyzed based on these measurements.

According to the actual site conditions, the stress disturbance area is located directly above the tunnel roof, which is most affected by the impact of dynamic load disturbances. Under the action of the dynamic impact load, the surrounding rock particles on the roof and sides of the tunnel mainly vibrate inward, causing tensile damage on the surface of the tunnel’s surrounding rock. The rock mass points on the tunnel floor vibrate in both positive and negative directions, with the floor primarily experiencing tensile and compressive damage. During the stress wave propagation process, the vibration period lasts from 0 to 0.02 s. In this period, the stress wave passes through various rock layers within the surrounding rock and reaches the tunnel surface, initiating vibration in the surface particles of the surrounding rock. From 0.02 to 0.08 s, the stress fluctuation period occurs, during which the dynamic stress wave acts on the tunnel surface. The surrounding rock on the tunnel surface undergoes periodic rapid vibrations, generating tensile and compressive stresses. This period corresponds to the most intense phase of destruction for the surrounding rock.

Figure 13 shows the stress magnitude of different stress waves transmitted to the roof, as monitored by the tunnel roof. When the disturbance stress is 100 MPa, the stress wave propagates to the tunnel roof at a speed of approximately 13 m/s. When the disturbance stress is 70 MPa, the stress wave propagates to the tunnel roof at a speed of approximately 9 m/s. When the disturbance stress is 40 MPa, the stress wave propagates to the tunnel roof at a speed of about 5 m/s. The vibration period of the stress wave increases during propagation, but the magnitude of the stress wave does not attenuate significantly.

Fig.13

Vibration speed of tunnel roof.

Plastic zone analysis

Accompanied by stress wave disturbances, the surrounding rock of the tunnel is affected to varying degrees. Figure 14 illustrates the plastic differentiation cloud diagram under different conditions. From the graph, it can be clearly seen that the plastic zone is primarily distributed around the roadway and near the disturbance zone. The forms of rock mass failure are relatively complex, including tension, shear, and a combination of both. Regardless of the support method used, when the tunnel is disturbed by a stress of 100 MPa, the surrounding rock’s plastic zone is the largest. When disturbed by a stress of 70 MPa, the plastic zone of the surrounding rock is second in size. When the roadway is disturbed by a stress of 40 MPa, the plastic zone is minimized. As the intensity of dynamic disturbance increases, the plastic zone of the surrounding rock also shows a linear increase. With Scheme II support, the plastic zone reaches its maximum when subjected to a disturbance stress of 100 MPa, with a volume of 2831.62 m³. In the first support tunnel, the plastic zone volume is 1793.65 m³, representing a 43.14% reduction in the plastic zone area.

Fig.14

Cloud diagram of plastic zone: (a) scheme I 100 MPa (b) scheme I 70 MPa (c) scheme I 40 MPa (d) scheme II 100 MPa (e) scheme II 70 MPa (f) scheme II 40 MPa.

Lateral force on anchor cable

To compare the supportive effects of two support methods, the changes in axial force of the roof bolts, anchor cables, and bolts on both sides of the roadway were monitored separately (Figs. 15, 16). As illustrated in Fig. 17, when the surrounding area of the tunnel is subjected to the same magnitude of dynamic disturbance, the axial force from wave propagation gradually increases and eventually stabilizes. The axial force borne by the two bolts in both support methods is essentially the same. The maximum axial force on the anchor rod is less than 100 kN, which does not exceed the bearing capacity of the bolt.

Fig.15

bolt and anchor cable stress: (a)two rod bolt force diagram (b)axial force diagram of roof bolt and cable.

Fig.16

Roof anchor cable force diagram.

Fig.17

Photos before and after tunnel treatment: (a) before tunnel support (b) after tunnel support.

Figure 15 shows a comparison of the axial forces on the bolts (cables) at the midpoint of the roof. In Scheme II, which uses only bolts, the stress on the central bolt in the roof is the only one monitored. As depicted in the figure, under the same disturbance magnitude, the axial force on the anchor cable exceeds that on the bolt. The axial force supported by the roof plate bolt is approximately 49% of the axial force of the roof plate anchor cable. The maximum axial force experienced by the anchor cable in Scheme I during support is around 378 kN. As disturbance stress increases, the axial stress on the anchor cable continues to rise. During intense dynamic disturbances, the anchor cable nearly reaches its axial force capacity. Therefore, anchor cables play a crucial role in supporting the tunnel roof.

Figure 16 illustrates the force distribution of the anchor cables on the roadway roof under dynamic disturbances of 40 MPa, 70 MPa, and 100 MPa. The figure shows that the force on the anchor cable increases gradually with the transfer of stress. When the disturbance stress is below 70 MPa, the anchor cable bears relatively low axial stress. However, when the disturbance stress reaches 100 MPa, the axial force on the anchor cable doubles. This doubling has a significant inhibitory effect on the deformation of the roof caused by disturbance stress, substantially reducing the roof’s deformation.

Control effect of tunnel surrounding rock

The middle section of the 1240 m level of the Sanshandao Gold Mine initially adopted a "bolt-net-shotcrete" support method for the through roadway. However, due to the dynamic disturbance caused by horizontal blasting in the preceding section, the roof and two sides of the tunnel experienced varying degrees of collapse and support failures, including bare bolt leakage. As marked in Fig. 17(a), this significantly impacted the normal production activities of the mine. To enhance the stability of the roadway and ensure continued production, a revised support method of "high prestressed anchor cable-bolt-hanging net-shotcrete" was implemented. A total of 10 bolts and 3 anchor cables were installed on the tunnel cross-section, with a shotcrete thickness of 0.15 m. As shown in Fig. 17(b), after the treatment, the tunnel’s stability was significantly improved.

To evaluate the effectiveness of tunnel support, monitoring equipment is installed on-site to observe the deformation of surrounding rock and the axial force of bolts before and after tunnel support. By monitoring the stress on anchor cables and bolts, it was observed that the axial force of the support components gradually increased within one week of tunnel excavation. After one week, it tends to stabilize, and the force on the anchor cable is higher than that on the bolt, as shown in Fig. 18(a). The maximum force on the anchor cable at the midpoint of the roof plate is about 350 kN, followed by the anchor cable on the roof side, which is about 320 kN. The force on the anchor rods is all below 250 kN. Therefore, anchor cables play a crucial role in tunnel support. Figure 18(b) illustrates the changes in the movement of the roof and two sides of the tunnel before and after treatment. The displacement of the midpoint of the roof after tunnel treatment decreased by 47.98%. The movement at the roof 45° position decreased by 42.47%, and the movement of the tunnel support point decreased by 51.07%. On average, the movement of tunnels decreased by 47.17%. Long-term monitoring has revealed that the displacement of the roadway is within 110 mm, meeting the safety production requirements of the mine.

Fig.18

tunnel management effect: (a) stress on anchor cable after treatment (b) comparison of tunnel displacement.

Combining true triaxial experiments under disturbance, theoretical calculations of high-stress dynamic disturbance tunnels, optimization of tunnel support parameters, and on-site industrial experiments. The tunnel is divided into five potential risk levels, I-V, based on stress levels and peak ground acceleration (PGA). As illustrated in Fig. 19, a lower level indicates a safer scenario, while a higher level indicates increased risk in the area. Proposed tunnel support strategies under high-stress disturbance are based on the risk level. As depicted in Table 5, this can offer significant reference for designing surrounding rock support for high-stress tunnels affected by disturbances.

Fig.19

Tunnel hazard classification by static and dynamic load.

Table 5 Tunnel support strategies.

Conclusion

• (1) Deeply buried rocks, subjected to dynamic loads under true triaxial high static stress, exhibit a transition in failure mode from pure shear to a combined shear-tension failure. Increased disturbance intensity accelerates crack propagation, ultimately weakening the rock. Specifically, a 30% increase in disturbance intensity results in an approximate 8.06% reduction in rock strength.

• (2) Impact damage to the overlying travertine is directly proportional to the concentrated static stress of the surrounding rock, the intensity of the impact source, and the length of the travertine. Conversely, damage decreases with increasing stress wave propagation distance, travertine thickness, and its inherent strength. Strengthening the travertine at the tunnel roof, both in thickness and material properties, enhances the surrounding rock’s resistance to damage.

• (3) Ordinary bolts are effective in resisting dynamic disturbances up to 40 MPa. However, when the disturbance intensity exceeds 70 MPa, the bolts reach their maximum bearing capacity. In contrast, highly prestressed anchor cables can withstand dynamic disturbances up to 100 MPa, proving to be more suitable for high-stress tunnel environments.

• (4) Anchor cable support in deeply buried, dynamically disturbed tunnels is characterized by shallow anchoring depths, low preload forces, and significant separation of deep surrounding rock. Additionally, anchor cables show limited damage resistance. The use of highly prestressed anchor cables significantly enhances the tunnel’s ability to resist damage. Field applications demonstrate that the “anchor net – high prestress anchor cable – bolt – shotcrete” support system reduces surrounding rock deformation by up to 51.07%, substantially improving stability.

• (5) By integrating stress and peak ground acceleration (PGA) data, tunnel hazards can be classified into five potential risk levels. A risk-based support strategy is proposed, offering practical guidance for designing surrounding rock support systems in high-stress tunnels exposed to similar dynamic disturbances.