Optimizing deep belief network for concrete crack detection via a modified design of ideal gas molecular dynamics

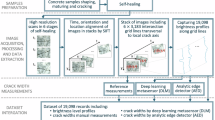
Abstract

Concrete structures are prone to developing cracks, which can have a negative impact on their overall performance and longevity. It is essential to promptly identify and repair these cracks in order to ensure the structural integrity of the building. The present research concentrates on the development of crack diagnosis algorithms based on vision using an optimized version of Deep Neural Network (DNN). The DNN model employed in the current study is the deep belief network (DBN), while the optimization technique is based on a newly designed variant of the Ideal Gas Molecular Movement (MIGMM). By combining these two components, a highly effective crack detection system is created, capable of achieving higher classification rates. To train the DNN model, an image dataset comprising two classes, namely “no-cracks” and “cracks”, has been utilized. The MIGMM has been applied to the DBN model, involving fine-tuning the network architecture’s weights, substituting the categorization layer with two classes of output (cracks and no-cracks), and augmenting the picture dataset using stochastic angles of rotation. The proposed DBN/MIGMM model achieves exceptional performance, with an accuracy of 90.189%, specificity of 94.502%, precision of 94.586%, recall of 94.529%, and an F1-score of 88.093%, outperforming state-of-the-art methods such as Fully Convolutional Networks (FCN), You Only Look Once (YOLO), CrackSegNet, Convolutional Neural Networks (CNN), and Convolutional Encoder-Decoder Networks (CedNet). The present outcomes prepare a comprehensive superior assessment of the proposed model’s effectiveness in accurately detecting and classifying cracks.

Introduction

Concrete is a remarkable material known for its exceptional hardness and durability, making it an optimal choice for an extensive variety of structure applications. From the foundations of towering skyscrapers to the creation of outdoor swimming pools, concrete proves its versatility¹. However, despite its impressive qualities, concrete is susceptible to cracking, which can occur in various parts of a structure, including the roof, foundation, and floor². These cracks pose common challenges for construction professionals and necessitate a thorough investigation and assessment of their origins, types, and impact on structural stability³. Understanding these aspects is of utmost importance. Once this knowledge is acquired, appropriate remedial measures can be implemented⁴. These measures may involve leaving the crack open, administering targeted material injections, or employing suitable methodologies to repair the concrete cracks⁵.

The increasing interest in automated crack detection systems in the field of structural health monitoring arises from their ability to provide a more reliable and efficient alternative to traditional manual inspection methods.

The utilization of deep learning algorithms shows considerable potential within the area of image identification tasks, particularly in analyzing visual data to identify cracks on concrete surfaces⁶. These advanced algorithms demonstrate a capability to process intricate visual information, enabling the accurate and efficient detection and localization of cracks⁷. As a result, these technological advancements have the potential to revolutionize the field of organizational health monitoring by simplifying the diagnosis and assessment of structural defects, hence improving the entire safety and integrity of civil infrastructure⁸.

Dung et al.⁹ introduced a method for detecting cracks in concrete on the basis of a deep FCN (Fully Convolutional Network) for segmentation of semantic of crack pictures. Three various previously trained network structures were tested for image classification using a dataset of 40,000 227 × 227 pixel pictures, with the VGG16-based encoder selected for additional training. The FCN network achieved an average precision of approximately 90% for semantic segmentation after training on a subset of 500 annotated crack-labeled images. Validation of the method was conducted using images from a cyclic loading test on a concrete specimen, showing effective crack detection and accurate evaluation of crack density. However, potential limitations of the study may involve the necessity for further validation on diverse datasets and real-world conditions, as well as the possible effect of varying lighting and environmental issues on the accuracy of crack detection.

Park et al.¹⁰ investigated the utilization of structured light and deep learning in conjunction with laser sensors and vision to identify and measure cracks in concrete constructions, which is essential for evaluating structural integrity amidst infrastructure decay. The YOLO algorithm enabled instantaneous crack detection, while crack size measurements were determined by the positions of laser beams on the surfaces. To mitigate potential misalignment issues, a correction algorithm incorporating a specialized jig module and distance sensor was created. The algorithm’s precision was confirmed through simulations and experiments, showcasing its effectiveness in real-time crack detection and measurement. Nevertheless, practical obstacles like surface texture discrepancies impacting laser beam reflections and the necessity for robustness testing in various environmental conditions to ensure applicability could present limitations.

Ren et al.¹¹ emphasized the significance of automated segmentation and diagnosis of concrete cracks within tunnels as a crucial task for civil engineers. Crack segmentation that is based on Image, utilizing CNNs for segmentation of image, was identified as an effective method. A new deep fully convolutional neural network, called CrackSegNet, was introduced to achieve crack segmentation of dense pixel-wise. This network incorporated various modules such as spatial pyramid pooling, skip connections, and dilated convolution to improve aggregation, resolution reconstruction, and multiscale feature extraction, resulting in a notable enhancement in crack segmentation performance. CrackSegNet exhibited superior accuracy and generalization in comparison to conventional methods, providing an efficient and cost-effective solution for tunnel inspection and monitoring that could potentially be automated. However, potential limitations of this work may include the necessity for further validation under different tunnel conditions and sizes, as well as considerations regarding real-time application feasibility and computational resource requirements for large-scale implementation.

Golding et al.¹² highlighted the importance of regularly inspecting infrastructure to maintain structural health, especially in detecting visual indicators of stress such as cracks and depressions that could result in failure if left undetected. Manual inspections conducted by skilled inspectors were time-consuming and subjective, causing delays that could compromise the integrity of the structure. To tackle the present problem, the research suggested an autonomous crack diagnosis approach on the basis of deep learning using CNN. The current approach involved processing 40,000 RGB images to train a previously trained VGG16 design for various models of CNN. While traditional image processing techniques like thresholding, grayscale, and edge diagnosis had been utilized for crack detection, their integration into deep learning was considered innovative. The study revealed that both grayscale and RGB models demonstrated similar performance, with accuracy improving as the models underwent much training. However, edge-diagnosis and thresholding models exhibited lower efficacy in comparison with RGB models, indicating that color was not a determining factor in DL crack detection. Despite these results, potential limitations of the research include the necessity for validation across various kinds of infrastructure and environmental conditions, as well as addressing challenges related to computational resources and model generalization in real-world applications.

Li et al.¹³ focused on the issue of identifying and quantifying cracks at a pixel level through the introduction of a CedNet (Convolutional Encoder-Decoder Network) and the utilization of image post-processing methods for measuring crack widths and orientations. Training and validation of CedNet were carried out using a dataset of 1800 images of cracked concrete structures, resulting in high levels of precision, accuracy, F-measure, Intersection Over Union (IoU), and recall. The model’s resilience and flexibility were assessed, and an experiment was conducted in a laboratory to fine-tune crack width and orientation measurements using a smartphone camera. Furthermore, perspective transformation was implemented to correct image distortions caused by skewed angles, and comparisons with existing deep learning methods were made to showcase the superior efficiency of the proposed methodology. Nevertheless, potential limitations of the study may involve the necessity for further validation under various environmental conditions and concrete structure types, along with considerations for real-world implementation challenges like scalability and adaptation to different imaging devices and environments.

Xu et al.¹⁴ proposed a recognition method for multimodal detection of concrete cracks, named YOLO-DL, based on the YOLO object detector, the encoder-decoder structure of DeepLabv3+, and the attention mechanism integrated calibration module, to perform multi-task at the same time, leading to the establishment of three branches for cracks classification, localization detection, and semantic segmentation. With a detection precision of 84.87%, mAP@0. 93.44%, 92.10%, 82.90%, 6 of 5349 and demonstrated an F1 score of 93.86%, 93.86%, 83.94%, 6 of 5502 and a mIoU of 95.24% An F2 DST scores of 80.93% and an mIoU of 94.94% for crack segmentation, the YOLO-DL model provides significantly shorter segmentation inference times than DeepLabv3+, FCN, U-Net, and SegNet, making it suitable for real-time crack recognition and it demonstrated its promise in detection of real structures for concrete cracks. The attention mechanism incorporates the local information of each image frame to optimize the robustness and performance of the model. A new measurement method for crack width based on the local element grid method is designed with sub-pixel-level measurement precision, and the maximum relative error is less than 10%, which can provide detailed crack width information. This study, however, is limited by the decreased accuracy in extremely complex or noisy environments and the extensive computational resources required to train the model, which may lead to unsuitability in low-resource areas.

Fan et al.¹⁵ systematically compared the performance of five deep learning object detection algorithms such as Faster R-CNN, SSD, YOLO v3 and v8, and RetinaNet based on their capability to generate bounding boxes for objects of interest and compared the performance of each algorithm in light of issues related to thin and small concrete cracks. Because of the difficulty of bounding cracks in their individual bounding box, model accuracy and consistency are usually compromised due to duplication of measurements. To tackle that, an enhanced confusion matrix based on linear presented in this paper was used to assess the performance of algorithms. Compared to the other evaluated methods, the SSD method achieved 90.6% overall accuracy on the VARI images and showed good performance in small cracks and data imbalance, indicating that the model was surprisingly stable. The comparative analysis highlights how different deep learning algorithms contribute to the emerging automatic damage detection methods. Despite its strengths, challenges remain, including possible accuracy decline in extremely complex or noisy settings, as well as the requirement of significant computing resources, potentially limiting the real-world usefulness of these models in resource-constrained environments.

Peng et al.¹⁶ provided a bridge defect detection method, which incorporates both spectral and spatial information with hyperspectral imaging to attain a simultaneously used structural performance indicator. To eliminate mutual interference, a dual-branch dense block convolutional neural network algorithm was proposed for spectral feature extraction, which consists of spectral and spatial branches, respectively. At the same time, it performs better than support vector machine and classification algorithms in traditional deep learning, achieving OA of 98.57%, AA of 98.16%, and Kappa coefficient of 0.9814 on small sample datasets. Challenges ahead: Could potentially find it difficult to operate on a larger scale, as well as compute high power requirement limiting practicality in resource-restricted environments.

While the utilization of deep learning methodologies has been observed in the field of crack detection, there is a pressing need to enhance the effectiveness of these models in order to achieve greater precision and resilience in real-world scenarios. It is evident that existing techniques may not fully exploit the potential of optimization strategies to enhance the recall rates and accuracy of crack diagnosis systems.

This study aims to overcome the limitations of current crack detection systems by combining deep learning with optimization algorithms, thereby harnessing the synergistic potential between the two. The research represents a new framework that combines a deep belief network with a customized Ideal Gas Molecular Movement optimization algorithm, resulting in the development of a model that demonstrates superior classification capabilities in identifying cracks on concrete surfaces. As a result, this research represents a significant advancement in the field of automated crack diagnosis technology, with the potential to enhance maintenance practices and strengthen safety protocols for concrete structures on a global scale.

Dataset and preprocessing

Dataset description

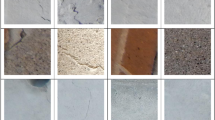
The study employs the SDNET2018 dataset, which is a carefully annotated collection of images specifically created for training, validating, and benchmarking crack diagnosis algorithms powered by artificial intelligence, tailored for concrete surfaces¹⁷. This dataset comprises more than 56,000 images that are divided into categories of non-cracked and cracked concrete decks of bridge, pavements, and walls. These images exhibit crack widths ranging from 0.06 mm to 25 mm and encompass various obstacles such as shadows, surface roughness, scaling, edges, holes, and background debris.

In terms of methodology, the pictures were taken employing a 16 MP Nikon digital camera, divided into sub pictures of 256 × 256 pixels, and labeled as “C” for cracks and “U” for uncracked areas. The pictures were sourced from locations, such as the Utah State University system, structural health (SMASH) laboratory, and the material for bridge decks, the Wanlass/Russell Performance Hall construction on the campus of USU for walls, and roads and sidewalks around the USU campus for pavements.

The SDNET2018 dataset is crucial for developing concrete crack diagnosis algorithms that utilize deep learning CNNs due to its wide range of crack types and real-world scenarios, making it a valuable asset for advancing research in structural health monitoring. This dataset has been cited in numerous research papers focusing on autonomous concrete crack detection, fatigue crack detection on steel components, and issues in inspection of bridge employing systems of minor unmanned aerial^18,19,20. Samples of concrete pavements, both uncracked and cracked, extracted from the SDNET2018 database have been illustrated in Fig. (1).

Fig. 1

Samples of concrete pavements, both cracked and uncracked, extracted from the SDNET2018 dataset: (A) cracked and (B) uncracked.

Within the scope of the current research, the SDNET2018 dataset plays a fundamental role in laying the groundwork for the development and assessment of the proposed DBN/MIGMM model for crack diagnosis on the basis of automatic vision employing concrete surfaces.

Contrast enhancement based on CLAHE

CLAHE, also known as Contrast Limited Adaptive Histogram Equalization, is an advanced technique employed within processing of image to improve the contrast within images. It is particularly beneficial for improving the visibility of features in images that have poor contrast. CLAHE is an extension of another technique called adaptive histogram equalization (AHE). AHE calculates multiple histograms for different sections of the image and utilizes them to redistribute the lightness values of the image. However, AHE can sometimes excessively amplify the contrast in areas of the image that have little variation, resulting in the amplification of noise.

To address this issue, CLAHE incorporates a limitation on the amplification. The main concept behind CLAHE is to perform AHE but restrict the histogram by a predetermined value before computing the cumulative distribution function (CDF). This predetermined value is determined based on the acceptable level of noise in the image. Once the histogram is clipped, it is redistributed in a way that ensures the height of the histogram does not exceed the clip limit. This redistribution is applied to each local region, and bilinear interpolation is employed to eliminate any artificially induced boundaries.

Let $\:I(x,\:y)$ be the intensity of the pixel at position ( $\:(x,\:y)$ ) within the image of input, and let ( $\:H$ ) be the histogram of the intensities in a region around ( $\:(x,\:y)$ ). The CLAHE algorithm is summarized in the following way:

• (1) The picture has been segmented into non-overlapping areas, denoted as $\:{R}_{i}$.

• (2) For each region $\:{R}_{i}$, the histogram $\:{H}_{i}$ of pixel intensities is computed.

• (3) The histogram $\:{H}_{i}$ is then clipped at a predefined clip limit $\:\tau\:$, ensuring that $\:{H}_{i}\left(v\right)$ is equal to the minimum value between $\:{H}_{i}\left(V\right)$ and $\:\tau\:$ for each intensity value $\:v$.

• (4) Any excess pixels in $\:{H}_{i}$ that exceed the clip limit $\:\tau\:$ are redistributed across all intensity levels.

• (5) The cumulative distribution function (CDF) $\:{C}_{i}$ is computed for each clipped and redistributed histogram $\:{H}_{i}$.

• (6) The pixel intensities in each region $\:{R}_{i}$ are mapped according to the CDF $\:{C}_{i}$.

• (7) Bilinear interpolation is used to smooth the transitions between adjacent regions.

The outcome is an image with improved contrast, which can be especially advantageous for crack detection algorithms as it enhances the visibility of crack edges against the concrete background. By manipulating the clip limit ($\:\tau\:$), one has the ability to regulate the level of contrast enhancement and noise amplification, customizing the procedure to meet the specific demands of the crack detection assignment.

CLAHE has been effectively utilized in various sectors, such as medical imaging and industrial inspection, to enhance the clarity of crucial features in images. In the context of automatic crack diagnosis based on vision employing concrete surfaces, CLAHE can greatly assist in emphasizing the subtle characteristics of cracks, thereby enhancing the precision of the detection algorithms. Figure (2) illustrates the implementation of CLAHE on images depicting cracks in concrete.

Fig. 2

Implementation of CLAHE on images depicting cracks in concrete. The image (A) input image (B) enhanced image, (C) the histogram of (A), (D) the histogram of (B).

In image (A), we observe the original image displaying cracks on the concrete surface. Image (B) exhibits the improved version of the image of input after applying CLAHE, which enhances the contrast and makes the cracks more visible. The histograms of images (A) and (B) are presented in (C) and (D) respectively, demonstrating the circulation of intensities of pixel before and after the implementation of CLAHE. This effectively showcases how CLAHE enhances the visual quality of images depicting concrete cracks by improving contrast and highlighting subtle details.

Data augmentation

Data augmentation is a key factor in improving the performance of deep learning models, particularly in tasks like image classification such as concrete crack detection. By expanding the dataset with modified versions of existing images, the model can improve its ability to generalize and become more resilient to variations it may encounter in real-world situations. Below are detailed explanations of the augmentation techniques discussed:

• (1) Convolution Filters: These filters are utilized to perform convolution operations that change the texture and quality of images. By adjusting sharpness or adding blur, the model is capable of learning to identify features and patterns that are not solely reliant on high-resolution details.

• (2) Random Erasure: This technique involves randomly deleting parts of the image to simulate occlusion. It helps the model learn to recognize features without depending on complete visual information, thus enhancing its crack detection capabilities even when cracks are partially obscured.

• (3) Color Space Transformations: Altering the RGB color channels, contrast, and brightness introduces variations in image appearance that replicate different lighting conditions. This is crucial for a model intended for use in various environments where lighting can significantly impact visibility.

• (4) Geometric Transformations: Operations like stretching, cropping, rotating, zooming, and flipping introduce spatial and perspective changes. These transformations assist the model in identifying cracks regardless of their orientation, scale, and position within the image.

Each of these techniques contributes to establishing a more diverse and comprehensive training dataset, which is essential for building a dependable crack detection system. By integrating a range of augmentations, the deep learning model can better handle the complexities of analyzing real-world concrete surfaces. Figure (3) illustrates different augmentation techniques employed in detecting concrete cracks.

Fig. 3

Different augmentation techniques employed in detecting concrete cracks.

The utilization of these methods is essential in improving the resilience of algorithms designed for crack detection. By incorporating a wider dataset through techniques like rotation, flipping, scaling, cropping, and color manipulation, the variability of crack images can be increased. This, in turn, enables the model to better adapt to unseen data and enhance its overall accuracy. Through the integration of these augmentation techniques, we can efficiently train DBN to detect concrete cracks with improved efficiency in real-world situations.

Modified ideal gas molecular movement

Gas molecules can be compared to possible individuals that efficiently traverse and explore the entire capacity of a vessel, aiming to optimize the area by investigating all possible areas for global optimal solutions²¹. These molecules collaborate and change data with each other after collisions, as the individuals navigate within the confined space. The data exchange has been observed through changes in the molecules’ velocity as they encounter new scenarios at different time intervals. The fundamental concept of the IGMM algorithm is to utilize these navigation and collision events to identify the global optimum. The optimization process will be elaborated in the subsequent section.

Initializing

The initial requirement involves the regular dispersion and stochastic movement of molecules along various paths. This requirement promotes the idea of employing a consistent dispersion to generate the primary population, which has been estimated to expedite the procedure of search to the optimal solutions. After stochastically designating the solutions’ primary population within the permissible range of design variables, the velocity equation is adjusted to regulate the initial temperature at 0°C.

Calculation of molecular masses

The present algorithm implemented a reasonable measure to evaluate the fitness of the normalized agent. This was achieved by assigning a mass parameter to all gas molecules on the basis of fitness of it. The calculation of the gas molecules’ velocity revealed an inverse correlation between velocity and mass. In other words, molecules with larger masses moved at lower velocities, while those with smaller masses moved at higher velocities²². Therefore, the mass calculation was designed to ensure that the appropriate molecules traveled at lower velocities. This was justified by their inclination to stay within the present area that was more likely to be reasonable. Conversely, fewer suitable molecules exhibited a different behavior. In order to minimize the objective of the study, all solutions were allocated a mass proportional to fitness of it employing the subsequent equation:

$${\raise0.7ex\hbox{${\frac{1}{{fit\left( i \right)}}}$} \!\mathord{\left/ {\vphantom {{\frac{1}{{fit\left( i \right)}}} {\frac{1}{{\sqrt {\sum \left( {fi{t^2}\left( i \right)} \right)} }}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${\frac{1}{{\sqrt {\sum \left( {fi{t^2}\left( i \right)} \right)} }}}$}}$$

(1)

Such that the molecule $\:i$’s mass has been denoted as $\:{m}_{i}$, while $\:fit\left(i\right)$ represents the molecule $\:i$’s fitness based on the problem cost. The highest-ranking molecule is determined by comparing their molecular masses during the iterations.

Calculation molecule’s collision possibility

Gas molecules interact with each other based on specific probabilities, which increase as the molecules move over time and distance. To optimize this interaction, a parameter known as MCP (Molecules Collision Probability) has been introduced. Within the initial stage of the optimization procedure, once the issue area has been unknown and there is not any data exchange between agents, MCP has been found to be at the least level of it²³. On the other hand, as optimality progresses and the optimal area has been identified, the probability of collision increases in an exponential manner, reaching its maximum level achievable.

$$MPC=1 - \exp \left( { - 0.63 \times iter} \right)$$

(2)

Calculation molecules’ novel velocity and situation

Both molecules are in collision with each other on the basis of their specific probability of collision or continue to travel without colliding based on their velocity relationship. In light of this event, the subsequent steps will compute the novel location and velocity of all molecules.

Computing molecular velocity at the collision incidence (MVCI)

The third and second features of each ideal gas demonstrates the communication between molecules. In this scenario, the heavier molecule is assumed to be stationary while the lighter molecule motions, following the hypotheses regarding elastic collisions among molecules. Additionally, the velocity of the individual’s motion can be calculated using the equation $\:x=\varDelta\:vt$ (for t = 1) through comparing the two molecules’ locations.

$${\left( {v_{1}^{d}} \right)^{{\prime }}}=\frac{{\left( {{m_1} - E{m_2}} \right)}}{{{m_1}+{m_2}}} \times v_{1}^{d}$$

(3)

$${\left( {v_{2}^{d}} \right)^{{\prime }}}=\frac{{\left( {1+E} \right){m_1}}}{{{m_1}+{m_2}}} \times v_{1}^{d}$$

(4)

Such that, $\:{v}_{1}^{d}$ represents the first molecule’ primary velocity prior to the collision, with $\:{v}_{2}^{d}$ expected to be 0. Subsequently, $\:{\left({v}_{1}^{d}\right)}^{{\prime\:}}$and $\:{\left({v}_{2}^{d}\right)}^{{\prime\:}}$ indicate the final velocities post-collision, respectively, where $\:d$ denotes the optimization issue’s dimension.

It was previously mentioned that the value of $\:E$ is fixed at one in elastic collisions, however, in the aforementioned equation, the current variable has been treated as a parameter for ensuring convergence within the optimizer. So, during the initial stages of the optimality procedure, the value of the current parameter is approximately one, but as the quantity of cycles of optimality increases, value of it significantly decreases on the basis of the subsequent linear formula.

$$\:E=1-\left(\frac{iter}{maxIt}\right)$$

(5)

The variables $\:iter$ represents the present iteration of the optimality procedure and $\:maxIt$ specifies the highest number iterations of the optimality procedure. Once the novel velocity of all molecules have been computed, its updated position is determined using the following formulas:

$$\left( {z_{1}^{d} } \right)^{\prime } = z_{2}^{d} + rand\left( {v_{2}^{d} } \right)^{\prime }$$

(6)

$$\left( {z_{1}^{d} } \right)^{\prime } = z_{2}^{d} + rand\left( {v_{2}^{d} } \right)^{\prime }$$

(7)

The state of the stationary molecule before the impact is denoted as $\:{z}_{2}^{d}$, while the new situations after the impact are represented by $\:{\left({z}_{1}^{d}\right)}^{{\prime\:}}$ and $\:{\left({z}_{2}^{d}\right)}^{{\prime\:}}$. The term “rand” refers to a randomly distributed value ranging between 0 and 1.

Calculation nocollision molecular velocity (NCMV)

In the context of ideal gases in an isolated environment, if there are no collisions between molecules, the velocity of the $\:{i}^{th}$ molecule can be defined as follows:

$$\left( {v_{i}^{d} } \right)^{\prime } = 1.7\sqrt {\frac{{kT_{i} }}{{m_{i} }}}$$

(8)

The Boltzmann coefficient is inversely related to the quantity of molecules, and value of it is controlled by the formula $\:k\:=\:1/nVar$, where $\:nVar$ represents the quantity of molecules within the optimality procedure. Each molecule’s velocity adjusts according to its mass and temperature. Hence, it is essential to compute the novel temperature for all molecules at the present stage. This is achieved by employing a subtractive formulation defined by the following equation:

$$T_{i}^{\prime } = T_{i} - 1/m_{i}$$

(9)

Once determination of the unique speed of all molecules has been accomplished, the novel scenario is calculated employing the formula provided.

$$\left( {z_{i}^{d} } \right)^{\prime } = z_{i}^{d} + rand\left( {v_{i}^{d} } \right)^{\prime }$$

(10)

Convergence principles

During the ultimate stage of optimality, the convergence has been verified. The process of optimization has been fully controlled, once the finest outcomes within the present iteration demonstrates minimal alterations in an acceptable tolerance for multiple iterations. The other suitable criterion of convergence happens when the gap between the value of average penalized cost and the best solution of each design within an iteration decreases to an intended level²⁴. Another frequently used ultimate criterion within meta-heuristic algorithms happens when the highest quantity of iterations has been fulfilled without achieving convergence. It happens when the optimality process might stop without reaching a typical convergence.

Modified ideal gas molecular movement

To enhance its performance and adaptability, we have introduced a revised version that incorporates elements of Chaos theory, specifically the Kent map and the Lévy flight mechanism.

The Kent shift map, which is a component of chaos theory, introduces a deterministic yet unpredictable element to the algorithm. This map is a simple 1-dimensional chaotic map that generates binary sequences with intricate and non-repetitive patterns. By integrating the Kent shift map into the Ideal Gas Molecular Movement algorithm, we aim to expand the search process and prevent premature fixation on local optima. This is achieved by disrupting the algorithm’s state space, thereby preserving the chaotic nature of the search process and enhancing its exploration capabilities. By utilizing the Kent map, we can introduce chaotic behavior in the optimizer’s initial population.

$$rand\left( {v_{i}^{d} } \right)^{\prime } _{{New}} = \left\{ {\begin{array}{*{20}c} {rand\left( {v_{i}^{d} } \right)^{'} /\beta ,~~~0 < rand\left( {v_{i}^{d} } \right)^{\prime } \le \beta } \\ {\frac{{1 - rand\left( {v_{i}^{d} } \right)^{'} }}{{1 - \beta }},\beta \le rand\left( {v_{i}^{d} } \right)^{\prime } < 1} \\ \end{array} } \right.$$

(11)

where, $\:\beta\:$ is a parameter between 0 and 1.

As the second adjustment, the Lévy flight approach entails making random moves with distances following a heavy-tailed probability distribution. This characteristic allows the algorithm to occasionally take large leaps across the search area, preventing it from being trapped in local optimal solutions and improving the exploration of the entire search space.

By integrating Lévy flights into the IGMM algorithm, a balanced combination of local exploitation and global exploration is attained, leading to greater adaptability when traversing complex terrains. In population-based metaheuristic algorithms, this method is commonly employed to thoroughly investigate various areas within the search space and avoid.

$$Levy\left( w \right) \approx \frac{w}{{1+\theta }}$$

(12)

$$w=\frac{A}{{{{\left| B \right|}^{1/\theta }}}}$$

(13)

$${\sigma ^2}={\left[ {\frac{{{\text{\varvec{\Gamma}}}\left( {1+\theta } \right)}}{{\theta {\text{\varvec{\Gamma}}}\left( {\left( {1+\theta } \right)/2} \right)}}\frac{{{\text{sin}}\left( {\pi \tau /2} \right)}}{{{2^{\left( {1+\theta } \right)/2}}}}} \right]^{\frac{2}{\tau }}}$$

(14)

The Lévy flight technique has been utilized to enhance $\:{\left({z}_{i}^{d}\right)}^{{\prime\:}}$, with the step size denoted as w and the Lévy index $\:\theta\:$ ranging between 0 and 2 (specifically, with $\:\theta\:=1.5$). $\:A$ and $\:B$ are normally distributed with a mean of 0, and the Gamma function is represented by $\:\varGamma\:(.)$. By employing the Lévy flight technique, notable advancements have been successfully attained. Therefore, the new scenario is intended by the following Eq. 

$$\left( {z_{i}^{d} } \right)^{\prime } = z_{i}^{d} + Levy$$

(15)

Algorithm validation

Within the present part, the efficacy of the suggested Modified algorithm was assessed n the basis of a comparison its evaluation with 20 state-of-the-art standard benchmarks, including 10 CEC 2019 and 10 CEC 2021 benchmark test suited²⁵. An annual tournament is held to evaluate the performance of various algorithms using tests based on the 100-Digit Challenge. The CEC04-CEC10 functions were made as 10-dimensional minimization problems with a boundary range between − 100 and 100 by the CEC benchmark’s developer.

In contrast, the CEC01-CEC03 functions had varying sizes. Consequently, the test functions of the CEC04-CEC10 undergo rotation and shifting, while the test functions of the CEC01-CEC03 require more balance. Scaling has been considered a choice for each test. Quality assurance measures have been implemented specifically for the CEC01 results to accommodate the additional 1000 dimensions introduced to a subset of the functions.

The efficacy of MIGMM was contrasted with several optimization algorithms, including African vultures optimization algorithm (AVOA)²⁶, Tunicate Swarm Algorithm (TSA)²⁷, Owl Search Algorithm (OSA)²⁸, and Multi-verse optimize (MVO)²⁹. Each algorithm undergoes 120 iterations and involves 80 agents. Table 1 tabulates the set parameters of the studied algorithms.

Table 1 The set parameters of the studied algorithms.

The study involved calculating important metrics such as the standard deviation and mean. To ensure a comprehensive analysis, all algorithms were run 35 times. Table 2 displays the comparative analysis of the proposed Modified Ideal Gas Molecular Movement algorithm against other advanced metaheuristics. The ultimate outcomes of the current algorithms on the CEC2019 benchmark have been illustrated in Table 1.

Table 2 The outcomes of the algorithms on the CEC2019 benchmark.

Based on the data provided in Table 2, the Modified Ideal Gas Molecular Movement (MIGMM) algorithm’s performance was evaluated alongside several state-of-the-art metaheuristic algorithms such as AVOA, TSA, OSA, and MVO across various CEC2019 benchmark test functions. In the case of CEC01, MIGMM achieved an average (AVG) value of 89638.3 with a standard deviation (StD) of 24272.92. Comparatively, AVOA, MVO, TSA, and OSA displayed notably higher AVG values with differing levels of StD. Similarly, for CEC02 and CEC03, MIGMM’s AVG and StD values showcased competitive performance when contrasted with the other algorithms, generally exhibiting lower AVG and StD values in these scenarios.

However, for CEC04-CEC10, MIGMM’s performance varied. In certain instances, MIGMM surpassed the other algorithms in terms of AVG and StD, while in others, it fell short. For instance, in CEC06, MIGMM demonstrated a relatively high AVG value compared to some of the other algorithms. Overall, the findings indicate that MIGMM’s performance is diverse across different test functions, displaying competitive performance in some cases but less consistent results in others. Further analysis and comparison are necessary to comprehensively comprehend the strengths and weaknesses of MIGMM in relation to several algorithms scrutinized within the present research. And the final results of the present algorithms on the CEC2021 benchmark have been illustrated in Table 3.

Table 3 The outcomes of the algorithms on the CEC2021 benchmark.

CEC01 highlights MIGMM as the standout performer, boasting an AVG and StD of 0, indicating its superior and consistent performance. On the other hand, AVOA, MVO, TSA, and OSA exhibit varying AVG and StD values, with MVO having a higher AVG but also a relatively elevated StD compared to MIGMM. Transitioning to CEC02, MIGMM continues to excel with an AVG and StD of 0, further emphasizing its effectiveness. AVOA and OSA demonstrate competitive performance, while MVO and TSA exhibit higher AVG and StD values.

In CEC03, MIGMM once again showcases exceptional performance with an AVG and StD of 0. AVOA and TSA have lower AVG values but higher StD, whereas MVO and OSA present higher AVG values. Throughout CEC04-CEC10, MIGMM consistently delivers impressive results with minimal deviation (0 StD), indicating its robust performance across these test functions. AVOA, MVO, TSA, and OSA exhibit varying AVG and StD values, suggesting that certain algorithms perform better on specific test functions than others.

In conclusion, the results strongly indicate that the MIGMM algorithm performs exceptionally well on the CEC2021 benchmark test functions, consistently achieving optimal results with minimal deviation. This underscores the efficacy of MIGMM as a metaheuristic algorithm for optimization tasks in comparison to the other algorithms studied. Further comprehensive examination and comparison could prepare extra insights into the weaknesses and strengths of all algorithms on specific test functions.

Deep belief networks using modified pelican optimizer

Deep belief networks

A DBN (Deep Belief Network) has been found to be a type of generative graphical model utilized in deep learning. It is composed of multiple layers of hidden units, known as latent variables, with associations between the layers but not within each layer. DBNs have the capability to learn how to probabilistically reconstruct their inputs through unsupervised learning on a given set of examples.

Following this unsupervised learning phase, a DBN can undergo further training with supervision to carry out tasks such as classification. The structure of a DBN typically includes stacking simpler, unsupervised networks such as autoencoders or RBMs (Restricted Boltzmann Machine). The concealed layer of all sub-networks serves as the layer that is visible for the subsequent one, enabling a layer-by-layer and rapid unsupervised procedure of training.

This training often utilizes a technique called contrastive divergence, which is an approximation to the maximum likelihood method typically employed for learning the weights in the network. DBNs are particularly renowned for their ability to capture and represent intricate data distributions, making them valuable for tasks related to feature detection and classification across various domains.

Restricted Boltzmann Machines are a specific type of Boltzmann machine that consist of hidden and visible unit layers. In RBMs, stochastic binary variables are assigned to the higher layer ($\:{L}_{h}$) and the hidden layer, which are respectively the visible layer ($\:{L}_{v}$). In order to create the joint distribution function, undirected weights ($\:w$) between the visible and hidden layers along with biases are considered. The energy function can be calculated as follows:

$$\rho \left( {{L_v},{\text{~}}{L_h}} \right)=\frac{1}{{{F_p}}}\exp \left( { - E\left( {{L_v},{\text{~}}{L_h}} \right)} \right)$$

(16)

where, $\:{F}_{p}$ defines the achieved partition function with gathering feasible visible and hidden layers, that is:

$${F_p}=\mathop \sum \limits_{{{L_v},{\text{~}}{L_h}}} \exp \left( { - E\left( {{L_v},{\text{~}}{L_h}} \right)} \right)$$

(17)

And the connection of the energy configuration for visible and hidden pairs is signified by the following:

$$E\left( {{L_v},~{L_h}} \right)= - \mathop \sum \limits_{{i=1}} {a_i}{L_{{v_i}}} - \mathop \sum \limits_{{j=1}} {b_j}{L_{{h_j}}} - \mathop \sum \limits_{{i,j}} {L_{{v_i}}}{L_{{h_j}}}{w_{ij}}$$

(18)

The weight connecting hidden and visible pairs is determined by $\:{w}_{ij}$, $\:{L}_{{v}_{i}}$ and $\:{L}_{{h}_{j}}$, which denote the binary state of hidden unit $\:j$ and visible unit $\:i$, while $\:{a}_{i}$ and $\:{b}_{j}$ represent the biases in the visible and hidden units. The RBM weights are adjusted using the equation below:

$$\:\varDelta\:{w}_{ij}={E}_{t}\left({L}_{{v}_{i}}{L}_{{h}_{j}}\right)-{E}_{m}\left({L}_{{v}_{i}}{L}_{{h}_{j}}\right)$$

(19)

The expectation for the training data and model is represented by $\:{E}_{m}\left(.\right)$ and $\:{E}_{t}\left(.\right)$, respectively. It is crucial to construct the layout architecture of DBN correctly in order to effectively handle various tasks. Several research studies have recently focused on achieving this objective. This study introduces a novel and enhanced metaheuristic approach that addresses this challenge.

Proposed MIGMM-based DBN

Developing the layout architecture in DBNs optimally requires a high level of problem-solving aptitude, as mentioned earlier. To address the challenges involved, implementing the MIGMM can be an effective solution. This approach helps overcome algorithmic limitations such as early convergence and being trapped in local minimums. In this study, the newly developed MIGMM is utilized to select and replace the network’s best-performing weights with new ones. This aids in reducing the gap between the output and the intended value. The performance index that needs to be diminished to the least amount in the network is the mean squared error (MSE). The definition of this function is given in the following:

$$\:MSE=\frac{1}{T}\sum\:_{j=1}^{N}\sum\:_{i=1}^{M}{\left({{Y}_{j}^{i}-D}_{j}^{i}\right)}^{2}$$

(20)

Such that, the output layers’ quantity and the data number are defined by $\:M$ and $\:N$, respectively. and $\:{Y}_{j}^{i}$ and $\:{D}_{j}^{i}$ represent the network output and the desired output for the $\:{j}^{th}$ unit in the DBN at period $\:t$. After improving the suggested optimal DBN, the image is categorized on the basis of the attributes extracted from the segmented images. The share of test and training data are 20% and 80%, respectively.

Simulation results

As mentioned before, this research aimed to enhance vision-based crack detection systems through a unique approach. By combining a Deep Belief Network (DBN) with a modified version of the algorithm, we have developed an improved DBN/MIGMM model that demonstrates exceptional classification accuracy. Additionally, the model’s robustness was tested by expanding the dataset to include images with random rotation angles, simulating various crack patterns. This enhancement has strengthened the model’s ability to reliably identify cracks under different conditions. The Matlab 2019b experimental setup is operated using an i7-6700HQ Asus N552 processor and 12GB of RAM.

An array of assessment metrics, comprising specificity, precision, AUC, accuracy, F1-score, and sensitivity, is utilized to evaluate the effectiveness of the DBN/MIGMM model. the current metrics prepare worthy insights into the capability of the model to accurately categorize concrete crack images and reduce errors or confusion among different categories. Additionally, a comparison evaluation has been carried out to contrast the results of the newly introduced DBN/MIGMM model with cutting-edge models like deep fully convolutional network (FCN)⁹, YOLO¹⁰, new deep fully convolutional neural network (CrackSegNet)¹¹, convolutional neural networks (CNN)¹², and convolutional encoder-decoder network (CedNet)¹³. Later on, the mathematical formulas for the measurements are showcased.

$$\:Precision=\frac{TP}{TP+FP}\times\:100$$

(21)

$$\:Specificity=\frac{TN}{TN+FP}\times\:100$$

(22)

$$\:Sensitivity=\frac{TP}{TP+FN}\times\:100$$

(23)

$$\:Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\times\:100$$

(24)

$$\:F1=2\times\:\frac{Precision\times\:Sensitivity}{Precision+Sensitivity}\times\:100$$

(25)

The confusion matrix of the DBN/MIGMM model in concrete crack detection provides essential insights into the neural network’s prediction capabilities. It categorizes predictions into four groups, including True Negatives (TN), False Negatives (FN), False Positives (FP), and True Positives (TP). TN signifies correct predictions, FN signifies incorrect predictions, FP signifies incorrect positive predictions, and TP signifies correct positive predictions.

TNs happen when the network correctly forecast the type of sport, while FNs have been found to be cases once the network incorrectly forecasts the sport type. On the other hand, FPs happen once the network incorrectly forecasts the sport type, and TPs have been considered samples once the network accurately predicts the sport type.

These metrics were chosen because they are widely used in other similar studies and show good potential for tackling the unique challenges of crack detection. Other examples include works like Zhang et al.³⁰ and Cha et al.³¹ have outlined precision and recall as being important factors in assessing crack detection tasks, with the F1-score being highlighted as an important metric when dealing with imbalanced data, confirming that in datasets where the distribution of cracked and non-cracked images is not equal, the F1- score commonly acts as a critical metric. With these metrics, this study provides a comprehensive and unbiased assessment of the performance of the proposed DBN/MIGMM model by following the standard practices frequently adopted in literature.

For ensuring an impartial evaluation, the 2-, 3-, and 5-fold cross-validation method is utilized to assess both the proposed DBN/MIGMM model and other advanced techniques. This method is well-established and trustworthy for assessing the efficacy of a model and its capacity for generalization. The process involves splitting the data into five equally sized and random subsets, utilizing each subset as a test set once, and employing the other four subsets as sets of training. The ultimate efficiency measurements were calculated by averaging the five folds outcomes.

The 5-fold cross-validation technique was utilized to compute the performance metrics for all methods, and the average performance of each method is displayed. To guarantee the reliability and validity of the outcomes, the experimental work was conducted on a dedicated platform with consistent hardware and software specifications. The efficiency metrics of the proposed DBN/MIGMM model, namely Precision, Recall, and Accuracy, were compared to those of other advanced approaches using different numbers of folds, such as 2-fold, 3-fold, and 5-fold, as well as the mean value across multiple runs.

The performance metrics for each method were computed employing the 5-fold cross-validation technique, and the average performance of each method is presented. For ensuring the validity and reliability of the outcomes, the experimental work was conducted on a specific platform with consistent software and hardware specifications. The efficiency metrics of the proposed DBN/MIGMM model, which include Recall, Precision, F1-score, specificity, and Accuracy were compared to those of other advanced approaches employing various numbers of folds, such as 2-fold, 3-fold, and 5-fold, as well as the mean value across different runs. The outcomes of the present comparison have been visually represented in Tables 4, 5 and 6, displaying the performance metrics for each method. Table 4 illustrates the 2-fold comparison results.

Table 4 The 2-fold comparison results.

The DBN/MIGMM model stands out as the top performer regarding specificity, accuracy, F1 score, precision, and recall. With an impressive accuracy rate of 87.601%, the DBN/MIGMM model demonstrates superior predictive accuracy compared to other models. It also excels in specificity, scoring 91.457%, indicating its proficiency in accurately recognizing true negatives while reducing FPs the least. While taking the F1-score into account that strikes a balance between recall and precision, the DBN/MIGMM model achieves a commendable score of 80.495%, highlighting its ability to strike a balance between these important metrics in detecting concrete cracks.

Moreover, the model exhibits high precision at 93.667%, indicating a low rate of false positive forecasts, and a recall rate of 90.062%, demonstrating effectiveness of it in capturing TP samples. Therefore, the comparison results emphasize the exceptional performance of the DBN/MIGMM model compared to other contemporary methods. It excels in accuracy, specificity, F1 score, precision, and recall, highlighting its superiority. These findings suggest that the integrated approach of combining Deep Belief Network with the modified Ideal Gas Molecular Movement optimization algorithm is highly effective in enhancing vision-based crack detection systems. The DBN/MIGMM model showcases remarkable classification accuracy and robustness. Table 5 tabulates the 3-fold analysis of the approaches.

Table 5 The 3-fold comparison results.

As can be observed, the FCN method attains an accuracy of 84.176%, with specificity of 75.948% and an F1 score of 67.015%. Precision and recall rates are 81.442% and 75.196%, respectively. YOLO showcases an accuracy of 74.797%, with higher specificity at 81.741% and an F1 score of 73.285%. Precision and recall rates are 84.38% and 77.119%, respectively. CrackSegNet achieves an accuracy of 78.835%, with specificity at 78.285% and an F1 score of 68.79%. Precision and recall rates are 77.913% and 81.652%, respectively. CNN demonstrates an accuracy of 82.029%, with specificity at 77.297% and an F1 score of 74.966%. Precision and recall rates are notably higher at 89.164% and 88.258%, respectively. CedNet achieves an accuracy of 81.554%, with specificity at 76.574% and an F1 score of 78.851%. Precision and recall rates are 85.109% and 85.654%, respectively. In contrast, the DBN/MIGMM model excels with the highest accuracy at 88.408%, along with the highest specificity at 92.15%. It also achieves a competitive F1 score of 80.901% and impressively high precision and recall rates of 93.051% and 91.961%, respectively. The current outcomes underscore the excellent efficiency of the DBN/MIGMM model in comparison with other approaches regarding specificity, accuracy, precision, recall, and F1-score, showcasing its effectiveness in concrete crack detection tasks. Table 6 tabulates the 5-fold analysis of the approaches.

Table 6 The 5-fold comparison results.

As can be observed from Fig. (3), The FCN method attains an accuracy of 84.442%, with a specificity of 82.571% and an F1 score of 75.139%. The precision and recall rates are 80.767% and 78.8%, respectively. YOLO showcases an accuracy of 83.911%, with a relatively high specificity of 87.414% and an F1 score of 79.687%. The precision and recall rates are 84.862% and 86.325%, respectively. CrackSegNet reaches an accuracy of 78.039%, with a specificity of 79.527% and an F1 score of 73.525%. The precision and recall rates are 80.476% and 88.188%, respectively. CNN demonstrates an accuracy of 80.325%, with a specificity of 80.486% and an F1 score of 78.906%. The precision and recall rates are notably higher at 88.792% and 93.311%, respectively. CedNet achieves an accuracy of 80.259%, with a specificity of 84.323% and an F1 score of 77.797%. The precision and recall rates are 89.542% and 95.11%, respectively. In contrast, the DBN/MIGMM model excels with the maximum accuracy at 90.189% and the maximum specificity at 94.502%. It also achieves an impressive F1 score of 88.093% and exceptionally high precision and recall rates of 94.586% and 94.529%, respectively. Overall, the findings emphasize the superior performance of the DBN/MIGMM model across all metrics in the 5-fold comparison, underscoring its effectiveness in concrete crack detection tasks compared to other contemporary methods.

The strong scalability of the DBN/MIGMM model makes it a powerful tool in large-scale structural health monitoring applications. The modular design of the architecture and the efficiency of the Modified Ideal Gas Molecular Movement (MIGMM) optimization algorithm result in a very fast convergence during training, minimizing computational overheads; also, the model can process large datasets such as the SDNET2018 dataset containing more than 56,000 photos. Its capabilities to generalize across a number of crack patterns and environmental conditions also make this scalable with respect to different structures ranging from small pavements to larger bridge decks.

Albeit scale and computational resources have a significant influence on this approach since it’ll need distributed or cloud-based systems to run against 100s of thousands or millions of images/sets/images. In terms of processing time, the DBN/MIGMM model is on par with state-of-the-art methods such as FCN, YOLO, and CNN-based approaches because of the speedy weight optimization using the MIGMM algorithm and due to the data augmentation techniques, that minimize extensive retraining.

But this depends on how high-resolution the images are or how complex is the architecture, and further optimization like parallel processing or hardware acceleration (e.g., GPU or TPU) could also help in making it faster. Therefore, the DBN/MIGMM model provides a sufficiently fast and scalable approach for real-world crack detection tasks, although our future work will need to focus on improving the computational efficiency further to allow for handling much larger datasets as well as operating in more challenging environments.

Applicability and reliability of the DBN/MIGMM model

The proposed DBN /MIGMM model can greatly improve the accuracy, specificity and robustness of the crack detection, which has shown good results in our performance metrics. Due to the nature of its applicability to images of surfaces such as bridge decks, pavements, and walls, it could easily adapt to various crack patterns as well as environmental conditions by using different data augmentation techniques. The performance of this method is subject to the quality and diversity of training data, and it may struggle with low-quality images, complex backgrounds, new types of crack, extreme environmental conditions, or corner cases such as hairline cracks.

Future work could address these limitations by increasing the training data size, utilizing more sophisticated preprocessing techniques, creating hybrid models, and including real-time feedback systems. The model can thus be more effective and reliable in actual structural health monitoring by catering these challenges.

The DBN/MIGMM model introduced shows great promise for improving vision-based concrete structure crack detection for empirical validation studies with high accuracy, specificity and robustness. It is generally applicable to high-resolution images of surfaces, such as bridge decks, pavements or walls, and is capable of adapting to a variety of crack patterns and environmental conditions through the application of widely used data augmentation methods like random rotations and contrast enhancement. Nonetheless, its accuracy is contingent upon the volume and variety of training data, making it potentially vulnerable to scenarios with poor image quality, intricate backgrounds, unseen crack patterns, harsh environmental conditions, or edge cases, such as hairline cracks. Each of these are aspects for model tuning. The key scientific contributions of this work include:

New Optimization Method: The proposed MIGMM, which offers significant improvement over the best-known performance metrics with minimum ‘time-data’ (in terms of training time) required to train deep belief networks in comparison to other methods.

Flat out Validation: A dedicated validation with significant performance measures and cross-validation methods, confirming an informative and objective validation of the model capability.

Field Applicability: Creating a trustworthy and fast-acting fracture examination apparatus that could be used for everyday structural health monitoring methods, decreasing dependence on manual inspection and enhancing upkeep techniques.

The study has some strong points, but it also admits to a few weaknesses. For example, it struggles with poor-quality images, busy backgrounds, and tricky situations like very thin cracks, which can make the model less accurate. Also, the model needs more computing power when working with high-quality images or bigger sets of data, so it needs to be improved to handle larger tasks more efficiently.

Conclusions

Concrete constructions are prone to cracking, which can affect their efficiency and longevity. It is essential to promptly identify and fix any cracks to ensure the structural integrity is preserved. This research proposed a combination of a deep belief network (DBN) with a modified version of Ideal Gas Molecular Movement (MIGMM) optimization algorithm to enhance the efficiency of vision-based crack detection systems. The enhanced DBN/MIGMM model showed outstanding classification accuracy, outperforming traditional methods in detecting cracks on concrete surfaces. By integrating MIGMM into the DBN structure, not only are the network’s parameters optimized, but also a specialized classification layer was introduced specifically for the binary categorization of “cracks” and “no-cracks”. Main highlight of the model involves achieving excellent performance metrics when validated against other state-of-the-art methods (i.e., Fully Convolutional Networks (FCN), You Only Look Once (YOLO), CrackSegNet, Convolutional Neural Networks (CNN) and Convolutional Encoder-Decoder Networks (CedNet) reported in previous literature) with an accuracy of 90.189%, specificity of 94.502%, precision of 94.586, recall of 94.529 and F1-score of 88.093. The data was improved (by randomly rotating the photos and increasing their contrast), making the model more dependable and responsive to various patterns and lighting conditions in the photographs. However, the research identifies significant limits, particularly with low-quality photos, complex backdrops, or unusual occurrences such as hairline fractures. These factors may have an impact on the model’s predictive accuracy. Furthermore, the model’s computational complexity might be problematic. Before putting the model into production, you may wish to optimize it if you are using a big data set or a high-resolution picture for training. Future work would include, perhaps increasing the training data-set to include other types of cracks and environmental conditions, offering additional preprocessing techniques to improve input image quality, experimenting with hybrid convolutional models with other generic structures for functional feature extraction, and integrating hardware exhibition (like GPUs or TPUs) to accelerate processing speed.