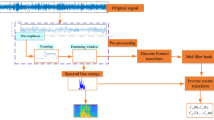
Abstract
This paper investigates the impact of variations in excitation frequency variations on the dielectric properties of coal gangue to enhance identification accuracy in challenging underground conditions. A dielectric identification methodology based on frequency shift characteristics is proposed, focusing on coal gangue samples collected from Zhujidong mine in Huainan mining area, for which a dielectric identification system was designed and constructed. This system facilitates the collection of dielectric response signals from coal gangue at frequencies of 0.4 MHz and 0.5 MHz. To analyze these response signals, a Variation Mode Decomposition (VMD) combined with a median noise reduction technique was implemented. The results indicate that this approach yields optimal noise reduction was achieved, improving the signal-to-noise ratio and root mean square error metrics. The effective voltage values and frequency components of the coal gangue at the specified frequencies were extracted, leading to the development of eight identification models. Notably, the support vector machine (SVM) identification model achieved an accuracy of 98.3%, significantly outperforming K-Nearest Neighbor (KNN), Probabilistic Neural Network (PNN), and Back Propagation (BP) models. This research presents a novel approach to addressing the identification challenges associated with the separation of coal gangue in underground environments.
Similar content being viewed by others
Introduction
Coal constitutes approximately 25% of the global energy supply, making it the second-largest energy source following oil1. The advancement of intelligent coal mines is essential for achieving high-quality development within the coal industry, with the detection, identification, and separation of underground coal gangue being a critical component of this process2. One of the most effective strategies for the clean utilization of coal gangue involves the separation of underground coal gangue and its subsequent use to fill goaf, which significantly enhances the productivity of coal shaft lifting, reduces transportation costs, and minimizes waste discharge3.
Traditional methods for the separation of coal gangue can be categorized into manual and mechanical techniques. However, with advancements in science and technology, manual separation has been largely phased out in leading coal-producing nations4. Currently, mechanical separation of coal gangue has been implemented. This process can be further classified based on the necessity of water: mechanical devices are categorized as either dry separation or wet separation systems. Common wet separation technologies include gas-solid fluidized beds5,6,7, jigs8, and cyclones9. Despite their effectiveness, wet separation methods are often criticized for their substantial water consumption and large spatial requirements, leading to their predominant use in well-based gangue selection10. Conversely, dry separation technologies exhibit a lower dependency on water resources, making them more suitable for the separation of underground gangue.
In the field of research concerning dry separation machinery, the identification characteristics of coal gangue are frequently assessed through its density11, hardness12, and various optical13, acoustic14, radiation attenuation15, and dielectric properties16. Wang et al.17 utilized the density characteristics of coal gangue as a basis for identification and proposed a separation method predicated on these density attributes. The volumes of coal and coal gangue were quantified using three-dimensional laser scanning technology, while their respective densities were estimated by integrating the results from weighing. Building on the premise that coal and gangue require different crushing forces, Yang et al.18 employed a hydraulic rotary sorting cylinder to facilitate the automated separation of coal from gangue. Due to the greater hardness of coal gangue compared to coal, it is less susceptible to fragmentation and does not pass through the openings beneath the supporting plate in the same manner as broken coal, thereby enabling the separation process. Density and hardness represent the most pronounced distinctions between coal and gangue, and they are the primary characteristics utilized in manual gangue separation.
The optical properties of coal gangue are notably diverse, particularly in terms of CCD19 and spectral imaging20, which encompass numerous identification features. In the context of image recognition for coal gangue, attributes such as gray-level21, texture22, and morphological23 characteristics are frequently employed in conjunction with deep learning algorithms24 for identification purposes. Zeng et al.25 introduced an intelligent detection methodology for coal gangue that leverages an enhanced version of the YOLOv8 algorithm, integrating coal gangue imagery with deep learning techniques. Images were captured under varying lighting conditions, and the CBAM attention mechanism was incorporated to emphasize critical features, while the EIOU loss function was introduced to enhance box regression, thereby improving detection accuracy.
Li et al.26 simulated the operational conditions pertinent to coal gangue separation and proposed a multiposition spectral feature fusion identification method. Among the classification models developed using various feature fusion techniques, the one-dimensional convolutional neural network model that employed feature layer fusion demonstrated the most robust classification performance. The Grad-CAM method was utilized to visualize the regions of interest in the model’s decision-making process, culminating in the development of a coal gangue identification system utilizing LabVIEW. Additionally, X-rays27, γ-rays28, and THz29 radiation are commonly employed for the identification of coal gangue. Wang et al.30 elucidated the effects of thickness, density, and coal type on separation by mitigating the impact of dual energy X-ray transmission (XRT) thickness on the identification of coal and gangue. By considering the imaging principles of coal gangue in R-I two-dimensional expansion space, a distance transform image processing and recognition method was proposed, utilizing a particle swarm optimization algorithm in conjunction with a support vector machine (SVM). This research offers novel methodologies and practical guidance for the selection and optimization of XRT separation parameters across varying thicknesses, densities, and coal types.
In the investigation of the dielectric properties of coal gangue, Giuntini et al.31 (1987) conducted measurements of the complex dielectric constant of non-desalted coal across a frequency range of 5 Hz to 100 MHz, utilizing this parameter to assess coal quality. Subsequently, in 1994, their research team examined the real component of the dielectric constant of coal as a function of frequency (100 Hz to 13 MHz), leading to the development of a straightforward model for the differentiation and classification of coals based on their distinct properties and origins32. Building upon the foundational work of previous researchers, my team and I have undertaken investigations into the dielectric33 identification of coal gangue, yielding significant results that integrate dielectric characteristics with imaging34 attributes of coal gangue.
To mitigate the effects of variations in the geometric size of coal gangue on the precision of its identification, this study introduces a dielectric identification methodology that capitalizes on frequency shift characteristics. The research encompasses the design of a system and the implementation of experimental studies. The results demonstrate that the dielectric identification process is characterized by rapid identification, low energy consumption, the absence of water usage, minimal noise generation, and no radiation emissions. Additionally, this method is considered appropriate for the demanding conditions typically encountered in underground environments, which are often marked by variable lighting, restricted spatial dimensions, and the presence of slime adhesion.
Principle of dielectric identification of coal gangue
Coal and coal gangue are distinct chemical substances that exhibit varying dielectric constant values within the framework of physics. It is generally observed that, in a time-varying electromagnetic field, the dielectric constant of materials decreases as the frequency increases. This paper proposes the design of a dielectric identification system for coal and gangue, utilizing the differences in their dielectric constants and the characteristics of frequency shifts. Figure 1 presents a schematic diagram of the dielectric identification system for coal and gangue based on frequency shift characteristics. The system consists of a capacitor formed by two copper electrode plates positioned on the left and right, with the coal or gangue medium situated in the center. The coal or gangue medium represents the material being transported on a conveyor belt, which passes through the parallel plate capacitor. To ensure accurate signal extraction, the coal or gangue medium is aligned prior to its passage through the capacitor, allowing only one medium to traverse the copper plates at any given time. The system employs two excitation sources operating at different frequencies. Under the control of a Field-Programmable Gate Array (FPGA), alternating high-frequency signals are input into the circuit. These excitation signals generate response signals at both ends of a constant resistance. The variation in the response signal results in two distinct changes: first, a modification in the frequency of the excitation signal leads to a change in the dielectric constant of the same medium; second, alterations in the properties of the medium also induce changes in the dielectric constant. To analyze these specific changes, the dielectric response signal is collected using a signal acquisition instrument and subsequently transmitted to a computer. The response signal undergoes a series of processing steps, including de-noising, feature analysis and extraction, and the construction of feature vectors. Ultimately, an identification model is established to facilitate the identification and classification of coal and gangue.
Variable dielectric capacitive sensor
The capacitance sensor utilizing a variable medium operates on the principle of differing dielectric constants associated with various materials, enabling the detection of the measured variable through alterations in the medium. Conversely, this principle can also be applied to ascertain the type and change of medium by analyzing the variations in the measured dielectric constant.
The operational principle of the plate structure variable dielectric capacitive sensor is illustrated in Fig. 2. Based on the varying distribution of the medium, which is situated between the two plates and characterized by its dielectric constant (denoted as εjec), the sensor can be categorized into two types: series and parallel configurations.
The principle of the flat plate structure variable dielectric capacitive sensor is illustrated in Fig. 2. This sensor can be categorized into series and parallel types based on the varying distribution positions of the medium, which possesses a dielectric constant denoted as εjec, situated between the two plates.
The series structure can be conceptualized as the series connection of two capacitive sensors that utilize different media, specifically εjec and εobj.
Therefore, the total capacitance value is:
When the dielectric constant (εjec) is not incorporated, the initial capacitance is:
The extent of capacitance variation following a change in the dielectric material is:
The observed variation in capacitance following the modification of the medium exhibits a nonlinear correlation with the dielectric constant εjec of the introduced medium.
The configuration can be characterized as a parallel arrangement of two capacitive sensors, with each sensor employing different media on the left and right sides, respectively.
Therefore, the total capacitance value is:
The initial capacitance, when the medium with permittivity εjec is not incorporated, is:
The alteration in capacitance subsequent to the modification of the medium is:
It is evident that the variation in capacitance following the alteration of the medium exhibits a linear correlation with the relative permittivity (εjec) of the introduced medium.
The methodology for detecting variable medium capacitance discussed in this article is based on the two previously mentioned principles, which are integrated in a hybrid configuration, as depicted in Fig. 3. This research employs rapid frequency-shift detection; thus, the displacement of the medium along the x-axis, characterized by a velocity of vpd and denoted as Δx, along with the fluctuation amplitude in the y-direction, represented as Δy, are minimal. Consequently, the changes in the capacitance value of the composite medium capacitor due to frequency variations can be considered negligible, and the analysis focuses solely on the capacitance value changes of the individual medium capacitor that are attributable to frequency variations.
In the design of capacitors, it is essential to minimize the thickness of the plates, within permissible limits, in order to mitigate the influence of edge effects on capacitance. The corrected capacitance can be expressed as follows:
Among them, ξ=0.163.
Excitation source and dielectric response signal
The schematic depiction of the recognition system can be understood as a conventional dual-frequency excitation RC circuit, as demonstrated in Fig. 4. In this arrangement, a standard sinusoidal alternating current voltage, referred to as \({\text{U}}_{\text{s}}\), is applied. The resistor R and the capacitor XC serve to partition the voltage. The excitation voltage source is set as:
In the formula, B denotes the amplitude of the alternating current voltage, f signifies the frequency of the alternating current voltage, t represents time, and φ indicates the initial phase angle, with the condition that φ=0.
In this RC series circuit, the phasor representation of the effective value of the input voltage \({\text{U}}_{\text{s}}\) is referred to as:
In a typical scenario involving a sine wave alternating voltage, when the phase angle (φ) is zero, the relationship can be represented as \(\dot{\text{U}}\text{=}{\text{B}}\). The impedance associated with the resistor R in the circuit is represented as \({\text{Z}}_{\text{R}}= \text{R}\), whereas the impedance of the capacitor (C) is defined as follows:
From the equation \({\text{X}}_{\text{c}}\text{=1/(2}\pi {\text{f}}\text{C)}\), it can be inferred that the impedance \({\text{Z}}_{\text{C}}\text{=-j}\frac{1}{{2}\pi {\text{f}}{\text{C}}}\). The effective value phasor of the voltage across the resistor (R) is as follows:
By substituting the value of \(\dot{\text{U}}\) into the formula and rearranging the terms, we can derive the following expression:
The effective value of the voltage across resistor R is as follows:
VMD--median signal denoising
The response signals obtained from the data logger are influenced by electromagnetic interference. To improve the analysis and feature extraction of these signals after collection, it is crucial to apply a denoising technique. For one-dimensional sinusoidal signals, this paper proposes a VMD—Median signal denoising method, and its denoising principle is as follows:
Assuming that the original signal x(t) is decomposed into k components, the decomposition sequence is guaranteed to be modal components with limited bandwidth with central frequency, and the sum of estimated bandwidths of each mode is the smallest, and the constraint condition is that the sum of all modes is equal to the original signal, the VMD constrained variational model is as follows:
Where (19) is each modal function:
Where (20) is the modal center frequency:
Median filtering: for a given window size, sort the values in the window, and then use the middle value as the output. The mathematical formula of median filtering is as follows:
Where \({u}_{k}\) is the original signal, \({w}_{k}\) is the filtered signal, n is the current position and b is the window size.
The flow of VMD—Median signal denoising method is shown in Fig. 5.
Feature extraction
The denoised sample data should be imported into the MATLAB feature extraction program. Maintaining a constant input excitation voltage and excitation frequency, it is apparent from (17) that the dielectric constant is exclusively influenced by the variation of UR. However, to calculate the dielectric constant, several constant parameters must be supplied as input. In subsequent experiments, the configuration of the capacitor may differ due to the varying dimensions of coal and coal gangue samples. To facilitate the feature extraction process, only UR1 and UR2, which denote the dielectric constant of each sample, along with the excitation frequencies f1 and f2, will be extracted to form the feature vector:
Experimental scheme design
Preparation of experimental materials
The coal and coal gangue samples employed in this study were sourced from the Zhujidong Coal Mine, situated in the Panji District of Huainan City, Anhui Province. The dielectric identification system designed for coal gangue, which operates on the principles of frequency shift characteristics, is depicted in Fig. 6.
The recognition system consists of two excitation sources, a computer, a signal recording device, a fixed resistor, a flat capacitor, several circuit boards, and connecting wires. The specifications for the relevant components are detailed in Table 1.
Exploring the effect of frequency variation on the dielectric constant of coal gangue
Under the influence of an alternating current power supply, the output voltage amplitude of the signal generator is calibrated to 10.00 V, with a bias of 0.00 V, a duty cycle of 50.0%, and an initial phase of 0.00°. Each experimental group initiates at a frequency of 100 kHz, which is subsequently increased in increments of 200 kHz. At each frequency increment, the frequency value and the corresponding effective voltage (UR) across the resistor (R) are documented. The single-sample experiment is concluded when the input frequency reaches 3.9 MHz. Employing this methodology, three sets of numerical measurements are performed on the coal gangue medium, with 50 sampling points collected for each specimen group.
The effective voltage (UR) across the terminals of the resistor (R) for each category of experimental coal gangue media is documented in Table 2, reflecting the impact of different frequencies. The data indicate that alterations in frequency lead to proportional changes in the effective voltage (UR), which demonstrates a progressive increase with rising frequency.
By integrating (11) with (17), one can derive the relationship between the relative dielectric constant of the medium within the capacitor, the effective voltage value (UR) across the resistor (R), and the frequency of the response signal.
It is evident from (24) that in an alternating RC series circuit, the effective voltage across the resistance R is measured. Furthermore, the relative dielectric constant of the capacitor’s dielectric material at a specified frequency or voltage can be determined based on the structural parameters of the capacitor and the characteristics of the excitation source.
The data pertaining to the dielectric constant are presented in Table 3. It is evident that the dielectric constant of the coal gangue medium exhibits significant variation at the same frequency.
To determine the frequency point at which the dielectric constant of coal gangue exhibits the most pronounced variation, a numerical analysis was conducted on the dielectric constants of six distinct categories of coal gangue media. The average dielectric constants for three categories of coal and three categories of coal gangue were computed, resulting in data that demonstrate the relationship between the average dielectric constant of coal gangue and frequency, as illustrated in Fig. 7. It was found that the average dielectric constant of coal gangue decreases as frequency increases.
The magnitude of this decrease is quantified by the rate of change of the average dielectric constant, as shown in Fig. 8. Importantly, the rate of change of the average dielectric constant for gangue is more significant than that for coal, with the most notable difference occurring at a frequency of 0.5 MHz. The frequencies of 0.4 MHz and 0.5 MHz are identified as critical variable frequency points, at which the dielectric constant of coal gangue experiences the most substantial changes, thereby effectively reflecting the dielectric identification characteristics of coal gangue.
Experimental verification and data analysis
Experimental samples collection of coal gangue
The investigation into the frequency variation of coal and coal gangue demonstrates notable differences in their dielectric constant properties. Specifically, the most significant variation in the average dielectric constant between coal and coal gangue occurs at frequencies of 0.3MHz and 0.5MHz. The excitation frequencies utilized in the experiment were established at 0.3MHz and 0.5MHz, with a voltage supply of 10V. A frequency-shifted dielectric extraction and identification system was employed to analyze a total of 200 specimens, comprising 100 samples of coal and 100 samples of coal gangue. Each specimen underwent analysis at both frequencies, yielding a total of 400 data points for each analysis. The resulting sample data were subsequently stored in CSV format.
Noise reduction of dielectric response signal
Data samples were obtained through the use of MATLAB software, focusing on a coal gangue sample analyzed at a frequency of 0.3 MHz as a case study. The noise present in this sample was mitigated by employing the Variational Mode Decomposition (VMD) algorithm. The initial step involved the decomposition of the data, as demonstrated in Fig. 9.
The decomposed signal is reconstructed to obtain a noise-reduced dielectric response signal, as illustrated in Fig. 10. The effectiveness of the noise reduction is assessed using the signal-to-noise ratio (SNR) and the root mean square error (RMSE) as evaluation metrics.
where \(\text{x(t)}\) is the original signal; \({\text{x}}{\prime}\text{(t)}\) is the signal after noise reduction; N is the number of sampling points.
The quantitative effects of noise reduction for the six denoising techniques are illustrated in Fig. 11. Among the methods evaluated, median filtering exhibits more effective noise reduction than Kalman filtering. Significantly, the outcomes derived from the VMD-Median denoising approach yield the highest signal-to-noise ratio and the lowest root mean square error, thereby indicating its superior performance in denoising. The response signals acquired during the experimental procedure were processed exclusively using the VMD-Median method and subsequently stored as samples in CSV format files.
Division of training set and test set
Two classification modes of coal and gangue are defined, and the labels are 1 and 2 respectively. Out of a total of 300 samples collected, the initial 150 samples are classified as the first group, while samples numbered 151 to 300 are assigned to the second group. From each category, 120 samples were chosen to form the training set, while the remaining 30 samples from each category were allocated to the test set. A selection of samples from the test set is provided in Fig. 12, with the coal and gangue samples presented in a randomized order.
Construction and testing of recognition model
Taking SVM as an example, the theoretical basis of this recognition model is demonstrated.
Construct a training set of samples:
Where \({x}_{i}\in X={R}^{n},{y}_{i}\in \left\{1,-1\right\}\left(i=1,2,\cdot \cdot \cdot ,l\right),\) and xi is the feature vector.
Select the linear kernel function \(K\left(x,x{\prime}\right)\) and suitable parameter C, and construct and solve the optimization problem:
Obtain the optimal solution:
Select a positive component of α*, \(0<{\alpha }_{j}^{*}<C\), and then calculate the threshold:
Build a decision function:
Eight kinds of recognition and classification models are established by using the training set in MATLAB software, and the recognition and classification results are shown in Fig. 13. The established models were subsequently applied to a test dataset. Among the 60 test samples comprising coal and coal gangue, logistic regression and random forest achieved a recognition accuracy of 93.3%. In comparison, the K-nearest neighbor, Quadratic Discriminant Analysis (QDA), and Naive Bayes models recorded a recognition accuracy of 95%. The Backpropagation (BP) achieved a recognition accuracy of 96.7%. Additionally, both the Support Vector Machine (SVM) and the Probabilistic Neural Network (PNN) classification models attained a recognition accuracy of 98.3%. Notably, the SVM model demonstrated the highest recognition speed among the evaluated models.
These findings indicate that it is indeed feasible to identify coal gangue by leveraging the differences in dielectric constants between coal and coal gangue. This approach exhibits enhanced real-time performance when applied to the test dataset.
Conclusion
This research focuses on the acquisition, noise reduction of response signals, extraction of feature values and vectors, and the development of a network identification model for coal gangue, leading to precise and swift identification and classification results. The key contributions of this study are as follows:
-
(1)
A novel dielectric identification method for coal gangue, based on frequency shift characteristics, is introduced for the first time, along with the creation of a corresponding coal gangue identification system.
-
(2)
To address the electromagnetic noise in the dielectric response signals of coal gangue, a noise reduction technique that combines Variational Mode Decomposition (VMD) with a Median filter is proposed. This method achieves a high signal-to-noise ratio and a low root mean square error.
-
(3)
A coal gangue identification system has been established based on the frequency-dependent characteristics of its dielectric properties, identifying two frequency points that show the most significant differences in these properties. These points serve as the working points for frequency shifts in the system.
-
(4)
Eight different identification models have been created using the frequencies of the two identified shift points along with the dielectric characteristic values to form feature vectors. Testing has shown that all models achieved high recognition accuracy, with the Support Vector Machine (SVM) reaching an accuracy of 98.3% and a processing time of 0.008003 seconds, thus functioning at the millisecond level. The method’s effectiveness is validated in terms of both accuracy and real-time performance, providing a theoretical basis for further research into underground coal gangue identification based on its dielectric characteristics.
Data availability
The research presented in this paper represents the most recent advancements achieved by our team at this stage, and the data remains unpublished. Interested researchers may obtain further information by contacting the corresponding author.
References
Yin, J. Q. et al. Intelligent photoelectric identification of coal and gangue − A review. Measurement https://doi.org/10.1016/j.measurement.2024.114723 (2024).
Li, D. Y. et al. An identification and positioning method for coal gangue based on lightweight mixed domain attention. Int. J. Coal Prep. Util. 43(9), 1542–1560 (2023).
Yang, Y. & Zeng, Q. L. Impact-slip experiments and systematic study of coal gangue “category” recognition technology Part I: Impact-slip experiments between coal gangue mixture and top coal caving hydraulic support and the study of coal gangue “category” recognition technology. Powder Technol. 392, 224–240 (2021).
Wang, X. et al. A detection method for densely distributed coal and gangue with uneven particle based on DeepLabV3+. Measurement https://doi.org/10.1016/j.measurement.2024.114756 (2024).
Zhao, P. F., Zhao, Y. M., Chen, Z. Q. & Luo, Z. F. Dry cleaning of fine lignite in a vibrated gas-fluidized bed: Segregation characteristics. Fuel 142, 274–282 (2015).
Lv, B. et al. Impact of vertical internals on the hydrodynamics and separation performance of a gas-solid separation fluidized bed. Powder Technol. 360, 577–587 (2020).
Oshitani, J. et al. Unstable sinking of spheres at higher air velocity in a gas-solid fluidized bed. Adv. Powder Technol. 32(4), 1278–1282 (2021).
Mackay, M. et al. Preparation of clean coal samples using the Roben Jig. Fuel https://doi.org/10.1016/j.fuel.2021.121729 (2021).
Ji, L., Kuang, S. B. & Yu, A. B. Numerical investigation of hydrocyclone feed inlet configurations for mitigating particle misplacement. Ind. Eng. Chem. Res. 58(36), 16823–16833 (2019).
Jiang, Z. G., He, K. Z. & Zhang, D. M. A review of intelligent coal gangue separation technology and equipment development. Int. J. Coal Prep. Util. 44(9), 1308–1324 (2024).
Guan, Z. L. et al. Coal/gangue volume estimation with convolutional neural network and separation based on predicted volume and weight. Cmc-Comput. Mater. Con. 79(1), 279–306 (2024).
Zheng, K. H. et al. Image-based numerical study of three-dimensional meso-structure effects on damage and failure of heterogeneous coal-rock under dynamic impact loads. Particuology 51, 132–141 (2020).
Li, M., Yuan, Y. X. & Cao, X. G. Experimental study on the influence of illuminance and spectral wavelength on image and spectral parameters of coal and gangue. Int. J. Coal Prep. Util. 44(10), 1521–1541 (2024).
Wan, L. R. et al. Vibration response analysis of the tail beam of hydraulic support impacted by coal gangue particles with different shapes. ACS Omega 71(4), 3656–3670 (2022).
Zhao, Y. Q. et al. Research on the fine identification of coal types and gangue based on X-ray diffraction principle. Int. J. Coal Prep. Util. 43(11), 1885–1896 (2023).
Wang, X. Q. et al. Dielectric and geometric feature extraction and recognition method of coal and gangue based on VMD-SVM. Powder Technol. 392, 241–250 (2021).
Wang, W. D. & Zhang, C. Separating coal and gangue using three-dimensional laser scanning. Int. J. Miner. Process. 169, 79–84 (2017).
Yang, D. L. et al. Impact-crush separation characteristics of coal and gangue. Int. J. Coal Prep. Util. 38(3), 127–134 (2018).
Zhao, G. Z. et al. Lightweight detection model for coal gangue identification based on improved YOLOv5s. J. Real-Time Image Pr. https://doi.org/10.1007/s11554-024-01518-5 (2024).
Liu, T. et al. Study on coal and gangue recognition by vis-NIR spectroscopy under different working conditions. Spectrosc. Spect. Anal. 44(3), 821–828 (2024).
Li, X. et al. A study on the influence of particle size on the identification accuracy of coal and gangue. Gospod Surowcami Min. 39(1), 109–129 (2023).
Luo, Q. S. et al. Research on identification of coal and gangue under complex working conditions based on relief feature. Int. J. Coal Prep. Util. 44(9), 1431–1446 (2024).
Fu, C. C., Lu, F. L. & Zhang, G. Y. Discrimination analysis of coal and gangue using multifractal properties of optical texture. Int. J. Coal Prep. Util. 42(7), 1925–1937 (2022).
Xu, M. Y. et al. Coal and gangue classification based on laser-induced breakdown spectroscopy and deep Learning. Acs Omega 81(50), 47646–47657 (2023).
Zeng, Q. L. et al. Detection of coal and gangue based on improved YOLOv8. Sensors https://doi.org/10.3390/s24041246 (2024).
Li, B. et al. Spectroscopy identification method and system for coal and gangue based on multilocation feature fusion. Int. J. Coal Prep. Util. 44(3), 993–1016 (2024).
Zhao, Y. Q. et al. Study on coal and gangue recognition method based on the combination of X-ray transmission and diffraction principle. Energ Source Part A 44(4), 9716–9728 (2022).
Zhang, N. B. et al. Precise detection of coal and gangue based on natural γ-ray. Sci. Rep. https://doi.org/10.1038/s41598-024-51424-w (2024).
Shao, D. et al. Classification method of coal and gangue using terahertz time-domain spectroscopy cluster analysis and principal component analysis. J. Appl. Spectrosc. 89(4), 719–725 (2022).
Wang, S. et al. Dual-energy X-ray transmission identification method of multi-thickness coal and gangue based on SVM distance transformation. Fuel https://doi.org/10.1016/j.fuel.2023.129593 (2024).
Giuntini, J. C., Zanchetta, J. V. & Diaby, S. Characterization of coals by the study of complex permittivity. Fuel 66(2), 179–184 (1987).
Brach, I., Giuntini, J. C. & Zanchetta, J. V. Real part of the permittivity of coals and their rank. Fuel 73(5), 738–741 (1994).
Wang, X. Q. et al. Recognition of coal and gangue based on dielectric characteristics and geometric constraints under multi factors. Energ Source Part A https://doi.org/10.1080/15567036.2021.1968546 (2021).
Wang, X. Q. et al. Coal gangue image segmentation method based on edge detection theory of star algorithm. Int. J. Coal Prep. Util. 43(1), 119–134 (2023).
Funding
This research has received support from the Key Scientific Research Project of Colleges and Universities in Henan Province (25A440007), the Innovation and Entrepreneurship Training Program for College Students in China (202410478002), and the Innovation and Entrepreneurship Training Program for College Students in Henan Province (202310478029).
Author information
Authors and Affiliations
Contributions
In the preparation of this manuscript, the authorship ranking was established by the entire staff prior to submission. Associate Professor X.Q.W. (ORCID:0000-0002-0983-5827) was instrumental in determining the research topic, designing the research plan, collecting experimental samples, constructing the experimental platform, and overseeing the entire research process. Assistant M.W. was responsible for the collection of experimental data and the creation of visual representations of the research findings. Furthermore, Teaching Assistant P.P.Z. verified the authenticity of the manuscript and the reliability of the experimental data, as well as contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, X., Wu, M. & Zhao, P. Dielectric identification method and system design of coal gangue based on frequency shift characteristics. Sci Rep 15, 8712 (2025). https://doi.org/10.1038/s41598-025-93401-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-93401-x