Abstract
Mathematical tools are crucial for dealing with uncertainty because they provide a rigorous and logical framework for evaluating, measuring, and making decisions in the presence of ambiguous information. The bipolar complex fuzzy is one of the mathematical methods for simultaneously handling dual aspect and second-dimensional information. Thus, in this script, we propound aggregation operators “partitioned Maclaurin symmetric mean and partitioned dual Maclaurin symmetric mean” within bipolar complex fuzzy set that is bipolar complex fuzzy partitioned Maclaurin symmetric mean and bipolar complex fuzzy partitioned dual Maclaurin symmetric mean, bipolar complex fuzzy weighted partitioned Maclaurin symmetric mean and bipolar complex fuzzy weighted partitioned dual Maclaurin symmetric mean operators. We also propound the related axioms of the invented operators. By employing the deduced aggregation operators, we produce a technique of multiattribute decision making within bipolar complex fuzzy sets to overcome awkward uncertainties. After that, we demonstrate an explanatory example for revealing the significance and practicability of the deduced theory and then we analyze the reliability and legitimacy of the propounded operators by comparing them with some prevailing work.
Similar content being viewed by others
Introduction
Research background
Decision making in everyday life scenarios comes with complex problems that need advanced mathematical tools that handle imprecision and unclear information. Fuzzy set (FS) theory together with its extended forms has enabled the development of these tools across different key stages. Zadeh1 established fuzzy sets as the foundation after which they became prominent for multiattribute decision making (MADM) applications2,3. The initial framework provided experts with a tool to transcend traditional crisp theory when describing alternative attributes and values. Mardani et al.4 demonstrated improved decision making capabilities through their interpretation of decision making based on fuzzy aggregation operators (AOs). The development of fuzzy aggregation theory received two important advancements through Vanicek et al.5 who introduced fuzzy aggregation and averaging for group decision making and Grabish et al.6 who proposed fuzzy aggregation of numerical preferences. Ralescu and Ralescu7 introduced new fuzzy aggregation approaches that expanded the existing concepts. Various researchers discuss the MCDM techniques in FS and its extended frameworks such as a new AI-based three-way decision making system for S-Box image encryption analysis developed by Abdullah et al.8 using the TOPSIS method. Nawaz et al.9 developed an integrated fuzzy neural network system that incorporated double hierarchy linguistic information to improve surgical approach decision making processes. Zhang et al.10 created a neural network system that successfully implements double hierarchy linguistic information for robot selection tasks while proving its worth in automation and robotics applications. Abdullah et al.11 developed a feed-forward double hierarchy linguistic neural network for heterogeneous wireless network selection to enhance network performance under uncertain conditions. Abdullah et al.12 evaluated different techniques that use double-hierarchy linguistic information for three-way decision making in deep learning applications. Abosuliman et al.13 demonstrated how fuzzy credibility neural networks can effectively select nanomaterials for nanosensor applications.
Assessment data complexities revealed the limitations of traditional FS methodologies while they were being employed. The original concept received an enhancement through Zhang’s14 development of bipolar fuzzy sets (BFS) which included both positive membership grades (PMG) ranging from 0 to 1 and negative membership grades (NMG) spanning from − 1 to 0. The extension resulted in various advancements in bipolar fuzzy theory through the work of Gul15 who established bipolar fuzzy operations and Jana et al.16 who developed Dombi operators in bipolar fuzzy contexts alongside Wei et al.17 who applied Hamacher operators to bipolar fuzzy information and Jana et al.18 who introduced Prioritized Dombi operators. Specialized MADM approaches along with TOPSIS and ELECTRE-I techniques and MULTIMOORA procedure expanded the field19,20,21. Theoretical research brought forward bipolar fuzzy graphs22 cubic bipolar fuzzy information23 bipolar picture fuzzy sets24 and bipolar soft sets25,26.
The assessment of multidimensional data required complex FS (CFS) which Ramot et al.27 introduced. The framework used membership grades which existed within the unit disc of the complex plane to represent both amplitude and phase terms. The Cartesian representation of CFS was presented by Tamir et al.28 after its initial introduction by Ramot et al.27. The research produced multiple predictive applications29 and rotational invariance solutions for complex fuzzy operations30 as well as complex fuzzy inference systems31,32 and complex fuzzy aggregation operators33,34,35,36, cosine similarity for CFS37 and complex hesitant FSs38 and complex picture fuzzy N-soft sets39. The latest advancement in this sequence comes from Mahmood and Rehman40 who created the bipolar complex fuzzy set (BCFS) framework which unites bipolar and complex fuzzy benefits. The unified framework provides a solution to manage the positive and negative aspects of multi-dimensional decision making problems within a single framework. Researchers in this field recently developed Dombi operators41 and Hamacher operators42 for BCFS.
Related work
Research in this field combines two essential areas of previous work which include BCFS developments alongside partitioned Maclaurin symmetric mean (PMSM) operator evolution. These fields have experienced major progress in recent times. BCFS has experienced multiple essential developments that both built its theoretical base and enabled practical usage of this framework. The research by Mahmood and Rehman40 presented BCFS as an advanced tool to handle dual-aspect multi-dimensional information through the complex representation of positive membership grades (PMG) and negative membership grades (NMG). Some theories produced multiple AOs which followed as a result of research development. Mahmood and Rehman43 developed Schweizer-Sklar AOs for BCFS to enable flexible bipolar complex fuzzy information combinations, and Naeem et al.44 devised Frank Power AOs to introduce a new method for BCFS information fusion applications.
Research on PMSM and PDMSM operators constitutes a major branch of aggregation theory investigation. The PMSM and PDMSM operators introduced by Bai et al.45 and Wang et al.46 respectively solve a fundamental problem with standard aggregation methods because they do not require attributes to be connected. The PMSM framework acknowledges that real-world applications show the natural partitioning of attributes into distinct classes because the interconnections exist only within each class and independence exists between different classes. The partitioned methodology has demonstrated success across different fuzzy frameworks which include Q-rung orthopair fuzzy sets (Bai et al.45) and Intuitionistic fuzzy sets (IFSs) through the IFPMSM and IFWPMSM operators (Liu et al.46) and Linguistic neutrosophic environment (Liu and You47) and IFSs with dual operators (IFPDMSM and WIFPDMSM) by Wang et al.48.
Motivation
The effectiveness of PMSM and PDMSM operators in their respective contexts stands proven but their application to bipolar complex fuzzy (BCF) information has not been investigated. The absence of PMSM and PDMSM operators becomes crucial because decision making scenarios today have become increasingly complex and involve:
-
Dual-aspect information (positive and negative evaluations)
-
Multi-dimensional data with real and imaginary parts (extra fuzzy information)
-
The information system divides its attributes into two parts: interconnected attributes alongside independent attributes
The BCFS framework becomes unable to address complex situations due to its absence of both PMSM and PDMSM operators. The current BCFS operators handle bipolar complex information yet they fail to consider the natural attribute partitioning which appears commonly in real-world applications. The existing PMSM systems manage partitioned features yet they cannot process the comprehensive dual-dimensional information which BCFS delivers. The research gap stands out most strongly in MADM applications because:
-
Information systems should represent data across positive and negative value ranges.
-
The evaluation needs to incorporate extra fuzzy information
-
Attributes organize themselves into distinct groups which show partial independence from other groups
Real-world applications demand the significance of this research because of their practical requirements. Real-world decision making scenarios often distribute their attributes into separate groups where linked attributes show strong relationships yet independent attributes stay distinct. Decision makers need tools that effectively manage such natural data partitions during the processing of complex multi-faceted information. The combination of increasing decision making scenarios using extra fuzzy data together with the requirement to handle positive and negative aspects creates an urgent need for advanced mathematical tools.
Novelties and advantages
The proposed approaches bring substantial breakthroughs that resolve current weaknesses in decision making systems. Our work introduces PMSM and PDMSM operators into BCFS environments for the first time to establish a new mathematical framework that handles multi-dimensional dual-aspect information with natural attribute partitioning. The integration of bipolar complex information handling with partitioned attribute processing represents the first successful attempt at decision making methodology development. The research develops new operator capabilities by creating BCFPMSM and BCFPDMSM operators and their weighted counterparts BCFWPMSM and BCFWPDMSM. The operators benefit from new theoretical properties and operational laws that guarantee both mathematical strength and practical usability. The methodology introduces fresh methods to address interdependent attributes in BCFS and develops new mechanisms to process extra fuzzy data in partitioned attributes while integrating positive and negative membership grades in complex systems.
The present proposed methods demonstrate comprehensive high-level benefits compared to current approaches in multiple ways. Our information processing approach presents better dual-aspect modeling capabilities than standard fuzzy methods and superior extra fuzzy data representation than BFSs. The method delivers superior attribute relationship modeling than BCFS approaches specifically in domains where attributes form naturally distinct groups. The proposed framework shows impressive versatility because it works with independent and interconnected attributes simultaneously and adjusts to different decision situations. The framework becomes more adaptable through specific parameter weighting methods for various attribute classifications which optimize its applicability to actual decisions. Our method provides three essential practical advantages which include better decision representation of real-world scenarios and enhanced uncertainty management together with natural grouping capabilities.
Contribution
The research presents multiple important original findings in both fuzzy mathematics and decision making theory domains. The research creates new AOs that unite partitioned MSM operators with BCFSs for their first application in the literature. This research presents the bipolar complex fuzzy PMSM (BCFPMSM) and bipolar complex fuzzy PDMSM (BCFPDMSM) operators while introducing their weighted variants as BCFWPMSM and BCFWPDMSM operators. The newly developed operators serve as the initial mathematical system that effectively processes dual-aspect data and extra fuzzy information together with naturally partitioned properties in BCF systems. Our second principal achievement involves creating an extensive theoretical basis for these newly developed operators. We prove fundamental mathematical properties together with operational laws and theorems that determine how BCFPMSM and BCFPDMSM operators function. The theoretical framework establishes original proofs of idempotency together with boundedness and monotonicity properties which provide strong mathematical foundations for practical usage of these operators. These properties establish new mathematical knowledge about partitioned mean operator behavior when applied to BCF information systems. The third major achievement involves creating a new MADM method that utilizes the distinctive features of our proposed operators. This method provides novel approaches to solving decision problems that contain attributes that belong to specific categories while maintaining independent relationships between different categories. Our method stands as the first solution that allows decision makers to evaluate bipolar information while handling extra fuzzy data and attribute division through a single mathematical framework thus advancing MADM techniques.
Layout of the paper
In Section "Preliminaries", the fundamental mathematical structure of BCFS, PMSM, and PDMSM operators, and their elementary laws are reminded. Section "PMSM and PDMSM operators for BCFNs", consists of BCFPMSM, BCFWPMSM, BCFPDMSM, BCFWPDMSM operators and their significant properties with numerous powerful results. In Section "Comparison" of this article, we invented a new technique of MADM by employing the invented operators within the setting of BCFS. In Section "MADM methodology established on invented PMSM operators", we reveal the applicability and effectiveness of the invented technique with the assistance of a genuine DM example. In Section "Explanatory example", we inspected the reliability and legitimacy of the propounded operators by comparing them with some prevailing theories. Section 7 has the concluding remarks.
Preliminaries
In this portion, the fundamental theories such as BCFS, PMSM, PDMSM operators, and their elementary laws are reminded. In the rest of the script, \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\hbox{K}} }}\) be a universal set.
Definition 1:
40 A BCFS \(\hbox{O}\) is of the formation
where \({\Psi }_{\hbox{O}}^{+}\left(\kappa \right):{K}\to \left[0, 1\right]\)\(+\iota \left[0, 1\right]\) and \({\Psi }_{\hbox{O}}^{-}\left(\kappa \right):{K}\to \left[-1, 0\right]\)\(+\iota \left[-1, 0\right]\), stated the PMG and NMG in the structure: \({\Psi }_{\hbox{O}}^{+}\left(\kappa \right)={\theta }_{\hbox{O}}^{+}\left(\kappa \right)+\iota {\vartheta }_{\hbox{O}}^{+}\left(\kappa \right)\) and \({\Psi }_{\hbox{O}}^{-}\left(\kappa \right)={\theta }_{\hbox{O}}^{-}\left(\kappa \right)+\iota {\vartheta }_{\hbox{O}}^{-}\left(\kappa \right)\), with \({\theta }_{\hbox{O}}^{+}\left(\kappa \right),{\vartheta }_{\hbox{O}}^{+}\left(\kappa \right)\in \left[0, 1\right]\) and \({\theta }_{\hbox{O}}^{-}\left(\kappa \right),{\vartheta }_{\hbox{O}}^{-}\left(\kappa \right)\in \left[-1, 0\right]\). We call \(\hbox{O}=(\kappa , {\Psi }_{\hbox{O}}^{+}(\kappa ), {\Psi }_{\hbox{O}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{\hbox{O}}^{+}(\kappa )+\iota {\vartheta }_{\hbox{O}}^{+}(\kappa ), {\theta }_{\hbox{O}}^{-}(\kappa )+\iota {\vartheta }_{\hbox{O}}^{-}(\kappa ))\) BCF number (BCFN).
Definition 2:
41 For a BCFN \(\hbox{O}=\left(\kappa , {\Psi }_{\hbox{O}}^{+}\left(\kappa \right), {\Psi }_{\hbox{O}}^{-}\left(\kappa \right)\right)=\left(\kappa , {\theta }_{\hbox{O}}^{+}\left(\kappa \right)+\iota {\vartheta }_{\hbox{O}}^{+}\left(\kappa \right), {\theta }_{\hbox{O}}^{-}\left(\kappa \right)+\iota {\vartheta }_{\hbox{O}}^{-}\left(\kappa \right)\right)\), the score value \({\mathbb{S}}_{\mathcal{B}}\) is characterized as
Definition 3:
41 The score value \({\mathbb{H}}_{\mathcal{B}}\) of a BCFN \(\hbox{O}=(\kappa , {\Psi }_{\hbox{O}}^{+}(\kappa ), {\Psi }_{\hbox{O}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{\hbox{O}}^{+}(\kappa )+\iota {\vartheta }_{\hbox{O}}^{+}(\kappa ),\)\({\theta }_{\hbox{O}}^{-}(\kappa )+\iota {\vartheta }_{\hbox{O}}^{-}(\kappa ))\) is characterized as
Definition 4:
41 In the presence of any two BCFNs \({\hbox{O}}_{1}=(\kappa , {\Psi }_{{\hbox{O}}_{1}}^{+}(\kappa ),\)\({\Psi }_{{\hbox{O}}_{1}}^{-}(\kappa ))\) and \({\hbox{O}}_{2}=(\kappa , {\Psi }_{{\hbox{O}}_{2}}^{+}(\kappa ),\)\({\Psi }_{{\hbox{O}}_{2}}^{-}(\kappa ))\), we establish
-
1.
If \({\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)<{\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right)\), then \({\hbox{O}}_{1}<{\hbox{O}}_{2}\)
-
2.
If \({\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)>{\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right)\), then \({\hbox{O}}_{1}>{\hbox{O}}_{2}\)
-
3.
If \({\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)={\mathbb{S}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right)\), then
-
i
If \({\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)<{\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right),\) then \({\hbox{O}}_{1}<{\hbox{O}}_{2}\)
-
ii
If \({\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)>{\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right),\) then \({\hbox{O}}_{1}>{\hbox{O}}_{2}\)
-
iii
If \({\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{1}\right)={\mathbb{H}}_{\mathcal{B}}\left({\hbox{O}}_{2}\right),\) then \({\hbox{O}}_{1}={\hbox{O}}_{2}\)
-
i
Definition 5:
41 In the presence of any two BCFNs \({\hbox{O}}_{1}=(\kappa , {\Psi }_{{\hbox{O}}_{1}}^{+}(\kappa ), {\Psi }_{{\hbox{O}}_{1}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{{\hbox{O}}_{1}}^{+}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{1}}^{+}(\kappa ), {\theta }_{{\hbox{O}}_{1}}^{-}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{1}}^{-}(\kappa ))\) and \({\hbox{O}}_{2}=(\kappa , {\Psi }_{{\hbox{O}}_{2}}^{+}(\kappa ), {\Psi }_{{\hbox{O}}_{2}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{{\hbox{O}}_{2}}^{+}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{2}}^{+}(\kappa ), {\theta }_{{\hbox{O}}_{2}}^{-}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{2}}^{-}(\kappa ))\), with \(\lambda >0\), then
-
1.
\({\hbox{O}}_{1}\oplus {\hbox{O}}_{2}=\left(\kappa , \left(\begin{array}{c}{\theta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)+{\theta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)-{\theta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right){\theta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)+\iota \left({\vartheta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)+{\vartheta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)-{\vartheta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right){\vartheta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)\right), \\ -\left({\theta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right){\theta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)\right)+\iota \left(-\left({\vartheta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right){\vartheta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)\right)\right)\end{array}\right)\right)\)
-
2.
\({\hbox{O}}_{1}\otimes {\hbox{O}}_{2}=\left(\kappa , \left(\begin{array}{c}{\theta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right){\theta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)+\iota \left({\vartheta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right){\vartheta }_{{\hbox{O}}_{2}}^{+}\left(\kappa \right)\right), \\ {\theta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)+{\theta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)+{\theta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right){\theta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)+\iota \left({\vartheta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)+{\vartheta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)+{\vartheta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right){\vartheta }_{{\hbox{O}}_{2}}^{-}\left(\kappa \right)\right)\end{array}\right)\right)\)
-
3.
\(\lambda {\hbox{O}}_{1}=\left(\kappa , \left(1-{\left(1-{\theta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)\right)}^{\lambda }+\iota \left(1- {\left(1-{\vartheta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)\right)}^{\lambda }\right),-{\left|{\theta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)\right|}^{\lambda }+\iota \left(-{\left|{\vartheta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)\right|}^{\lambda }\right)\right)\right)\)
-
4.
\({{\hbox{O}}_{1}}^{\lambda }=\left(\kappa , \left({\left({\theta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)\right)}^{\lambda }+\iota {\left({\vartheta }_{{\hbox{O}}_{1}}^{+}\left(\kappa \right)\right)}^{\lambda }, -1+{\left(1+{\theta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)\right)}^{\lambda }+\iota \left(-1+{\left(1+{\vartheta }_{{\hbox{O}}_{1}}^{-}\left(\kappa \right)\right)}^{\lambda }\right)\right)\right)\)
Theorem i:
41 In the presence of any two BCFNs \({\hbox{O}}_{1}=(\kappa , {\Psi }_{{\hbox{O}}_{1}}^{+}(\kappa ), {\Psi }_{{\hbox{O}}_{1}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{{\hbox{O}}_{1}}^{+}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{1}}^{+}(\kappa ), {\theta }_{{\hbox{O}}_{1}}^{-}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{1}}^{-}(\kappa ))\) and \({\hbox{O}}_{2}=(\kappa , {\Psi }_{{\hbox{O}}_{2}}^{+}(\kappa ), {\Psi }_{{\hbox{O}}_{2}}^{-}(\kappa ))\)\(=(\kappa , {\theta }_{{\hbox{O}}_{2}}^{+}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{2}}^{+}(\kappa ), {\theta }_{{\hbox{O}}_{2}}^{-}(\kappa )+\iota {\vartheta }_{{\hbox{O}}_{2}}^{-}(\kappa ))\), with \(\lambda , {\lambda }_{1}, {\lambda }_{2}>0\), then
-
1.
\({\hbox{O}}_{1}\oplus {\hbox{O}}_{2}={\hbox{O}}_{2}\oplus {\hbox{O}}_{1}\)
-
2.
\({\hbox{O}}_{1}\otimes {\hbox{O}}_{2}={\hbox{O}}_{2}\otimes {\hbox{O}}_{2}\)
-
3.
\(\lambda \left({\hbox{O}}_{1}\oplus {\hbox{O}}_{2}\right)=\lambda {\hbox{O}}_{1}\oplus \lambda {\hbox{O}}_{2}\)
-
4.
\({\left({\hbox{O}}_{1}\otimes {\hbox{O}}_{2}\right)}^{\lambda }={{\hbox{O}}_{1}}^{\lambda }\otimes {{\hbox{O}}_{2}}^{\lambda }\)
-
5.
\({\lambda }_{1}{\hbox{O}}_{1}\oplus {\lambda }_{2}{\hbox{O}}_{1}=\left({\lambda }_{1}+{\lambda }_{2}\right){\hbox{O}}_{1}\)
-
6.
\({{\hbox{O}}_{1}}^{{\lambda }_{1}}\otimes {{\hbox{O}}_{1}}^{{\lambda }_{2}}={{\hbox{O}}_{1}}^{{\lambda }_{1}+{\lambda }_{2}}\)
-
7.
\({\left({{\hbox{O}}_{1}}^{{\lambda }_{1}}\right)}^{{\lambda }_{2}}={{\hbox{O}}_{1}}^{{\lambda }_{1}{\lambda }_{2}}\)
Definition 6:
45 In the presence of a group of positive numbers \({\hbox{O}}_{\mathcalligra{s}}\), the PMSM operator is established as
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\,\hbox{is}\) a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\,\hbox{integer}\) obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial.
Subsequent are the obvious characteristics of PMSM.
-
1.
\(PMS{M}^{\left(\mathcalligra{f}\right)}\left(\hbox{O}, \hbox{O}, \hbox{O}, \dots , \hbox{O}\right)= \hbox{O}\)
-
2.
\(PMS{M}^{\left(\mathcalligra{f}\right)}\left({\hbox{O}}_{1}, {\hbox{O}}_{2}, {\hbox{O}}_{3}, \dots , {\hbox{O}}_{\mathfrak{n}}\right)\le PMS{M}^{\left(\mathcalligra{f}\right)}\left({\hbox{O}}_{1}^{\prime}, {\hbox{O}}_{2}^{\prime}, {\hbox{O}}_{3}^{\prime}, \dots , {\hbox{O}}_{\mathfrak{n}}^{\prime}\right)\) if \({\hbox{O}}_{\mathcalligra{s}}\le {\hbox{O}}_{\mathcalligra{s}}^{\prime} \forall \mathcalligra{s}\)
-
3.
\(\underset{\mathcalligra{s}}{\text{min}}\left\{{\hbox{O}}_{\mathcalligra{s}}\right\}\le PMS{M}^{\left(\mathcalligra{f}\right)}\left({\hbox{O}}_{1}, {\hbox{O}}_{2}, {\hbox{O}}_{3}, \dots , {\hbox{O}}_{\mathfrak{n}}\right)\le \underset{\mathcalligra{s}}{\text{max}}\left\{{\hbox{O}}_{\mathcalligra{s}}\right\}\)
Definition 7:
48 In the presence of a group of positive numbers \({\hbox{O}}_{\mathcalligra{s}}\), the PDMSM operator is established as
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\,\hbox{is}\) a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\,\hbox{integer}\) obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial.
PMSM and PDMSM operators for BCFNs
The beneficial theme of this study is to expose the novel methodologies of BCFPMSM, BCFWPMSM, BCFPDMSM, and BCFWPDMSM operators. The terms \({\hbox{O}}_{\mathcalligra{r}}=\left({\Psi }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}, {\Psi }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\right)=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\right) \left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\) stated the family of BCFNs in the following study.
BCFPMSM operator
Following, we interpreted the BCFPMSM operator.
Definition 8:
The BCFPMSM operator \(BCFPMS{M}^{\left(\mathcalligra{f}\right)}\) is simplified by:
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\) is a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\) integer obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial.
Theorem ii:
For Eq. (4) we diagnose
Proof:
From Def. 5, we have
and
then we obtain
consequently
Therefore, we obtain
this implies that
completed the proof of the results.
Furthermore, the BCFPMSM has the necessary properties as follows
In the accessibility of two collections of BCFNs \({\hbox{O}}_{\mathcalligra{r}}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\right)\) and \({\hbox{O}}_{\mathcalligra{r}}^{\prime}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\right)\), \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), we have
a) Idempotency: If \({\hbox{O}}_{\mathcalligra{r}}=\hbox{O} \forall \mathcalligra{r}\), then
b) Monotonicity: If \({\hbox{O}}_{\mathcalligra{r}}\le\) \({\hbox{O}}_{\mathcalligra{r}}^{\prime}\) for \(\hbox{all}\,\mathcalligra{r}\), i.e. \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}\), \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\), then
c) Boundedness: If \({\hbox{O}}_{\mathcalligra{r}}^{*}=\underset{\mathcalligra{r}}{\text{max}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\) and \({{\hbox{O}}_{\mathcalligra{r}}}^{**}=\underset{\mathcalligra{r}}{\text{min}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\), then
BCFWPMSM operator
In MADM, each attribute has various significance and is necessary to be given distinct weights. Thus, AO should consider the weights of attributes. Following, we interpreted the BCFWPMSM operator.
Definition 9:
The BCFWPMSM operator \(BCFWPMS{M}^{\left(\mathcalligra{f}\right)}\) is simplified by:
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\,\hbox{is}\) a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\,\hbox{integer}\) obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial and \({\tilde{\omega}}=\left({\tilde{\omega}}_{1}, {\tilde{\omega}}_{2}, {\tilde{\omega}}_{3}, \dots , {\tilde{\omega}}_{\mathfrak{n}}\right)\) is the WV of \({\hbox{O}}_{\mathcalligra{r}}\) \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), where \({\tilde{\omega}}_{\mathcalligra{r}}\) denotes the significant degree of \({\hbox{O}}_{\mathcalligra{r}}\) such that \({\tilde{\omega}}_{\mathcalligra{r}}\in \left[0, 1\right]\) and \(\sum_{k=1}^{\mathfrak{n}}{\tilde{\omega}}_{\mathcalligra{r}}=1\).
Theorem iii:
For Eq. (6) we diagnose
Additionally, the BCFWPMSM has the necessary properties as follows
In the accessibility of two collections of BCFNs \({\hbox{O}}_{\mathcalligra{r}}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\right)\) and \({\hbox{O}}_{\mathcalligra{r}}^{\prime}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\right)\), \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), we have
d) Idempotency: If \({\hbox{O}}_{\mathcalligra{r}}=\hbox{O} \forall \mathcalligra{r}\), then
e) Monotonicity: If \({\hbox{O}}_{\mathcalligra{r}}\le\) \({\hbox{O}}_{\mathcalligra{r}}^{\prime}\) for \(\hbox{all}\,\mathcalligra{r}\), i.e. \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}\), \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\), then
f) Boundedness: If \({\hbox{O}}_{\mathcalligra{r}}^{*}=\underset{\mathcalligra{r}}{\text{max}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\) and \({{\hbox{O}}_{\mathcalligra{r}}}^{**}=\underset{\mathcalligra{r}}{\text{min}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\), then
BCFPDMSM operator
In this subsection, we produce the BCFPDMSM operator.
Definition 10:
The BCFPDMSM operator \(BCFPDMS{M}^{\left(\mathcalligra{f}\right)}\) is simplified by:
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\,\hbox{is}\) a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\,\hbox{integer}\) obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial.
Theorem iv:
For Eq. (8), we diagnose
Proof:
From Def. 5, we have
and
then we obtain
consequently,
Therefore, we obtain
this implies that
completed the proof of the results.
Additionally, the BCFPDMSM has the necessary properties as follows
In the accessibility of two collections of BCFNs \({\hbox{O}}_{\mathcalligra{r}}=({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+},\)\({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-})\) and \({\hbox{O}}_{\mathcalligra{r}}^{\prime}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\right)\), \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), we have
g) Idempotency: If \({\hbox{O}}_{\mathcalligra{r}}=\hbox{O} \forall \mathcalligra{r}\), then
h) Monotonicity: If \({\hbox{O}}_{\mathcalligra{r}}\le\) \({\hbox{O}}_{\mathcalligra{r}}^{\prime}\) for \(\hbox{all}\,\mathcalligra{r}\), i.e. \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}\), \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\), then
i) Boundedness: If \({\hbox{O}}_{\mathcalligra{r}}^{*}=\underset{\mathcalligra{r}}{\text{max}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\) and \({{\hbox{O}}_{\mathcalligra{r}}}^{**}=\underset{\mathcalligra{r}}{\text{min}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\), then
BCFWPMSM operator
In MADM, each attribute has various significance and is necessary to be given distinct weights. Thus, AO should consider the weights of attributes. Following, we interpreted the BCFWDPMSM operator.
Definition 11:
The BCFWPDMSM operator \(BCFWPDMS{M}^{\left(\mathcalligra{f}\right)}\) is simplified by:
where \(\mathcalligra{v}\) signifies the number of partitions, \(\mathcalligra{f}\, \hbox{is}\) a parameter, \(\mathcalligra{f}=1, 2, 3, \dots , {\mathfrak{t}}_{\mathcalligra{u}}\), where \({\mathfrak{t}}_{\mathcalligra{u}}\) signifies the quantity of attributes in the partition \({\mathcal{P}}_{\mathcalligra{u}}\), \({\mathcalligra{r}}_{1}, {\mathcalligra{r}}_{2}, {\mathcalligra{r}}_{3}\dots , {\mathcalligra{r}}_{\mathcalligra{f}}\) are \(\mathcalligra{f}\,\hbox{integer}\) obtained from the set \(\left\{1, 2, \dots ,{\mathfrak{t}}_{\mathcalligra{u}}\right\}\) of \({\mathfrak{t}}_{\mathcalligra{u}}\) integers such that \(1\le {\mathcalligra{r}}_{1}<{\mathcalligra{r}}_{2}<\dots <{\mathcalligra{r}}_{\mathcalligra{f}}\le {\mathfrak{t}}_{\mathcalligra{u}}\). The term \({\mathcal{C}}_{{\mathfrak{t}}_{\mathcalligra{u}}}^{\mathcalligra{f}}\)=\(\frac{{\mathfrak{t}}_{\mathcalligra{u}}!}{\mathcalligra{f}!\left({\mathfrak{t}}_{\mathcalligra{u}}-\mathcalligra{f}\right)!}\) demonstrates the binomial and \({\tilde{\omega}}=\left({\tilde{\omega}}_{1}, {\tilde{\omega}}_{2}, {\tilde{\omega}}_{3}, \dots , {\tilde{\omega}}_{\mathfrak{n}}\right)\) is the WV of \({\hbox{O}}_{\mathcalligra{r}}\) \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), where \({\tilde{\omega}}_{\mathcalligra{r}}\) denotes the significant degree of \({\hbox{O}}_{\mathcalligra{r}}\) such that \({\tilde{\omega}}_{\mathcalligra{r}}\in \left[0, 1\right]\) and \(\sum_{k=1}^{\mathfrak{n}}{\tilde{\omega}}_{\mathcalligra{r}}=1\).
Theorem v:
For Eq. (10), we diagnose
Additionally, the BCFWPDMSM has the necessary properties as follows.
In the accessibility of two collections of BCFNs \({\hbox{O}}_{\mathcalligra{r}}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\right)\) and \({\hbox{O}}_{\mathcalligra{r}}^{\prime}=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\right)\), \(\left(\mathcalligra{r}=1, 2, 3, \dots , \mathfrak{n}\right)\), we have.
j) Idempotency: If \({\hbox{O}}_{\mathcalligra{r}}=\hbox{O} \forall \mathcalligra{r}\), then
k) Monotonicity: If \({\hbox{O}}_{\mathcalligra{r}}\le\) \({\hbox{O}}_{\mathcalligra{r}}^{\prime}\) \(\hbox{for\,all}\,\mathcalligra{r},\) i.e. \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{+}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{+}\), \({\theta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\theta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}, {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}}^{-}\le {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}}^{\prime}}^{-}\), then
l) Boundedness: If \({\hbox{O}}_{\mathcalligra{r}}^{*}=\underset{\mathcalligra{r}}{\text{max}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\) and \({{\hbox{O}}_{\mathcalligra{r}}}^{**}=\underset{\mathcalligra{r}}{\text{min}}\left\{{\hbox{O}}_{\mathcalligra{r}}\right\}\), then
MADM methodology established on invented PMSM operators
Here, we invent a new MADM method depending on the invented PMSM and PDMSM operators in the setting of BCFNs.
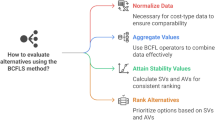
For resolving the DM issues, below, we will employ an invented MADM approach. Let the family of alternative be \(\mathfrak{T}=\left\{{\mathfrak{T}}_{1}, {\mathfrak{T}}_{2}, .., {\mathfrak{T}}_{\mathfrak{m}}\right\}\), the group of attributes is \(\mathfrak{D}=\left\{{\mathfrak{D}}_{1}, {\mathfrak{D}}_{2}, .., {\mathfrak{D}}_{\mathfrak{n}}\right\}\) and \({\tilde{\omega}}=\left({\tilde{\omega}}_{1}, {\tilde{\omega}}_{2}, {\tilde{\omega}}_{3}, \dots , {\tilde{\omega}}_{\mathfrak{n}}\right)\) be the WVs of attributes with the condition that \(\sum_{\mathcalligra{r}=1}^{\mathfrak{n}}{\tilde{\omega}}_{\mathcalligra{r}}=1\), and \({\tilde{\omega}}_{\mathcalligra{r}}\in \left[0, 1\right]\) for all \(\mathcalligra{r}\). To assess the alternative \({\mathfrak{T}}_{\mathcalligra{r}}\) concerning the attribute \({\mathfrak{D}}_{\mathcalligra{s}}\), an expert will employ the BCFNs and illustrate it as \({\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}=\left({\Psi }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{+}, {\Psi }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{-}\right)=\left({\theta }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{+}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{+}, {\theta }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{-}+\iota {\vartheta }_{{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}}^{-}\right)\), we can obtain a decision matrix \(\mathfrak{M}={\left[{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}\right]}_{\mathfrak{m}\times \mathfrak{n}}\). Let \(\mathfrak{D}=\left\{{\mathfrak{D}}_{1}, {\mathfrak{D}}_{2}, .., {\mathfrak{D}}_{\mathfrak{n}}\right\}\) be partitioned into \(\mathcalligra{v}\) different classes \({\mathcal{P}}_{1}, {\mathcal{P}}_{2}, \dots , {\mathcal{P}}_{\mathcalligra{u}}\). There is a connection between the attributes of the same classes and doesn’t have a connection among the attributes of different classes. Following are the steps of the invented methodology.
Step 1: Normalization of Decision Matrix.
The first step transforms the decision matrix \(\mathfrak{M}={\left[{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}\right]}_{\mathfrak{m}\times \mathfrak{n}}\) into normalized matrix \({\mathfrak{M}}^{\prime}={\left[{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}^{\prime}\right]}_{\mathfrak{m}\times \mathfrak{n}}\) because it handles different attribute types including benefit and cost attributes. The normalization technique preserves benefit-type attribute values because they lead to better decision results. The values from cost-type attributes require appropriate normalization formulas to transform them during the process. This formula is devised as follows.
The standardized procedure maintains an equal and just evaluation process between different attribute formats while minimizing variation from measurement complexity.
Step 2: Information Aggregation.
The selection of one operator from four key operators including BCFPMSM, BCFWPMSM, BCFPDMSM, or BCFWPDMSM occurs in this step. The selected operator unifies normalized information by accounting for inner-class attribute relationships without permitting information transfer between distinct classes. The aggregation method unifies normalized values into complete scores for assessing each available alternative.
Step 3: Score and Accuracy Calculation.
Use Definitions 2 and 3 to determine score and accuracy values from the aggregated results after the aggregation process is completed. Score values function as the main performance indicator for alternatives but accuracy values act as a backup differentiator when score values match. The calculations produce numerical measures from fuzzy information which enables systematic evaluation of alternatives against each other.
Step 4: Ranking and Selection.
The last stage requires the sorting of alternatives according to their calculated score and accuracy values. The ranking system depends mainly on score values yet accuracy values determine the final placement when score values match. The systematic ranking procedure determines the best alternative through a complete assessment of criteria and their relationships.
Explanatory example
In this part, the applicability and effectiveness of the invented technique are tested through the following genuine DM example.
In the discipline of supply chain management (SCM), the selection of suppliers is one of the significant problems in DM. The procedure of selection is crucial for improving the organization’s effectiveness and needs the evaluation of various alternatives (options) of the suppliers in light of various attributes. Supplier selection is one of the vital parts of SCM, it is MADM issues that include both quantitative and qualitative attributes. The selection of the finest supplier would decrease buying costs, reduce item lead time, enhance profits, develop consumer loyalty, and reinforce effectiveness. For that reason, it has turned into a fundamental concentration for each buying company, yet there is no norm for the selection of suppliers, and it ought to be applied given the circumstances. Usually, the producer of the selection of suppliers includes four stages i.e. stage 1: finding suppliers, stage 2: gathering data about these suppliers, stage 3: haggling with suppliers, stage 4: assessing suppliers and selecting the finest one. From the point of view of MADM, the stage of gathering data about the suppliers indicates defining the attributes that should have been assessed. Stage 3 implies defining the attributes and values of every supplier. The primary job of assessing suppliers is to rank the suppliers and select the finest ones as per the attribute values. Here, we will employ the interpreted technique for the selection of suppliers. A company intends to select a supplier. After the essential selection, \(\mathfrak{T}=\left\{{\mathfrak{T}}_{1}, {\mathfrak{T}}_{2}, .., {\mathfrak{T}}_{\mathfrak{m}}\right\}\) are only the remaining 4 applicants. A decision maker is hired to assess the applicants by considering the 4 attributes \({\mathfrak{D}}_{1}=Clear\,recordkeeping\), \({\mathfrak{D}}_{2}=Strives\,to\,continually\,improve\), \({\mathfrak{D}}_{3}=Reliability\), \({\mathfrak{D}}_{4}=Demonstrates\,innovat\iota on\) and select the finest. The WV is \({\tilde{\omega}}=\left(0.2, 0.27, 0.23, 0.3\right)\). Let the attributes \({\mathfrak{D}}_{1}\), \({\mathfrak{D}}_{2}\),\({\mathfrak{D}}_{3}\), and \({\mathfrak{D}}_{4}\) be divided into two classes \({\mathcal{P}}_{1}=\left\{{\mathfrak{D}}_{1}, {\mathfrak{D}}_{3}\right\}\) and \({\mathcal{P}}_{2}=\left\{{\mathfrak{D}}_{2}, {\mathfrak{D}}_{4}\right\}\). The decision maker assesses the suppliers \({\mathfrak{T}}_{\mathcalligra{r}} \left(\mathcalligra{r}=1, 2, 3, 4\right)\) By considering the attribute \({\mathfrak{D}}_{\mathcalligra{s}} \left(\mathcalligra{s}=1, 2, 3, 5\right)\) in the setting of BCFNs. Thus, we obtained a decision matrix \(\mathfrak{M}={\left[{\hbox{O}}_{\mathcalligra{r}\mathcalligra{s}}\right]}_{4\times 4}\) which is described in Table 1.
Step 1. Since all the attributes are of the same type, so no need for normalization.
Step 2: Utilize the invented BCFPMSM, BCFWPMSM, BCFPDMSM, and BCFWPDMSM operators to obtain all preference values of \({\mathfrak{T}}_{\mathcalligra{r}} \left(\mathcalligra{r}=1, 2, 3, 4\right)\) which have appeared in Table 2.
Step 3: Determine the score and accuracy values by employing Def 2 and 3 for each aggregated outcome \({\mathfrak{T}}_{\mathcalligra{r}} \left(\mathcalligra{r}=1, \text{2,3}, 4\right)\) which have appeared in Table 3.
Step 4: Place all the alternatives \({\mathfrak{T}}_{\mathcalligra{r}} \left(\mathcalligra{r}=1, 2, 3, 4\right)\) in descending order in Table 4 by utilizing the determined score and accuracy values to get the finest alternative.
The graphical interpretation of Table 4 is given in Fig. 1.
The graphical explanation of Table 4.
By overhead analysis, it is noticeable that the invented BCFPMSM, BCFWPMSM, and BCFWPDMSM operators provide us with that the supplier \({\mathfrak{T}}_{3}\) is the best one among all other suppliers and the operator BCFPDMSM delivers us that the supplier \({\mathfrak{T}}_{1}\) is the optimal one among all the other suppliers. It is obvious, that the selection of one of the invented operators depends on the preference of an expert. In addition, it should be seen that all of them can give us different results, and having comparable results is not a necessary choice. In our above example, we are considering the value of the parameter \(\dot{\mathcalligra{f}}=2\) in both partitions.
Comparison
This section performs an extensive evaluation of our proposed operators through a comparison with existing methods found in the literature to assess their reliability and legitimacy.
Multiple AOs exist for BCFS frameworks to manage information through their advanced mathematical structure that preserves ambiguous data without information loss. Our comparison encompasses multiple established works, including the intuitionistic fuzzy domain operators that are IFPMSM and IFWPMSM by Liu et al.46, IFPDMSM and WIFPDMSM by Wang et al.48 bipolar complex fuzzy operators that are Dombi AOs for BCFNs by Mahmood and Rehman41, Hamacher AOs for BCFNs by Mahmood et al.42, and bipolar fuzzy operators that are Dombi AOs by Jana et al.16, Hamacher AOs by Wei et al.17, and Prioritized Dombi AOs by Jana et al.18. We observe multiple substantial differences between existing operators and our proposed operators when applying them to the illustrative example from the previous section and the result is displayed in Table 5 and Fig. 2.
The graphical explanation of Table 5.
The Dombi and Hamacher operators using BCFS produce outcome variations from our proposed operators. The operators fail to capture relationships between various attributes because they lack this functionality. The proposed operators improve decision making by recognizing that attributes exist within separate categories which maintain independent relationships between their members but allow connections between categories.
The intuitionistic fuzzy operators (IFPMSM, IFWPMSM, IFPDMSM, and WIFPDMSM) show major drawbacks when processing information from BCFS. The mathematical structure of these operators shows two main limitations because it lacks negative aspect representation and second-dimensional information. The limitation hinders their ability to handle complex real-world scenarios because they fail to model positive and negative aspects together at the same time. The bipolar fuzzy operators (BFDA, BFDPA, and BFHA) experience natural processing limitations when working with BCF information because their mathematical model lacks support for second-dimensional data representation. The absence of second-dimensional representation makes these operators less useful for situations demanding accurate multi-dimensional data processing. We introduced PMSM and PDMSM operators as a pioneering advancement in the BCFN environment. Previous AOs for BCFNs failed to address situations where multiple connected attributes exist within a single class while preserving different class independence. Our method solves this issue specifically and integrates positive and negative features alongside second-dimensional information. The proposed methodology proves essential for complex decisions because standard methods prove inadequate in similar environments. Our operators showcase superior attributes and relations handling capabilities in combination with mathematical precision for effective decision making processes. Our enhancement provides critical value to real-world applications because it enables decision makers to analyze multiple connected factors at once. These proposed operators smoothly supplement existing approaches while filling critical technical deficiencies that arise in complex interlinked attribute systems. The results confirm the essential and beneficial nature of our proposed approach for handling more advanced real-life decision support problems alongside providing improved information aggregation mechanisms.
Special cases
-
1.
By taking \(\dot{\mathcalligra{v}}=1\)
-
2.
By taking the real and unreal parts equal to zero in the NMG the proposed operators will be transformed in the setting of CFS.
-
3.
By taking the unreal part equal to zero in both PMG and NMG the proposed operators will be transformed in the setting of BFS.
-
4.
By taking the real and unreal parts equal to zero in the NMG and also putting the real part of PMG equal to zero, the proposed operators will be transformed in the setting of FS.
Practical implication
The application of partitioned Maclaurin symmetric mean operators within bipolar complex fuzzy contexts produces significant practical outcomes that benefit multiple real-world domains. The theoretical progress of partitioned Maclaurin symmetric mean operators creates practical advantages for professionals who need to solve complex decision problems.
The business sector utilizes these operators to give managers advanced decision making tools for complex choices. Decision makers who select suppliers gain the ability to assess both beneficial and detrimental attribute aspects through a system that tracks their interdependent relationships. Financial analysts use these operators to conduct extensive risk assessments by combining gain and loss modeling of interconnected market elements which helps improve portfolio management and investment planning. These operators deliver substantial advantages to healthcare providers in their operations. Medical professionals now have improved capabilities to analyze multiple interconnected treatment factors while they assess potential advantages against risks and how health parameters influence each other. Hospital departments benefit from these operators through improved resource distribution and healthcare professionals develop advanced treatment plans which integrate short-term and long-term patient outcomes. These operators provide urban developers and environmental managers with improved capabilities to evaluate different projects. Planning officials together with environmental scientists have gained better capabilities to analyze complex environmental relationships that link environmental results with social outcomes and financial elements. The model enables decisions to become more effective in projects combining various environmental influences during urban development and policy execution.
These operators enable manufacturing companies to enhance their production optimization by analyzing the interdependent quality factors and resource utilization throughout multiple manufacturing phases. Supply chain management benefits from these operators because companies gain improved coordination of suppliers and their dependencies which enhances inventory management and distribution networks. Project managers from all sectors would gain from better risk evaluation tools that combine opportunity analysis with threat assessment and component interdependency understanding. Evaluation of complicated proposals in research and development environments becomes more effective because decision makers must determine resource allocations for connected research projects. The educational sector should use these operators to develop complete curricula and allocate resources by understanding how various academic programs and learning outcomes affect each other. The system allows for better educational planning and student assessment that considers multiple criteria that depend on each other.
These operators prove most beneficial in situations where standard approaches prove inadequate because they help make decisions involving uncertain situations and complex interdependent elements. Decision making methodology experienced a major advancement through the development of tools that enable simultaneous management of positive and negative aspects and their interrelated components. The work becomes highly beneficial for real-world practitioners who need to manage multiple factors in their professional scenarios. These operators show promise to impact theoretical and practical aspects of decision science because they work well in multiple sectors. These operators enable decision makers to approach complex scenarios with advanced and detailed methods which results in improved organizational outcomes across different business sectors.
Conclusion
The PMSM and PDMSM operators along with their partitioned forms remain significant data aggregation tools. This research field lacks investigation into these operators when applied to BCFNs. We established the BCFPMSM, BCFWPMSM, BCFPDMSM, and BCFWPDMSM operators through an assumption that divides attributes into separate classes that maintain internal connection between attributes but maintain external independence between classes. The AOs served as the foundation for our development of a new MADM technique for BCFNs. The method effectively detects interrelated multiple attributes within one class without compromising the independent nature of attributes between different classes. An illustrative example validated our proposed technique together with its practicality while demonstrating better performance compared to existing methodologies. The proposed method establishes a refined and systematic framework to handle uncertainty in MADM problems according to our research findings. The research field should develop these concepts by applying them to complex dual hesitant fuzzy sets complex fuzzy neutrosophic soft sets and complex hesitant fuzzy sets to boost decision making applications.
Advantages and limitations of the proposed approach
The main benefit of developed operators emerges from their capability to handle multi-dimensional uncertainty during decision making processes. The proposed operators surpass traditional fuzzy and bipolar fuzzy approaches because they analyze both positive and negative aspects in complex environments which makes them suitable for bipolar multi-dimensional uncertain situations. The partitioning attribute mechanism protects class dependencies and maintains separate independence for class attributes which results in better structured and accurate decision processes. Weighted operators BCFWPMSM and BCFWPDMSM enable users to assign different weights to attributes which enhances decision reliability because it allows for controlled flexibility. The proposed method demonstrates several benefits yet it contains specific constraints. The handling of bipolar complex fuzzy information becomes computationally complex as the number of attributes and partitions increases in the system. Expert assessments regarding class partitioning and weight assignment introduce subjectivity that can negatively affect the stability of decision outcomes. The proposed method successfully tracks dependencies within a class but does not explicitly represent relationships between different classes which might be vital for particular decision contexts. Future research should develop combination techniques of aggregation methods that address present limitations through new dependency modeling elements and perform optimization of computational speed.
Future direction
In the future, we aim to expand this proposed theory in various aggregation operators like Dombi49, Aczel Alsina50,51 and probability aggregation operators52. Further, we would like to apply this work in real-life applications of various fields such as healthcare, AI, Machine learning, Management, etc.
The acronyms of this article are shown in Table 6.
Data availability
All data generated or analyzed during this study are included in this published article.
References
Zadeh, L. A. Information and control. Fuzzy Sets 8(3), 338–353 (1965).
Chu, T. C. A fuzzy number interval arithmetic based fuzzy MCDM algorithm. Int. J. Fuzzy Syst. 4(4), 867–872 (2002).
Xu, Z. S. Study on method for triangular fuzzy number-based multiattribute decision making with preference information on alternatives. Syst. Eng. Electron. 24(8), 9–12 (2002).
Mardani, A. et al. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. Mak. 17(02), 391–466 (2018).
Vaníček, J., Vrana, I. & Aly, S. Fuzzy aggregation and averaging for group decision making: a generalization and survey. Knowl. Based Syst. 22(1), 79–84 (2009).
Grabisch, M., Orlovski, S. A. & Yager, R. R. Fuzzy aggregation of numerical preferences. In Fuzzy sets in decision analysis, operations research and statistics (pp. 31–68). Springer, Boston, MA (1998).
Ralescu, A. L. & Ralescu, D. A. Extensions of fuzzy aggregation. Fuzzy Sets Syst. 86(3), 321–330 (1997).
Abdullah, S., Almagrabi, A. O. & Ullah, I. A new approach to artificial intelligent based three-way decision making and analyzing S-Box image encryption using TOPSIS method. Mathematics 11(6), 1559 (2023).
Nawaz, M., Abdullah, S. & Ullah, I. An integrated fuzzy neural network model for surgical approach selection using double hierarchy linguistic information. Comput. Biol. Med. 186, 109606 (2025).
Zhang, Y., Abdullah, S., Ullah, I. & Ghani, F. A new approach to neural network via double hierarchy linguistic information: Application in robot selection. Eng. Appl. Artif. Intell. 129, 107581 (2024).
Abdullah, S., Ullah, I. & Ghani, F. Heterogeneous wireless network selection using feed forward double hierarchy linguistic neural network. Artif. Intell. Rev. 57(8), 191 (2024).
Abdullah, S., Ullah, I. & Khan, F. Analyzing the deep learning techniques based on three way decision under double hierarchy linguistic information and application. IEEE Access (2023).
Abosuliman, S. S., Abdullah, S. & Ullah, I. Using a fuzzy credibility neural network to select nanomaterials for nanosensors. Eng. Appl. Artif. Intell. 136, 108958 (2024).
Zhang, W. R. Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis. In NAFIPS/IFIS/NASA’94. Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige (pp. 305–309). IEEE (1994).
Gul, Z. Some bipolar fuzzy aggregations operators and their applications in multicriteria group decision making (Doctoral dissertation, M. Phil Thesis) (2015).
Jana, C., Pal, M. & Wang, J. Q. Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision making process. J. Ambient Intell. Hum. Comput. 10(9), 3533–3549 (2019).
Wei, G., Alsaadi, F. E., Hayat, T. & Alsaedi, A. Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision making. Int. J. Fuzzy Syst. 20(1), 1–12 (2018).
Jana, C., Pal, M. & Wang, J. Q. Bipolar fuzzy Dombi prioritized aggregation operators in multiple attribute decision making. Soft Comput. 24(5), 3631–3646 (2020).
Alghamdi, M. A., Alshehri, N. O. & Akram, M. Multi-criteria decision making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 20(6), 2057–2064 (2018).
Akram, M. & Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 39(1), 1–21 (2020).
Stanujkic, D., Karabasevic, D., Zavadskas, E. K., Smarandache, F. & Brauers, W. K. A bipolar fuzzy extension of the MULTIMOORA method. Informatica 30(1), 135–152 (2019).
Akram, M. Bipolar fuzzy graphs. Inf. Sci. 181(24), 5548–5564 (2011).
Riaz, M. & Tehrim, S. T. Multiattribute group decision making based on cubic bipolar fuzzy information using averaging aggregation operators. J. Intell. Fuzzy Syst. 37(2), 2473–2494 (2019).
Riaz, M., Garg, H., Farid, H. M. A. & Chinram, R. Multi-criteria decision making based on bipolar picture fuzzy operators and new distance measures. Comput. Model. Eng. Sci. 127(2), 771–800 (2021).
Mahmood, T. A novel approach towards bipolar soft sets and their applications. J. Math. 2020. Article ID 4690808 (2020).
Abdullah, S., Aslam, M. & Ullah, K. Bipolar fuzzy soft sets and its applications in decision making problem. J. Intell. Fuzzy Syst. 27(2), 729–742 (2014).
Ramot, D., Milo, R., Friedman, M. & Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 10(2), 171–186 (2002).
Tamir, D. E., Jin, L. & Kandel, A. A new interpretation of complex membership grade. Int. J. Intell. Syst. 26(4), 285–312 (2011).
Ma, J., Zhang, G. & Lu, J. A method for multiple periodic factor prediction problems using complex fuzzy sets. IEEE Trans. Fuzzy Syst. 20(1), 32–45 (2011).
Dai, S. A generalization of rotational invariance for complex fuzzy operations. IEEE Trans. Fuzzy Syst. 29(5), 1152–1159 (2020).
Man, J. Y., Chen, Z. & Dick, S. Towards inductive learning of complex fuzzy inference systems. In NAFIPS 2007–2007 Annual Meeting of the North American Fuzzy Information Processing Society (pp. 415–420). IEEE (2007).
Lan, L. T. H. et al. A new complex fuzzy inference system with fuzzy knowledge graph and extensions in decision making. IEEE Access 8, 164899–164921 (2020).
Bi, L., Dai, S., Hu, B. & Li, S. Complex fuzzy arithmetic aggregation operators. J. Intell. Fuzzy Syst. 36(3), 2765–2771 (2019).
Bi, L., Dai, S. & Hu, B. Complex fuzzy geometric aggregation operators. Symmetry 10(7), 251 (2018).
Li, S., Han, X., Bi, L., Hu, B. & Dai, S. Complex fuzzy aggregation operations with complex weights. J. Intell. Fuzzy Syst. (Preprint), 1–7 (2021).
Shams, M. & Abdullah, S. Selection of best industrial waste management technique under complex non-linear Diophantine fuzzy Dombi aggregation operators. Appl. Soft Comput. 148, 110855 (2023).
Guo, W., Bi, L., Hu, B. & Dai, S. Cosine similarity measure of complex fuzzy sets and robustness of complex fuzzy connectives. Math. Probl. Eng. 2020.
Mahmood, T., Ur Rehman, U., Ali, Z. & Mahmood, T. Hybrid vector similarity measures based on complex hesitant fuzzy sets and their applications to pattern recognition and medical diagnosis. J. Intell. Fuzzy Syst. 40(1), 625–646 (2021).
Mahmood, T. & ur Rehman, U., & Ahmmad, J.,. Complex picture fuzzy N-soft sets and their decision making algorithm. Soft Comput. 25, 13657–13678 (2021).
Mahmood, T. & Ur Rehman, U. A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intell. Syst. 37(1), 535–567 (2022).
Mahmood, T. & Ur Rehman, U. A method to multiattribute decision making technique based on Dombi aggregation operators under bipolar complex fuzzy information. Comput. Appl. Math. 41(1), 1–23 (2022).
Mahmood, T., Ur Rehman, U., Ahmmad, J. & Santos-García, G. Bipolar complex fuzzy hamacher aggregation operators and their applications in multiattribute decision making. Mathematics 10(1), 23 (2022).
Mahmood, T. & ur Rehman, U.,. Digital technology implementation and impact of artificial intelligence based on bipolar complex fuzzy Schweizer-Sklar power aggregation operators. Appl. Soft Comput. 143, 110375 (2023).
Naeem, M., Mahmood, T. & ur Rehman, U., & Mehmood, F.,. Classification of renewable energy and its sources with decision making approach based on bipolar complex fuzzy frank power aggregation operators. Energy Strategy Rev. 49, 101162 (2023).
Bai, K., Zhu, X., Wang, J. & Zhang, R. Some partitioned Maclaurin symmetric mean based on q-rung orthopair fuzzy information for dealing with multiattribute group decision making. Symmetry 10(9), 383 (2018).
Liu, P., Chen, S. M. & Wang, Y. Multiattribute group decision making based on intuitionistic fuzzy partitioned Maclaurin symmetric mean operators. Inf. Sci. 512, 830–854 (2020).
Liu, P. & You, X. Linguistic neutrosophic partitioned Maclaurin symmetric mean operators based on clustering algorithm and their application to multi-criteria group decision making. Artif. Intell. Rev. 53(3), 2131–2170 (2020).
Wang, H., Liu, Y., Liu, F. & Lin, J. Multiple attribute decision making method based upon intuitionistic fuzzy partitioned dual maclaurin symmetric mean operators. Int. J. Comput. Intell. Syst. 14(1), 1–20 (2021).
Jaleel, A. WASPAS technique utilized for agricultural robotics system based on dombi aggregation operators under bipolar complex fuzzy soft information. J. Innov. Res. Math. Comput. Sci. 1(2), 67–95 (2022).
Jabeen, K., Ullah, K., Akram, M. & Haleemzai, I. Interval valued picture fuzzy Aczel-Alsina aggregation operators and their application by using the multiattribute decision making problem. J. Math. 2023(1), 1707867 (2023).
Hussain, A., Ullah, K., Pamucar, D., Haleemzai, I. & Tatić, D. Assessment of solar panel using multiattribute decision-making approach based on intuitionistic fuzzy Aczel Alsina Heronian mean operator. Int. J. Intell. Syst. 2023(1), 6268613 (2023).
Ur Rehman, U. Selection of database management system by using multiattribute decision making approach based on probability complex fuzzy aggregation operators. J. Innov. Res. Math. Comput. Sci. 2(1), 1–16 (2023).
Acknowledgement
All authors are thankful to the referees for their valuable suggestions in the improvement of the manuscript. Also, the authors extend their appreciation to Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) for funding this research work through grant number IMSIU-DDRSP2502.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Author information
Authors and Affiliations
Contributions
Ubaid ur Rehman prepared the main manuscript, Meraj Ali Khan validate the results while Ibrahim Aldayel and Tahir Mahmood proofread the whole manuscript, check and fix language issues and made other corrections wherever needed.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Rehman, U.u., Aldayel, I., Khan, M.A. et al. Partitioned Maclaurin symmetric mean operators in bipolar complex fuzzy sets for multiattribute decision making. Sci Rep 15, 14118 (2025). https://doi.org/10.1038/s41598-025-93452-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-93452-0