Study of harmful gas migration law and influencing factors after tunnel blasting in high-altitude tunnels under push ventilation conditions

Abstract

Multiple toxic gases, such as carbon monoxide (CO), are generated after blasting of plateau tunnel. To investigate the migration patterns of CO during the ventilation process following blasting in high-altitude tunnels, this paper employs a three-dimensional model of tunnel blasting excavation under push ventilation. The study utilizes computational fluid dynamics to explore the temporal and spatial evolution characteristics of CO under various operational conditions. The influence of relevant factors was quantified using the grey relational analysis method. Numerical simulations were then used to derive distribution functions for CO concentration in relation to altitude, ventilation time, and other factors. The results indicate that under the influence of push ventilation, multiple vortex regions form due to the interaction between ventilation jets and several recirculation areas, where the airflow velocity is slower and CO concentrations are higher compared to other nearby regions. The grey relational analysis method yielded correlation factors of 0.634039, 0.6572, and 0.6560 for altitude (H), distance from duct outlet to working face (L₀), and ventilation volume (Q), respectively. Notably, altitude plays a significant role in CO migration; as altitude increases from 0 to 6000 m, the peak CO equivalent mass concentration at the tunnel exit increases by 77.10%. A correction coefficient K_H = exp(0.0952H) was derived for the relationship between altitude and CO concentration peaks. Finally, the CO distribution function based on tunnel ventilation parameters is established. The derived formula was compared with actual field data, confirming that this distribution function can guide environmental safety assessments following tunnel blasting.

Introduction

As China’s “Western Development” policy progresses, tunnel construction is increasingly trending towards projects at higher altitudes and of greater lengths¹. In this context, the tunnel blasting excavation process, due to the elevated altitudes, has led to increased CO emissions, presenting new challenges for ventilation during construction. It is essential to conduct more in-depth research on the migration patterns of CO at high altitudes to ensure the occupational health of the construction personnel and the smooth progression of construction.

Currently, the pollutants generated from tunnel blasting are primarily expelled through an efficient ventilation system, which reduces pollutant concentration and ensures a safe and comfortable working environment within the tunnel. In the context of tunnel construction ventilation, scholars both domestically and internationally have extensively studied air flow fields during ventilation, the migration patterns of pollutants, and the optimization of ventilation schemes^2,3,4. For instance, Gidhagen et al.⁵ and Feng et al.⁶ have developed numerical models of tunnels to understand the distribution of wind speeds and pollutant diffusion during ventilation. Chen et al.⁷ created a full-scale tunnel model that considers canyon winds, identifying the hydraulic diameter of the tunnel as the primary factor influencing the internal airflow field due to external winds. Zhou et al.⁸ established a similar experimental platform for tunnel ventilation, discovering a negative correlation between the effectiveness of push ventilation and the distance from the ventilation opening to the tunnel face. The effective length of action was identified as a critical factor influencing ventilation effectiveness, with Nan et al.⁹ deriving a semi-empirical formula for the average velocity distribution of air recirculation, leading to a formula for effective length based on tunnel parameters.

During tunnel blasting and excavation, the placement of the ventilation system and tunnel structure directly affect the working environment, which in turn impacts workers’ health^10,11,12,13. In high-altitude tunnel construction, dynamic loads and environmental factors such as atmospheric pressure and temperature cause changes in the mechanical properties of concrete, which can, in turn, affect tunnel stability and ventilation efficiency^14,15,16,17. As a result, many researchers have focused on the arrangement of ventilation systems within tunnels to explore the diffusion patterns of pollutants under ventilated conditions^18,19,20,21. For instance, Chang et al.²² simulated the effects of various parameters such as duct wind speed and ventilation distance on the diffusion patterns of CO, and derived a function describing the spatial and temporal distribution of CO concentration within the tunnel. Guo et al.²³ combined field testing and numerical simulation to study the impact of the amount of air pushed by ventilation on the movement of blasting dust under push ventilation conditions. Sasmito et al.²⁴ have investigated the distribution and movement patterns of gas produced during tunnel operations and CO emissions from large machinery.

In high-altitude tunnels, the oxygen content and environmental temperature are lower, while humidity and atmospheric pressure exhibit greater variability²⁵. Therefore, ventilation theories applicable at lower altitudes may not be suitable for high-altitude tunnels^26,27,28,29. In response to the impact of altitude on CO ventilation parameters, numerous scholars have conducted extensive research. Yan et al.³⁰ derived formulas for the altitude coefficient of smoke from different vehicle types by measuring CO emissions at various altitudes in situ. Zhang et al.³¹ analyzed the distribution patterns of airflow and the forces on dust in tunnels based on the characteristics of turbulent flow in circular tubes, establishing a theoretical model for the minimum dust-clearing wind speed at different altitudes. Cao et al.³² developed a full-scale numerical model of a tunnel, deriving a formula that correlates altitude with CO concentration. Chen et al.³³ noted that the ventilation time required to dilute blasting smoke in plateau mines correlates with the distance from the ventilation opening to the tunnel face. Zhang et al.³⁴ observed the distribution characteristics of dust and CO in plateau tunnels through field monitoring, suggesting that the choice of fan significantly affects the dilution effectiveness for blasting pollutants. Huang et al.³⁵ employed the computational fluid dynamics (CFD) method to study the migration patterns of CO following blasting in plateau mines, indicating that the ventilation time needed to dilute CO in plains is significantly less than that required in high-altitude areas.

Although scholars both domestically and internationally have conducted extensive research on tunnel ventilation, most studies focus on plain areas, with fewer investigations into the CO distribution functions and influencing factors under the ventilation conditions of plateau area tunnels. Therefore, this paper relies on the Duomuge Tunnel project of the Sichuan-Tibet Railway to establish a three-dimensional tunnel blasting excavation push ventilation model. By employing CFD, this paper examines the temporal and spatial evolution of CO under different working conditions. Using the grey relational analysis method, the influencing factors are identified. The distribution functions relating CO concentration with variables such as altitude and ventilation time are derived and compared against actual field data. These functions can guide the environmental safety evaluation after tunnel blasting.

Numerical methods and model analysis

Mathematical model

To better simulate the migration of CO in a tunnel, the following assumptions are made:

• 1. The gas within the tunnel is an incompressible ideal gas.

• 2. The CO produced post-blasting does not undergo any chemical reactions.

• 3. The sole source of CO is from blasting, with no other pollutants present.

• 4. Given the moderate temperatures in the tunnel, the impact of temperature on the airflow field is neglected.

Based on these assumptions, it is postulated that CO is the primary pollutant following blasting. It does not react with other gases and is expelled from the tunnel solely through ventilation, with a uniform distribution of initial CO smoke within the tunnel after blasting. The air flow in the tunnel during ventilation can be regarded as non-stable incompressible air flow, so Navier–Stokes equation can be used as the governing equation of gas^36,37,38,39.

Continuity equation:

$$\frac{\partial \rho }{{\partial t}} + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} } \right) = 0$$

(1)

Momentum equation:

$$\frac{{\partial u_{i} }}{\partial t} + u_{j} \frac{{\partial u_{i} }}{{\partial x_{i} }} = f_{i} - \frac{1}{\rho }\frac{\partial p}{{\partial x_{i} }} + \frac{\mu }{\rho }\frac{{\partial^{2} u_{i} }}{{\partial x_{i} \partial x_{j} }}$$

(2)

Energy equation:

$$\frac{\partial }{\partial t}\left( {\rho T} \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} T} \right) = \frac{\partial }{{\partial x_{i} }}\left( {\frac{{\mu_{t} }}{\sigma T}\frac{\partial T}{{\partial x_{i} }}} \right) + \frac{{C_{pv} - C_{pa} }}{{C_{p} }}\left[ {\left( {\frac{{\mu_{t} }}{\sigma T}} \right)\frac{\partial \omega }{{\partial x_{i} }}} \right]\frac{\partial T}{{\partial x_{i} }}$$

(3)

Species transport equation:

$$\frac{\partial }{\partial t}\left( {\rho \omega } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} \omega } \right) = \frac{\partial }{{\partial x_{i} }}\left( {u_{t} \frac{\partial \omega }{{\partial x_{i} }}} \right)$$

(4)

where ρ is the density, kg/m³; t is the time, s; u_i and u_j are the components of the velocity vector, m/s; x_i and x_j are the components of the coordinate system, m; f_i is the volume force in the i direction, m/s²; p is the pressure, Pa; μ is the dynamic viscosity, Pa s; μ_t is the turbulent viscosity, Pa s; T is the temperature, K; C_p, C_pv, C_pa respectively denote the specific heat at constant pressure of mixed fluid, leakage material and air, J/(kg K); u_t is the diffusion velocity of species, m/s; ω is the mass fraction.

During the construction process in the tunnel, substantial quantities of pollutants such as CO are generated. The flow of gases within the tunnel is treated as an incompressible fluid, and is controlled in CFD simulations using the turbulent $k-\varepsilon$ model. The flow field often includes jets, recirculation, and stagnation zones, making the three-dimensional transient RNG $k-\varepsilon$ model an effective approach. In this model, k represents the turbulent kinetic energy, and $\epsilon$ represents the rate of dissipation of turbulent kinetic energy. The $k-\varepsilon$ equations are as follows^40,41:

$$\frac{\partial }{\partial t}\left( {\rho k} \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho ku_{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{k} }}} \right).\frac{\partial k}{{\partial x_{j} }}} \right] + G_{k} - \rho \varepsilon + S_{k}$$

(5)

$$\frac{\partial }{\partial t}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho \varepsilon u_{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}} \right).\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + \frac{{c_{1\varepsilon } G_{k} \varepsilon }}{k} + \frac{{c_{2\varepsilon } \rho \varepsilon^{2} }}{k} - R_{\varepsilon } + S_{\varepsilon }$$

(6)

where k is the turbulent kinetic energy, J; $\varepsilon$ is the turbulent kinetic energy dissipation rate, m²/s³; G_k is the turbulence kinetic energy produced by the laminar velocity gradient; $\mu$ and μ_t respectively denote the molecular viscosity and the turbulent viscosity, pa s, μ_t = ${\mu }_{t}=\rho {c}_{\mu }\frac{{k}^{2}}{\varepsilon }$; S_k and ${S}_{\varepsilon }$ denote the source terms; R_ε is an additional term of ε equation; c_1ε, c_2ε, $c_{\mu }$, $\sigma_{\varepsilon }$ and ${\sigma }_{k}$ are the model constants with c_1ε = 1.44, c_2ε = 1.92, ${c}_{\mu }$ = 0.09, ${\sigma }_{\varepsilon }$ = 1.3, ${\sigma }_{k}$ = 1.0.

Relationship between gas parameters and altitude

As the altitude increases, the atmospheric pressure, temperature, and environmental gas density of the region change accordingly. The variations in atmospheric pressure at different altitudes are derived as follows⁴²:

$$P_{H} = P_{0} \left[ {1 - \frac{{\left( {\gamma - 1} \right)MgH}}{{\gamma RT_{0} }}} \right]^{{\frac{\gamma }{\gamma - 1}}}$$

(7)

where, P_H is the atmospheric pressure at altitude H, Pa; P₀ is the standard atmospheric pressure, 101325 Pa; M is the molar mass of air, 28 kg/mol; g is the acceleration of gravity, which is 9.8 m/s²; R is the gas constant, 8.314 J/(mol.K); T₀ is the air temperature under the standard condition, 293.15 K; H is the altitude, m; γ is the atmospheric specific heat capacity ratio, which is 1.232.

With increasing altitude, according to the ideal gas law PV = nRT, the mass remains constant but the volume of the gas increases. This leads to the derivation of the gas density formula at different altitudes:

$$\frac{{\rho_{coH} }}{{\rho_{co} }} = \frac{{P_{H} }}{{P_{0} }}.\frac{{T_{0} }}{{T_{H} }} = \frac{{q_{0} }}{{q_{H} }}$$

(8)

where ρ_co and ρ_coH are the densities of CO at standard conditions and at altitudes of H, respectively, kg/m³; T_H is the gas temperature at altitudes of H, ${T}_{H}={T}_{0}-0.0065H$, K; q₀ and q_H are the volume of gun smoke produced per kilogram of explosive at standard conditions and at altitudes of H, m³, q₀ = 0.04m³.

From the above equations, it is evident that the same amount of explosives will produce more CO at higher altitudes, as the volume of CO increases with altitude. Therefore, the concept of equivalent CO mass concentration C is introduced, and the formula is as follows⁴³:

$$\left\{ {\begin{array}{*{20}l} {C = \omega_{v} \rho_{co} k_{h} } \hfill \\ {\omega_{m} = mq_{0} M_{co} /\left( {L_{c} AM_{air} } \right)} \hfill \\ {\omega_{v} = \omega_{m} M_{co} /M_{air} } \hfill \\ {L_{c} = 15 + m/5} \hfill \\ {k_{h} = {{\rho_{co} } \mathord{\left/ {\vphantom {{\rho_{co} } {\rho_{coH} }}} \right. \kern-0pt} {\rho_{coH} }}} \hfill \\ \end{array} } \right.$$

(9)

where C is the equivalent CO mass concentration at an altitude of H m, mg/m³; ${\omega }_{m}$ is the mass fraction of CO in the standard condition; ${\omega }_{v}$ is the volume fraction of CO in the standard condition; k_h is the proportional coefficient of CO density with altitude; m is the amount of explosive used in a blast, kg; M_co and M_air are the molar mass of CO and air, respectively; A is the tunnel section area, m²; L_c is the initial length of smoke after blasting, m.

Based on the above formulations, Fig. 1 is produced showing how atmospheric pressure, CO density, and the volume of smoke per kilogram of explosives vary with altitude. As altitude increases, both CO density and atmospheric pressure show a decreasing trend, while the volume of CO produced per kilogram of explosives increases.

Fig. 1

Gas parameters vary with altitude.

The tunnel is located at an altitude of 3000 m. After calculations, the atmospheric pressure is determined to be 70073.8 Pa, the air density is 0.9069 kg/m³, the CO density is 0.8788 kg/m³, and the volume of CO produced per kilogram of explosives is 0.057 m³.

Physical model and boundary conditions

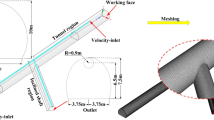
The tunnel is located at an altitude of 3000 m in the Bomi County area of Linzhi, Tibet, and is constructed as part of the Ya’an to Linzhi section. It is a single-head tunnel employing push ventilation. By simplifying the interior components of the tunnel and retaining only the main areas that affect CO migration, a 1:1 scale model of the 300-m area in front of the tunnel face is created, as illustrated in Fig. 2. The cross-sectional dimensions of the tunnel are 300 m by 7.8 m by 7.52 m, with a cross-sectional area of 68.6m². The ventilation outlet is located 30 m from the tunnel face, and the amount of explosives used in a single blast is 178.6 kg, resulting in an initial smoke length of 50 m and an initial CO volume fraction of 0.28%. The total length of the tunnel is 300 m. The model is designed using ANSYS 2022R1 SpaceClaim (https://www.ansys.com/products/3d-design/ansys-spaceclaim), and then meshed using the ANSYS 2022R1 Meshing (https://www.ansys.com/products/meshing) into hexahedral grids.

Fig. 2

Tunnel physical model.

When simulating gas transport behavior using ANSYS 2022R1 Fluent (https://www.ansys.com/products/fluids/ansys-fluent), the quality of the mesh is crucial. Thus, it is necessary to conduct a mesh independence test. In this paper, the speed of the air significantly influences the migration of pollutants like CO, and thus it was selected as the primary parameter for the independence test. Different mesh sizes were applied to the geometric model using ANSYS 2022R1 Meshing (https://www.ansys.com/products/meshing) to validate mesh independence. The mesh counts for the geometric model were 256,458, 683,215, and 1,046,608. As shown in Fig. 3a, the simulation results for mesh counts of 683,215 and 1,046,608 are virtually identical, whereas the results for a mesh count of 256,458 show a slightly lower peak velocity of air within a 20-meter range from the tunnel face. Considering computational performance and mesh quality, a mesh count of 683,215 was ultimately chosen for the geometric model. The quality of the divided mesh is shown in Fig. 3b.

Fig. 3

Mesh independence analysis: (a) Air flow velocity under different mesh sizes and (b) Mesh quality.

In accordance with the actual conditions of tunnel construction, the remaining boundary conditions are set as follows: The entrance boundary is defined as a velocity inlet, with fresh air uniformly entering the tunnel through the duct at a rate of 38 m³/s. The exit of the tunnel is defined as a pressure outlet boundary, with the CO recirculation volume fraction set to zero. Both the tunnel walls and the tunnel face are defined as wall. The relevant model parameters are presented in Table 1.

Table 1 Calculation model settings.

Results and discussion

Analysis of the airflow field

After blasting in the tunnel, the generated CO flows with the air inside the tunnel. Therefore, when employing push ventilation, it is essential to study the movement patterns of the airflow field within the tunnel. As depicted in Fig. 4, the distribution of airflow velocity inside the tunnel is illustrated. This is achieved by taking cross-sectional average velocities at intervals of 10 m, thus determining the overall average air speed within the tunnel.

Fig. 4

Air flow field analysis.

From the Fig. 4, it becomes evident that as the airflow moves towards the tunnel face, the core velocity of the airflow gradually decreases. Moreover, due to the obstruction by the tunnel face and the muck truck, gas recirculation occurs along with the interaction with the blown air from the ventilation ducts. This interaction results in the formation of multiple vortex zones before and after the muck truck, where airflow velocities are lower than in surrounding areas. Within 75 m of the tunnel face, the gas velocity is notably chaotic and unstable, gradually decreasing outward until it stabilizes at 0.55 m/s.

Analysis of CO migration law

The transport of CO following tunnel blasting under ventilated conditions is simulated by numerical simulation. Figure 5a illustrates the variation of CO within the tunnel over time with ventilation. Figure 5b shows the calculation of average CO concentrations at cross-sections taken every 10 m, thereby determining the distribution of CO concentrations throughout the tunnel at different times.

Fig. 5

CO migration law analysis: (a) CO cloud image under different ventilation time. (b) CO distribution in tunnel under different ventilation time.

From Fig. 5a, it can be observed that as ventilation time increases, the migration of CO forms a “匚”-shaped gas cloud, and the concentration of CO within the cloud decreases with increasing distance from the tunnel face, eventually spreading throughout the entire tunnel. By the time ventilation reaches 550 s, the CO concentration throughout the tunnel has reduced to within safe limits (30 mg/m³). As depicted in Fig. 5b, with increasing ventilation time, the peak CO concentrations in the tunnel gradually decrease, and high-concentration areas of CO move towards the exit. At 300 s, the peak CO concentration decreases from 3637.8 to 2013.9 mg/m³, a reduction of 44.6%; by 550 s, the peak CO concentration drops to 27 mg/m³, a reduction of 99.3%, ensuring that the tunnel environment is safe for workers.

Numerical simulation verification

To validate the accuracy of the simulation process, the CO mass concentration at a position 100 m from the tunnel face and 1.6 m away from the ground was chosen as the verification metric. The test process was shown in Fig. 6. ADKS-4 Four-in-one gas detector was used to detect the changing process of CO concentration. Collect one data point every 20 s. It can be seen from Fig. 6 that the field measured values and simulated values generally show the same trend, and the CO mass concentration first increases rapidly and then gradually decreases. The simulation results are basically consistent with the measured data in the field, and the measurement error is less than 20%. Therefore, the transport law of CO after tunnel blasting can be predicted and analyzed, so as to provide reference for pollution gas control.

Fig. 6

Numerical simulation verification process.

Analysis of factors influencing CO migration

The impact of the altitude H on CO migration law

As indicated by the formula presented earlier, the production of CO increases with rising altitude for the same quantity of explosives. This results in a corresponding increase in the CO mass fraction. Consequently, this paper investigates the impact of altitude on CO migration following tunnel blasting, with simulations conducted at altitudes of 0, 1000, 2000, 3000, 4000, 5000, and 6000 m. The parameters are outlined in Table 2, with all other variables held constant. The airflow from the ventilation duct is maintained at 38 m³/s, and the duct is positioned 30 m from the tunnel face. When the ventilation time reaches 260 s, CO has diffused throughout the entire tunnel, which is the focus of our analysis regarding the distribution of CO within the tunnel at different altitudes at this time. Figure 7a shows the average CO concentration at tunnel sections taken every 10 m after 260 s, thereby illustrating the distribution of CO concentration throughout the tunnel. Figure 7b displays the CO concentration distribution 240 m from the tunnel face at different altitudes after 260 s of ventilation.

Table 2 Gas simulation parameters at different altitudes.

Fig. 7

Changes of CO concentration at different altitudes: (a) CO concentration distribution in tunnels at different altitudes. (b) Cloud map of CO concentration in cross-section 240 m away from the palm surface.

As shown in Fig. 7a, at 260 s of ventilation, CO diffuses throughout the tunnel, and the peak mass fraction of CO in the tunnel gradually increases with altitude. Compared to the plain area (altitude of 0 m), the increase in mass fraction of CO at altitudes of 1000, 2000, 3000, 4000, 5000, and 6000 m are respectively $\Delta C_{1}$ = 0.0126%, $\Delta C_{2}$ = 0.0264%, $\Delta C_{3}$ = 0.0417%, $\Delta C_{4}$ = 0.0584%, $\Delta C_{5}$ = 0.0768%, and $\Delta C_{6}$ = 0.0971%. From an altitude of 0 m to 6000 m, the corresponding increase in CO equivalent mass concentration is 1252.2 mg/m³, an increase rate of 77.04%. At 260 s, the peak CO concentration occurs 240 m from the tunnel face, as depicted in Fig. 7b. The Fig. 7b indicates that as altitude increases, the CO mass fraction also increases, and the CO concentration at the center of the tunnel section is lower than in the surrounding areas. This pattern is due to the influence of the airflow field, where the air velocity is higher in the center of the tunnel section and lower near the tunnel walls due to the boundary layer effect on the walls, resulting in higher concentrations of CO at the walls compared to the center.

As CO continues to diffuse towards the tunnel exit, Fig. 8 illustrates the variation in CO concentration at the tunnel exit over time at different altitudes. As shown in Fig. 8, CO spreads to the tunnel exit by 260 s, and by 340 s, the CO concentration at the tunnel exit reaches its peak. From an altitude of 0 to 6000 m, the peak CO equivalent mass concentration at the tunnel exit increases from 1535.1 to 2718.7 mg/m³, marking an increase of 77.10%.

Fig. 8

Changes of CO concentration at the outlet with time at different altitudes.

As altitude increases, a corresponding rise in the peak values of CO equivalent mass concentration is observed. To address this variation, a correction factor K_H (K_H = C_H/C₀) is introduced, where C_H represents the peak CO equivalent mass concentration at an altitude H, and C₀ denotes the peak CO concentration at an altitude of 0 m. Figure 9 presents the correction factors for CO at various altitudes over different time periods, leading to a derived relationship between the correction factor and altitude:

$$K_{H} = e^{0.0952H}$$

(10)

Fig. 9

Relationship between altitude and correction factor.

As shown in Fig. 10, the time required for CO concentration to decrease to a safe level at different altitudes is presented for distances of 50 m, 100 m, 150 m, 200 m, and 250 m from the tunnel face. Compared to sea level, at an altitude of 6000 m, the time needed for CO concentration to reach a safe level is, on average, 32 s longer. This analysis indicates that as altitude increases, the peak CO equivalent mass concentration also rises, necessitating longer ventilation times to reduce CO to safe levels. Consequently, the impact of altitude must be considered when calculating the safe entry times for workers in tunnels.

Fig. 10

The relationship between altitude and the time required to reach a safe concentration.

The impact of the distance from duct outlet to working face L ₀ on CO migration

During tunnel excavation employing the drill-and-blast method, as the excavation depth increases, the ventilation ducts are extended. The distance from the ventilation duct outlets to the tunnel face significantly affects the airflow field distribution near the tunnel face, and thereby influences CO emissions within the tunnel. Studies were conducted with the distance from duct outlet to working face set at 20 m, 25 m, 30 m, 35 m, and 40 m, keeping other parameters constant. Simulations at 260 s post-ventilation examined the coupled airflow and CO processes and the CO concentration profiles along the tunnel, as depicted in Fig. 11.

Fig.11

Transport law of CO under different ventilation distance: (a) Volume cloud map of CO concentration. (b) CO concentration distribution in tunnels at different ventilation distances.

Figure 11a shows the volumetric distribution of CO at various ventilation distances L₀. At 20 m, the emission of CO is the slowest, with residual concentrations persisting near the secondary lining trolley. At 35 m, the area of high CO concentration is closest to the outlet, indicating the fastest overall emission rate. Figure 11b illustrates the CO concentration distribution inside the tunnel at 260 s for different ventilation distances. At a distance of 35 m, the peak CO concentration in the tunnel is 1844.7 mg/m³, compared to 2360.7 mg/m³ at 20 m, an increase of 516 mg/m³. This indicates that the CO mass concentration in the tunnel initially decreases and then increases as the ventilation distance is extended, suggesting that an optimal ventilation distance facilitates efficient CO emission.

Figure 12 compares the time required to reduce CO concentrations to safe levels and the maximum CO concentrations observed during the process. According to Fig. 12a, at 100 m from the tunnel face, a ventilation distance of 25 m more effectively expels CO, while beyond 150 m, a distance of 35 m is more efficient. Figure 12b shows that increasing the ventilation distance maximizes the reduction of peak CO concentrations across sections. Compared to a distance L₀ of 20 m, at L₀ set as 35 m, the time required to lower concentrations to safe levels at distances of 50 m and 250 m from the tunnel face is reduced by 20 s and 60 s, respectively, with the peak CO concentration at 250 m being reduced by 419.8 mg/m³.

Fig. 12

CO concentration at different ventilation distances: (a) Ventilation time required for CO dilution to a safe value. (b) Peak concentration of CO in each tunnel section.

The impact of the ventilation volume Q on CO migration

The air supply volume provided by fans is a crucial technical benchmark in tunnel ventilation; an adequate ventilation rate can expedite the removal of harmful gases from the tunnel and enhance energy efficiency. Therefore, ventilation rates of 22.8 m³/s, 30.4 m³/s, 38.0 m³/s, 45.6 m³/s, and 53.2 m³/s were selected, with other parameters held constant, to simulate the distribution of CO within the tunnel at 260 s, as shown in Fig. 13. Figure 14 illustrates the time required to dilute CO concentrations to safe levels at different ventilation volume.

Fig. 13

Effect of different ventilation volume on CO migration: (a) Cloud image of CO distribution in tunnel under different ventilation volume. (b) CO distribution in tunnel under different ventilation volume.

Fig. 14

The time required for the CO concentration in each section to fall to the safe value under different air volume: (a) The time required for CO concentration to fall to a safe value at different sections. (b) The time required for CO concentration to fall to a safe value within 100 m from the working face.

From Fig. 13a, it is evident that as the ventilation volume increases, the speed of CO movement accelerates. Compared to a ventilation volume of 22.8 m³/s, where CO spreads only to the middle of the tunnel, at 53.2 m³/s, CO has diffused to the tunnel exit. Furthermore, with increased ventilation volume, the dilution of CO concentrations to safe levels within 100 m of the tunnel face occurs more rapidly, as depicted in Fig. 13b.

Figure 14a shows that as the ventilation volume increases, the time required to reduce CO concentrations to safe levels at various tunnel sections becomes shorter. At a ventilation volume of 53.2 m³/s compared to 22.8m³/s, the time needed to lower CO concentrations to safe levels at tunnel sections 50 m and 250 m from the face is reduced by 260 s and 480 s, respectively. Figure 14b, which details the time required to achieve safe CO levels at 100 m from the tunnel face under different ventilation volumes, indicates that the effectiveness of CO expulsion gradually decreases with increasing ventilation volumes. Additionally, a functional relationship between the time required to reach safe levels at 100 m from the tunnel face and the ventilation volume can be represented as: T = 0.29Q²− 32.10Q + 1133.17. Thus, when selecting the ventilation volume for tunnel fans, it is essential to set an appropriate ventilation volume to maximize electrical energy savings and enhance worker efficiency.

Grey relational analysis

To investigate the impact of three factors—altitude H, distance from duct outlet to working face L₀, and ventilation volume Q—on the efficiency of CO emission, the grey relational analysis method was employed to determine the degree of correlation and influence between these factors and CO emission efficiency. The time required to reduce the CO concentration to safe levels within a 200 m range of the tunnel face was selected as the reference sequence Y₀, representing the degree of CO migration after blasting when ventilation is activated. Altitude H, distance from duct outlet to working face L₀, and ventilation volume Q were used as sub-sequences, represented as Y₁, Y₂, and Y₃, respectively, as shown in Table 3.

Table 3 The main factors affecting safety time.

The analysis proceeded as follows:

(1) Establish the initial matrix Y, with the first column Y₀ as the reference sequence, and the second (Y₁), third (Y₂), and fourth (Y₃) columns as sub-sequences.

$$Y = \left( {Y_{0} ,Y_{1} ,Y_{2} ,Y_{3} } \right) = \left[ {\begin{array}{*{20}c} {Y_{0} \left( 1 \right)} & {Y_{1} \left( 1 \right)} & {Y_{2} \left( 1 \right)} & {Y_{3} \left( 1 \right)} \\ {Y_{0} \left( 2 \right)} & {Y_{1} \left( 2 \right)} & {Y_{2} \left( 2 \right)} & {Y_{3} \left( 2 \right)} \\ \vdots & \vdots & \vdots & \vdots \\ {Y_{0} \left( {15} \right)} & {Y_{1} \left( {15} \right)} & {Y_{2} \left( {15} \right)} & {Y_{3} \left( {15} \right)} \\ \end{array} } \right]$$

(11)

(2) Given the different units of data in each column of the initial matrix Y, dimensionless processing was necessary. The range method was used to process each sequence, resulting in the dimensionless matrix $Z=\left({Z}_{0},{Z}_{1},{Z}_{2},{Z}_{3}\right)$, where k = 1, 2 … 15, and i = 0, 1, 2, 3.

$$Z_{i} \left( k \right) = \frac{{Y_{i} \left( k \right) - \min Y_{i} }}{{\max Y_{i} - \min Y_{i} }}$$

(12)

(3) Calculate the difference matrix $\Delta$, comprised of the absolute differences between each dimensionless sub-sequence and the reference sequence, i.e., ${\Delta }_{i}=\left|{Z}_{i}-{Z}_{0}\right|$, thus obtaining the difference matrix $\Delta =\left[{\Delta }_{1},{\Delta }_{2},{\Delta }_{3}\right]$.

(4) Compute the maximum (M) and minimum (N) values in the difference matrix $\Delta$.

Where, $M=max\left[max\left({\Delta }_{1}\right),max\left({\Delta }_{2}\right),max\left({\Delta }_{3}\right)\right]$,$N=min\left[min\left({\Delta }_{1}\right),min\left({\Delta }_{2}\right),min\left({\Delta }_{3}\right)\right]$

(5) Calculate the grey relational coefficient matrix X, where each X_ki is calculated using the following formula:

$$X_{ki} = \frac{N + \eta M}{{\Delta_{ki} + \eta M}}$$

(13)

where $\eta$ is resolution coefficient, $\eta$=0.5.

(6) Compute the relational degree factor R_i for each sub-sequence relative to the reference sequence, ${R}_{i}=\frac{1}{15}{\sum }_{k=1}^{15}{L}_{ki}$, where i = 1, 2, 3, and k = 1, 2, 3 … 15; substituting the data yields the relational degree factors R₁ = 0.634039, R₂ = 0.6572, and R₃ = 0.6560 within the 200 m range.

The larger the grey relational degree factor R_i, the greater the influence on the migration of CO following tunnel blasting, and vice versa. According to the sizes of the grey relational degree factors, the ranking is: distance from duct outlet to working face L₀ > ventilation volume Q > altitude H. This result is also consistent with previous research, which found that the impact of altitude on the diffusion of CO after blasting is minimal³⁵. This indicates that distance L₀ and volume Q are the principal factors affecting CO migration, while altitude also impacts the peak concentration of CO post-blasting and cannot be overlooked in terms of reducing CO to safe levels. In summary, to improve the post-blasting tunnel environment, increasing the supply of ventilation and possibly shortening the distance from the air duct exit to the working face can accelerate the expulsion of harmful gases. Additionally, the impact of altitude on reducing CO to safe levels should be considered when designing ventilation parameters.

CO distribution function fitting and verification

CO distribution functions

To calculate the distribution function of CO concentration over time and space under various construction conditions in a tunnel, the relationship between the CO mass concentration (in mg/m³) and several variables was investigated. These variables include ventilation time t (in seconds), distance from the tunnel face x (in meters), altitude H (in kilometers), the distance L₀ from duct outlet to working face (in meters), tunnel section area A (in m²), and ventilation volume Q (in m³/s). Initially, the CO mass concentrations were log-transformed to a dimensionless form, expressed as ln(C/C₀), where C represents the current mass concentration, and C₀ is the initial concentration at an altitude of 3000 m. The area from the ventilation duct outlet to the tunnel face, defined as the turbulent zone (x < L), is characterized by uneven CO distribution. Conversely, the area from the ventilation duct outlet to the tunnel exit, defined as the stable zone (x > L), and the movement speed of CO in this area is regular, as shown in Fig. 15, and the simulation scheme is shown in Table 3.

Fig. 15

The distribution of turbulent and stable zone.

Distribution function in the turbulent zone

The distribution function of CO in the turbulent zone was first discussed. In this zone, although the relationship between CO concentration and distance from the tunnel face is not clear, the average CO mass concentration follows a linear relationship with ventilation time. Figure 16 illustrates this relationship for Condition 1 in the turbulent zone. By employing the same methodology, the average ln(C/C₀) as a function of ventilation time t was calculated for Conditions 1 through 15, as shown in Table 4. Thus, the distribution function within the turbulent zone can be expressed as:

$$\ln \left( {\frac{C}{{C_{0} }}} \right) = k_{1} t + b_{H1} + b_{lq1} \quad (x \le L_{0} )$$

(14)

where k₁ is a function containing ventilation volume Q, distance L₀ and tunnel section area A, k₁ = -0.0223 $\ln \left( {\frac{Q}{{AL_{0} }}} \right)\,$ − 0.10549; b_H1 is related to altitude H, b_H1 = 0.11748H; b_lq1 is a function of ventilation volume Q, distance L₀ and tunnel section area A, b_lq1 = − 0.1598 ${\text{ln}(\frac{Q}{A{L}_{0}})}^{2}$ − 1.19ln($\frac{Q}{A{L}_{0}}$) + 1.862.

Fig. 16

Function relation of ln(C/C₀) of the turbulent zone with ventilation time in Condition 1.

Table 4 CO distribution function in tunnel turbulent zone under different working conditions (x ≤ L₀).

Distribution function in the stable zone

When the distance from the tunnel face x exceeds the ventilation distance L₀, the time taken for the peak CO concentration to reach the tunnel exit is set as t₀. Under these circumstances, the distribution pattern of CO concentration differs substantially before and after t₀, represented as t ≤ t₀ and t > t₀ respectively. t₀ can be calculated using the following theoretical formula:

$${t}_{0}={t}_{t}=\left({L}_{a}-{L}_{c}+0.5{L}_{c}\right)A/Q$$

(15)

where L_a is the total length of the tunnel, m; L_c is the initial length of smoke after blasting, m; A is the tunnel area, m².

A numerical simulation was used to validate t₀ against the theoretical prediction, as shown in Fig. 17, which led to adjustments in the theoretical formula. The actual time t_a required for the peak CO concentration to shift towards the tunnel exit is computed as:

Fig. 17

The relationship between theoretical ventilation time and actual ventilation time.

$${t}_{0}={t}_{a}=0.91{t}_{t}+6.64=0.91\left[\left({L}_{a}-{L}_{c}+0.5{L}_{c}\right)A/Q\right]+6.64$$

(16)

Figure 18 shows the distribution pattern of CO in the stable zone of the tunnel for Condition 1. For t ≤ t₀, the distribution pattern of CO concentration gradually transitions from a quadratic to a linear relationship. Conversely, for t > t₀, the relationship between ln(C/C₀) and the distance from the tunnel face x becomes linear, with the CO distribution function within 750 s of ventilation shown in Table 5. Using a similar method, the CO distribution functions in the stable zone for Conditions 1 to 15 are compiled in Table 6.

Fig. 18

The distribution of CO in the tunnel stationary region in Condition 1.

Table 5 CO distribution in the tunnel stable region in Condition 1 (x > L).

Table 6 Distribution of CO in the tunnel stable region (x > L).

By processing the data in Table 6 and Eq. 14, the distribution function C_tx of CO in the tunnel as a function of time and space is derived, and the parameters in the formula 17 are shown in Table 7:

$$C_{tx} = \left\{ {\begin{array}{*{20}l} {C_{0} e^{{k_{1} t + b_{H1} + b_{lq1} }} } \hfill & {\left( {x \le L} \right)} \hfill \\ {C_{0} e^{{A\left( t \right)\left( {1 - t/t_{0} } \right)^{2} x^{2} + B_{1} \left( {1 - t/t_{0} } \right)x + C_{1} t + D_{H1} + D_{lq1} }} } \hfill & {\left( {x > L,t \le t_{0} } \right)} \hfill \\ {C_{0} e^{{B_{2} x + C_{2} t + D_{H2} + D_{lq2} }} } \hfill & {\left( {x > L,t > t_{0} } \right)} \hfill \\ \end{array} } \right.$$

(17)

Table 7 Distribution function coefficient values.

Compared with previous studies⁶, this paper focuses on the variation of CO mass concentration within the tunnel during the entire ventilation process after tunnel face blasting (x ≤ L, t ≥ 0). Based on five fundamental ventilation parameters of the tunnel (cross-sectional area, ventilation volume, distance from the tunnel face to the air duct , altitude H, and initial CO mass concentration C₀), these parameters are substituted into Eq. (17) to derive the CO mass concentration at a distance x meters from the tunnel face after t seconds of ventilation. This distribution function is applicable to tunnels of the same type that use pressurized ventilation.

Validation of the distribution function

To verify the accuracy of the distribution functions of post-blasting CO under ventilation conditions described in the previous section, a comparison was made between the function derived and field measurement data. The field tests were conducted in a tunnel section with a cross-sectional area A of 50.2 m² and a ventilation distance L₀ of 30 m, tunnel ventilation volume Q of 38 m³/s, and an initial CO mass concentration C₀ of 4050.0 mg/m³ over a ventilation period of 15 min. Additional details are shown in Table 8, and the site of these field operations is depicted in Fig. 18.

Table 8 Tunnel blasting ventilation parameters.

The test location was selected at the Duomuge Tunnel No. 2 cross-passage in Bomi County, Linzhi City, Tibet. The field data were collected using a quadruple gas detector to monitor combustible gases, oxygen, hydrogen sulfide, and carbon monoxide. The CO monitoring was conducted at a section 260 m from the tunnel face, at a height of 1.6 m above the ground, as shown in Fig. 19. Data points were collected every 5 s for 11 min following the blast, and this data was then incorporated into Eq. 17 for comparison with theoretical predictions, as illustrated in Fig. 19. The comparison and error analysis charts in Fig. 20 indicate that the trends of the measured data closely align with those of the theoretical data, with an average error ranging between − 40 and 24 mg/m³. The theoretical formula developed in the previous section can thus serve as a reference for practical engineering applications, enabling more accurate determinations of safe entry times for workers into the tunnel. This contributes to enhancing both the environmental quality of tunnel construction and the efficiency of worker construction.

Fig. 19

Field test procedure.

Fig. 20

Comparison between measured data and theoretical data: (a) Measured and theoretical data. (b) Error graphs of measured and theoretical data.

Conclusion

In this paper, we initially investigated the airflow field and CO migration in a tunnel under the influence of forced ventilation. Subsequently, we examined the effects of three factors on CO migration, ultimately deriving a distribution function for CO within the tunnel. The following conclusions were drawn:

• 1. Under forced ventilation, obstructions caused by the muck truck and tunnel face led to the formation of multiple recirculation zones. In the interplay between the jet and several recirculating areas, multiple vortex regions formed near the tunnel face. These regions exhibited slower velocities compared to nearby areas, thereby impacting the efficiency of CO dispersal.

• 2. As the altitude increased from 0 to 6000 m, the peak CO mass concentration at the tunnel exit rose from 1535.1 to 2718.7 mg/m³, a 77.10% increase. This also resulted in a longer ventilation time required for high-altitude tunnels to dilute the CO concentration to safe levels.

• 3. Through grey relational analysis, we found that the impact of altitude on CO diffusion is minimal, while the distance from the duct outlet to the working face and ventilation volume are the key factors. Increasing ventilation volume and appropriately shortening the distance from the duct outlet to the working face can facilitate the expulsion of harmful gases after blasting. The correlation coefficients correspond to 0.634039, 0.6572, and 0.6560 respectively.

• 4. A distribution function for CO in the tunnel was established based on seven factors: tunnel cross-sectional area A, distance from the tunnel face x, ventilation time t, altitude H, distance from duct outlet to working face L₀, ventilation volume Q and initial CO mass concentration C₀. The derived formula was compared with actual field data, showing a high degree of fit, thus validating that the distribution function can guide practical field operations effectively.