Improved genetic algorithm based on bi-level co-evolution for coverage path planning in irregular region

Abstract

Irregular region coverage path planning has been widely applied in robot search tasks and has attracted a lot of attention. This study proposes an improved genetic algorithm based on bi-level co-evolution for coverage path planning (IGA–CPP) in irregular region. The processes of the method are region decomposition, sub-region selection and coverage path generation. The difficult problem is to plan the coverage path of sub-regions after decomposition. The key idea is to design a bi-level co-evolutionary strategy for planning optimized order and coverage path of sub-regions. The genetic algorithm has been improved by introducing the bi-level co-evolutionary strategy into the genetic framework and linearly reducing the population size in each iteration to achieve fast convergence. The improved genetic algorithm is used as computing engine for path length optimization. The performance of IGA–CPP is evaluated by simulation experiments. Optimal control parameters are obtained through multiple comparison experiments. Statistical analysis with other algorithms shows that IGA–CPP is more efficient. It can be concluded that IGA–CPP is workable to obtain optimized coverage path of irregular region.

Introduction

Path planning of irregular region has always been an important technique for robots in exploration missions, especially in ocean environmental observation missions. In ocean surveys^1,2, detection of sand waves or coral reefs in irregular regions is a common task³. Planning coverage path based on evolutionary algorithms can generate optimized paths for irregular regions, which is beneficial for efficiency of exploration. It also alleviates the lack of range caused by the robot’s energy limitations. Therefore, it is important to study the coverage path planning of irregular region.

The traditional coverage path planning method of irregular region is to transform the region into a regular one, and then visit the entire transformed area in a ’back and forth’ manner. This way inevitably increases the invalid working area and reduces the efficiency. Moreover, this method can not be applied to the area where the boundary can not be crossed. We propose an improved genetic algorithm based on bi-level co-evolution for coverage path planning (IGA-CPP), which can solve these problems. The proposed method is divided into three steps: region decomposition, sub-region selection and coverage path planning. Region decomposition is to divide the irregular region into several regular sub-regions for path planning; Sub-region selection is to select the large sub-regions and eliminate the minimal sub-regions to reduce the cost of planning algorithm. Coverage path planning is to optimize the coverage order and path of sub-regions by improved genetic algorithm.

Since the region is decomposed into several sub-regions, and there are many possible coverage paths in each sub-region, so it is inevitable to optimize the traversal order of the sub-region and choose the appropriate internal path. We improve genetic algorithm so that it can be more efficiently. One improvement is to introduce a mechanism to accelerate the convergence speed. This mechanism allows the population to shrink during the iterative process, thus reducing the computational effort. The other improvement is to propose a bi-level co-evolution strategy to make the coverage order and path of sub-regions evolve at the same time.

Population reduction mechanism sets a minimum population size. With the increase of the number of iterations, the population size decreases linearly. When the iteration is completed, the population size reaches the minimum. This mechanism can effectively reduce computing consumption. The key idea of bi-level co-evolution strategy is design two optimization planners. The first planner encodes sub-regions and optimizes the coverage order. The second planner encodes paths of sub-regions and optimizes the coverage path in each sub-region. The encoded order and paths are decoded by a decoder to generate a coverage path of irregular region. IGA is used as the computing engine for optimization. The co-evolution strategy combines the two evolution processes through a decoder to realize the synchronous evolution of coverage order and sub-paths. The strategy plays an important role in the application of IGA in planning coverage path of irregular region.

Related works

Coverage path planning is a part of path planning and was developed in the mid-1960s⁴. Algorithms have been put forward over years to improve coverage efficiency, according to previous studies there are three categories of them: exact cellular decomposition method⁵, grid-based coverage method⁶ and optimal coverage method^7,8. Exact cellular decomposition method (ECDM) presents the concept of “cell”, the region is divided into multiple cells in which there is no obstacles. Cells are visited by motions as seed spreader⁹. in order to overcome the drawbacks of the traditional ECDM, Oksanen and Visala proposed a merging process, which merges multiple cells to generate convex cells¹⁰. An improved cell decomposition algorithm is proposed and optimized paths are generated with safety as the goal, workspace was divided into manageable free areas to find a safe path¹¹. Jung et al.¹² proposed Opposite Angle-Based Exact Cell Decomposition (OAECD) for the mobile robot path planning problem and obtained more efficient path than that generated by vertical cell decomposition algorithm. Sanjoy et al.¹³ reviewed different cell decomposition path planning methods, these algorithms were discussed for their advantages and drawbacks. Grid-based coverage method is similar to ECDM, dividing the region into grid cells with the same shape. The shape of the grid cells can be set to approximate the shape of the region. For this reason, it is classified as an approximate cell decomposition. The resolution of the grid map has a large impact on the coverage efficiency. This approach was first applied to traversal path planning by Zelinsky et al.¹⁴. The environment was represented by a set of uniform grid cells. The region coverage path planning was solved using this method. Later, a wavefront algorithm was proposed to plan covered paths in an unknown environment¹⁵. Cabreira et al. proposed some improved coverage path planning method dealing with irregular-shaped regions¹⁶ and the grid-based solution was determined based on the information about the workspace¹⁷. Alia Ghaddar and Ahmad Merei proposed a grid-based approach to cover a region with the goal of reducing completion time and energy consumption¹⁸. The goal of optimal coverage method is to find the optimized traversal path, which needs to be determined based on the prior information of the region. In order to obtain coverage path with the minimum number of turns, Huang et al. proposed a coverage path planning method with Line-sweep-based decomposition¹⁹. The coverage path has multiple possible sweep directions in each cell, and this method finds the optimal sweep direction in a cell, however, it cannot accommodate coverage path planning for multiple regions because the inter-region path cost is not considered. Sharma et al.²⁰ constructed a tree map and used depth first search method to solve the problem of covering an unknown polygonal environment.

ECDM and grid-based coverage path planning method are easy leading to the exponential increase of CPU consumption. Therefore, it is difficult to apply to coverage path planning for complex region shapes. The traditional optimal coverage path planning method treats a cell as a node and transforms the inter-cell traversal problem into a traveler problem, thus avoiding multi-region path planning. A common problem in coverage path planning is to find the better coverage path from the many feasible paths. The optimal coverage methods can solve this problem more effectively than ECDM and grid-based coverage method. They use evolutionary algorithms as the computational engine, which can effectively improve the search speed of the optimal solution. Evolutionary algorithms are suitable to deal with path planning problems of an NP-hard nature. Genetic algorithm is one of the most popular evolutionary algorithms, it was used to generate optimized coverage path and achieved good results²¹. Juan Irving et al. proposed a method for obtaining coverage path for disjoint regions. The experiments proved that the method obtained the best paths compared to other related methods²². The trapezoidal cellular decomposition method was used to decompose region into cells, then genetic algorithm was used to plan coverage path. Whale Cuckoo Search Optimization Algorithm (WCSOA) was proposed to solve the path planning problem of oil spill detection. From the simulation results, it can be seen that WCSOA reduces the energy consumption of autonomous underwater vehicle (AUV)²³. Le et al.²⁴ tested the efficiency of evolutionary algorithms for coverage path planning, including genetic algorithm (GA) and ant colony optimization (ACO). Zheping Yan et al. applied the water wave optimization (WWO) algorithm into path planning of autonomous underwater vehicle (AUV). Experimental results showed that WWO can effectively solve the AUV path planning problem²⁵. Jinchao Chen et al.²⁶ improved the mixed integer linear programming and constructed an exact formula in order to obtain the optimal coverage path for multiple regions.

Although there have been many evolutionary algorithms applied to path planning problems, there has been little research on covered path planning for irregular regions. Aiming at the problem of coverage path optimization in irregular region, we propose an improved genetic algorithm to generate optimized coverage path of irregular region. Exact cellular decomposition method is introduced to the optimal path planning method. The goal of this paper is to find an optimized coverage path of irregular region to improve exploration efficiency. The contribution is to propose an IGA-based coverage path planning method for irregular regions and to design three scenarios to verify the effectiveness of the proposed method. In addition, the optimal control parameters of IGA are determined in this study.

Method

IGA-CPP is proposed for coverage of irregular region. Firstly, the irregular region is decomposed and the smaller sub-regions are rejected. Then, planning the traversal order and sub-paths for the remaining sub-regions. Finally, generate the coverage path of irregular region.

Region decomposition and selection

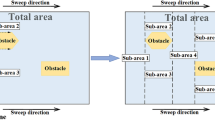
In most cases, there are concave angles in the irregular region to be covered. It is hard to plan coverage paths directly because it is easy to encounter two points that cannot be connected directly in the region. Regions with all convex angles are easier to plan than regions with concave angles. It makes great convenient to break down a region with concave angles into several sub-regions with convex angles. We break down concave regions based on a partitioning method that eliminates concave angles²⁷. The decomposition process is shown in Fig. 1.

Fig. 1

The decomposition process.

• Step 1 Identify concave angles

  Figure 1a shows the process of determining a concave angle. The vertices of irregular region is noted by $V = \{V_{1},\cdots ,V_{n}\}$. $V_{M}$ is the midpoint of $V_{i-1}$ and $V_{i+1}$. Connect $V_{M}$ and $V_{i}$ into a straight line. $P_{1}$ and $P_{2}$ are two points on the line $V_{M},V_{i}$. $P_{1}$ is close to $V_{M}$ and $P_{2}$ is close to $V_{i}$. If both of $P_{1}$ and $P_{2}$ are not in the irregular region, then $V_{i}$ is the vertex of a concave angle, where $i\in [2,{\cdots },n-1]$. When i equals 1, $V_{n}$ replaces $V_{i-1}$. When i equals n, $V_{1}$ replaces $V_{i+1}$. Use the ray intersection method to verify the position of points $P_{1}$ and $P_{2}$ in relation to the irregular region.

• Step 2 Decompose the irregular region

  Four rays are made from $P_{1}$ and $P_{2}$ in four directions: up, down, left and right. If one of the rays does not intersect the region boundary or if there are multiple intersections with an even number, then the ray endpoint is outside the region. If one of the rays has an odd number of intersections with the boundary of the region, then the endpoint of the ray is in the region. Figure 1b shows all the concave angles in irregular region.

• Step 3 Iterative processing of subregions

  The process of decomposition based on the concave angle is shown in Fig. 1c. From vertex $V_{1}$ to $V_{n}$, if the angle corresponding to vertex $V_{i}$ is concave, then the edge $V_{i-1},V_{i}$ is extended and the extension divides the region into two subregions. Repeat dealing the vertices of all sub-regions in this way until all sub-regions no longer have concave angles.

• Step 4 Filter subregions by area

  After sub-regions are generated, there may be some small sub-regions. These regions are not worth traversing because they contain little information. Therefore, a threshold value is set. When the area of the sub-region is less than the threshold value, the sub-region is rejected. Only sub-regions with larger area are selected.

  Fig. 2

  

  The four possible paths in sub-region.

Coverage path generation

The coverage path generation is implemented by improved genetic algorithm. First, the coverage mode of sub-region is determined. Then, the improved genetic algorithm is used to determine the order to cover and the optimized coverage paths of sub-regions. Finally, the coverage path of irregular region is generated.

Sub-region path generation

The back and force method is used to sweep each sub-region along the long edge. Select the longest edge as the baseline and find the vertex farthest from the edge. Several parallel lines are generated between the vertex and the edge. The number of parallel lines is determined by the detection range of the agent. Each parallel line has two intersections with the boundary of sub-region. Every two intersection points generated by a parallel line are placed in a set. Take the last point in the first set and calculate the distance between this point and the two points in the second set. The point with a shorter distance in the second set is placed in the first position. According to this method, the positions of the points in the set are adjusted in turn. After adjustment, connect all the points in sets to generate coverage path of sub-region. The difference in starting position leads to four possible coverage paths in sub-region, as shown in Fig. 2.

Improved genetic algorithm

Improved genetic algorithm is used to determine coverage order and optimized paths of sub-regions. The sub-regions are encoded to $R = [1,2,\ldots ,N]$. Four possible coverage paths shown in Fig. 2 in the i-th sub-region are encoded to $P_{i} = [1,2,3,4]$, where $i \in {R}$. Co-evolution begins with the co-generation of initial population. Every chromosome in the population is composed of two encoded components: A sequential visitation order of sub-regions $S_{c}$, and numeric identifiers mapping each visitation order to its associated sub-region path $S_{p}$. Assume the population size is $N_p$, then the i-th $S_{c}$ can be represented as $(I_{1},I_{2},\ldots ,I_{k},\ldots ,I_{N})$, the i-th $S_{p}$ can be represented as $(J_{1},J_{2},\ldots ,J_{k},\ldots ,J_{N})$, where $i\in \{1, 2, \ldots , N_p\}$, $I_k \in [1,\ldots , N]$, $J_k \in [1,\ldots ,4]$, $I_k$ represents the $k{-}th$ sub-region, and $J_k$ represents the path number in the $k{-}th$ sub-region. For instance, after an irregular region is decomposed, it encompasses six sub-regions, which are respectively numbered as [1, 2, 3, 4, 5, 6]. One possible traversal sequence is [2, 3, 5, 6, 4, 1], with the corresponding sub-region path numbers being [1, 3, 1, 2, 3, 2]. This indicates that the sub-region numbered 2 is traversed first, and the selected traversal path is the first of the four possible paths within the sub-region; subsequently, the sub-region numbered 3 is traversed, and the chosen traversal path is the third of the four possible paths within the sub-region, and so on.

The crossover operation is carried out at a level above the chromosome level. Individuals in the population consist of two parts: the sub-region traversal order and the sub-region path encoding. The mutation operation is performed on the chromosome, while the crossover operation involves crossover between the original individual and the mutated individual for the sub-region traversal order, as well as crossover between the original individual and the mutated individual for the sub-region path encoding. After the crossover operation is completed, new individuals will be formed. The mutation operation introduces new genetic material to the population, preventing it from converging too quickly to a local optimum. Although the crossover operation is an important operation to combine the characteristics of different individuals and create new offspring, the mutation operation plays a complementary role. The crossover operation can combine the good features of the parents, but it may not always be able to generate entirely new solutions. Mutation fills this gap by introducing random changes, which may lead to the discovery of entirely new and potentially better solutions. The combination of crossover and mutation operations enables the algorithm to both utilize the good features of existing solutions and explore new possibilities.

Fig. 3

The co-evolutionary process of IGA. At the chromosome level, each chromosome undergoes mutation with a certain probability. The mutated chromosome is calculated according to Eqs. (1) and (2). If the generated random number is greater than F, the chromosome does not mutate. If the generated random number is less than F, the chromosome mutates. At the individual level, individuals after formula calculation are regarded as mutated individuals, and mutated individuals form the mutated population.

The co-evolution process is shown in Fig. 3. Feasible solutions $(I_{1},I_{2},\ldots ,I_{N})$ and $(J_{1},J_{2},\ldots ,J_{N})$ form the next generation feasible solution through mutation, crossover, selection and combination. Define F and C are mutation factor and crossover factor. $\textbf{rand}$ denotes a random number in the interval [0, 1]. Suppose $I_{m}$ is the mutation individual. $I_{m}$ and $J_{m}$ is generated by formula as follows:

$$\begin{aligned} I_{m,i}=\left\{ \begin{array}{ll} I_{i} & \quad \textbf{rand}>F \\ \textbf{round}(\textbf{rand}\cdot (N-1))+1 & \quad \textbf{rand}\le F \end{array}\right. \end{aligned}$$

(1)

$$\begin{aligned} J_{m,i}=\left\{ \begin{array}{ll} J_{i} & \quad \textbf{rand}>F \\ \textbf{round}(\textbf{rand}\cdot 3)+1 & \quad \textbf{rand}\le F \end{array} \right. \end{aligned}$$

(2)

In the formula $i\in [1,\ldots ,N]$, $I_{m,i}\in [1,\ldots ,4]$. $\textbf{round}$ rounds element to the nearest integer. When $\textbf{rand}>F,$ there is no mutation. When $\textbf{rand}\le F$, the i-th element in I and J mutate to $I_{m}$ and $J_{m}$. The crossover formula is as follows:

$$\begin{aligned} I_{c,i}=\left\{ \begin{array}{ll} I_{i} & \quad \textbf{rand}>{{ C}} \\ I_{m_i} & \quad \textbf{rand}\le {{ C}} \end{array}\right. \end{aligned}$$

(3)

$$\begin{aligned} J_{c,i}=\left\{ \begin{array}{ll} J_{i} & \quad \textbf{rand}>{{ C}} \\ J_{m_i} & \quad \textbf{rand}\le {{ C}} \end{array}\right. \end{aligned}$$

(4)

when $\textbf{rand}>{C}$, the element in crossover individual is the same as element in original individual. When $\textbf{rand}\le {C}$, the element in crossover individual becomes the element in mutation individual. After crossover, the element in $I_{c}$ may not conform to the encoding rules. We rank the elements in the crossover individual by size. If the smallest element is in the i-th position of individual, the i-th element modified to 1. If the second smallest element is in the j-th position of individual, the j-th element modified to 2, and so on. The crossover individuals that conform to the encoding rules can be obtained through this modification strategy.

Original individuals I and J are combined and decoded to generate original coverage path $P_{o}$. Crossover individuals $I_{c}$ and $J_{c}$ are combined and decoded to generate coverage path $P_{c}$. Take the length of coverage path as fitness function, as follows:

$$\begin{aligned} F_{cn} = D_{s}+D_{e}+\sum _{i=1}^{N-1}D_{i} + \sum _{i=1}^{N}L_{i} \end{aligned}$$

(5)

$D_{s}$ is the distance between starting point and the entry point of first sub-region. $D_{e}$ is the distance between ending point and the exit point of last sub-region. $D_{i}$ is the distance between the exit point of the sub-region numbered i and the entrance point of the subregion numbered (i + 1). $L_{i}$ is the length of coverage path in the i-th sub-region. From the original individuals and crossover individuals, the individuals with higher fitness were selected as $I_{b}$. The improved algorithm also has linear population reduction, the population size decreases linearly as by iterations. Let the population size of the g-th generation be $\textit{Np}_{g}$.

$$\begin{aligned} \textit{Np}_{g+1} = \textbf{round} \left( \textit{Np}_{0}-\frac{\textit{Np}_{0}-{N_{p_{min}}}}{G}\cdot g \right) \end{aligned}$$

(6)

where $\textbf{round}$ rounds element to the nearest integer. $N_{p_{min}}$ is the smallest population size, G is the number of generation at the termination of iterations. $\textit{Np}_{0}$ is the size of initial population. This mechanism has been applied in differential evolution algorithm²⁸, which can improve the computational efficiency. $\textit{Np}_{g+1}$ individuals with high fitness are selected from $I_{b}$ for next iteration.

Table 1 The UTM coordinates of the irregular region vertices.

Fig. 4

The irregular region for simulation.

Fig. 5

The path length obtained by different initial population sizes.

Fig. 6

The path length obtained by different mutation factors.

Fig. 7

The path length obtained by different crossover factors.

Simulation results and discussion

An irregular region is used for simulation, shown as Fig. 4. The red circles represent the vertices of irregular region, and the black solid line represents the boundary. The vertices coordinates are represented by Universal Transverse Mercartor Grid Systems (UTM), shown as Table 1.

Optimized control parameters of IGA

The most important control parameters of IGA are initial population size $\textit{Np}_{0}$, mutation factor F and crossover factor C. In order to explore the influence of these parameters on the results and get optimized control parameters, ten different values of each parameter are selected , and each value is calculated ten times for simulation experiment. The initial population size $\textit{Np}_{0}$ is set at 16, 32, 48, 64, 80, 96, 112, 128, 144 and 160, respectively. The mutation factor F is set at 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0, respectively. The values of crossover factor C are same as F. In the simulation experiment, the number of iterations is set to 150, the scanning range is set to 50, the starting point is (253857.603, 3992260.524), the minimum population size is set to 4²⁸.

The path length obtained by IGA with various parameters is shown in Figs. 5, 6 and 7. The lower boundary of the box represents the first quartile, the upper boundary represents the third quartile, the red line in the middle indicates the median, and the straight line extending from the edge of the box is called whisker, indicating the maximum and minimum values. The ‘+’ represents the outlier points. Figure 5 shows the path length obtained by IGA with different values of $\textit{Np}_{0}$. Although the optimal solution can’t be obtained by evolutionary algorithm, an acceptable optimized solution can be obtained. As can be seen from the box plot in Fig. 5, the red horizontal line, representing the average path length, keeps moving downward as the population size increases, which indicates that the average planned path length decreases with the increase of population size. The possible reason is that the increase of population size enables the algorithm to explore a larger feasible solution space, which is conducive to finding better paths.

We set the null hypothesis that the path lengths are not significantly different. A function named $\textbf{friedman}$ in MATLAB is used to calculate the statistics of the experimental results. For a chosen $\alpha$, the null hypothesis is rejected if p-value$<\alpha$²⁹. Here we choose $\alpha =0.05$. The p-values of control parameters $\textit{Np}_{0}$, F and C about path lengths are 0.037, 0.6 and 0.031 respectively. The p-values of F is higher than $\alpha$, so the null hypothesist cannot be rejected indicating that there is no significant change in path lengths when the values of mutation factor vary. The p-values of $\textit{Np}_{0}$ and C is lower than $\alpha$, so the null hypothesis is rejected, indicating that there are significant changes in path lengths when the values of initial population size and crossover factor vary. Since p-values is less than $\alpha =0.05$, post-hoc tests can be continued to compare significant performance differences between algorithms.

The non-parametric Friedman test mean ranks of $\textit{Np}_{0}=[16, 32, 48, 64, 80, 96, 112, 128, 144, 160]$ are 7.45, 7.4, 6.15, 5.25, 5.1, 3.45, 4.55, 6.1, 4.65, 4.9. The mean ranks of ${C}=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]$ are 3.85, 4.65, 4.05, 6.1, 6.65, 4.75, 4.55, 5.8, 7.5, 7.1, shown as Table 2. Bonferroni-Dunn post hoc test is used to perform multiple comparisons of experimental data sets. For $k=10$ values and number of exprimental data sets $N=10$, the critical distance is written as $\textit{CD}$. With $\alpha =0.05$ and $q_{0.05}=2.773$, $\textit{CD}$ for Bonferroni-Dunn post hoc test is

$$\begin{aligned} \textit{CD}= q_{0.05}\sqrt{(k(k+1)/(6N))}\approx 3.755 \end{aligned}$$

(7)

In the Bonferroni-Dunn post hoc test, the following parameters are used: $k=10$: This represents the number of groups being compared, which in our case is the number of different initial population sizes. $N=10$: This represents the number of experiments conducted for each group, which is the number of simulation runs for each initial population size. If the difference between all ranks is not less than $\textit{CD}$, then the null hypothesis is rejected, indicating that there is a significant difference between these parameter values. When the value of $\textit{Np}_{0}$ is 96, the ranking is the highest. When the value of C is 0.1, the ranking is the highest. Therefore, $\textit{Np}_{0}=96$ and ${C}=0.1$ can be selected as the optimized parameter.

Table 2 Ranks of $\textit{Np}_{0}$ and C.

Comparison with other algorithms

The other four algorithms: genetic algorithm (GA), particle swarm optimization (PSO), differential evolution (DE) and successful history-based adaptive differential evolution (SHADE) are used to compare. The four algorithms are applied to three scenes: (1) fixed starting point and unfixed ending point (2) fixed starting and ending point; (3) unfixed starting and ending point.

The parameters used for IGA are as follows: initial population size $N_{p_0}=96$, minimum population size $N_{p_{min}}=4$, mutation factor $F=0.1$, crossover probability $C=0.1$, and the maximum number of iterations is 150; The parameters used for GA are as follows: population size $N_p=96$, mutation factor $F=0.1$, crossover probability $C=0.1$, and the maximum number of iterations is 150; The parameters used for PSO are as follows: population size $N_p=96$, inertia weight $w=0.8$, maximum velocity $w_t=0.8$, learning factor $c=2,$ and the maximum number of iterations is 150; The parameters used for SHADE are as follows: population size $N_p=96,$ historical parameter length $H=6,$ initial historical parameter $F=0.5,C=0.7,$ and the maximum number of iterations is 150; The parameters used for DE are as follows: population size $N_p=96$, scaling factor $F=0.1,$ crossover probability $C=0.1,$ and the maximum number of iterations is 150.

Fig. 8

The optimal coverage path in irregular region when the starting point is fixed.

Fig. 9

Path lengths obtained by different algorithms when the starting point is fixed.

Fig. 10

Convergence graph of different algorithms when the starting point is fixed.

Fig. 11

The optimal coverage path in irregular region when the starting point and ending point are fixed.

Fig. 12

Path lengths obtained by different algorithms when the starting and ending points are fixed.

Fig. 13

Convergence graph of different algorithms when the starting and ending point are fixed.

In scene (1), the starting point is S(253857.60, 3992260.52) and the ending point is unfixed. The optimal coverage paths in irregular region is obtained by calculating all possible path lengths. The length of optimal coverage path is 6630.03. The path is shown in Fig. 8. The blue dots and the red pentagram represent the starting points and ending points of coverage path in irregular regions respectively. The solid black line indicates the boundary of sub-regions. The red lines in irregular region indicate the coverage path. Figure 9 shows path lengths obtained by IGA, GA, PSO, DE and SHADE respectively. The control parameters of these algorithms are selected from several groups that perform better. To test the differences between the IGA and the other four algorithms, 10 calculations were performed for each method. The lower boundary of the box represents the first quartile, the upper boundary represents the third quartile, the red line in the middle indicates the median, and the straight line extending from the edge of the box is called whisker, indicating the maximum and minimum values. The ‘+’ represents the outlier points. It can be seen that the results of IGA are similar to those of SHADE, and better than other algorithms. The number of iterations required to reach the steady state varies. IGA requires the least number of iterations. SHADE the second least. They converged to the optimized result with an acceptable number of iterations. GA, PSO and DE do not perform as well as IGA and SHADE in terms of convergence speed. The convergence graph is shown in Fig. 10. The results in the figure show that IGA can converge more quickly than other compared algorithms.

In scene (2), the starting point is (253857.60, 3992260.52) and the ending point is (254332.53, 3993603.33). The optimal coverage paths in irregular region is obtained by calculating all possible path lengths. The length of optimal coverage path is 6853.97. The path is shown in Fig. 11. The blue dots and the red pentagram represent the starting points and ending points of coverage path in irregular regions respectively. The solid black line indicates the boundary of sub-regions. The red lines in irregular region indicate the coverage path. Figure 12 shows the path lengths obtained by IGA, GA, PSO, SHADE and DE respectively. Ten calculations were performed using each method. The lower boundary of the box represents the first quartile, the upper boundary represents the third quartile, the red line in the middle indicates the median, and the straight line extending from the edge of the box is called whisker, indicating the maximum and minimum values. The ‘+’ represents the outlier points. It can be seen that the results of IGA are similar to those of PSO and SHADE, and better than other algorithms. The number of iterations required to reach the steady state varies, with IGA requiring the least number of iterations and SHADE the second. IGA and SHADE are able to converge faster than the other compared algorithms The convergence graph is shown in Fig. 13.

Fig. 14

The optimal coverage path in irregular region when the starting point and ending point are unfixed.

Fig. 15

Path lengths obtained by different algorithms when the starting and ending points are unfixed.

Fig. 16

Convergence graph of different algorithms when the starting and ending point are unfixed.

In scene (3), the starting point and the ending point is unfixed. The optimal coverage paths in irregular region is obtained by calculating all possible path lengths. The length of optimal coverage path is 6152.53. The coverage path is shown in Fig. 14. The blue dots and the red pentagram represent the starting points and ending points of coverage path in irregular regions respectively. The solid black line indicates the boundary of sub-regions. The red lines in irregular region indicate the coverage path. Figure 15 shows the path lengths obtained by IGA, GA, PSO, SHADE and DE respectively. Ten calculations were performed using each method. It can be seen that the results of IGA are better than those of other algorithms. The convergence graph is shown in Fig. 16. The number of iterations required to reach the steady state varies. IGA converge more fast than other algorithms.

A comparative analysis of Figs. 9, 12, and 15 clearly demonstrates the advantages of the proposed IGA algorithm. In Fig. 9, which shows the path lengths obtained by different algorithms when the starting point is fixed, IGA and SHADE exhibit similar performance, with IGA having a slightly lower median path length and a tighter interquartile range (IQR), indicating more consistent results compared to GA, PSO, and DE. Figure 12 presents the path lengths when both the starting and ending points are fixed. IGA and SHADE still show similar performance, but the difference between them and the other algorithms is less pronounced than in Fig. 9. Figure 15 shows the path lengths when both the starting and ending points are unfixed. IGA significantly outperforms the other algorithms, with the lowest median path length and the tightest IQR, highlighting its flexibility and efficiency in optimizing path lengths. Overall, IGA consistently outperforms GA, PSO, SHADE, and DE across all three scenarios, demonstrating its superiority in terms of path length optimization.

Experiments on complex irregular regions

Experiments were conducted using IGA on more complex regions, which consist of 5, 6, 7, and 8 sub-regions respectively, to evaluate the scalability of the proposed method. Vertices coordinates of the regions are as follows:

Table 3 Vertices of complex region.

Fig. 17

Coverage path in irregular region with 5 sub-regions.

Fig. 18

Coverage path in irregular region with 6 sub-regions.

Fig. 19

Coverage path in irregular region with 7 sub-regions.

Fig. 20

Coverage path in irregular region with 8 sub-regions.

Using the IGA method with a fixed starting point and an unfixed ending point, where the starting point coordinates are [0,0], a scanning width of 0.1, $N_{p_0}=96$,$F=0.1$, $C=0.1$, the resulting coverage paths are shown in Figs. 17, 18, 19, and 20. In the figures, blue dots represent the starting points of the paths, and red pentagrams represent the ending points of the paths. It can be seen that, for complex irregular regions, the proposed algorithm still achieves optimized results, demonstrating scalability.

Fig. 21

Conveergence graph of complex irregular regions.

The convergence graph of the coverage path lengths obtained from different regions is shown in Fig. 21.

The blue curve marked with dots in the figure represents the convergence graph for 5 sub-regions, the orange curve marked with triangles represents the convergence graph for 6 sub-regions, the yellow curve marked with vertical lines represents the convergence graph for 7 sub-regions, and the purple curve marked with hexagons represents the convergence graph for 8 sub-regions. The x-axis indicates the number of iterations, with a total of 150 iterations. The y-axis represents the average path length of the population obtained in each iteration. It can be seen that when the number of sub-regions is 5 or 6, the curves become relatively stable after 150 iterations. However, when the number of sub-regions is 7 or 8, the convergence curves still show a downward trend. Therefore, when there are more sub-regions, a larger number of iterations should be set. Theoretically, the more iterations, the closer the path length obtained by the algorithm is to the optimal solution. Considering the balance between computational resources and algorithm performance, it is not recommended to use an excessively large number of iterations. Figure 21 proves that the performance of the algorithm in more complex regions is still reliable.

Discussion

This section discusses the performance of the IGA algorithm in three scenarios: fixed starting point only, fixed starting and ending points, and unfixed starting and ending points. It also discusses the algorithm’s convergence characteristics, complexity, limitations, and future work.

Performance of IGA in three scenarios

IGA performs better than other algorithms in three scenarios. In the first scene, although the length of coverage path is not much different from other algorithms, the convergence speed is faster than other algorithms. In the second scene, the advantage of IGA becomes smaller. Because the starting point and the end point are fixed, the distances between the starting, ending point and the irregular region in the coverage path can not be ignored, the space that can be optimized is very small, so it has an impact on the optimization results. In the third scene, the advantage of IGA is the most obvious . Because the starting point and the end point are not fixed, the distance from the starting point to the irregular region and the distance from the irregular to the ending point can be ignored, which can better reflect the advantages of IGA. IGA is a kind of evolutionary algorithm, so it has the same disadvantages as other evolutionary algorithms. When the scale of problem increases to a certain extent, IGA can get the optimized solution in a limited time, but cannot get the optimal solution.

Convergence properties and computational complexity

Regarding the convergence of the algorithm, a bi-level co-evolution strategy is adopted, enabling the simultaneous evolution of the coverage order and path of sub-regions. The population size is dynamically adjusted, starting from a larger initial size and decreasing linearly during iterations. This mechanism helps maintain a balance between exploration and exploitation. Initially, a larger population size enhances the exploration capability, allowing the algorithm to search a broader solution space and avoid premature convergence. As the population size decreases, the exploitation capability is strengthened, enabling the algorithm to more effectively optimize the solutions and converge towards the optimal solution. Furthermore, the mutation and crossover operations enhance the algorithm’s ability to explore the solution space and avoid local optima.

In terms of the computational complexity of the algorithm, several factors need to be considered. The first is the region decomposition process, which is crucial for breaking down the irregular region into manageable sub-regions. The complexity of this process depends on the number of vertices and the intricacy of the region’s shape. For a region with N vertices, the decomposition step may involve operations such as identifying concave angles and extending edges, which can be completed in O(N) or $O(N^2)$ time depending on the implementation.

The second factor is the genetic algorithm operations. For a population size of Np and each individual having a chromosome length of L, the mutation and crossover operations have a time complexity of $O(N_p \times L)$. The fitness evaluation, which involves calculating the path length for each individual, also contributes to the computational cost. Fitness evaluation for each individual typically requires O(M) time, where M is the number of sub-regions or the complexity of the path planning.

Additionally, the co-evolutionary process between the coverage order and path of sub-regions adds another layer of complexity. However, this process is designed to improve the algorithm’s efficiency by optimizing both aspects simultaneously. The overall computational complexity of the algorithm can be considered as $O(N_p \times L \times G)$, where G is the number of generations. This complexity is manageable for medium-sized problems and can be further optimized through parameter tuning and efficient implementation strategies.

In conclusion, the convergence characteristics of the proposed algorithm benefit from its dynamic population adjustment and co-evolutionary strategy, enabling it to effectively balance exploration and exploitation. Its computational complexity is primarily influenced by the population size, chromosome length, and the number of generations, making it suitable for practical applications with appropriate parameter settings.

Limitations of IGA and future work

Although extensive simulation experiments have been conducted, and the results effectively demonstrate the validity of the proposed algorithm, it should be noted that real-world experimental outcomes may be influenced by various factors, such as environmental conditions and the precision of equipment control. If the experiments are conducted in an indoor environment where there are no obstacles within each area, and the robot can move freely with control effects fully meeting the requirements, the results of the simulation experiments can be replicated. However, if the experiments are conducted in a complex outdoor environment or if the control effects are significantly affected, such as when the robot produces larger errors in moving from one path point to the next according to instructions, or if the task area contains many obstacles, the effectiveness of this algorithm will also be correspondingly reduced. There are two directions for future research: one is to consider the distribution of obstacles in the task area and improve the current algorithm; the other is to consider the actual control effects of the robot and further analyze and improve the algorithm in combination with real-world errors.In addition, the more sub-regions an irregular area contains, the more computational resources the planning algorithm consumes. Therefore, this algorithm is more suitable for offline planning.

Conclusion

We presented a method of coverage path planning in irregular region based on IGA. Our proposed method can output optimized coverage paths of irregular region based on a co-evolutionary strategy. In order to verify the superiority of the proposed method, a series of experiments were implemented. The experimental results show that IGA-CPP is able to obtain shorter coverage paths of irregular region in acceptable time than the traditional optimization methods.

The region decomposition method was introduced and IGA was applied to compute the optimized coverage path of irregular region. We designed a co-evolutionary optimization mechanism for planning optimized order and coverage path of sub-regions. The mechanism realized the synchronous evolution of coverage order and sub-paths, which is the key to the application of coverage path planning method in irregular region. Optimized parameters of IGA were selected from multiple sets of simulation experiments. Comparisons of IGA and four other optimization methods supported the rationale for the proposed method. Three scenes were considered in the comparison. All the results showed IGA performed better than the other algorithms. In the future, we plan to apply more optimization algorithms to coverage path planning, and consider multi-objective obstacle-free path planning in unknown environments.