Introduction

Driver drowsiness is a critical safety concern on roads worldwide, contributing significantly to traffic accidents, injuries, and fatalities1. Drowsy driving was responsible for 91,000 accidents, 50,000 injuries, and 795 deaths in the United States in 2017 alone2. These disheartening statistics underscore the pressing necessity for developing efficacious drowsiness detection systems. Moreover, drivers who had slept for less than four hours over 24 h exhibited a comparable traffic accident risk to that observed in drivers who were under the influence of alcohol3. Given that drowsiness-related accidents are often underreported due to the difficulty in identifying drowsiness as the cause post-crash, the figures may be even higher. These sobering statistics highlight the critical importance of studying driver drowsiness and developing robust detection methods to enhance road safety and potentially save thousands of lives annually.

The critical nature of drowsy driving has prompted extensive research into methodologies for discovery through sensor-driven systems. These methodologies generally encompass techniques centered on the vehicle, driver conduct analysis, and physiological measurements4. Vehicle-based methods utilize sensors to monitor characteristics, including lane deviation, automobile velocity, and steering wheel orientation. However, their accuracy can be significantly affected by external factors like road geometry and weather conditions5. Driver behavior-based techniques employ cameras within the car cabin to observe symptoms of drowsiness in the driver’s head and face, encompassing eyelid closure proportion, eye-blinking behaviors, cranial orientation, countenance changes, and involuntary jaw opening. These methods may be compromised by unfavorable lighting conditions or in cases where the operator dons spectacles or facial coverings6. Physiological process-based approaches directly measure the driver’s physical conditions using electrodes placed on the body, monitoring factors including brain signals, cardiac rhythm, and respiration rate. While physiological signal methods offer high accuracy and are minimally influenced by human subjective intentions1, applying sensors to the operator’s physique can occasionally present practical difficulties6.

While each driver drowsiness detection technique has its own limitations, physiological approaches have emerged as promising due to their ability to detect drowsiness effects on physiological signals almost instantaneously, offering superior dependability and precision in identification relative to the two alternative approaches7. Electroencephalogram (EEG)-based techniques have emerged as particularly effective among physiological signals for accurately identifying driver drowsiness in comparable scenarios4. Due to its non-invasive nature and high-time resolution, EEG is widely used to study neural dynamics in human behavior8. Research has demonstrated a significant correlation between a driver’s level of drowsiness and the power of EEG signals6. This relationship has led to EEG being recognized as one of the most dependable features for drowsiness detection. The sensitivity of EEG signals to changes in alertness, combined with their ability to provide real-time data on brain activity, makes them a valuable tool in the ongoing efforts to enhance road safety through improved drowsiness detection methods.

To effectively detect drowsiness using EEG signals, a crucial first step involves transforming the signal into a new domain for analysis. This transformation can be achieved through two principal techniques: the Fourier transform and the wavelet transform. Fourier transform translates the signal into frequency components by employing a sequence of sinusoidal waves. In contrast, WT converts the signal into a time–frequency representation utilizing various wavelet functions. The choice between these methods depends on the nature of the signal being analyzed. Fourier transform is particularly effective for stationary signals, whereas wavelet transform excels in handling non-stationary signals9. Since EEG signals are inherently non-stationary10, wavelet transform is generally considered the more suitable approach for this application. Following the signal transformation, artificial intelligence can classify driver drowsiness based on the extracted EEG signal features. This process enables a more nuanced and accurate assessment of a driver’s alertness, potentially improving the reliability of drowsiness detection systems.

Numerous machine learning techniques have been successfully employed for modeling EEG signals so far11. Machine learning algorithms have proven particularly effective in scenarios involving multidimensional data with intricate relationships12. However, the low signal-to-noise ratio and spatial resolution of EEG signals, combined with their high-dimensional complexity and the subtle temporal patterns associated with drowsiness onset, necessitate highly accurate signal processing methods13. Recently, deep learning techniques have advanced swiftly and found widespread application in driver behavior identification identification14 and driver EEG monitoring. Deep learning demonstrates excellent prospects for solving complex tasks based on EEG data, offering significant improvements over traditional signal processing approaches15, primarily due to their remarkable prowess in acquiring intricate feature representations and their ability to fuse more information16,17. The capacity of deep learning to automatically discern hierarchical characteristics from unprocessed data, identify intricate temporal relationships, and discern subtle patterns in EEG signals offers the potential for more precise and resilient models in a range of EEG-based applications, including drowsiness detection18. Convolutional neural network (CNN) has emerged as a dominant deep learning approach for processing and interpreting EEG data, indicating its efficacy over traditional methods such as support vector machine19,20. EEG signals, characterized by high-dimensional, noisy data with temporal dependencies, present challenges for traditional machine learning models. CNNs, however, can capture the complex patterns within EEG data by applying convolutional filters that identify essential local and global features across time and channels21,22,23. Various CNN architectures have been developed for EEG analysis, leveraging different aspects of the signal structure, including 1D, 2D, and 3D models. For instance, Alnaanah et al. (2023) proposed CNN1D for temporal convolution, CNN2D for combined temporal and spatial analysis, and CNN3D for treating EEG signals as video-like data, all yielding promising results in EEG tasks24. Sadiq et al. (2022) highlighted the potential of transfer learning by utilizing pre-trained CNN models for robust EEG-based brain-computer interfaces23. Hybrid approaches like the LSTM-CNN architecture by Omar et al. (2023) effectively combine spatial feature extraction with temporal learning for high accuracy in epileptic EEG classification25. Additionally, in the realm of drowsiness detection, Balam et al. (2021) demonstrated the effectiveness of a CNN with single-channel EEG signals26, while Chaabene et al. (2021) achieved 90.42% accuracy using a multi-channel system that incorporated data augmentation to enhance performance27. Collectively, these studies underscore the versatility and efficacy of CNNs in analyzing EEG signals across various applications, particularly in detecting driver drowsiness.

As various model configurations can significantly influence both training time and identification accuracy11, the optimization of deep learning architectures—encompassing the learning process and hyperparameter tuning—remains one of the most challenging problems in the field. While gradient-based backpropagation methods have been widely used to optimize deep learning algorithms, they suffer from significant drawbacks, such as getting trapped in local minima, high computational costs due to numerous iterations, and the requirement for continuous cost functions28. Since training deep learning models is an NP-hard optimization problem, there has been a growing interest in utilizing meta-heuristic algorithms for its optimization. Meta-heuristic algorithms offer potential advantages in avoiding local optima, reducing computational costs, and handling non-continuous cost functions. Meta-heuristic approaches show promise in accurately estimating optimal deep learning components, providing a robust alternative to traditional gradient-based methods and potentially improving the overall performance and efficiency of deep learning models28.

While existing literature acknowledges the effectiveness of CNN in EEG signal modeling, a significant gap persists in optimizing CNNs, particularly in the context of EEG-based drowsiness detection. While CNNs have shown promise, their performance is often limited by the challenges in hyperparameter tuning and optimization. Addressing this gap is crucial for improving the accuracy and robustness of drowsiness detection systems. This study presents a novel approach by integrating Teaching Learning-Based Optimization (TLBO) and Student Psychology-Based Optimization (SPBO)—two advanced meta-heuristic algorithms that mimic human learning behaviors to optimize CNNs. Unlike traditional meta-heuristic optimization methods, TLBO and SPBO leverage pedagogical and psychological principles to guide the search process, offering a more adaptive and dynamic approach to CNN optimization. Specifically, TLBO facilitates knowledge sharing to enhance solution quality29, while SPBO encourages a balanced exploration and exploitation strategy in the search space, improving the optimization process30. Moreover, these algorithms reduce dependency on specific algorithmic parameters and significantly enhance convergence rates by leveraging structured learning mechanisms30,31.

To the best of our knowledge, applying TLBO and SPBO for CNN optimization in EEG-based drowsiness detection is unprecedented, marking a novel contribution to the field. This study highlights how these algorithms provide a fresh perspective on CNN performance improvement. By evaluating the impact of TLBO and SPBO individually, this work seeks to demonstrate how these techniques can refine CNN architectures to achieve more precise modeling of drowsy EEG signals. Ultimately, this approach aims to improve the reliability of driver drowsiness detection, contributing to enhanced road safety and better real-time drowsiness monitoring systems.

Research design and implementation

Research framework

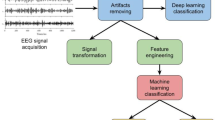
As illustrated in Fig. 1, this study comprises three primary phases:

  • EEG data acquisition: EEG data were collected from individual participants during simulator experiments, using the dataset reported by Farhangi (2022). Further details on the specific experimental conditions and protocols are provided in "Simulator study".

  • EEG signal processing: EEG signals were segmented into 3-s epochs, each containing 1,536 data records based on a 512 Hz sampling rate. Epochs were labeled as “wakeful” or “drowsy” according to participants’ self-reported drowsiness levels, reflecting reduced alertness over time. To eliminate power line interference, a third-order notch Butterworth filter was applied. The signals were then transformed into the time–frequency domain using a level 4 discrete wavelet transform (DWT), producing detail and approximation coefficients per epoch. Finally, seven statistical features were extracted for further analysis.

  • Model optimization and validation: A CNN model was optimized using TLBO and SPBO algorithms. After optimization, the model was trained and validated using EEG features derived from the preprocessed signals. The dataset was split into 70% for training and 30% for validation. Performance evaluation metrics included the receiver operating characteristic (ROC) curve, area under the curve (AUC), mean absolute error (MAE), and mean squared error (MSE).

Fig. 1
figure 1

Research methodology.

Full size image

Simulator study

We used data from experiments involving a lone-driver simulator provided by Farhangi (2022) to study driving behavior (Fig. 2). This study was conducted at the Virtual Reality Laboratory of K. N. Toosi University of Technology. All experimental protocols were approved by the K. N. Toosi University of Technology in accordance with the Declaration of Helsinki. Before the simulator-based experiment, participants were provided detailed information about the research, including its purpose, procedures, potential risks and benefits, and their rights. A commitment to maintaining the confidentiality and privacy of all participant information was reaffirmed. Informed consent was obtained from all participants.

Fig. 2
figure 2

Driving simulator experiment (above) and the virtual road (below). Reproduced with permission from4 under the Lincese Number 5976581430047.

Full size image

The virtual roadway was an expressway measuring 108 km long, with lanes measuring 3.65 m in width. The maximum grade was 4%, and the superelevation was 8%. The participants were equipped with a MindWave™ mobile 2 EEG headset throughout the experiment. The study involved 20 adult participants, comprising male and female individuals with an average age of 31.9 years (ranging from 25 to 39 years). Every participant held a current driving permit for at least 12 months and had previously navigated expressways in actual traffic situations. To induce drowsiness, participants were required to refrain from sleeping for a minimum of two hours prior to testing and were prohibited from consuming caffeine or other stimulants. Prior to the commencement of the primary experiment, participants were required to complete a 10-min training session in the simulator. They were instructed to operate the vehicle at the maximum permitted speed of 110 km/h. During the test phase, the laboratory environment was maintained at a low noise level, and drivers were prohibited from conversing, eating, or drinking. The experiment was terminated if a participant exhibited drowsiness or deviated from the designated route.

Convolutional neural network (CNN)

CNNs represent a specialized category within deep learning architectures. These models extract abstract features from data and have proven effective in image analysis tasks. Moreover, CNNs possess layers capable of learning patterns in sequential multivariate data, making them versatile for various prediction challenges6. A typical CNN architecture consists of several vital layers that work together to process and analyze complex data efficiently (Fig. 3). This architecture contributes to the widespread adoption of CNN in various modeling applications:

  • Convolutional layer: The convolutional layer is the main component of the CNN network, utilizing sliding windows and weight sharing to reduce processing complexity. In this layer, a kernel function is employed to extract various features from the input data32.

  • Pooling layer: The pooling layer follows, designed to reduce the feature map size by minimizing connections between layers and processing feature maps independently. This layer aims to enhance model training efficiency by decreasing dimensionality and extracting dominant features33.

  • Flattening layer: The flattening layer is applied before the fully connected layer, converting the data into a one-dimensional vector, which is crucial for further processing34.

  • Fully connected layer: The fully connected layer incorporates weights and biases, connecting neurons across different network layers34.

This layered structure enables CNNs to process and analyze complex data efficiently, contributing to their widespread adoption in machine learning applications.

Fig. 3
figure 3

The architecture of the CNN network. Reproduced with permission from32 under Creative Common CC BY license of MDPI.

Full size image

.

Human-based meta-heuristic optimization

Teaching learning-based optimization (TLBO)

TLBO is a population-based metaheuristic algorithm with superior performance in solving large-scale constrained and unconstrained problems across various applications35. Inspired by the educational process, it operates on the principle that a teacher’s guidance enhances student performance. The algorithm consists of two key phases: the Teacher phase, which simulates instructional influence, and the Learner phase, where knowledge is gained through peer interaction36. The popularity of TLBO in real-world optimization stems from its fast convergence, parameter-free nature, and ease of implementation, making it a widely adopted and effective tool in the field37.

Teacher stage: The teacher’s effectiveness influences students’ performance, making the teacher the optimal solution. In this phase, the class’s average grades improve due to the teacher’s knowledge transfer. Each student’s solution is then updated using the following equation37:

$${\text{z}}_{i,new}={\text{z}}_{i,old}+ramd({z}_{teacher}-TF\times {\text{z}}_{mean})$$
(1)

where \({z}_{i}\in ({z}_{i}^{1},\dots ,{z}_{i}^{d},\dots ,{z}_{i}^{D})\) represents the ith student score and \({\text{Z}}_{teacher}\) the best solution for the specific iteration. Average class solution with NL learners is

$${\text{z}}_{mean}=\frac{1}{NL}\sum_{i=1}^{NL}{z}_{i};{z}_{i,new}\in ({z}_{i}^{1},\dots ,{z}_{i}^{d},\dots ,{z}_{i}^{D})$$
(2)

where \(\in ({z}_{i}^{1},\dots ,{z}_{i}^{d},\dots ,{z}_{i}^{D})\) represent the latest and previous scores of the ith student, respectively. Rand represents a randomly generated number from 0 to 1, and TF is the teacher factor, heuristically chosen as either 1 or 2. If \({z}_{i,new}\) is better than \({z}_{i,old}\), it will be accepted as the new solution; otherwise, \({z}_{i,old}\) will be retained as the current solution.

Learner stage: At this stage, a student \({\text{z}}_{i}\) interacts randomly with a different student \({\text{z}}_{j}\) (where \({\text{z}}_{i}\ne {\text{z}}_{j}\)) to further enhance its grades, and the solutions are updated according to the following equation37:

$${z}_{i,new}= \left\{\begin{array}{c}{z}_{i,old}+rand\left({\text{z}}_{i}-{\text{z}}_{j}\right) if {\text{z}}_{i}\ge f({\text{z}}_{j})\\ {z}_{i,old}+rand\left({\text{z}}_{i}-{\text{z}}_{j}\right) if {\text{z}}_{i}<f({\text{z}}_{j})\end{array}\right.$$
(3)

In the given equation, the objective function \(f({\text{z}}_{j})\) consists of D design variables, and \({z}_{i,new}\) will only be accepted if it provides a better fitness value.

Student psychology-based optimization (SPBO)

The SPBO algorithm is designed to emulate human behavior and functions by capitalizing on psychological tendencies observed among students who seek to excel academically and enhance their performance to attain the highest ranking within their academic cohort. Attainment of the highest level of academic achievement necessitates the attainment of higher overall grades than those of one’s peers. This objective can be achieved by investing additional effort into all subjects30. However, it is essential to note that students’ capabilities, efficiency, and interests can vary significantly, which leads to a range of performance outcomes. In any given class, students can typically be grouped into four categories based on their performance on a specific topic: those who demonstrate the highest levels of proficiency, those who perform at a commendable level, those who exhibit average proficiency, and those who attempt to improve their performance in a somewhat haphazard manner38.

Best student: The learner with the highest mean score strives to retain their leading position by demonstrating consistently superior performance compared to their peers. To achieve this, they must exert effort that exceeds the class average across all subjects30. The algorithm models the top student’s advancement using the following expression:

$${X}_{best new}= {X}_{best}+{(-1)}^{k} rand \times ({X}_{best}-{X}_{j})$$
(4)

where \({X}_{best}\) symbolizes the top score attained by the highest-performing student, \({X}_{j}\) represents the score of the student j in a randomly selected field, the variable k is assigned a value at random, either 1 or 2, and rand denotes a random value within the range of 0 to 1.

Good student: This group of learners exhibits increased effort and superior performance in their areas of interest. The algorithm incorporates psychological diversity among these students through random selection. Some individuals within this category strive to surpass the top performers, aiming to achieve the highest test scores38. The behavior of this student category is modeled as follows:

$${X}_{new i}= {X}_{best}+ rand \times ({X}_{best}-{X}_{i})$$
(5)

Concurrently, a subset of students sought to improve their academic standing by mirroring the successful strategies of their top-performing classmates38. This tendency towards emulation can be represented mathematically as follows:

$${X}_{new i}= {X}_{mean}+ rand \times \left({X}_{best}-{X}_{i}\right)+rand$$
(6)

where \({X}_{mean}\) symbolizes the mean score achieved by the entire class in a specific field and \({X}_{i}\) denotes the score obtained by the student i in this field.

Average student: Learners who lack enthusiasm for a particular subject typically invest only minimal effort in their studies. These individuals are classified as “average” within that specific academic domain30. The algorithm randomly selects students for this category based on their simulated psychological profiles, as outlined in the following expression:

$${X}_{new i}= {X}_{i}+ rand \times \left({X}_{mean}-{X}_{i}\right)$$
(7)

Students who attempt to enhance at random: Some learners strive to enhance their level by utilizing diverse tactics and applying varying degrees of effort across different subjects and periods. These learners demonstrate fluctuating levels of commitment to various disciplines in their pursuit of overall improvement30. This behavior can be modeled as follows:

$${X}_{new i}= {X}_{min}+ rand \times \left({X}_{max}-{X}_{min}\right)$$
(8)

where \({X}_{max}\) represents the highest possible grade achievable in the subject, and \({X}_{min}\) denotes the lowest possible grade for that same subject.

Hyperparameters under optimization

According to the literature39,40,41, we identified seven critical hyperparameters for optimization in our CNN model. These hyperparameters, each playing a crucial role in model performance, are:

  • Number of epochs: The number of epochs specifies how many times the training algorithm will iterate over the entire training dataset. While increasing the number of epochs can enhance performance, it also raises the likelihood of overfitting42.

  • Batch size: The batch size parameter determines the quantity of training samples processed in a single iteration. Utilizing smaller batches can result in more variable gradient estimates, potentially aiding in avoiding local optima but often at the cost of extended training durations. In contrast, larger batches offer more consistent gradient estimates but may increase the risk of overfitting43.

  • Dropout rate: Dropout is a regularization method in CNNs, designed to mitigate overfitting. This technique operates by randomly deactivating a portion of input neurons during the training process, which helps prevent the model from becoming excessively dependent on specific features. The dropout rate, a crucial hyperparameter, determines the fraction of neurons to be deactivated and typically requires fine-tuning44.

  • Filter size: The size of filters in convolutional layers is an important hyperparameters as well. Larger filters capture broader context but may overlook finer details, while smaller filters are better suited for capturing detailed features45.

Validation metrics

The efficiency of the CNN was measured by applying AUC, MAE, and MSE metrics. The ROC is a graphical representation that assesses the performance of a model by comparing two probabilistic measures of sensitivity (on the y-axis) and specificity (on the x-axis). These two parameters range from 0 to 1 and are calculated using Eqs. 9 and 10, respectively. Sensitivity represents the likelihood of correctly identifying a positive sample, while specificity indicates the probability of accurately classifying a negative sample. The AUC, which represents the area beneath the ROC curve, signifies the model’s ability to classify a random sample correctly. A higher AUC value, closer to 1, indicates superior model performance38.

$$\text{Sensitivity}=\frac{TP}{TP+FN}$$
(9)
$$\text{Specificity}=\frac{TN}{TN+FP}$$
(10)

where TP (true positive) refers to correctly classified positive samples, TN (true negative) represents correctly classified negative samples, FP (false positive) denotes instances where negative samples were incorrectly labeled as positive, and FN (false negative) indicates positive samples that were mistakenly classified as negative.

Both MAE and MSE are widely used measures for assessing modeling error. The model efficiency improves as these metrics approach zero. MAE calculates the average of the absolute differences between actual and predicted values, treating all errors equally regardless of their direction. On the other hand, MSE squares the errors, which amplifies the impact of large errors and outliers, making them more prominent in the final score46. These metrics are computed using Eqs. 11 and 12, respectively:

$$MAE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {y_{i} - \hat{y}_{i} } \right|$$
(11)
$$MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2}$$
(12)

where yi signifies the true value of sample i and ŷi represents its forecasted value.

Results and discussion

EEG signal analysis

The EEG data underwent processing and modeling to evaluate drowsy driving detection. When examining EEG signals, power line interference frequency was considered within the 49–51 Hz range. The fourth-level DWT produced four detailed parameters alongside a single approximation parameter (Fig. 4). From each coefficient, seven characteristics were derived: variance, mean, kurtosis, skewness, power, entropy, and root mean square, culminating in 35 total signal attributes. The extracted features and categorized EEG signals were subsequently analyzed using both CNN-TLBO and CNN-SPBO model.

Fig. 4
figure 4

(A) original unprocessed EEG epoch, (B) EEG epoch after power line interference removal using a 3rd-order notch Butterworth filter, (C) time–frequency domain representation of the EEG epoch following level 4 DWT.

Full size image

We investigated the relationship between EEG signal features and driver alertness states (wakeful = 1, drowsy = 0) without any noise removal or outlier detection, except for removing power line interference. The correlation analysis results between the signal features and alertness states are presented in Fig. 5.

Fig. 5
figure 5

Heatmap depicting the correlation between EEG signal features and driver alertness states (drowsy state = 0, wakeful state = 1).

Full size image

Notably, the correlation coefficients for the approximation coefficient 4, and detail coefficients 4, 3, and 2 show negative values across most statistical features, suggesting a weak inverse relationship with driver alertness. These results indicate that lower signal feature values in these coefficients are generally associated with a drowsy state, consistent with previous studies that report a reduction in EEG signal complexity and amplitude during drowsiness36. In contrast, detail coefficient 1 demonstrates positive correlations with several features, suggesting a stronger association with wakefulness than other coefficients. This finding aligns literature indicating that increased power in higher frequency bands correlates with wakefulness47.

Overall, our findings are consistent with the literature48, suggesting that dynamic changes in wavelet coefficients can provide valuable insights for detecting changes in driver alertness in real-time monitoring applications.

To enhance the performance of the CNN, we employed two human-inspired meta-heuristic algorithms: TLBO and SPBO. These algorithms were run for 100 iterations and a population size of 10, to identify and optimize the values of the hyperparameters introduced in "Hyperparameters under Optimization". The overarching goal of this optimization effort was to minimize the MSE value. By utilizing these advanced techniques, we aimed to fine-tune the CNN model for improved accuracy and effectiveness.

The optimization process started with the initialization phase of the algorithm. Once initialized, the next step involved assessing the tunning, which was established through the evaluation of the CNN efficiency using the MSE metric. Reduced MSE scores suggest superior fitness and greater alignment between the model’s forecasts and the actual values. Upon reaching the 100 iterations, the optimal set of hyperparameters was identified as the one that achieved the best performance in the final population (Table 1). Lastly, the CNN model was trained with these optimized hyperparameters, completing the fine-tuning process.

Table 1 Optimized hyperparameters of CNN by TLBO and SPBO.
Full size table

A powerful server, equipped with 128 GB of RAM and a 64-core processor, was utilized to fine-tune the CNN using TLBO and SPBO. The tuning process using TLBO took 148 min, approximately 1.3 times longer than SPBO, yet both methods yielded similar results in minimizing the objective function. The CNN-TLBO model contained 4,145 parameters, whereas CNN-SPBO had 264,065 parameters, indicating a significant difference in model complexity. Similar to49, we found that TLBO resulted in a simpler optimized model structure than SPBO. The architectures of the optimized CNN models are presented in Table 2.

Table 2  The architectures of optimized CNN models.
Full size table

To achieve a near-real-time detection approach, it is crucial to consider computational complexity50. Optimizing the model for driver drowsiness detection requires balancing performance and efficiency to ensure real-time feasibility while maintaining high accuracy. While both CNN-TLBO and CNN-SPBO performed similarly in minimizing the objective function, their optimization strategies led to distinct differences in model architecture and computational cost.

The reason CNN-TLBO contained significantly fewer parameters can be attributed to the inherent limitations of the TLBO algorithm in its standard form. TLBO, despite its improved searchability and accelerated convergence process, still struggles with premature convergence and insufficient learning processes. This means that during CNN optimization, TLBO may favor simpler architectures that converge quickly but do not fully explore the potential complexity of the model. Since TLBO follows a fixed learning strategy (teacher and learner phases) without dynamic parameter tuning, it lacks the adaptability needed to fine-tune deeper architectures effectively51. As a result, the optimization process may lead to selecting a minimalistic CNN structure with fewer layers, filters, or neurons, ultimately resulting in a model with significantly fewer parameters. In contrast, the SPBO algorithm enhances exploration and mitigates premature convergence by integrating adaptive learning mechanisms inspired by student behaviors, such as motivation and curiosity30. This adaptability allows SPBO to optimize more intricate CNN architectures, potentially leading to models with a higher number of parameters compared to those optimized by the more rigid TLBO approach.

Finally, the effectiveness of a meta-heuristic algorithm is influenced by a triad of crucial factors: the unique characteristics of the optimization problem being tackled, the specific settings of the algorithm’s control parameters, and the inherent randomness within the algorithm’s processes52. Consequently, the success of meta-heuristic approaches can vary considerably depending on the specific context and nature of the problem to which they are applied.

Validation results

To validate the effectiveness of the optimization methods, we conducted a comparative analysis of the baseline CNN, CNN-TLBO, and CNN-SPBO. Figure 6 presents the MAE and MSE values for training and test data across these models. The results indicate that the performance of CNN-TLBO and CNN-SPBO was closely similar, with both models achieving lower error rates than the baseline CNN. CNN-TLBO achieved the lowest error values, with a test MAE of 0.223 and test MSE of 0.113, demonstrating superior performance. CNN-SPBO also exhibited a reduction in error, with a test MAE of 0.226 and test MSE of 0.107, outperforming the baseline CNN, which had a test MAE of 0.241 and test MSE of 0.127.

Fig. 6 
figure 6

Measured MAE and MSE values for CNN models.

Full size image

As demonstrated in Fig. 6, the modeling errors of CNN-TLBO and CNN-SPBO for the training data were markedly lower than those for the testing data, indicating a subtle overfitting. CNNs are susceptible to overfitting due to various factors. One primary reason is the scarcity of training data, which can lead the model to over-learn specific characteristics of the limited dataset, hindering its ability to generalize to new, unseen examples53. Moreover, excessive model complexity, characterized by abundant layers or parameters, can enable CNNs to memorize training data instead of extracting generalizable patterns54. Extended training durations may exacerbate this issue, causing the model to assimilate noise and extraneous information in the training set55. Overfitting in CNNs can also be attributed to the quality and composition of the training data. Including noisy or irrelevant information can lead the model to learn spurious patterns that do not accurately represent the authentic underlying relationships in the data54. Moreover, a lack of diversity in the training set can result in a model that struggles to perform well on new, more varied data56. The absence of regularization techniques, such as dropout or L1/L2 regularization, can exacerbate the overfitting problem57. Similarly, neglecting data augmentation strategies may limit the model’s exposure to diverse examples, hindering its ability to generalize effectively58.

In this study, we employed human-based meta-heuristic optimization techniques to fine-tune our CNN architecture. However, the observed overfitting in our proposed CNN models can be attributed to several interrelated factors. Firstly, the initial CNN architecture may have introduced inherent limitations despite our optimization efforts. Secondly, the constraints of our training data, particularly in quantity and diversity, likely contributed to the model’s tendency to overfit. It is crucial to note that EEG signals are inherently prone to noise and artifacts4. Our decision not to implement specialized noise removal techniques in the preprocessing stage may have allowed non-generalizable, noise-related patterns to persist in the data, potentially exacerbating the overfitting issue. Additionally, we may have overlooked opportunities for EEG-specific data augmentation, which could have enhanced the model’s robustness to input variations. These factors collectively underscore the challenges in developing generalizable CNN models for EEG signal analysis and highlight areas for potential improvement in future research.

The CNN-TLBO and CNN-SPBO models demonstrated accurate predictions compared to the target values. Nevertheless, Fig. 7 reveals that these models still produced some significant errors in their predictions. Notably, there is a discernible difference between the predictions for drowsy and wakeful states of both training and test data sets. This distinction suggests that the models could differentiate between drowsy and alert conditions, despite occasional large errors in their estimations.

Fig. 7
figure 7

Predictions of CNN-TLBO and CNN-SPBO.

Full size image

The ROC curves for the CNN models were generated using a dataset of 615 drowsy and 585 wakeful records. In this classification task, drowsy states were labeled as 1, while wakeful states were labeled as 0. As shown in Fig. 8, both TLBO and SPBO optimization methods significantly enhanced the model’s ability to differentiate between the two states. CNN-TLBO achieved the highest AUC of 0.926, indicating superior classification performance, while CNN-SPBO followed closely with an AUC of 0.920. Both optimized models outperformed the baseline CNN (AUC = 0.876), demonstrating the effectiveness of TLBO and SPBO in improving predictive accuracy and overall model performance.

Fig. 8
figure 8

Assessment of CNN-SPBO and CNN-TLBO using ROC and AUC metrics.

Full size image

In our study, we utilized the benchmark EEG dataset from Farhangi (2022), which classified brain signals using six different machine learning algorithms, including decision tree, extra trees, k-nearest neighbor, multi-layer perceptron, random forest, and support vector classification, all optimized via the random search method. To assess the effectiveness of our proposed approach, we compared the performance of CNN models optimized with TLBO and SPBO against the highest performance reported in the benchmark study. CNN-TLBO demonstrated a 0.029 improvement in MAE and a 0.10 increase in AUC, indicating enhanced predictive accuracy and robustness. Similarly, CNN-SPBO achieved a 0.026 improvement in MAE and a 0.11 increase in AUC, further validating the effectiveness of the proposed optimization techniques.

Lastly, it should be noted that due to the high computational cost associated with model tuning, cross-validation was not performed in this study, which could impact the generalizability of the results.

Conclusion

In this study, two human-inspired meta-heuristic algorithms, TLBO and SPBO, were applied to optimize the CNN model for driver drowsiness detection in a simulator-based environment, focusing on minimizing the modeling error. Both methods demonstrated strong predictive performance, achieving similar accuracy in distinguishing between drowsy and wakeful states, with only slight differences in their error metrics. While CNN-TLBO resulted in a simpler model, SPBO’s efficiency in optimization time—requiring 116 min compared to TLBO’s 148—made it the more cost-effective option. Despite the models’ strong performance, subtle overfitting was observed, likely due to the limited diversity of training data and the absence of specialized noise reduction or augmentation techniques. The study concludes that SPBO is a preferable optimizer for EEG-based drowsiness detection, balancing high accuracy and lower computational demands. Our observations underscore the importance of carefully selecting meta-heuristic methods to achieve optimal results, considering not only the final performance metrics but also factors such as model complexity, optimization time, and computational demands.