Estimation of state of health for lithium-ion batteries using advanced data-driven techniques

Abstract

Accurate estimation of the State of Health (SOH) is crucial for ensuring the performance, safety, and longevity of lithium-ion batteries in electric vehicles. Traditional methods, such as Coulomb Counting and the Extended Kalman Filter, often lack the accuracy and computational efficiency required for modern applications. This study proposes an advanced framework that leverages machine learning models to model the nonlinear degradation patterns of lithium-ion batteries by focusing on key features such as voltage, current, internal resistance, and temperature. The proposed framework incorporates optimized pre-processing techniques, including normalization, to improve data quality and ensure consistency across varying battery conditions. Advanced machine learning models, including Adaboost, Xgboost, Ridge Regression, Decision Trees, Random Forests, Artificial Neural Networks, and Long Short-Term Memory Networks (LSTM), are employed to analyze battery performance. Among these, the LSTM network demonstrates outstanding capability in capturing long-term dependencies in sequential battery data, achieving a mean squared error of 0.000115 and an R2 score of 0.9982. It also accurately predicts the remaining life cycle of the battery using temporal patterns derived from MATLAB model datasheets, significantly reducing estimation errors. A comprehensive comparison using performance metrics such as root mean squared error, mean absolute error, and R2 scores highlights the LSTM model’s superiority while evaluating the suitability of other approaches. The proposed method not only improves estimation accuracy but also reduces computational demands through optimized feature selection and model training strategies, making it highly suitable for real-time applications in lightweight electric vehicles with limited computational resources. This research bridges the gap between theoretical advancements in data-driven techniques and their practical deployment in real-world battery management systems.

Introduction

The performance and dependability of lithium-ion (Li-ion) batteries are receiving a lot of attention due to the rising demand for portable electronic devices, electric vehicles (EVs), and renewable energy storage systems¹. Due to their high energy density, long cycle life, and relatively low self-discharge rates, these batteries are among the top choices for EV applications.

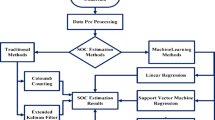
However, ensuring the optimal performance and longevity of Li-ion batteries necessitates an accurate estimation of their state of health (SOH). SOH estimation is crucial for predicting battery life, optimizing charging strategies, and preventing unexpected failures, thus ensuring the safety and efficiency of battery-operated systems². Li-ion batteries offer many benefits, but a significant drawback is that their capacity fades with prolonged usage. Furthermore, it’s critical to precisely monitor and estimate capacity because overcharging or overcharging a battery due to an inaccurate estimate may permanently damage it. Because of their excellent energy density, extended cycle life, and comparatively low self-discharge rates, these batteries are the go-to option for a variety of uses³. Furthermore, the remaining useful life (RUL) forecast and the SOH estimation are complicated by the nonlinear decline of battery capacity⁴. Numerous investigations have been carried out in an effort to accurately estimate the SOH, including experimental, model-based, and machine-learning methods, shown in Fig. 1.

Model-based approaches use a battery model and account for the internal degradation process to estimate the SOH of a battery. For instance, an analogous circuit model combined with an improved Kalman filter was employed to predict the SOH, incorporating dynamic error boundaries for enhanced accuracy⁶. Similarly, a NARX network optimized with an adaptive weighted square-root cubature Kalman filter (AWSC-KF) has been utilized for dynamic State-of-Charge (SOC) estimation in Li-ion batteries. This approach improves SOC accuracy and real-time performance, making it suitable for battery management systems, though it demands significant computational resources and may face scalability challenges³⁴. Furthermore, an ASTSEKF optimizer with nonlinear condition adaptability has been introduced for precise SOC estimation under dynamic conditions. While it enhances estimation accuracy, it also suffers from high computational demands and limited scalability³⁵. These methods collectively highlight the advancements in battery state estimation while underscoring the need for improved computational efficiency and better scalability for real-world applications.

Data-driven approaches use machine learning or statistical models to forecast the SOH of batteries. To increase the estimation’s accuracy⁶ presented sparse Bayesian predictive modeling using a sample entropy of brief sequences of voltage. A hidden Markov model was used to calculate and evaluate a battery’s SOH. To estimate the SOH⁷, Using Gaussian process regression, which combines the mean and covariance functions.

Fig. 1

Categorization of battery SOH evaluations¹.

An enhanced relevance vector machine approach was also put forth⁸ to calculate a battery’s RUL. By using the Gaussian process regression model as indirect health markers.

It was suggested⁹ to use a deep neural network to estimate battery charging curves, which are necessary for computing SOH. To anticipate a battery’s feasible capacity¹⁰, suggested a deep convolutional neural network (CNN) technique using current and voltage measurement data. To improve the accuracy of an RUL forecast, multichannel charging profiles and long-short temporary memory (LSTM) model were combined¹¹.

Data-driven algorithms, on the other hand, have made tremendous progress in enhancing SOH accuracy with enhanced performance and enhancing learning capabilities for high accuracy¹². Due to their flexibility in capturing complex, non-linear relationships, higher accuracy when compared to traditional methods, data-driven nature, robustness to noise, scalability, ability to extract features automatically, and integration capabilities with other systems, machine learning (ML) approaches are preferred for SOH estimation of Li-ion batteries³⁴.

Adaboost may estimate SOH better than Xgboost due to its simplicity and robustness in handling small datasets and reducing variance¹³. It focuses on improving weak learners iteratively, which can capture the nuances of battery degradation patterns more effectively in certain scenarios compared to the more complex Xgboost.

As Xgboost can handle complex relationships in data and reduce overfitting with regularisation, it could be able to estimate SOH more accurately than Adaboost. It optimizes speed and performance through advanced techniques, making it more suitable for large datasets and capturing intricate battery degradation patterns¹³. Decision Trees (DT) may estimate SOH better than Xgboost due to their interpretability and handling ability of non-linear relationships, which are crucial for understanding complex battery degradation patterns¹⁴. However, Xgboost’s advanced techniques can lead to higher accuracy and efficiency, especially with large datasets and intricate patterns.

DT for SOH estimation in Li-ion batteries offers interpretability, non-linear relationship handling, and no data preprocessing requirements¹⁵. However, they are prone to overfitting, have high variance, and may struggle with complex patterns. Combining them with ensemble methods can enhance accuracy and mitigate limitations. To reduce model complexity and overfitting for SOH estimation, ridge regression is a linear regression technique that incorporates a regularisation term to penalize large coefficients¹⁶. Its advantages include handling multicollinearity and providing a simpler model, but it may oversimplify complex relationships and require tuning of the regularization parameter. Since Ridge Regression penalizes large coefficients to prevent overfitting and can manage multicollinearity, it may be able to estimate SOH more accurately than decision tree models¹⁷. It provides a simpler and more interpretable model, which can be advantageous for understanding the relationship between features and SOH in Li-ion batteries. Although Random Forest (RF) can handle high-dimensional data and capture complex non-linear correlations, it may be able to predict SOH more accurately than Ridge regression¹⁸. It can help in understanding the factors influencing SOH in Li-ion batteries by reducing overfitting and providing feature importance rankings. Using numerous decision trees and averaging their estimations, random forest is an ensemble learning technique that estimates the SOH¹⁹. It reduces overfitting, handles nonlinearities, and provides feature importance rankings. However, it can be computationally intensive and less interpretable than individual decision trees.

Artificial neural networks (ANNs) can represent intricate non-linear relationships, they might be able to predict SOH more accurately than random forests. They can adapt to varying data patterns and capture nuances in battery degradation, which may be challenging for a random forest’s ensemble of decision trees²⁰. However, ANNs require more data and computational resources.

ANNs for SOH estimation use a network of interconnected nodes to model complex relationships. They can learn from data without explicitly programmed rules, potentially capturing intricate battery degradation patterns²¹. However, ANNs require large datasets, are computationally intensive, and can be challenging to interpret.

The recurrent neural network (RNN) utilized for the SOH estimate is LSTM. It is appropriate for time-series battery data since it can capture long-term dependencies in sequential data²². Advantages include handling sequential data, but disadvantages include complexity, computational cost, and potential overfitting with small datasets.

LSTMs may estimate SOH better than traditional ANNs because of their capacity to capture long-term dependencies and model sequential data²³. Because of their suitability for time-series battery data, they can successfully identify intricate patterns of degradation that conventional ANNs might find difficult to identify.

The energy level of a battery significantly influences its characteristics, necessitating an effective pre-processing technique to enhance the precision and effectiveness of State of Health (SOH) estimates in machine learning (ML) models. Various techniques, including Adaboost Regression, Xgboost Regression, Ridge Regression, DT Regression, RF Regression, ANN, and LSTM, have been widely employed for SOH estimation²³. Building upon this, an enhanced SOC estimation method integrates LSTM with an adaptive state update filter that incorporates battery parameters, improving estimation accuracy and robustness. However, this comes at the cost of high computational demands³⁶. Furthermore, an extended-input LSTM model, coupled with an adaptive singular value decomposition unscented Kalman filter, leverages full-cycle current rate and temperature data, further enhancing SOC accuracy and adaptability, though computational intensity remains a challenge³⁷. These advancements underscore the potential of ML approaches for precise battery state estimation while emphasizing the need for computational efficiency in real-world applications. This paper proposes an ML-based approach for the long-term health prognosis of lithium-ion batteries, improving SOH prediction accuracy and enabling better battery management and lifespan estimation. The approach’s merits include high precision in life cycle prediction and the ability to handle complex data patterns, yet it faces limitations due to its dependency on specific datasets, which restricts generalizability, and its inherent computational complexity³⁸. Additionally, the paper introduces an ML model that predicts the remaining useful life (RUL) of lithium-ion batteries, utilizing a bi-directional recurrent network to capture complex temporal dependencies, which improves RUL predictions. While this offers enhanced accuracy, effective temporal data handling, and practical applications, it also faces challenges like data dependency, computational complexity, and limited generalizability³⁹. These studies collectively highlight the effectiveness of ML techniques in battery state estimation while pointing to the need for addressing scalability and computational efficiency.

Thus, to use the models, training data must be gathered to estimate and predict results. The SOH of Li-Ion batteries is predicted in the current work, and seven ML techniques are employed to forecast the SOH in the suggested three-wheeler EV design. At the end of the process, their performance indices are utilized to compare all aforesaid seven algorithms²⁴. The proposed concept for integrating a BMS technology in the battery system into a lightweight three-wheeled EV will provide new research opportunities, emphasizing range, weight, and battery life. The field of battery SOH estimation has evolved significantly, with traditional methods like CC and EKF providing initial insights but often struggling to capture complex degradation patterns in Li-ion batteries. Recent advancements have incorporated ML techniques to improve estimation accuracy. The proposed study advances this research by introducing an energy-level-based pre-processing framework, which enhances input data quality by focusing on key battery features related to energy levels. This targeted pre-processing reduces noise and improves the relevance of the data, leading to more accurate SOH estimation. Additionally, a comprehensive comparison of various ML algorithms, including Adaboost, Xgboost, Ridge Regression, DT, RF, ANN, and LSTM, provides a broader evaluation than previous works. It also addresses the specific needs of lightweight three-wheeled electric vehicles, highlighting new applications and considerations for battery management.

This approach refines data pre-processing and applies diverse ML models to practical scenarios, pushing the boundaries of current SOH estimation research. The complete structure of SOH estimation is represented in Fig. 2.

Fig. 2

Graphical representation structure of battery SOH estimation.

It is structured into six sections. Section “System description” offers a brief description of the EV prototype and its battery datasets. Section “SOH estimation approach and key findings” discusses the SOH estimation approach and highlights key findings. Section “Machine learning process” outlines the machine learning process for SOH estimation using the proposed preprocessing method. Section “Results and discussion” compares SOH estimation results of using different MLA, section “Conclusion” presents the conclusions.

System description

The proposed concept for integrating a Battery management system (BMS) technology in the battery system into a lightweight three-wheeled EV (LEV) will provide new research opportunities, emphasizing range, weight, and battery life⁵. The technical specifications for LEVs are displayed in Table 1, whereas the characteristics involved in the planned work are specified in Table 2. Figure 3 displays the LEV prototype model of the battery-electric supercharger (BESS) electric propulsion system.

The battery has been used in this instance as the main power source⁵. The electric driver controller and batteries are linked via. The Indian road is the intended use for this suggested model. It has been designed in accordance with the Research Association of India (ARAI) norm by taking that norm into consideration. The total force calculation shown in Eq. (1),

$${F_{Total}}={F_r}+{F_d}+{F_g}+{F_{a~}}$$

(1)

where ${F_r}~$ is rolling resistance force, ${F_d}~$ is aero- dynamic drag force, ${F_g}$ is gradient force, ${F_{a~}}$ is acceleration force,${M_g}$ is the gravitational mass, θ is the grade angle (degree) and ${F_{Total}}$ is the total resistive force that the vehicle experiences, considering only factors like air resistance, tire friction, and gravitational pull. It is important when analyzing deceleration, energy consumption, and efficiency, which are considered in the EV design.

Fig. 3

LEV prototype model⁵.

Table 1 Technical specification of the lab designed three-wheeler.

Table 2 Specification considered for the proposed work.

Modelling of Li-ion battery

In an equivalent circuit model of a lithium-ion battery as represented in Fig. 4, ${V_{ocv}}$ represents the open circuit voltage, reflecting the battery’s internal electrochemical potential when no current flows, and is influenced by SOC and temperature²⁶. ${R_0}$, symbolizes the series resistor, accounting for internal ohmic resistance from electrodes, electrolyte, and contact points, causing an immediate voltage drop under current flow. The diffusive resistances$~{R_1}$,$~{R_2}$, model the resistive effects of ion diffusion within the battery, while the diffusive capacitances ${C_1}$,$~{C_2}$, repsent the capacitive storage behavior arising from ion diffusion.${V_1},{V_2},{V_3}$, represents the voltage drop across the RC parallel branches. Together, these parameters enable the circuit to accurately capture the battery’s dynamic behavior under varying operating conditions. The diffusion charge is taken into account by the parallel RC branch. ${V_t}~,$ is the battery’s terminal voltage as measured across its terminals, which is given by Eq. (2),

$${V_t}={V_{ocv}} - {V_1} - {V_2} - {V_3}~~$$

(2)

Fig. 4

Equivalent electrical circuit–based Li-ion model.

The battery pack has a terminal voltage of 48 V, and the motor drive receives power directly from it. The battery operates with a SOC range between 30% and 100%. To achieve a maximum range of 100 km, the BES system reduces the energy demand from the battery to 220.98 N or 4.8 kWh. Details of the Li-ion battery bank are provided in Table 3. To store 4.8 kWh of energy for a 100 km range on a single charge, the battery pack is composed of 520 cells, organized into 40 stacks of 13 cells in series. The cells used in the battery pack are Li-ion 18,650 NMC cells with a capacity of 2500 mAh each.

Table 3 Specification of Li-ion battery pack.

Fig. 5

Li-ion cell charging and discharging board.

Fig. 6

Li-ion battery grading system.

To design the battery pack, first, cell charging and discharging has been done to know the cell capacity, shown in Fig. 5, and then cell internal resistance obtained through IR tester and after then the cells has been arranged in series and parallel connection and connected the BMS, here CAN protocol BMS is integrated to monitor and balance the battery pack performance, through the mulita-meter and capacity tester, the voltage and capacity variation are observed, shown in Fig. 6.Switched mode power supply(SMPS) are used to give the controlled power supply to the charging module and when the battery has done deep discharging, to recover it, boost charging is applied to the battery. The data of the battery pack like, voltage, current, IR, temperatures are collected from the CAN bus BMS. Theses collected data will be analyzed using different MLA algorithm for the SOC estimation, which is clearly described in the chapter.

SOH Estimation approach and key findings

Battery performance can be referred to as the SOH, and several indirect health indicators are frequently used in assessment methodologies. These techniques fall into four categories: data-driven, hybrid, model-based, and differential analysis²⁷.

The SOH of a Li-ion battery quantitatively evaluates its capacity degradation and increase in internal impedance over time. This estimation considers two key parameters, i.e. the overall rated capacity (${Q_{Rated}}~$) and the total charge capacity (${Q_{BOL}}$). ${Q_{BOL}}$, represents the total charge capacity of the battery when it is new, as specified by the manufacturer, while ${Q_{Rated}},~$refers to the maximum charge capacity achievable when the battery is fully charged at the start of its life. These values are essential for calculating SOH, which measures the extent of capacity loss due to aging and usage. The same relationship is represented mathematically through Eqs. (3, 4):

$$~~SOC=\frac{{{Q_{BOL}}}}{{{Q_{Rared}}}}~ \times 100\% ~~~$$

(3)

The resulting SOH percentage indicates the battery’s health, whereas a lower SOH value signifies higher degradation and reduced performance.

To determine the SOH of a battery, the initial State of Health (SOH) must first be obtained. This can either be retrieved from the manufacturer’s data sheet or, for greater accuracy, measured using a charging and discharging machine, as shown in Fig. 6. To measure the initial SOH, the battery is first charged at a constant current of 1 A using the charging machine. After the battery is fully charged, it is discharged at a constant current of 0.1 A using the discharging machine. The capacity recorded during this process will represent the initial SOH of the battery.

Once the initial SOH is obtained, the battery is subjected to a certain number of charge and discharge cycles. After these cycles, the remaining SOH can be calculated using the following formula, represented in Eq. (4). Here, ${Q_{Current~capacity}}~$is the current capacity of the battery after a set number of cycles, and ${Q_{Intial~Capcity}}$ is the initial capacity of the battery.

$$SOH=~\frac{{{Q_{Current~capacity}}}}{{{Q_{Intial~Capcity}}}}~ \times 100\% ~$$

(4)

This formula provides the percentage of the battery’s health remaining after use. A number of parameters are needed to calculate the Depth of Discharge (DOD). The ratio of the released charge capacity to the overall rated capacity is known as the DOD. Equations (5–7) are used to express the discharge current $~{I_d}$, which is another way it takes into account the discharge capacity.

$$DOD=~\frac{{{Q_{Released~Rated~capacity}}}}{{{Q_{Rated}}}}~ \times 100\%$$

(5)

$$\Delta DOD=~\frac{{\mathop \smallint \nolimits_{{{t_0}}}^{{{t_0}+\tau }} {I_d}}}{{{Q_{Rated}}}}~ \times 100\% ~$$

(6)

$$DOD\left( t \right)=DOD\left( {{t_0}} \right)+100\% ~$$

(7)

Equation (8) represents the SOC without taking battery aging and operating efficiency into account.

Equation (9)²⁸ is used to calculate the SOH in direct measuring procedures.

$$SOC\left( t \right)=100\% - DOD\left( t \right)~$$

(8)

$$SOC\left( t \right)=SOH\left( t \right) - DOD\left( t \right)~$$

(9)

These methods can only be applied in limited experimental settings and are not suitable for real-world web applications. Since indirect analytic techniques are currently widely used through a variety of means and are the most practical, they are of great importance. These methods can only be applied in limited experimental settings and are not suitable for real-world web applications. Since data-driven methods are currently widely used through a variety of means and are the most practical, they are of great importance.

Machine learning process

The suggested method for estimating the SOH of batteries included three stages, as illustrated in Fig. 7, data pre-processing, model training, and a performance assessment. During the data preparation step, the missing and anomalous values were eliminated from the raw data from the batteries. The battery features were extracted once the data was cleaned². A training dataset and a test dataset were created from the feature data. The training dataset was divided into training and validation data during the model training phase.

Using the training data, trained Ad boost, Xgboost, Ridge, DT, RF, ANN, and LSTMs. Using the validation results, the architecture’s hyper-parameters were changed. The trained model was tested using the test dataset during the performance evaluation stage, and the R2 score, mean absolute percentage error (MAE), mean squared error (MSE), and root mean squared error (RMSE) were used to assess the model’s performance.

Data preprocessing

Pre-processing of the data was done to make it fit for a ML model. Because there were anomalous and missing values in the raw data, data cleaning was necessary. After data cleaning, features were retrieved from the raw data, which was based on time series. Equation (10) was used to represent the feature format. As a result, used min-max normalisation² to normalise the SOH dataset as follows:

$$z_{{nm}}^{k}=~\frac{{x_{{nm - {\text{min}}\left( {{X_n}} \right)}}^{k}}}{{\hbox{max} \left( {{X_n}} \right) - {\text{min}}\left( {{X_n}} \right)}}~~~~n \in \left\{ {1, \ldots ,5} \right\},m \in \left\{ {1, \ldots ,s} \right\}$$

(10)

Here, m is the m-th sampling point, k denotes the number of cycles, and $\:{X}_{n}$ is an array of the n-th row in Eq. (11) of all charging cycles. Additionally, applied min-max normalisation to normalise the capacity in the following manner:

Fig. 7

Overview of the proposed process for Li-ion battery SOH estimation.

$${c^k}=\frac{{{C^k} - {\text{min}}\left( C \right)}}{{\hbox{max} \left( C \right) - {\text{min}}\left( C \right)}}$$

(11)

Where C is a group of capacity for all charging cycles and k is the number of cycles. After normalization, the data was divided into two sets: the test dataset was used to evaluate the final models, and the training dataset was used to fit the model parameters. In SOH estimation for batteries using machine learning algorithms, data pre-processing is essential. Data re-sampling addresses class imbalances or irregular distributions by either increasing the number of samples in underrepresented classes or reducing them in overrepresented ones. Outlier detection identifies and handles anomalies that could skew results, using box plots. Data normalization scales features to a uniform range or distribution, improving model convergence and performance. Techniques like Min-Max Normalization ensure features contribute equally, leading to more accurate and reliable estimations. These pre-processing steps are crucial for enhancing model performance and achieving precise SOH estimates.

Model training

The training dataset has been divided into training and validation data for the model training phase. In this paper used seven distinct machine learning models with the dataset: Adaboost, Xgboost, Ridge, DT, RF, ANN, and LSTM architectures.

Ridge regression

A linear regression technique known as ridge regression is used to examine the relationship between input factors and a continuous target variable is called ridge regression, shown in Fig. 8.

It is particularly useful when the input variables are correlated or when there is multicollinearity present in the data²⁸. Ridge regression helps to regularise the model and lessen the effect of multicollinearity by adding a penalty term to the usual linear regression objective function.

Fig. 8

Ridge regression for SOH estimation.

The mathematical relationship between cell voltage, cell current, and cell internal resistance, temperature, and SOH estimation using Ridge regression can be represented by the following Eqs. (12, 13):

$$\widehat {{SoH}}=~{\beta _0}+~{\beta _1}.{V_{cell}}+{\beta _2}.I+{\beta _3}.{R_{cell}}+{\beta _4}.T$$

(12)

Where, $\widehat {{SoH}}~$ is the predicted State of Health, ${\beta _0},{\beta _1},{\beta _2},{\beta _3},{\beta _4}$ are the coefficients (weights) of the Ridge regression model,${V_{cell}}$ represents the voltage of the cell, I represents the current of the cell, ${R_{cell}}$ represents the internal resistance of the cell, T represents the temperature.

In Ridge regression, the coefficients$~{\beta _0},~{\beta _1},~{\beta _2}$,$~{\beta _3},{\beta _4}$ are estimated by minimizing the following objective function:

Minimize

$$\mathop \sum \limits_{{i=1}}^{N} {\left( {{y_i} - \left( {{\beta _0}+~{\beta _1} \cdot {V_{cell}}+{\beta _2} \cdot I+{\beta _3} \cdot {R_{cell}}+{\beta _4} \cdot T~} \right)} \right)^2}+~\lambda ~\mathop \sum \limits_{{j=1}}^{p} \beta _{j}^{2}~$$

(13)

Where ${\text{N}}$ represents the number of samples, ${\text{P}}$ represents the number of features, ${{\text{y}}_{\text{i}}}~$represents the observed SOH for the sample i,$~{\text{\varvec{\uplambda}}}$ represents the regularization parameter, $\mathop \sum \limits_{{{\text{j}}=1}}^{{\text{p}}} {\text{\varvec{\upbeta}}}_{{\text{j}}}^{2}{\text{~represents~}}$the penalty term that penalizes large coefficients.

The objective is to find the values of$~~{\beta _0},~{\beta _1},~{\beta _2}$,$~{\beta _3},{\beta _4}~{\text{that}}$ minimize the sum of squared errors plus the Ridge penalty. Ridge regression helps to minimize the effects of multicollinearity and stabilizes the model by shrinking the coefficients towards zero.

Decision tree

In this, the feature space is divided into regions, and each region is fitted with a basic model. To support decisions and their possible outcomes, a DT uses a hierarchical model based on chance events, resource costs, and utility²⁹. The tree structure is made up of leaf, internal, branch, and root nodes, arranged in a tree-like hierarchy, shown in Fig. 9. The DT working principle in mathematical form is presented in Eq. (14).

Fig. 9

Pictorial representation of decision tree algorithms SOH estimation.

The mathematical relationship between cell voltage, cell current, cell internal resistance, temperature, and SOH estimation using decision tree regression can be represented by the following equation:

$$\widehat {{SoH}}=~\mathop \sum \limits_{{i=1}}^{N} {w_i}.{y_i}~$$

(14)

Where,$\widehat {{SoH}}$ is the predicted State of Health, N represents the number of samples in the region to which the new data point belongs, ${w_i}$ represents the weight assigned to each training sample i, and ${y_i}~$ represents the SOH value of training sample i.

In order to forecast the target variable in DT regression, the model learns a series of if-then-else decision rules from the training set. The goal of the model’s training is to reduce the target variable’s variation within each leaf node.

The DT model equation for SOH estimation does not have a fixed form like linear regression, as it depends on the specific structure of the DT learned from the training data. The series of choices the DT makes, culminating in the ultimate estimation at the leaf node that corresponds to the new data point, represents the relationship between the input features and SOH.

Adaboost

A machine learning technique called Adaboost is applied to regression and classification problems. It is an ensemble learning technique that builds a strong learner by combining several weak learners³⁰, shown in Fig. 10. Using the same dataset, Adaboost trains weak learners iteratively and modifies the weights of the training examples in response to the past weak learners’ performance. This allows Adaboost to focus more on the instances that are difficult to classify or predict.

Fig. 10

Pictorial representation of Adaboost algorithms SOH estimation.

The method known as Adaboost regression is applied to regression projects in which the objective is to predict a continuous target variable. The mathematical relationship between cell voltages, cell current, and cell internal resistance, temperature, and SOH estimation using Adaboost can be represented by the following Eq. (15):

$$\widehat {{SoH}}=~\mathop \sum \limits_{{t=1}}^{T} {\alpha _t}{h_t}~\left( {{V_{cell}},I,{R_{cell}},T} \right)$$

(15)

Where, $\widehat {{SoH~}}$represents the predicated State of Health, T represents the number of weak learners (base models), ${\alpha _t}~{\text{represents}}~$the weight assigned to the t-th weak learner, and ${h_t}~{\text{represents~}}$ the t-th weak learner that predicts SOH based on the input features.

The Adaboost algorithm sequentially adds weak learners to the ensemble, with each new weak learner focusing on the instances misclassified or poorly predicted by the previous weak learners. The weights ${\alpha _t}$ ​are computed based on the performance of the weak learners, giving more weight to the more accurate learners. A weighted summation of the estimations made by each of the ensemble’s weak learners makes up the final SOH forecast, where the weights are determined by the Adaboost algorithm. This allows Adaboost to create a strong learner that can effectively predict SOH based on the input features.

Xgboost

Xgboost is a widely used MLA, popularly for both regression and classification tasks. It utilizes ensemble learning method to create a robust predictive model by sequentially combining multiple weak models, typically DT, shown in Fig. 11.

Fig. 11

Pictorial representation of Xgboost algorithms SOH estimation.

The Xgboost regression technique adds DTs to the ensemble iteratively, with each new tree fixing mistakes produced by the preceding trees³⁰. The weighted total of the estimations made by each tree in the ensemble represents the final forecast. The following Eq. (16) represents the mathematical link between temperature, internal resistance, cell voltage, current, and SOH estimate using Xgboost:

$$\widehat {{SoH}}=f\left( {{V_{cell}},I,{R_{cell}},T} \right)~$$

(16)

Where, $\widehat {{SoH}}~$represents the predicted State of Health, ${V_{cell}}~$ represents the cell voltage, I represents the cell current,${R_{cell}}~$represents the cell’s internal resistance, T represents the temperature, f represents the function learned by the Xgboost model.

The exact form of the function f is learned during the training of the Xgboost model using a dataset that includes measurements of SOH, cell voltage, cell current, cell internal resistance, and temperature. By maximizing the weights given to each feature and the ensemble’s DT parameters, Xgboost discovers the correlation between these input features and SOH. It’s crucial to remember that the Xgboost model has acquired a complex and non-linear connection, which enabled it to fully comprehend the subtleties of the input data and how they affected the estimation of SOH.

Random forest algorithm

Random forest regression is an MLA that involves a collection of DT to perform regression tasks. Each DT in the RF is trained on a random subset of the training data and a random subset of the features, which reduces overfitting and enhances the model generalization capabilities³¹. The final estimation of the RF is the average of the estimations of all the individual trees. The mathematical relationship between cell voltages, cell current, and cell internal resistance, temperature, and SOH estimation using RF regression can be represented by the following Eq. (17):

$$\widehat {{SoH~}}=~\frac{1}{N}~\mathop \sum \limits_{{i=1}}^{N} \widehat {{So{H_i}}}~$$

(17)

Where $\widehat {{SoH~}}~$ represents the predicted SOH, N represents the number of decision trees in the RF, $\widehat {{So{H_i}}}$ ​ represents the predicted SOH from the i-th decision tree.

Each DT in RF regression is trained using a random selection of both the features and the training data. This unpredictability aids in lowering overfitting and enhances the model’s overall effectiveness. The average of each individual tree’s forecasts makes up the RF’s final estimation, which serves to smooth out the estimations and raise the model’s accuracy, as shown in Fig. 12. As a result, complicated correlations in the data can be captured using RF regression, enabling precise estimations for the target variable.

Fig. 12

Pictorial representation of random forest algorithms SOH estimation.

Artificial neural network (ANN)

A class of ML techniques called ANNs is motivated by the composition and operations of the human brain. They are applied to many different tasks, such as pattern recognition, grouping, regression, and classification³². After being received by the input layer, the data is processed in one or more hidden layers before being sent to the output layer, which makes the estimation, shown in Fig. 13. This Eq. (18), for a basic feedforward neural network with one hidden layer, represents the mathematical link between cell voltage, cell current, cell internal resistance, temperature, and SOH estimate using an ANN:

$$\widehat {{SoH}}=f\left( {\mathop \sum \limits_{{i=1}}^{n} {w_{i2}}.g\left( {\mathop \sum \limits_{{j=1}}^{m} {w_{j1}}.{x_j}+~{b_j}~} \right)+{b_2}} \right)~$$

(18)

Where, $\widehat {{SoH}}~~$ represents the predicted State of Health, f and g are activation ReLU functions used in the hidden and output layers, respectively, ${w_{ij~}}$ represents the weights connecting neurons in adjacent layers, ${x_j}~$ represents the input features (e.g., cell voltage, cell current, cell internal resistance, temperature), ${b_j}~~$ represents the bias terms, $n~$ represents the number of neurons in the hidden layer, $m~$ represents the number of input features.

By modifying the weights and biases to reduce the discrepancy between the predicted and actual SOH in the training data, the network learns to map the input features to the target variable. Because of their reputation for capturing intricate non-linear relationships in data.

Fig. 13

Artificial neural network SOH estimation.

Long-Short-Term memory (LSTM)

The LSTM model is a type of RNN that captures long-term dependencies in sequential data, as shown in Fig. 14. For battery SOH estimation³², it analyzes historical data, i.e. voltage, current, cycles, etc. to predict battery health and remaining life, ensuring optimal performance and longevity, represents in Eqs. (19–23)

$${i_t}=~\sigma ~\left( {{W_{ix}}.{x_t}+~{W_{ih}}.{h_{t - 1}}+~{W_{ic}}.{c_{t - 1}}+{b_i}} \right)~$$

(19)

$${f_t}=\sigma \left( {{W_{fx}}.{x_t}+~{W_{fh}}.{h_{t - 1}}+{W_{fc}}.{c_{t - 1}}+~{b_f}} \right)$$

(20)

$$~{c_t}=~{f_t}.{c_{t - 1}}+{i_t}.\tanh \left( {{W_{cx}}.{x_t}+~{W_{ch}}~.~{h_{t - 1}}+~{b_c}} \right)~~~$$

(21)

$${o_t}=~\sigma ({W_{ox}}.{x_t}+{W_{oh}}.{h_{t - 1}}+{W_{oc}}.{c_t}+{b_0}$$

(22)

$${h_t}=~{o_t}.\tanh \left( {{c_t}} \right)~$$

(23)

Where, ${i_t},{f_t},~~{o_t}~$ represent the input, forget, and output gates, ${c_t}$ represents the state of the cell, ${h_t}~$ represents the hidden state, ${x_t}~$ represents the input at time step t (e.g., cell voltage, cell current, cell internal resistance, temperature), W represents the weight matrices, $b~$ represents the bias terms, $\sigma$ represents the sigmoid activation function, $tanh$ represents the hyperbolic tangent activation function. The LSTM cell processes the input sequence ${x_1},{x_2}, \ldots \ldots .{x_t}$ sequentially, updating its cell state and hidden state at each time step. The cell state retains information over long sequences, allowing the LSTM to capture long-term dependencies in the data. The final estimation for the SOH is made based on the hidden state ${h_t}$ or by passing it through additional layers of the LSTM or other neural network architectures.

Fig. 14

Long-short temporary memory SOH estimation.

Model testing

Model testing involves testing the previously constructed MLA LSTM model mentioned above using test data. The model will be tested using one to seven input parameters according to the test plan³³. To facilitate comparison of the estimation result, only the last 66,302 data are taken after the data is converted into a series for the subsequent step.

Performance evaluation

The MSE and RMSE were computed to assess the models’ performance using the test data set. Furthermore, the following formulas were used to calculate the MAE and R2 score for a performance evaluation: Evaluation using MSE, RMSE, MAE, and R-squared. The outcomes of the model test are utilized to compute performance using:

Mean absolute error

The average squared difference between the actual and anticipated values is computed via MSE². MSE is sensitive to outliers since squaring the differences penalises greater errors more than smaller ones, represented in Eq. (24). Since the estimations are closer to the actual values, a model with a lower mean square error (MSE) has superior predictive accuracy.

$$MSE=~\frac{1}{N}\mathop \sum \limits_{{i=1}}^{N} {\left( {{C_i} - \widehat {{{C_i}}}} \right)^2}$$

(24)

Where ${C_i}$, represents the actual capacity, and ${\hat {C}_i}$ represents the estimated capacity, and N represents the number of datasets.

In the SOH estimation for Li-ion batteries, MSE is used to assess how accurately a model predicts the SOH.

Root Mean Squared Error (RMSE)

By figuring out the root of the error value between the expected and actual values, RMSE is one method of evaluating the precision of the estimation findings²⁴. The RMSE value can be found using the following Eq. (25):

$$RMSE=\sqrt {\frac{1}{N}\mathop \sum \limits_{{i=1}}^{N} {{\left( {{C_i} - \widehat {{{C_i}}}} \right)}^2}~~}$$

(25)

Where ${C_i}$, represents the actual capacity,${\hat {C}_i}$ represents the estimated capacity, and N represents the number of datasets.

Mean absolute error (MAE)

Whether the error is positive or negative, the MAE measures the absolute error between the actual data and the anticipated data²⁶. The formula used to get the MAE value is shown in Eq. (26);

$$MAE=~\frac{1}{N}\mathop \sum \limits_{{i=1}}^{N} \left| {\left( {{C_i} - \widehat {{{C_i}}}} \right)} \right|~$$

(26)

Where ${C_i}$ represents the actual capacity, ${\hat {C}_i}$ represents the estimated capacity, and N represents the number of datasets.

R-Squared (R2)

The R-squared tool for examining the relationship between actual and expected data is the coefficient of determination. The value of R2 ranges from -∞ to 1, with a closer value indicating greater suitability of the current model with the dataset^11,24. The formula used to determine R2’s value is shown in Eq. (27);

$${R^2}=1 - ~\frac{{\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{C_i} - {{\hat {C}}_i}} \right)}^2}}}{{\mathop \sum \nolimits_{{i=1}}^{N} {{\left( {{C_i} - \bar {C}} \right)}^2}}}$$

(27)

Where ${C_i}$ represents the actual capacity,${\hat {C}_i}$ represents the estimated capacity, $\bar {C}$ represents mean of the actual capacity, and N represents the number of datasets

Results and discussion

To perform the simulation udds (Urban Dynamometer Driving Schedule) drive cycle, shown in Fig. 15, is applied to the EV power train model, and shown in Fig. 16. In the system, the udds drive cycle is considered as the reference speed signal in terms of mph. It is a standardized test cycle used to simulate urban driving conditions for vehicles³⁴.

Fig. 15

Udds drive cycle signal in mph.

Fig. 16

Overall EV powertrain design block diagram of the purposed system.

This speed is compared with the actual speed and the error is fed to the PI controller, within the PI controller, the error is converted to a duty cycle. This duty cycle is fed to the driver circuit which is within the EV control unit. In the control unit MOSFET driver circuit is used, which feeds the pulse to the BLDC motor. The out of the BLDC motor is given to the wheel of the EV through the mechanical transmission system, whole system is represented in Fig. 16. The controller unit is connected to the Li-ion battery, which serves as the energy supply for the entire system. MATLAB simulation was used to assess the performance of Li-ion battery characteristics. One of the most important metrics for determining a Li-ion batteries overall health and remaining useful life is its SOH. Internal resistance is one of the most important markers of a batteries SOH. The efficiency and performance of the battery are impacted by internal resistance, which tends to rise with battery age. The resistance that prevents electric current from flowing through a battery is known as internal resistance. Internal components of the battery deteriorate after cycles of charge and discharge, increasing internal resistance, as shown in Fig. 17.The batteries SOH, which is sometimes represented as a percentage, indicates how well the battery can store and release energy in comparison to its initial, perfect state.

The following is a frequently used mathematical model that illustrates the connection between internal resistance and SOH, shown in Eqs. (28),

$${R_{int}}=~{R_0}+\left( {1+k\left( {1 - SOH} \right)} \right)~~$$

(28)

The internal resistance, initial internal resistance, and SOH constants denoted as R_int, R_0, k, and SOH, indicate the rate of increase in internal resistance as the battery’s SOH falls.

Fig. 17

Plot between R vs. SOH.

However, the actual relationship between internal resistance and SOH can be more complex due to factors such as temperature, cycling conditions, and specific battery chemistry. In practice, this relationship may be modeled using non-linear functions to better fit experimental data. A Li-ion battery’s SOH deteriorates with time as a result of aging, environmental variables, and cycling.

The relationship between time and SOH can be expressed through mathematical equations that model the degradation process. One common model to describe the SOH over time is an exponential decay model, which is represented by Eq. (29):

$$SOH\left( t \right)=~SO{H_{0~}}~.~{e^{ - \lambda t~}}$$

(29)

In this Eq. (29), $SOH\left( t \right)$ represents the state of health of the battery at the time (t). $~SO{H_{0~}}~$ represents the initial state of health of the battery when it is new (typically 100% or 1). $~\lambda$ represents the degradation rate constant, which characterizes the rate at which the battery’s health deteriorates over time, and t represents the time elapsed. This exponential decay plot suggests that the SOH decreases exponentially over time, which a common pattern is observed in many Li-ion batteries, as shown in Fig. 18.

The parameter $\lambda$ is crucial as it encapsulates the effects of various factors influencing battery degradation, such as charge-discharge cycles, temperature, and load conditions. A higher value of $\lambda ~$ indicates a faster degradation rate.

Fig. 18

Plot between SOH with respect to time.

This model captures the additional impact of usage on the SOH. Over time, the battery undergoes both time-dependent aging and cycle-dependent aging, both contributing to the overall SOH decline. To improve the accuracy of SOH estimation, a MLA was implemented. In this approach, cell voltage, cell current, pack current, pack voltage, temperature, and internal resistance were used as inputs to compute the SOC for the EV system model, as depicted in Fig. 19.

Fig. 19

ML block diagram.

The data of 66,302 of the aforesaid parameters are collected, which are divide up into training and testing datasets in an 80–20% ratio, as illustrated in Table 4. The training dataset was used to train the model, and the testing dataset was used to evaluate its performance.

Table 4 Battery dataset splitting.

Performance metrics

The model’s evaluation employs various metrics, including MSE, RMSE, and MAE, mean absolute percentage error (MAPE), and R2 score, to assess performance.

Fig. 20

Scatter Plot of True SOC vs. Predicted SOC of: (a) Adaboost regression, (b) Xgboost regression, (c) Decision tree regression, (d) Ridge regression, (e) Random forest regression, (f) Artificial neural network, (g) Long-short term memory algorithms.

The neural network model for battery SOH estimation consists of an input layer, two hidden layers with 64 neurons each, and an output layer with one neuron. The hidden layers use the ReLU (Rectified Linear Unit) activation function, while the output layer employs a linear activation function, suitable for regression tasks. The model is optimized using the Adam optimizer with a learning rate of 0.001 and a MSE loss function, trained over 13 epochs with a batch size of 32. To prevent overfitting, regularization techniques such as a dropout rate of 0.2 and L2 regularization with a value of 0.01 are applied. He Initialization is used to initialize the model weights, effective for ReLU-based networks. An Early Stopping mechanism with a patience of 5 epochs and a minimum delta of 0.001 is implemented to halt training when improvements plateau. The model’s performance is evaluated using metrics such as MAE, RMSE, and R² Score to ensure accuracy and generalization. Performance analysis of the model is conducted through scatter plots for the seven machine learning models, assessing the relationship between predicted and actual SOH. These plots help identify trends, outliers, and the strength of relationships between parameters. If the predicted and actual SOH points are scattered randomly without any pattern, it indicates inaccurate model estimations. As shown in Fig. 20a–c, random scatter suggests poor model performance. Conversely, a positive relationship between actual and predicted SOH, as observed in Fig. 20d and e, indicates good model accuracy. When the points form a diagonal line from the origin, as seen in Fig. 20f and g, it demonstrates a strong correlation, signifying highly accurate model estimations. The LSTM approach outperforms all other methods, achieving an R² score of 1, indicating superior efficiency. Its performance is validated with a training accuracy of 0.9215 and training loss of 0.0785. Among all models, ANN and LSTM show the lowest error rates, with LSTM reaching the highest accuracy of 0.9982, demonstrating its ability to capture complex data patterns. Xgboost also performs well, achieving 0.9402 accuracy and low error rates through its gradient-boosting framework. While both LSTM and ANN are more computationally intensive, their superior performance justifies the trade-off. On the other hand, Xgboost and RF effectively handle non-linear relationships, reducing overfitting despite being less complex. The performance evaluation of these machine learning algorithms is detailed in Table 5, with the corresponding metrics visualized in Fig. 21.

Fig. 21

Performance metrics of the proposed ML algorithms.

Table 5 Performance analysis of the battery.

Simpler models, such as DT and Ridge Regression, struggle with higher error rates, indicating difficulties in capturing data complexity. Ridge and DT’s higher variance and bias suggest potential overfitting or under fitting, while Adaboost exhibits moderate performance, potentially due to sensitivity to noisy data, reducing bias but still struggling with variance in complex datasets.

Additionally, the remaining life cycle of the battery was obtained using LSTM MLA, considering the manufacture data of the NMC 18,650 cell, which is 1250 cycles at 40% DOD, yielding a remaining life cycle of 9.7. The error between the actual and predicted remaining life cycles is minimal, with an MAE of 0.065, MSE of 0.018, and RMSE of 0.135, indicating that the model accurately predicts battery health and remaining life cycle, as shown in Fig. 22.

Fig. 22

Plot between remaining life cycle and time steps.

Conclusion

In conclusion, this paper highlights the significant advantages of advanced machine learning algorithms for accurate SOH estimation in Li-ion batteries, crucial for optimizing BMS in electric vehicles. While traditional methods like Constant Current and the Extended Kalman Filter provide a baseline for SOH estimation, advanced algorithms such as DT, RF, ANN, and LSTM networks offer superior performance by effectively handling nonlinearities and complex data patterns. Among these, the LSTM model excels by capturing long-term dependencies in sequential battery data, making it the most accurate for SOH estimation. This demonstrates the importance of selecting robust machine learning algorithms that account for the dynamic, nonlinear nature of battery systems. Accurate SOH estimation plays a critical role in maintaining battery health, extending electric vehicle lifespan, and optimizing BMS performance. Using the LSTM model, the remaining life cycle of the NMC 18,650 cell was predicted with high accuracy. Based on the manufacturer’s data for 1250 cycles at 40% DOD, the LSTM model predicted a remaining life of 9.7 years. With minimal error, demonstrated by an MAE of 0.065, MSE of 0.018, and RMSE of 0.135, the model shows strong capability in predicting both SOH and remaining life.

Future research will focus on integrating these machine learning models into real-time BMS systems, considering factors such as battery aging, operating conditions, and real-world degradation patterns to further improve SOH predictions. However, the models were trained on specific datasets, which may limit their generalizability across different battery chemistries and degradation patterns. To address this, future work will aim to enhance model adaptability and reliability, with a focus on validating the model’s accuracy under varying battery chemistries, operating conditions, and ambient temperatures to improve generalization and robustness.